1 Introduction

Silicon planar microring resonators (MRRs) waveguide have been investigated through wide scope of photonics applications including multiplexers (Alavi et al. 2014a, b), sensors (Ahmed et al. 2016b), switches (Gundogdu et al. 2007), filters (Malka et al. 2015), coupler (Jalas et al. 2011) routers, modulators, delayers, and detectors (Feng et al. 2012). MRR provide large Q-factor, thus it has a long light-analyte effective interaction length which can be beneficial for reducing the device’s dimensions (Chao and Guo 2006). Conventional fiber-based sensors face many limitation issues, where the MRRs effectively influence the efficient performance of the sensing devices (Ahmed et al. 2016c). In this case the sensing performance affected by the size of the device (Sun and Fan 2011; Harun et al. 2006; Ahmad et al. 2005). Moreover, additional features of the MRR incorporating faster response, lack of electromagnetic interference, low consumption of power, a smaller footprint and simple multiplexibility are the positive advantages over the electrical and mechanical based sensors (Ciminelli et al. 2014). The critical parameters of the microrings such as the free spectral range (FSR), sensitivity, detection limit and full width at half maximum (FWHM) have the highly impact on the Q-factor of the device. Also, better sensitivity for the large Q factor MRR indicating longer length of light-analyte interaction.

A sufficiently intense pulse of light inputted into a MRR will trigger nonlinear light behaviour (Spyropoulou et al. 2011). The system characterization can be performed via several methods (Almeida et al. 2004), and suitable system parameters allow for ring resonators to act as filter devices by which soliton signals can be generated (Lin and Crozier 2011; Amiri et al. 2015a, b; Amiri and Ahmad 2014). Add-drop filters are appropriate for on-chip design (Soltanian et al. 2015; Amiri et al. 2014a, b). A system containing an add-drop filter ring resonator connected to a smaller ring for filtering chaotic signals is capable of multiple mode-locked soliton transmissions. Mode-locked fiber lasers which produce picosecond time-duration optical pulses at gigahertz repetition rates are ideal candidates for use in time-division multiplexed (TDM) optical interconnects (Runser et al. 2001; Seo et al. 1996).

The techniques to generate the mode-locking in a laser may be Arranged into classes either ‘active’ or ‘passive’ (Fermann 2016). The active techniques generally involve utilizing an external signal to cause a modulation of the intracavity light (Li et al. 2014). The passive techniques do not utilize an external signal, but require placing some element into the laser cavity which induces self-modulation of the light (Ducasse et al. 2013). MRRs have a number of qualities which make them attractive for ultra-fast pulse generation via active or passive mode-locking (Amiri et al. 2014a, b, c, d). Semiconductors have been well demonstrated as a suitable material for the saturable absorber (SA) necessary for mode-locking (Chen et al. 2014; Alves et al. 2014). The potential of a semiconductor mode-locked laser with a dense mode spacing (30 ps) as an optical source is used to generate 25 GHz multiple mode-locked soliton pulses within the MRRs system is studied. The pulses are applicable in wavelength division multiplexing (Tsatourian et al. 2013; Amiri et al. 2015a, b, c, d). In this research, a mode-locked spectrum was generated by a laser cavity, which incorporated a laser and a SA, and input into a ring resonator system that consisted of an add-drop filter system connected to a smaller ring resonator.

In order to form the multi-function operations, for instance, control, tune, amplify, the additional input such as Gaussian with spectral profile is introduced into the system. The function of the proposed MRRs is to combine and filter the inputs as mode-locked laser and Gaussian. The filtering process performed during round-trip of the inputs within the MRRs, therefore, slicing the spectrums obtained. The advantage of using the add-drop filter system is to generate spatially uniform multi-solitons that can be filtered (Amiri et al. 2014a, b, c, d). Multiple mode-locked laser output was produced, and thus validated the proposed system as a suitable device for applications involving WDM.

2 Time-domain travelling-wave model

The traveling-wave equations describing the propagation of the optical field inside the MRR cavity along the longitudinal z and transverse r directions can be written as

$$\frac{1}{{\nu_{g} }}\frac{{\partial \underline{\psi }^{ \pm } (r,z,t)}}{\partial t} \pm \frac{{\partial \underline{\psi }^{ \pm } (r,z,t)}}{\partial z} = \frac{i}{2\beta }[H(r,z,t)]\underline{\psi }^{ \pm } (r,z,t)$$
(1)

where the expression on the right side of the Eq. 1 is complex and the symbols presented as \(\nu_{g} = (c/n_{g} ),\) n g , c and β are respectively the group velocity, the group refractive index, the light velocity in free space, and the longitudinal propagation coefficient. The slowly varying envelopes of the forward and backward traveling wave along the longitudinal direction are shown as \(\underline{\psi }^{ + }\) and \(\underline{\psi }^{ - }\). Furthermore, the mathematical propagation fields distribution along with the effective one-dimensional (1-D) (longitudinal direction) (Yu 1996) and in quasi-three dimensional (3-D) (longitudinal and transverse directions) (Yu and Lo 1996) are respectively stated in \([H(r,z,t)]\) (i.e. Eq. 1), where corresponding formula presented as follows:

$$[H(r,z,t)] = \left\{ {\begin{array}{*{20}l} {\Delta \varepsilon_{eff} (z,t)k_{0}^{2} ,} \hfill & {1{ - }D} \hfill \\ {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}} \right) + \Delta \varepsilon (r,z,t)k_{0}^{2} ,} \hfill & { 3 { - }D} \hfill \\ \end{array} } \right.$$
(2)

Within the above equation \(k_{0} = (2\pi /\lambda_{0} )\) means the wavevector for each term, and λ 0 accordingly, is the operating wavelength. Besides, Δε eff and Δε in term 1 and 2 of Eq. 2 are respectively the effective modification of the permittivity along the 1-D and quasi-3-D geometry of the waveguide. As such, the aforesaid expression in Eq. 1 can be used to define the general behavior of the optical fields propagating either along 1-D direction or quasi-3-D space inside the MRR cavity. The time-domain traveling-wave method as the solution of the time–space \([H(r,z,t)]\) can be exploited according to Zhang et al. (1994). Thus, the time and spatial variation of wave equations can be linearly treated by a first-order difference approximation to the partial differential in Eq. 1, thus through selecting the relation between time and the spatial step as \(\Delta z = \nu_{g} \cdot \Delta t,\) we have

$$\psi^{ \pm } (r,z \pm \Delta z,t + \Delta t) = \left[ {1 + i[H(r,z,t)] \cdot \Delta z/2\beta } \right]\psi^{ \pm } (r,z,t)$$
(3)

where Δt is a constant time step and Δz is the propagation distance. If the initial value of \(\psi^{ \pm } (r,z,t)\) at time t and location z is known, the fields \(\psi^{ \pm } (r,z,t + \Delta t)\) at the next time step t + Δt can be determined at the position z + Δz from Eq. 3.

3 Proposed microring resonator system

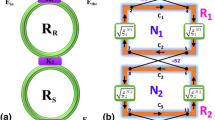
The proposed system for multi mode-locked soliton generation is shown in Fig. 1. A mode-locked laser and a Gaussian laser beam are used as inputs. The Gaussian laser beam is used to control the output signals.

Fig. 1
figure 1

Top MRR structure, E electric fields, κ coupling coefficient, R radius of the rings. Bottom waveguide cross sectional for both straight and rings sections, effective waveguide cross section A eff is 0.92 µm2

Full size image

The MRRs are made of silicon semiconductor with Si core having refractive index of 3.65 surrounded by SiO2 (n = 1.45). The nonlinear refractive index is 2.7 × 10−16 m2 W−1 for wavelengths around 1555 nm. Silicon photonic semiconductors are an ideal platform for nonlinear because they exhibit some strong nonlinear effects such as Kerr nonlinearity.

Considering a high-Q MRR after applying the nonlinear Kerr effect, there is a possibility to obtain a wide spectral optical comb generation with ultra-low consumption (Kippenberg et al. 2004; Del’Haye et al. 2007). The chance of generation optical comb is more promising for silicon or III–V compound semiconductor materials in the structure of resonators due to benefiting from strong nonlinear Kerr effects. The geometry of the waveguide plays an important role on the effective area of the nonlinear interaction (Koos et al. 2008). Such an optical nonlinearity effect can be measured for nonlinear waveguide through the parameter γ as given by Leuthold et al. (2010), Foster et al. (2004)

$$\gamma = (2\pi /\lambda )(n_{2} /A_{eff} )$$
(4)

From the above expression, we can easily see that the high nonlinear Kerr coefficient n 2 and very small cross sectional area A eff ensure the maximum value of parameter γ. In this research, the obtained γ has been calculated to 1185.23 W−1 m−1.

The used semiconductor layers sequence (from top to bottom) is shown as follows:

  • SiO2 cap (0.71 µm) (n 1 = 1.45)

  • Si (0.3 µm) (n 2 = 3.65)

  • Si etch stop layer (0.05 µm) (n 3 = 3.65)

  • Si (0.3 µm) (n 2 = 3.65)

  • SiO2 substrate (0.5 µm) (n 1 = 1.45)

The coupling between the rings and the “bus” waveguides and between adjacent rings is represented by power couplers. These are not proper directional couplers since they have no optical length. But the effect of a power coupler plus additional waveguide sections (25 μm) to create the necessary delays, is virtually the same as a directional-coupler of finite length. Directional couplers are well designed, characterized, and optimized respect to their structural parameters in Ahmed et al. (2016a).

4 Theory of the microring resonator system

This system consists of an add-drop filter system with an attached smaller MRR. This MRR is positioned subsequent to the throughput port and prior to the add port in terms of the filter system circulation, and is used to filter chaotic signals in order to attain clear signals from the output ports. The mode-locked laser pulse spectrum, which can be generated by a loop consisting of two fiber optics reflectors, a semiconductor gain medium laser, and a SA, is injected into the ring system. The input optical fields into the MRRs then, are given by Ahmad et al. (2015), Amiri et al. (2015b)

$$E_{in} = A\sec \,h\left[ {\frac{T}{{T_{0} }}} \right]\exp \left[ {\left( {\frac{iz}{{2L_{D} }}} \right) - i\omega_{0} t} \right],$$
(5)
$$E_{add} = E_{0} \exp \left[ {\left( {\frac{iz}{{2L_{D} }}} \right) - i\omega_{0} t} \right]$$
(6)

A (and E 0) and z are introduced as optical amplitudes propagation distance respectively. \(T = t - \beta_{1} \times z\) is a soliton pulse propagation time, and in which β 1 and β 2 are the linear and second order terms of the Taylor expansion coefficients of the propagation constant (Amiri and Ali 2014; Alavi et al. 2014a, b). The dispersion length of the soliton pulse is \(L_{D} = T_{0}^{2} /|\beta_{2} |,\) while the frequency shift of the soliton represented as ω 0 (Zhang et al. 2014; Alavi et al. 2016). The initial propagation time, T 0, can be determined once soliton peak intensity \((|\beta_{2} /\varGamma T_{0}^{2} |)\) is known. For the soliton pulse, a balance should be achieved between the dispersion length, L D, and the nonlinear length, \(L_{NL} = 1/\varGamma \phi_{NL} ,\) such that \(L_{D} = L_{NL}\) where \(\varGamma = n_{2} \times k_{0}\) is the length scale over which dispersion or nonlinear effects will widen or narrow the beam. The total refractive index of the system is given by Amiri et al. (2013b, 2015c):

$$n = n_{0} + n_{2} I = n_{0} + \left( {\frac{{n_{2} }}{{A_{eff} }}} \right)P$$
(7)

where n 0 and n 2 are the linear and nonlinear Kerr coefficients respectively (Leblond and Mihalache 2013), I is the optical intensity, and P is the optical power. The effective waveguide cross section is given by A eff (Liu et al. 2012). The normalized output can be expressed as (Amiri and Ali 2013; Amiri et al. 2013a):

$$\left| {\frac{{E_{out} (t)}}{{E_{in} (t)}}} \right|^2 = (1 - \gamma )\left[ {\frac{{\left( {1 - (1 - \gamma )x^{2} } \right)\kappa }}{{\left( {1 - x\sqrt {1 - \gamma } \sqrt {1 - \kappa } } \right)^{2} +\,4x\sqrt {1 - \gamma } \sqrt {1 - \kappa } \sin^{2} \left( {\frac{\phi }{2}} \right)}}} \right]$$
(8)

The coupling coefficient is \(\kappa ,\) the \(x = \exp ( - \alpha L/2)\) represents a round-trip loss, the γ is the fractional coupler intensity loss (Rand and Steiglitz 2012), \(\phi = \phi_{0} + \phi_{NL}\) in which \(\phi_{0} = \, kLn_{0}\) and \(\phi_{NL} = kLn_{2} |E_{in} |^{2}\) are the linear and nonlinear phase shifts, \(k = 2\pi /\lambda\) is the wave number, and L and α are waveguide length absorption coefficient respectively (Lederer and Aitchison 2013). In reference to Fig. 1, the equations are given by Amiri and Afroozeh (2014):

$$E_{1} = \sqrt {1 - \gamma } \times \left[ {E_{3} \times \sqrt {1 - \kappa_{1} } + j\sqrt {\kappa_{1} } \times E_{in} } \right]$$
(9)
$$E_{2} = E_{R} \times E_{1} \times e^{{\frac{{ - \alpha L_{R} }}{4} - jk_{n} \frac{{L_{R} }}{2}}}$$
(10)
$$E_{3} = \sqrt {1 - \gamma } \times \left[ {E_{2} \times \sqrt {1 - \kappa_{2} } + j\sqrt {\kappa_{2} } \times E_{add} } \right]$$
(11)
$$E_{R} = E_{1} \times \left\{ {\frac{{\sqrt {(1 - \gamma ) \times (1 - \kappa )} - (1 - \gamma ) \times e^{{\frac{ - \alpha }{2}L_{R} - jk_{n} L_{R} }} }}{{1\sqrt {(1 - \gamma ) \times (1 - \kappa ) \times e^{{\frac{ - \alpha }{2}L_{R} - jk_{n} L_{R} }} } }}} \right\}$$
(12)
$$\begin{aligned} E_{t1} & = - x_{2} y_{2} \sqrt {\kappa_{1} } E_{add} e^{{\frac{ - \alpha L}{2}}} - jk_{n} \frac{L}{2} \\ & \quad + \left[ {\frac{{x_{1}^{3/2} \kappa_{1} \sqrt {\kappa_{2} } E_{R} E_{in} \left( {e^{{\frac{ - \alpha L}{2}}} - jk_{n} \frac{L}{2}} \right)^{2} +\,x_{2}^{2} y_{1} y_{2} \sqrt {\kappa_{1} \times \kappa_{2} } E_{R} E_{add} \left( {e^{{\frac{ - \alpha L}{2}}} - jk_{n} \frac{L}{2}} \right)^{3} }}{{1 - x_{2} y_{1} y_{2} E_{R} \left( {e^{{\frac{ - \alpha L}{2}}} - jk_{n} \frac{L}{2}} \right)^{2} }}} \right] \\ \end{aligned}$$
(13)
$$\begin{aligned} E_{t2} & = - x_{2} y_{2} E_{add} \\ & \quad + \left[ {\frac{{x_{2} \kappa_{1} \sqrt {\kappa_{1} \times \kappa_{2} } E_{R} E_{in} e^{{\frac{-\alpha L}{2} - jkn\frac{L}{2}}} + x_{1}^{3/2} y_{1} y_{2} \sqrt {\kappa_{2} } E_{R} E_{add} \left( {e^{{ - \alpha \frac{L}{2} - jk_{n} \frac{L}{2}}} } \right)^{2} }}{{1 - x_{2} y_{1} y_{2} E_{R} \left( {e^{{\frac{ - \alpha L}{2} - jk_{n} \frac{L}{2}}} } \right)^{2} }}} \right] \\ \end{aligned}$$
(14)

E t1 and E t2 are the add-drop outputs. Here, \(L_{R} = 2\pi R_{R}\) where R R is the radius and E R is the electric field within the ring. \(x_{1} = \sqrt {1 - \gamma } ,\) \(y_{1} = \sqrt {1 - \kappa_{1} } ,\) \(x_{2} = 1 - \gamma ,\) \(y_{2} = \sqrt {1 - \kappa_{2} }\) and \(L = 2\pi R_{ad} .\)

5 Mode-locking by a saturable absorber (SA) using a laser cavity

Employing the nonlinear Kerr effect in a high-Q MRR, has a chance to achieve wideband optical comb generation with ultra-low power consumption (Kippenberg et al. 2004; Del’Haye et al. 2007). Moreover, a resonator in silicon or III–V compound semiconductor might be desired for the optical comb generation due to benefiting from strong nonlinear Kerr effects. Mode-locking in the proposed system requires an SA, which is located within the laser cavity along with the laser. This SA is modeled in PICWave as a gain section with a very short non-radiative recombination time. The active layer of the SA section is made of InGaAsP, labeled “InGaAsP_SA”, with a length of 40 µm. The schematic of the mode-locked laser generation system is shown in Fig. 2.

Fig. 2
figure 2

Mode-locked laser generation using a semiconductor gain medium laser connected to an SA. Reflection coefficient is 30 % and current is 80 mA

Full size image

Results were generated using the photonic circuits simulator PICWave made by photon design (PICWave, Photon Design Inc. http://www.photond.com/products/picwave/picwave_applications_00.htm), which is centered on the time-domain travelling wave (TDTW) method and capable of modeling both active and passive photonic circuits. Molecular beam epitaxial (MBE) growth on patterned substrates is a one-step growth process which makes possible local variation of composition and quantum well thickness. This could be used to make quantum wires, and to fabricate integrated structures requiring different regions having different bandgap wavelengths. Indium gallium arsenide phosphide (In1−xGaxAsyP1−y) is a quaternary compound semiconductor material, an alloy of gallium arsenide and indium phosphide. This compound has applications in photonic devices, due to the ability to tailor its band gap via changes in the alloy mole ratios, x and y. Indium phosphide-based photonic integrated circuits, or PICs, commonly use alloys of In1−xGaxAsyP1−y to construct quantum wells, waveguides and other photonic structures, lattice matched to an InP substrate, enabling single-crystal epitaxial growth onto InP. Many devices operating in the near-infrared 1.55 μm wavelength window, utilize this alloy, and are employed as optical components (such as laser transmitters, photodetectors and modulators) in C-band communications systems (Pearsall 1982; Moerman et al. 1991; Xin et al. 2009; Sands 2004).

Figure 3 shows the waveguide structure of the InGaAsP_SA constructed device that was calculated with the fully vectorial finite difference mode (FDM) solver. The utilized layers sequence from bottom to top, with corresponding layer thickness and refractive index, was InP substrate (1.5 µm) (n = 3.18), InGaAsP (0.3 µm) (n = 3.34), InGaAsP-SA (0.04 µm) (n = 3.39), InGaAsP (0.3 µm) (n = 3.34), InGaAsP (0.2 µm) (n = 3.34), and InP cap (0.7 µm) (n = 3.18). The center wavelength is 1.55 μm.

Fig. 3
figure 3

Waveguide-cross section for the fundamental TE-like mode

Full size image

6 Characterization of the saturable absorber (SA)

The mode propagation profile of the SA is shown in Fig. 4.

Fig. 4
figure 4

Left single mode propagating within the SA. Right mode profile for the fundamental TE-like mode calculated with the fully vectorial finite difference mode solver (FDM) solver

Full size image

In the case of bent dielectric waveguides, the optical mode is a leaky mode, where the bending loss increases according to a decrease of the bending radius. Therefore, a small radius MRR has lower intrinsic Q at a defined resonant wavelength. A waveguide has only a finite number of guided propagation modes, the intensity distributions of which have a finite extent around the waveguide core. The number of guided modes, their transverse amplitude profiles and their propagation constants depend on the details of the waveguide structure and on the optical frequency. Here, the fundamental and purely TE-like modes propagating within the waveguide obtained and presented as follows.

The used SA has composition of In0.76Ga0.24As0.53P0.47 with As fraction (y) of 0.53 and Ga fraction (x) of 0.24. The variation of the refractive index versus the As fraction (y) is shown in Fig. 5. As shown, different As fraction (y) of the InGaAsP-SA have different refractive indices. This information obtained from the used software.

Fig. 5
figure 5

Refractive index versus the As fraction (y)

Full size image

The bandgap energy varies with respect to the following equation (Agrawal and Dutta 1986; Adachi 1982),

$$E_{\text{g}} = 1.35 - 0.72y + 0.12y^{2} \,[{\text{eV}}]$$
(15)

Figure 6a shows the bandgap energy versus the As fraction (y) of the waveguide. Different As fraction (y) were applied to the Eq. 15 to obtain the bandgap energy. Figure 6b shows the mode absorption loss versus the As fraction (y). It shows a significant increase of the mode absorption when the As fraction (y) increases in the InGaAsP-SA.

Fig. 6
figure 6

a The bandgap energy versus the As fraction (y), b the mode absorption loss versus the As fraction (y)

Full size image

7 Mode-locked laser characterization

The spectrum of the mode-locked laser is shown in Fig. 7a and the time domain profile of the peak is presented in Fig. 7b. It can be seen below the output of the laser in the time domain. The Q-switching can be clearly observed to occur at the beginning of the simulation. After 2 ns, the mode-locked laser reaches a steady state. Close observation of the steady-state output reveals the expected train of Gaussian-like pulses to have a spacing of 30 ps and an FWHM of 10 ps.

Fig. 7
figure 7

a Mode-locked laser and b picosecond mode-locked laser output

Full size image

8 Parameters of the microring resonator system and output analysis

Table 1 shows the ring’s parameters.

Table 1 Parameters of the MRR system
Full size table

The output signal from the throughput port of the ring resonator system is shown in Fig. 8.

Fig. 8
figure 8

Throughput port output signals

Full size image

To obtain flat-top spectral passbands and uniform intensity distribution, the photonics devices such as switches and Filters are desired and utilized for significant reduction of the inter-channel interference in optical communication networks and on-chip interconnects applications (Harun et al. 2005; Zulkifli et al. 2010). MRR can be used to generate flat-top passbands owing steep edges by accurate controlling of its critical parameters such as radius, coupling coefficient and dimension. Figure 9 shows multiple mode-locked soliton pulses with FSR of 25 GHz and FWHM of 630 MHz generated from the drop port. Figure 9b, is a magnified view of the Fig. 9a.

Fig. 9
figure 9

a Drop port output signals, and b signals with 25 GHz FSR and 630 MHz FWHM

Full size image

The corresponding FSR and FWHM of the generate pulses shown in Fig. 9b in the wavelength domain were 0.2 nm and 5 pm respectively, and the train mode-locked pulses had a pulse duration of 40 ps and repetition rate of 200 GHz. The finesse \(F = \Delta f_{FSR} /\Delta f_{FWHM}\) (Ahmed and Ullah 2011) is ~39.7, the Q-factor, \(Q = f_{ref} /f_{FWHM}\) is ~3×105, and the interaction length, \(L_{eff} = (Q \times \lambda )/(2\pi n)\) (Ahmed and Ullah 2011) is 2 cm, where the \(\lambda = 1.55\,\upmu{\text{m}}\), Q = 3×105, π = 3.14 and n = 3.65.

We have simulated a 25-GHz mode-locked solitons as a potential multi-wavelength source for WDM applications. The output contains over 182 modes within 4.5 THz frequency range, each having a linewidth of 630 MHz and FSR of 25 GHz which varies slightly along with the wavelength. For applications such as on-chip, chip–chip, or short reach WDM, the output directly from this system is likely to be sufficient.

When different optical waves interact coherently in a nonlinear medium, the optical four-wave mixing (FWM) phenomenon occurs. The magnitude of the FWM phenomenon depends on the channel spacing and waveguide dispersion. The FWM efficiency increases dramatically with respect to small channel spacing between pulses, where it is inversely proportional to the waveguide dispersion. At the zero-dispersion point, therefore the FWM efficiency is maximum. Due to the above explanation and the existence of dispersion in the used waveguide and also the large channel spacing (spacing in the range of 25 GHz), in this research, the FWM effect is negligible (Goff 2002; Habib and Ngah 2007).

9 Conclusion

As conclusion, nonlinear light behaviour inside a silicon MRR was exploited in the design of an add-drop filter intended for including particular WDM channels. The proposed system, consisting of a silicon add-drop filter ring resonator connected to a smaller ring, was used to generate multiple mode-locked solitons. These presented MRRs are simulated using silicon (Si) on a SiO2 substrate. An SA was a necessary addition in order to achieve mode-locked pulses, and semiconductor material was used for this purpose. This apparatus enabled generation of multi-channels and transmission of optical mode-locked soliton pulses. The SA was modeled by PICWave software based on the TDTW method. Generated Gaussian-like mode-locked pulses had a spacing of 30 ps and FWHM of 10 ps. The MRR system was able to filter the input pulses and generate a comb of mode-locked pulses possessing the properties of solitons. These generated multi-mode-locked soliton pulses had a 25 GHz FSR and 630 MHz FWHM, which corresponded to 0.2 nm and 5 pm respectively, and are applicable for optical communications devices. Analysis of results included a calculated soliton pulse Q-factor of approximately 3 × 105, which was indicative of the system having a high performance characteristic.