1 Introduction

III–V based TL has already proven its performance (Feng et al. 2005, 2007; Holonyak and Feng 2006) but the cost of device is high and so not suitable for commercial use. Group IV semiconductor like Si and Ge are always a good choice of materials for devices particularly for integrated circuit devices because of their low cost and matured growth technology. Yet these materials are not suitable for light emitting devices because of their indirect bandgap nature. However, direct Γ valley of the Ge conduction band is only 134 meV higher than the indirect L valley. It says that with band-structure engineering, Ge has the potential to become a direct band gap material which can be used for efficient light emitting devices (Kouvetakis et al. 2006). Although several approaches have reported in this context (Goodman 1982; Soref and Perry 1991; Fischetti and Laux 1996; Kurdi et al. 2009), incorporation of Sn into Ge lattice is most promising route to obtain direct band gap in Ge (Kouvetakis et al. 2006).

Some studies on GeSn alloy based optoelectronic devices such as lasers (Chang et al. 2010), detectors (Werner et al. 2011) etc. have already been reported in literature. But, GeSn alloy based TL has not yet been reported to the best of authors knowledge. Moreover, due to large lattice mismatch between Ge and Sn, strain energy builds up and it plays important role on the nature of transition in GeSn alloy. As TL is QW based devices, the study of quantum mechanical behavior of GeSn active layer is also important. Thus, proper design of GeSn based TL considering the design criteria like significant carrier and optical confinement is really a big challenge. To the best of authors knowledge no such design aspects has yet been discussed and reported in literature. Theoretical model for Group-IV based TL to predict Sn composition dependent optical gain have already been proposed by the authors elsewhere (Das and Ranjan 2015). The work has been extended further to study the characteristic of quantum mechanical behavior of the active layer of proposed TL and is reported here. Also, subband carrier distribution is considered for determination of optical gain and threshold carrier density. Rest of the paper is organized as follows. Design aspect and proposed device structure for strain balanced GeSn-based TL is described in Sect. 2. Simulation results are discussed in Sect. 3 and in last section, conclusion is made.

2 Design aspects and proposed model

Band edges of Г and L valleys in conduction band, heavy hole (HH) and light hole (LH) in valance band are calculated using model solid theory (Van de Walle 1989) where parameters for Si, Ge and Sn are taken from different literatures. Values of relevant material parameters along with the references from where they are taken are summarized in Table 1 for quick reference. Model solid theory uses self-consistent first principle calculation to derive the relative energies of the valance and the conduction band at semiconductor interfaces. In our calculation, interface between two lattice matched surfaces is assumed to be ideal, whereas pseudomorphic potential due to strain in each layer is considered for the interface between two lattice mismatched surfaces. Band edges in Ge and in Ge0.85Sn0.15 are calculated considering strain and are shown in Fig. 1a, b respectively. It is seen from Fig. 1a that the direct bandgap can be obtained in tensile strained Ge layer at a minimum strain of 1.61 %. Moreover, in the case of tensile strained Ge, LH is higher than HH band and so, the TM polarized gain will be dominating over TE mode gain. But the optical confinement factor, high value of which is required for lasing operation, is poorer in TM mode than that in TE mode (Chuang 2009). Now, it is seen from Fig. 1b that the direct bandgap can also be obtained in compressively strained Ge0.85Sn0.15 layer and minimum value of required strain is 0.72 % (absolute value) for Sn composition of 15 %. It is also seen from Fig. 1b that in case of compressively strained GeSn, HH is higher than LH band and so, the TE polarized gain will dominate. So, GeSn alloy material is preferred to be the active layer material of a light emitting device. In this context, it may be mentioned that the range of compressive strain, for which GeSn shows direct bandgap nature, varies with Sn concentration in GeSn alloy. This range is 0–72 % for Sn concentration of 15 % as shown in Fig. 1b. For larger values of Sn composition, this range will be higher. However, in summary, it can be accomplished that, higher value of absolute strain is required in tensile strained Ge than compressively strained Gesn to achieve direct band gap in Group-IV material. Lower value of strain reduces the misfit dislocation density in strained layer and hence improves the fabrication quality of deposited layer. Now, the barrier region requires higher bandgap and lower refractive index material like Si, Ge etc. to ensure carrier and optical confinement. But the bandgap between direct (Г valley) and indirect (L valley) is much higher in Si than Ge. Thus, by choosing Si-incorporated alloy, e.g. SiGeSn as a material for barrier serves both the purposes. So, the ternary material SiGeSn is used as a barrier for better optical and carrier confinement. However, with increasing Sn concentration in SiGeSn, energy difference between Г and L valley in the barrier reduces but refractive index of barrier increases which causes reduced optical confinement. Thus a tradeoff occurs between carrier and optical confinement. So, choice of Sn concentration for both, well and barrier is very important.

Table 1 Parameters of Si, Ge, α-Sn (Chang et al. 2010; Van de Walle 1989; Menendez and Kouvetakis 2004)
Full size table
Fig. 1
figure 1

a Band edges of Ge as a function of Strain. Indirect to direct band edge at tensile strain 1.61 %. In tensile strain LH is above then HH. 1. b Band edges of Ge0.85Sn0.15 as a function of Strain. Indirect to direct band edge at compressive strain 0.72 %. In compressive strain HH is above then LH

Full size image

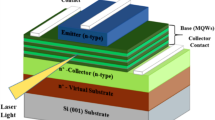
The schematic diagram of the proposed TL considered in our model is shown in Fig. 2. The n-type Si material forms an emitter, the p-type Si0.12Ge0.73Sn0.15 as a base and n-type Si0.11Ge0.73Sn0.16 as a collector. For lasing action, an intrinsic Ge0.85Sn0.15 QW is inserted in the Si0.12Ge0.73Sn0.15 base which acts as a barrier. The collector layer is lattice matched with strain-relaxed Ge0.87Sn0.13 buffer layer which is used for subsequent growth of barrier and well. The composition of buffer is chosen such that the strains observed by well and barrier are equal but opposite in nature. Thus, 0.18 % of tensile strain in barrier compensates 0.29 % compressive strain in the well. The well width is selected such that single bound state exists in each of conduction band and valence band. Also, width of the well is chosen by taking critical thickness of GeSn layer into consideration. Barrier width of 80 Ǻ is calculated for 100 Ǻ thick well using strain balanced condition for a cubic based multilayer system grown along (001) axis (Van de Walle 1989). The growth of such strained layer GezSn1−z is demonstrated experimentally (Oeheme et al. 2014).

Fig. 2
figure 2

Schematic structure of npn Si–Si0.12Ge0.73Sn0.15–Si0.11Ge0.73Sn0.16 based transistor laser (TL) with strain-balanced i-Ge0,85Sn0.15 single quantum well (QW) in the base. Strain relaxed Ge0.87Sn0.13 buffer layer is used to create compressive strain in well and tensile strain in barrier

Full size image

3 Theoretical calculation and results

The bandgaps of unstrained GeSn and SiGeSn material system are calculated from the expression given by (Chang et al. 2010):

$$\begin{aligned} E_{g\eta \_SiGeSn} & = xE_{g\eta \_Si} + yE_{g\eta \_Ge} + (1 - x - y)E_{g\eta \_Sn} - xyb_{\eta \_SiGe} \\&\quad- x(1 - x - y)b_{\eta \_SiSn} - y(1 - x - y)b_{\eta \_GeSn} \\ E_{g\eta \_GeSn} & = zE_{g\eta \_Ge} + (1 - z)E_{g\eta \_Sn} - z(1 - z)b_{\eta \_GeSn} \\ \end{aligned}$$
(1)

where η stands for Г and L valley. Bowing parameters, \(b_{\eta\_SiGe}\), \(b_{\eta\_{Si}{Sn}}\) and \(b_{\eta\_GeSn}\) of SiGe, SiSn and GeSn are listed in Table 2 (Chang et al. 2010). Linear interpolation technique is used to obtain other material parameters of GezSn1−z and SixGeySn1−x−y. In the model solid theory, average of three valance band (VB) at Г valley are taken as a reference level so all the band edges are calculated at Г point of the Brillouin zone. Due to deformation potential and spin orbit effect the valance band shifted from average valance band. The VB energy of unstrained GezSn1−z given by:

$$E_{v\_GeSn} = E_{v\_avg\_GeSn} + \tfrac{1}{3}\Delta_{0\_GeSn}$$
(2)

where, \(E_{v\_avg\_GeSn}\) and \(\Delta_{0\_GeSn}\) is average valance band and spin orbit splitting energy of GeSn respectively.

Table 2 Bowing parameter of SiGe, GeSn, SiSn (Chang et al. 2010)
Full size table

The conduction band (CB) of unstrained GeSn is calculated using:

$$E_{c\eta \_GeSn} = E_{v\_GeSn} + E_{g\eta \_GeSn}$$
(3)

Since our growth direction along (001) axis, strain along the surface (x, y) is same. The CB for strained GezSn1−z given by:

$$E_{c\eta \_GeSn\_strain} = E_{c\eta \_GeSn} + a_{c\eta \_GeSn} \left( {e_{xx\_GeSn} + e_{yy\_GeSn} + e_{zz\_GeSn} } \right)$$
(4)

where, \(a_{c\eta\_GeSn}\) is hydrostatic deformation potential for CB. \(e_{xx\_GeSn}\), \(e_{yy\_GeSn}\) and \(e{zz\_GeSn}\) are strain along x, y and z axis respectively. Due to shear strain, VB splits into HH and LH band. The expression of HH and LH valance band given by:

$$\begin{aligned} E_{v\_HH\_GeSn} & = E_{v\_avg\_GeSn} + a_{v\_GeSn} \left( {e_{xx\_GeSn} + e_{yy\_GeSn} + e_{zz\_GeSn} } \right) + \tfrac{1}{3}\Delta_{0\_GeSn} - \tfrac{1}{2}\delta E_{\_GeSn} \, \\ E_{v\_LH\_GeSn} & = E_{v\_avg\_GeSn} + a_{v\_GeSn} \left( {e_{xx\_GeSn} + e_{yy\_GeSn} + e_{zz\_GeSn} } \right) \\ & \quad - \tfrac{1}{6}\Delta_{0\_GeSn} + \tfrac{1}{4}\delta E_{\_GeSn} + \tfrac{1}{2}\left[ {\Delta_{0\_GeSn}^{2} + \Delta_{0\_GeSn} \delta E_{\_GeSn} + \tfrac{9}{4}\delta E^{2}_{\_GeSn} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \\ \end{aligned}$$
(5)

where change in energy due to shear strain is

$$\delta E_{\_GeSn} = 2b_{v\_gesn} \left( {e_{zz\_GeSn} - e_{xx\_GeSn} } \right)$$
(6)

The band offsets between the well and the barrier in Г-CB and HH, LH valance band are as follows:

$$\begin{aligned} \Delta E_{C\varGamma } &= E_{C\varGamma \_SiGeSn\_strain} - E_{C\varGamma \_GeSn\_strain} \hfill \\ \Delta E_{V\_HH} &= E_{V\_HH\_GeSn} - E_{V\_HH\_SiGeSn} {\text{ and }}\Delta E_{V\_LH} = E_{V\_LH\_GeSn} - E_{V\_LH\_SiGeSn} \hfill \\ \end{aligned}$$
(7)

where \(a{v\_GeSn}\) is deformation potential of VB and \(b{c\eta\_GeSn}\) is deformation potential for shear strain.

The band offsets of Si0.12Ge0.73Sn0.15 barrier and Ge0.85Sn0.15 well are used to find Eigen energies and corresponding wave functions in Г-CB, HH and LH VB. In Г-conduction band, following Schrödinger equation with effective mass approximation is used to obtain the Eigen energy and the wave function (Chuang 2009):

$$\, \left[ {\frac{{ - \hbar^{ 2} }}{ 2}\frac{\partial }{{\partial {\text{z}}}}\frac{ 1}{{m_{\text{C}} }}\frac{\partial }{{\partial {\text{z}}}} + \frac{{\hbar^{2} k_{t}^{2} }}{{2m_{C} }} + {\text{V}}_{\text{C}} ( {\text{z)}}} \right]\uppsi = {\text{E}}_{\text{C}} \psi \,$$
(8)

where z is position variable, ψ is wave function. EC, m c are Eigen energy and effective mass in Г-CB respectively. k t is wave vector perpendicular to k z (growth axis) and directed along \(\langle 110\rangle\) in k x −k y plane. VC is the potential profile of Г-CB which includes strain effect. In the above Schrödinger equation ψ does not contain the Bloch function because effect of periodic potential created by crystal lattice is replaced by effective mass m c . To reduce the complexity of problem, all calculation are around Г point of the Brillouin zone thus, we take k t  = 0. The Schrödinger equation is solved using one of the numerical techniques, Finite Difference Method (FDM) (Datta 2005). The lowest Eigen energy value is 1st subband energy in Г CB and its corresponding Eigen vector is wave function. The VB is degenerate in energy so interaction between the bands cannot be neglected. The effect of HH band on LH band and vice versa are shown by an extra coupling term in the Schrödinger equation (Coldren et al. 2012). Due to strain effect HH and LH band are split and it is assume that if difference between band edge of HH and LH at Г point (kt = 0) is large enough then the coupling between HH and LH can be neglected (Coldren et al. 2012). With this assumption we take Schrödinger equation for HH and LH valance band as follows (Chuang 2009):

$$ \left[ {\frac{{ - \hbar^{ 2} }}{ 2}\frac{\partial }{{\partial {\text{z}}}}\frac{ 1}{{m_{{{\text{V\_hh,lh}}}} }}\frac{\partial }{{\partial {\text{z}}}} + \frac{{\hbar^{2} k_{t}^{2} }}{{2m_{V\_hh,lh} }} + {\text{V}}_{\text{hh,lh}} ( {\text{z)}}} \right]{{\psi }} = {\text{E}}_{{{\text{V\_hh,lh}}}} \psi $$
(9)

where \(m_{V\_hh} = \frac{{m_{0} }}{{\gamma_{1} - 2\gamma_{2} }}\,\,\,and\,\,\,m_{V\_lh} = \frac{{m_{0} }}{{\gamma_{1} + 2f_{ + } \gamma_{2} }}\) uses to replace the effect of Bloch function. f + is dimensionless strain dependent factor which comes from spin orbit effect.

Calculated band alignment, Eigen energies and wave function for well and barrier in base are shown in Fig. 3a and band diagram at equilibrium for the region of emitter to collector of the device considering Г-valley CB and HH VB is shown in Fig. 3b. In Fig. 3a, band offset between the well and the barrier is finite thus wave function is not confined only in the well region. However, it is sufficiently large to ensure carrier confinement in the well. Compressive strain is present in the well so, HH valance band is above the LH valance band but it is reverse in barrier region. It is also observed that the band edges of L valley in the well and the barrier are higher than the band edge of Г-valley in the well and thus, the direct bandgap is obtained in the well. It is clear from the figure that a single quantized level in Г-conduction band, HH band and LH band is present for the said dimension of well.

Fig. 3
figure 3

a The Energy band structure, Eigen energy and wave function for Ge0.85Sn0.15/Si0.12Ge0.73Sn0.15 QW is shown in figure. In well, compressive strain is present so HH valance band is above then LH valance band and reverse in barrier region. b Band structure of the device (from emitter to collector) at equilibrium considering Г-valley conduction band and HH valance band

Full size image

Optical gain is an important parameter for analysis of laser performance and it estimated for the strain-balanced QW structure with the help of Fermi golden rule (Chuang 2009). Eigen energies and wave function are taken along z-direction in the conduction band and HH band. The expression for gain coefficient is given by:

$${\text{g(}}\hbar \omega )= {\text{C}}_{ 0} \left| {I_{h1}^{e1} } \right|^{2} \int\limits_{ 0}^{\infty } {{\text{dE}}_{\text{t}} {{\uprho }}_{\text{r}}^{{ 2 {\text{D}}}} } \left| {{\hat{\text{e}}} .p_{cv} } \right|^{ 2}\frac{{\rm H}/2{\uppi}}{{\left[ {{\text{E}}_{\text{h1}}^{\text{c1}} ( 0 )+ {\text{E}}_{\text{t}} - \hbar \omega } \right]^{ 2} + \,\left({\rm H}/2 \right)^{ 2} }}\left[ {{\text{f}}_{\text{c}}^{ 1} (\hbar \omega )- {\text{f}}_{\text{v}}^{ 1} (\hbar \omega )} \right] \,$$
(10)

where

$$\begin{aligned} C_{0} = \frac{{\pi e^{2} }}{{n_{r} c\varepsilon_{0} m_{0}^{2} w}}, \, \rho_{\text{r}}^{{ 2 {\text{D}}}} = \frac{{m_{r} }}{{\pi \hbar^{2} L_{z} }},{\text{ I}}_{\text{h1}}^{\text{e1}} = \sum\limits_{{ - L_{z} /2}}^{{L_{z} /2}} {\phi_{1} (z)g_{1} (z)} { , } \hfill \\ \left| {\hat{e}.p_{cv} } \right|^{2} = 1.5\left( {\frac{{m_{0} }}{{m_{e} }} - 1} \right)\frac{{m_{0} E_{g} (E_{g} + \Delta )}}{{6\left( {E_{g} + \tfrac{2}{3}\Delta } \right)}} \, \hfill \\ \end{aligned}$$
(11)

where n r is refractive index of GeSn, \(\rho_{r}^{2D}\) is reduced density of state function, L z is width of QW along z-direction, and m r is reduced effective mass. I is overlap integral of the conduction subband wave function (Φ 1(z)) and valance subband wave function (g 1(z)). \(\left| {\hat{e} \cdot p_{cv} } \right|^{2}\) is momentum matrix element between the CB and the VB, where ê is polarization unit vector. H is the full-width at half-maximum (FWHM) of the Lorentzian function, which is taken as 20 meV (Chang et al. 2010). \({\text{E}}_{{{\text{h}}1}}^{\text{c1}}\) is the bandgap between E c1 and E h1 which are bound state Eigen energies in Г conduction band and HH valance band respectively. The Fermi occupation probabilities(\({\text{f}}_{\text{c}}^{\text{n}}\) and \({\text{f}}_{\text{v}}^{\text{m}}\)) are expressed as follows:

$$\begin{aligned}f_{c}^{n} (\hbar \omega ) &= \frac{1}{{1 + \exp \left\{ {{{[E_{C1} + ({{m_{r} } \mathord{\left/ {\vphantom {{m_{r} } {m_{e} }}} \right. \kern-0pt} {m_{e} }})(\hbar \omega - E_{g} ) - F_{c} ]} \mathord{\left/ {\vphantom {{[E_{C1} + ({{m_{r} } \mathord{\left/ {\vphantom {{m_{r} } {m_{e} }}} \right. \kern-0pt} {m_{e} }})(\hbar \omega - E_{g} ) - F_{c} ]} {K_{B} T}}} \right. \kern-0pt} {K_{B} T}}} \right\}}},\\ f_{v}^{m} (\hbar \omega ) &= \frac{1}{{1 + \exp \left\{ {{{[E_{h1} - ({{m_{r} } \mathord{\left/ {\vphantom {{m_{r} } {m_{h} }}} \right. \kern-0pt} {m_{h} }})(\hbar \omega - E_{g} ) - F_{v} ]} \mathord{\left/ {\vphantom {{[E_{h1} - ({{m_{r} } \mathord{\left/ {\vphantom {{m_{r} } {m_{h} }}} \right. \kern-0pt} {m_{h} }})(\hbar \omega - E_{g} ) - F_{v} ]} {K_{B} T}}} \right. \kern-0pt} {K_{B} T}}} \right\}}} \end{aligned}$$
(12)

here the F c and F v are the quasi-Fermi level which are calculated for a given injected carrier density (Chuang 2009). We considered charge neutrality condition and neglected the effect of p-type barrier because our model has intrinsic QW.

In the proposed structure injected carriers reach to the well through the barrier. Carrier density distribution in Г conduction valley and L conduction valley is required to predict more accurate value of optical gain. The carrier density in different subbands with total injected carrier density in the well is shown in Fig. 4. In the barrier region L conduction valley has lower potential compared to Г conduction valley so large amount of carrier goes to L valley in the barrier region that further transport to L valley in the well. However the difference in L and Г conduction valley in the barrier region is very less so a significant amount of carrier goes to Г conduction valley in the well. Although the current injection efficiency is poor, the significient amount of carriers in gamma valley in the well will recombine rediatively which is sufficient for lasing action. We can increase the gain by heavily doped emitter or by changing Sn concentration in well and barrier. So GeSn QW has the potential to provide gain medium for optoelectronic applications. Benefits of GeSn quantum well are its ease of integrability by matured CMOS technology and its intoxicity. In Fig. 5, optical gain for different total injected carrier densities is plotted as a function of photon energy. Out of total injected carrier, the leakage carrier density in L valley does not contribute to the optical gain. It is clear from figure that, with increase in injected carrier density, the optical gain increases, as the difference in fermi occupation probabilities increases. The spectral width also increases with increasing injected carrier density (\({\text{E}}_{\text{c1}}^{\text{h1}} > {\text{h}}\nu > {\text{F}}_{\text{CV}}\)) as shown in Fig. 5. As injected carrier density increases, quasi-fermi level separation (FCV = FC − FV) also increases. Hence, the range of positive gain (\({\text{E}}_{\text{c1}}^{\text{h1}} > {\text{h}}\nu > {\text{F}}_{\text{CV}}\)) is increased. The peak TE gain is obtained at 460 meV, corresponding to a emission wavelength of 2.68 μm, which lies in mid-infrared region. To predict the transparency carrier density and the threshold carrier density, the modal gain and the threshold modal gain are plotted as a function of total injected carrier density and are shown in Fig. 6. It is observed from figure that modal gain increases with total injected carrier density and reaches to the threshold value for the carrier density of 4.9 × 1018 cm−3 which is nothing but threshold carrier density (Nth). Modal gain crosses the zero value at carrier density of 2.1 × 1018 cm−3 which is the transparency carrier density, Ntr. In this calculation, optical confinement factor is taken as 5 %, the cavity length is taken as 500 µm, the reflectivities (R1&R2)for both the facets of the cavity are taken as 0.357 and modal loss is taken from (Chang et al., 2010). The differential gain g is obtained as 4.32 × 10−17 cm2.

Fig. 4
figure 4

Carrier densities of Г and L conduction valley as a function of total injected carrier density

Full size image
Fig. 5
figure 5

TE mode gain spectra for different total injected carrier densities. The peak TE gain is obtained at 460 meV, corresponding to a emission wavelength of 2.68 μm, which is in mid-infrared region

Full size image
Fig. 6
figure 6

The Modal gain and threshold modal gain as a function of total injected carrier density

Full size image

One of the important parameters, DC current gain of the transistor can be obtained from base current and collector current calculation which again need solution of continuity and rate equations in the base. An estimation of current gain is obtained and it is approximately in the range of 100–120 for the doping in the barrier ~1019 cm−3. Also, it is found that, with increasing base current, the dc current gain remains constant initially and after the base threshold current it decreases. This is due to the fact that, above the base threshold current, lasing action starts and due to the significant recombination of carriers in the base, collector current and, hence, current gain decreases. Further study is required for dc and ac analysis of the transistor in detail.

4 Conclusion

In the present work we proposed an analytical model for Tin incorporated n–p–n TL. The effect of concentration of α-Sn and strain in well and barrier regions on optical and carrier confinement, is studied. The GezSn1−z well is chosen to be compressive strained as it supports TE mode which is crucial for higher optical confinement. Ternary material SixGeySn1−x−y add more flexibility in barrier region to control carrier distribution in L and Г valley. The effect of subband carrier distribution in L valley and Г valley was also considered in our analysis. The calculated optical gain is used to find transparency carrier density, Ntr = 2.2 × 1018 cm−3, threshold carrier density, Nth = 4.9 × 1018 cm−3 and differential optical gain g = 4.32 × 10−17 cm2. The peak value of optical gain occurs at 2.68 µm. So, this device is a potential candidate for low cost monolithic TL for infrared applications. Now, as the barrier height is very less in the proposed structure for TL, effect of temperature on the performance of the device is significant. Rate of escape (inverse of escape lifetime) of carriers, from the well, increases significantly with temperature where as the rate carrier capture in the well varies insignificantly with temperature. Since, the ratio of escape rate to the capture rate has important role on the laser gain, low temperature of operation is always preferred for such devices.