1 Introduction

Quantum communication refers to the distribution of quantum states between two parties, traditionally called Alice and Bob. The quantum states could be entangled states or quantum dense coding (Bennett and Wiesner 1992). Many of the initial works in quantum communication applied discrete quantum variables. However, continuous variables are verified to be appropriate for a quantum communication (Andersen et al. 2009). Quantum key distribution (QKD) is another major branch of quantum communication. It concerns with the establishment of a joint secret key between Alice and Bob, through a quantum channel (Scarani et al. 2009). QKD techniques have been considered as a useful component in network communication systems that need high security (Elliott 2002). Currently, there are large numbers of private networks around the world which offer consumers’ desired secured and private communications. A traditional communication system is applied as the data communication link. The traditional channel can be wired or wireless. In the past two decades, wireless communications has attracted great popularity in which, Radio Frequency (RF) and Optical Wireless (OW) have been applied for transferring data (Majumdar and Ricklin 2007). OW has the potential to be an alternative to RF and fiber optic communication systems, because of the license-free operation (in contrast to the RF communication), immunity to electromagnetic interference, ease of deployment, low power consumption, high security caused by the high directionality and narrowness of the beam (Popoola and Ghassemlooy 2009). OWC can be applied for both indoor (Ghassemlooy and Boucouvalas 2005) and outdoor (Ghassemlooy et al. 2007) applications.

In fact, the Quantum channel establishes the key using quantum cryptography. Then the key will be used for the data encryption and data decryption in OWC channel. The quantum channel also can be wired or wireless. Optical wireless QKD uses the air as the medium for the transmission of photons between the quantum transmitter and receiver. Optical wireless QKD over the free space was first proposed in 1996 (Jacobs and Franson 1996). After that, a number of preparation, measurement and entanglement based structures have been investigated in free space (Scarani et al. 2009). The current longest quantum channel distance is 144 km (Schmitt-Manderbach et al. 2007; Ursin et al. 2007) and satellite quantum communication was investigated in (Villoresi et al. 2008; Perdigues Armengol et al. 2008).

MRR has many interesting and effective applications because of its own nature. It shows an effective performance for generating mm-wave and micro wave generation (Xu et al. 2009; Jia et al. 2007; Seo et al. 2005; Jiang et al. 2010; Ferreira da Silva et al. 2012) and it can be an interesting tool to generate solitonic pulses needed in quantum communication and OWC systems. Yupapin et al. have shown that MRR can be used to generate multi wavelength when a soliton pulse is propagating inside the system (Yupapin and Suwancharoen 2007). The entangled photon pair can be performed via the MRR system, where it can be used to generate secured key codes (Yupapin 2010). Dense wavelength of optical pulses, whether bright or dark type can be generated when the soliton pulse is propagating within the nonlinear MRR system and causes large bandwidth signals to be achieved and offered for continuous dense coding and quantum packet switching applications (Yupapin et al. 2010). Therefore, signals encoding is implemented using multi orthogonal bright and dark soliton signals and Quantum key can be performed and generated using a nonlinear MRR system with appropriate parameters.

In this paper, we have used a nonlinear MRR system to form the multi wavelength, applicable for digital codes generation used in quantum communication and OWC system. By using the proposed system, orthogonal soliton pulses which are bright and dark soliton can be localized and transferred through a digital signal processing system. The rest of this paper is organized as follows. Section 2 describes the theoretical modeling of the proposed system and Sect. 3 demonstrates simulation results and contribution. Finally conclusions are presented in Sect. 4.

2 Theoretical modeling

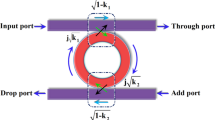
An optical soliton pulse can be inputted into the nonlinear MRRs, where large optical bandwidth of the output signals can be generated. The nonlinear behavior of self-phase modulation (SPM) keeps the large output power. Chaotic signals cancelation can be performed using an optical add/drop filter system (Yupapin and Suwancharoen 2007). The schematic of the proposed systems is shown in Fig. 1.

Fig. 1
figure 1

Systems of multi optical soliton pulse generation, where, \(\text{ R}_{\mathrm{s}}\): ring radii, \(\kappa _{\mathrm{s}}\): coupling coefficients, \(\kappa _{4 }\) and \(\kappa _{5}\) are coupling losses

Full size image

The bright or dark soliton pulse is inserted into the proposed system. The input optical field \((E_{in})\) of the optical powers can be expressed as (Mitatha et al. 2009) follow, where Eq. (1) and Eq. (2) show the optical bright and dark soliton, respectively.

$$\begin{aligned} E_{in} =A\sec h\left[ {\frac{T}{T_0 }} \right]\exp \left[ {\left( {\frac{z}{2L_D }} \right)-i\omega _0 t} \right]\end{aligned}$$
(1)
$$\begin{aligned} E_{in} =A\tanh \left[ {\frac{T}{T_0 }} \right]\exp \left[ {\left( {\frac{z}{2L_D }} \right)-i\omega _0 t} \right] \end{aligned}$$
(2)

A and z are the optical field amplitude and propagation distance, respectively. \(T\) is a soliton pulse propagation time in a frame moving at the group velocity, \(T = t-\beta _{1}\times z\), where \(\beta _{1}\) and \(\beta _{2}\) are the coefficients of the linear and second order terms of Taylor expansion of the propagation constant. \(L_D ={T_0^2 }/{\left| {\beta _2 } \right|}\) is the dispersion length of the soliton pulse. The frequency shift of the soliton is \(\omega _{0}\). This soliton describes a pulse that keeps its temporal width invariance as it propagates, and thus is called a temporal soliton. When soliton peak intensity \(\left( {\left| {\beta _2 /\Gamma T_0^2 } \right|} \right)\) is given then, is known. For the temporal optical soliton pulse in the microring device, a balance should be achieved between the dispersion length \((L_{D})\) and the nonlinear length of \(L_{NL} =(1/{\Gamma _{\Phi NL} })\), where \(\Gamma = n_{2}\times k_{0}\) is the length scale over which dispersive or nonlinear effects makes the beam becoming wider or narrower, hence \(L_{D}=L_{NL}\). When light propagates within the nonlinear medium, the refractive index (n) of light within the medium is given by (Yupapin and Pornsuwancharoen 2009).

$$\begin{aligned} n=n_0 +n_2 I=n_0 +\left(\frac{n_2 }{A_{eff} }\right)P, \end{aligned}$$
(3)

\(n_{0}\) and \(n_{2}\) are the linear and nonlinear refractive indexes, respectively. \(I\) and \(P\) are the optical intensity and optical power, respectively. The effective mode core area of the device is given by \(A_{eff}\). For the MRR and NRR, the effective mode core areas ranges from 0.50 to 0.10 \(\upmu \mathrm{m}^{2}\) (Kokubun et al. 2005). The resonant output can be formed; therefore the normalized output signals of the light field which is the ratio between the output and input fields \((\text{ E}_{\mathrm{out}}(\text{ t})\) and \(\text{ E}_{\mathrm{in}}(\text{ t}))\) in each roundtrip can be expressed by (Yupapin et al. 2007).

$$\begin{aligned} \left| {\frac{E_{out} (t)}{E_{in} (t)}} \right|^{2}=(1-\gamma )\times \left[ {1-\frac{(1-(1-\gamma ) x^{2})\kappa }{(1-x \sqrt{1-\gamma }\sqrt{1-\kappa })^{2}+4{}{}x{}{}\sqrt{1-\gamma }\sqrt{1-\kappa }\sin ^{2}(\frac{\phi }{2})}} \right]\nonumber \\ \end{aligned}$$
(4)

Equation (4) specifies that a ring resonator in the exacting case is very similar to a Fabry-Perot cavity, which has an input and output mirror with a field reflectivity \((1-\kappa )\), and a fully reflecting mirror. \(\kappa \) is the coupling coefficient, and \(\text{ x}=\text{ exp}(-\alpha \text{ L}/2)\) represents a roundtrip loss coefficient, \(\Phi _{0}=kLn_{0}\) and \(\Phi _{NL}=kLn_{2} {\vert }E_{in} {\vert }^{2}\) are the linear and nonlinear phase shifts and \(k=2\pi /\lambda \) is the wave propagation number in a vacuum. \(L\) and \(\alpha \) are waveguide length and linear absorption coefficient, respectively. In this investigation, the iterative method is introduced to obtain the results as shown in Eq. (4), similarly, when the output field is connected and input into the next ring resonators. In order to retrieve the signals from the chaotic noise, we propose to use the add/drop device with the appropriate parameters. The optical outputs of a ring resonator add/drop filter are given by Eqs. (5) and (6) (Yupapin et al. 2008).

$$\begin{aligned} \left| {\frac{E_t }{E_{in} }} \right|^{2}=\frac{\left( {1-\kappa _1 } \right)-2\sqrt{1-\kappa _1 }\cdot \sqrt{1-\kappa _2 }e^{-\frac{\alpha }{2}L}\cos \left( {k_n L} \right)+\left( {1-\kappa _2 } \right)e^{-\alpha L}}{1+\left( {1-\kappa _1 } \right)\left( {1-\kappa _2 } \right)e^{-\alpha L}-2\sqrt{1-\kappa _1 }\cdot \sqrt{1-\kappa _2 }e^{-\frac{\alpha }{2}L}\cos \left( {k_n L} \right)} \end{aligned}$$
(5)

and

$$\begin{aligned} \left| {\frac{E_d }{E_{in} }} \right|^{2}=\frac{\kappa _1 \kappa _2 e^{-\frac{\alpha }{2}L}}{1+\left( {1-\kappa _1 } \right)\left( {1-\kappa _2 } \right)e^{-\alpha L}-2\sqrt{1-\kappa _1 }\cdot \sqrt{1-\kappa _2 }e^{-\frac{\alpha }{2}L}\cos \left( {k_n L} \right)} \end{aligned}$$
(6)

\(E_{t}\) and \(E_{d}\) represent the optical fields of the through port and drop ports, respectively. \(\beta = kn_{\mathrm{eff}}\) is the propagation constant, \(n_{\mathrm{eff}}\) is the effective refractive index of the waveguide, and the circumference of the ring is \(L=2 \pi R\), with \(R\) as the radius of the ring. New parameters are introduced for simplification with \(\phi =\beta \text{ L}\) as the phase constant. By using the specific parameters of the add/drop device, the chaotic noise cancellation can be obtained and the required signals can be retrieved by the specific users. \(\kappa _{1}\) and \(\kappa _{2}\) are the coupling coefficients of the add/drop filters, \(k_{n} =2\pi /\lambda \) is the wave propagation number in a vacuum, and the waveguide (ring resonator) loss is \(\alpha = 0.5\,\mathrm{dB\,mm}^{-1}\) (Tanaram et al. 2011). The fractional coupler intensity loss is \(\gamma = 0.1\). In the case of the add/drop device, the nonlinear refractive index is neglected (Piyatamrong et al. 2010). High capacity of optical pulses can be obtained when the full width at half maximum (FWHM) of these pulses are very small, where the amplification is performed inside the micro or nano ring system (Suhailin et al. 2009).

3 Results and discussion

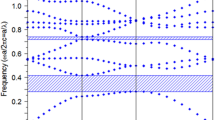
From Fig. 1, the input bright soliton pulse has 50 ns pulse width and peak power of 2 W. The ring radii are \(R_{1}= 15\,\upmu \mathrm{m}, R_{2}= 9\,\upmu \mathrm{m}, R_{3}= 9\) and \(R_{d }= 70 \,\upmu \mathrm{m}\). The fixed parameters are selected to \(\lambda _{0} = 1.55 \,\upmu \mathrm{m}, n_{0} = 3.34\) (InGaAsP/InP), \(A_{eff} = 0.25\,\upmu \mathrm{m}^{2}, \alpha = 0.5\,\mathrm{dB mm}^{-1}\), and \(\gamma = 0.1\). The coupling coefficients range from 0.1 to 0.96, where the nonlinear refractive index is \(n_{2} = 2.2\times 10^{-17} \text{ m}^{2}/\text{ W}\) and the wave guided loss used is \(0.5\,\mathrm{dB\,mm}^{-1}\). Optical signals are sliced into smaller signals broadening over the band as shown in Fig. 2b–d. Therefore, a large bandwidth signal is formed within the first ring device, where a compress bandwidth with smaller group velocity is attained inside the ring \(R_{2 }\) and \(R_{3}\), such as filtering signals. Localized soliton pulses are formed within the add/drop filter system, where resonant condition is performed, given in Fig. 2e–h. However, there are two types of dark and bright soliton pulses. In this paper, the multi soliton pulses with FSR and FHWM of 1,440, and 50 pm are simulated.

Fig. 2
figure 2

Results of the multi-soliton pulse generation, (a): input bright soliton, (b–d): large bandwidth signals, (e–f): bright soliton with FSR of 1,440 pm, and FWHM of 50 pm, (g–h): dark soliton with FSR of 1,440 pm, and FWHM of 50 pm

Full size image

Figure 3 shows the generation of optical multi soliton signals, where the input dark soliton pulse with power of 10 W propagates inside the microring system. Figure 3 b–d shows the filtering process within \(R_{1}, R_{2}\) and \(R_{3}\) with ring radii of 15, 9 and 9 \(\upmu \mathrm{m}\), respectively, where the amplification of output signals occurred. Using the dark soliton input, the security of the optical transmission can be performed along the fiber due to very low power of the central wavelength, which protects the signals to be undetected by any types of conventional laser detectors. Therefore, by using suitable add/drop filter system, powerful bright and dark soliton can be generated shown in Fig. 3e–h. Amplification of optical soliton is an advantage for long transmission links. The power distribution of the output pulses can be executed via the add/drop filter with radius of \(\text{ R}_{\mathrm{d}}\).

Fig. 3
figure 3

Results of the multi-soliton pulse generation, (a): input dark soliton, (b–d): large bandwidth signals, (e–f): bright soliton, (g–h): dark soliton with FSR of 1,440 pm, and FWHM of 50  pm

Full size image

Therefore, the proposed system is suitable for the multi soliton pulses generation, which is available for high performance network. An optical soliton communication has been realized as a good candidate for long distance communication. Therefore, increasing soliton wavelengths is recommended, where the security aim can be obtained by using the dark soliton signals. Generated multi soliton pulses can be transmitted into the OWC systems. Increasing communication capacity is provided by increasing soliton pulses \((\lambda _i)\), which can be performed by generating bright and dark optical soliton pulses. Furthermore, the communication security is formed by using the dark soliton. Therefore, the high capacity and secured signals can be transmitted and retrieved via quantum codes. Here the quantum codes can be generated by using of dark and bright optical solitons.

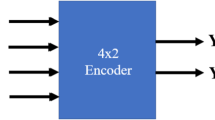
Generated dark and bright soliton pulses can be converted to digital codes of “0” and “1” by using analog to digital electronic convertor system. This system is known as optical binary to decimal convertor system which is applicable to generate digital codes. Therefore, in operation, the large bandwidth within the MRR can be generated by using an optical soliton input into the device. The localized soliton pulse is generated, whereas the required signals, included specific wavelengths, can perform the secure communication network. The security code can be formed by using the spatial soliton pulses. The proposed optical binary to decimal convertor system is shown in Fig. 4. The input and control light pulse trains are inputted into the first add/drop optical filter (MRR1) using dark soliton (logic ‘0’) or the bright soliton (logic ‘1’). First, the dark soliton is converted to become a dark and bright soliton via the add/drop optical filter, which can be seen at the through and drop ports with \(\pi \) phase shift. By using the add/drop optical filter (MRR2 and MRR3), both input signals are generated by the first stage add/drop optical filter. Next, the input data ”Y” with logic “0” (dark soliton) and logic “1” (bright soliton) are added into the both add ports, where the dark-bright soliton conversion with \(\pi \) phase shift is operated again.

Fig. 4
figure 4

System of binary to decimal convertor, where T and D are the through and drop ports of the system

Full size image

From Fig. 4, the optical pulse train X,Y is fed into MRR2 from input and add ports, respectively, in which the optical pulse trains appear at the through and drop ports of MRR2 will be \(X \overline{{\text{ Y}}}\) and \(X \text{ Y}\), respectively. Then the optical pulse train \(\overline{{X}},\overline{{\text{ Y}}}\) is fed into MRR3 from input and add ports, respectively. The optical pulse trains that appear at the through and drop ports of MRR3 will be \(\overline{{X}} \text{ Y}\) and \(\overline{{X}}\, \overline{{\text{ Y}}}\), respectively. Therefore, the generation of logic codes of “0” and “1” can be easily done by using series of beam splitters (B.S) connected to the binary to decimal convertor system. In our simulation, the add/drop optical filter parameters are fixed for all coupling coefficients to be \(\kappa _s =0.05, R_{ad} =300\) nm, \(A_{eff} =0.25\,\upmu \mathrm{m}^{2}\), and \(\alpha =0.05\,\mathrm{dB\,mm}^{-1}\). Here, the results show the generation of optical logic codes of “00”, “01”, “10” and “11”, using the MRRs proposed system.

As shown in Fig. 5, a highly secured OWC consists of two different channels; quantum channel and a classical channel. OWC is chosen as the classical channel. The quantum channel is the line of sight optical wireless path which can apply the proposed system to transmit polarization photons. First of all, the quantum channel determines the key used for the data encryption and decryption using quantum cryptography. After the quantum handshake, OWC system will either refuse or confirm the data communication via the OWC channel. As can be seen in Fig. 5, the applied OWC system as the OWC channel can be an indoor (Ghassemlooy and Boucouvalas 2005) or outdoor (Ghassemlooy et al. 2007) OWC system. An outdoor OWC system is mostly utilized for bridging two different networks. While, an indoor optical wireless can be used to connect PCs,laptops, shopping areas, manufacturing floors and so on.

Fig. 5
figure 5

Block diagram of a highly secure OWC network

Full size image

On the other hand, Balsells et al. proposed solitonic pulse shape for OWC for the first time and they mathematically analyzed a solitonic pulse shape for an OWC system. Their results confirm the significant superiority of the solitonic pulse shape for atmospheric an OWC links. However they stated that solitonic pulse generation is more complicated than generating other pulses and new techniques are needed to generate solitonic pulse shape appropriate for OWC systems (Balsells et al. 2012). The obtained results in this research (as shown in Figs. 2, 3) can be used for OWC system as well. In fact, the proposed system can be integrated to the existing OWC transmitter. It can generate solitonic pulses, which show better performance compared to other pulse shapes applied in OWC systems.

4 Conclusion

We proposed an interesting concept of the digital codes generation, where the system of micro ring resonator was used to generate high capacity of multi optical bright and dark soliton, connected to an analog to digital convertor system. A chaotic signal generation using a soliton pulse in the nonlinear MRRs was presented. Optical communication capacity can be increased by the multi soliton pulses generation, where more soliton channels can be generated by using the MRR system. The required channels were obtained by filtering the large bandwidth signals using an add/drop filter system. The proposed system consists of a series of MRR devices, where the digital codes of “0” and “1” can be generated within the optical binary to decimal convertor system. The advantage of the system is that the clear signal can be retrieved by the specific add/drop filter. Generated results can be applied for both the QKD and OWC systems.