1 Introduction

Detection of biological and chemical agents using far infrared (terahertz, THz) radiation is very promising due to the great successes in research of THz sources, THz spectroscopy and imaging systems. Since rotational and vibrational spectra of many molecules are located in the terahertz domain, specific terahertz absorption patterns allow the identification and quantification of these molecules (Pala and Shur 2008). Currently, terahertz spectroscopy and imaging systems have been used in explosive detection, medicine quality control, and nondestructive evaluation, as a result of the gradual maturation THz technology in the last decade (Pala and Shur 2008; Federici and Moeller 2010). Furthermore, far infrared remote sensing technology can potentially be used in astronomy and atmospheric studies. However, these systems prefer THz detectors with fast response time and room-temperature operation, as well as tunability in frequency. The quality of a detected image is strongly restricted by device performance. Currently, the most common THz detectors available include bolometers (Kroug et al. 2001), pyroelectric detectors, and schottky diodes (Barbieri et al. 2004). However, those detectors cannot completely meet demands of THz systems.

Recently, there has been growing interest in semiconductor-transistor-based plasmonic detectors which utilize plasma waves for generating and detecting THz signals (Dyakonov and Shur 1996). Common transistors used in plasmonic detections are Si MOSFETs, InGaAs/InP or GaAs/AlGaAs high electron mobility transistors (HEMTs), and GaN HEMTs. The collective motion of two dimensional electron gases (2DEG) behaves like shallow water under a gate. A plasma wave frequency in a gated two-dimensional (2D) system follows this simple linear relation: \(\omega = { sk,}\) where \(s\) is the plasma wave velocity \((s= (eV_{\mathrm{gs}}/m^{*})^{0.5})\) and \(k\) is the plasma wave vector. Hydrodynamic nonlinearity can produce photoresponse in the form of continuous source-drain voltage (under open circuit condition) or direct current (with fixed drain voltage) under the irradiation of THz electromagnetic field, even at room temperature (Popov et al. 2003; Popov et al. 2008; Coquillat et al. 2010), if an appropriate antenna structure (such as slot antenna, bow tie antenna, or grating-gate structure) is chosen. In the regime of non-resonance, the photoresponse is a smooth function of gate voltage as well as frequency, while the resonant structure in the photoresponse can be achieved if the resonant condition is satisfied. Since the resonant frequency is proportional to the square root of gate voltage, the devices have inherent advantage of tunability by gate bias. These would eliminate bulky filters, mirrors and other element to realize compact monolithic detector array (Otsuji and Kitamura 2001).

In GaAs semiconductor-transistor-based plasmonic THz detectors, typical sheet electron concentration is \(10^{12}\text{ cm}^{-2}\). This requires a very short gate length in order to utilize the plasma wave for resonance detection (Shaner et al. 2008). The gate length usually lies in the deep sub-micrometer domain for a GaAs plasmonic THz detector. Therefore, devices with higher electron density and mobility are important in the reduction of the complexity of device fabrication. More recently, GaN plasmonic THz detectors (typically, based on GaN HEMTs) have attracted great interest due to their unique properties such as a large band gap and a strong polarization effect. As compared with other III-V HEMT devices, GaN HEMTs have received wider recognition as potential devices for high-frequency and high-power microwave applications (Wang et al. 2012). The electron density in the channel of AlGaN/GaN HEMT can be an order of magnitude higher than for a GaAs HEMT. This will reduce the limitation of deep-submicron meter gate length devices like GaAs HEMT for THz detection according to the dispersion law of plasma wave. One of the main choices for improving the couple between short-wavelength plasmon resonant and relatively long-wavelength THz radiation is to deposit a periodic grating gate to substitute a single-gated antenna. The working principle of the periodic grating gate structures on HEMTs/FETs can be summarized as followed according to the references (Popov 2011a). Diffracted electromagnetic waves with the in-plane wavevectors can be excited, when an electromagnetic wave incident on the grating gate. The in-plane wavevectors are expressed as \(q=2\pi n/L\) with \(n=0, \pm 1,\,\pm 2{\ldots }\) where \(L\) is the period of the grating gate. As THz wavelength is much larger than the period in a typical grating-gate HEMT/FET structure, the excited in-plane wavevectors \((\text{ n}\ne 0)\) are evanescent waves decaying away from the grating gate. The in-plane evanescent waves excite the near-field plasmonic oscillations with the same wavevectors in the gated 2D channel at the coincidence of their frequency. In the previous GaAs HEMTs, a periodic grating gate has been used to expand the frequency domain in THz detection (Popov 2011a). This relies on the higher order resonant plasmon mode excitations with the help of spatial dispersion of the grating gate. The plasmonic wave resonant detector based on the slit-grating-gate transistor is one important device that can achieve tunability and room-temperature THz detection. However, the detection frequency, quantum efficiency, and working temperature of the device cannot fulfill all the requirements of imaging and sensing applications. The maximum resonant frequency has not yet exceeded 5THz with the length of gate finger around 1 \(\mu \text{ m}\) due to the low frequency of the fundamental plasmon mode and radiative damping of the higher order plasmon mode. In our recent papers, we have performed electromagnetic simulation of the plasmon resonant oscillations of GaN HEMTs with the grating gate serving as both as coupler and electrodes (Wang et al. 2012a; Wang et al. 2012b; Wang et al. 2011). However, interactions of the double channel at different channel separations and slit lengths with uniform sheet density are not discussed in detail.

In this paper, numerical simulations of the tunable plasmonic resonant detectors based on slit-grating-gate single-channel and double-channel HEMTs are carried out by FDTD method. The plasmonic resonant phenomenon in the terahertz wave band for AlN/GaN HEMTs is investigated. The results of this work can offer a great advance to realizing tunable and room-temperature THz detections.

2 Device structure and simulation models

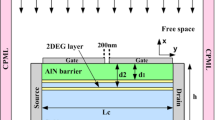
Figure 1a shows the typical structure of grating-gate single channel (SC). For SC GaN HEMTs, AlN/GaN structures with a 2.5-\(\,\upmu \text{ m}\)-thick undoped GaN buffer layer and a 5-nm-thick AlN barrier layer on a 2-inch sapphire substrate are used in the simulations. Conventional SC GaN HEMTs usually have an \(\text{ Al}_{x}\text{ Ga}_{1-x}\text{ N}\) barrier with \(x=0.25-0.3\). Using AlN substituting \(\text{ Al}_{x}\text{ Ga}_{1-x}\text{ N}\) as a thin barrier layer has been reported recently (Wang et al. 2012; Chu et al. 2005). An AlN barrier not only supplies the high density of 2DEG in the channel as a strong polarization effect, but also improves the gate controllability due to the ultra-thin thickness and wide bandgap. Figure 1b shows the typical structure of grating-gate DC GaN HEMTs. The structure consists of a 2.5-\(\,\upmu \text{ m}\)-thick undoped GaN buffer layer, a 21-nm-thick AlGaN bottom barrier layer with the Al composition graded from 3 to 6 %, a 14-nm-thick GaN channel layer, and a 5-nm-thick AlN top barrier layer. In fact, \(\text{ Al}_{0.3}\text{ Ga}_{0.7}\text{ N}\) (20–30 nm) or InAlN (15–20 nm) can also be used as the top barrier layer. The only difference in the simulations is the dielectric constant. However, different materials for the top barrier layers may cause significant differences on material growth as well as device fabrication.

Fig. 1
figure 1

Schematic of a single-channel and b double-channel HEMT structures with THz wave incident from top side. The current vibration, electric field distribution of grating gate, and electron density striction are also shown along the channel

Full size image

Due to the small net dipole moment of gated plasmons, a grating coupler is required to improve the coupling efficiency. The coupler, also serving as electrodes (Muravjov et al. 2010), can be formed by electron-beam etching. The period of the grating gate is \(0.6\,\upmu \text{ m}\). A 0.7 duty-cycle is implemented to ensure uniformity of the 2D channel. In the simulation, \(n_{s1}:n_{s2}\) are used to represent the ratios between the sheet densities of upper and lower channels where total densities value \(n_{s1}+n_{s2}\) is 3\(\times 10^{13}\text{ cm}^{-2}\). A TM polarization THz wave is incident from the top side of the device. The simulation is performed in the FDTD scheme with Drude-optical conductivity to describe electromagnetic wave transport and damping along the channel. The mobility used in this paper is approximately \(1200\,\text{ cm}^{2}\text{/Vs}\, \text{ at}\, 300K\) (Wang et al. 2012) and the electron relaxation time \(\tau \) is about 0.14 ps. The thickness of 2DEG layer modeled is 10 nm, an intermediate thickness after considering the wave function and electron density distributions (Wang et al. 2012a). The plasmon oscillations along the channel are obtained by solving the Maxwell equations in the time domain with the electromagnetic wave solver EMW in Sentaurus-TCAD (Synopsys 2010). Periodic boundary conditions are imposed in the x direction for the grating gates, while perfect matched layers are imposed in the y direction. The electromagnetic response of 2DEG is described by Drude conductivity \(\sigma (x)=n(x)e^{2}\tau /\text{ m}^{*}(1-i\omega \tau )\), in which \(m\)* is the effective electron mass, \(\tau \) is the scattering time caused by the phonons, impurities etc., \(e\) is the elementary charge, and \(n(x)\) is the sheet electron density along the channel. Generally speaking, the electron density \(n(x)\) in the gated region of a channel is different from that in the ungated one, even though there is no electric field added. The electron density distributions can be obtained by solving the Poisson equation as in Wang et al. (2012b). Finally, the Drude-conductivity is embedded by a convolution method to describe the plasmonic oscillation along the channel of grating gate.

A gated conductive channel layer can support two elementary plasmons with symmetrical (SM plasmon) and asymmetrical (ASM plasmon) charge distributions. In the long-wavelength approximation (kd \(<<1, d\) is the thickness of barrier layer), the dispersions of SM plasmons in the gated channel can be written as (Popov 2011a; Popov et al. 2011b)

$$\begin{aligned} (\omega _p )_{\mathrm{gated}-\text{ SM}} =sk=\sqrt{\frac{e^{2}n(x)d}{\varepsilon _0 \varepsilon _r m^{*}}}k \end{aligned}$$
(1)

where \(\varepsilon _{0},\,\varepsilon _{\mathrm{r}}\) and \(\varepsilon _{2}\) are the vacuum permittivity, and dielectric constants of the barrier layer and substrate, respectively. For a device with narrow gate slit and weak spatial modulation of electron density, the wavevector \(k\) of gated plasmon satisfies the selection rule 2 \(\pi \text{ n}/L (L\) is the grating period, \( n = 1, 2, 3, 4{\ldots })\) due to the fact that the spatial waveform of the plasmon occupies almost the entire period of the transistor structure (Allen et al. 1975; Popov 2011a).

With the electromagnetic boundary condition being included, the eigen-frequency of ASM mode can be approximated as follows (Wang et al. 2012a):

$$\begin{aligned} (\omega )_{\mathrm{ASM}}&\approx \frac{\omega _p }{(1+\varepsilon _2 )^{1/2}}\frac{1+\exp (-kd_1 )}{1-\gamma \exp (-kd_1 )}\nonumber \\&\approx \frac{\omega _p }{(1+\varepsilon _2 )^{1/2}}, \text{ for} \gamma =\frac{\varepsilon _2 -1}{\varepsilon _2 +1},kd_1 <<\text{1} \end{aligned}$$
(2)

where \(\omega _{p}\) is the plasma frequency of free electron gas given by \((n(x)e^{2}/\varepsilon _{0}m^{*})^{0.5}\), and \(d_{1}\) is the finite thickness of electron channel layer used in this model.

3 Results and discussion

This new type of plasmonic resonant detector based on slit-grating-gate single-channel and double-channel AlN/GaN HEMTs is chosen for the following reasons. First, the designs of the double channel and high-Al mole-fraction barrier into the HEMTs, as shown in Fig. 1, can supply the HEMTs with high density two-dimensional electron gas, high mobility, and long momentum relaxation time making the detector suitable for room-temperature THz detection. Secondly, a slit grating gate design is used to better couple the plamson wave with the incoming THz signal. The slit grating gate provides the near-field interaction with the two-dimensional electron gas plasmonic resonant making the device tunable under variations in gate voltage (Wang et al. 2011; Wang et al. 2012a).

Figure 2 show the absorption spectra of SC-HEMTs and DC-HEMTs under uniform sheet density. Three kinds of characteristic plasmonic absorption peaks, marked with a, b, and c, can be obtained under THz illuminations. For SC-HEMTs, peaks a and b are the first order and second order resonant absorption peaks of gated plasmons (symmetrical mode), respectively. Their resonance oscillations are shown in Fig. 3a, b. Peak c is related with the plasmonic resonant of dipole-oscillation vertical to the 2D channel plane. It is also called the asymmetrical mode as shown in Fig. 3c. Note that there are no resonant absorption peaks of ungated plasmons in the absorption spectrum due to the ultra-short length of slit. The frequency of the ungated plasmon runs out of the range of 1-18THz according to the ungated dispersion relationship reported in Ref. Wang et al. (2012a).

Fig. 2
figure 2

Absorption spectra of DC-HEMTs are shown under uniform sheet density, where gate voltage is set to zero. \(n_{s1}: n_{s2}\) represents ratios between sheet densities of upper and lower channels with total densities value of \(n_{s1}+n_{s2}=3\times 10^{13}\text{ cm}^{-2}\). Three kinds of plasmonic peaks are marked with (a), (b), and (c). For comparison, the absorption spectrum of SC HEMTs is also shown with the uniform electron density distributions of 2\(\times 10^{12}\text{ cm}^{-2}\)

Full size image
Fig. 3
figure 3

Plasmon-induced electric field distribution in SC-HEMT with a 1st order symmetrical resonant mode, b 2nd order symmetrical resonant mode, and c asymmetrical resonant mode, and in DC-HEMT with d hybrid resonant mode (\(E\)y) with both symmetrical and asymmetrical oscillations in the two channels. The dashed-lined rectangular denotes the channel region

Full size image

For DC-HEMTs, the plasmonic resonant absorption of peak b is very different from that of the SC-HEMTs. The strength of peak b is significantly enhanced. These effects occur because interactions between plasmons in the two channels are enhanced. This conclusion is verified by the plasmon-induced electric field distribution in DC-HEMT, as shown in Fig. 3d. It is found that the second order resonance of gated plasmons in the upper channel couples with the asymmetrical plasmonic resonance in the lower channel. Peak b is the linear combination of the two different absorption modes. A change of the ratios between the sheet densities of upper and lower channels from 7:3 to 8:2 can cause a redshift of peak b. This is because the effective sheet density contributing to the plasmon resonance for the ratio of 8:2 is much closer to the metal grating gate, namely a little bit thinner in effective barrier thickness than that for the ratio of 7:3. Such ratio-dependent plasmonic resonant modes are quite important for the design of DC-HEMT plasmonic THz detectors. It is also found that the frequency of peak c for the ratio of 8:2 is much higher than that for the ratio of 7:3. The reason is that peak c is the asymmetrical plasmonic resonant absorption of the upper channel. An increase sheet density of the upper channel induces a higher absorption frequency for the asymmetrical mode according to the dispersion relationship of asymmetrical mode.

To further understand the interaction of the upper and lower channels, the absorption spectra of DC HEMTs with the separation of upper and lower channels ranging from 15 nm to 45nm are numerically calculated. The results are shown in Fig. 4. Due to the plasmonic oscillation induced in the lower channel, a blue shift and enhancement of the first and second resonant peaks are displayed in the spectrum of DC-HEMT, compared to that of the SC HEMT. Peak b is significantly increased due to the enhanced resonant interaction between plasmonic oscillations along these two channels when the separations are reduced.

Fig. 4
figure 4

Absorption spectra of DC-HEMTs (solid line) and SC-HEMT (dashed line) under uniform zero gate voltages with \(n_{1}:n_{2}=7:3\). Three kinds of plasmonic peaks are marked with (a), (b), and (c). The separation of upper and lower channels is changed from 15 to 45 nm

Full size image

Figure 5 shows the absorption spectra of DC-HEMTs at the different lengths of grating-gate period and slit. It is obvious that the plasmon resonances of peaks \(a_{1}\) and \(a_{2}\) are related to the 1st and 2nd order oscillations of symmetrical plasmon along the upper gated channel where the grating period is \(2\,\upmu \text{ m}\). Similar oscillations of symmetrical plasmon can be found for the grating period of \(1\,\upmu \text{ m}\) and the slit of \(0.2\,\upmu \text{ m}\). Therefore, peaks b are still caused by the hybrid modes between upper-channel symmetrical and lower-channel asymmetrical oscillations despite different device dimensions from those in Fig. 2. For the grating gate with the period of \(1\,\upmu \text{ m}\) and slit of \(0.2\,\upmu \text{ m}\), peak b is the hybrid resonant mode with 3rd order upper-channel symmetrical and lower-channel asymmetrical oscillations. However, for the grating gate with the period of \(1\,\upmu \text{ m}\) and slit of \(0.4\,\upmu \text{ m}\), peak b is the hybrid resonant mode with 2nd order upper-channel symmetrical and lower-channel asymmetrical oscillations. Therefore, resonance b can be caused by different plasmon modes relying on the relative position between the frequency of single plasmon resonance in upper and lower channels without lump them together. This also explains why the absorption strength of peak b for the grating period of \(1\,\upmu \text{ m}\) and slit of \(0.4\,\upmu \text{ m}\) is lowest. For the other dimensions in Fig. 5, the resonant frequency of 3rd order upper-channel symmetrical plasmon is closer to the resonant frequency of lower-channel asymmetrical oscillations. Thus the absorption coupling is stronger for the corresponding dimensions in Fig. 5. Note that, due to the strong background absorption, some higher order upper-channel symmetrical plasmons cannot be found in the absorption spectra. So it is possible that an even higher order upper-channel symmetrical plasmon (4th or 5th) for the grating period of \(2\,\upmu \text{ m}\) interacts with the lower-channel asymmetrical oscillations forming peak b.

Fig. 5
figure 5

Absorption spectra of DC-HEMTs with the period of \(2\,\upmu \text{ m}\) (solid line, and the slit lengths are 0.2, 0.4, and \(0.6\,\upmu \text{ m})\) and \(1\,\upmu \text{ m}\) (dashed line, and the slit lengths are 0.2 and \(0.4\,\upmu \text{ m})\), respectively

Full size image

4 Conclusions

The plasmonic resonant phenomenon in terahertz wave band for single–channel and double channel AlN/GaN HEMTs are investigated by using the finite difference time domain method. Strong resonant absorptions can be obtained when the grating-gate serves as a coupler. These plasmonic absorption peaks for double-channel HEMTs are ratio-dependent and can be tuned in the terahertz frequency domain by changing the length of period and slit, as well as the distribution of electron density in the channels. The channel separation of DC-HEMTs is also very important to absorption strength, which can be significantly affected by the hybrid resonant mode of symmetrical and asymmetrical oscillations of two channels. Our results demonstrate the potential of these devices for THz applications.