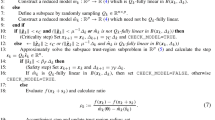On two-subspace randomized extended Kaczmarz method for solving large linear least-squares problems

Abstract

For solving the large-scale linear least-squares problem, we propose a block version of the randomized extended Kaczmarz method, called the two-subspace randomized extended Kaczmarz method, which does not require any row or column paving. Theoretical analysis and numerical results show that the two-subspace randomized extended Kaczmarz method is much more efficient than the randomized extended Kaczmarz method. When the coefficient matrix is of full column rank, the two-subspace randomized extended Kaczmarz method can also outperform the randomized coordinate descent method. If the linear system is consistent, we remove one of the iteration sequences in the two-subspace randomized extended Kaczmarz method, which approximates the projection of the right-hand side vector onto the orthogonal complement space of the range space of the coefficient matrix, and obtain the generalized two-subspace randomized Kaczmarz method, which is actually a generalization of the two-subspace randomized Kaczmarz method without the assumptions of unit row norms and full column rank on the coefficient matrix. We give the upper bound for the convergence rate of the generalized two-subspace randomized Kaczmarz method which also leads to a better upper bound for the convergence rate of the two-subspace randomized Kaczmarz method.

1 Introduction

The Kaczmarz method [17], also known as the algebraic reconstruction technique (ART), is a classic while effective row-action iteration solver for solving the large sparse system of linear equations Ax = b, with $A\in {\mathbb {C}}^{m \times n}$ being an m-by-n complex matrix, $b\in {\mathbb {C}}^{m}$ being an m-dimensional complex vector, and $x\in {\mathbb {C}}^{n}$ being the n-dimensional unknown vector. Due to its simplicity, the Kaczmarz method has been widely used in the area of signal and image processing [8, 9, 16, 20].

When the coefficient matrix $A\in {\mathbb {C}}^{m\times n}$ is of full row rank, the iteration sequence of the Kaczmarz method is linearly convergent to the least Euclidean norm solution of the linear system Ax = b with a rate of $(1-\det (Y^{*}Y))^{\frac {1}{2m}}$, where (⋅)^∗ is the conjugate transpose of the corresponding matrix or vector, the i-th column of the matrix $Y\in {\mathbb {C}}^{n\times m}$ is (A⁽ⁱ⁾)^∗/∥A⁽ⁱ⁾∥₂, i.e., the unit vector which is parallel to the conjugate transpose of the i-th row A⁽ⁱ⁾ of the matrix A, and $\det (Y^{*}Y)$ is the determinant of the matrix Y^∗Y. When the coefficient matrix is of deficient row rank, the iteration sequence of the Kaczmarz method can be proved to be convergent to the least Euclidean norm solution of the consistent linear system, but the convergence rate is hard to formulate explicitly. We refer to [1, 13] for more details on the convergence theory for the Kaczmarz method.

Based on the Kaczmarz method, by choosing each row of the coefficient matrix randomly with probability proportional to its squared Euclidean norm, rather than sequentially in the given order, Strohmer and Vershynin constructed the randomized Kaczmarz (RK) method [25] for solving the consistent linear system. Whether the coefficient matrix A of the consistent linear system Ax = b is of full row rank or not, the RK method can converge not only faster than the Kaczmarz method but also with an expected linear convergence rate expressed explicitly in terms of a natural linear-algebra condition measure $\kappa _{F, 2}(A):=\|A\|_{F}^{2}\|A^{\dag }\|_{2}^{2}$, i.e., the product of the squared Frobenius norm of the matrix A and the squared Euclidean norm of the Moore-Penrose pseudoinverse of the matrix A. A better upper bound for the convergence rate of the RK method was given in [5], a randomized block Kaczmarz method for solving consistent linear systems was proposed in [22], a greedy RK method was proposed in [3, 4], and a non-randomized greedy Kaczmarz method was given in [26]; see also [14, 19, 21] and the references therein.

Since the RK method can not converge to the least-norm least-squares solution when the linear system is not consistent, Zouzias and Freris [27] extended the RK method and proposed the randomized extended Kaczmarz (REK) method to iteratively compute the least Euclidean norm solution x_⋆ := A^‡b of the least-squares problem

$$ \begin{array}{@{}rcl@{}} \min_{x\in{\mathbb{C}}^{n}}\|Ax-b\|_{2}, \quad\text{with}\quad A \in {\mathbb{C}}^{m \times n} \quad\text{and}\quad b \in {\mathbb{C}}^{m}. \end{array} $$

(1.1)

The k-th iterate of the REK method contains two parts: the first part is one RK iteration applied on the linear system Ax = b − z_k, that is

$$ \begin{array}{@{}rcl@{}} x_{k+1} =x_{k}+\frac{\left( b^{(i_{k})}-z_{k}^{(i_{k})}-A^{(i_{k})} x_{k}\right)} {\|A^{(i_{k})}\|_{2}^{2}} (A^{(i_{k})})^{*}, \end{array} $$

where $A^{(i_{k})}$ is the i_k-th row of the matrix A and selected with probability $\text {Pr}(\text {row}=i_{k})=\frac {\|A^{(i_{k})}\|_{2}^{2}}{\|A\|_{F}^{2}}$, $b^{(i_{k})}$ is the i_k-th entry of the vector b, z_k is the vector obtained in the second part of the (k − 1)-th iterate, and $z_{k}^{(i_{k})}$ is the i_k-th entry of the vector z_k; the second part is one randomized orthogonal projection iteration applied on the linear system A^∗z = 0 to obtain the approximation of the projection of the vector b onto the orthogonal complement space of the range space of the matrix A, that is

$$ \begin{array}{@{}rcl@{}} z_{k+1}=z_{k}-\frac{A_{(j_{k})}^{*} z_{k}}{\|A_{(j_{k})}\|_{2}^{2}} A_{(j_{k})}, \end{array} $$

where $A_{(j_{k})}$ is the j_k-th column of the matrix A and selected with probability $\text {Pr}(\text {column}=j_{k})=\frac {\|A_{(j_{k})}\|_{2}^{2}}{\|A\|_{F}^{2}}$, and $A_{(j_{k})}^{*}$ is the conjugate transpose of $A_{(j_{k})}$. Starting with the initial vectors x₀ = 0 and z₀ = b, Zouzias and Freris [27] gave the expected convergence rate of the iteration sequence $\{x_{k}\}_{k=0}^{\infty }$ generated by the REK method as

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|x_{k}-x_{\star}\|_{2}^{2} \leq \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right)^{\lfloor\frac{k}{2}\rfloor} \left( 1+2\kappa^{2}(A)\right) \|x_{\star}\|_{2}^{2}, \end{array} $$

(1.2)

where $\kappa (A)=\sqrt {\frac {\lambda _{\max \limits }(A^{*}A)}{\lambda _{\min \limits }(A^{*}A)}}$ is the condition number of A, $\lambda _{\min \limits }(A^{*}A)$ and $\lambda _{\max \limits }(A^{*}A)$ are the smallest nonzero and the largest eigenvalue of the matrix A^∗A, and $\lfloor \frac {k}{2}\rfloor$ is the largest integer which is smaller than or equal to $\frac {k}{2}$. For more discussions about the REK method, we refer to [7, 12]. Another randomized method which can be used to solve the least-squares problem (1.1) with full column-rank coefficient matrix A is the randomized coordinate descent (RCD) method [18], and it chooses a unit coordinate direction as a search direction randomly according to a probability which is proportional to the squared Euclidean norm of the corresponding column of A. For more discussions about the RCD method, we refer to [2, 6].

To improve the convergence speed, a block version of the REK method was given in [24]. However, this randomized block Kaczmarz method requires good row and column pavings, which are difficult to obtain when the row norms or the column norms of the matrix A are not the same constant, especially when the row norms or the column norms of A are varied in a wide range. In addition, the construction of good pavings may lead to a lot of extra costs. In this paper, we propose a new block version of the REK method, called the two-subspace randomized extended Kaczmarz (TREK) method, and establish its convergence theory. The TREK method does not require any row or column paving. The upper bound for the convergence rate of the TREK method is smaller than the square of the upper bound for the convergence rate of the REK method. The experimental results show that the TREK method outperforms the REK method, and for solving the least-squares problem (1.1) with full column-rank coefficient matrix, the TREK method can also outperform the RCD method.

For the consistent linear system, we can remove the iteration of z_k in the TREK method and obtain the generalized two-subspace randomized Kaczmarz (GTRK) method. Actually, the GTRK method is a generalization of the two-subspace randomized Kaczmarz (TRK) method, which is a block RK method proposed by Needell and Ward [23] with each block submatrix owning two rows of the coefficient matrix, to solve the consistent linear system without the assumptions of unit row norms and full column rank on the coefficient matrix. We give the estimate for the convergence rate of the GTRK method. If the coefficient matrix is of full column rank and with unit-norm rows, the GTRK method will degenerate to the TRK method, and in this case, our upper bound for the convergence rate of the TRK method is smaller than that given in [23].

The organization of this paper is as follows. After introducing necessary notation in Section 2, we give the TREK method for solving the least-squares problem (1.1) and the GTRK method for solving the consistent linear system in Section 3. In Section 4, we establish the convergence theory for the TREK and the GTRK method. We report and discuss the numerical results in Section 5. Finally, in Section 6, we end this paper with concluding remarks.

2 Notation

For a matrix $G\in {\mathbb {C}}^{m \times n}$, we use G^T, G^‡, ∥G∥_F and ∥G∥₂ to denote its transpose, Moore-Penrose pseudoinverse, Frobenius norm and Euclidean norm, respectively. In particular, if G is Hermitian, we use $\lambda _{\min \limits }(G)$ and $\lambda _{\max \limits }(G)$ to represent its smallest nonzero and largest eigenvalues, respectively. Let G⁽ⁱ⁾ and G_(j) denote the i-th row and the j-th column of the matrix G. In particular, we clarify that $G_{(j)}^{*}$ is adopted to denote the conjugate transpose of G_(j). For a vector $u \in {\mathbb {C}}^{m}$, u⁽ⁱ⁾ and u^T are used to indicate its i-th entry and transpose. Let ${\mathcal R}(G)$ denote the range space of the matrix G and ${\mathcal R}(G)^{\perp }$ denote the orthogonal complement subspace of ${\mathcal R}(G)$. Then for any $u \in {\mathbb {C}}^{m}$ it holds that $u = u_{{\mathcal R}(G)}+u_{{\mathcal R}(G)^{\perp }}$, with $u_{{\mathcal R}(G)}$ and $u_{{\mathcal R}(G)^{\perp }}$ being the orthogonal projections of the vector u onto ${\mathcal R}(G)$ and ${\mathcal R}(G)^{\perp }$, respectively. In addition, I_s denotes the identity matrix of dimension s and, for a constant $\upsilon \in {\mathbb {C}}$, $\bar {\upsilon }$ denotes its conjugate. In particular, if υ is a real number, then ⌊υ⌋ represents the largest integer which is smaller than or equal to υ.

For the coefficient matrix $A\in {\mathbb {C}}^{m\times n}$ in (1.1), we always assume that any two rows or any two columns are independent with each other. Define the row coherence parameters of A as

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\delta = \underset{p\neq q}{\min}\frac{|\mathit{A}^{(p)}(\mathit{A}^{(q)})^{*}|} {\|\mathit{A}^{(p)}\|_{2}\|\mathit{A}^{(q)}\|_{2}} \quad\!\!\text{and}\!\!\quad {\Delta} = \underset{p\neq q}{\max}\frac{|A^{(p)}(A^{(q)})^{*}|} {\|\mathit{A}^{(p)}\|_{2}\|\mathit{A}^{(q)}\|_{2}},\!\! \quad \mathit{p}, \mathit{q} = 1, 2, \ldots, m, \end{array} $$

(2.1)

and the column coherence parameters of A as

$$ \tilde{\delta} = \underset{p\neq q}{\min}\frac{|(A_{(p)})^{*}A_{(q)}|} {\|\mathit{A}_{(p)}\|_{2}\|\mathit{A}_{(q)}\|_{2}} \quad\!\!\text{and}\!\!\quad \tilde{\Delta} = \underset{p\neq q}{\max}\frac{|(A_{(p)})^{*}A_{(q)}|} {\|\mathit{A}_{(p)}\|_{2}\|\mathit{A}_{(q)}\|_{2}}, \quad p, q = 1, 2, \ldots, n. $$

(2.2)

Then, we have 0 ≤ δ ≤Δ < 1 and $0\leq \tilde {\delta }\leq \tilde {\Delta }<1$.

We use ${\mathbb {E}}_{k}$ to denote the expected value conditional on the first k iterations, that is,

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}[\cdot] ={\mathbb{E}}[\cdot \mid i_{0_{1}}, i_{0_{2}}, j_{0_{1}}, j_{0_{2}}, i_{1_{1}}, i_{1_{2}}, j_{1_{1}}, j_{1_{2}}, \ldots, i_{(k-1)_{1}}, i_{(k-1)_{2}}, j_{(k-1)_{1}}, j_{(k-1)_{2}}], \end{array} $$

where $i_{l_{1}}, i_{l_{2}}, j_{l_{1}}, j_{l_{2}}$ (l = 0,1,…, k − 1) are the rows and the columns chosen at the l-th iterate. Then, from the law of the iterated expectation, we have ${\mathbb {E}}[ {\mathbb {E}}_{k}[\cdot ] ]={\mathbb {E}}[\cdot ]$.

3 The TREK method

For solving the least-squares problem (1.1), the REK method extends the RK method, by introducing an iterative sequence $\{z_{k}\}_{k=0}^{\infty }$ to approach the orthogonal projection vector $b_{{\mathcal R}(A)^{\perp }}$, and projecting the k-th iteration vector x_k onto the hyperplane $\{x | A^{(i_{k})}x=b^{(i_{k})}-z_{k}^{(i_{k})}\}$. A block version of the REK method, which requires good row and column pavings of the coefficient matrix A, was proposed in [24]. The crucial condition for the existence of a good paving is that the row and column norms are all one, or at least varied in a small range. However, when the row norms are not fixed to be a constant or even varied in a wide range, as the least-norm least-squares solution of the linear system DAx = Db, with $D=\text {diag}\left \{\frac {1}{\|A^{(1)}\|_{2}}, \frac {1}{\|A^{(2)}\|_{2}}, \ldots , \frac {1}{\|A^{(m)}\|_{2}}\right \}$ being a diagonal matrix whose diagonal entries are $\frac {1}{\|A^{(i)}\|_{2}}, i=1, 2, \ldots , m$, may not be that of the linear system Ax = b and we can not compute the least-norm least-squares solution of the linear system Ax = b by solving the linear system DAx = Db whose row norms are all one, a good row paving of A will be difficult to obtain. In addition, to find good row and column pavings may require a lot of extra costs. Therefore, to improve the convergence rate of the REK method, we consider to construct a new block REK method without the use of row and column pavings of A.

At the k-th iterate of the RK method, the row $A^{(i_{k})}$ is chosen randomly, and the current iteration vector x_k is projected onto the hyperplane $\{x | A^{(i_{k})}x=b^{(i_{k})}\}$. To accelerate the RK method, for solving the consistent linear system Ax = b, when the coefficient matrix $A\in {\mathbb {C}}^{m\times n}$ is of full column rank with m ≥ n and each row of A has unit Euclidean norm, Needell and Ward [23] proposed the TRK method. At the k-th iterate of the TRK method, two distinct rows $A^{(i_{k_1})}$ and $A^{(i_{k_2})}$ are chosen uniformly at random, and the current iteration vector x_k is projected onto the hyperplane $\{x | A_{\tau _{k}}x=b_{\tau _{k}}\}$ with

$$ \begin{array}{@{}rcl@{}} A_{\tau_{k}}=\left( (A^{(i_{k_1})})^{T}, (A^{(i_{k_2})})^{T}\right)^{T} \quad\text{and}\quad b_{\tau_{k}}=\left( b^{(i_{k_1})}, b^{(i_{k_2})}\right)^{T}. \end{array} $$

(3.1)

In this way, the next iteration vector x_k+ 1 will be closer to the least-norm solution x_⋆ than the vector obtained by directly projecting x_k onto the hyperplane $\{x | A^{(i_{k_1})} x=b^{(i_{k_1})}\}$ and then onto the hyperplane $\{x | A^{(i_{k_2})} x=b^{(i_{k_2})}\}$.

Inspired by the TRK method, at the k-th iterate, after selecting two distinct rows $A^{(i_{k_1})}$ and $A^{(i_{k_2})}$ randomly, we project the iteration vector x_k onto the hyperplane $\{x | A^{(i_{k_2})} x=b^{(i_{k_2})}-z_{k}^{(i_{k_{2}})}\}$ and then onto the hyperplane $\{x | u_{k}^{*}x=\beta _{k}\}$, i.e,

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\! y_{k} = x_{k} + \frac{\left( \!b^{(i_{k_2})} - z_k^{(i_{k_2})} - A^{(i_{k_2})} x_{k}\!\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*} \ \text{ and } \ x_{k+1} = y_{k} + \frac{\left( \beta_{k} - u_{k}^{*}y_{k}\right)}{\|u_{k}\|_{2}^{2}} u_{k}, \end{array} $$

(3.2)

where

$$ \begin{array}{@{}rcl@{}} \mu_{k}&=&\frac{A^{(i_{k_2})}(A^{(i_{k_1})})^{*}}{\|A^{(i_{k_2})}\|_{2}\|A^{(i_{k_1})}\|_{2}}, \\ u_{k}&=&\frac{(A^{(i_{k_1})})^{*}}{\|A^{(i_{k_1})}\|_{2}}-\mu_{k}\frac{(A^{(i_{k_2})})^{*}}{\|A^{(i_{k_2})}\|_{2}} \quad\text{and}\\ \beta_{k}&=&\frac{b^{(i_{k_1})}-z_k^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}} -\bar{\mu}_{k}\frac{\left( b^{(i_{k_2})}-z_k^{(i_{k_2})}\right)}{\|A^{(i_{k_2})}\|_{2}}; \end{array} $$

(3.3)

and after selecting two distinct columns $A_{(j_{k_1})}$ and $A_{(j_{k_2})}$ randomly, we project the iteration vector z_k onto the hyperplane $\{z | A_{(j_{k_2})}^{*}z=0\}$ and then onto the hyperplane $\{z | v_{k}^{*}z=0\}$, i.e.,

$$ \begin{array}{@{}rcl@{}} \mathscr{Z}_{k}=z_{k}-\frac{A_{(j_{k_2})}^{*} z_{k}}{\|A_{(j_{k_2})}\|_{2}^{2}} A_{(j_{k_2})} \quad\text{and}\quad z_{k+1}=\mathscr{Z}_{k}-\frac{v_{k}^{*}\mathscr{Z}_{k}}{\|v_{k}\|_{2}^{2}} v_{k}, \end{array} $$

(3.4)

where

$$ \begin{array}{@{}rcl@{}} \nu_{k}=\frac{A_{(j_{k_2})}^{*}A_{(j_{k_1})}}{\|A_{(j_{k_2})}\|_{2}\|A_{(j_{k_1})}\|_{2}} \quad\text{and}\quad v_{k}=\frac{A_{(j_{k_1})}}{\|A_{(j_{k_1})}\|_{2}}-\nu_{k}\frac{A_{(j_{k_2})}}{\|A_{(j_{k_2})}\|_{2}}. \end{array} $$

Since the vectors $A^{(i_{k_2})}$ and u_k are orthogonal to each other and the vectors $A_{(j_{k_2})}$ and v_k are orthogonal to each other, the next iteration vectors x_k+ 1 and z_k+ 1 will be on the hyperplane $\{x | A_{\tau _{k}}x=b_{\tau _{k}}-(z_{k})_{\tau _{k}}\}$ and $\{z | A_{\omega _{k}}^{*}z=0\}$ respectively, where $A_{\tau _{k}}$ and $b_{\tau _{k}}$ are defined as in (3.1) and

$$ \begin{array}{@{}rcl@{}} (z_{k})_{\tau_{k}}=(z_{k}^{(i_{k_{1}})}, z_{k}^{(i_{k_{2}})})^{T} \quad\text{and}\quad A_{\omega_{k}}=(A_{(j_{k_1})}, A_{(j_{k_2})}). \end{array} $$

(3.5)

In this way, the next iteration vectors x_k+ 1 and z_k+ 1 will be closer to x_⋆ and $b_{{\mathcal R}(A)^{\perp }}$, respectively, than the vectors obtained by applying two REK iterations on x_k and z_k with the working rows $A^{(i_{k_1})}$ and $A^{(i_{k_2})}$ and the working columns $A_{(j_{k_1})}$ and $A_{(j_{k_2})}$. In addition, when the angle between $A^{(i_{k_1})}$ and $A^{(i_{k_2})}$ or the angle between $A_{(j_{k_1})}$ and $A_{(j_{k_2})}$ is smaller, this acceleration will be more significant.

To save the computation cost, we simplify the iteration schemes in (3.2) and (3.4) by respectively substituting the first equality into the second one, and propose the TREK method in Method 1.

At each iterate, the TREK method utilizes two rows and two columns of the matrix A, while the REK method only utilizes one row and one column. Thus, to be fair, we compare one iteration of the TREK method with two iterations, instead of one iteration, of the REK method. For the convenience of the discussion in the sequel, we call the method, each iteration of which consists of two REK iterations, the REK2 method. If $\|A^{(i)}\|_{2}^{2}$, i = 1,2,…, m, and $\|A_{(j)}\|_{2}^{2}$, j = 1,2,…, n, are precomputed, each iteration step of the TREK method will cost 10m + 10n + 20 flops, and that of the REK2 method will cost 8m + 8n + 4 flops.

When the linear system Ax = b is consistent, we do not need the iteration of z_k any more. Thus, in this case, we set z_k = 0, k = 0,1,2,…, in the TREK method, and obtain the GTRK method for solving the consistent linear system Ax = b in Method 2.

The GTRK method is actually a generalization of the TRK method, without the assumptions of tall and full column-rank coefficient matrix A with unit row norms, that is, the matrix A can be flat or tall, and full rank or rank deficient, and the Euclidean norm of each row of A can be any nonnegative real number.

We remark here that the GTRK method is not the generalization of the TRK method mentioned in Remark 4 of [23] which selects the pair of distinct rows $A^{(i_{k_1})}$ and $A^{(i_{k_2})}$ at the k-th iterate with probability proportional to $\|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2}$. In fact, at the k-th iterate of Method 2, the row pair $(A^{(i_{k_1})}, A^{(i_{k_2})})$ is selected with the probability $\frac {\|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2}} {\|A\|_{F}^{2}(\|A\|_{F}^{2}-\|A^{(i_{k_1})}\|_{2}^{2})}$, while at the k-th iterate of the generalization of the TRK method mentioned in Remark 4 of [23] for the coefficient matrix with arbitrary row norms, the row pair $(A^{(i_{k_1})}, A^{(i_{k_2})})$ is selected with the probability $\frac {\|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2}}{\|A\|_{F}^{4}-{\sum }_{i=1}^{m}\|A^{(i)}\|_{2}^{4}}$.

4 Convergence analysis

To analyze the convergence of the TREK method, we need to give the convergence property of the GTRK method first. Based on Theorem 1.1 in [23] for the convergence of the TRK method, by improving the estimate of the solution error for the vector obtained by utilizing two RK iterations on the current iteration vector with two different working rows and analyzing the convergence without the assumptions of unit row norms and full column rank on the coefficient matrix, we can obtain the following lemma. We refer to Appendix for its proof.

Lemma 4.1

If the linear system Ax = b, with $A\in {\mathbb {C}}^{m\times n}$ and $b\in {\mathbb {C}}^{m}$, is consistent, then the iteration sequence $\{x_{k}\}_{k=0}^{\infty }$ generated by the GTRK method starting from an initial guess $x_{0}\in {\mathbb {C}}^{n}$ in the column space of A^∗, converges to the least-norm solution x_⋆ = A^‡b in expectation. Moreover, the solution error in expectation for the iteration sequence $\{x_{k}\}_{k=0}^{\infty }$ obeys

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|x_{k+1}-x_{\star}\|_{2}^{2} \leq \left[ \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tau_{\max}}\right) \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right) -\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \frac{\tau_{\min}}{\tau_{\max}} \gamma \right] \|x_{k}-x_{\star}\|_{2}^{2}, \end{array} $$

where $\gamma =\min \limits \left \{\frac {\delta ^{2}(1-\delta )}{1+\delta }, \frac {{\Delta }^{2}(1-{\Delta })}{1+{\Delta }}\right \}$ with δ and Δ being defined as in (2.1), and

$$ \begin{array}{@{}rcl@{}} \tau_{\min}=\|A\|_{F}^{2}-\max_{1\leq i\leq m}\|A^{(i)}\|_{2}^{2}, \quad \tau_{\max}=\|A\|_{F}^{2}-\min_{1\leq i\leq m}\|A^{(i)}\|_{2}^{2}. \end{array} $$

As a result, it holds that

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|x_{k}-x_{\star}\|_{2}^{2} \leq \left[ \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tau_{\max}}\right) \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right) -\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \frac{\tau_{\min}}{\tau_{\max}} \gamma \right]^{k} \|x_{0}-x_{\star}\|_{2}^{2}. \end{array} $$

When the coefficient matrix $A\in {\mathbb {C}}^{m\times n}$ of the consistent linear system is of full column rank and the Euclidean norm of each row of A is one, the GTRK method will degenerate to the TRK method. In this case, it follows from Lemma 4.1 that, starting from any initial guess $x_{0}\in {\mathbb {C}}^{n}$, the solution error in expectation for the iteration sequence $\{x_{k}\}_{k=0}^{\infty }$ generated by the TRK method obeys

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|x_{k} - x_{\star}\|_{2}^{2} \!\leq\! \left[ \left( 1 - \frac{\lambda_{\min}(A^{*}A)}{m-1}\right) \left( 1 - \frac{\lambda_{\min}(A^{*}A)}{m}\right) - \frac{\lambda_{\min}(A^{*}A)}{m} \gamma \right]^{k} \|x_{0} - x_{\star}\|_{2}^{2}. \end{array} $$

Then, we can observe that our upper bound for the expected convergence rate of the TRK method is smaller than that given in Theorem 1.1 of [23], i.e.,

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|x_{k}-x_{\star}\|_{2}^{2} \leq \left[ \left( 1-\frac{\lambda_{\min}(A^{*}A)}{m}\right)^{2} -\frac{\lambda_{\min}(A^{*}A)}{m} \gamma \right]^{k} \|x_{0}-x_{\star}\|_{2}^{2}. \end{array} $$

Based on the above discussion, we can establish the convergence theory for the TREK method in the following theorem.

Theorem 4.1

The iteration sequence $\{x_{k}\}_{k=0}^{\infty }$ generated by the TREK method converges in expectation to the least-norm solution x_⋆ = A^‡b of the least-squares problem (1.1). Moreover, the solution error in expectation for the iteration sequence $\{x_{k}\}_{k=0}^{\infty }$ obeys

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!{\mathbb{E}}\|x_{k} - x_{\star}\|_{2}^{2} \!\leq\! (\max\{\alpha, \beta\})^{\lfloor\frac{k}{2}\rfloor} \left( \!1 + \frac{4}{(1 - {\Delta})(1 - \alpha)} \frac{\tau_{\max}}{\tau_{\min}} \frac{\lambda_{\max}(A^{*}A)}{\|A\|_{F}^{2}}\!\right) \|x_{\star}\|_{2}^{2}, \end{array} $$

(4.1)

where

$$ \begin{array}{@{}rcl@{}} \alpha=\left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tau_{\max}}\right) \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right) -\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \frac{\tau_{\min}}{\tau_{\max}} \gamma \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \beta=\left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tilde{\tau}_{\max}}\right) \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right) -\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \frac{\tilde{\tau}_{\min}}{\tilde{\tau}_{\max}} \tilde{\gamma}, \end{array} $$

with $\gamma =\min \limits \left \{\frac {\delta ^{2}(1-\delta )}{1+\delta }, \frac {{\Delta }^{2}(1-{\Delta })}{1+{\Delta }}\right \}$, $\tilde {\gamma }=\min \limits \left \{\frac {\tilde {\delta }^{2}(1-\tilde {\delta })} {1+\tilde {\delta }}, \frac {\tilde {\Delta }^{2}(1-\tilde {\Delta })} {1+\tilde {\Delta }}\right \}$, δ and Δ being defined as in (2.1), $\tilde {\delta }$ and $\tilde {\Delta }$ being defined as in (2.2), and

$$ \begin{array}{@{}rcl@{}} \tau_{\min}=\|A\|_{F}^{2}-\max_{1\leq i\leq m}\|A^{(i)}\|_{2}^{2}, \quad \tau_{\max}=\|A\|_{F}^{2}-\min_{1\leq i\leq m}\|A^{(i)}\|_{2}^{2}, \\ \tilde{\tau}_{\min} =\|A\|_{F}^{2}-\max_{1\leq j\leq n}\|A_{(j)}\|_{2}^{2}, \quad \tilde{\tau}_{\max} =\|A\|_{F}^{2}-\min_{1\leq j\leq n}\|A_{(j)}\|_{2}^{2}. \end{array} $$

Proof

Define $\tilde {x}_{k+1}$ as

$$ \begin{array}{@{}rcl@{}} \tilde{x}_{k+1}=x_{k} +\frac{\tilde{r}_{k_{1}}-\bar{\mu}_{k} \tilde{r}_{k_{2}}}{(1-|\mu_{k}|^{2})\|A^{(i_{k_1})}\|_{2}} (A^{(i_{k_1})})^{*} +\frac{\tilde{r}_{k_{2}}-\mu_{k} \tilde{r}_{k_{1}}}{(1-|\mu_{k}|^{2})\|A^{(i_{k_2})}\|_{2}} (A^{(i_{k_2})})^{*}, \end{array} $$

where

$$ \begin{array}{@{}rcl@{}} \tilde{r}_{k_{1}}=\frac{b_{{\mathcal R}(A)}^{(i_{k_{1}})}-A^{(i_{k_1})} x_{k}}{\|A^{(i_{k_1})}\|_{2}} \quad\text{and}\quad \tilde{r}_{k_{2}}=\frac{b_{{\mathcal R}(A)}^{(i_{k_{2}})}-A^{(i_{k_2})} x_{k}}{\|A^{(i_{k_2})}\|_{2}}. \end{array} $$

It is easy to find that $\tilde {x}_{k+1}$ is actually obtained by applying one GTRK iteration on the vector x_k for the consistent linear system $Ax=b_{{\mathcal R}(A)}$. Similar to the proofs of the convergence theorems for the REK-type methods in [7, 10, 12, 24, 27], we illuminate the orthogonality of $x_{k+1}-\tilde {x}_{k+1}$ and $\tilde {x}_{k+1}-x_{\star }$ first.

From the iteration scheme of x_k we have

$$ \begin{array}{@{}rcl@{}} x_{k+1}-\tilde{x}_{k+1} &=&\frac{\tilde{s}_{k_{1}}-\bar{\mu}_{k} \tilde{s}_{k_{2}}}{(1-|\mu_{k}|^{2})\|A^{(i_{k_1})}\|_{2}} (A^{(i_{k_1})})^{*} +\frac{\tilde{s}_{k_{2}}-\mu_{k} \tilde{s}_{k_{1}}}{(1-|\mu_{k}|^{2})\|A^{(i_{k_2})}\|_{2}} (A^{(i_{k_2})})^{*} \\ &=&\frac{\tilde{s}_{k_{2}}}{\|A^{(i_{k_2})}\|_{2}} (A^{(i_{k_2})})^{*} +\left( \tilde{s}_{k_{1}}-\bar{\mu}_{k}\tilde{s}_{k_{2}}\right) \frac{u_{k}}{\|u_{k}\|_{2}^{2}}, \end{array} $$

(4.2)

where u_k is defined as in (3.3) with $\|u_{k}\|_{2}^{2}=1-|\mu _{k}|^{2}$, and

$$ \begin{array}{@{}rcl@{}} \tilde{s}_{k_{1}}=r_{k_{1}}-\tilde{r}_{k_{1}} =\frac{b_{{\mathcal R}(A)^{\perp}}^{(i_{k_{1}})}-z_k^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}} \quad\text{and}\quad \tilde{s}_{k_{2}}=r_{k_{2}}-\tilde{r}_{k_{2}} =\frac{b_{{\mathcal R}(A)^{\perp}}^{(i_{k_{2}})}-z_k^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}}. \end{array} $$

Besides, we can also find that

$$ \begin{array}{@{}rcl@{}} \tilde{x}_{k+1} = x_{k} + \frac{\left( \!b_{{\mathcal R}(A)}^{(i_{k_{2}})} - A^{(i_{k_2})} x_{k}\!\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*} + \left( \!\frac{b_{{\mathcal R}(A)}^{(i_{k_{1}})}}{\|A^{(i_{k_1})}\|_{2}} - \bar{\mu}_{k}\frac{b_{{\mathcal R}(A)}^{(i_{k_{2}})}}{\|A^{(i_{k_2})}\|_{2}} - u_{k}^{*} x_{k}\!\right) \frac{u_{k}}{\|u_{k}\|_{2}^{2}}. \end{array} $$

Since $b_{{\mathcal R}(A)}=Ax_{\star }$, we have

$$ \begin{array}{@{}rcl@{}} x_{k} - x_{\star} + \frac{\left( b_{{\mathcal R}(A)}^{(i_{k_{2}})} - A^{(i_{k_2})} x_{k}\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*} &=&x_{k}-x_{\star}+ \frac{\left( A^{(i_{k_2})} x_{\star} - A^{(i_{k_2})} x_{k}\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*} \\ &=&\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}} {\|A^{(i_{k_2})}\|_{2}^{2}}\right)(x_{k}-x_{\star}) \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \frac{b_{{\mathcal R}(A)}^{(i_{k_{1}})}}{\|A^{(i_{k_1})}\|_{2}} - \bar{\mu}_{k}\frac{b_{{\mathcal R}(A)}^{(i_{k_{2}})}}{\|A^{(i_{k_2})}\|_{2}} - u_{k}^{*} x_{k} = \frac{A^{(i_{k_1})} x_{\star}}{\|A^{(i_{k_1})}\|_{2}} -\bar{\mu}_{k}\frac{A^{(i_{k_2})} x_{\star}}{\|A^{(i_{k_2})}\|_{2}} -u_{k}^{*} x_{k} =u_{k}^{*}(x_{\star}-x_{k}). \end{array} $$

Therefore, it holds that

$$ \begin{array}{@{}rcl@{}} \tilde{x}_{k+1}-x_{\star} =\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}} {\|A^{(i_{k_2})}\|_{2}^{2}} -\frac{u_{k}u_{k}^{*}}{\|u_{k}\|_{2}^{2}}\right)(x_{k}-x_{\star}). \end{array} $$

Hence, combining this equality with the equality (4.2), it follows from the orthogonality of the vectors $A^{(i_{k_2})}$ and u_k that

$$ \begin{array}{@{}rcl@{}} (x_{k+1}-\tilde{x}_{k+1})^{*}(\tilde{x}_{k+1}-x_{\star})=0. \end{array} $$

This means that $x_{k+1}-\tilde {x}_{k+1}$ is perpendicular to $\tilde {x}_{k+1}-x_{\star }$. Thus, it holds that

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|x_{k+1}-x_{\star}\|_{2}^{2} ={\mathbb{E}}_{k}\|x_{k+1}-\tilde{x}_{k+1}\|_{2}^{2} +{\mathbb{E}}_{k}\|\tilde{x}_{k+1}-x_{\star}\|_{2}^{2}. \end{array} $$

(4.3)

Then, we give the estimates for ${\mathbb {E}}_{k}\|x_{k+1}-\tilde {x}_{k+1}\|_{2}^{2}$ and ${\mathbb {E}}_{k}\|\tilde {x}_{k+1}-x_{\star }\|_{2}^{2}$, respectively. From equality (4.2), using the facts $A^{(i_{k_2})} u_{k}=0$ and $\|u_{k}\|_{2}^{2}=1-|\mu _{k}|^{2}$ we have

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|x_{k+1}-\tilde{x}_{k+1}\|_{2}^{2} &=&\sum\limits_{i_{k_{1}}=1}^{m}\frac{\|A^{(i_{k_1})}\|_{2}^{2}}{\|A\|_{F}^{2}} \underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \frac{\|A^{(i_{k_2})}\|_{2}^{2}}{\|A\|_{F}^{2}-\|A^{(i_{k_1})}\|_{2}^{2}} \|x_{k+1}-\tilde{x}_{k+1}\|_{2}^{2}\\ & \leq& \frac{1}{\|A\|_{F}^{2} \tau_{\min}} \sum\limits_{i_{k_{1}}=1}^{m} \underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2}\\ && \cdot \left( |\tilde{s}_{k_{2}}|^{2} +\frac{|\tilde{s}_{k_{1}}-\bar{\mu}_{k}\tilde{s}_{k_{2}}|^{2}}{1-|\mu_{k}|^{2}}\right). \end{array} $$

(4.4)

For p, q ∈{1,2,…, m} and p≠q, define

$$ \begin{array}{@{}rcl@{}} \xi_{p,q} =\frac{1}{\sqrt{1-\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}}} \quad\text{and}\quad \eta_{p,q} =\frac{\frac{A^{(p)}(A^{(q)})^{*}}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}}} {\sqrt{1-\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}}}. \end{array} $$

Since for any $\xi , \eta , \phi , \psi \in {\mathbb {C}}$, it holds that

$$ \begin{array}{@{}rcl@{}} |\xi \phi-\eta \psi|^{2}+|\xi \psi-\bar{\eta} \phi|^{2} \leq (|\xi|+|\eta|)^{2}(|\phi|^{2}+|\psi|^{2}), \end{array} $$

we have

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i_{k_{1}}=1}^{m}\underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2} \frac{|\tilde{s}_{k_{1}}-\bar{\mu}_{k}\tilde{s}_{k_{2}}|^{2}}{1-|\mu_{k}|^{2}} \\ &=&\sum\limits_{p<q}\|A^{(p)}\|_{2}^{2}\|A^{(q)}\|_{2}^{2} \left( \left|\xi_{p,q}\tilde{s}_{p}-\eta_{p,q}\tilde{s}_{q}\right|^{2} +\left|\xi_{p,q}\tilde{s}_{q}-\bar{\eta}_{p,q}\tilde{s}_{p} \right|^{2}\right) \\ &\leq&\sum\limits_{p<q}\|A^{(p)}\|_{2}^{2}\|A^{(q)}\|_{2}^{2} \left( |\xi_{p,q}|+|\eta_{p,q}|\right)^{2} \left( |\tilde{s}_{p}|^{2}+|\tilde{s}_{q}|^{2}\right) \end{array} $$

where p, q ∈{1,2,…, m}, p≠q and

$$ \begin{array}{@{}rcl@{}} \tilde{s}_{p}=\frac{b_{{\mathcal R}(A)^{\perp}}^{(p)}-z_{k}^{(p)}}{\|A^{(p)}\|_{2}} \quad\text{and}\quad \tilde{s}_{q}=\frac{b_{{\mathcal R}(A)^{\perp}}^{(q)}-z_{k}^{(q)}}{\|A^{(q)}\|_{2}}. \end{array} $$

From the inequality

$$ \begin{array}{@{}rcl@{}} \left( |\xi_{p,q}|+|\eta_{p,q}|\right)^{2} =\left( \frac{1+\frac{|A^{(p)}(A^{(q)})^{*}|}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}}} {\sqrt{1-\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}}}\right)^{2} =\frac{1+\frac{|A^{(q)}(A^{(p)})^{*}|}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}}} {1-\frac{|A^{(q)}(A^{(p)})^{*}|}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}}} \leq \frac{1+{\Delta}}{1-{\Delta}}, \end{array} $$

we have

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i_{k_{1}}=1}^{m}\underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2} \frac{|\tilde{s}_{k_{1}}-\bar{\mu}_{k}\tilde{s}_{k_{2}}|^{2}}{1-|\mu_{k}|^{2}} \\&\leq& \frac{1+{\Delta}}{1-{\Delta}} \sum\limits_{p<q}\|A^{(p)}\|_{2}^{2}\|A^{(q)}\|_{2}^{2} \left( |\tilde{s}_{p}|^{2}+|\tilde{s}_{q}|^{2}\right) \\ &=&\frac{1+{\Delta}}{1-{\Delta}} \sum\limits_{p=1}^{m}\underset{q \neq p}{\sum\limits_{q=1}^{m}} \|A^{(q)}\|_{2}^{2}\left|b_{{\mathcal R}(A)^{\perp}}^{(p)}-z_{k}^{(p)}\right|^{2} \\ &\leq& \frac{1+{\Delta}}{1-{\Delta}} \tau_{\max}\|b_{{\mathcal R}(A)^{\perp}}-z_{k}\|_{2}^{2}. \end{array} $$

(4.5)

Besides, it holds that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i_{k_{1}}=1}^{m}\underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2} |\tilde{s}_{k_{2}}|^{2} &=&\sum\limits_{i_{k_{2}}=1}^{m}\underset{i_{k_{1}}\neq i_{k_{2}}}{\sum\limits_{i_{k_{1}}=1}^{m}} \|A^{(i_{k_1})}\|_{2}^{2}\left|b_{{\mathcal R}(A)^{\perp}}^{(i_{k_{2}})}-z_k^{(i_{k_2})}\right|^{2} \\ &\leq& \tau_{\max}\|b_{{\mathcal R}(A)^{\perp}}-z_{k}\|_{2}^{2}. \end{array} $$

(4.6)

Therefore, by substituting (4.5) and (4.6) into (4.4), we can obtain

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|x_{k+1} - \tilde{x}_{k+1}\|_{2}^{2} \!& \leq&\! \frac{1}{\|A\|_{F}^{2} \tau_{\min}} \left( \!\tau_{\max}\|b_{{\mathcal R}(A)^{\perp}} - z_{k}\|_{2}^{2} + \frac{1 + {\Delta}}{1 - {\Delta}} \tau_{\max}\|b_{{\mathcal R}(A)^{\perp}} - z_{k}\|_{2}^{2}\right) \\ \!& =&\! \frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} \|b_{{\mathcal R}(A)^{\perp}}-z_{k}\|_{2}^{2}. \end{array} $$

(4.7)

Since $\tilde {x}_{k+1}$ can be obtained by utilizing one GTRK iteration on the vector x_k for the consistent linear system $Ax=b_{{\mathcal R}(A)}$ whose least-norm solution is also x_⋆, from Lemma 4.1 and $x_{k}\in {\mathcal R}(A^{*})$, we know

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|\tilde{x}_{k+1}-x_{\star}\|_{2}^{2} \leq \alpha\|x_{k}-x_{\star}\|_{2}^{2}. \end{array} $$

(4.8)

Then, by substituting inequalities (4.7) and (4.8) into equality (4.3) we get

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|x_{k+1}-x_{\star}\|_{2}^{2} & \leq \alpha\|x_{k}-x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} \|b_{{\mathcal R}(A)^{\perp}}-z_{k}\|_{2}^{2}. \end{array} $$

(4.9)

In the TREK method, the iteration of $z_{k}-b_{{\mathcal R}(A)^{\perp }}$ is just the GTRK iteration for solving the consistent linear system A^∗z = 0, where z is the m-dimensional unknown vector and the least-norm solution is the zero vector. Thus, it follows from $z_{0}-b_{{\mathcal R}(A)^{\perp }}=b_{{\mathcal R}(A)}\in {\mathcal R}(A)$ and Lemma 4.1 that

$$ \begin{array}{@{}rcl@{}} && {\mathbb{E}}_{k}\|b_{{\mathcal R}(A)^{\perp}}-z_{k+1}\|_{2}^{2} \\ & \leq & \left[ \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tilde{\tau}_{\max}}\right) \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right) -\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \frac{\tilde{\tau}_{\min}}{\tilde{\tau}_{\max}} \tilde{\gamma} \right] \|b_{{\mathcal R}(A)^{\perp}}-z_{k}\|_{2}^{2}. \end{array} $$

Then for any nonnegative integer l ≥ 0 we have

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|b_{{\mathcal R}(A)^{\perp}}-z_{l}\|_{2}^{2} \leq \beta^{l}\|b_{{\mathcal R}(A)^{\perp}}-z_{0}\|_{2}^{2} = \beta^{l}\|b_{{\mathcal R}(A)}\|_{2}^{2} \leq \|b_{{\mathcal R}(A)}\|_{2}^{2}. \end{array} $$

(4.10)

Using the similar technique in the proofs of the convergence theorems for the REK-type methods in [7, 24, 27], for any nonnegative integer k, define $k_{p} := \lfloor \frac {k}{2}\rfloor$ and k_q := k − k_p. Then it follows from inequalities (4.9) and (4.10) that

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|x_{k_{p}}-x_{\star}\|_{2}^{2} &\leq& \alpha{\mathbb{E}}\|x_{k_{p}-1}-x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} {\mathbb{E}}\|b_{{\mathcal R}(A)^{\perp}}-z_{k_{p}-1}\|_{2}^{2} \\ & \leq& \alpha^{k_{p}}\|x_{0}-x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} \sum\limits_{l=0}^{k_{p}-1}\alpha^{l} {\mathbb{E}}\|b_{{\mathcal R}(A)^{\perp}}\\&&-z_{k_{p}-l-1}\|_{2}^{2} \\ & \leq& \alpha^{k_{p}}\|x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} \|b_{{\mathcal R}(A)}\|_{2}^{2} \sum\limits_{l=0}^{k_{p}-1}\alpha^{l} \\ & \leq& \alpha^{k_{p}}\|x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} \|b_{{\mathcal R}(A)}\|_{2}^{2} \sum\limits_{l=0}^{\infty}\alpha^{l} \\ & =& \alpha^{k_{p}}\|x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})(1-\alpha)} \frac{\tau_{\max}}{\tau_{\min}} \frac{\|b_{{\mathcal R}(A)}\|_{2}^{2}}{\|A\|_{F}^{2}}. \end{array} $$

(4.11)

For any nonnegative integer l ≥ 0 we have

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|b_{{\mathcal R}(A)^{\perp}}-z_{l+k_{p}}\|_{2}^{2} \leq \beta^{l+k_{p}}\|b_{{\mathcal R}(A)^{\perp}}-z_{0}\|_{2}^{2} \leq \beta^{k_{p}}\|b_{{\mathcal R}(A)}\|_{2}^{2}. \end{array} $$

(4.12)

Then, using inequalities (4.9) and (4.12), for any nonnegative integer k, we can get

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|x_{k}-x_{\star}\|_{2}^{2} &=&{\mathbb{E}}\|x_{k_{p}+k_{q}}-x_{\star}\|_{2}^{2} \\ & \leq& \alpha{\mathbb{E}}\|x_{k_{p}+k_{q}-1}-x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} {\mathbb{E}}\|b_{{\mathcal R}(A)^{\perp}}\\&&-z_{k_{p}+k_{q}-1}\|_{2}^{2} \\ & \leq& \alpha^{k_{q}}{\mathbb{E}}\|x_{k_{p}}-x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})\|A\|_{F}^{2}} \frac{\tau_{\max}}{\tau_{\min}} \sum\limits_{l=0}^{k_{q}-1}\alpha^{l} {\mathbb{E}}\|b_{{\mathcal R}(A)^{\perp}}\\&&-z_{k_{p}+k_{q}-l-1}\|_{2}^{2} \\ & \leq& \alpha^{k_{q}}{\mathbb{E}}\|x_{k_{p}}-x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})} \frac{\tau_{\max}}{\tau_{\min}} \frac{\beta^{k_{p}}\|b_{{\mathcal R}(A)}\|_{2}^{2}}{\|A\|_{F}^{2}} \sum\limits_{l=0}^{k_{q}-1}\alpha^{l}. \end{array} $$

As a result, it follows from inequality (4.11) and $b_{{\mathcal R}(A)}=Ax_{\star }$ that

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}\|x_{k}-x_{\star}\|_{2}^{2} & \leq& \alpha^{k_{q}}\left( \alpha^{k_{p}}\|x_{\star}\|_{2}^{2} +\frac{2}{(1-{\Delta})(1-\alpha)} \frac{\tau_{\max}}{\tau_{\min}} \frac{\|b_{{\mathcal R}(A)}\|_{2}^{2}}{\|A\|_{F}^{2}}\right) \\&&+\beta^{k_{p}}\frac{2}{(1-{\Delta})(1-\alpha)} \frac{\tau_{\max}}{\tau_{\min}} \frac{\|b_{{\mathcal R}(A)}\|_{2}^{2}}{\|A\|_{F}^{2}} \\ & = &\alpha^{k}\|x_{\star}\|_{2}^{2} +(\alpha^{k_{q}}+\beta^{k_{p}}) \frac{2}{(1-{\Delta})(1-\alpha)} \frac{\tau_{\max}}{\tau_{\min}} \frac{\|b_{{\mathcal R}(A)}\|_{2}^{2}}{\|A\|_{F}^{2}} \\ & \leq& \alpha^{k}\|x_{\star}\|_{2}^{2} +(\alpha^{k_{q}}+\beta^{k_{p}}) \frac{2}{(1-{\Delta})(1-\alpha)} \frac{\tau_{\max}}{\tau_{\min}} \frac{\lambda_{\max}(A^{*}A)}{\|A\|_{F}^{2}} \|x_{\star}\|_{2}^{2} \\ & \leq& (\max\{\alpha, \beta\})^{k_{p}} \left( 1+\frac{4}{(1-{\Delta})(1-\alpha)} \frac{\tau_{\max}}{\tau_{\min}} \frac{\lambda_{\max}(A^{*}A)}{\|A\|_{F}^{2}}\right) \|x_{\star}\|_{2}^{2}, \end{array} $$

which is just the estimate in (4.1). □

From (1.2) and (4.1), we know that the convergence rates for the mean squared errors of the REK2 method and the TREK method are bounded by

$$ \begin{array}{@{}rcl@{}} 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \quad\text{and}\quad (\max\{\alpha, \beta\})^{\frac{1}{2}}, \end{array} $$

respectively. Since it holds that

$$ \begin{array}{@{}rcl@{}} \max\{\alpha, \beta\}< \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right)^{2}, \end{array} $$

the upper bound for the convergence rate of the TREK method is smaller than that of the REK2 method.

Actually, Step 5 of the TREK method is mathematically equivalent to

$$ \begin{array}{@{}rcl@{}} x_{k+1}=x_{k}+(A_{\tau_{k}})^{\dag}(b_{\tau_{k}}-(z_{k})_{\tau_{k}}-A_{\tau_{k}}x_{k}), \end{array} $$

(4.13)

and Step 9 of the TREK method is mathematically equivalent to

$$ \begin{array}{@{}rcl@{}} z_{k+1}=z_{k}-A_{\omega_{k}}(A_{\omega_{k}})^{\dag} z_{k}, \end{array} $$

(4.14)

where $A_{\tau _{k}}$, $b_{\tau _{k}}$, $(z_{k})_{\tau _{k}}$ and $A_{\omega _{k}}$ are defined as in (3.1) and (3.5).

When $A^{(i_{k_1})}$ is parallel to $A^{(i_{k_2})}$, that is $A^{(i_{k_2})}=cA^{(i_{k_1})}$ with $c\in {\mathbb {C}}$ being a constant, the iteration (4.13) is equivalent to

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!x_{k+1}=x_{k}+\left( \frac{b^{(i_{k_1})}-z_k^{(i_{k_1})}+\bar{c}(b^{(i_{k_2})}-z_k^{(i_{k_2})})}{\|A^{(i_{k_1})}\|_{2}^{2}+\|A^{(i_{k_2})}\|_{2}^{2}} -\frac{A^{(i_{k_1})} x_{k}}{\|A^{(i_{k_1})}\|_{2}^{2}}\right)(A^{(i_{k_1})})^{*}, \end{array} $$

(4.15)

which can be used to replace Step 5 of the TREK method; when $A_{(j_{k_1})}$ is parallel to $A_{(j_{k_2})}$, the iteration (4.14) is equivalent to

$$ \begin{array}{@{}rcl@{}} z_{k+1}=z_{k}-\frac{A_{(j_{k_1})}^{*}z_{k}}{\|A_{(j_{k_1})}\|_{2}^{2}} A_{(j_{k_1})}, \end{array} $$

(4.16)

which can be used to replace Step 9 of the TREK method.

We can also extend the TREK method by changing $A_{\tau _{k}}$ and $A_{\omega _{k}}$ in the iterations (4.13) and (4.14) to the submatrices of A, which consist of arbitrary number of rows and columns of A selected randomly from the matrix A but not from the row and column pavings of A. This will be a valuable topic to be discussed in the future.

5 Experimental results

In this section, we implement the TREK method and the REK2 method (each iteration of which consists of two REK iterations), and show that the former can outperform the latter in terms of both the number of iteration steps (denoted as “IT”) and the computing time in seconds (denoted as “CPU”). Here, the IT and CPU mean the medians of the required numbers of iteration steps and the elapsed computing times with respect to 30 times of repeated runs of the corresponding method. In the TREK method, when $A^{(i_{k_1})}$ is parallel to $A^{(i_{k_2})}$, i.e., |μ_k| = 1, we use the iteration (4.15) instead of Step 5; and when $A_{(j_{k_1})}$ is parallel to $A_{(j_{k_2})}$, i.e., |ν_k| = 1, we use the iteration (4.16) instead of Step 9. For the least-squares problem (1.1) with full column-rank coefficient matrix A, we also implement the RCD method [18], and show that, in this case, the TREK method can also outperform the RCD method in terms of both the iteration count and the CPU time.

All computations of the TREK and REK2 methods are started from the initial vectors x₀ = 0 and z₀ = b. In accordance with the stopping criterion in [27], for solving the least-squares problem (1.1) iteratively, we check for convergence every $4\min \limits (m, n)$ iterations, and terminate the computation once

$$ \begin{array}{@{}rcl@{}} \frac{\|b-z_{k}-Ax_{k}\|_{2}}{\|A\|_{F}\|x_{k}\|_{2}}\leq 10^{-5} \quad\text{and}\quad \frac{\|A^{*}z_{k}\|_{2}}{\|A\|_{F}^{2}\|x_{k}\|_{2}}\leq 10^{-5}. \end{array} $$

For the RCD method, the computations are started from the initial vector x₀ = 0, and we check for convergence every $4\min \limits (m, n)$ iterations, and terminate the computation once

$$ \begin{array}{@{}rcl@{}} \frac{\|A^{*}(b-Ax_{k})\|_{2}}{\|A^{*}b\|_{2}}\leq \varepsilon, \end{array} $$

where ε is chosen to ensure that the relative solution error of the RCD method, which is defined as

$$ \begin{array}{@{}rcl@{}} \text{RSE}=\frac{\|x_{\text{IT}}-x_{\star}\|_{2}^{2}}{\|x_{\star}\|_{2}^{2}} \end{array} $$

with x_IT representing the average of the approximate solution vectors obtained from 30 times of repeated runs of the corresponding method, is of the same order of magnitude as those of the TREK and REK2 methods. In addition, all experiments are carried out using MATLAB (version R2020a) on a personal computer with 2.4 GHz central processing unit (Intel Core i9), 64.00 GB memory, and macOS Catalina operating system (version 10.15.4).

Example 5.1

We solve the least-squares problem (1.1) with the entries of the coefficient matrix $A\in {\mathbb {R}}^{m\times n}$ being the independent identically distributed uniform random variables in the interval (t,1), and the right-hand side vector being b = Ax_∗ + r, where one of the solutions $x_{*}\in {\mathbb {R}}^{n}$ of the least-squares problem (1.1) is generated randomly with the MATLAB function randn, and $r\in {\mathbb {R}}^{m}$ is a nonzero vector in the null space of A^T generated by the MATLAB function null. To guarantee the existence of the nonzero vector r, when m > n, the matrix $A\in {\mathbb {R}}^{m\times n}$ is generated by the MATLAB function rand; while when m ≤ n, the first m − 1 rows of A are generated by the MATLAB function rand and the m-th row of A is the average of the first and second rows of A. Thus, when m > n, the rank of A is n; and when m ≤ n, the rank of A is m − 1.

For solving the least-squares problems in Example 5.1, we list the numbers of iteration steps and the computing times for the REK2 and TREK methods in Tables 1, 2, 3, 4, 5, 6. For the least-squares problems with full column-rank coefficient matrix A, we also list the numbers of iteration steps and the computing times for the RCD method in Tables 1, 3 and 5. Besides, in Tables 1–6, we report the relative solution errors of each method and the Euclidean condition number (i.e., cond(A)) of the matrix A.

Table 1 IT, CPU and RSE of REK2, RCD and TREK for m-by-n matrices A with t = 0.1, n = 500 and different m

Table 2 IT, CPU and RSE of REK2 and TREK for m-by-n matrices A with t = 0.1, m = 500 and different n

Table 3 IT, CPU and RSE of REK2, RCD and TREK for m-by-n matrices A with t = 0.5, n = 500 and different m

Table 4 IT, CPU and RSE of REK2 and TREK for m-by-n matrices A with t = 0.5, m = 500 and different n

Table 5 IT, CPU and RSE of REK2, RCD and TREK for m-by-n matrices A with t = 0.9, n = 500 and different m

Table 6 IT, CPU and RSE of REK2 and TREK for m-by-n matrices A with t = 0.9, m = 500 and different n

From these tables, we see that the TREK method outperforms the REK2 method in terms of both iteration counts and CPU times. This advantage is more obvious with larger t, i.e., with the stronger correlation between the rows and the stronger correlation between the columns of the matrix A. Although when t = 0.1 and the matrix A is of full column rank, the TREK method costs slightly more computing time than the RCD method, for the cases when t = 0.5 and t = 0.9, and the matrix A is of full column rank, the TREK method vastly outperforms the RCD method in terms of both iteration counts and CPU times.

When m ≤ n, the condition number of A is infinity since A is rank deficient. When m > n, we can find that, for fixed t and n = 500, the condition number of A is decreasing with respect to the increase of m. Besides, when m > n and the size of A is fixed, the condition number of A is increasing with respect to the increase of t. Thus, in this case, the advantage of the TREK method over the REK2 and RCD methods with respect to the iteration count and the CPU time is also more obvious with larger condition number of A.

The RSEs in these tables show that the REK2, RCD and TREK methods can all converge to the least-norm solution x_⋆ of the least-squares problem (1.1). Besides, we can also find that the RSE of the TREK method is always smaller than that of the REK2 method, that is, the approximate solution obtained by the TREK method is always closer to the exact solution x_⋆ than that obtained by the REK2 method.

In Figs. 1 and 2, we depict the curves of the iteration step in base-10 logarithm and the CPU time in base-10 logarithm of the REK2 and TREK methods versus the number of rows or columns of the matrix A. From these figures, we can also see that the number of iteration steps and the computing time of the TREK method are much less than those of the REK2 method. In addition, for both of the REK2 and TREK methods, when t is fixed and n = 500, the number of iteration steps is decreasing with respect to the increase of m for 1000 ≤ m ≤ 5000, and the CPU time is increasing with respect to the increase of m for 2000 ≤ m ≤ 5000; when t is fixed and m = 500, the number of iteration steps is decreasing with respect to the increase of n for 1000 ≤ n ≤ 5000, and the CPU time is increasing with respect to the increase of n for 2000 ≤ n ≤ 5000. The performance of the REK2 method is much sensitive to the change of t while that of the TREK method is not. When t becomes larger, the number of iteration steps and the CPU time of the REK2 method increase rapidly, while those of the TREK method do not change very much and even decrease.

Fig. 1

Pictures of $\log _{10}$(IT) (left) and $\log _{10}$(CPU) (right) versus m for REK2 and TREK when n = 500. REK2 for t = 0.1: “−∘−”, REK2 for t = 0.5: “− ⊳ −”, REK2 for t = 0.9: “−∗−”, TREK for t = 0.1: “—”, TREK for t = 0.5: “−⋅−” and TREK for t = 0.9: “⋅⋅⋅”

Fig. 2

Pictures of $\log _{10}$(IT) (left) and $\log _{10}$(CPU) (right) versus n for REK2 and TREK when m = 500. REK2 for t = 0.1: “−∘−”, REK2 for t = 0.5: “− ⊳ −”, REK2 for t = 0.9: “−∗−”, TREK for t = 0.1: “—”, TREK for t = 0.5: “−⋅−” and TREK for t = 0.9: “⋅⋅⋅”

Example 5.2

We solve the least-squares problem (1.1) with the entries of the rank-deficient coefficient matrix $A\in {\mathbb {R}}^{m\times n}$ being in the interval (0.5,1), and the right-hand side vector being b = Ax_∗ + r, where one of the solutions $x_{*}\in {\mathbb {R}}^{n}$ of the least-squares problem (1.1) is generated randomly with the MATLAB function randn, and $r\in {\mathbb {R}}^{m}$ is a nonzero vector in the null space of A^T generated by the MATLAB function null. The rank of the matrix A, i.e., rank(A), is 250, 300, 350, 400 or 450. When m = 5000 and n = 500, the first rank(A) columns of A are generated by the MATLAB function rand, the (rank(A) + j)-th column of A, j = 1,2,…, n − 1 −rank(A), is the average of the j-th and (j + 1)-th columns of A, and the n-th column of A is the average of the first and (n −rank(A))-th columns of A; when m = 500 and n = 5000, the first rank(A) rows of A are generated by the MATLAB function rand, the (rank(A) + i)-th row of A, i = 1,2,…, m − 1 −rank(A), is the average of the i-th and (i + 1)-th rows of A, and the m-th row of A is the average of the first and (m −rank(A))-th rows of A.

For solving the least-squares problems in Example 5.2, we list the numbers of iteration steps, the computing times and the relative solution errors for the REK2 and TREK methods in Tables 7–8. From these two tables, we see that the TREK method outperforms the REK2 method in terms of both iteration counts and CPU times. Besides, whether m = 5000, n = 500 or m = 500, n = 5000, the numbers of iteration steps and the computing times of the REK2 and TREK methods are increasing with respect to the increase of the rank of the matrix A. Moreover, the RSE of the TREK method is always smaller than that of the REK2 method.

Table 7 IT, CPU and RSE of REK2 and TREK for m-by-n matrices A with m = 5000 and n = 500

Table 8 IT, CPU and RSE of REK2 and TREK for m-by-n matrices A with m = 500 and n = 5000

Example 5.3

We solve the X-ray CT problem generated by a MATLAB package AIR Tools II [15]. The full column-rank sparse coefficient matrix A of the least-squares problem (1.1) is obtained from the discretization schemes of the line integrals along the straight X-rays of the attenuation coefficient of the object which the X-rays penetrate. The object domain is the square [− 30,30] × [− 30,30]. The source is placed infinitely far from a flat detector with equal spacing between the 90 pixels and each detector pixel being hit by a single X-ray. These rays are parallel and the distance between the first and the last ray is 89. Moreover, the source-detector pair is rotated around the object, and measurements are recorded for angles 0:0.5:179.5. The Euclidean condition number of A is 520.66. The right-hand side vector is b = Ax_⋆ + r, where the unique solution x_⋆ of the least-squares problem (1.1) is obtained by reshaping the 60 × 60 image of the well-known Shepp-Logan medical phantom, and r is a nonzero vector in the null space of A^T generated by the MATLAB function null.

For solving the least-squares problem in Example 5.3, we list the numbers of iteration steps, the computing times and the relative solution errors for the REK2, RCD and TREK methods in Table 9. From this table, we can also see that the TREK method outperforms the REK2 method in terms of both iteration count and CPU time. Besides, the RSE of the TREK method is smaller than that of the REK2 method. Although the RCD method needs the largest number of iteration steps, it costs the least computing time.

In Fig. 3, we give the 60 × 60 images of the exact Shepp-Logan medical phantom and the approximate solutions obtained by the REK2, RCD and TREK methods. From this figure, we can find that, inside of the ellipse, there exist relatively obvious mesh lines in the image of the approximate solution obtained by the REK2 method, while the images of the approximate solutions obtained by the TREK and RCD methods are smoother and closer to the exact phantom.

Fig. 3

Pictures of the exact Shepp-Logan medical phantom, and the approximate solutions obtained by REK2, RCD and TREK a exact phantom b REK2 c RCD d TREK

Table 9 IT, CPU and RSE of REK2, RCD and TREK for m-by-n matrix A with m = 32400 and n = 3600

Example 5.4

We solve the test problem in the MATLAB package AIR Tools II [15] which simulates the geophysical problem where one records the travel time of seismic waves between sub-surface sources and detectors located either at or below the surface. The goal is to determine the sub-surface attenuation in the square domain of size [0,12] × [0,12]. There are 12 equally spaced sources located at the right side of the domain and 480 receivers equally spaced on the top (the surface) and the left side of the domain. The wave between the source and the receiver is assumed to travel within the first Fresnel zone shaped as an ellipse with focal points at the source and the receiver. The dominating frequency of the propagating wave is 4.5. The recorded travel time is modeled as an integral of the attenuation coefficient over the Fresnel zone. The full column-rank sparse coefficient matrix A of the least-squares problem (1.1) is obtained from the discretization schemes of these integrals, and the Euclidean condition number of A is 11104.91. The right-hand side vector is b = Ax_⋆ + r, where the unique solution x_⋆ of the least-squares problem (1.1) is obtained by reshaping the 12 × 12 image of the tectonic phantom, and r is a nonzero vector in the null space of A^T generated by the MATLAB function null.

For solving the least-squares problem in Example 5.4, we list the numbers of iteration steps, the computing times and the relative solution errors for the REK2, RCD and TREK methods in Table 10. From this table, we can see that the TREK method outperforms the REK2 and RCD methods in terms of both iteration count and CPU time, and the RSE of the TREK method is smaller than those of the REK2 and RCD methods. In Fig. 4, we give the 12 × 12 images of the exact tectonic phantom, and the approximate solutions obtained by the REK2, RCD and TREK methods. From this figure, we can see that the REK2, RCD and TREK methods can all converge to the exact solution successfully.

Fig. 4

Pictures of the exact tectonic phantom, and the approximate solutions obtained by REK2, RCD and TREK a exact phantom b REK2 c RCD d TREK

Table 10 IT, CPU and RSE of REK2, RCD and TREK for m-by-n matrix A with m = 5760 and n = 144

Example 5.5

We solve the least-squares problem (1.1) with the coefficient matrix $A\in {\mathbb {R}}^{m\times n}$ chosen from the SuiteSparse Matrix Collection [11] and originating from combinatorial problem and linear programming, and the right-hand side vector being b = Ax_∗ + r, where one of the solutions $x_{*}\in {\mathbb {R}}^{n}$ of the least-squares problem (1.1) is generated randomly with the MATLAB function randn, and $r\in {\mathbb {R}}^{m}$ is a nonzero vector in the null space of A^T. Since the matrix A is too large, the vector r is not generated by the MATLAB function null, but is generated by projecting the vector $\tilde {r}\in {\mathbb {R}}^{m}$, which is generated randomly with the MATLAB function randn, onto the null space of A^T. That is, $r=\tilde {r}-AA^{\dag }\tilde {r}$, where $A^{\dag }\tilde {r}$ is generated by the MATLAB function lsqminnorm.

For solving the least-squares problems in Example 5.5, we list the numbers of iteration steps, the computing times and the relative solution errors for the REK2 and TREK methods in Table 11. The density, which is defined as

$$ \begin{array}{@{}rcl@{}} \text{density} =\frac{\text{number of nonzeros of an \textit{m}-by-\textit{n} matrix}} {m n}, \end{array} $$

Table 11 IT, CPU and RSE of REK2 and TREK for m-by-n matrices A with different m and n

rank (i.e., rank(A)), and Euclidean condition number (i.e., cond(A)) of the tested matrices are also reported in this table. From this table, we can see that for the matrices GL7d13 and relat8, the TREK method outperforms the REK2 method in terms of both iteration counts and CPU times. For the matrix lp_nug30, the numbers of iteration steps of the REK2 and TREK methods are the same, thus the computing time of the TREK method is slightly more than that of the REK2 method. Besides, for all the three tested matrices, the RSEs of the REK2 and TREK methods are of the same order of magnitude.

6 Concluding remarks

For solving large linear least-squares problems, we construct a new block REK method, called the TREK method, without the use of row and column pavings of the coefficient matrix. Both theoretical analysis and numerical results show that the TREK method outperforms the REK method. For solving the least-squares problem with full column-rank coefficient matrix, the TREK method can also outperform the RCD method.

If the linear system is consistent, by removing one of the iteration sequences in the TREK method, we construct the GTRK method, and it is actually a generalization of the TRK method without the assumptions of unit row norms and full column rank on the coefficient matrix. We give the upper bound for the convergence rate of the GTRK method, and when the coefficient matrix is of full column rank and the Euclidean norms of its rows are all one, this upper bound for the convergence rate of the TRK method is better than the existing one.

When the angle between the two rows or the two columns used in each iteration is smaller, the TREK iteration will converge more faster than two REK iterations. However, each TREK iteration will cost 2m + 2n + 16 extra flops compared to two REK iterations. When the two rows used in each iteration are nearly orthogonal and the two columns used in each iteration are also nearly orthogonal, two REK iterations can already perform well. Therefore, we can consider to combine the TREK iteration and the REK iteration together and construct a more efficient hybrid method. This is an interesting and valuable topic to be studied in the future.

Appendix

Proof of Lemma 4.1

From the definition of the GTRK method we can obtain

$$ \begin{array}{@{}rcl@{}} x_{k+1} &=&x_{k}+ \frac{\left( b^{(i_{k_2})}-A^{(i_{k_2})} x_{k}\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*} \\&&+\left( \frac{b^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}}-\bar{\mu}_{k}\frac{b^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}} -u_{k}^{*} x_{k}\right) \frac{u_{k}}{\|u_{k}\|_{2}^{2}}, \end{array} $$

where u_k is defined as in (3.3) with $\|u_{k}\|_{2}^{2}=1-|\mu _{k}|^{2}$. Since the linear system Ax = b is assumed to be consistent, it holds that b = Ax_⋆, then we have

$$ \begin{array}{@{}rcl@{}} x_{k} - x_{\star}+ \frac{\left( b^{(i_{k_2})}-A^{(i_{k_2})} x_{k}\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*} &=&x_{k} - x_{\star}+ \frac{\left( A^{(i_{k_2})} x_{\star} - A^{(i_{k_2})} x_{k}\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*} \\ &=&\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}} {\|A^{(i_{k_2})}\|_{2}^{2}}\right)(x_{k}-x_{\star}) \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \frac{b^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}} - \bar{\mu}_{k}\frac{b^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}} - u_{k}^{*} x_{k} = \frac{A^{(i_{k_1})} x_{\star}}{\|A^{(i_{k_1})}\|_{2}} - \bar{\mu}_{k}\frac{A^{(i_{k_2})} x_{\star}}{\|A^{(i_{k_2})}\|_{2}} -u_{k}^{*} x_{k} =u_{k}^{*}(x_{\star}-x_{k}). \end{array} $$

Therefore, it holds that

$$ \begin{array}{@{}rcl@{}} x_{k+1}-x_{\star} =\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}} -\frac{u_{k}u_{k}^{*}}{\|u_{k}\|_{2}^{2}}\right)(x_{k}-x_{\star}). \end{array} $$

(A.1)

We denote $\check {y}_{k}$ and $\check {x}_{k+1}$ as the vectors obtained by utilizing one RK iteration on x_k and $\check {y}_{k}$ with the working rows $A^{(i_{k_1})}$ and $A^{(i_{k_2})}$ for the consistent linear system Ax = b, respectively. That is,

$$ \check{y}_{k} = x_{k} +\frac{\left( b^{(i_{k_1})}-A^{(i_{k_1})} x_{k}\right)} {\|A^{(i_{k_1})}\|_{2}^{2}} (A^{(i_{k_1})})^{*} $$

and

$$ \check{x}_{k+1} =\check{y}_{k} + \frac{\left( b^{(i_{k_2})}-A^{(i_{k_2})} \check{y}_{k}\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*}. $$

Then, it follows from b = Ax_⋆ that

$$ \begin{array}{@{}rcl@{}} \check{x}_{k+1}-x_{\star} &=&\check{y}_{k}-x_{\star}+ \frac{\left( A^{(i_{k_2})} x_{\star}-A^{(i_{k_2})} \check{y}_{k}\right)} {\|A^{(i_{k_2})}\|_{2}^{2}} (A^{(i_{k_2})})^{*}\\ &=&\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}}\right) (\check{y}_{k}-x_{\star}) \\ & =&\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}}\right) \left( x_{k}-x_{\star} +\frac{\left( A^{(i_{k_1})} x_{\star}-A^{(i_{k_1})} x_{k}\right)} {\|A^{(i_{k_1})}\|_{2}^{2}} (A^{(i_{k_1})})^{*}\right) \\ & =&\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}}\right) \left( I_{n}-\frac{(A^{(i_{k_1})})^{*}A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}^{2}}\right) (x_{k}-x_{\star}). \end{array} $$

(A.2)

From the definition of u_k we have

$$ \begin{array}{@{}rcl@{}} \check{x}_{k+1} - x_{\star} \!& =&\!\left( \!I_{n} - \frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}} - \left( I_{n} - \frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}}\right) \frac{(A^{(i_{k_1})})^{*}A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}^{2}}\!\right) (x_{k} - x_{\star}) \\ \!& =&\!\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}}- \frac{u_{k}A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}}\right) (x_{k}-x_{\star}) \\ \!& =&\!\left( I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}}- \frac{u_{k} u_{k}^{*}}{\|u_{k}\|_{2}^{2}}\right)(x_{k}-x_{\star}) \\&&\!+\left( \frac{u_{k} u_{k}^{*}}{\|u_{k}\|_{2}^{2}}- \frac{u_{k}A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}}\right)(x_{k}-x_{\star}). \end{array} $$

From the orthogonality of the vectors $A^{(i_{k_2})}$ and u_k that

$$ \begin{array}{@{}rcl@{}} A^{(i_{k_2})} u_{k} =A^{(i_{k_2})}\left( \frac{(A^{(i_{k_1})})^{*}}{\|A^{(i_{k_1})}\|_{2}} -\mu_{k}\frac{(A^{(i_{k_2})})^{*}}{\|A^{(i_{k_2})}\|_{2}}\right) =0, \end{array} $$

we have

$$ \begin{array}{@{}rcl@{}} &&\!\!\|\check{x}_{k+1}-x_{\star}\|_{2}^{2} \\ \!\! & =& \!\!\left\|\!\left( \!I_{n} - \frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}} - \frac{u_{k} u_{k}^{*}}{\|u_{k}\|_{2}^{2}}\right)\!(x_{k}\! -\! x_{\star})\right\|_{2}^{2} \! +\! \left\|\!\left( \frac{u_{k} u_{k}^{*}}{\|u_{k}\|_{2}^{2}}\! -\! \frac{u_{k}A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}}\right)\! (x_{k}\! -\! x_{\star})\right\|_{2}^{2}. \end{array} $$

Then, it follows from (A.1) that

$$ \begin{array}{@{}rcl@{}} \|x_{k+1}-x_{\star}\|_{2}^{2} =\|\check{x}_{k+1}-x_{\star}\|_{2}^{2} -\left|\frac{A^{(i_{k_1})} (x_{k}-x_{\star})}{\|A^{(i_{k_1})}\|_{2}} -\frac{u_{k}^{*}(x_{k}-x_{\star})}{\|u_{k}\|_{2}^{2}} \right|^{2}\|u_{k}\|_{2}^{2}. \end{array} $$

By taking the conditional expectation on both sides of this equality, we can obtain

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|x_{k+1}-x_{\star}\|_{2}^{2} &=&{\mathbb{E}}_{k}\|\check{x}_{k+1}-x_{\star}\|_{2}^{2} \\&&-{\mathbb{E}}_{k}\left|\frac{A^{(i_{k_1})} (x_{k}-x_{\star})}{\|A^{(i_{k_1})}\|_{2}} -\frac{u_{k}^{*}(x_{k}-x_{\star})}{\|u_{k}\|_{2}^{2}}\right|^{2}\|u_{k}\|_{2}^{2}. \end{array} $$

(A.3)

Next, we give the estimates for the first and second parts of the right-hand side of the equality (A.3) respectively. Denote the two orthogonal projection matrices as

$$ \begin{array}{@{}rcl@{}} Q_{i_{k_{1}}}=I_{n}-\frac{(A^{(i_{k_1})})^{*}A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}^{2}} \quad\text{and}\quad Q_{i_{k_{2}}}=I_{n}-\frac{(A^{(i_{k_2})})^{*}A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}^{2}}, \end{array} $$

then from equality (A.2) we have

$$ \begin{array}{@{}rcl@{}} &&{\mathbb{E}}_{k}\|\check{x}_{k+1}-x_{\star}\|_{2}^{2} \\& =&\sum\limits_{i_{k_{1}}=1}^{m}\frac{\|A^{(i_{k_1})}\|_{2}^{2}}{\|A\|_{F}^{2}} \underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \frac{\|A^{(i_{k_2})}\|_{2}^{2}}{\|A\|_{F}^{2}-\|A^{(i_{k_1})}\|_{2}^{2}} (x_{k}-x_{\star})^{*} Q_{i_{k_{1}}}Q_{i_{k_{2}}}Q_{i_{k_{1}}} (x_{k}-x_{\star}) \\ & =& \sum\limits_{i_{k_{1}}=1}^{m}\frac{\|A^{(i_{k_1})}\|_{2}^{2}}{\|A\|_{F}^{2}} (x_{k}-x_{\star})^{*}Q_{i_{k_{1}}} \left( I_{n}-\frac{A^{*}A-(A^{(i_{k_1})})^{*}A^{(i_{k_1})}}{\|A\|_{F}^{2}-\|A^{(i_{k_1})}\|_{2}^{2}}\right)Q_{i_{k_{1}}} (x_{k}-x_{\star}) \\ & =& \sum\limits_{i_{k_{1}}=1}^{m}\frac{\|A^{(i_{k_1})}\|_{2}^{2}}{\|A\|_{F}^{2}} (x_{k}-x_{\star})^{*}Q_{i_{k_{1}}} \left( I_{n}-\frac{A^{*}A}{\|A\|_{F}^{2}-\|A^{(i_{k_1})}\|_{2}^{2}}\right) Q_{i_{k_{1}}}(x_{k}-x_{\star}). \end{array} $$

Since $x_{k}-x_{\star }\in {\mathcal R}(A^{*})$ and $Q_{i_{k_{1}}}(x_{k}-x_{\star })\in {\mathcal R}(A^{*})$, it holds that

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|\check{x}_{k+1}-x_{\star}\|_{2}^{2} & \leq& \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tau_{\max}}\right) \sum\limits_{i_{k_{1}}=1}^{m}\frac{\|A^{(i_{k_1})}\|_{2}^{2}}{\|A\|_{F}^{2}} (x_{k}-x_{\star})^{*}Q_{i_{k_{1}}}(x_{k}-x_{\star}) \\ & =& \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tau_{\max}}\right) (x_{k}-x_{\star})^{*} \left( I_{n}-\frac{A^{*} A}{\|A\|_{F}^{2}}\right) (x_{k}-x_{\star}) \\ & \leq& \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tau_{\max}}\right) \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\|A\|_{F}^{2}}\right)\|x_{k}-x_{\star}\|_{2}^{2}. \end{array} $$

(A.4)

From the definition of u_k and $\|u_{k}\|_{2}^{2}=1-|\mu _{k}|^{2}$, we have

$$ \begin{array}{@{}rcl@{}} && {\mathbb{E}}_{k}\left|\frac{A^{(i_{k_1})} (x_{k}-x_{\star})}{\|A^{(i_{k_1})}\|_{2}} -\frac{u_{k}^{*}(x_{k}-x_{\star})}{\|u_{k}\|_{2}^{2}}\right|^{2}\|u_{k}\|_{2}^{2}\\ & =& {\mathbb{E}}_{k}\left|\|u_{k}\|_{2}\frac{A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}}(x_{k}-x_{\star}) -\frac{1}{\|u_{k}\|_{2}}\left( \frac{A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}} -\bar{\mu}_{k}\frac{A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}}\right)(x_{k}-x_{\star}) \right|^{2} \\ & =& \sum\limits_{i_{k_{1}}=1}^{m}\frac{\|A^{(i_{k_1})}\|_{2}^{2}}{\|A\|_{F}^{2}} \underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \frac{\|A^{(i_{k_2})}\|_{2}^{2}}{\|A\|_{F}^{2}-\|A^{(i_{k_1})}\|_{2}^{2}} \left|\frac{|\mu_{k}|^{2}}{\|u_{k}\|_{2}}\frac{A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}}(x_{k}-x_{\star}) \right.\\&&\left.-\frac{\bar{\mu}_{k}}{\|u_{k}\|_{2}}\frac{A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}}(x_{k}-x_{\star}) \right|^{2} \\ & \geq& \sum\limits_{i_{k_{1}}=1}^{m} \underset{i_{k_{2}}\neq i_{k_{1}}}{\sum\limits_{i_{k_{2}}=1}^{m}} \frac{\|A^{(i_{k_1})}\|_{2}^{2}\|A^{(i_{k_2})}\|_{2}^{2}} {\|A\|_{F}^{2} \tau_{\max}} \left|\frac{|\mu_{k}|^{2}}{\|u_{k}\|_{2}}\frac{A^{(i_{k_1})}}{\|A^{(i_{k_1})}\|_{2}}(x_{k}-x_{\star}) \right.\\&&\left.-\frac{\bar{\mu}_{k}}{\|u_{k}\|_{2}}\frac{A^{(i_{k_2})}}{\|A^{(i_{k_2})}\|_{2}}(x_{k}-x_{\star}) \right|^{2}. \end{array} $$

Then, with the notations

$$ \begin{array}{@{}rcl@{}} \theta_{p,q} =\frac{\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}} {\sqrt{1-\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}}} \quad\text{and}\quad \eta_{p,q} =\frac{\frac{A^{(p)}(A^{(q)})^{*}}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}}} {\sqrt{1-\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}}} \end{array} $$

for p, q ∈{1, 2,…, m} and p≠q, we can obtain

$$ \begin{array}{@{}rcl@{}} && {\mathbb{E}}_{k}\left|\frac{A^{(i_{k_1})} (x_{k}-x_{\star})}{\|A^{(i_{k_1})}\|_{2}} -\frac{u_{k}^{*}(x_{k}-x_{\star})}{\|u_{k}\|_{2}^{2}}\right|^{2}\|u_{k}\|_{2}^{2} \\ & \geq& \frac{1}{\|A\|_{F}^{2} \tau_{\max}} \sum\limits_{p<q}\|A^{(p)}\|_{2}^{2}\|A^{(q)}\|_{2}^{2} \left( \left|\theta_{p,q}\frac{A^{(p)}}{\|A^{(p)}\|_{2}}(x_{k}-x_{\star}) \right.\right.\\&&\left.-\eta_{p,q}\frac{A^{(q)}}{\|A^{(q)}\|_{2}}(x_{k}-x_{\star})\right|^{2} \\ &&+\left.\left|\theta_{p,q}\frac{A^{(q)}}{\|A^{(q)}\|_{2}}(x_{k}-x_{\star}) -\bar{\eta}_{p,q}\frac{A^{(p)}}{\|A^{(p)}\|_{2}}(x_{k}-x_{\star})\right|^{2}\right). \end{array} $$

Since for any $\theta , \eta , \phi , \psi \in {\mathbb {C}}$, it holds that

$$ \begin{array}{@{}rcl@{}} |\theta \phi-\eta \psi|^{2}+|\theta \psi-\bar{\eta} \phi|^{2} \geq (|\eta|-|\theta|)^{2}(|\phi|^{2}+|\psi|^{2}), \end{array} $$

we have

$$ \begin{array}{@{}rcl@{}} && {\mathbb{E}}_{k}\left|\frac{A^{(i_{k_1})} (x_{k}-x_{\star})}{\|A^{(i_{k_1})}\|_{2}} -\frac{u_{k}^{*}(x_{k}-x_{\star})}{\|u_{k}\|_{2}^{2}}\right|^{2}\|u_{k}\|_{2}^{2} \\ & \geq& \frac{1}{\|A\|_{F}^{2} \tau_{\max}} \sum\limits_{p<q}\|A^{(p)}\|_{2}^{2}\|A^{(q)}\|_{2}^{2} (|\eta_{p,q}|-|\theta_{p,q}|)^{2}\\ &&\cdot\left( \left|\frac{A^{(p)}}{\|A^{(p)}\|_{2}}(x_{k}-x_{\star})\right|^{2} +\left|\frac{A^{(q)}}{\|A^{(q)}\|_{2}}(x_{k}-x_{\star})\right|^{2}\right). \end{array} $$

Then from

$$ \begin{array}{@{}rcl@{}} (|\eta_{p,q}|-|\theta_{p,q}|)^{2} &=&\left( \frac{\frac{|A^{(p)}(A^{(q)})^{*}|}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}} -\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}} {\sqrt{1-\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}}}}\right)^{2} \\&=&\frac{\frac{|A^{(q)}(A^{(p)})^{*}|^{2}}{\|A^{(q)}\|_{2}^{2}\|A^{(p)}\|_{2}^{2}} \left( 1-\frac{|A^{(q)}(A^{(p)})^{*}|}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}}\right)} {1+\frac{|A^{(q)}(A^{(p)})^{*}|}{\|A^{(q)}\|_{2}\|A^{(p)}\|_{2}}} \geq \gamma, \end{array} $$

we know that

$$ \begin{array}{@{}rcl@{}} && {\mathbb{E}}_{k}\left|\frac{A^{(i_{k_1})} (x_{k}-x_{\star})}{\|A^{(i_{k_1})}\|_{2}} -\frac{u_{k}^{*}(x_{k}-x_{\star})}{\|u_{k}\|_{2}^{2}}\right|^{2}\|u_{k}\|_{2}^{2} \\ & \geq& \frac{\gamma}{\|A\|_{F}^{2} \tau_{\max}} \sum\limits_{p<q}\left( \|A^{(q)}\|_{2}^{2}\left|A^{(p)}(x_{k}-x_{\star})\right|^{2} +\|A^{(p)}\|_{2}^{2}\left|A^{(q)}(x_{k}-x_{\star})\right|^{2}\right) \\ & =&\frac{\gamma}{\|A\|_{F}^{2} \tau_{\max}} \sum\limits_{p=1}^{m}\underset{q \neq p}{\sum\limits_{q=1}^{m}} \|A^{(q)}\|_{2}^{2}\left|A^{(p)}(x_{k}-x_{\star})\right|^{2} \\ & =&\frac{\gamma}{\|A\|_{F}^{2} \tau_{\max}} \sum\limits_{p=1}^{m}(\|A\|_{F}^{2}-\|A^{(p)}\|_{2}^{2}) \left|A^{(p)}(x_{k}-x_{\star})\right|^{2} \\ & \geq& \frac{\gamma \tau_{\min}} {\|A\|_{F}^{2} \tau_{\max}} \sum\limits_{p=1}^{m}\left|A^{(p)}(x_{k}-x_{\star})\right|^{2} =\frac{\gamma \tau_{\min}} {\|A\|_{F}^{2} \tau_{\max}} \|A(x_{k}-x_{\star})\|_{2}^{2}. \end{array} $$

It follows from $x_{k}-x_{\star }\in {\mathcal R}(A^{*})$ that

$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!{\mathbb{E}}_{k}\left|\frac{A^{(i_{k_1})} (x_{k} - x_{\star})}{\|A^{(i_{k_1})}\|_{2}} - \frac{u_{k}^{*}(x_{k}-x_{\star})}{\|u_{k}\|_{2}^{2}}\right|^{2}\|u_{k}\|_{2}^{2} \!\geq\! \frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \frac{\tau_{\min}}{\tau_{\max}} \gamma\|x_{k} - x_{\star}\|_{2}^{2} . \end{array} $$

(A.5)

Substituting (A.4) and (A.5) into (A.3), we have

$$ \begin{array}{@{}rcl@{}} {\mathbb{E}}_{k}\|x_{k+1} - x_{\star}\|_{2}^{2} &\leq& \left[ \left( 1-\frac{\lambda_{\min}(A^{*}A)} {\tau_{\max}}\right) \left( 1-\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}}\right) -\frac{\lambda_{\min}(A^{*}A)}{\|A\|_{F}^{2}} \frac{\tau_{\min}}{\tau_{\max}} \gamma \right]\\&& \cdot \|x_{k}-x_{\star}\|_{2}^{2}. \end{array} $$

Finally, taking full expectation on both sides of this inequality, we will obtain the result in Lemma 4.1 by induction on the iteration index k. □