A color image encryption and hiding algorithm based on hyperchaotic system and discrete cosine transform

Abstract

Some existing image encryption schemes based on chaotic systems have various security defects, such as non-uniform distribution of the chaotic system's phase trajectory, narrow chaotic range, and the encryption algorithm easily to be cracked, etc. To solve these problems, a new color image encryption and hiding algorithm is proposed in this paper. Firstly, a two-dimensional cross-coupled chaotic model (2D-CCCM) is designed, which can generate a variety of hyperchaotic maps. Performance analysis demonstrates that they exhibit more complex chaotic behavior and a wider range of chaotic distribution than existing chaotic systems, and all of them enter the hyper-chaotic state when the system parameters are in the range of [1, ∞). Further, based on this chaotic system, a new color image encryption algorithm is proposed. The algorithm applies the cyclic shift operation and the improved out-inside shuffling algorithm to simultaneously scramble and diffuse the R, G, and B planes of the color image. Finally, two-dimensional discrete cosine transform is employed to embed the ciphertext image into the visually meaningful carrier image to further improve the security of the encryption algorithm. The main contributions of this study are twofold: firstly, the 2D-CCCM is proposed, and the generated chaotic system overcomes the drawbacks of existing chaotic systems; secondly, simulation analysis and security evaluation demonstrate that the proposed color image encryption and hiding algorithm has better encryption performance and higher security than several advanced image encryption algorithms.

1 Introduction

With the rapid development of computer networks and wireless communication technology, large amounts of information are generated and transmitted every day. Image is one of the main carriers of information, which can be intuitively felt by human vision, so the research on image transmission has become a hot research field. Security is one of the most important performances in the process of image transmission. Because the image contains a wealth of information, only using traditional encryption algorithms such as advanced encryption standard (AES) [1] and data encryption standard (DES) [2] are no longer meet the requirements [3, 4]. With the deepening of research, many new image encryption methods have been proposed, such as the improved AES and DES [5], cellular automata [6], frequency domain transforms [7], DNA coding [8], compressed sensing [9], chaotic systems [10,11,12,13,14], and so on. Chaotic systems are widely used in image encryption communication because of their excellent ergodic properties, pseudo-randomness, and initial sensitivity [15,16,17,18,19].

The security of image encryption algorithms based on chaotic systems is related to the performance of chaotic systems. In recent years, many researchers have proposed different chaotic systems for image encryption [20,21,22,23,24,25], which can be divided into one-dimensional chaotic systems and high-dimensional chaotic systems. Generally speaking, the one-dimensional chaotic system has a simple structure, few control parameters, and a small chaotic range. Chaotic sequences generated by one-dimensional chaotic systems have low pseudo-randomness and small key space. To improve the security of encryption algorithms, many researchers have proposed different hyperchaotic systems. For example, Liu et al. [23] proposed a two-dimensional sinusoidal ICMIC mapping (2D-SIMM), and Gao et al. [26] proposed a chaotic circuit based on memristor–memcapacitor to generate a four-dimensional continuous chaotic system. These systems have improved performance compared to one-dimensional chaotic systems, but there are still issues such as low ergodicity and low complexity. Therefore, in order to further enhance the performance of chaotic systems, a new two-dimensional cross-coupled chaotic model (2D-CCCM) is proposed in this paper, which can be used to generate a variety of two-dimensional hyperchaotic systems. Various dynamic analyses show that these chaotic systems have a wider range of chaotic characteristic and a higher complexity.

The color images have R, G, and B channels, which can transmit more information than gray images, so the encryption algorithm of color images has more practical significance. The existing color image encryption algorithms are mainly divided into two types. One is to scramble and diffuse the R, G, and B planes respectively. This method ignores the internal relationship between the R, G, and B color channels, and the encryption effect is not good enough. For example, Wang et al. [27] proposed a gray image encryption algorithm based on row scrambling and zigzag transformation and extended it to color images. The other is to rearrange and combine the three planes R, G, and B into one plane, and then carry out scrambling and diffusion operations on this large plane. This method increases the number of iterations of the chaotic system and reduces the efficiency of encryption. For instance, Teng et al. [12] combined the three planes R, G, and B into a plane vertically, and then scrambled and diffused the two-dimensional pixel matrix. Different from the above two methods, in this paper, a color image encryption algorithm including cross-plane scrambling and cyclic shift diffusion is proposed. The algorithm scrambles and diffuses three color channels simultaneously, which greatly improves the encryption effect and reduces the time complexity.

Most of the existing image encryption algorithms are to encrypt the plaintext image into a chaotic pixel image, which is visually similar to the noise image [3, 28,29,30,31]. However, such ciphertext images can be seen as encrypted images at a glance, which is easy to attract the attention of attackers and increase the risk of cracking. Therefore, it is of practical significance to encrypt and hide images into visually meaningful images. Bao et al. [32] first proposed an image encryption and hiding algorithm based on discrete wavelet transform (DWT). Based on this idea, Huang et al. [9] designed an image encryption and hiding scheme based on integer wavelet transform (IWT). These algorithms can hide the ciphertext image information very well, but the size of the visually meaningful image is four times that of the ciphertext image, which requires extra transmission bandwidth and storage space. To solve this problem, we propose a novel image encryption and hiding algorithm using two-dimensional discrete cosine transform (DCT). DCT is a transformation technique widely used in digital signal processing and image compression, which can achieve the time–frequency transformation of signals. The DCT-based image hiding algorithm proposed in this article requires the same size of the carrier image as the cipher image, which improves the security of image encryption and reduces the time and space complexity.

Based on the above analysis, the main contributions of this paper can be summarized as follows:

• 1. A new two-dimensional hyperchaotic system model is proposed, which can be used to generate multiple chaotic maps with good performance. The security of image encryption algorithms based on these chaotic maps has been greatly improved.

• 2. Considering the internal relationship between the three channels of the color image, a new image encryption algorithm including cross-plane scrambling and cyclic shift diffusion is put forward. The algorithm uses the improved out-inside shuffling algorithm, which greatly improves the encryption effect and reduces the time complexity.

• 3. A new color image encryption and hiding algorithm is designed based on 2D DCT. By hiding the encrypted image in the carrier image with visual significance, the security of the encryption algorithm is further improved.

The rest of this article is organized as follows. Section 2 introduces the chaotic system model and analyzes the performance of the chaotic maps generated by this model. 2D DCT is also introduced. Section 3 introduces the proposed algorithm for image encryption and decryption. In Sect. 4, the simulation effect and safety analysis results of the algorithm are obtained. Finally, Sect. 5 draws a brief conclusion.

2 Chaotic system and 2D DCT

2.1 Definition of 2D-SICM

The nonlinearity and pseudo-randomness of chaotic systems play an important role in chaotic encryption communication. Some classical chaotic maps have poor pseudo-randomness, so there are security risks when employing this system for image encryption. To solve this problem, a new two-dimensional hyperchaotic system is proposed in this paper, and the system model is shown in Fig. 1. There are two inputs x_n and y_n and two outputs x_n+1 and y_n+1, ⊕ stands for addition, F and G are two one-dimensional chaotic maps, to improve their nonlinearity and pseudo-randomness, it is modulated by functions f and g to obtain 2D-CCCM. The 2D-CCCM can be defined by.

$$ \left\{ \begin{gathered} x_{n + 1} = F(f(y_{n} ) + g(x_{n} )) \hfill \\ y_{n + 1} = G(g(y_{n} ) + f(x_{n} )) \hfill \\ \end{gathered} \right. $$

(1)

Fig. 1

Structure diagram of 2D-CCCM

In Fig. 1, f is chosen as the Sine function, g is chosen as the Cosine function, F and G are set as Sine map and the iterative chaotic map with infinite collapse (ICMIC), Sine map and ICMIC are two one-dimensional chaotic maps, which is defined as Eqs. (2) and (3) respectively.

$$ x_{n + 1} = \alpha \sin (\pi x_{n} )/4 $$

(2)

$$ x_{n + 1} = \sin (c/x_{n} ) $$

(3)

Then a novel two-dimensional Sine-ICMIC coupling map (2D-SICM) is obtained as

$$ \left\{ {\begin{array}{*{20}l} {x_{{n + 1}} = \alpha \sin (\pi (\sin y_{n} + \cos x_{n} ))} \hfill \\ {y_{{n + 1}} = \sin \left( {\frac{\beta }{{\sin x_{n} + \cos y_{n} }}} \right)} \hfill \\ \end{array} } \right. $$

(4)

where α and β are the system parameters, when α, β ∈ [1, + ∞), the system is in a hyperchaotic state.

2.2 Performance evaluation of 2D-SICM

In order to analyze the nonlinearity, complexity, unpredictability, and other chaotic characteristics of 2D-SICM, some analytical methods such as bifurcation diagram, phase diagram, Lyapunov exponents, permutation entropy, Spectral entropy, and 0–1 test are used [33,34,35,36]. At the same time, we compare the features of the 2D-SICM with those of classical one-dimensional chaotic systems such as Logistic map, Sine map, ICMIC, and two-dimensional chaotic systems such as 2D-SIMM [23], 2D-Logistic map [37], 2D-SLMM [38], Hénon map [39], etc.

2.2.1 Phase diagram

The attractor phase diagram can directly reflect the nonlinearity and complexity of chaotic maps. When the initial values (x₀, y₀) of 2D-SICM are set to (0.2, 0.2) and the system parameters are adjusted to α = 100 and β = 100, the phase diagram is shown in Fig. 2a. Compared with the phase diagram of 2D-SLMM, 2D-Logistic map, and Hénon map, whose parameters are adjusted to the best, the phase diagram of 2D-SICM are more evenly distributed and extensive. Therefore, 2D-SICM has more complex dynamic behavior and wider chaotic distribution.

Fig. 2

Attractor phase diagram. a The proposed 2D-SICM with α = 100, β = 100; b 2D-SLMM with α = 1, β = 3; c 2D-Logistic map with r = 1.19; d Hénon map with α = 1.4, β = 0.3

2.2.2 Bifurcation diagram

The bifurcation diagram reflects the motion state of the chaotic system changes with the system parameters. Therefore, the bifurcation diagram can be used to analyze the dynamical behaviors of the chaotic system [40,41,42,43]. The bifurcation diagram of 2D-SICM is shown in Fig. 3, where (a) is the bifurcation diagram of x varying with system parameters α and β, the variation range of α and β is (10, 30), and (b) is the bifurcation diagram of y varying with system parameters α and β, the variation range of α and β is (0, 100). It can be seen from the figure that 2D-SICM is in chaotic states at a wide range, but does not exhibit periodic states, indicating that 2D-SICM has a large chaotic range.

Fig. 3

Bifurcation diagram of 2D-SICM. a Bifurcation diagram of x; b Bifurcation diagram of y

2.2.3 Lyapunov exponent

Lyapunov exponent (LE) effectively represents the evolution process of the system over time and the sensitivity of the system to the initial value. A positive LE indicates that the system is sensitive to the changes of initial values, so chaotic systems have at least one positive LE [44,45,46]. When the system has two or more positive LEs, the system is in a hyperchaotic state.

The LE of 2D-SICM is shown in Fig. 4, where (a) is the diagram of the first Lyapunov exponent LE₁ of 2D-SICM varying with the system parameters α and β, and (b) is the diagram.of the second Lyapunov exponent LE₂ of 2D-SICM varying with the system parameters α and β. It can be seen that when α > 1 and β > 1, the system has two positive LEs, and at this time, the system is in a hyperchaotic state. With the increase of α and β, the LEs of the system increase, which indicates that 2D-SICM has a wide chaotic range and with the increase of the system parameters, the chaotic characteristics of the system become better, and the sensitivity to the initial value becomes higher.

Fig. 4

Lyapunov exponents of 2D-SICM. a LE₁, b LE₂

2.2.4 Complexity analysis

The complexity of chaotic systems refers to the degree to which chaotic sequences produced by chaotic systems are close to random sequences. At present, there is no unified method to measure the complexity of chaotic systems, and the value range of the results obtained by measuring the system complexity with different methods is different. However, under the same measurement method, the greater the complexity value is, the more complex the chaotic sequence is, and the closer it is to the random sequence.

In this paper, permutation entropy (PE) and normalized spectral entropy (SE) are used to analyze the complexity of chaotic systems. Figure 5a, c show the comparison results of the PE and SE of the proposed chaotic system 2D-SICM and three classical one-dimensional chaotic systems Logistic, Sine, and ICMIC respectively; Fig. 5b, d show the comparison results of the PE and SE of 2D-SICM and the three newly proposed two-dimensional chaotic systems 2D-SIMM, 2D Logistic map, and 2D-SLMM, respectively. It can be seen from Fig. 5 that the PE and SE of 2D-SICM are significantly higher than some classical one-dimensional chaotic systems and some newly proposed two-dimensional chaotic systems, and the performance is stable and close to the ideal value of 1. The results indicate that the chaotic sequences generated by 2D-SICM have higher complexity and unpredictability, and can be used to generate more secure key sequences for image encryption.

Fig. 5

Permutation entropy and spectral entropy of different chaotic systems. a PE of 2D-SICM, Logistic map, Sine map, and ICMIC; b PE of 2D-SICM, 2D-SIMM, 2D-Logistic map, and 2D-SLMM; c SE of 2D-SICM, Logistic map, Sine map, and ICMIC; d SE of 2D-SICM, 2D-SIMM, 2D-Logistic map, and 2D-SLMM

2.2.5 0–1 test

The 0–1 test is a test method to show whether a time series is chaotic. Different from the LE, it does not need phase space reconstruction, and directly determines whether the system is chaotic by observing whether the output is close to 1. According to the LE analysis in Fig. 4, it is concluded that when α > 1 and β > 1, the system is in a hyperchaotic state. The 0–1 test is carried out for the system parameters (α, β) = (0.1, 0.2) and (α, β) = (5, 20), respectively, and the (p, s) diagram is shown in Fig. 6, where (a) and (b) correspond to periodic motion and Brownian motion, respectively, indicating that the system is in non-chaotic state and chaotic state, respectively. Obviously, the results of the 0–1 test are consistent with the analysis of the LE.

Fig. 6

0–1 test results of 2D-SICM. a α = 0.1, β = 0.2; b α = 5, β = 20

2.3 Definition of 2D-LICM and 2D-LSM

Based on the model of 2D-CCCM shown in Fig. 1, different two-dimensional chaotic systems can be obtained by keeping f and g fixed and changing F and G into different one-dimensional chaotic maps. Therefore, it can be shown that 2D-CCCM has a certain degree of universality for finding new two-dimensional chaotic systems.

When F and G are set as the Logistic map and ICMIC, respectively, where the logistic map is defined as

$$ x_{n + 1} = \mu x_{n} (1 - x_{n} ) $$

(5)

Then two-dimensional Logistic-ICMIC coupling map (2D-LICM) is obtained as

$$\left\{ {\begin{array}{*{20}l} {x_{{n + 1}} = \alpha (\sin y_{n} + \cos x_{n} )(1 - (\sin y_{n} + \cos x_{n} ))} \hfill \\ {y_{{n + 1}} = \sin \left( {\frac{\beta }{{\sin x_{n} + \cos y_{n} }}} \right)} \hfill \\ \end{array} } \right. $$

(6)

where α, β ∈ [1, + ∞).

When F and G are set as the Logistic map and Sine map, respectively, then the two-dimensional Logistic-Sine coupling map (2D-LSM) is obtained as

$$ \left\{ {\begin{array}{*{20}l} {x_{n + 1} = \alpha \left( {\sin y_{n} + \cos x_{n} } \right)\left( {1 - \left( {\sin y_{n} + \cos x_{n} } \right)} \right)} \hfill \\ {y_{n + 1} = \beta \sin \left( {\pi \left( {\sin x_{n} + \cos y_{n} } \right)} \right)} \hfill \\ \end{array} } \right. $$

(7)

where α, β ∈ [1, + ∞).

The phase diagram and LEs of 2D-LICM and 2D-LSM are shown in Figs. 7 and 8. It can be seen from Figs. 7 and 8 that these two chaotic maps are similar to 2D-SICM in that they both have good chaotic performance and are hyperchaotic in a wide range. It is further shown that 2D-CCCM is superior in finding new two-dimensional chaotic systems.

Fig. 7

Phase diagram and Lyapunov exponents of 2D-LICM. a Phase diagram with α = 100, β = 100; b Lyapunov exponents of α (β = 20)

Fig. 8

Phase diagram and Lyapunov exponents of 2D-LSM. a Phase diagram with α = 100, β = 100; b Lyapunov exponents of α (β = 20)

2.4 2D DCT

DCT is a separable transform method that converts time-domain signals into frequency-domain signals, with cosine functions as its transform kernel. It is a special type of Discrete Fourier Transform (DFT). The special feature of DCT is that it only uses real numbers instead of complex numbers. Therefore, it is widely used in digital signal processing, especially in compression transforms of speech and image signals. The formula for DCT is as

$$ \left\{ {\begin{array}{*{20}l} {F(u) = C(u)\sqrt{\frac{2}{N}} \sum\limits_{x = 0}^{N - 1} f (x)\cos \frac{(2x + 1)u\pi }{{2N}}(u,x = 0,1,2, \ldots ,N - 1)} \\ {C(u) = \left\{ {\begin{array}{*{20}l} {\sqrt{\frac{1}{2}} ,u = 0} \hfill \\ {1,u \ne 0} \hfill \\ \end{array} } \right.} \\ \end{array} } \right. $$

(8)

where f (x) is the original signal, F(u) is the transformed frequency signal, and N is the length of the signal.

In this paper, we perform 2D DCT on the R, G, and B color planes of the encrypted image, and embed the transformed image into a meaningful carrier image for practical transmission. 2D DCT is a second-level DCT transformation performed on top of a one-dimensional DCT transformation. For a two-dimensional image matrix of size M × N, the 2D DCT formula is given in Eq. (9), while the formula for the two-dimensional inverse discrete cosine transform (IDCT) is given in Eq. (10).

$$ F(u,v) = \frac{2}{{\sqrt {MN} }}\sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{N - 1} f } (x,y)C(u)C(v)\cos \left[ {\frac{(2x + 1)u\pi }{{2M}}} \right]\cos \left[ {\frac{(2y + 1)v\pi }{{2N}}} \right] $$

(9)

$$ f(x,y) = \frac{2}{{\sqrt[{}]{MN}}}\sum\limits_{u = 0}^{M - 1} {\sum\limits_{v = 0}^{N - 1} C } (u)C(v)F(u,v)\cos \left[ {\frac{(2x + 1)u\pi }{{2M}}} \right]\cos \left[ {\frac{(2y + 1)v\pi }{{2N}}} \right] $$

(10)

where x, u = 0, 1, 2, …, M-1; y, v = 0, 1, 2, …, N-1.

3 The proposed encryption and decryption algorithm

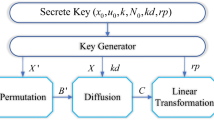
Based on the above two-dimensional chaotic system 2D-SICM, a new color image encryption and hiding algorithm is proposed in this paper. Suppose the original color image is P and the size is M × N × 3, where M and N are the numbers of rows and columns of the color image, respectively, and the flow chart of the algorithm is shown in Fig. 9. As can be seen from the figure, the algorithm includes key generation, cross-plane scrambling, row and column shuffling, cyclic shift diffusion, and embedding the encrypted image into the carrier image. The specific implementation process of the algorithm is described below.

Fig. 9

Flowchart of the proposed image encryption algorithm

3.1 Generate keys and obtain system parameters

The Secure Hash Algorithm (SHA) is the most widely used Hash function. SHA is highly sensitive to input volume and can effectively resist plaintext attacks. Therefore, SHA is unidirectional and uncrackable [9, 12]. There are many forms of SHA. In this paper, SHA-512 is applied to generate the initial values and system parameters of the chaotic system. Through the SHA-512 function, get the hash key h with 512 bits length from the original color image, combine every 8 bits to get 64 keys, and then convert these keys into 8 sub keys k through Eq. (11).

$$ k(i) = \sqrt[8]{{{\text{h}}(8 \times i - 7) \oplus h(8 \times i - 6)... \oplus h(8 \times i)}},\quad i = 1,2 \ldots 8 $$

(11)

where ⊕ indicates bitwise XOR operation. By using the subkeys k, the system parameters α, β, and the initial values x₀ and y₀ of the chaotic system can be obtained by

$$ \left\{ {\begin{array}{*{20}l} {\alpha = \bmod ({\text{sqrt}} (k(1) \times k(5)) \times M,5) + 15} \hfill \\ {\beta = \bmod ({\text{sqrt}} (k(2) \times k(6)) \times M,5) + 20} \hfill \\ {x_{0} = \bmod ({\text{sqrt}} (k(3) \times k(7)) \times N,0.5) + 0.5} \hfill \\ {y_{0} = \bmod ({\text{sqrt}} (k(4) \times k(8)) \times N,0.5) + 0.5} \hfill \\ \end{array} } \right. $$

(12)

where mod () is the modulo operation and sqrt () is the square root operation.

3.2 Cross-plane scrambling

Most of the existing image encryption algorithms scramble in a single plane, which can be roughly divided into two types. One is to scramble rows and columns of the two-dimensional image matrix successively or to do row and column scrambling at the same time. The other is to scan the two-dimensional image matrix into a one-dimensional pixel vector with different scanning methods, and then scramble the position of the one-dimensional vector. These two methods ignore the relationship between the three color planes of color images, which makes these encryption algorithms have some problems such as poor effect and low efficiency. To overcome these defects, this paper proposes a cross-plane three-dimensional color image scrambling algorithm. This algorithm connects the R, G, and B color planes of color images, so that a pixel can appear anywhere in the three color planes, which greatly improves the encryption effect and efficiency. The schematic diagram of the scrambling algorithm is shown in Fig. 10. The detailed steps are described below.

Fig. 10

Schematic diagram of cross-plane scrambling

Step1. The parameters and initial values of the chaotic system 2D-SICM are generated by Eq. (12). Iterating 2D-SICM for M × N × 3 + o times to get chaotic sequences x and y, and dropping the first o values of x and y to eliminate the transient response, here we choose o = 100. Then, the chaotic sequences x and y are transformed by Eq. (13) to obtain the sequences X, Y, and Z. Where floor (x) stands for taking the largest integer not greater than x, and abs(x) stands for taking the absolute value of x.

$$ \left\{ {\begin{array}{*{20}l} {X = floor \left( {\bmod \,\left( {{\text{abs}} (x(o + 1:o + 2 \times M \times N)) \times 10^{10} ,3} \right)} \right)} \hfill \\ {Y = \bmod \left( {{\text{abs}} (y(o + 1:o + 3 \times (M + N))) \times 10^{10} ,256} \right)} \hfill \\ {Z = {\text{floor}} \left( {\bmod \left( {{\text{abs}} (x(o + 1:o + 3 \times M \times N)) \times 10^{10} ,256} \right)} \right)} \hfill \\ \end{array} } \right. $$

(13)

Step2. Chaotic matrix I₁ with M rows and N columns is obtained by reshaping the first M × N values of sequence X, and chaotic matrix I₂ with M rows and N columns is obtained by reshaping the M × N + 1: 2 × M × N values of sequence X. The chaotic matrix J with 3 rows and M + N columns is obtained by reshaping the sequence Y. The index sequences J₁ and J₂ are obtained by sorting the values of the first M columns of J and the values of the M + 1: M + N columns by rows, respectively. The specific transformation method is shown as

$$ \left\{ {\begin{array}{*{20}l} {I_{1} = reshape (X(1:M \times N),[M,N])} \hfill \\ {I_{2} = {\text{reshape}} (X(M \times N + 1:2 \times M \times N),[M,N])} \hfill \\ {J = {\text{reshape}} (Y,[3,M + N])} \hfill \\ {\left[ {\sim ,J_{1} (i,:)} \right] = {\text{sort}} (J(i,1:M)),\quad i = 1,2,3} \hfill \\ {\left[ {\sim ,J_{2} (i,:)} \right] = {\text{sort}} (J(i,M + 1:M + N)),\quad i = 1,2,3} \hfill \\ \end{array} } \right. $$

(14)

where, reshape (x, [M, N]) represents realigning the sequence x into a matrix of size M × N, and sort (x) represents arranging the elements of the sequence x in ascending order.

Step3. By utilizing the chaotic matrix I₁ and cyclic shift method, pixels in the color plane R, G, and B of the original color image P are scrambled according to Eq. (15) to obtain P₁.

$$ P_{1} (i,j,:) = {\text{circshift}} \left( {P(i,j,:),I_{1} (i,j)} \right) $$

(15)

where circshift (x, y) represents that the loop shifts the elements in vector x by y positions.

Step4. The Inside-Out Algorithm is a classical shuffling algorithm. Its basic idea is to traverse the array from front to back, insert the value of the i-th position in the array into any position in the first i positions of the array (assumed to be k), and its actual effect is equivalent to exchanging the i-th and k-th positions in the newly generated array. In this paper, we use the chaotic system-based Inside-Out Algorithm to shuffle the rows and columns of P₁. First, the row shuffles: employ the index matrix J₁ as the random number required in the shuffle algorithm to shuffle the row vectors of the three color planes of P₁ by Eq. (16) to get P₂. Before shuffling the rows of P₁ with Eq. (16), it is necessary to initialize and assign P₂. The initial value of P₂ is P₁.

$$ \left\{ {\begin{array}{*{20}l} {u(i) = \bmod \left( {J_{1} (k,i),i} \right) + 1,\quad i = 1,2 \ldots M;k = 1,2,3} \hfill \\ {P_{2} (i,:,k) = P_{2} (u(i),:,k),\quad i = 1,2 \ldots M;k = 1,2,3} \hfill \\ {P_{2} (u(i),:,k) = P_{1} (i,:,k),\quad i = 1,2 \ldots M;k = 1,2,3} \hfill \\ \end{array} } \right. $$

(16)

Step5. Then, column shuffling: similar to row shuffling, column shuffling uses index matrix J₂ to shuffle the column vectors of the three color planes of P₂ by Eq. (17) to obtain the scrambled 3D pixel matrix P₃. Similarly, P₃ needs to be initialized, and P₃'s initialization value is P₂.

$$ \left\{ {\begin{array}{*{20}l} {v(j) = \bmod \left( {J_{2} (k,j),j} \right) + 1,\quad j = 1,2 \ldots N;k = 1,2,3} \hfill \\ {P_{3} (:,j,k) = P_{3} (:,v(j),k),\quad j = 1,2 \ldots N;k = 1,2,3} \hfill \\ {P_{3} (:,v(j),k) = P_{2} (:,j,k),\quad j = 1,2 \ldots N;k = 1,2,3} \hfill \\ \end{array} } \right. $$

(17)

As shown in Fig. 10, after cross-plane arrangement and row shuffling, and column shuffling of the 3D pixel matrix by the chaotic system-based Inside-Out Algorithm, the probability of every point on the original color image appearing at any point on the 3D plane is equal. Therefore, this scrambling algorithm proposed in this paper has a good scrambling effect.

3.3 Cyclic shift diffusion

The purpose of diffusion is to transmit a change in the value of one pixel to other pixels to improve the plaintext sensitivity of the encryption system. Most of the existing diffusion algorithms follow a fixed diffusion order, and the current pixel value is only affected by the previous pixel value, which greatly reduces the encryption effect. To solve this problem, we propose a cyclic shift diffusion algorithm, whose algorithm flow is shown in Fig. 11. In this algorithm, the current pixel value may be affected by any previous pixel value, which greatly improves the plaintext sensitivity of the encryption system. The operation of the cyclic shift diffusion process is as follows:

Fig. 11

Schematic diagram of cyclic shift diffusion

Step1. The chaotic sequence Z in Eq. (13) is reshaped to obtain the three-dimensional diffusion matrix K with the same size as the original color image and the operation is as

$$ K = {\text{reshape}}(Z,[M,N,3]) $$

(18)

Step2. Diffusion matrix K and index matrix I₂ are used to carry out cyclic shift diffusion operation on scrambled image P₃, as shown in Eq. (19). Diffusion starts from the first point of each color plane and is accompanied by a cyclic shift in the vertical direction at the same time, and I₂ is the cyclic shift value.

$$ \left\{ {\begin{array}{*{20}l} {P_{4} (i,j,:) = {\text{circshift}} \left( {\,\bmod \,\left( {P_{3} (i,j,:) + K(i,j,:),256} \right),I_{2} (i,j)} \right),i = 1;j = 1} \hfill \\ {P_{4} (i,j,:) = {\text{circshift}} \left( {\,\bmod \,\left( {P_{3} (i,j,:) + P_{4} (i,j - 1,:) + K(i,j,:),256} \right),I_{2} (i,j)} \right),i = 1;j \ne 1} \hfill \\ {P_{4} (i,j,:) = {\text{circshift}} \left( {\,\bmod \,\left( {P_{3} (i,j,:) + P_{4} (i - 1,j,:) + K(i,j,:),256} \right),I_{2} (i,j)} \right),i \ne 1} \hfill \\ \end{array} } \right. $$

(19)

Step3. After the above steps, the final cipher image P₄ is obtained.

3.4 Embed encrypted image into the carrier image

Embedding the encrypted image into a carrier image that has visual meaning for actual transmission can reduce the probability of attacks by attackers and further enhance the security of image encryption. Existing image hiding algorithms based on DWT and IWT require a carrier image size that is four times the size of the encrypted image, which increases the transmission bandwidth and storage space. To address this issue, this paper applies 2D DCT to image hiding algorithms, and the specific operation is described as follows. This method requires a carrier image size that is the same as the encrypted image, which overcomes the drawbacks of DWT and IWT.

Step1. Select a meaningful color image T with the same size as the cipher image P₄ as the carrier image.

Step2. Apply 2D DCT to the three color planes of the carrier image T to obtain the processed TR, TG, and TB components.

Step3. Embed the pixel values P₄R, P₄G, and P₄B of the three color planes of cipher image P₄ into TR, TG, and TB. The specific operation is shown as

$$ \left\{ {\begin{array}{*{20}l} {TR^{\prime } = TR + c \times P_{4} R} \hfill \\ {TG^{\prime } = TG + c \times P_{4} G} \hfill \\ {TB^{\prime } = TB + c \times P_{4} B} \hfill \\ \end{array} } \right. $$

(20)

where c is the embedding coefficient, which we set as (x₀ + y₀)/10.

Step4. Perform 2D IDCT on TR', TG', and TB' to obtain the carrier image T₁ which contains the information of cipher image P₄.

3.5 Decryption algorithm

Step1. Apply 2D DCT to T₁ to obtain TR', TG', TB', and then separate P₄R, P₄G, and P₄B components through Eq. (21) to obtain cipher image P₄.

$$ \left\{ {\begin{array}{*{20}l} {P_{4} R = (TR^{\prime } - TR)/c} \hfill \\ {P_{4} G = (TG^{\prime } - TG)/c} \hfill \\ {P_{4} B = (TB^{\prime } - TB)/c} \hfill \\ \end{array} } \right. $$

(21)

Step2. The cipher image P₄ obtains the scrambled image P₃ through inverse diffusion which described as

$$ \left\{ {\begin{array}{*{20}l} {P_{3} (i,j,:) = \bmod \left( {{\text{circshift}} \left( {P_{4} (i,j,:), - I_{2} (i,j)} \right) - K(i,j,:),256} \right),i = 1;j = 1} \hfill \\ {P_{3} (i,j,:) = \bmod \left( {{\text{circshift}} \left( {P_{4} (i,j,:), - I_{2} (i,j)} \right) - P_{4} (i,j - 1,:) - K(i,j,:),256} \right),i = 1;j \ne 1} \hfill \\ {P_{3} (i,j,:) = \bmod \left( {{\text{circshift}} \left( {P_{4} (i,j,:), - I_{2} (i,j)} \right) - P_{4} (i - 1,j,:) - K(i,j,:),256} \right),i \ne 1} \hfill \\ \end{array} } \right. $$

(22)

Step3. Reverse column shuffling P₃ to get P₂, the operation is as

$$ \left\{ {\begin{array}{*{20}l} {v(j) = \bmod (J_{2} (k,j),j) + 1,\quad j = N,N - 1, \ldots 1;k = 1,2,3} \hfill \\ {temp = P_{2} (:,j,k),\quad j = N,N - 1, \ldots 1;k = 1,2,3} \hfill \\ {P_{2} (:,j,k) = P_{2} (:,v(j),k),\quad j = N,N - 1, \ldots 1;k = 1,2,3} \hfill \\ {P_{2} (:,v(j),k) = temp,\quad j = N,N - 1, \ldots 1;k = 1,2,3} \hfill \\ \end{array} } \right. $$

(23)

where the temp is a temporary variable.

Step4. Reverse row shuffling P₂ to get P₁ and the operation is described as

$$ \left\{ {\begin{array}{*{20}l} {u(i) = \bmod (J_{1} (k,i),i) + 1,\quad i = M,M - 1, \ldots 1;k = 1,2,3} \hfill \\ {temp = P_{1} (i,:,k),\quad i = M,M - 1, \ldots 1;k = 1,2,3} \hfill \\ {P_{1} (i,:,k) = P_{1} (u(i),:,k),\quad i = M,M - 1, \ldots 1;k = 1,2,3} \hfill \\ {P_{1} (u(i),:,k) = temp,\quad i = M,M - 1, \ldots 1;k = 1,2,3} \hfill \\ \end{array} } \right. $$

(24)

Step5. Reverse cross-plane scrambling of P₁ to get the decrypted image P, the operation is as

$$ P(i,j,:) = {\text{circshift}} (P_{1} (i,j,:), - I_{1} (i,j)) $$

(25)

4 Simulation results and performance analysis

In this chapter, we analyze the performance of the encryption algorithm by observing the encryption effect of color images of different sizes and combining with a variety of test methods. The selected images are 256 × 256 Lena, 512 × 512 Baboon, 512 × 512 Satellite map, 1024 × 1024 Aircraft and 768 × 512 Parrot, respectively. The simulation results are shown in Fig. 12. It can be seen that the encryption algorithm can well hide the plaintext image information, and there is no visual difference between the carrier image and the carrier image containing ciphertext image information, which greatly improves the security of the encryption algorithm.

Fig. 12

Simulation results of different color images. a Original Lena image, b Encrypted Lena image, c Carrier image A, d Carrier image A containing Lena, e Decrypted Lena Image; f Original Baboon image, g Encrypted Baboon image, h Carrier image B, i Carrier image B containing Baboon, j Decrypted Baboon Image; k Original Satellite map, l Encrypted Satellite map, m Carrier image C, n Carrier image C containing Satellite map, o Decrypted Satellite map; p Original Aircraft image, q Encrypted Aircraft image, r Carrier image D, s Carrier image D containing Aircraft, t Decrypted Aircraft Image; u Original Parrot image, v Encrypted Parrot image, w Carrier image E, x Carrier image E containing Parrot, y Decrypted Parrot Image

4.1 Histogram analysis

The histogram of a digital image reflects its statistical properties and shows the quantity distribution of different gray values. A good encryption algorithm should be able to disrupt the gray distribution of the plaintext image and make the gray distribution of the ciphertext image as uniform as possible [47,48,49]. Figure 13 analyzes the performance of the proposed encryption algorithm by comparing the histogram distribution of the original color image and its encrypted image in Fig. 12. As shown in Fig. 13, the gray value distribution of ciphertext images of different sizes is very uniform, so the encryption algorithm has good statistical characteristics and can resist statistical attacks.

Fig. 13

Histogram analysis results of original image and encryption image

4.2 Information entropy

Information entropy is a physical quantity to measure the uncertainty of image information. The greater the information entropy, the greater the uncertainty of image information. Equation (26) defines the calculation method of information entropy.

$$ H(x) = - \sum\limits_{i = 1}^{L} p \left( {x_{i} } \right)\log_{2} p\left( {x_{i} } \right) $$

(26)

where, L is the length of information x, and p (x_i) is the probability of occurrence of x_i. For a color image with a gray level of 256, the L of R, G, and B channels is 256, and the ideal value of information entropy is 8.

Table 1 shows the calculation results of the information entropy of R, G, and B channels of plaintext images and ciphertext images, and compares them with other algorithms. It can be seen that the information entropy of R, G, and B channels of the ciphertext image in our algorithm is close to the ideal value of 8, so the proposed encryption algorithm has high security.

Table 1 Information entropy analysis

4.3 Correlation analysis of adjacent pixels

In natural images, two adjacent pixels are highly correlated. Attackers can use the correlation between adjacent pixels to crack some information from ciphertext images, which makes the process of image encryption communication have security risks. To improve the security of the encryption algorithm, the correlation between adjacent pixels of the ciphertext image should be as small as possible, that is, its correlation coefficient should be as close as possible to 0. The calculation process of the correlation coefficient is shown in Eq. (27).

$$ \left\{ {\begin{array}{*{20}l} {E(x) = \frac{1}{N}\sum\limits_{i = 1}^{N} {x_{i} } } \hfill \\ {D(x) = \frac{1}{N}\sum\limits_{i = 1}^{N} {(x_{i} - E(} x))^{2} } \hfill \\ {{\text{cov}} (x,y) = \frac{1}{N}\sum\limits_{i = 1}^{N} {(x_{i} - E(} x))(y_{i} - E(y))} \hfill \\ {r_{xy} = \frac{{{\text{cov}} (x,y)}}{{\sqrt {D(x)D(y)} }}} \hfill \\ \end{array} } \right. $$

(27)

where x and y are two adjacent pixels, and N = 10,000 is the number of adjacent pixels selected in each direction. E (x) and D (x) represent the expectation and variance of x, and cov (x, y) is the covariance of x and y. r_xy is the correlation coefficient of x and y.

Randomly select the adjacent pixels in the horizontal direction of Lena's R channel, the vertical direction of Lena's G channel, and the diagonal direction of Lena's B channel, and their correlation distribution is shown in Fig. 14. Table 2 shows the correlation coefficients of adjacent pixels in the horizontal, vertical, and diagonal directions of different images. The results show that the correlation coefficients of adjacent pixels of different directions in different images are close to 0, so the proposed encryption algorithm can greatly reduce the correlation between adjacent pixels and improve the security of image encryption.

Fig. 14

Correlation analysis of adjacent pixels of plaintext image and ciphertext image. a R channel in the horizontal direction, b G channel in the vertical direction, c B Channel in the diagonal direction

Table 2 Correlation coefficients of adjacent pixels

4.4 Key analysis

Key space refers to the collection of all keys in the encryption or decryption system. To effectively resist exhaustive attacks, the key space of the image encryption system should be large enough. Some cryptologists suggest that the password length should be at least 128 bits. The encryption algorithm proposed in this paper utilizes SHA-512 to generate the key, and the length of the generated password is 512 bits, greater than 128 bits, so the encryption algorithm proposed in this paper can effectively resist exhaustive attacks.

A good encryption system needs not only enough key space but is also very sensitive to key changes. Key sensitivity means that when the encryption and decryption keys change slightly, the encryption and decryption images obtained have significant differences. Figure 15 shows the decrypted image obtained when one key in the key system is changed during decryption. It can be seen from the results that when any key changes slightly, the correct decryption image cannot be obtained, so our proposed algorithm is extremely sensitive to the key.

Fig. 15

Key sensitivity analysis. a original image, b decrypted image using α + 10^–14, c decrypted image using β + 10^–14, d decrypted image using x₀ + 10^–14, e decrypted image using y₀ + 10^–14, f decrypted image using the correct key

4.5 Differential attack analysis

The differential attack is an attack method that attacks the encryption algorithm by comparing and analyzing the propagation of differences between two ciphertext images obtained by two plaintext images with specific differences. To resist the differential attack, the encryption algorithm needs to be very sensitive to the plaintext image, that is, a small change in the plaintext image can cause a large change in the ciphertext image. The number of pixels change rate (NPCR) and unified average changing intensity (UACI) can be used to measure the difference between the ciphertext images encrypted by two slightly changed plaintext images. The NPCR and UACI values are computed by

$$ {\text{NPCR}} = \frac{{\sum\limits_{ij} D (i,j)}}{M \times N} \times 100\% $$

(28)

$$ {\text{UACI}} = \frac{1}{M \times N}\left[ {\sum\limits_{ij} {\frac{{\left| {C_{1} (i,j) - C_{2} (i,j)} \right|}}{255}} } \right] \times 100\% $$

(29)

where c₁ and c₂ are ciphertext images obtained by encrypting two plaintext images with slight differences, M and N are the numbers of rows and columns of the ciphertext image, respectively, and the D (i, j) is calculated as

$$ D(i,j) = \left\{ {\begin{array}{*{20}l} {1,C_{1} (i,j) \ne C_{2} (i,j)} \hfill \\ {0,C_{1} (i,j) = C_{2} (i,j)} \hfill \\ \end{array} } \right. $$

(30)

For the image with 256 Gy levels, the ideal values of NPCR and UACI are 99.6094% and 33.4635%, respectively. Table 3 shows the NPCR and UACI values of different images encrypted by the proposed algorithm, both of them were very close to the ideal values. Table 4 shows the comparison of UPCR and UACI values between our proposed encryption algorithm and other algorithms. The results show that the UPCR and UACI of our proposed encryption algorithm are closer to the ideal values, so our proposed algorithm can better resist differential attacks.

Table 3 Values of NPCR and UACI

Table 4 Comparison of NPCR and UACI values obtained by different methods

4.6 Clipping and noise attack analysis

In the process of image encryption communication, the transmitted ciphertext image will inevitably encounter the impact of data loss or noise interference. A good encryption algorithm should be able to resist these impacts. Even if the ciphertext image is affected by these disturbances, it should be able to decrypt the correct original image information.

We tested the ability of the proposed algorithm to resist cropping attack and noise respectively. Among them, the test result of resistance to cropping attack is shown in Fig. 16. It can be seen from the figure that when the ciphertext image loses more data, the decrypted image is less clear. However, even if 25% of the data is lost, the decrypted image still retains most of the information of the original image, and we can still clearly identify the original image visually.

Fig. 16

Ciphertext images subjected to different degrees of cropping attacks and their decryption images. a 6.25% cropped, b 12.5% cropped, c 14.1% cropped, d 25% cropped

Figure 17 shows the ability of our algorithm to resist noise attacks. As shown in the figure, when different degrees of salt & pepper noise (SPN) and gaussian noise (GN) are added to the ciphertext image, although the decrypted image is affected to different degrees, most of the information of the original image can be decrypted.

Fig. 17

Ciphertext image added with different degrees and different types of noise and its decryption image. a 0.005 GN, b 0.01 GN, c 0.05 SPN, d 0.1 SPN

To further verify the robustness of the proposed encryption algorithm, we tested the mean squared error (MSE) and peak signal to noise ratio (PSNR) of the recovered image compared to the plaintext image. PSNR is an objective standard for evaluating the quality of an image, where a higher PSNR value indicates less distortion in the recovered image compared to the original image. The calculation formula is given as

$$ \left\{ {\begin{array}{*{20}l} {MSE = \frac{1}{M \times N}\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{N} {(P_{1} (} } i,j) - P(i,j))^{2} } \hfill \\ {PSNR = 10\log_{10} \left( {\frac{255 \times 255}{{MSE}}} \right)} \hfill \\ \end{array} } \right. $$

(31)

where M and N represent the size of the image, P₁ denotes the recovered image, and P denotes the plaintext image.

Tables 5 and 6 respectively show the PSNR values of the recovered images compared to the original Lena512 image under data loss and noise attacks, and are compared with another algorithm. The results indicate that our algorithm has a significantly higher PSNR value of over 32 dB, and is superior to the other algorithm, demonstrating that our encryption scheme has better robustness and can better resist cropping and noise attacks.

Table 5 Comparison of resistance to cropping attacks

Table 6 Comparison of resistance to noise attacks

4.7 Running performance

To meet the actual needs, a good encryption algorithm should also have excellent running performance. In our algorithm, the 3D pixel matrix is simultaneously scrambled and diffused, instead of the three color planes respectively, so the proposed algorithm theoretically improves the running performance and reduces the running time. We tested different sizes of color images using MATLAB R2021a with Intel(R) Core (TM) i5-8300H CPU @ 2.30 GHz and 8.0G RAM on Windows 10 Home OS. Table 7 shows the test results and compares them with other algorithms. The results show that the proposed algorithm has good running performance and can meet the actual needs of image encryption communication.

Table 7 Comparison of running performance (Unit: s)

4.8 Comparison of hidden effects

The current visually meaningful image hiding schemes include DWT and IWT, while this paper adopts DCT. Table 8 shows the sizes of the carrier images required by these three different methods. It can be seen that the carrier image size required by the DCT-based image hiding algorithm in this paper is one-fourth of the other two methods, which greatly saves transmission bandwidth and storage space. Table 9 shows the PSNR values between the meaningful carrier image and the carrier image under the same size and embedding coefficient, and compares them with other visual meaningful image encryption schemes. As can be seen from the table, the PSNR value of our scheme is above 44 dB, which is better than ref [9, 53, 54], indicating that our DCT-based image hiding scheme has better imperceptibility and visual security.

Table 8 Sizes of carrier images required by different methods

Table 9 Comparison of PSNR values

5 Conclusion

This paper proposes a color image encryption and hiding algorithm based on the two-dimensional hyperchaotic system 2D-SICM and DCT. First, a two-dimensional chaotic mapping model 2D-CCCM is designed, which is composed of one-dimensional chaotic mapping and nonlinear function cross-coupling. Based on this model, a novel two-dimensional hyperchaotic system 2D-SICM is generated by using the Sine map and ICMIC. Phase diagram, bifurcation diagram, Lyapunov exponent spectrum, spectral entropy complexity, permutation entropy complexity, and 0–1 test results indicate that 2D-SICM has complex dynamic behavior and is suitable for image encryption. Based on 2D-CCCM, two new hyperchaotic systems, 2D-LICM and 2D-LSM, are also generated by using one-dimensional chaotic maps, which shows that 2D-CCCM is superior in looking for new two-dimensional chaotic maps. The key of the algorithm is generated by SHA-512, which improves the plaintext sensitivity and key space. The encryption process includes cross-plane permutation, row and column shuffle based on the improved out-inside shuffling algorithm, and cyclic shift diffusion. The cross-plane scrambling and diffusion of the R, G, and B channels of the color image greatly improve the encryption effect and efficiency. Finally, DCT is used to embed the ciphertext image into the visually meaningful carrier image. There is no visual difference between the carrier image before and after embedding the ciphertext image information, which further improves the security of the encryption algorithm. A series of simulations and security tests are carried out on color images of different sizes and compared with other algorithms, the results verify that the algorithm has higher security performance, and can resist various attacks.

At last, in our image encryption hiding scheme, only a single color image can be encrypted, which cannot meet the requirements of encrypting multiple images in the era of big data. Additionally, the encryption and decryption key of this scheme is generated by the plaintext image through the Hash function and needs to be transmitted separately from the ciphertext image, which reduces the transmission security. To address these issues, in our future research, we will focus on exploring efficient encryption methods for simultaneously encrypting multiple images, as well as methods for embedding the keys into the carrier image for simultaneous transmission.