Harmonic resonances of graphene-reinforced nonlinear cylindrical shells: effects of spinning motion and thermal environment

Abstract

This work investigates nonlinear harmonic resonance behaviors of graded graphene-reinforced composite spinning thin cylindrical shells subjected to a thermal load and an external excitation. The volume fraction of graphene platelets varies continuously in the shell’s thickness direction, which generates position-dependent useful material properties. Natural frequencies of shell traveling waves are derived by considering influences of the initial hoop tension, centrifugal and Coriolis forces, thermal expansion deformation, and thermal conductivity. A new Airy stress function is introduced. Harmonic resonance behaviors and their stable solutions for the spinning cylindrical shell are analyzed based on an equation of motion which is established by adopting Donnell’s nonlinear shell theory. The necessary and sufficient conditions for the existence of the subharmonic resonance of the spinning composite cylindrical shell are given. Besides the shell’s intrinsic structural damping, the Coriolis effect due to the spinning motion has a contribution to the damping terms of the system as well. Comparisons between the present analytical results and those in other papers are made to validate the existing solutions. Influences of main factors on vibration characteristics, primary resonance, and subharmonic resonance behaviors of the novel composite cylindrical shell are discussed. Furthermore, the mechanism of how the spinning motion affects the amplitude–frequency curves of harmonic resonances of the cylindrical shell is analyzed.

1 Introduction

Carbon-based materials, like carbon nanotubes (CNTs) and graphene platelets (GPLs) [1], have attracted considerable attention and been used as reinforcement nanofillers for many years. Among these materials, the GPLs are preferred nanofillers to exhibit better reinforcement effects resulting from their higher Young’s modulus, outstanding tensile strength, and larger specific surface area [2]. As GPLs are mixed with polymers, a novel polymer composite belonging to a multiphase solid material can be formed. It can exhibit the higher stiffness, excellent thermal properties, and lower mass density which are not presented in the pure polymers [3]. The novel polymer composites present significant potential for utilization in ultra-lightweight equipment elements of various structures in the practical engineering, such as the gas barrier, flexible touchscreens, and coating and sensing devices. Extensive works [4, 5] on the GPLs-reinforced polymer composites have been carried out considering their engineering significance.

Rafiee et al. [6] studied the mechanical properties of epoxy composites reinforced by GPLs and those by CNTs. Their experimental result revealed that the tensile strength, Young’s modulus, and fracture toughness of the GPLs-reinforced composite were all greater than those of the CNTs-reinforced composite at the same weight fraction of nanofillers. Parashar and Mertiny [7] investigated buckling behaviors of the GPLs-reinforced composite by using a multiscale modeling technique, where the graphene was simulated in a atomistic scale and the polymer deformation was addressed as a continuum. Based on a GPLs-reinforced multilayer composite model, Yang and his co-workers studied the bending deformation [8, 9], buckling and post-buckling behaviors [10,11,12], and linear and nonlinear vibration characteristics [13,14,15,16,17] of GPLs-reinforced composite structures, where GPLs were non-uniformly distributed in a specific direction with various patterns. In their works, the pronounced enhancement effect of GPLs nanofillers on stiffness of the neat polymers was proved.

As one of the gyration shell structures, the cylindrical shell is widely adopted in some practical engineering such as the flight vehicles, guided missile, and centrifugal separator. In the past decades, extensive research work has been made on the vibrations of cylindrical shells. However, a part of them [18,19,20,21] failed to consider the spinning motion. The spinning motion of cylindrical shells is a common situation in the engineering fields and important to the mechanical performances of the shell structures, as a result that the initial hoop tension, Coriolis force, and centrifugal force generated by the spinning motion can significantly affect dynamic behaviors of shell structures with spinning motion [22, 23]. Besides, the thermal environment in these engineering fields is a crucial point to be considered. It can change the stiffness of these structures and affect their mechanical behaviors. For this purpose, Wang [24] investigated the frequency response of nonlinear vibration of a composite spinning cylindrical shell. Dong et al. [14, 15] analyzed dynamic responses of GPLs-reinforced spinning cylindrical shells, in which they discussed influences of in-plane inertia on the natural frequencies of cylindrical shells.

Fig. 1

A spinning cylindrical shell

When an external excitation is applied on the structures, a significant amplitude vibration may exhibit where resonances can occur that sometimes results in instabilities of the systems [25]. The primary and subharmonic resonances are two particular phenomenons of the resonances for these nonlinear systems. In the primary resonance, vibration amplitudes of the structure have a maximum value, while in the 1/3 subharmonic resonance, vibration amplitudes of the structure have its minimum value [26]. Also, there are many different behaviors between these two resonances. Parametric controls for these two resonances of the structures can be conducted by engineers who can make use of the resonances or avoid it. Therefore, studies on the primary resonance and subharmonic resonance of cylindrical shell structures are important and essential. Up to date, lots of research work on the resonance behaviors of engineering structures subjected to an external harmonic excitation has been carried out. By employing the Galerkin method, Sheng and Wang [27] analyzed the chaotic oscillation and primary resonance of a spinning cylindrical shell considering the thermal expansion deformation. Wang and Li [28] presented the primary resonance of a nanobeam through the multiple scale method. Li and Yao [29] analyzed the amplitude–frequency relation of the 1/3 subharmonic resonance for a laminated nonlinear cylindrical shell, where the stability problem was discussed as well.

Because of ideal performances of the FG carbon-based nanofillers- reinforced composite structures, an effort to investigate the resonance behaviors of graphene-reinforced composite structures subjected to an external harmonic excitation is essential and exciting. Considering graphene-reinforced composite, Gao et al. [30] studied the amplitude–frequency responses of GPLs-reinforced porous cylindrical shells. Li et al. [31] investigated the primary, superharmonic, subharmonic, and combination resonances of GPLs-reinforced beams, and numerical results revealed that the amplitude peak decreases with the GPLs weight fraction.

Up to date, few studies on resonance behaviors of spinning cylindrical shells can be found in the literature. However, there are no works in the literature on resonance behaviors of GPLs-reinforced composite spinning cylindrical shell. Therefore, primary resonance and 1/3 subharmonic resonance behaviors of FG graphene-reinforced composite thin spinning cylindrical shell in a thermal environment are investigated in this paper. In Sect. 2, the differential equation of motion concerning the radial displacement of composite spinning cylindrical shells is obtained, where the thermal conductivity and thermal expansion deformation are considered. Useful material properties of the novel composite material for different GPL patterns are obtained as well. In Sect. 3, the natural frequency of traveling waves is derived. In Sect. 4, frequency–amplitude relations and stability conditions of primary and 1/3 subharmonic resonances of the cylindrical shell are studied, respectively, by employing the multiple scale method. In Sect. 5, numerical examples are presented to validate the analytical formulation. Numerical examples are executed to highlight the effects of spinning speeds, damping coefficients, temperature variations, and the external excitation on the primary and subharmonic resonances behaviors of the graphene-reinforced spinning cylindrical shell, and mainly, influence of the Coriolis force generated by the spinning motion on the damping of the system is analyzed.

2 Theoretical formulation

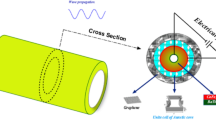
Figure 1 presents a GPLs-reinforced cylindrical shell which spins about its longitudinal axes in a thermal environment. As shown, $\varOmega$ (rad/s) represents the constant angular speed of the spinning cylindrical shell. L, r, and h denote the length, radius, and shell thickness of the cylindrical shell, respectively. An orthogonal coordinate system (x, $\theta$, z) is adopted. $u_{0}$, $v_{0}$, and $w_{0}$ are components of displacements of the middle surface ($z = 0$) in the x-, $\theta$-, and z-directions, respectively.

Assume that the GPLs-reinforced cylindrical shell is subjected to a thermal load, and the temperature field of the shell across the thickness is $T\left( z \right) =\hat{T}+\Delta \hat{T}\left( z \right)$, where $\hat{T}$ represents the initial temperature under the free stress state, and $\Delta \hat{T}\left( z \right)$ is the temperature variation. Following the Fourier law of heat conduction and considering the Dirichlet boundary on the inner $T\left( {-h/2} \right) =T_\mathrm{i}$ and outer $T\left( {h/2} \right) =T_\mathrm{o}$ surfaces, the one-dimensional steady temperature field of the shell through the thickness can be calculated by [32, 33]

(1)

where $k_c \left( \eta \right)$ is the useful thermal conductivity coefficient of the GPLs-reinforced composite.

In what follows, some material parameters concerning useful material properties of the GPLs-reinforced composite are introduced

$$\begin{aligned}&Q_{11} =Q_{22} =\frac{E_c \left( z \right) }{1-\nu _c^2 \left( z \right) },\,\,Q_{12} =Q_{21} =\frac{E_c \left( z \right) \nu { }_c\left( z \right) }{1-\nu _c^2 \left( z \right) },\\&Q_{44} =\frac{E_c \left( z \right) }{2\left[ {1+\nu { }_c\left( z \right) } \right] } \\&\left\{ {{\begin{array}{ccc} {A_{ij}^{*} }&{} {B_{ij}^{*} }&{} {D_{ij}^{*} } \\ \end{array} }} \right\} {=}\int _{-h/2}^{h/2} {Q_{ij} \left\{ {{\begin{array}{ccc} 1&{} z&{} {z^{2}} \\ \end{array} }} \right\} \hbox {d}z} \quad \left( {i,j{=}1,\,\,2,\,\,4} \right) , \\&I_0 =\int _{-h/2}^{h/2} {\rho _c \left( z \right) \hbox {d}z} , \end{aligned}$$

where $E_c \left( z \right)$, $\nu _c \left( z \right)$, and $\rho _c \left( z \right)$ are useful Young’s modulus, Poisson’s ratio, and mass density of the GPLs-reinforced composite, respectively. $Q_{ij} \,\left( {i,j=1,2,4} \right)$ are elements of the stiffness matrix for the present composite materials. $A_{ij}^{*}$, $B_{ij}^{*}$, and $D_{ij}^*$ denote the extension, extension-bending coupling, and bending stiffnesses of the cylindrical shell, respectively. $I_{0}$ represents the shell inertia.

In order to facilitate derivation, some new parameters, such as $A_{ij}$, $B_{ij}$, $C_{ij}$, $D_{ij} \,\left( {i,\,j=1,\,2,\,4} \right)$ related to extension, extension-bending coupling, and bending stiffnesses of the cylindrical shell, are firstly introduced as the following

$$\begin{aligned}&\Delta =\left( {A_{11}^{*} } \right) ^{2}-\left( {A_{12}^{*} } \right) ^{2};\,\,A_{11} =\frac{A_{11}^{*} }{\Delta };\\ A_{12}= & {} -\frac{A_{12}^{*} }{\Delta };\,\,A_{00} =\frac{1}{A_{11}^{*} +A_{12}^{*} }; \\ B_{11}= & {} \frac{A_{11}^{*} B_{11}^{*} -A_{12}^{*} B_{12}^{*} }{\Delta };\,\,B_{12} =\frac{A_{11}^{*} B_{12}^{*} -A_{12}^{*} B_{11}^{*} }{\Delta }; \\ A_{44}= & {} \frac{1}{A_{44}^{*} };\,\,B_{44} =2\frac{B_{44}^{*} }{A_{44}^{*} }; \\ C_{12}= & {} A_{12} B_{11}^{*} +A_{11} B_{12}^{*} ; \\ C_{11}= & {} A_{11} B_{11}^{*} +A_{12} B_{12}^{*} ; \\ C_{44}= & {} A_{44} B_{44}^{*} ; \\ D_{11}= & {} B_{11} B_{11}^{*} +B_{12} B_{12}^{*} -D_{11}^{*} ; \\ D_{12}= & {} B_{11} B_{12}^{*} +B_{12} B_{11}^{*} -D_{12}^{*} ; \\ D_{44}= & {} B_{44} B_{44}^{*} -2D_{44}^{*} ; \end{aligned}$$

2.1 Basic equations

The strain field of cylindrical shells is directly given as

$$\begin{aligned} \left\{ {{\begin{array}{c} {\varepsilon _{xx} } \\ {\varepsilon _{\theta \theta } } \\ {\gamma _{x\theta } } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {\varepsilon _{xx}^0 } \\ {\varepsilon _{\theta \theta }^0 } \\ {\gamma _{x\theta }^0 } \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{c} {k_{xx} } \\ {k_{\theta \theta } } \\ {2\chi _{x\theta } } \\ \end{array} }} \right\} . \end{aligned}$$

(2)

where $\varepsilon _{xx}$, $\varepsilon _{\theta \theta }$, and $\gamma _{x\theta }$ are the normal and shear strains of the thin cylindrical shell. Following Donnell’s nonlinear shell theory, the normal and shear strains ($\varepsilon _{xx}^0$, $\varepsilon _{\theta \theta }^0$ and $\gamma _{x\theta }^0$) and the changes in the curvature and torsion in the middle surface ($k_{xx}$, $k_{\theta \theta }$, and $\chi _{x\theta } )$ of the cylindrical shell in Eq. (2) are:

$$\begin{aligned}&\varepsilon _{xx}^0 =u_{0,x} +\frac{1}{2}w_{0,x}^2 ,\,\,\varepsilon _{\theta \theta }^0 =\frac{1}{r}\left( {v_{0,\theta } +w_0 } \right) +\frac{1}{2r^{2}}w_{0,\theta }^2 ,\nonumber \\&\gamma _{x\theta }^0 =\frac{1}{r}u_{0,\theta } +v_{0,x} +\frac{1}{r}w_{0,x} w_{0,\theta } , \nonumber \\&k_{xx} =-w_{0,xx} ,\,\,k_{\theta \theta } =-\frac{1}{r^{2}}w_{0,\theta \theta } ,\,\,\chi _{x\theta } =-\frac{1}{r}w_{0,x\theta } ,\nonumber \\ \end{aligned}$$

(3)

The linear constitutive equation considering the thermal expansion deformation of the functionally graded composite is [34]

$$\begin{aligned} \left\{ {{\begin{array}{c} {\sigma _{xx} } \\ {\sigma _{\theta \theta } } \\ {\sigma _{x\theta } } \\ \end{array} }} \right\} =\left[ {{\begin{array}{ccc} {Q_{11} }&{} {Q_{12} }&{} 0 \\ {Q_{21} }&{} {Q_{22} }&{} 0 \\ 0&{} 0&{} {Q_{44} } \\ \end{array} }} \right] \left\{ {{\begin{array}{cc} {\varepsilon _{xx} -\varepsilon _{xx}^T } \\ {\varepsilon _{\theta \theta } -\varepsilon _{\theta \theta }^T } \\ {\gamma _{x\theta } -\gamma _{x\theta }^T } \\ \end{array} }} \right\} , \end{aligned}$$

(4)

where $\varepsilon _{xx}^T$, $\varepsilon _{\theta \theta }^T$, and $\gamma _{x\theta }^T$ denote the thermal strains generated by the thermal expansion deformation. The relationship between the thermal strains and the temperature variation $\Delta \hat{T}\left( z \right)$ is given as

(5)

where $\alpha _c$ is the useful thermal expansion coefficient of the GPLs-reinforced composite.

On the base of the stress fields, stress results $N_{ij}$ and moments $M_{ij}$ of the cylindrical shell are expressed as

$$\begin{aligned} \left\{ {{\begin{array}{cc} {N_{ij} }&{} {M_{ij} } \\ \end{array} }} \right\} =\int _{-h/2}^{h/2} {\sigma _{ij} \left\{ {{\begin{array}{cc} 1&{} z \\ \end{array} }} \right\} \hbox {d}z} ,\,\,\left( {i,j} \right) =\left( {x,\theta } \right) , \end{aligned}$$

(6)

and

(7)

where $N_{ij}^T$ and $M_{ij}^T$ represent the stress resultant and moment caused by the thermal expansion deformation. Inserting Eq. (4) into Eq. (6) and considering Eqs. (5) and (7), one can derive

$$\begin{aligned} \begin{aligned} N_{xx}&=A_{11}^{*} \varepsilon _{xx}^0 -B_{11}^{*} w_{0,xx} +A_{12}^{*} \varepsilon _{\theta \theta }^0 \\&\quad -B_{12}^{*}r^{-2}w_{0,\theta \theta } -N_{xx}^T , \\ N_{\theta \theta }&=A_{12}^{*} \varepsilon _{xx}^0 -B_{12}^{*} w_{0,xx} +A_{11}^{*} \varepsilon _{\theta \theta }^0 \\&\quad -B_{11}^{*} r^{-2}w_{0,\theta \theta } -N_{\theta \theta }^T , \\ N_{x\theta }&=A_{44}^{*} \gamma _{x\theta }^0 -2B_{44}^{*} r^{-1}w_{0,x\theta } , \\ M_{xx}&=B_{11}^{*} \varepsilon _{xx}^0 +B_{12}^{*} \varepsilon _{\theta \theta }^0 -D_{11}^{*} w_{0,xx} \\&\quad -D_{12}^{*} r^{-2}w_{0,\theta \theta } -M_{xx}^T ; \\ M_{\theta \theta }&=B_{12}^{*} \varepsilon _{xx}^0 +B_{11}^{*} \varepsilon _{\theta \theta }^0 -D_{12}^{*} w_{0,xx} \\&\quad -D_{11}^{*} r^{-2}w_{0,\theta \theta } -M_{\theta \theta }^T ; \\ M_{x\theta }&=B_{44}^{*} \gamma _{x\theta }^0 -2D_{44}^{*} r^{-1}w_{0,x\theta } ; \end{aligned} \end{aligned}$$

(8)

Reversing Eqs. (8)$_{1-3}$, the normal and shear strains of the middle surface are derived as functions of the stress results

$$\begin{aligned} \begin{aligned} \varepsilon _{xx}^0&=A_{11} N_{xx} +A_{12} N_{\theta \theta } +B_{11} w_{0,xx} \\&\quad +r^{-2}B_{12} w_{0,\theta \theta } +A_{00} N_{xx}^T , \\ \varepsilon _{\theta \theta }^0&=A_{11} N_{\theta \theta } +A_{12} N_{xx} +B_{12} w_{0,xx} \\&\quad +r^{-2}B_{11} w_{0,\theta \theta } +A_{00} N_{\theta \theta }^T , \\ \gamma _{x\theta }^0&=A_{44} N_{x\theta } +r^{-1}B_{44} w_{0,x\theta } . \end{aligned} \end{aligned}$$

(9)

Considering the external harmonic excitation p and temperature variation $\Delta \hat{T}\left( z \right)$, the governing equations of the spinning cylindrical shell are [15]

$$\begin{aligned}&N_{xx,x} +r^{-1}N_{x\theta ,\theta } \nonumber \\&\quad =I_0 \left( {\ddot{u}_0 -\Omega ^{2}u_{0,\theta \theta } } \right) , \quad r^{-1}N_{\theta \theta ,\theta } +N_{x\theta ,x} \nonumber \\&\quad =I_0 \left[ {\ddot{v}_0 -2\Omega \dot{w}_0 -\Omega ^{2}(v_{0,\theta \theta } +2w_{0,\theta } )} \right] , \nonumber \\&M_{xx,xx} +r^{-2}M_{\theta \theta ,\theta \theta } -r^{-1}N_{\theta \theta }\nonumber \\&\quad +\,2r^{-1}M_{x\theta ,x\theta } +\hat{{N}}+p \nonumber \\&\quad =I_0 \left[ {\ddot{w}_0 +2\Omega \dot{v}_0 -\Omega ^{2}\left( {w_{0,\theta \theta } -2v_{0,\theta } } \right) +ch\dot{w}_0 } \right] ,\nonumber \\ \end{aligned}$$

(10)

where c ($\hbox {kg}/\hbox {m}^{3}\hbox {s}$) is the cylindrical shell’s intrinsic structural damping coefficient. Expression of the nonlinear term $\hat{N}$ is

$$\begin{aligned} \hat{{N}}= & {} r^{-1}\left[ \left( {rN_{xx} w_{0,x} +N_{x\theta } w_{0,\theta } } \right) _{,x} \right. \\&+\left. \left( {r^{-1}N_{\theta \theta } w_{0,\theta } +N_{x\theta } w_{0,x} } \right) _{,\theta } \right] . \end{aligned}$$

Besides, the external harmonic excitation can be assumed as $p\left( t \right) =\bar{Q}\cos nt\cos \omega t$, where $\omega$ and $\bar{Q}$ are the excitation frequency and amplitude of p, respectively.

In accordance with Eq. (3), the nonlinear kinematic compatibility equation is derived readily as

$$\begin{aligned}&r^{-2}\varepsilon _{xx,\theta \theta }^0 +\varepsilon _{\theta \theta ,xx}^0 -r^{-1}\gamma _{x\theta ,x\theta }^0 =r^{-2}w_{0,x\theta }^2 \nonumber \\&\quad -\,r^{-2}w_{0,xx} w_{0,\theta \theta } +r^{-1}w_{0,xx} . \end{aligned}$$

(11)

2.2 Equations of motion

In this section, the nonlinear kinematic compatibility equilibrium (11) is solved firstly. Similar to contributions of the in-plane Airy stress functions, in the present study, a new stress function $\psi$ is introduced with the following relationship

$$\begin{aligned}&N_{xx} =r^{-2}\psi _{,\theta \theta } -N^{T};\,\,N_{\theta \theta } =\psi _{,xx} -N^{T};\\&\quad N_{x\theta } =-r^{-1}\psi _{,x\theta } , \end{aligned}$$

Substituting Eq. (9) into Eq. (11) and considering the above relationship, the nonlinear kinematic compatibility equation becomes

$$\begin{aligned}&r^{-4}A_{11} \psi _{,\theta \theta \theta \theta } +r^{-2}\left( {A_{44} +2A_{12} } \right) \psi _{,xx\theta \theta } \nonumber \\&\quad +\,A_{11} \psi _{,xxxx} +B_{12} w_{0,xxxx} +r^{-4}B_{12} w_{0,\theta \theta \theta \theta } \nonumber \\&\quad +\,r^{-2}\left( {2B_{11} -B_{44} } \right) w_{0,xx\theta \theta } =r^{-2}w_{0,x\theta }^2 \nonumber \\&\quad -\,r^{-2}w_{0,xx} w_{0,\theta \theta }+r^{-1}w_{0,xx} , \end{aligned}$$

(12)

Fig. 2

Distribution of different GPL patterns

The assumed model method [29, 35] is adopted to solve the nonlinear kinematic compatibility equation. Approximate solutions $w_0 =W_{mn} \left( t \right) \varphi _m \left( x \right) \cos n\theta$, $u_0 =U_{mn} \left( t \right) \varphi _m \left( x \right) _{,x} \cos n\theta$, $v_0 =V_{mn} \left( t \right) \varphi _m \left( x \right) \sin n\theta$ are used, where $W_{mn}$, $U_{mn}$, $V_{mn}$ are the natural model amplitudes of the cylindrical shell in the radial, axial, and circumferential directions, respectively. Circumferential and axial half waves numbers are n and m, respectively. $\varphi _m \left( x \right)$ is the model function and dependent on constraint conditions of both ends of the cylindrical shell [15].

Assuming both ends of the cylindrical shell are simply-supported, $\varphi _m \left( x \right) =\sin \alpha x$ exists [36], where $\alpha =m\pi /L$. And then, Eq. (12) can be rewritten as

$$\begin{aligned}&r^{-4}A_{11} \psi _{,\theta \theta \theta \theta } +r^{-2}\left( {A_{44} +2A_{12} } \right) \psi _{,xx\theta \theta } \nonumber \\&\quad +\,A_{11} \psi _{,xxxx} = F_1 \sin \left( {\alpha x} \right) \cos \left( {n\theta } \right) W_{mn} \nonumber \\&\quad +\,\frac{1}{2}\left[ {\cos \left( {2\alpha x} \right) -\cos \left( {2n\theta } \right) } \right] r^{-2}\alpha ^{2}n^{2}W_{mn}^2 ; \end{aligned}$$

(13)

where the coefficient $F_{1}$ is

$$\begin{aligned} F_1= & {} -r^{-1}\alpha ^{2}-B_{12} \alpha ^{4}-B_{12} r^{-4}n^{4}\\&-\,r^{-2}\left( {2B_{11} -B_{44} } \right) \alpha ^{2}n^{2}. \end{aligned}$$

Then, solving $\psi$ from Eq. (13) yields

$$\begin{aligned} \psi= & {} C_1 \cos \left( {2\alpha x} \right) W_{mn}^2 -C_2 \cos \left( {2n\theta } \right) W_{mn}^2 \nonumber \\&+\,C_3 \sin \left( {\alpha x} \right) \cos \left( {n\theta } \right) W_{mn} ; \end{aligned}$$

(14)

where the coefficients $C_\mathrm{i} \,\left( {i=1,\,2,\,3} \right)$ are

$$\begin{aligned} \begin{aligned} C_1&=\frac{r^{-2}n^{2}}{32\alpha ^{2}A_{11} };\,\,C_2 =\frac{r^{2}\alpha ^{2}}{32n^{2}A_{11} }; \\ C_3&=\frac{F_1 }{r^{-2}\left( {A_{44} +2A_{12} } \right) \alpha ^{2}n^{2}+A_{11} \alpha ^{4}+A_{11} r^{-4}n^{4}}. \end{aligned} \end{aligned}$$

In Eq. (10), it is noticed that the governing equation in the radial direction of the cylindrical shell is coupled with that in circumferential direction when the spinning motion ($\varOmega \ne 0)$ is considered in the present model. Thus, it is unreasonable to ignore Eqs. (10)$_{1-2}$, directly. Following the procedure in Refs. [14, 15] and according to Eqs. (10)$_{1-2}$, the natural model amplitudes in the axial $U_{mn}$ and circumferential $V_{mn}$ can be derived as

$$\begin{aligned} U_{mn} =\Gamma _{11} W_{mn} ,\,\,V_{mn} =\Gamma _{12} W_{mn} . \end{aligned}$$

(15)

where $\varGamma _{ij}$ ($i,j=1,\,2$) are the coefficients given in “Appendix B”. Considering Eq. (15) and the new stress function $\psi$, Eq. (10)$_{3}$ becomes

$$\begin{aligned}&C_{12} \psi _{,xxxx} +2r^{-2}\left( {C_{11} -C_{44} } \right) \psi _{,xx\theta \theta } \nonumber \\&\qquad +r^{-4}C_{12} \psi _{,\theta \theta \theta \theta } +D_{11} w_{0,xxxx} \nonumber \\&\qquad +2r^{-2}\left( {D_{12} +D_{44} } \right) w_{0,xx\theta \theta } +r^{-4}D_{11} w_{0,\theta \theta \theta \theta } \nonumber \\&\qquad -r^{-1}\psi _{,xx} +r^{-1}N^{T} +\left( {r^{-2}\psi _{,\theta \theta } -N^{T}} \right) w_{0,xx} \nonumber \\&\qquad +r^{-2}\left( {\psi _{,xx} -N^{T}} \right) w_{0,\theta \theta } -2r^{-2}\psi _{,x\theta } w_{0,x\theta } \nonumber \\&\qquad +\bar{{Q}}\cos \left( {n\theta } \right) \cos \left( {\omega t} \right) \nonumber \\&\quad =I_0 \left[ \ddot{w}_0 +\left( {2\Omega \Gamma _{12} +ch} \right) \dot{w}_0 \right. \nonumber \\&\qquad -\left. \Omega ^{2}\left( {w_{0,\theta \theta } -2\Gamma _{12} w_{0,\theta } } \right) \right] , \end{aligned}$$

(16)

Substituting the obtained solution of stress function $\psi$ into Eq. (16) and using Galerkin approach, a final equation of motion in terms of the radial displacement of the spinning cylindrical shell is obtained as follows

$$\begin{aligned}&I_0 \ddot{W}_{mn} +I_0 \tilde{\mu }\dot{W}_{mn} +\tilde{\beta }_1 W_{mn} +\tilde{\beta }_3 W_{mn}^3 \nonumber \\&\quad +\frac{2\bar{{Q}}r_m \cos \left( {\omega t} \right) }{m\pi }=0. \end{aligned}$$

(17)

where the external harmonic excitation and thermal load are considered. Coefficients are given as

$$\begin{aligned} \begin{aligned} \tilde{\mu }&=2\Omega \Gamma _{12} +ch; \\ \tilde{\beta }_1&=I_0 \Omega ^{2}n^{2}-\left( {C_{12} C_3 +D_{11} } \right) \left( {\alpha ^{4}+r^{-4}n^{4}} \right) \\&\quad -r^{-1}C_3 \alpha ^{2} -2r^{-2}\left[ \left( {C_{11} -C_{44} } \right) C_3 \right. \\&\quad +\left. \left( {D_{12} +D_{44} } \right) \right] \alpha ^{2}n^{2}-\left( {\alpha ^{2}+r^{-2}n^{2}} \right) N^{T};\\ \tilde{\beta }_3&=2r^{-2}\alpha ^{2}n^{2}\left( {C_1 +C_2 } \right) ; \\ r_m&=-1+\left( {-1} \right) ^{m}; \\ \end{aligned} \end{aligned}$$

As shown in Eq. (17), the Coriolis effect due to spinning motion plays a role in the damping terms besides shell’s intrinsic structural damping. This unusual phenomenon can be seen in the following numerical analysis.

2.3 Effective material properties

Figure 2 demonstrates the distribution of GPLs in the novel composite cylindrical shell in which three different GPLs distribution patterns are plotted. As shown, volume fractions ($V_{GPL}$) of GPLs in patterns A and B are graded and continuously change through the shell thickness direction, while it is uniformly dispersed in the GPL pattern C. We assume that the matrix and GPLs nanofillers are in perfect bond.

Then, we define the following functions in terms of z to characterize the distributions of GPLs in which GPL patterns A, B, and C are denoted by shape functions $\Theta _{i}$ ($i = 1,\,2,\,3$), respectively.

$$\begin{aligned} \Theta _\mathrm{i} \left( z \right)= & {} \left\{ {{\begin{array}{ccc} {\Theta _1 \left( z \right) }&{} {\Theta _2 \left( z \right) }&{} {\Theta _3 \left( z \right) } \\ \end{array} }} \right\} \nonumber \\= & {} \left\{ {{\begin{array}{ccc} {1-\cos \left( {\frac{\pi z}{h}} \right) }&{} {1-\cos \left( {\frac{\pi z}{2h}+\frac{\pi }{4}} \right) }&{} 1 \\ \end{array} }} \right\} . \end{aligned}$$

(18)

The relationship between the shape functions $\Theta _{i}$ and the volume fraction $V_{GPL}$ of GPLs is

$$\begin{aligned} V_{GPL} =S_\mathrm{i} \Theta _\mathrm{i} \left( z \right) , \end{aligned}$$

where the peak values $S_{i}$ ($i = 1,\,2,\,3$) of the GPLs’ volume fraction are functions of $\varLambda _{\mathrm{GPL}}$. They are expressed by

$$\begin{aligned} \frac{S_\mathrm{i} }{h}\int _{-h/2}^{h/2} {\Theta _\mathrm{i} (z)} \hbox {d}z=\frac{\Lambda _{GPL} \rho _m }{\Lambda _{GPL} \rho _m +\rho _{GPL} -\Lambda _{GPL} \rho _{GPL} }.\nonumber \\ \end{aligned}$$

(19)

The geometrical sizes of GPLs can change the useful Young’s modulus of the GPLs-reinforced composite. Therefore, the modified Halpin–Tsai micromechanics model validated by Rafiee et al. [6] is adopted to calculate the useful Young’s modulus rather than the rule of mixtures. Rafiee’s experiment revealed that this micromechanics model just generates $\sim$13% relative error to predict the useful Young’s modulus as the GPLs weight fraction is 0.1%. The useful Poisson’s ratio, mass density, and thermal expansion coefficient can be estimated by the rule of mixtures. The micromechanics theory [37, 38] is used to predict the useful thermal conductivity coefficient of the novel composite. Their expressions are given as follows:

$$\begin{aligned} E_c \left( z \right)= & {} E_m \left[ \frac{3}{8}\left( {\frac{1+\xi _L \eta _L V_{GPL} }{1-\eta _L V_{GPL} }} \right) \right. \nonumber \\&+\left. \frac{5}{8}\left( {\frac{1+\xi _B \eta _B V_{GPL} }{1-\eta _B V_{GPL} }} \right) \right] , \nonumber \\ \nu _c \left( z \right)= & {} \nu _{GPL} V_{GPL} +\nu _m \left( {1-V_{GPL} } \right) , \nonumber \\ \rho _c \left( z \right)= & {} \rho _{GPL} V_{GPL} +\rho _m \left( {1-V_{GPL} } \right) , \nonumber \\ \alpha _c \left( z \right)= & {} \alpha _{GPL} V_{GPL} +\alpha _m \left( {1-V_{GPL} } \right) , \nonumber \\ k_c \left( z \right)= & {} k_m \left[ \frac{V_{GPL} }{3}\left( \frac{2}{H+1/(k_x /k_m -1)}\right. \right. \nonumber \\&+\left. \left. \frac{1}{(1-H)/2+1/(k_z /k_m -1)}\right) +1 \right] ,\nonumber \\ \end{aligned}$$

(20)

where the subscripts ‘GPL’ and ‘m’ represent the corresponding material properties of the GPLs and polymer matrix, respectively. $\xi _{L}$, $\xi _{B}$, $\eta _{L}$, and $\eta _{B}$ are geometrical parameters of the GPLs with the following expressions

$$\begin{aligned} \xi _L= & {} 2\frac{L_{GPL} }{t_{GPL} },\,\,\eta _L =2\frac{E_{GPL} -E_m }{E_{GPL} -\xi _L E_m }, \\ \xi _B= & {} 2\frac{b_{GPL} }{t_{GPL} },\,\,\eta _B =2\frac{E_{GPL} -E_m }{E_{GPL} -\xi _B E_m }, \end{aligned}$$

where $L_{\mathrm{GPL}}$, $b_{\mathrm{GPL}}$, and $t_{\mathrm{GPL}}$ are the GPLs’ average length, width, and thickness, respectively. In Eq. (20), $k_{z}$ and $k_{x}$, respectively, are the thermal conductivity coefficients of the GPLs through the thickness and in-plane directions. H is a parameter related to the GPL’s geometrical sizes given by

$$\begin{aligned} H= & {} \frac{\hbox {ln}\left[ {\left( {\xi _L /2+\sqrt{(\xi _L /2)^{2}-1}} \right) \xi _L /2} \right] }{\left( {(\xi _L /2)^{2}-1} \right) ^{1.5}}\\&-\,\frac{1}{(\xi _L /2)^{2}-1} \end{aligned}$$

and

$$\begin{aligned} k_x= & {} \frac{k_{GPL} }{2R_k k_{GPL} /L_{GPL} +1},\\ k_z= & {} \frac{k_{GPL} }{2R_k k_{GPL} /t_{GPL} +1}, \end{aligned}$$

where $R_{k}$ is a constant that is dependent on composite material properties.

3 Undamped free vibration

In this section, vibration characteristics of backward and forward traveling waves of the spinning cylindrical shell subjected to the thermal load are studied. By ignoring the external excitation and the shell’s intrinsic structural damping effect, the following governing equations of the spinning cylindrical shell can be derived on the basis of Eq. (10).

$$\begin{aligned}&\left[ {{\begin{array}{ccc} {L_{\mathrm{11}} }&{}\quad {L_{\mathrm{12}} }&{}\quad {L_{\mathrm{13}} } \\ {L_{\mathrm{21}} }&{}\quad {L_{\mathrm{22}} }&{}\quad {L_{\mathrm{23}} } \\ {L_{\mathrm{31}} }&{}\quad {L_{\mathrm{32}} }&{}\quad {L_{\mathrm{33}} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {u_0 } \\ {v_0 } \\ {w_0 } \\ \end{array} }} \right\} +\left\{ {{\begin{array}{c} {N_1^\mathrm{non} } \\ {N_2^\mathrm{non} } \\ {N_3^\mathrm{non} } \\ \end{array} }} \right\} +\left\{ {{\begin{array}{c} 0 \\ 0 \\ {r^{-1}N^{T}} \\ \end{array} }} \right\} \nonumber \\&\quad =I_0 \left\{ {{\begin{array}{c} {\ddot{u}_0 } \\ {\ddot{v}_0 } \\ {\ddot{w}_0 } \\ \end{array} }} \right\} +I_0 \left[ {{\begin{array}{ccc} 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {-2\Omega } \\ 0&{}\quad {2\Omega }&{}\quad \hbox {0} \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\dot{u}_0 } \\ {\dot{v}_0 } \\ {\dot{w}_0 } \\ \end{array} }} \right\} \end{aligned}$$

(21)

where differential operators $L_{gh}$ ($g, h = 1,\,2,\,3$) are given in “Appendix A”. Expressions of nonlinear items $N_k^\mathrm{non}$ ($k = 1,\, 2,\,3$) can be found in Ref. [15].

Inserting the assumed shell model in Sect. 2.2 into the linear parts of Eq. (21), the following determinant related to the shell natural frequencies can be derived

$$\begin{aligned} \left| {{\begin{array}{ccc} {\Gamma _{11}^{*} +I_0 \varpi ^{2}}&{} {\Gamma _{12}^{*} }&{} {\Gamma _{13}^{*} } \\ {\Gamma _{21}^{*} }&{} {\Gamma _{22}^{*} +I_0 \varpi ^{2}}&{} {\Gamma _{23}^{*} -2I_0 \Omega \varpi } \\ {\Gamma _{31}^{*} }&{} {\Gamma _{32}^{*} -2I_0 \Omega \varpi }&{} {\Gamma _{33}^{*} +I_0 \varpi ^{2}} \\ \end{array} }} \right| =0.\nonumber \\ \end{aligned}$$

(22)

where determinant coefficients $\varGamma _{gh}^*$ ($g,h=1,\,2,\,3)$ are listed in “Appendix B”. Three coupled roots for natural frequencies ($\varpi$) can be calculated, and they are the frequencies along $u_{0}$, $v_{0}$, and $w_{0}$ directions, respectively, in which the first two lowest values of $\varpi$ are the natural frequencies of forward and backward traveling waves in the $w_{0}$ direction. As shown in Eq. (22), when the spinning motion is ignored ($\varOmega = 0$), $\varpi$ just occurs in the principal diagonal of the determinant, and a standing wave forms replacing traveling waves.

4 Harmonic resonances

In this section, perturbation analyses of the harmonic resonances for the GPLs-reinforced composite cylindrical shell are implemented by using the multiple scale method [39, 40]. The multiple scales method is one of the perturbation techniques to obtain approximate analytical solutions of problems whose exact solution cannot be found. This method is always adopted to study harmonic resonance behaviors of structures [25,26,27,28,29,30] and problems where the solutions include more than one temporal or spatial scale [41]. In this method, we introduce independent fast time-scale and slow time-scale variables to capture the slow modulation of the pattern and treat these as separated variables in addition to the original variables that must be retained to describe the pattern state itself.

Introducing an internal damping parameter, i.e., $\tilde{\mu }=2\hat{\omega }_{mn}\zeta$, where $\hat{\omega }_{mn}$ is a frequency parameter defined by $\hat{\omega }_{mn}^2 =\hat{\beta }_1 /I_0$, Eq. (17) can be rewritten as

$$\begin{aligned} \ddot{W}_{mn} \,+\,2\hat{{\omega }}_{mn} \zeta \dot{W}_{mn} \,+\,\hat{{\omega }}_{mn}^2 W_{mn} \,+\,\beta _3 W_{mn}^3 =\beta _0 \cos \left( {\omega t} \right) , \end{aligned}$$

(23)

where expressions of coefficients are given as

$$\begin{aligned} {\beta _{\mathrm{3}} =\tilde{\beta }_{\mathrm{3}} }/{I_{\mathrm{0}} };\quad \beta _0 =\frac{-2\bar{{Q}}r_m }{m\pi I_{\mathrm{0}} }. \end{aligned}$$

4.1 Primary resonance

Introducing the following variables $w_1 =W_{mn}$, $\varepsilon \bar{\mu }=\hat{\omega }_{mn}\zeta$, $\varepsilon \bar{\beta }_3 =\beta _3$, and $\varepsilon \bar{\beta }_0 =\beta _0$ to express the damping and external excitation as small parameters, and ignoring the overlines of all the parameters, Eq. (23) becomes

$$\begin{aligned} \ddot{w}_1 +2\varepsilon \mu \dot{w}_1 +\hat{{\omega }}_{mn}^2 w_1 +\varepsilon \beta _3 w_1^3 =\varepsilon \beta _0 \cos \left( {\omega t} \right) ; \end{aligned}$$

(24)

where $\varepsilon$ is a dimensionless small parameter. The approximate solution of Eq. (24) is assumed as:

$$\begin{aligned} w_1= & {} w_1^{\left( 0 \right) } \left( {T_0 ,T_1 ,T_2 } \right) +\varepsilon w_1^{\left( 1 \right) } \left( {T_0 ,T_1 ,T_2 } \right) \nonumber \\&+\,\varepsilon ^{2}w_1^{\left( 2 \right) } \left( {T_0 ,T_1 ,T_2 } \right) \end{aligned}$$

(25)

where $T_{0}=\tau$, $T_{1}=\varepsilon \tau$ and $T_{2}=\varepsilon ^{2} \tau$ represent different temporal scales. Assuming that $\omega -\hat{\omega }_{mn}$ is an infinitesimal and $\omega =\hat{\omega }_{mn} +\varepsilon \sigma$ exists, where $\sigma$ is a detuning parameter to measure difference of shell natural frequencies and excitation frequencies. Combining Eqs. (24) and (25) and obeying a convention track yield

$$\begin{aligned}&D_0^2 w_1^{\left( 0 \right) } +\hat{{\omega }}_{mn}^2 w_1^{\left( 0 \right) } =0,\nonumber \\&D_0^2 w_1^{\left( 1 \right) } +\hat{{\omega }}_{mn}^2 w_1^{\left( 1 \right) } =-2D_0 D_1 w_1^{\left( 0 \right) } -2\mu D_0 w_1^{\left( 0 \right) } \nonumber \\&\quad -\beta _3 w_1^{\left( 0 \right) } w_1^{\left( 0 \right) } w_1^{\left( 0 \right) }+\beta _0 \cos \left( {\hat{{\omega }}_{mn} T_0 +\sigma T_1 }\right) , \end{aligned}$$

(26)

The solution for $w_1^{\left( 0 \right) }$ in Eq. (26)$_{1}$ can be expressed as

$$\begin{aligned} w_1^{\left( 0 \right) } \left( {T_0 ,T_1 } \right) =A_1 \left( {T_1 } \right) \hbox {e}^{\mathrm{i}\hat{{\omega }}_{mn} T_0 }+\bar{{A}}_1 \left( {T_1 } \right) \hbox {e}^{-\mathrm{i}\hat{{\omega }}_{mn} T_0 },\qquad \quad \end{aligned}$$

(27)

where $A_1 \left( {T_1 } \right)$ is complex-valued amplitude function with conjugates $\bar{A}_1 \left( {T_1 } \right)$. $\hbox {i}=\sqrt{-1}$. Inserting Eq. (27) into Eq. (26)$_{2}$ leads to

$$\begin{aligned}&D_0^2 w_1^{\left( 1 \right) } +\hat{{\omega }}_{mn}^2 w_1^{\left( 1 \right) } =\left[ -2\hbox {i}\hat{{\omega }}_{mn} \left( {D_1 A_1 +\mu A_1 } \right) \right. \\&\quad -\left. 3\beta _3 A_1^2 \bar{{A}}_1 +\frac{\beta _0 }{2}e^{\mathrm{i}\sigma T_1 } \right] e^{\mathrm{i}\hat{{\omega }}_{mn} T_0 }+{\text {coco}}+{\text {NST}}; \end{aligned}$$

where coco is the complex conjugate of the preceding terms. NST is the non-secular terms. The secular terms can be ignored by setting

$$\begin{aligned} 2\hbox {i}\hat{{\omega }}_{mn} \left( {D_1 A_1 +\mu A_1 } \right) +3\beta _3 A_1^2 \bar{{A}}_1 -\frac{\beta _0 }{2}e^{\mathrm{i}\sigma T_1 }=0.\qquad \quad \end{aligned}$$

(28)

Let

$$\begin{aligned} A_1 \left( {T_1 } \right) =\frac{1}{2}a\left( {T_1 } \right) e^{\mathrm{i}\varphi \left( {T_1 } \right) }, \end{aligned}$$

(29)

where $a\left( {T_1 } \right)$ and $\varphi \left( {T_1 } \right)$ are the real-valued functions. Inserting Eq. (29) into Eq. (28) yields

$$\begin{aligned} \begin{aligned}&D_1 a=-\mu a+\frac{\beta _0 }{2\hat{{\omega }}_{mn} }\sin \gamma ; \\&aD_1 \gamma =a\sigma -\frac{3\beta _3 }{8\hat{{\omega }}_{mn} }a^{3}+\frac{\beta _0 }{2\hat{{\omega }}_{mn} }\cos \gamma ; \end{aligned} \end{aligned}$$

(30)

where $\gamma =\sigma T_1 -\varphi$. A steady-state solution determining the amplitude and phase of the system can be derived by setting $D_1 a=0$ and $D_1 \gamma =0$ in Eq. (30). One can obtain

$$\begin{aligned}&\left[ {\mu ^{2}+\left( {\sigma -\frac{3\beta _3 }{8\hat{{\omega }}_{mn} }a^{2}} \right) ^{2}} \right] a^{2}=\left( {\frac{\beta _0 }{2\hat{{\omega }}_{mn} }} \right) ^{2}, \nonumber \\&\quad \tan \gamma =\frac{8\hat{{\omega }}_{mn}^2 \zeta }{3\beta _3 a^{2}-8\hat{{\omega }}_{mn} \left( {\omega -\hat{{\omega }}_{mn} } \right) }. \end{aligned}$$

(31)

Multiplying $\varepsilon ^{2}$ to both sides of Eq. (31)$_{1}$ and replacing corresponding variables by the original ones, Eq. (31)$_{1}$ can be rewritten as

$$\begin{aligned}&\left[ {\left( {\hat{{\omega }}_{mn} \zeta } \right) ^{2}+\left( {\omega -\hat{{\omega }}_{mn} -\frac{3\beta _3 }{8\hat{{\omega }}_{mn} }a^{2}} \right) ^{2}} \right] a^{2}\nonumber \\&\quad =\left( {\frac{\beta _0 }{2\hat{{\omega }}_{mn} }} \right) ^{2}. \end{aligned}$$

(32)

It is noted that Eq. (32) characterizes amplitude–frequency relations for the primary resonance of the composite cylindrical shell system. If $0<a<\beta _0 /2\zeta \hat{\omega }_{mn}^2$, real roots of $\omega$ can be calculated for a given amplitude. We introduce two perturbation variables $\Delta \hbox {a}_s$ and $\Delta \upgamma _s$ satisfying $\hbox {a}=\hbox {a}_s +\Delta \hbox {a}_s$ and $\upgamma =\upgamma _s +\Delta \upgamma _s$, respectively. Substituting these two equations into Eq. (30) and neglecting nonlinear items belonging to the small increments, the following perturbation equations can be derived

$$\begin{aligned} \begin{aligned} D_1 \Delta a_s&=-\mu \Delta a_s +\frac{\beta _0 \cos \gamma _s }{2\hat{{\omega }}_{mn} }\Delta \gamma _s ; \\ D_1 \Delta \gamma _s&=\left( {\frac{\sigma }{a_s }-\frac{9\beta _3 a_s }{8\hat{{\omega }}_{mn} }} \right) \Delta a_s -\frac{\beta _0 \sin \gamma _s }{2\hat{{\omega }}_{mn} a_s }\Delta \gamma _s ; \end{aligned} \end{aligned}$$

(33)

And then, considering Eq. (30) and eliminating $\upgamma _s$, Eq. (33) can be rewritten as

$$\begin{aligned} \left\{ {{\begin{array}{c} {D_1 \Delta a_{\mathrm{s}} } \\ {D_1 \Delta \gamma _s } \\ \end{array} }} \right\} {=}\left[ {{ \begin{array}{c@{\quad }c} {-\mu }&{} {\frac{3\beta _3 a_s^3 }{8\hat{{\omega }}_{mn} }-a_s \sigma } \\ {\left( {\frac{\sigma }{a_s }-\frac{9\beta _3 a_s }{8\hat{{\omega }}_{mn} }} \right) }&{} {-\mu } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\Delta a_s } \\ {\Delta \gamma _s } \\ \end{array} }} \right\} , \end{aligned}$$

and the characteristic determinant of the above equation is

$$\begin{aligned} \det \left| {\left( {\lambda _p } \right) } \right| =\lambda _p^2 +2\mu \lambda _p +\mathrm{X}_p , \end{aligned}$$

where

$$\begin{aligned} \mathrm{X}_p =\frac{27\beta _3^2 }{64\hat{{\omega }}_{mn}^2 }a^{4}-\frac{3\beta _3 \sigma }{2\hat{{\omega }}_{mn} }a^{2}+\sigma ^{2}+\mu ^{2}. \end{aligned}$$

(34)

Therefore, the necessary and sufficient conditions of the spinning composite cylindrical shell under the stable primary resonance are $\mu >0$ and $\hbox {X}_p >0$.

4.2 1/3 subharmonic resonance

In this section, analytical solutions for 1/3 subharmonic resonance ($\omega =3\hat{\omega }_{mn} +\varepsilon \sigma$) are derived. Introducing the following variables $w_1 =W_{mn}$, $\varepsilon \bar{\mu }=\hat{\omega }_{mn}\zeta$, and $\varepsilon \bar{\beta }_3 =\beta _3$, and ignoring the overlines of all the parameters, Eq. (23) becomes

$$\begin{aligned} \ddot{w}_1 +2\varepsilon \mu \dot{w}_1 +\hat{{\omega }}_{mn}^2 w_1 +\varepsilon \beta _3 w_1^3 =\beta _0 \cos \left( {\omega t} \right) , \end{aligned}$$

(35)

Following the procedure of the above section and considering $\omega =3\hat{\omega }_{mn} +\varepsilon \sigma$, Eq. (26) becomes

$$\begin{aligned}&D_0^2 w_1^{\left( 0 \right) } +\hat{{\omega }}_{mn}^2 w_1^{\left( 0 \right) } -\beta _0 \cos \left( {\omega t} \right) =0, \nonumber \\&D_0^2 w_1^{\left( 1 \right) } +\hat{{\omega }}_{mn}^2 w_1^{\left( 1 \right) } =-2D_0 D_1 w_1^{\left( 0 \right) } -2\mu D_0 w_1^{\left( 0 \right) } \nonumber \\&\quad -\beta _3 w_1^{\left( 0 \right) } w_1^{\left( 0 \right) } w_1^{\left( 0 \right) } . \end{aligned}$$

(36)

Table 1 Material properties of composite components [42]

The solution for $w_1^{\left( 0 \right) }$ in Eq. (36)$_{1}$ can be expressed as

$$\begin{aligned}&w_1^{\left( 0 \right) } \left( {T_0 ,T_1 } \right) =A_1 \left( {T_1 } \right) e^{\mathrm{i}\hat{{\omega }}_{mn} T_0 }+\Lambda e^{\mathrm{i}\omega T_0 }\nonumber \\&\quad +\bar{{A}}_1 \left( {T_1 } \right) e^{-\mathrm{i}\hat{{\omega }}_{mn} T_0 }+\Lambda e^{-\hbox {i}\omega T_0 }, \end{aligned}$$

(37)

where

$$\begin{aligned} \Lambda =\frac{\beta _0 }{2\left( {\hat{{\omega }}_{mn}^2 -\omega ^{2}} \right) }. \end{aligned}$$

Inserting Eq. (37) into Eq. (36)$_{2}$ leads to

$$\begin{aligned} \begin{aligned}&D_0^2 w_1^{\left( 1 \right) } +\hat{{\omega }}_{mn}^2 w_1^{\left( 1 \right) } =-\left[ 2\hbox {i}\hat{{\omega }}_{mn} \left( {D_1 A_1 +\mu A_1 } \right) \right. \\&\quad +\left. 6\beta _3 A_1 \Lambda ^{2}+3\beta _3 A_1^2 \bar{{A}}_1 \right] e^{\mathrm{i}\hat{{\omega }}_{mn} T_0 } \\&\quad -\Lambda \left[ {2\mu \hbox {i}\omega +3\beta _3 \Lambda ^{2}+6\beta _3 A_1 \bar{{A}}_1 } \right] e^{\mathrm{i}\omega T_0 }\\&\quad -\beta _3 \left[ A_1^3 e^{\mathrm{3i}\hat{{\omega }}_{mn} T_0 }+\Lambda ^{3}e^{\mathrm{3i}\omega T_0 }+3A_1^2 \Lambda e^{\mathrm{i}\left( {2\hat{{\omega }}_{mn} +\omega } \right) T_0 }\right. \\&\quad +3\bar{{A}}_1^2 \Lambda e^{\mathrm{i}\left( {\omega -2\hat{{\omega }}_{mn} } \right) T_0 } + 3A_1 \Lambda ^{2}e^{\mathrm{i}\left( {\hat{{\omega }}_{mn} +2\omega } \right) T_0 }\\&\quad \left. +3A_1 \Lambda ^{2}e^{\mathrm{i}\left( {\hat{{\omega }}_{mn} -2\omega } \right) T_0 } \right] +cc. \end{aligned} \end{aligned}$$

The secular terms in the above equation can be ignored by setting

$$\begin{aligned}&2\hbox {i}\hat{{\omega }}_{mn} \left( {D_1 A_1 +\mu A_1 } \right) +3\beta _3 A_1^2 \bar{{A}}_1 \nonumber \\&\quad +6\beta _3 A_1 \Lambda ^{2}+3\beta _3 \bar{{A}}_1^2 \Lambda e^{\mathrm{i}\sigma T_1 }=0. \end{aligned}$$

(38)

Inserting Eq. (29) into Eq. (38) yields

$$\begin{aligned} \begin{aligned} D_1 a&=-\mu a-\frac{3\beta _3 \Lambda }{4\hat{{\omega }}_{mn} }a^{2}\sin \gamma , \\ D_1 \gamma&=\sigma -\frac{9\beta _3 }{\hat{{\omega }}_{mn} }\left( {\frac{a^{2}}{8}+\Lambda ^{2}+\frac{\Lambda }{4}a\cos \gamma } \right) , \end{aligned} \end{aligned}$$

(39)

where $\gamma =\sigma T_1 -3\varphi$. In order to obtain a steady-state solution determining the amplitude of the system, one can obtain the following equation by setting $D_1 a=0$ and $D_1 \gamma =0$.

$$\begin{aligned} \left( {\hbox {3}\mu } \right) ^{\mathrm{2}}+\left[ {\sigma -\frac{9\beta _3 }{\hat{{\omega }}_{mn} }\left( {\frac{a^{2}}{8}+\Lambda ^{2}} \right) } \right] ^{\mathrm{2}}=\left( {\frac{3\beta _3 \Lambda }{4\hat{{\omega }}_{mn} }a} \right) ^{\mathrm{2}}.\nonumber \\ \end{aligned}$$

(40)

Replacing corresponding variables by the original ones from Eq. (40), the amplitude–frequency relationships for 1/3 subharmonic resonance of the cylindrical shell system can be obtained

$$\begin{aligned}&\left( {\hbox {3}\hat{{\omega }}_{mn} \zeta } \right) ^{\mathrm{2}}+\left[ {\omega -3\hat{{\omega }}_{mn} -\frac{9\beta _3 }{\hat{{\omega }}_{mn} }\left( {\frac{a^{2}}{8}+\Lambda ^{2}} \right) } \right] ^{\mathrm{2}}\nonumber \\&\quad =\left( {\frac{3\beta _3 \Lambda }{4\hat{{\omega }}_{mn} }a} \right) ^{\mathrm{2}}. \end{aligned}$$

(41)

Equation (41) is an algebraic equation, and it can also be rewritten as the following form

$$\begin{aligned}&a^{4}+\left( {12\Lambda ^{2}-\frac{16\sigma \hat{{\omega }}_{mn} }{9\beta _3 }} \right) a^{2}\\&\quad +\frac{64}{81\beta _3^2 }\left[ {9\mu ^{2}\hat{{\omega }}_{mn}^2 +\left( {\sigma \hat{{\omega }}_{mn} -9\beta _3 \Lambda ^{2}} \right) ^{2}} \right] =0, \end{aligned}$$

where a is real and positive if and only if

$$\begin{aligned}&\Lambda ^{2}-\frac{4\sigma \hat{{\omega }}_{mn} }{27\beta _3 }<0; \\&\Lambda ^{4}-\frac{8\sigma \hat{{\omega }}_{mn} }{63\beta _3 }\Lambda ^{2}+\frac{16\mu ^{2}\hat{{\omega }}_{mn}^2 }{63\beta _3^2 }<0; \end{aligned}$$

The above inequality can ensure the occurrence of 1/3 subharmonic resonance. And then, the necessary and sufficient conditions ensuring stable 1/3 subharmonic resonance need to be discussed. Following procedures of the derivation of Eq. (33), perturbation equations in case of the 1/3 subharmonic resonance can be given as

$$\begin{aligned} \begin{aligned} D_1 \Delta a_{\mathrm{s}}&=-\left( {\mu +\frac{3\beta _3 \Lambda a_{\mathrm{s}} \sin \gamma _s }{2\hat{{\omega }}_{mn} }} \right) \Delta a_s \\&\quad -\frac{3\beta _3 \Lambda a_s^2 \cos \gamma _s }{4\hat{{\omega }}_{mn} }\Delta \gamma _s , \\ D_1 \Delta \gamma _s&=-\frac{9}{4}\left( {\frac{\beta _3 a_{\mathrm{s}} +\beta _3 \Lambda \cos \gamma _s }{\hat{{\omega }}_{mn} }} \right) \Delta a_s \\&\quad +\frac{9\beta _3 \Lambda a_{\mathrm{s}} \sin \gamma _s }{4\hat{{\omega }}_{mn} }\Delta \gamma _s , \end{aligned} \end{aligned}$$

(42)

Inserting Eq. (39) into Eq. (42) and ignoring the phase angle $\upgamma _s$, Eq. (42) is rewritten as

$$\begin{aligned}&\left\{ {{\begin{array}{c} {D_1 \Delta a_{\mathrm{s}} } \\ {D_1 \Delta \gamma _s } \\ \end{array} }} \right\} \\&\quad =\left[ {{\begin{array}{c@{\quad }c} \mu &{} {-\frac{a_s }{3}\left( {\sigma -\frac{9\beta _3 a_s^2 }{8\hat{{\omega }}_{mn} }-\frac{9\beta _3 \Lambda ^{2}}{\hat{{\omega }}_{mn} }} \right) } \\ {-\frac{9\beta _3 a_s }{4\hat{{\omega }}_{mn} }-\frac{1}{a_s }\left( {\sigma -\frac{9\beta _3 a_s^2 }{8\hat{{\omega }}_{mn} }-\frac{9\beta _3 \Lambda ^{2}}{\hat{{\omega }}_{mn} }} \right) }&{} {-3\mu } \\ \end{array} }} \right] \\&\qquad \left\{ {{\begin{array}{c} {\Delta a_s } \\ {\Delta \gamma _s } \\ \end{array} }} \right\} , \end{aligned}$$

and the characteristic determinant of the above equation can be expressed as

$$\begin{aligned} \det \left| {\left( {\lambda _s } \right) } \right| =\lambda _s^2 +2\mu \lambda _s +\mathrm{X}_s , \end{aligned}$$

where the coefficient $X_s$ can be calculated from

$$\begin{aligned} \mathrm{X}_s= & {} -\frac{27\beta _3^2 }{\hat{{\omega }}_{mn}^2 }\Lambda ^{4}+\frac{6\beta _3 \sigma }{\hat{{\omega }}_{mn} }\Lambda ^{2}+\frac{27\beta _3^2 }{64\hat{{\omega }}_{mn}^2 }a^{4}\nonumber \\&-\frac{1}{3}\sigma ^{2}-3\mu ^{2}. \end{aligned}$$

(43)

Therefore, the necessary and sufficient conditions for the spinning composite cylindrical shell under the stable 1/3 subharmonic resonance are $\mu >0$ and $\hbox {X}_s >0$.

5 Results and discussion

Assume the novel composite material is constituted by a mixture of graded GPLs and the epoxy resin. The geometrical sizes of the GPLs mentioned in Sect. 2.3 are $t_{\mathrm{GPL}}= 2.5\,\hbox {nm}$, $L_{\mathrm{GPL}}= 2.5\,\upmu \hbox {m}$, and $b_{\mathrm{GPL}}=1.25\,\upmu \hbox {m}$. Material properties of these two components are listed in Table 1. Numerical examples are carried out which focus on the vibration characteristics and nonlinear harmonic resonance behaviors of the spinning composite cylindrical shell in thermal environment.

Table 2 Lists of $\bar{\upomega }_/2\uppi$ ($\Omega = 0 \hbox { rad}/\hbox {s}$, $L/r=2$, $r=0.1\,\hbox {m}$, $h=0.247\,\hbox {mm}$)

To characterize the thermal environment of the graphene-reinforced cylindrical shell, we define temperature variation $\Delta T=T_\mathrm{o} -\hat{T}$ and $T_\mathrm{i} =\hat{T}$. Besides, a viscous damping factor $\xi$ is introduced to make $c={\xi \rho _m \hat{{\omega }}_{mn} }/{120}$ exist and examine the intrinsic structural damping that is different from the damping effect caused by the Coriolis effect. The following dimensionless linear natural frequency $\omega _{mn}$ and amplitude of the external excitation Q are introduced

$$\begin{aligned} \omega _{mn} =\varpi r\sqrt{\left( {1-\nu _m^2 } \right) \rho _m /E_m }, \ Q=2.85\times 10^{5}{\bar{{Q}}}/{E_m }. \end{aligned}$$

5.1 Validation

Vibration characteristics of traveling waves are calculated from Eq. (22). Nonlinear harmonic resonance responses are derived from analyses in Sect. 4. Present solutions on vibration characteristics and the amplitude–frequency relationship of the primary resonance are compared with those of other works to validate the analytical solution. Isotropic materials and a functionally graded material described by a power-law function model [32, 43] are introduced as

$$\begin{aligned} \begin{aligned}&\hbox {Isotropic material I}:E_\mathrm{o} =E_\mathrm{i} =71.02\hbox {GPa},\\&\quad \nu _\mathrm{o} =\nu _\mathrm{i} =0.3\hbox {1},\,\,\rho _\mathrm{o} =\rho _\mathrm{i} =2796\,\hbox {kg/m}^{\mathrm{3}}, \\&\hbox {Isotropic material II}:E_\mathrm{o} =E_\mathrm{i} =200\hbox {GPa},\\&\quad \nu _\mathrm{o} =\nu _\mathrm{i} =0.3,\,\,\rho _\mathrm{o} =\rho _\mathrm{i} =7971.8\,\hbox {kg/m}^{\mathrm{3}}, \\&\hbox {FG material}:E_\mathrm{o} =207.788\hbox {GPa},\,\,\nu _\mathrm{o} =0.317756,\\&\quad \rho _\mathrm{o} =8166\,\hbox {kg}/\hbox {m}^{\mathrm{3}}, \\&E_\mathrm{i} =205.098\hbox {GPa},\,\,\nu _\mathrm{i} =0.31,\,\,\rho _\mathrm{i} =8900\,\hbox {kg/m}^{\mathrm{3}}, \\ \end{aligned} \end{aligned}$$

where the subscripts ‘i’ and ‘o’ represent the corresponding material properties of inner and outer surfaces of the cylindrical shell, respectively.

Table 3 Dimensionless natural frequencies of a cylindrical shell ($\Omega = 10\,\hbox {rad}/\hbox {s}$, isotropic material II, $L/r = 5$, $h/r = 0.002$)

Natural frequencies of traveling waves of cylindrical shells are listed in Tables 2 and 3, where stationary and spinning cylindrical shells are considered, respectively. For different axial and circumferential wave numbers, the natural frequencies calculated from present analytical solutions agree well with the experimental results [19] of the cylindrical shell made of isotropic material I. In Table 3, $\left( {\upomega _{mn} } \right) ^{f}$ and $\left( {\upomega _{mn} } \right) ^{b}$ denote dimensionless natural frequencies of the forward and backward traveling waves, respectively. Spinning speed $\Omega =10$ rad/s is considered. The primary resonance responses for the functionally graded cylindrical shell are plotted in Fig. 3, where the power-law index is 0.5. Present analytical solutions and numerical calculations about harmonic resonance behaviors are verified.

5.2 Natural frequencies of traveling waves

As discussed in Sect. 3, a standard traveling wave bifurcates into backward and forward traveling waves [14] when spinning motion exists.

Fig. 3

Amplitude–frequency relationship of the primary resonance

Fig. 4

Dimensionless natural frequencies of traveling waves versus spinning speed: influences of a GPL weight fraction and b temperature variations

The dimensionless natural frequencies of traveling waves of given modes ($m,n) = (1, 1)$ for various GPL weight fractions and temperature variations are plotted in Fig. 4, where solid and dash-dot lines represent backward and forward traveling waves, respectively. When the spinning speed lower than the critical spinning speed, frequencies of forward traveling waves decrease with the spinning speed, while frequencies of backward traveling waves increase with the spinning speed, and the interpretation of this phenomenon can be seen in Ref. [14]. In Fig. 4a, dimensionless natural frequencies of traveling waves increase with GPL weight fractions. It proves the pronounced enhancement effect on the effective stiffness of the cylindrical shell. With the GPLs weight fraction reaches 0.1%, dimensionless natural frequency is increased by around 104.1%. As shown in Fig. 4b, lower temperature variations of the graphene-reinforced cylindrical shell correspond to higher dimensionless natural frequencies of traveling waves, since the stiffness of the cylindrical shell decreases with temperature variations.

5.3 Numerical simulation for the primary resonance

In this section, primary resonance behaviors of the graphene-reinforced composite cylindrical shell are presented, including amplitude–frequency curves, stability solutions, and the variation of the vibration amplitude. Influences of GPLs parameters, spinning speeds, the external excitation, structural damping coefficients, and temperature variations on results are investigated. Circumferential waves number is $n=6$. The cylindrical shell with geometrical sizes $L/r = 20$ and $r/h = 30$ is adopted. Figures 5, 6, 7, and 8 present amplitude–frequency curves of primary resonance of the graphene-reinforced cylindrical shell, where the dashed and solid lines denote unstable and stable solutions, respectively. As a result of the positive coefficient of nonlinearity item $\left( {\beta _3 >0} \right)$ in Eq. (24) for the present cylindrical shell system, all the amplitude–frequency curves on primary resonances bend toward the right side, and the system stiffness exhibits hardening behavior.

Fig. 5

Primary resonance responses for the graphene-reinforced composite cylindrical shell: influences of a$\varLambda _{GPL}$ and b GPL disperse patterns

Fig. 6

Primary resonance responses for the graphene-reinforced composite cylindrical shell versus temperatures variations

Figure 5 displays influences of GPL weight fractions and disperse patterns on the amplitude–frequency curves of primary resonance for the graded graphene-reinforced cylindrical shell. The cylindrical shell with $\varOmega =40$ rad/s and $\Delta T=30$ K is studied. The solid circle line in Fig. 5a represents a nonlinear free vibration of the undamped cylindrical shell. In Fig. 5a, compared to the curves with $\varLambda _{GPL} =0.0$ wt. %, another two amplitude peaks exhibit a considerable decrease, and their hardening behaviors are weakened, pronouncedly, when 0.1% and 0.2% weight fraction GPLs are added into the neat epoxy resin cylindrical shell. For example, when the GPLs weight fraction reaches 0.2 %, the amplitude peak is decreased by around 89%. In Fig. 5b, we find that the amplitude peak in the case of GPL pattern A is the lowest among the present three GPLs patterns. This phenomenon reveals that GPL pattern A can achieve a better reinforcement effect judging from the response of the primary resonance.

Figure 6 plots amplitude–frequency curves of primary resonance for the graded graphene-reinforced cylindrical shell for different $\varDelta T$. The dimensionless amplitude of external excitation $Q=3$ is considered. Higher temperature variation corresponds to a substantially increased amplitude peak and hardening behavior, since the stiffness of the graphene-reinforced composite cylindrical shell decreases with the temperature variation.

Fig. 7

Primary resonance responses for the graphene-reinforced composite cylindrical shell: influences of a dimensionless amplitude of external excitation and b viscous damping factors

Fig. 8

Primary resonance responses for the graphene-reinforced composite cylindrical shell versus spinning speed

Figure 7 shows the effects of dimensionless excitation amplitudes and viscous damping factors on the amplitude–frequency curves of primary resonance for the graded graphene-reinforced cylindrical shell. In Fig. 7a, except the nonlinear free vibration, the amplitude peak and the hardening behavior increase as the excitation amplitude increases, since the higher external excitation amplitude corresponds to greater vibration amplitude under the same nonlinear frequency. As shown in Fig. 7b, a, significant drop in the amplitude peak and the hardening behavior can be seen as the shell’s intrinsic structural viscous damping factor increased. Variation of the amplitude–frequency curves is much sensitive to the structural damping effect.

Effect of spinning motion on the amplitude–frequency curves of primary resonance for the graded graphene-reinforced cylindrical shell is plotted in Fig. 8. As discussed in Figs. 5 and 6, higher stiffness of the cylindrical shell corresponds to lower amplitude peak of amplitude–frequency curves and weakened hardening behavior. This phenomenon can also be found in Fig. 8b. Let $2\varOmega \varGamma _{12} =0$, which means the damping term caused by the spinning motion is ignored and the spinning motion just affects the stiffness of the cylindrical shell. In Fig. 8b, the higher spinning speed corresponds to lower amplitude peak of amplitude–frequency curves and weakened hardening behavior, since the spinning motion of cylindrical shell structures can improve their stiffness [14].

Fig. 9

Variation of vibration amplitude with external excitation amplitude for different frequency ratios

However, in Fig. 8a, amplitude peaks of amplitude–frequency curves and hardening behavior increase with the spinning speeds, because the Coriolis effect due to spinning motion plays a role in the damping terms besides shell’s intrinsic structural damping. The parameter $\varGamma _{12}$ is negative $\left( {\varGamma _{12} <0} \right)$. The contribution of the decreased damping generated by the increase in the spinning speed (which increases the amplitude peak and hardening behavior) on amplitude–frequency responses is more significant than that of increased stiffness generated by the same spinning speed variation (which decreases the amplitude peak and hardening behavior).

Considering the influences of frequencies of the external excitation, variations of vibration amplitudes with external excitation amplitudes are presented in Fig. 9. In the cases of frequency ratios $\upomega /\hat{\upomega }_{mn} \le 1$, vibration amplitudes increase with the external excitation amplitudes from zero. In the cases of frequency ratios $\upomega /\hat{\upomega }_{mn} >1$, as the external excitation amplitude increases from zero and reaches a specific value, a jump phenomenon can be observed where the corresponding value of vibration amplitude a is called jump height. After the jump phenomenon, vibration amplitudes increase with the external excitation amplitudes. We can also find that higher frequency ratio corresponds to higher vibration amplitudes and higher jump values.

5.4 Numerical simulation for the 1/3 subharmonic resonance

In this section, influences of GPL weight fractions, spinning speeds, and temperature variations on 1/3 subharmonic resonance behaviors are analyzed.

Fig. 10

Regions of 1/3 subharmonic resonance for the graphene-reinforced cylindrical shell versus GPL weight fractions

Fig. 11

Regions of 1/3 subharmonic resonance for the graphene-reinforced cylindrical shell versus spinning speeds

Fig. 12

Regions of 1/3 subharmonic resonance for the graphene-reinforced cylindrical shell versus temperature variations

Firstly, we define the relationships between the excitation frequency and excitation amplitude which enable the 1/3 subharmonic resonance to occur as existence region. Existence regions for the mode $\left( {m,n} \right) =\left( {1,6} \right)$ of the graphene-reinforced composite cylindrical shell are given in Figs. 10, 11, and 12. GPL pattern A and the shell’s intrinsic structural viscous damping factors $\xi =0.05$ are considered. We can find that only if the amplitude of the external excitation exceeds a specific small value and the frequency ratio $\omega /\hat{\omega }_{mn}$ of the external excitation exceeds three can the 1/3 subharmonic resonance occur. The maximum excitation amplitudes increase with the corresponding excitation frequency.

Fig. 13

1/3 subharmonic resonance responses for the graphene-reinforced cylindrical shell: influences of GPL weight fractions

Fig. 14

1/3 subharmonic resonance response for the graphene-reinforced cylindrical shell: influences of temperature variations

In Fig. 10, the maximum excitation amplitude under the same excitation frequency significantly increases as 0.4% weight fraction GPLs are added into the neat epoxy resin. The minimum value for the frequency ratio of the 1/3 subharmonic resonance increases with the GPL weight fraction.

Fig. 15

1/3 subharmonic resonance responses for the graphene-reinforced cylindrical shell: influences of spinning speeds

In Fig. 11, higher spinning speeds correspond to broader existence region of the 1/3 subharmonic resonance. In Fig. 12, lower temperature variations correspond to a larger region of the 1/3 subharmonic resonance, because higher spinning speeds and lower temperature variations increase the stiffness of the cylindrical shell, which can enlarge regions of the 1/3 subharmonic resonance. Higher spinning speeds correspond to lower frequency ratio of the 1/3 subharmonic resonance, while it is not sensitive to the temperature variation.

Moreover, the effect of GPL weight fractions, temperature variation, and spinning speed on the amplitude–frequency relations and the stabilities of 1/3 subharmonic resonance for the graded graphene-reinforced cylindrical shell are studied. The amplitude–frequency relation is characterized by Eq. (41), and their stable conditions are examined according to Eq. (43). In Figs. 13, 14, and 15, the excitation amplitudes applied on the cylindrical shells are chosen from solutions as shown in Figs. 10, 11, and 12. We find that the lower branch is always an unstable solution.

The amplitude–frequency curves are shown in Fig. 13; the minimum amplitude of the 1/3 subharmonic resonance increases with the GPL weight fraction, and the minimum frequency ratio increases with the GPL weight fraction. This phenomenon can be interpreted by the variation of stiffness of the shell structure. Similarly, in Fig. 14, lower temperature variation increases the stiffness of the shell structure which corresponds to the decreased length of the interval of frequency ratio and the increased minimum amplitude of the 1/3 subharmonic resonance. For the same frequency of the external excitation, amplitudes of the 1/3 subharmonic resonance decrease with the temperature variations.

In Fig. 15, the influence of spinning motion on amplitude–frequency curves of 1/3 subharmonic resonance of the graded graphene-reinforced cylindrical shell is displayed. As discussed before, spinning motion not only can increase the stiffness of the shell, also it can decrease the damping of the system. Therefore, in Fig. 15a, setting $2\varOmega \varGamma _{12} =0$ and ignoring the damping term caused by spinning motion, this phenomenon that the minimum amplitude of the 1/3 subharmonic resonance increases with the spinning speed can be found. In Fig. 15b, higher spinning speed corresponds to a greater length of the interval of frequency ratio and smaller minimum amplitude of the 1/3 subharmonic resonance.

6 Conclusions

Nonlinear primary resonance and 1/3 subharmonic resonance behaviors of the GPLs-reinforced composite cylindrical shell are conducted, and influences of the spinning motion, GPL weight fractions, temperature variations, and the viscous damping factor on the amplitude–frequency relations and stabilities of the resonances are investigated.

Numerical results reveal that the cylindrical shell with higher GPLs volume fraction has lower vibration amplitudes in the primary resonance and broader existence regions and increased minimum amplitude in the 1/3 subharmonic resonance. Temperature variation has critical influences on active stiffnesses and resonance behaviors of the novel composite cylindrical shell.

The Coriolis effect generated by the spinning motion has a contribution to the damping terms of the system besides the shell’s intrinsic structural damping. The contribution of the decreased damping generated by the increase in the spinning speed (which increases the amplitude peak and hardening behavior) on amplitude–frequency responses is more significant than that of increased stiffness generated by the same spinning speed variation (which decreases the amplitude peak and hardening behavior).

Appendices

Appendix A

Expressions of the differential operators in Eq. (21) are given as

$$\begin{aligned} \begin{aligned} L_{11}&=A_{11}^{*} ()_{,xx} +\left( {r^{-2}A_{44}^{*} +I_0 \Omega ^{2}} \right) ()_{,\theta \theta } , \\ L_{12}&=r^{-1}\left( {A_{12}^{*} +A_{44}^{*} } \right) ()_{,x\theta } , \\ L_{13}&=r^{-1}A_{12}^{*} ()_{,x} -B_{11}^{*} ()_{,xxx}\\&\quad -r^{-2}\left( {B_{12}^{*} +2B_{44}^{*} } \right) ()_{,x\theta \theta } , \\ L_{21}&=L_{12} , \\ L_{22}&=A_{44}^{*} ()_{,xx} +\left( {r^{-2}A_{11}^{*} +I_0 \Omega ^{2}} \right) ()_{,\theta \theta } , \\ L_{23}&=\left( {r^{-2}A_{11}^{*} +2I_0 \Omega ^{2}} \right) ()_{,\theta }\\&\quad -r^{-3}B_{11}^{*} ()_{,\theta \theta \theta } -r^{-1}\left( {B_{12}^{*} +2B_{44}^{*} } \right) ()_{,xx\theta } , \\ L_{31}&=-L_{13} ,\,\,L_{32} =-L_{23} , \\ L_{33}&=-r^{-2}A_{11}^*()+\left( {2r^{-1}B_{12}^*-N^{T}} \right) ()_{,xx} \\&\quad +\left( {2r^{-3}B_{11}^*+I_0 \Omega ^{2}-r^{-2}N^{T}} \right) ()_{,\theta \theta } \\&\quad -D_{11}^*()_{,xxxx} -r^{-4}D_{11}^*()_{,\theta \theta \theta \theta } \\&\quad -2r^{-2}\left( {D_{12}^*+2D_{44}^*} \right) ()_{,xx\theta \theta } . \\ \end{aligned} \end{aligned}$$

(A.1)

Appendix B

Elements of the determinant of matrix (22) have the following forms

$$\begin{aligned} \Gamma _{11}^{*}= & {} A_{\mathrm{11}}^{*} \frac{\Lambda _{\mathrm{2}} }{\Lambda _{\mathrm{1}} }-n^{2}\left( {r^{-2}A_{\mathrm{44}}^{*} +I_0 \Omega ^{2}} \right) ,\nonumber \\ \Gamma _{12}^{*}= & {} nr^{-1}\left( {A_{\mathrm{12}}^{*} +A_{\mathrm{44}}^{*} } \right) ,\nonumber \\ \Gamma _{13}^{*}= & {} r^{-1}A_{\mathrm{12}}^{*} -B_{\mathrm{11}}^{*} \frac{\Lambda _{\mathrm{2}} }{\Lambda _{\mathrm{1}} }+n^{2}r^{-2}\left( {B_{\mathrm{12}}^{*} +2B_{44}^{*} } \right) , \nonumber \\ \Gamma _{21}^{*}= & {} -\,nr^{-1}\left( {A_{\mathrm{12}}^{*} +A_{44}^{*} } \right) \frac{\Lambda _4 }{\Lambda _3},\nonumber \\ \Gamma _{22}^{*}= & {} A_{44}^{*} \frac{\Lambda _4 }{\Lambda _3 }-n^{2}\left( {r^{-2}A_{\mathrm{11}}^{*} +I_0 \Omega ^{2}} \right) ,\nonumber \\ \Gamma _{23}^{*}= & {} -\,n\left( {r^{-2}A_{\mathrm{11}}^{*} +2I_0 \Omega ^{2}} \right) -n^{3}r^{-3}B_{\mathrm{11}}^{*} \nonumber \\&\quad +\,nr^{-1}\left( {B_{\mathrm{12}}^{*} +2B_{44}^{*} } \right) \frac{\Lambda _4 }{\Lambda _3 }, \nonumber \\ \Gamma _{31}^{*}= & {} -\,r^{-1}A_{\mathrm{12}}^{*} \frac{\Lambda _4 }{\Lambda _3 }+B_{\mathrm{11}}^{*} \frac{\Lambda _5 }{\Lambda _3}\nonumber \\&\quad -\,n^{2}r^{-2}\left( {B_{\mathrm{12}}^{*} +2B_{44}^{*} } \right) \frac{\Lambda _4 }{\Lambda _3 }, \nonumber \\ \Gamma _{32}^{*}= & {} \Gamma _{23} , \nonumber \\ \Gamma _{33}^{*}= & {} -\,r^{-2}A_{\mathrm{11}}^{*} +\left( {2r^{-1}B_{12}^*-N^{T}} \right) \frac{\Lambda _4 }{\Lambda _3 }\nonumber \\&\quad -\,n^{2}\left( {2r^{-3}B_{11}^*+I_0 \Omega ^{2}-r^{-2}N^{T}} \right) \nonumber \\&\quad -\,D_{\mathrm{11}}^{*} \frac{\Lambda _{\mathrm{5}} }{\Lambda _3 }-n^{4}r^{-4}D_{\mathrm{11}}^{*} \nonumber \\&\quad +\,2n^{2}r^{-2}\left( {D_{\mathrm{12}}^{*} +2D_{44}^{*} } \right) \frac{\Lambda _4 }{\Lambda _3 }, \end{aligned}$$

(B.1)

and

$$\begin{aligned} \Gamma _{11} =\frac{\Gamma _{12}^{*} \Gamma _{23}^{*} -\Gamma _{22}^{*} \Gamma _{13}^{*} }{\Gamma _{11}^{*} \Gamma _{22}^{*} -\Gamma _{12}^{*} \Gamma _{21}^{*} },\,\,\Gamma _{12} =\frac{\Gamma _{21}^{*} \Gamma _{13}^{*} -\Gamma _{11}^{*} \Gamma _{23}^{*} }{\Gamma _{11}^{*} \Gamma _{22}^{*} -\Gamma _{12}^{*} \Gamma _{21}^{*} },\nonumber \\ \end{aligned}$$

(B.2)

where the coefficients $\varLambda _\mathrm{i} \left( {i=1,\,2,\,3,\,4,\,5} \right)$ related to the assumed shell models can be calculated from

$$\begin{aligned}&\left\{ {{\begin{array}{ccccc} {\Lambda _1 }&{} {\Lambda _2 }&{} {\Lambda _3 }&{}{\Lambda _4 }&{} {\Lambda _5 } \\ \end{array} }} \right\} \\&\quad =\int _0^L {\left\{ {{\begin{array}{ccccc} {\left( {\frac{\hbox {d}\phi }{\hbox {d}x}} \right) ^{2}}&{} {\frac{\hbox {d}^{3}\phi }{\hbox {d}x^{3}}\frac{\hbox {d}\phi }{\hbox {d}x}}&{} {\phi ^{\mathrm{2}}}&{} {\phi \frac{\hbox {d}^{\mathrm{2}}\phi }{\hbox {d}x^{\mathrm{2}}}}&{} {\phi \frac{\hbox {d}^{4}\phi }{\hbox {d}x^{4}}} \\ \end{array} }} \right\} } \hbox {d}x. \\ \end{aligned}$$