The non-linear vibrations of rotating functionally graded cylindrical shells

Abstract

This paper reports the result of an investigate on the non-linear vibrations of rotating functionally graded cylindrical shell in thermal environment, based on Hamilton’s principle, von Kármán non-linear theory and the first-order shear deformation theory. The formulation includes the initial hoop tension, the centrifugal and Coriolis forces due to rotation of the shell. The effects of in-plane and rotary inertia are taken into account in the equations of motion. Galerkin’s method is utilised to convert the governing partial differential equations to non-linear ordinary differential equations. A reduction in the model is presented to investigate non-linear dynamics, including primary resonance responses, quasi-periodic and chaotic responses to harmonic transverse external forces. The modal coefficients of quadratic and cubic nonlinearities are calculated by Galerkin integration and superimposed on the linear part of equation to establish the non-linear reduction equation. To validate the approach proposed in this paper, a series of comparison are performed and the investigations demonstrate good reliability and low computational cost of the present approach.

1 Introduction

Functionally graded (FG) cylindrical shells are being used as structural components in modern industries such as aerospace, mechanical and nuclear engineering [1–5]. Usually, they operate in high-temperature environments and in some applications undergo rotations with constant angular velocities. The effects of Coriolis and centrifugal forces in rotating shell structures can change their vibration characteristics to be become different from those of stationary FG shells. Hence, for the purpose of their engineering design and manufacture, the accurate evaluation of their vibration characteristics under rotating condition becomes essential.

In the previous works, most of rotating shells have been concerned to linear theory. Based on the first-order shear deformation theory and Hamilton’s principle, Malekzadeh and Heydarpour [6] investigated the linear vibration of rotating FG cylindrical shells subjected to thermal environment. Based on Sanders’ shell equations, Sun et al. [7] presented a general approach for the vibration studies of rotating cylindrical shells having arbitrary edges. The frequency equations are derived by taking the characteristic orthogonal polynomial series and the Rayleigh–Ritz method.

Using the first-order shear deformation theory, Nejad et al. [8] investigated the semi-analytical solution for the rotating thick truncated conical shells made of functionally graded materials under non-uniform pressure. Using vertically and obliquely reinforced 1–3 piezoelectric composite materials as the constraining layer, Kumar and Ray [9] presented the active vibration control of thin rotating laminated composite truncated conical shells. In addition, Dai et al. [10] extracted an exact one-dimensional solution for a rotating FG piezoelectric hollow cylinder subjected to electric, thermal and mechanical loads.

The plates and shells can be vibrated with large amplitude in a dynamic behaviour. It is not sufficient to employ linear theory to analyze their large amplitude vibration behaviour. Therefore, one should analyze the non-linear vibration characteristics to design a stable and reliable structure. Using the Donnell’s nonlinear shallow-shell theory, Catellani et al. [11] studied the dynamic behaviour of a parametrically excited cylindrical shell having geometric imperfections. The experimental and theoretical analysis of circular cylindrical shells under base excitation is presented by Pellicano [12], taking into account geometric shell nonlinearities; numerical analyses furnish useful explanations about the instability phenomena that are observed experimentally. Strozzi and Pellicano [13] studied the non-linear vibrations of functionally graded cylindrical shells; they used the Sanders–Koiter theory and considered simply supported, clamped and free boundary conditions. Using the first-order shear deformation theory and stress function, Duc and Thang [14] present an analytical approach to investigate the non-linear dynamic response and vibration of imperfect eccentrically stiffened functionally graded thick cylindrical shells surrounded on elastic foundations. The geometrically non-linear free vibration of functionally graded thick plates resting on the elastic Pasternak foundation is investigated by Taczała et al. [15] based on the first- order shear deformation theory; the material properties are assumed to be temperature dependent and expressed as a non-linear function of temperature. In the research works, only limited literature can be found on the non-linear vibration of rotating shells. Using the Ritz–Galerkin method, Lee and Kim [16] derived the non-linear frequency equation of the thin rotating hybrid cylindrical shell with simply supported boundary condition. Utilising the multiple scales method, Han and Chu [17] studied parametric instability of a rotating cylindrical shell under periodic axial loads. Analytical expressions of instability boundaries for various modes are obtained. Using the Donnell’s non-linear shallow-shell theory, Wang et al. [18] obtained the equations of motion of a cantilever rotating circular cylindrical shell subjected to a harmonic excitation.

To obtain the non-linear response of cylindrical shells, large numerical models are usually employed. These analyses involving a large number of degrees of freedom are very expensive with respect to both storage and CPU time. An attractive alternative is to derive consistent reduced-order models that can capture the main characteristics of the shell behaviour. Many attempts have been made to develop suitable and simple mathematical models for predicting the non-linear behaviour of shells [19–21].

In this paper, based on the first-order shear deformation theory, von Kármán theory and Hamilton’s principle, a theoretical analysis and a reduction model are presented to study non-linear vibrations of rotating FG cylindrical shells together with consideration of the initial hoop tension, centrifugal and Coriolis forces. The equations of motion are reduced using the Galerkin method to a system of non-linear ordinary differential equations with quadratic and cubic nonlinearities. This study is an extension of earlier works by the author [22] on non-linear vibration of FG cylindrical shells. In the present formulation, the in-plane and rotary inertias are both taken into account. The effects of rotating speeds and the amplitude of the external modal excitation on the non-linear vibration characteristics are investigated, including primary resonance responses, quasi-periodic and chaotic responses to harmonic transverse external forces. The present analysis is validated by comparing the numerical results with existing results, and very good agreement is obtained.

Fig. 1

Coordinate system of the rotating functionally graded cylindrical shell

2 Theoretical formulations

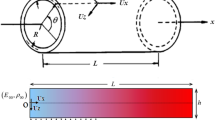
The geometry of an FG cylindrical shell and coordinate system are shown in Fig. 1. The cylindrical shell is assumed to have length L, constant thickness h and mean radius R and is also assumed to rotate about its horizontal axis with a constant angular speed $\varOmega$. Both ends of the shell are simply supported.

Form the first-order shear deformation theory, the displacements $(u_1,\,v_1,\,w_1)$ of a point $(x,\,\theta ,\,z)$ in the FG cylindrical shell are expressed as sum of the mid-surface displacements $(u,\,v,\,w)$ along the x, $\theta$ and z direction, and rotations $(\varphi _x,\,\varphi _\theta )$ of the normals to the mid-surface along x and $\theta$ axes, as follows

$$\begin{aligned}&u_1 \left( {x,\theta ,z,t} \right) =u\left( {x,\theta ,t} \right) +z\varphi _x (x,\theta ,t),\nonumber \\&v_1 \left( {x,\theta ,z,t} \right) =v\left( {x,\theta ,t} \right) +z\varphi _\theta \left( {x,\theta ,t} \right) ,\\&w_1 \left( {x,\theta ,z,t} \right) =w\left( {x,\theta ,t} \right) .\nonumber \end{aligned}$$

(1)

The geometrically non-linear membrane strain, the transverse shear strains and curvatures are given by adding the von Kármán terms to the linear strain displacement relations

$$\begin{aligned} \begin{aligned}&\varepsilon _x =\frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2},\\&\varepsilon _\theta = \frac{1}{R}\left( \frac{\partial v}{\partial \theta }+w\right) +\frac{1}{2}\left( \frac{1}{R}\frac{\partial w}{\partial \theta }\right) ^{2},\\&\gamma _{x\theta } =\frac{\partial v}{\partial x}+\frac{1}{R}\frac{\partial u}{\partial \theta }+\frac{1}{R}\frac{\partial w}{\partial x}\frac{\partial w}{\partial \theta },\\&\gamma _{xz} = \varphi _x +\frac{\partial w}{\partial x}, \quad \gamma _{\theta z} =\varphi _\theta +\frac{1}{R}\frac{\partial w}{\partial \theta },\\&\kappa _x =\frac{\partial \varphi _x }{\partial x},\\&\kappa _\theta =\frac{1}{R}\frac{\partial \varphi _\theta }{\partial \theta },\\&\kappa _{x\theta } = \frac{\partial \varphi _\theta }{\partial x}+\frac{1}{R}\frac{\partial \varphi _x }{\partial \theta }. \end{aligned} \end{aligned}$$

(2)

In this paper, the variation of temperature is assumed to occur in the thickness direction only and a heat flows from the inner surface to the outer surface of the FG cylindrical shell. The analytical solution is provided for the non-linear vibration characteristics of the rotating FG cylindrical shell under the linear temperature field:

$$\begin{aligned} T(x,\theta ,z)=\frac{T_m +T_c }{2}+\frac{T_m -T_c }{h}z, \quad T_{cm} =T_c -T_m \end{aligned}$$

(3)

where $T_{c}$ and $T_{m}$ are the temperature of the inner surface and the outer surface of the FG cylindrical shell, respectively. $T_{cm}$ is the temperature difference between the inner surface and the outer surface.

In order to accurately model the material properties of functionally graded materials, the properties must be both temperature dependent and position dependent. The volume fraction is a spatial function, and the properties of the constituents are functions of the temperature. Suppose that a typical material property $F_\mathrm{{eff}}$ is varied along the shell thickness according to the expressions [23] (a power low)

$$\begin{aligned} F_\mathrm{{eff}} (z,T)= & {} F_m (T)V(z)+F_c (T)(1-V(z)),\nonumber \\ V(z)= & {} \left( \frac{z+h/2}{h}\right) ^{\varPhi } \quad (0\le \varPhi \le \infty ), \end{aligned}$$

(4)

where $F_m (T)$ and $F_c (T)$ denote the property of the outer (metal) and inner (ceramic) surface of the shell, respectively, and $\varPhi$ expresses the volume fraction exponent. Here we assume that the effective mass densities $\rho _\mathrm{{eff}} (z)$, the effective Young’s modulus $E_\mathrm{{eff}}$, the effective Poisson’s ratio $\nu _\mathrm{{eff}}$ and the effective thermal expansion coefficients $\alpha _\mathrm{{eff}}$ vary according to Eq. 4.

The material properties of the metal and ceramic can be expressed as a function of temperature (in Kelvin), as

$$\begin{aligned} P=P_0 (P_{-1} T^{-1}+1+P_1 T+P_2 T^{2}+P_3 T^{3}) \end{aligned}$$

(5)

in which $P_0$; $P_{-1}$; $P_1$; $P_2$; and $P_3$ are the coefficients and are unique to the constituent materials.

The stress–strain relation including the temperature effects is given by

$$\begin{aligned} {{\varvec{\upsigma }} }=\mathbf{C}(z)[{\bar{{{\varvec{\upvarepsilon }} }}}-{{\varvec{\upalpha }} }(z)\Delta T], \end{aligned}$$

(6)

where ${{\varvec{\upsigma }}}=\left[ {{\begin{array}{lllll} {\sigma _x }&{} {\sigma _\theta }&{} {\tau _{x\theta } }&{} {\tau _{\theta z} }&{} {\tau _{xz} } \\ \end{array} }} \right] ^{T}$ (stresses), ${\bar{{{\varvec{\upvarepsilon }} }}}=\left[ {{\begin{array}{lllll} {\bar{{\varepsilon }}_x }&{} {\bar{{\varepsilon }}_\theta }&{} {\bar{{\gamma }}_{x\theta } }&{} {\bar{{\gamma }}_{\theta z} }&{} {\bar{{\gamma }}_{xz} }\\ \end{array} }} \right] ^{T}$ (strains) ,$\Delta T=T(x,\theta ,z)-T_0$ and $T_0 =T_m$ (room temperature, stress free state). $\mathbf{C}(z)$ and ${{\varvec{\upalpha }} }(z)$ is the elasticity matrix and thermal expansion coefficients matrix of functionally graded materials, respectively ( see “Appendix 1”). The strains ${\bar{{{\varvec{\upvarepsilon }} }}}$ of an arbitrary point are related to the mid-surface strains ($\varepsilon _x$, $\varepsilon _\theta$, $\gamma _{x\theta }$, $\gamma _{xz}$ and $\gamma _{\theta z}$) and curvatures ($\kappa _x$, $\kappa _\theta$ and $\kappa _{x\theta }$).

To derive the equations of motion, the formulation is based on Hamilton’s principle and the first-order shear deformation theory. The variational principle can be stated as

$$\begin{aligned} \int _0^t {(\delta K-\delta H+\delta W)\hbox {d}t} =0, \end{aligned}$$

(7)

where K, H and W are the kinetic energy, strain energy and the work done by the applied loads of the FG cylindrical shell, including the effect of the rotation. Considering the in-plane and rotary inertia, the equations of motion for the rotating FG cylindrical shell under thermal load are obtained as [22, 23]

$$\begin{aligned}&\delta u: \quad \frac{\partial (N_{x} -N_{x}^{T})}{\partial x}+\frac{1}{R}\frac{\partial (N_{x\theta } -N_{x\theta }^{T})}{\partial \theta }\nonumber \\&\qquad +\,\bar{{N}}_{\theta } (\frac{1}{R^{2}}\frac{\partial ^{2}u}{\partial \theta ^{2}}-\frac{1}{R}\frac{\partial w}{\partial x})\nonumber \\&\qquad +\,q_{x} (x,\theta ,t)=I_{0} \ddot{{u}}+I_{1} \ddot{{\varphi }}_{x}\nonumber \\&\delta v: \quad \frac{1}{R}\frac{\partial (N_{\theta } -N_{\theta }^{T})}{\partial \theta }+\frac{\partial (N_{x\theta } -N_{x\theta }^{T})}{\partial x}\nonumber \\&\qquad +\,\frac{1}{R}(Q_{\theta } -Q_{\theta }^{T})\nonumber \\&\qquad +\,\frac{\bar{{N}}_{\theta } }{R}\frac{\partial ^{2}u}{\partial x\partial \theta }+q_{\theta } (x,\theta ,t)=I_{0} \ddot{{v}}+I_{1} \ddot{{\varphi }}_{\theta }\nonumber \\&\qquad +\,I_{0} (2\varOmega \dot{{w}}-\varOmega ^{2}v)\nonumber \\&\delta w: \quad \frac{1}{R}\frac{\partial (Q_{\theta } -Q_{\theta }^{T})}{\partial \theta }+\frac{\partial (Q_{x} -Q_{x}^{T})}{\partial x}\nonumber \\&\qquad -\,\frac{1}{R}(N_{\theta } -N_{\theta }^{T})+\eta (u,v,w,\varphi _{x} ,\varphi _{\theta } )\nonumber \\&\qquad +\,\frac{\bar{{N}}_{\theta } }{R^{2}}(\frac{\partial ^{2}w}{\partial \theta ^{2}}-\frac{\partial v}{\partial \theta })+q_{z} (x,\theta ,t) \nonumber \\&\quad =I_{0} (\ddot{{w}}-2\varOmega \dot{{v}}-\varOmega ^{2}w)\nonumber \\&\delta \varphi _{x} : \quad \frac{\partial (M_{x} -M_{x}^{T})}{\partial x}+\frac{1}{R}\frac{\partial (M_{x\theta } -M_{x\theta }^{T})}{\partial \theta }\nonumber \\&\qquad -\,(Q_{x} -Q_{x}^{T}) +m_{x} (x,\theta ,t)=I_{1} \ddot{{u}}+I_{2} \ddot{{\varphi }}_{x}\nonumber \\&\delta \varphi _{\theta } : \quad \frac{1}{R}\frac{\partial (M_{\theta } -M_{\theta }^{T})}{\partial \theta }+\frac{\partial (M_{x\theta } -M_{x\theta }^{T})}{\partial x}\nonumber \\&\quad -\,(Q_{\theta } -Q_{\theta }^{T})+m_{\theta } (x,\theta ,t)=I_{1} \ddot{{v}}+I_{2} \ddot{{\varphi }}_{\theta } \end{aligned}$$

(8)

where

$$\begin{aligned}&\eta \left( u,v,w,\varphi _x ,\varphi _\theta \right) =\frac{\partial }{\partial x}\left[ \left( N_x -N_x^{T}\right) \frac{\partial w}{\partial x}\right] \\&\quad +\,\frac{1}{R^{2}}\frac{\partial }{\partial \theta }\left[ \left( N_\theta -N_\theta ^{T}\right) \frac{\partial w}{\partial \theta }\right] \\&\quad +\,\frac{1}{R}\frac{\partial }{\partial \theta }\left[ \left( N_{x\theta } -N_{x\theta }^{T}\right) \frac{\partial w}{\partial x}\right] \\&\quad +\,\frac{1}{R}\frac{\partial }{\partial x}\left[ \left( N_{x\theta } -N_{x\theta }^{T}\right) \frac{\partial w}{\partial \theta }\right] , \end{aligned}$$

is the non-linear contribution to the equilibrium equations due to the von Kármán non-linear strains, including the effects of the thermal loading. $2\varOmega \dot{w}$ and $2\varOmega \dot{v}$ are the Coriolis terms. $\varOmega ^{2}v$ and $\varOmega ^{2}w$ are the centrifugal terms. $\bar{{N}}_\theta =I_0 R^{2}\varOmega ^{2}$ is the initial hoop tension due to the centrifugal force. These additional terms arise due to the rotation of the shell. $q_x$, $q_\theta$, $q_z$, $m_x$ and $m_\theta$ are the surface forces intensities. Superscripts T denote resultants due to thermal effects, and $N_x$, $N_\theta$, $N_{x\theta }$, $M_x$, $M_\theta$, $M_{x\theta }$, $Q_x$ and $Q_\theta$ are the usual stress resultants. The thermal stress resultants and usual stress resultants are described in “Appendix 2”.

The mass term is defined as

$$\begin{aligned} \left( I_0, I_1, I_2\right) =\int _{-h/2}^{h/2} {\rho _\mathrm{{eff}} \left( z\right) \left( 1, z, z^{2}\right) \hbox {d}z} \end{aligned}$$

(9)

where $\rho _\mathrm{{eff}} (z)$ is the effective mass densities of the FG cylindrical shell (see Eq. 4).

Utilising Eq. (2) and “Appendixes 1 and 2”, the non-linear equations of motion can be expressed in terms of generalised displacement ($u,v,w,\varphi _x ,\varphi _\theta$) as follows:

$$\begin{aligned}&L_{11}u+L_{12}v+L_{13}w+L_{14} \varphi _{x}\nonumber \\&\quad +\,L_{15} \varphi _{\theta }+w'_{x}L_{16} w+w'_{\theta }L_{17}w\nonumber \\&\quad +\,\left( \frac{1}{R^{2}}\frac{\partial ^{2}u}{\partial \theta ^{2}}-\frac{1}{R}\frac{\partial w}{\partial x}\right) I_0 R^{2}\varOmega ^{2}+q_x\nonumber \\&\quad =I_0 \ddot{u}+I_1 \ddot{\varphi }_x \end{aligned}$$

(10)

$$\begin{aligned}&L_{21}u+L_{22}v+L_{23}w+L_{24} \varphi _{x}+L_{25} \varphi _{\theta }\nonumber \\&\quad +\,w'_{x}L_{26} w+w'_{\theta }L_{27}w\nonumber \\&\quad +\,I_0 R\varOmega ^{2}\frac{\partial ^{2}u}{\partial x\partial \theta }+I_0 \varOmega ^{2}v+q_\theta \nonumber \\&\quad =I_0 \ddot{v}+I_1 \ddot{\varphi }_\theta +2I_0 \varOmega \dot{w} \end{aligned}$$

(11)

$$\begin{aligned}&L_{31}u+L_{32}v+L_{33}w+L_{34} \varphi _{x}+L_{35} \varphi _{\theta }\nonumber \\&\quad +\,\eta \left( u,v,w,\varphi _{x},\varphi _{x}\theta \right) +w'_{x}L_{36} w+w'_{\theta }L_{37}w\nonumber \\&\quad +\,I_0 \varOmega ^{2}\left( \frac{\partial ^{2}w}{\partial \theta ^{2}}-\frac{\partial v}{\partial \theta }\right) +I_0 \varOmega ^{2}w+q_z\nonumber \\&\quad =I_0 \ddot{w}-2I_0 \varOmega \dot{v} \end{aligned}$$

(12)

$$\begin{aligned}&L_{41} u+L_{42} v+L_{43} w+L_{44} \varphi _x +L_{45} \varphi _\theta \nonumber \\&\quad +\,{w}'_x L_{46} w+{w}'_\theta L_{47} w+m_x =I_1 \ddot{u}+I_2 \ddot{\varphi }_x \end{aligned}$$

(13)

$$\begin{aligned}&L_{51} u+L_{52} v+L_{53} w+L_{54} \varphi _x +L_{55} \varphi _\theta \nonumber \\&\quad +\,{w}'_x L_{56} w+{w}'_\theta L_{57} w+m_\theta =I_1 \ddot{v}+I_2 \ddot{\varphi }_\theta \end{aligned}$$

(14)

where $L_{ij}$ are linear operators for the generalised displacement, described in “Appendix 3”.

2.1 Linear free vibrations of rotating FG cylindrical shells

The shell assumed is simply supported, and there exists a solution for the above five equations in the form

$$\begin{aligned} u= & {} U\cos \lambda _m x\cos (n\theta +\omega t) \end{aligned}$$

(15)

$$\begin{aligned} v= & {} V\sin \lambda _m x\sin (n\theta +\omega t) \end{aligned}$$

(16)

$$\begin{aligned} w= & {} W\sin \lambda _m x\cos (n\theta +\omega t) \end{aligned}$$

(17)

$$\begin{aligned} \varphi _x= & {} \varPhi _x \cos \lambda _m x\cos (n\theta +\omega t) \end{aligned}$$

(18)

$$\begin{aligned} \varphi _\theta= & {} \varPhi _\theta \sin \lambda _m x\sin (n\theta +\omega t) \end{aligned}$$

(19)

where $\lambda _m =\frac{m\pi }{L}$, U, V, W, $\varPhi _x$ and $\varPhi _\theta$ are displacement amplitudes, m and n are the axial and circumferential wave numbers, respectively, and $\omega$ is the natural frequency. For linear free vibration, we set the non-linear terms, the thermal and mechanical loads to zero in Eqs. (10)–(14). Substituting Eqs. (15)–(19) into Eqs. (10)–(14) yields the eigenvalue problem described by the following equations

$$\begin{aligned}&C_{11}^{mn} U+C_{12}^{mn} V+C_{13}^{mn} W+C_{14}^{mn} \varPhi _x +C_{15}^{mn} \varPhi _\theta \nonumber \\&\quad =\omega ^{2}I_0 U+\omega ^{2}I_1 \varPhi _x \end{aligned}$$

(20)

$$\begin{aligned}&C_{21}^{mn} U+C_{22}^{mn} V+C_{23}^{mn} W+C_{24}^{mn} \varPhi _x +C_{25}^{mn} \varPhi _\theta \nonumber \\&\quad =\omega ^{2}I_0 V+\omega ^{2}I_1 \varPhi _\theta +2\omega I_0 \varOmega W \end{aligned}$$

(21)

$$\begin{aligned}&C_{31}^{mn} U+C_{32}^{mn} V+C_{33}^{mn} W+C_{34}^{mn} \varPhi _x +C_{35}^{mn} \varPhi _\theta \nonumber \\&\quad =\omega ^{2}I_0 W+2\omega I_0 \varOmega V \end{aligned}$$

(22)

$$\begin{aligned}&C_{41}^{mn} U+C_{42}^{mn} V+C_{43}^{mn} W+C_{44}^{mn} \varPhi _x +C_{45}^{mn} \varPhi _\theta \nonumber \\&\quad =\omega ^{2}I_1 U+\omega ^{2}I_2 \varPhi _x \end{aligned}$$

(23)

$$\begin{aligned}&C_{51}^{mn} U+C_{52}^{mn} V+C_{53}^{mn} W+C_{54}^{mn} \varPhi _x +C_{55}^{mn} \varPhi _\theta \nonumber \\&\quad =\omega ^{2}I_1 V+\omega ^{2}I_2 \varPhi _\theta \end{aligned}$$

(24)

$C_{ij}^{mn}\,(i=1,2,\ldots 5;j=1,2,\ldots 5.)$ are the coefficients in terms of the rotating speed, wave numbers, the material elastic constants and geometric parameters and can be determined by linear operators $L_{ij}\,(i=1,2,\ldots 5;j=1,2,\ldots 5.)$ in Eqs. (10)–(14).

Using the static condensation method [23] from Eqs. (20, 21) and (23, 24), we can write

$$\begin{aligned} \left[ {{\begin{array}{llll} {C_{11}^{mn} }&{} {C_{12}^{mn} }&{} {C_{14}^{mn} }&{} {C_{15}^{mn} } \\ {C_{21}^{mn} }&{} {C_{22}^{mn} }&{} {C_{24}^{mn} }&{} {C_{25}^{mn} } \\ {C_{41}^{mn} }&{} {C_{42}^{mn} }&{} {C_{44}^{mn} }&{} {C_{45}^{mn} } \\ {C_{51}^{mn} }&{} {C_{52}^{mn} }&{} {C_{54}^{mn} }&{} {C_{55}^{mn} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} U \\ V \\ {\varPhi _x } \\ {\varPhi _\theta } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {-C_{13}^{mn} } \\ {-C_{23}^{mn} } \\ {-C_{43}^{mn} } \\ {-C_{53}^{mn} } \\ \end{array} }} \right\} W \end{aligned}$$

(25)

Solving Eq. (25) with respect to the amplitudes of in-plane displacements and rotations (U, V, $\varPhi _x$, $\varPhi _\theta$) and then substituting the results into the right of Eqs. (20, 21) and (23, 24), we have

$$\begin{aligned}&\left[ {{\begin{array}{llll} {C_{11}^{mn} }&{} {C_{12}^{mn} }&{} {C_{14}^{mn} }&{} {C_{15}^{mn} } \\ {C_{21}^{mn} }&{} {C_{22}^{mn} }&{} {C_{24}^{mn} }&{} {C_{25}^{mn} } \\ {C_{41}^{mn} }&{} {C_{42}^{mn} }&{} {C_{44}^{mn} }&{} {C_{45}^{mn} } \\ {C_{51}^{mn} }&{} {C_{52}^{mn} }&{} {C_{54}^{mn} }&{} {C_{55}^{mn} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} U \\ V \\ {\varPhi _x } \\ {\varPhi _\theta } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {-C_{13}^{mn} } \\ {-C_{23}^{mn} } \\ {-C_{43}^{mn} } \\ {-C_{53}^{mn} } \\ \end{array} }} \right\} W\nonumber \\&\quad +\left\{ {{\begin{array}{l} 0 \\ {2I_0 \varOmega } \\ 0 \\ 0 \\ \end{array} }} \right\} \omega W+\left\{ {{\begin{array}{l} {C_1 } \\ {C_2 } \\ {C_3 } \\ {C_4 } \\ \end{array} }} \right\} \omega ^{2}W \end{aligned}$$

(26)

$C_i\,(i=1,2,3,4)$ are coefficients expressed by the radial direction, in-plane and rotary inertias. Repeating the procedure to eliminate U, V, $\varPhi _x$ and $\varPhi _\theta$, solving Eq. (26) and then substituting the results into Eq. (22), the eigenvalue equation of rotating FG cylindrical shells can be simplified as

$$\begin{aligned} -M_{mn} (I_0 ,I_1 ,I_2 )\omega ^{2}+C_{mn} (\varOmega )\omega +K_{mn} =0 \end{aligned}$$

(27)

where $M_{mn} (I_0 ,I_1 ,I_2)$, $C_{mn} (\varOmega )$ and $K_{mn}$ are the generalised mass, generalised damping and generalised stiffness of the system, respectively. The coefficient of cubic term ($\omega ^{3})$ is omitted in Eq. (27). Solving the above equation, one obtains a positive root and a negative root. The positive root represents the forward natural frequency of the rotating FG cylindrical shell. The backward natural frequency can be obtained accordingly when the shell rotates in the reverse direction. The natural frequency $\omega$ is a function of mode numbers (m, n), rotating speeds $\varOmega$ and the mass inertia terms (including in-plane and rotary inertias). If $\varOmega =0$ (i.e. generalised damping $C_{mn} (\varOmega )=0.)$ is taken into Eq. (27), the eigenproblems for the motion of a rotating shell are transformed into the equations for the non-rotating shell.

2.2 Non-linear vibrations of rotating FG cylindrical shells

The in-plane displacements (u, v) and the rotations ($\varphi _x$, $\varphi _\theta$) are much smaller than the transverse displacement w, so the linear forms of displacement functions (u, v, $\varphi _x$, $\varphi _\theta$) are used

$$\begin{aligned} \begin{aligned}&u=\sum \limits _{m=\text{0 }}^M {\sum \limits _{n=\text{0 }}^N {u_{mn} (t)} } \cos \lambda _{m} x\cos n\theta ,\\&v=\sum \limits _{m=1}^M {\sum \limits _{n=1}^N {v_{mn} (t)} } \sin \lambda _{m} x\sin n\theta ,\\&\varphi _{x} =\sum \limits _{m=\text{0 }}^M {\sum \limits _{n=\text{0 }}^N {\phi _{xmn} (t)} } \cos \lambda _{m} x\cos n\theta ,\\&\varphi _{\theta }=\sum \limits _{m=1}^M {\sum \limits _{n=1}^N {\phi _{\theta mn} (t)} } \sin \lambda _{m} x\sin n\theta . \end{aligned} \end{aligned}$$

(28)

The non-linear form of transverse displacement is written in the present model as [24]

$$\begin{aligned} w= & {} \sum \limits _{m=1}^M {\sum \limits _{n=\text{0 }}^N {w_{mn} (t)} } \sin \lambda _{m} x\cos n\theta \nonumber \\&\quad -\sum \limits _{m=1}^M {\frac{w_{mn}^{2}(t)}{2R}} \sin \lambda _{m} x, \end{aligned}$$

(29)

The generalised loads in Eqs. (10)–(14) can also be expanded in double Fourier series

$$\begin{aligned} q_{x}= & {} \sum \limits _{m=1}^M {\sum \limits _{n=\text{0 }}^N {q_{mn1} } } (t)\cos \lambda _{m} x\cos n\theta , \nonumber \\ q_{\theta }= & {} \sum \limits _{m=1}^M {\sum \limits _{n=1}^N {q_{mn2} } } (t)\sin \lambda _{m} x\sin n\theta ,\nonumber \\ q_{z}= & {} \sum \limits _{m=1}^M {\sum \limits _{n=0}^N {q_{mn3} } } (t)\sin \lambda _{m} x\cos n\theta , \nonumber \\ m_{x}= & {} \sum \limits _{m=1}^M {\sum \limits _{n=0}^N {q_{mn4} } } (t)\cos \lambda _{m} x\cos n\theta ,\nonumber \\ m_{\theta }= & {} \sum \limits _{m=1}^M {\sum \limits _{n=1}^N {q_{mn5} } } (t)\sin \lambda _{m} x\sin n\theta . \end{aligned}$$

(30)

Substituting Eqs. (28)–(30) into Eqs. (10)–(14), and based on multiterm Galerkin procedure, the coupled non-linear equations of motion are obtained for the time-dependent variables $u_{mn} (t), v_{mn} (t), w_{mn} (t), \phi _{xmn} (t)$ and $\phi _{\theta mn} (t)$ [25, 26]:

$$\begin{aligned}&I_0 \ddot{u}_{mn} (t)+I_1 \ddot{\phi }_{xmn} (t)+C_{11}^{mn} u_{mn} (t)+C_{12}^{mn} v_{mn} (t)\nonumber \\&\quad +\,C_{13}^{mn} \phi _{xmn} (t)+C_{14}^{mn} \phi _{\theta mn} (t)+C_{15}^{mn} w_{mn} (t)\nonumber \\&\quad +\,\sum _{ijkl} C_{umn}^{ijkl} w_{ij} (t)w_{kl} (t)\nonumber \\&\quad +\,\sum _{ijklpq} {C_{umn}^{ijklpq} w_{ij} (t)w_{kl} (t)w_{pq} (t)} =q_{mn1} (t)\nonumber \\ \end{aligned}$$

(31)

$$\begin{aligned}&I_0 \ddot{v}_{mn} (t)+I_1 \ddot{\phi }_{\theta mn} (t)+C_{21}^{mn} u_{mn} (t)+C_{22}^{mn} v_{mn} (t)\nonumber \\&\quad +\,C_{23}^{mn} \phi _{xmn} (t)+C_{24}^{mn} \phi _{\theta mn} (t)+C_{25}^{mn} w_{mn} (t)\nonumber \\&\quad +\,\sum _{ij} {C_w^{ijmn} } \dot{w}_{ij} (t)+\sum _{ijkl} C_{vmn}^{ijkl} w_{ij} (t)w_{kl} (t)\nonumber \\&\quad +\,\sum _{ijklpq} {C_{vmn}^{ijklpq} w_{ij} (t)w_{kl} (t)w_{pq} (t)} =q_{mn2} (t) \nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned}&I_1 \ddot{u}_{mn} (t)+I_2 \ddot{\phi }_{xmn} (t)+C_{41}^{mn} u_{mn} (t)+C_{42}^{mn} v_{mn} (t)\nonumber \\&\quad +\,C_{43}^{mn} \phi _{xmn} (t)+C_{44}^{mn} \phi _{\theta mn} (t)+C_{45}^{mn} w_{mn} (t)\nonumber \\&\quad +\,\sum _{ijkl} C_{\phi xmn}^{ijkl} w_{ij} (t)w_{kl}(t)\nonumber \\&\quad +\,\sum _{ijklpq} {C_{\phi xmn}^{ijklpq} w_{ij} (t)w_{kl} (t)w_{pq} (t)} =q_{mn4} (t) \nonumber \\ \end{aligned}$$

(33)

$$\begin{aligned}&I_1 \ddot{v}_{mn} (t)+I_2 \ddot{\phi }_{\theta mn} (t)+C_{51}^{mn} u_{mn} (t)+C_{52}^{mn} v_{mn} (t)\nonumber \\&\quad +\,C_{53}^{mn} \phi _{xmn} (t)+C_{54}^{mn} \phi _{\theta mn} (t)+C_{55}^{mn} w_{mn} (t)\nonumber \\&\quad +\,\sum _{ijkl} C_{\phi \theta mn}^{ijkl} w_{ij} (t)w_{kl}(t)\nonumber \\&\quad +\,\sum _{ijklpq} {C_{\phi \theta mn}^{ijklpq} w_{ij} (t)w_{kl} (t)w_{pq} (t)} =q_{mn5} (t) \nonumber \\ \end{aligned}$$

(34)

$$\begin{aligned}&I_0 \ddot{w}_{mn} (t)+C_{31}^{mn} u_{mn} (t)+C_{32}^{mn} v_{mn} (t)+C_{33}^{mn} w_{mn} (t)\nonumber \\&\quad +\,C_{34}^{mn} \phi _{xmn} (t)+C_{35}^{mn} \phi _{\theta mn} (t)\nonumber \\&\quad +\,\sum _{ij} {C_v^{ijmn} } \dot{v}_{ij} (t)+\sum _{ijkl} {C_{1mn}^{ijkl} w_{ij} (t)u_{kl} (t)}\nonumber \\&\quad +\,\sum _{ijkl} {C_{2mn}^{ijkl} w_{ij} (t)v_{kl} (t)} +\sum _{ijkl} {C_{3mn}^{ijkl} w_{ij} (t)w_{kl} (t)}\nonumber \\&\quad +\,\sum _{ijkl} {C_{4mn}^{ijkl} w_{ij} (t)\phi _{xkl} (t)} +\sum _{ijkl} {C_{5mn}^{ijkl} w_{ij} (t)\phi _{\theta kl} (t)}\nonumber \\&\quad +\,\sum _{ijklpq} {C_{6mn}^{ijklpq} w_{ij} (t)w_{kl} (t)w_{pq} (t)} =q_{mn3} (t)\nonumber \\ \end{aligned}$$

(35)

where the coefficients of linear (see Eqs. 20–24) and non-linear terms can be determined by operators $L_{ij}$ and the von Kármán non-linear term $\eta (u,v,w,\varphi _x ,\varphi _\theta )$ in Eq. (12). The shell deflections are small so that only quadratic and cubic non-linear terms are retained for the present studied case. Based on the static condensation method [23], solving Eqs. (31)–(34) with respect to the modal coordinates of in-plane displacements and rotations ($u_{mn} (t)$, $v_{mn} (t)$, $\phi _{xmn} (t)$ and $\phi _{\theta mn} (t)$) and then substituting the results into the Eq. (35) , the equation of motion is transformed into a reduced equation in the generalised transverse displacement $w_{mn} (t)$ (see Eqs. 20–27):

$$\begin{aligned}&M_{mn} (I_0 ,I_1 ,I_2 )\ddot{w}_{mn} (t)+C_{mn} (\varOmega )\dot{w}_{mn} (t)\nonumber \\&\quad +\,K_{mn} w_{mn} (t)+\sum _{ijkl} {C_{mn2}^{ijkl} w_{ij} (t)w_{kl} (t)}\nonumber \\&\quad +\,\sum _{ijklpq} {C_{mn3}^{ijklpq} w_{ij} (t)} w_{kl} (t)w_{pq} (t)=Q_{mn} (t)\nonumber \\ \end{aligned}$$

(36)

where the generalised mass $M_{mn}$, damping $C_{mn}$ and linear stiffness $K_{mn}$ of the non-linear vibration system can be given by Eq. (27). $C_{mm2}^{ijkl}$ and $C_{mn3}^{ijklpq}$ are the non-linear components of the stiffness. The non-linear stiffness is calculated using assumed mode shapes by Galerkin integration and superimposed on the linear part of the equation to establish the non-linear modal equation. The generalised forces $Q_{mn}(t)$ consist of the double Fourier coefficients $q_{mn1} (t)$, $q_{mn2} (t)$, $q_{mn3} (t)$, $q_{mn4} (t)$ and $q_{mn5} (t)$.

Equation (36) represents a coupled non-linear ordinary differential equations with quadratic and cubic non-linearities. As long as the system does not possess internal resonances between modes, we can limit ourselves to solving equation by neglecting the modal interaction terms of Eq. (36) [24, 27]. Here only a single harmonic load $q_z$ (acting in direction z) is considered

$$\begin{aligned} Q_{mn} (t)=F_{mn} \cos \varpi t \end{aligned}$$

(37)

where $\varpi$ is the transverse excitation frequency. This assumption consists on neglecting all of the contributions except the contribution of the desired mode (m, n):

$$\begin{aligned}&M_{mn} (I_0 ,I_1 ,I_2 )\ddot{w}_{mn} (t)+C_{mn} (\varOmega )\dot{w}_{mn} (t)\nonumber \\&\quad +\,K_{mn} w_{mn} (t)+C_{mn}^2 w_{mn}^{2}(t)+C_{mn}^3 w_{mn}^{3}(t)\nonumber \\&\quad =F_{mn} \cos \varpi t, \end{aligned}$$

(38)

Equation (38) represents a non-linear ordinary differential equations with quadratic and cubic non-linearities. An approximate analytical solution will be obtained using the method of multiple scales. In order to utilise the perturbation technique, Eq. (38) is rewritten in the following form:

$$\begin{aligned}&\ddot{w}_{mn} (t)+\omega _{mn}^{2}w_{mn} (t)+2\varepsilon ^{2}\mu _{mn} \dot{w}_{mn} (t)\nonumber \\&\quad +\varepsilon \alpha _{2mn} w_{mn} (t)^{2}\!+\!\varepsilon ^{2}\alpha _{3mn} w_{mn} (t)^{3}\!=\!\varepsilon ^{2}\kappa _{mn} \cos \varpi t\nonumber \\ \end{aligned}$$

(39)

where $\varepsilon$ is perturbation parameter, coefficients in Eq. (32) are as follows:

$$\begin{aligned}&\omega _{mn}^{2}={K_{mn} }/{M_{mn} }, \quad \mu _{mn} ={C_{mn} }/{2\varepsilon ^{2}M_{mn} }, \nonumber \\&\alpha _{2mn}={C_{mn}^2}/{\varepsilon M_{mn} },\nonumber \\&\alpha _{3mn} ={C_{mn}^3 }/{\varepsilon ^{2}M_{mn} }, \quad \kappa _{mn} ={F_{mn} }/{\varepsilon ^{2}M_{mn} } \end{aligned}$$

(40)

For the case of the primary resonance considered in the present study, the detuning parameter, $\sigma$, is introduced to confine the excitation frequency ($\varpi$) near the linear frequency of the system, $\omega _{mn}$, by the following relation [28]:

$$\begin{aligned} \varpi =\omega _{mn} +\varepsilon ^{2}\sigma \end{aligned}$$

(41)

By applying the method of multiple scales to Eq. (39), we can obtain a second-order approximation of the frequency–response curve of the rotating FG cylindrical shell for the desired mode (m, n):

$$\begin{aligned} \sigma =\varLambda _{mn} a^{2}\pm \sqrt{\frac{\kappa _{mn} ^{2}}{4\omega _{mn}^{2}a^{2}}-\mu _{mn}^{2}}, \end{aligned}$$

(42)

where

$$\begin{aligned} \varLambda _{mn} =\frac{1}{8\omega _{mn} }\left[ 3\alpha _{3mn} -\frac{10\alpha _{2mn}^{2}}{3\omega _{mn}^{2}}\right] , \end{aligned}$$

(43)

which determines the hardening or softening behaviour, and a is the vibration amplitude.

Table 1 Comparison of frequency parameter $\omega ^{*}=\omega R\sqrt{(1-\upsilon ^{2})\rho /E}$ for a non-rotating simply supported (S–S) cylindrical shell ($R/L=0.05$, $h/R=0.05$, $\upsilon =0.3$, $m=1$)

Table 2 Comparison of frequency parameter $\omega ^{*}=\omega R\sqrt{(1-\upsilon ^{2})\rho /E}$ for rotating simply supported (S–S) cylindrical shell ($L/R=5$, $h/R=0.002$, $\upsilon =0.3$, $\varOmega =10$ rad/s, $m=1$)

The Eq. (38) can also be numerically solved by the Runge–Kutta algorithm [29] to analyze the non-linear dynamic response of rotating FG cylindrical shells.

3 Results and discussions

3.1 Simple validation of the present method

Example 1

To check the validity of the present analysis, comparisons are made with results available in open literature. Firstly, the natural frequency $\omega$ (rad/s) of non-rotating isotropic (rotating speed $\varOmega =0.$, volume fraction exponent $\varPhi =0$.) cylindrical shells is calculated from Eq. (27). The non-dimensional frequency parameters $\omega ^{*}=\omega R\sqrt{(1-\upsilon ^{2})\rho /E}$ are compared with those results obtained by Markus [30] and Liew et al. [31] in the vibration studies. The comparison shows excellent agreement in Table 1.

Example 2

For rotating isotropic (volume fraction exponent $\varPhi =0$.) cylindrical shells, the frequency parameters (forward and backward waves) are calculated from Eq. (27). Results are compared with those of Liew et al. [31], Jafari and Bagheri [32] for the verification of the validity of the present formulation. The comparisons are presented in Table 2, in which $\omega _f^*$ and $\omega _b^*$ are the non-dimensional frequency parameters associated with forward and backward waves, respectively. As can be seen from the comparisons, the agreement with those in the literature is good.

Example 3

Numerical results, based on Eqs. (38)–(43), have been computed and plotted for non-rotating isotropic cylindrical shells, in order to establish reasonable comparisons. The geometric properties and the material constants used are $R=0.1$ m, $h=0.000247$ m, $L=0.2$ m, $E_m =7.102 \times 10^{10}$ Pa, $\upsilon _m =0.31$ and $\rho _m =2796$ kg/m$^{3}$. The mode is ($m=1$, $n=6$). The external force used in the calculus is $F_{mn}=0.0012h^{2}\rho _m \omega _{mn}^{2}$ without damping (see Fig. 2a) and with damping (the damping ratio is $\zeta _{1,6}=0.0005$, see Fig. 2b). In Fig.2, the forced non-linear vibration case is given, showing a good agreement with Rougui et al. [24] and Pellicano et al. [26]. In this figure, a / h and $\varpi /\omega _{mn}$ denote the amplitude to thickness ratio and the excitation to linear frequency ratio, respectively.

Fig. 2

Comparison of results obtained in present work with previous results obtained by Rougui et al. (without damping, a) and Pellicano et al. (with damping, b)

Table 3 Temperature-dependent coefficients of elastic modulus E (GPa), Poisson’s ratio $\upsilon$; mass density $\rho$ (kg/m$^{3}$) and thermal expansion coefficient $\alpha$ (1/K) for ceramics and metals [33]

3.2 Dynamic behaviour of rotating FG cylindrical shells

Numerical results are presented for ceramic–metal FG cylindrical shell. The functionally graded material is ceramic rich (ZrO$_{2}$) at the inner surface and metal (Ti–6Al–4V) rich at the outer surface, with temperature difference $T_{cm} =200$ K (zero thermal stress state, $T_m =300$ K). The material properties are listed in Table 3 [33]. The geometric properties used are $R=0.1$ m, $h=0.000247$ m, $L=0.2$ m. The mode is $(m, n) = (1, 6)$.

Fig. 3

The influence of volume fraction exponents ($\varPhi$) together with rotating speeds ($\varOmega$) on the frequency parameters (backward and forward waves) of a rotating FG cylindrical shell

Based on Eq. (27), Fig. 3 illustrates the effects of volume fraction exponents ($\varPhi$) and rotating speeds ($\varOmega$) on the non-dimensional frequency parameters $\omega ^{*}$ (backward waves and forward waves) of rotating FG cylindrical shells. The frequency parameter $\omega ^{*}$ of the backward travelling wave is higher than that of the forward wave at each rotating speed $\varOmega$. It can be seen that the frequencies increase with the increase in volume fraction exponents and rotating speeds for both the backward and forward waves. However, it is also seen in Fig. 3 that the frequencies of rotating FG cylindrical shells show very minimal increase when the volume fraction exponent is increased from 10 to 50. It is expected that the frequencies will converge when the volume fraction exponent $\varPhi$ is sufficiently large. This is due to the fact that the material properties exhibit small variations for $\varPhi >10$, and when $\varPhi =\infty$, the shell is fully ceramic (ZrO$_{2}$).

Fig. 4

Influence of rotating speeds ($\varOmega$) on primary resonance responses of rotating FG cylindrical shells

Based on Eqs. (38)–(43), Fig. 4 illustrates the influence of the rotating speed ($\varOmega$) on the primary resonance responses of rotating FG cylindrical shells to harmonic transverse external forces. The volume fraction exponent is taken to be $\varPhi =0.5$. The excitation amplitude used in the calculus is $F_{mn} =0.004h^{2}\rho _c \omega _{mn}^{2}$. $\rho _c$ is the mass density of ceramic (ZrO$_{2}$). In this case, the rotating FG cylindrical shell considered is without damping. However, the forced non-linear vibration shows a similar damping behaviour (see Fig. 4). This can be expected as there is a generalised damping force $C_{mn} (\varOmega )\dot{w}_{mn} (t)$ when rotating speed $\varOmega \ne 0$ (see . Eq. 38). It can also be seen that an increase in the rotating speed $\varOmega$ leads to a decrease in the softening nonlinearity. The reason of this change in behaviour can be explained by the fact that the generalised damping coefficient $C_{mn} (\varOmega )$ (see Eq. 38) increases as the value of $\varOmega$ increases ($C_{mn} (2)=8.7432$, $C_{mn} (3)=13.1134$, $C_{mn} (4)=17.4845$). Increasing the damping coefficient results in a decreasing of the nonlinearity.

Fig. 5

Influence of excitation amplitudes on primary resonance responses of rotating FG cylindrical shells

The frequency-response curves with different transverse excitation amplitudes are plotted in Fig. 5, which shows the nonlinearity of the rotating FG cylindrical shell increases with the increasing in excitation amplitudes. This is consistent with the results presented by Nayfeh and Mook [28]. The data of the problem are $\varOmega =3.0$ r.p.s. and $\varPhi =0.5$. The excitation amplitude used in the calculus is $F_{mn} =\kappa h^{2}\rho _c \omega _{mn}^{2}$ ($\kappa =0.002, 0.004$ and 0.006) without damping.

Fig. 6

Chaotic oscillation for the rotating FG cylindrical shell at $\varOmega =0.0$ rad/s, a time trace, b phase-plane diagram, c Poincaré map

Fig. 7

Periodic response for the rotating FG cylindrical shell at $\varOmega =8.5$ rad/s, a time trace, b phase-plane diagram, c Poincaré map

Fig. 8

Period-4 oscillation for the rotating FG cylindrical shell at $\varOmega =16.0$ rad/s, a time trace, b phase-plane diagram, c Poincaré map

Fig. 9

Bifurcation diagram of Poincaré maps for the rotating FG cylindrical shell. $T\,=\,$periodic response, $nT\,=\,$ period-n response, $C\,=\,$chaos

Solving Eq. (38) by the Runge–Kutta method, the time traces, phase-plane diagrams, Poincaré maps and bifurcation diagram of rotating FG cylindrical shells are obtained by means of the software Fortran and shown in Figs. 6, 7, 8 and 9. The data of the problem are $\varpi =0.8\omega _{mn}$, $F_{mn} =10.0h^{2}\rho _c \omega _{mn}^{2}$ (without damping) and $\varPhi =0.5$. Simple periodic motion, quasi-periodic motion and chaotic response have been detected, as indicated in Figs. 6, 7, 8 and 9. This indicates a very rich and complex non-linear dynamics. The results for the rotating speed $\varOmega =0.0$ rad/s are presented in Fig. 6. From the time trace (a), phase-plane diagram (b) and Poincaré map (c), one can see that this is a very irregular motion. It is concluded that the motion is chaotic. Typical periodic oscillation is illustrated for the rotating speed $\varOmega =8.5$ rad/s in Fig. 7 through the time trace (a), phase-plane diagram (b) and Poincaré map (c), respectively. Typical characteristics of the period-4 oscillation for the rotating speed $\varOmega =16.0$ rad/s is depicted in Fig. 8. The bifurcation diagram of Poincaré maps for the rotating FG cylindrical shell is shown in Fig. 9. As shown in Fig. 9, the system displays chaotic response in the rotating speed interval of [0.0, 6.0]. As the rotating speed $\varOmega$ is increased, the motion displays several behaviour including periodic and period-n motion. When the rotating speed $V> 32.0$ rad/s, the bifurcation diagram of Poincaré maps presents simple periodic response. We see that, as the rotating speed $\varOmega$ increases, the motion of the FG cylindrical shell passes from chaotic to quasi-periodic and periodic and finally to periodic. The reason of this change in behaviour can be explained by the fact that the generalised damping increases as the rotating speed increases, and the nonlinearity decreases. Non-periodic motions are much more likely if damping is small. With larger damping, the oscillations were periodic. Figures 6, 7, 8 and 9 show that the relations between the nonlinearity and the rotating speed agree with the ones of the Fig. 4.

4 Conclusions

In the present work, the non-linear dynamics of rotating FG cylindrical shells have been studied by developing a non-linear theoretical model. The shear deformation, in-plane and rotary inertias are taken into account in the present formulation. Von Kármán theory and Hamilton’s principle are employed to obtain the non-linear governing equations. The objective of the study is to present a reduction in the model to investigate non-linear dynamics, including primary resonance responses, quasi-periodic and chaotic responses to harmonic transverse external forces. The method has been tested in the cases of linear and non-linear; also in the cases the comparison with authoritative literature shows a good accuracy. Some numerical examples are demonstrated for the present theoretical method. It is shown that the frequencies increase with the increase in volume fraction exponents and rotating speeds for both the backward and forward waves. Trends toward frequency convergence when the volume fraction exponent is sufficiently large are observed. It was also verified that rotating speeds and excitation amplitudes have a strong influence on the non-linear behaviour of rotating FG cylindrical shells. As the rotating speed increases, the motion of the FG cylindrical shell passes from chaotic to quasi-periodic and periodic and finally to periodic. The nonlinearity of the rotating FG cylindrical shell increases with the increasing in excitation amplitudes.

Appendices

Appendix 1

$$\begin{aligned} \mathbf{C}(z)= & {} \left[ {{\begin{array}{lllll} {C_{11} }&{} {C_{12} }&{} 0&{} 0&{} 0 \\ {C_{21} }&{} {C_{22} }&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {C_{33} }&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {C_{44} }&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {C_{55} } \\ \end{array} }} \right] ,\nonumber \\ {{\varvec{\upalpha }} }= & {} \left[ {{\begin{array}{lllll} {\alpha _{xxe} }&{} {\alpha _{\theta \theta e} }&{} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{T}. \end{aligned}$$

The effective thermal expansion coefficients ($\alpha _{xxe}$, $\alpha _{\theta \theta e}$) in the two principle directions (x, $\theta$) are equal due to in-plane uniform distribution of the functionally graded material properties ($\alpha _{xxe} =\alpha _{\theta \theta e} =\alpha _\mathrm{{eff}})$. The stiffness coefficients are defined according to

$$\begin{aligned} C_{11}= & {} \frac{E_\mathrm{{eff}}}{1-\nu _\mathrm{{eff}}^{2}},\\ C_{12}= & {} \frac{\nu _\mathrm{{eff}} E_\mathrm{{eff}}}{1-\nu _\mathrm{{eff}}^{2}},\nonumber \\ C_{21}= & {} \frac{\nu _\mathrm{{eff}} E_\mathrm{{eff}}}{1-\nu _\mathrm{{eff}}^{2}},\\ C_{22}= & {} \frac{E_\mathrm{{eff}}}{1-\nu _\mathrm{{eff}}^{2}},\\ C_{33}= & {} C_{44} =C_{55} =\frac{E_\mathrm{{eff}}}{2(1+\nu _\mathrm{{eff}})}. \end{aligned}$$

For a given volume fraction exponent $\varPhi$, the effective Young’s modulus $E_\mathrm{{eff}}$, the effective Poisson’s ratio $\nu _\mathrm{{eff}}$ and the effective thermal expansion coefficients $\alpha _\mathrm{{eff}}$ can be obtained according to Eq. (4).

Appendix 2

$$\begin{aligned}&\left\{ {{\begin{array}{ll} {N_x^{T}}&{} {M_x^{T}} \\ {N_\theta ^{T}}&{} {M_\theta ^{T}} \\ {N_{x\theta }^{T}}&{} {M_{x\theta }^{T}} \\ \end{array} }} \right\} =\int _{-\frac{h}{2}}^{\frac{h}{2}}\\&\quad \times {\left\{ {{\begin{array}{l} {Q_{11} (z)\alpha _{xxe} (z)+Q_{12} (z)\alpha _{\theta \theta e} (z)} \\ {Q_{12} (z)\alpha _{xxe} (z)+Q_{22} (z)\alpha _{\theta \theta e} (z)} \\ 0 \\ \end{array} }} \right\} \Delta T(z)\left( {{\begin{array}{ll} 1&{} z \\ \end{array} }} \right) \hbox {d}z},\\&Q_x^{T}=Q_\theta ^{T}=0.,\\&\left\{ {\begin{array}{l} N_x \\ N_\theta \\ N_{x\theta } \\ M_x \\ M_\theta \\ M_{x\theta } \\ \end{array}} \right\} \quad =\left[ {{\begin{array}{llllll} {A_{11} }&{} {A_{12} }&{} 0&{} {B_{11} }&{} {B_{12} }&{} 0 \\ {A_{21} }&{} {A_{22} }&{} 0&{} {B_{21} }&{} {B_{22} }&{} 0 \\ 0&{} 0&{} {A_{66} }&{} 0&{} 0&{} {B_{66} } \\ {B_{11} }&{} {B_{12} }&{} 0&{} {D_{11} }&{} {D_{12} }&{} 0 \\ {B_{21} }&{} {B_{22} }&{} 0&{} {D_{21} }&{} {D_{22} }&{} 0 \\ 0&{} 0&{} {B_{66} }&{} 0&{} 0&{} {D_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _x \\ \varepsilon _\theta \\ \gamma _{x\theta } \\ \kappa _x \\ \kappa _\theta \\ \kappa _{x\theta } \\ \end{array}} \right\} , \quad \left\{ {\begin{array}{l} Q_x \\ Q_\theta \\ \end{array}} \right\} \\&\quad =\left[ {{\begin{array}{ll} {E_{44} }&{} 0 \\ 0&{} {E_{55} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\gamma _{xz} } \\ {\gamma _{\theta z} } \\ \end{array} }} \right\} ,\\&(A_{ij} , B_{ij} , D_{ij} )\!=\!\int _{-\frac{h}{2}}^{\frac{h}{2}} {Q_{ij} } (1,z,z^{2})dz\, (i,j\!=\!1,2,6), E_{44}\\&\quad =\int _{-\frac{h}{2}}^{\frac{h}{2}} {Q_{\hbox {55}} } dz , E_{55} =\int _{-\frac{h}{2}}^{\frac{h}{2}} {Q_{\hbox {44}} } dz, \end{aligned}$$

where the effective elasticity coefficients $Q_{ij} (z)$ of the FG cylindrical shell are given

$$\begin{aligned} Q_{11}= & {} C_{11}, \quad Q_{12} =C_{12} /A, \quad Q_{21} =C_{21}, \quad Q_{22}\\&=C_{22} /A, \quad Q_{66} =C_{55} /A,\\ Q_{44}= & {} \kappa _G C_{44},\quad Q_{55} =Q_{44} /A, \quad A=1+z/R. \end{aligned}$$

A shear correction factor ($\kappa _G )$ of $\frac{5}{6}$ is used during the evaluation of $E_{44}$ and $E_{55}$ [34].

Appendix 3

$$\begin{aligned} L_{11}= & {} A_{11} \frac{\partial ^{2}}{\partial x^{2}}+\frac{1}{R^{2}}A_{66} \frac{\partial ^{2}}{\partial \theta ^{2}},\\ L_{12}= & {} \frac{A_{12} +A_{66} }{R}\frac{\partial ^{2}}{\partial x\partial \theta },\quad L_{13} =\frac{A_{12} }{R}\frac{\partial }{\partial x},\\ L_{16}= & {} L_{11},\quad L_{14} =B_{11} \frac{\partial ^{2}}{\partial x^{2}}+\frac{B_{66} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}, \\ L_{15}= & {} \frac{B_{12} +B_{66} }{R}\frac{\partial ^{2}}{\partial x\partial \theta },\\ L_{17}= & {} \frac{L_{12} }{R}, \quad L_{21} =\frac{A_{66} +A_{12} }{R}\frac{\partial ^{2}}{\partial x\partial \theta },\\ L_{22}= & {} A_{66} \frac{\partial ^{2}}{\partial x^{2}}+\frac{A_{22} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}-\frac{E_{55} }{R^{2}},\\ L_{23}= & {} \frac{A_{22} +E_{55} }{R^{2}}\frac{\partial }{\partial \theta },\\ L_{24}= & {} \frac{B_{66} +B_{12}}{R}\frac{\partial ^{2}}{\partial x\partial \theta }, \\ L_{25}= & {} B_{66} \frac{\partial ^{2}}{\partial x^{2}}+\frac{B_{22} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}+\frac{E_{55} }{R},\\ L_{26}= & {} L_{21},\quad L_{27} =\frac{A_{66} }{R}\frac{\partial ^{2}}{\partial x^{2}}+\frac{A_{22} }{R^{3}}\frac{\partial ^{2}}{\partial \theta ^{2}},\\ L_{31}= & {} -\frac{A_{21} }{R}\frac{\partial }{\partial x},\\ L_{32}= & {} -\frac{E_{55} }{R^{2}}\frac{\partial }{\partial \theta }-\frac{A_{22} }{R^{2}}\frac{\partial }{\partial \theta },\\ L_{33}= & {} E_{44} \frac{\partial ^{2}}{\partial x^{2}}+\frac{E_{55} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}-\frac{A_{22} }{R^{2}},\\ L_{34}= & {} E_{44} \frac{\partial }{\partial x}-\frac{B_{21} }{R}\frac{\partial }{\partial x}, \\ L_{35}= & {} \frac{E_{55} }{R}\frac{\partial }{\partial \theta }-\frac{B_{22} }{R^{2}}\frac{\partial }{\partial \theta },\\ L_{36}= & {} -\frac{A_{21} }{2R}\frac{\partial }{\partial x}, \quad L_{37} =-\frac{A_{22} }{2R^{3}}\frac{\partial }{\partial \theta },\\ L_{41}= & {} B_{11} \frac{\partial ^{2}}{\partial x^{2}}+\frac{B_{66} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}, \quad L_{42} =\frac{B_{12} +B_{66} }{R}\frac{\partial ^{2}}{\partial x\partial \theta },\\ L_{43}= & {} \left( \frac{B_{12} }{R}-E_{44} \right) \frac{\partial }{\partial x},\\ L_{44}= & {} D_{11} \frac{\partial ^{2}}{\partial x^{2}}+\frac{D_{66} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}-E_{44}, \\ L_{45}= & {} \frac{D_{12} +D_{66} }{R}\frac{\partial ^{2}}{\partial x\partial \theta },\\ L_{46}= & {} L_{41} , L_{47} =\frac{L_{42} }{R},\\ L_{51}= & {} \frac{B_{66} +B_{12} }{R}\frac{\partial ^{2}}{\partial x\partial \theta },\\ L_{52}= & {} B_{66} \frac{\partial ^{2}}{\partial x^{2}}+\frac{B_{22} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}+\frac{E_{55} }{R},\\ L_{53}= & {} \frac{B_{22} -E_{55} R}{R^{2}}\frac{\partial }{\partial \theta }, \\ L_{54}= & {} \frac{D_{12} +D_{66} }{R}\frac{\partial ^{2}}{\partial x\partial \theta }, \quad L_{55} =\frac{D_{22} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}\\&\,-E_{55} +D_{66} \frac{\partial ^{2}}{\partial x^{2}},\\ L_{56}= & {} L_{51},\quad L_{57} =\frac{B_{66} }{R}\frac{\partial ^{2}}{\partial x^{2}}+\frac{B_{22} }{R^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}}. \end{aligned}$$