1 Introduction

In recent years, the generation of chaotic attractor which attracts extensive attention of researchers in different fields has become an important part in the investigation of chaos theory and application. Especially, the generation of multi-wing chaotic attractor has become a key issue recently, and some multi-wing chaotic attractors have been proposed [1–7]. The multi-wing chaotic systems can be classified into two totally different groups. The one group is the system with smooth nonlinear function, in which the number of wings is not equal to that of the equilibria [1–4]. The other group is the system with piecewise nonlinear function [5–7]. The number of wings in these systems [1–7] is more than two. However, the systems in [1–7] have only one positive Lyapunov exponent, and they belong to normal chaos systems.

Since the first hyperchaotic attractor was introduced by Rossler [9], hyperchaotic systems have been intensively studied, and they can be widely applied in many realms such as cryptosystem [10–15], neural network [16, 17], secure communication [18], and laser design [19]. We take cryptosystem as example. Chaos as a special kind of nonlinear system, due to its pseudorandom motion trajectory, extreme sensitivity to initial conditions, unpredictability, and complexity, has unique advantages in the image encryption technology [11, 12]. For hyperchaotic system, because of its better unpredictability, more complex dynamic behavior, and larger key space, the applications of chaotic sequence as a key for image and video encryption have a greater advantage and research space [13–15].

Hyperchaotic multi-wing attractors with more complex dynamic are recently proposed [20, 21]. A multi-wing attractor is constructed in an existing hyperchaotic system by coordinate transition and absolute value transition [20]. The state feedback control is used in an existing multi-wing system in order to obtain hyperchaotic attractor [21]. The common methods to obtain hyperchaotic multi-wing attractor are proposed in [20, 21].

Recently, the method of generating hyperchaotic attractor is proposed since the fabrication of memristor is successfully realized in 2008 [25]. By adding one extra flux-controlled memristor into three-dimensional (3D) chaotic system, the 4D hyperchaotic memristive systems can be presented in [22, 23]. However, the researches in [22] focus on two-wing system, and in [23], a cross-product item must be added in order to generate real four-wing attractor. Moreover, the position of extra memristor in memristive system is not discussed.

Inspired by the [22] and [23], we propose a novel method to generate hyperchaotic multi-wing attractor in this paper. The method is only by replacing the resistor in the circuit of the modified Lü system with a flux-controlled memristor. Compared with the methods in [20–23], the method proposed in this paper is relatively easy to realize, and it can be easily extended to the generalized Lorenz system family. By introducing the memristor, the new memristive system has infinitely many stable and unstable equilibrium points. Moreover, we discuss whether the resistor in the circuit of modified Lü system can be replaced, and how the characteristic of new memristive system changes after replacing the resistor with memristor. The paper is organized as follows. In Sect. 2, the brief introduction of memristor is stated. The modified Lü system after replacing resistor with memristor and its basic dynamical properties are analyzed in Sect. 3. In Sect. 4, the circuit implementation of the new memristive hyperchaotic multi-wing system is proposed. Some conclusions are finally drawn in Sect. 5.

2 The memristor

The memristor which was originally envisioned by Professor Chua is a nonlinear element [24]. Encouraged by the physical implementation of memristive devices at nanoscale [25], the potential applications of memristor have been exploited in many fields, such as cellular neural network [26], nonlinear systems [27–29], nonvolatile random access memory (NRAM) [30, 31].

The definition of a memristor is based on the relationship between charge q and flux \(\varphi \). The relationship between the current across a charge-controlled memristor and the voltage is given by the differential form shown in (1).

$$\begin{aligned} v_{m} =M(q)i, \quad \dot{q}=i. \end{aligned}$$
(1)

where M(q) is the charge-controlled memristance [24].

The relationship between the voltage across a flux-controlled memristor and the current is given by the differential form shown in (2).

$$\begin{aligned} i_{m} =W(\varphi )v, \quad \dot{\varphi }=v. \end{aligned}$$
(2)

where \(W(\varphi )\) is a memductance function. A cubic nonlinearity is frequently chosen for the q function [22, 23, 32–34].

$$\begin{aligned} W(\varphi )=\frac{dq(\varphi )}{d\varphi }=\frac{d(a\varphi +b\varphi ^{3})}{d\varphi }=a+3b\varphi ^{2}. \end{aligned}$$
(3)

where a and b are two positive constants.

3 The proposed memristive hyperchaotic multi-wing system

Lü proposed a system with two-wing attractor in 2002 [8]. We consider the modified Lü system with \(2(N+1)\) wings proposed in [6]. It can be described as follows:

$$\begin{aligned}&\left\{ {\begin{array}{l} \dot{x}=\alpha (y-x) \\ \dot{y}=\beta y-xz/P \\ \dot{z}=f(x)-\gamma z \\ \end{array}} \right. \end{aligned}$$
(4)
$$\begin{aligned}&f(x)=F_0 x^{2}-{\mathop {\sum }\limits ^{N}_{i=1} {F_{i} }} [10.5\hbox {sgn}(\hbox {x}-\hbox {E}_{i})\nonumber \\&\qquad - 0.5\hbox {sgn}(\hbox {x}+\hbox {E}_{i} )] \nonumber \\&\quad F_{0} =\frac{k}{P}\,\,\,F_{i} =\frac{2AP}{k_{i}}\,\,\,E_{i}=\frac{0.5(i+1)AP}{k}. \end{aligned}$$
(5)

where N is a positive integer; A, P, k,  and \(k_{i}\) are constants; the values of \(\alpha , \beta \), and \(\gamma \) are positive; the specific parameters are configured as \(\alpha =36, \beta =20, \gamma =3, A=30, P=0.05, k=5\); and f(x) is the multi-segment quadratic function with duality symmetry. The equilibrium points of the system (4) are (0, 0, 0) and \((\pm u,\pm u, P\beta )\), where u satisfies: \(f(u)= P\beta \gamma \). The system belongs to normal chaos.

In this paper, the resistor in the implement circuit of system (4) is replaced with a flux-controlled memristor. Five cases are taken into consideration by replacing \(R_{1}, R_{2}, R_{3}, R_{4}\), and \(R_{5}\) with the memristor, respectively. The proposed system has many interesting complex dynamical behaviors such as periodic orbits, torus, chaos, and hyperchaos.

Fig. 1
figure 1

Circuit diagram for the original modified Lü system (4) after replacing \(R_{1}\)

Full size image

3.1 Case1: replacing \({R_{1}}\)

Firstly, the resistor \(R_{1}\) is replaced with flux-controlled memristor, and the circuit implementation is shown in Fig. 1. From Fig. 1 and (2), we obtain that

$$\begin{aligned} \left\{ {\begin{array}{lll} C_{x} \dot{v}_{x} =v_{y} /R_{2} -W(\varphi )v_{x} \\ C_{y} \dot{v}_{y} =v_{y} /R_{3} -v_{x} v_{z} /R_{4} \\ C_{z} \dot{v}_{z} =f(x)/R_{6} -v_{z} /R_{5} \\ \dot{\varphi }=v_{x} \\ \end{array}} \right. . \end{aligned}$$
(6)

where \(v_{x}, v_{y}\), and \(v_{z}\) indicate the voltage of x, y, and z.

Let \(\tau =t\cdot RC\) be the physical time, where t is the dimensionless time, R is a reference resistor, and C is a reference capacitor. When \(C_{x}=C_{y}=C_{z}=C, \alpha =R/R_{2}, \beta =R/R_{3}, \gamma =R/R_{5},\) and \(P=R_{4}/R\), the dimensionless equations can be expressed as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=\alpha y-\rho W(\varphi )x \\ \dot{y}=\beta y-xz/P \\ \dot{z}=f(x)-\gamma z \\ \dot{\varphi }=x \\ \end{array}} \right. . \end{aligned}$$
(7)

where \(\rho \) is a positive parameter indicating the strength of the memristor.

The memristive system (7) keeps the symmetry of original 3D system (4), and it is invariant under the transformation \((x, y, z, \varphi )\leftrightarrow (-x,-y, z,-\varphi )\) with z-axis symmetry.

The equilibria of system (7) can be derived by solving the following equations:

$$\begin{aligned} \left\{ {\begin{array}{l} \alpha y-\rho W(\varphi )x=0 \\ \beta y-xz/P=0 \\ f(x)-\gamma z=0 \\ x=0 \\ \end{array}} \right. . \end{aligned}$$
(8)

We can easily observe that the system (7) has infinitely many equilibria \(O=\{( x, y, z, \varphi )\vert x=y=z=0, \varphi =c\}\), where c is any real constant. By linearizing system (7) at point O, we can obtain the Jacobian matrix.

$$\begin{aligned} Jo=\left( {{\begin{array}{llll} {-\rho W(c)}&{} \alpha &{} 0&{} 0 \\ 0&{} \beta &{} 0&{} 0 \\ 0&{} 0&{} {-\gamma }&{} 0 \\ 1&{} 0&{} 0&{} 0 \\ \end{array} }} \right) . \end{aligned}$$
(9)

The dissipativity of system (7) is described as

$$\begin{aligned} \nabla V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z}+\frac{\partial \dot{\varphi }}{\partial \varphi }=-\rho W(c)+\beta -\gamma .\nonumber \\ \end{aligned}$$
(10)

When \(\rho , \beta ,\) and \(\gamma \) satisfy \(-\rho W(c)+\beta -\gamma <0\), the system is dissipative. This means that asymptotic motion settles onto an attractor and each volume containing the system trajectory shrinks to zero at an exponential rate as \(t \rightarrow \infty \). Moreover,

$$\begin{aligned} \frac{\hbox {d}V}{\hbox {d}t}=e^{-\rho W(c)+\beta -\gamma }=e^{r}. \end{aligned}$$
(11)

It implies that the volume of the attractor decreases by a factor of \(\hbox {e}^{r}\). And the memristor should satisfy:

$$\begin{aligned} \rho W(c)>\beta -\gamma . \end{aligned}$$
(12)

According to (9), the characteristic equation is given by

$$\begin{aligned} \lambda (\lambda +\rho W(c))(\lambda -\beta )(\lambda +\gamma )=0. \end{aligned}$$
(13)
Fig. 2
figure 2

First three LEs of system (7) by adjusting \(\rho \): a \(6<\rho <10\), b \(6<\rho <6.5\)

Full size image

It is very easy to solve its eigenvalues

$$\begin{aligned} \lambda _{1} =0,\lambda _{2} =-\rho W(c),\lambda _{3} =\beta ,\lambda _{4} =-\gamma . \end{aligned}$$
(14)

The values of \(\rho , a, b, \beta \), and \(\gamma \) are all positive, so \(\lambda _{2}\) and \(\lambda _{4}\) are always negative, and \(\lambda _{3}\) is always positive. Therefore, there are one positive eigenvalue, one zero eigenvalue, and two negative eigenvalues, and the system (7) has unstable saddle point.

In the following, the system (7) is further investigated by means of Lyapunov exponent analysis, bifurcation analysis, Poincaré map, and phase portrait. The parameters of the system (7) are similar to the original system, which are configured as \(\alpha =36, \beta =20, \gamma =3, P=0.05, N=4\), the parameters of f(x) are configured as \(F_{0}=100, F_{1}=10, F_{2}=12, F_{3}=16.67, F_{4}=18.18, E_{1}=0.3, E_{2}=0.45, E_{3}=0.6\), and \(E_{4}=0.75\). The memductance function of memristor is given by (3), where \(a=4,\) and \(b=0.01\).

When \(\rho \) is chosen from 6 to 10 and the initial condition is set to (1 0 1 0), the numerical results are described in Fig. 2 (The last one is not displayed because it is always a big negative number). The LEs describe the rate of exponential divergence from perturbed initial conditions. The method of Lyapunov characteristic exponents serves as a useful tool to quantify chaos, and specially, two positive maximum LEs are usually interpreted as an indication that the system is hyperchaotic. To accurately calculate the LE of system (7) with f(x), the continuous differentiable function tanh \((K_{0}(x\pm E_{i}))\) should be adopted to approximate the sign function sgn \((x\pm E_{i})\) [21, 35]. We choose the parameter \(K_{0} =1000\), which is so large that the calculated exponent is independent of its value to high precision. And we take the Dormand–Prince method (RK45) as the ODE solver and use the famous Wolf method.

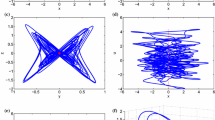
From Fig. 2, the dynamical behaviors of system (7) can be clearly observed, and the system can evolve into torus, chaotic attractor, and hyperchaotic attractor.

Fig. 3
figure 3

Simulated phase portraits of system (7) with different \(\rho \): a \(\rho =6\), b \(\rho =6.2\), c \(\rho =9\)

Full size image
Fig. 4
figure 4

Poincaré sections of system (7) with parameters \(\rho =6.2\). a Projection on \(y-z\) plane with \(x=0\); b projection on \(x-z\) plane with \(\varphi =3\); c projection on \(x-y\) plane with \(z=1\)

Full size image
Fig. 5
figure 5

Poincaré sections of system (7) with parameters \(\rho =9\). a Projection on \(y-z\) plane with \(x=0\); b projection on \(x-z\) plane with \(\varphi =0\); c projection on \(x-y\) plane with \(z=1\)

Full size image

At the beginning, the strength \(\rho \) begins from 6. It can be seen that system (7) has a torus when \(\rho \) changes from 6 to 6.13. And a typical torus is shown in Fig. 3a, when \(\rho =6\) the four LEs are 0.000, 0.00, −3.49, and −3.50, respectively. When \(\rho \) is near to 6.14, the LEs are 0.153, 0.00, −0.941, and −7.016. There exists one positive Lyapunov exponent, and the system is chaotic. From Fig. 2b, the maximum Lyapunov exponent approximates to zero (The LEs are 0.00, 0.00, −0.697856, and −7.262967 when \(\rho =6.24\), and the system (7) has a torus.) when the parameter \(\rho \) changes from 6.24 to 6.25. Therefore, the system (7) is chaotic (\(\rho \in [6.14, 6.23] \cup [6.26, 6.38])\), a typical chaotic attractor is shown in Fig. 3b when \(\rho =6.2\). When \(\rho \approx 6.38\), the LEs are 1.083, 0.126, −0.04, and −10.821, and the system (7) is hyperchaotic \((\rho \in [ 6.38, 10])\) except the critical value 9.95. A typical hyperchaotic attractor is shown in Fig. 3c when \(\rho =9\), and the Lyapunov exponents are \(L_{1} =4.18, L_{2} = 0.82, L_{3} = -0.008, L_{4} = -24.002\); therefore, system (7) is hyperchaotic. At the same time, the Lyapunov dimension of the system (7) is calculated by

$$\begin{aligned} D_{L}= & {} j+\frac{1}{\left| {L_{j+1} } \right| }\sum \limits ^{j}_{i=1} {L_{i} }\nonumber \\= & {} 3+\frac{4.18+0.82-0.008}{24.002}=3.208 \end{aligned}$$
(15)

From (15), it can be seen that the system (7) is really a dissipative system, and the Lyapunov dimension of this system is fractional. Therefore, system (7) is really a new hyperchaotic system.

Fig. 6
figure 6

Bifurcation diagram of system (7) by adjusting \(\rho \): a \(6<\rho <10\), b \(6<\rho <6.5\)

Full size image
Table 1 Dynamic analysis of systems after replacing \(R_{2}, R_{3}, R_{4},\) and \(R_{5}\) with the memristor, respectively
Full size table
Fig. 7
figure 7

LEs of memristive systems in Table 1. a Case 2, b Case 3, c Case 4, d Case 5

Full size image

As an important analysis technique, the Poincaré map can reflect bifurcation and folding properties of chaos. Figures 4 and 5 show the Poincaré sections of system (7) with different parameters.

It can be seen that the points of Poincaré map in Fig. 5 are denser than those in Fig. 4, which indicates that the system (7) with parameter \(\rho =9\) has extremely richer dynamics. From Figs. 4b and 5b, the Poincaré maps prove the existence of the multi-wing attractor. It is also obviously found that the system (7) with parameter \(\rho =9\) exhibits better multi-wing feature.

In order to make further study for the proposed system (7), its behavior with respect to the bifurcation parameter \(\rho \) is discovered. The bifurcation diagram shown in Fig. 6 is obtained by plotting the local maxima of the state variable x when changing the value of \(\rho \) in the interval [6, 10]. From Figs. 2 and 6, it can be seen that the LEs and the bifurcation diagram match very well. Both of them show that the memristive system can demonstrate complex dynamic behaviors.

3.2 Other cases: replace \(R_{2}, R_{3}, R_{4}\), and \(R_{5}\), respectively

Then, we replace the resistor \(R_{2}, R_{3}, R_{4}\), and \(R_{5}\) with the memristor, respectively (\(R_{6}\) cannot be replaced because the function f(x) is the key to generate the multi-wing attractor). When \(\alpha =36, \beta = 20, \gamma = 3, P=0.05, a = 4, b = 0.01\) and f(x) defined by (5), the dynamic analysis is shown in Table 1, and their LEs are described in Fig. 7 (The last one is not displayed because it is always a big negative number).

From Table 1, we can easily observe that all systems have only one equilibrium point \(O= \{(x, y, z, \varphi )\vert x=y=z=0, \varphi =c\}\), where c is any real constant. At the same time, \(\lambda _{3}\) is always positive, and it implies that the equilibrium point O is unstable.

Fig. 8
figure 8

Bifurcation diagram of systems in Table 1. a Case 2, b Case 3, c Case 4, d Case 5

Full size image
Fig. 9
figure 9

Simulated phase portraits of system in Case 3 when \(\rho =3.1\)

Full size image

From Figs. 7 and 8, the dynamical behaviors of systems in Table 1 can be clearly observed, and the systems have period orbits and torus, chaotic attractor, hyperchaotic attractor.

Case 2: In Fig. 7a, the strength \(\rho \) is 0 at the beginning. As \(\rho \) increases from 0, the chaotic attractor exists until \(\rho \approx \) 4.1, and the system transits to hyperchaos at \(\rho \approx \) 6. After \(\rho \approx \) 12, the system is also chaotic.

Case 3: In Fig. 7b, the positive LE appears until the parameter \(\rho \approx \) 1.5, and the system transits to hyperchaos at \(\rho \approx \) 1.6. Then, when \(\rho \approx \) 2.1, the system is begin to appear chaotic attractors except the critical value \(\rho \approx \) 3.1(The LEs are 0.00, 0.00, −0.638807, and −25.641281, and the system has a torus. And a typical torus is shown in Fig. 9). After \(\rho \approx \) 3.7, the system is also hyperchaotic.

Case 4: In Fig. 7c, as the strength \(\rho \) increasing, the system is firstly chaotic and transits to hyperchaos at \(\rho \approx \) 0.18. Then, it returns to chaotic when \(\rho \approx \) 0.33.

Case 5: In Fig. 7d, the strength \(\rho \) is 0 at the beginning. When \(\rho \) changes from 0.1 to 0.022, the system is chaotic, and it transits to hyperchaos at \(\rho \approx \) 0.008.

Fig. 10
figure 10

Circuit diagrams for realizing memristive hyperchaotic multi-wing attractors

Full size image
Fig. 11
figure 11

Experimental observations of memristive multi-wing system (7). a \(\rho =6\), b \(\rho =6.2\). c \(\rho =9\)

Full size image

Based on the above analysis, the new systems can obviously exhibit hyperchaotic property after replacing resistor \(R_{1}, R_{2}, R_{3}, R_{4}\), and \(R_{5}\) in multi-wing chaotic circuit with memristor. Especially, the two positive LEs shown in Figs. 2 and 7 are relatively larger, and the ranges of parameter \(\rho \) for generating hyperchaotic multi-wing attractor in first four cases are much larger than that in the last case. From Table 1, it is easy to observe that the symmetry of the Case 5 has changed, and it is not with z-axis symmetry.

4 Circuit implementation of the memristive system

In order to further observe the hyperchaotic multi-wing attractor, the memristive system (7) has been implemented by electronic circuits. In the circuit design, we use operational amplifiers TL082, and multipliers AD633JN. Their supply voltages are taken as \(E = \pm 15\) V, and their saturated voltages are \(V_{\mathrm{sat}}\) \(\approx \pm 13.5\) V. We take the Case1 replacing \(R_{1}\) with memristor as an example.

By putting a timescale factor RC on the dimensionless time and putting a multiplication factor 0.1/V on each multiplication with AD633JN, we can obtain:

$$\begin{aligned} \left\{ {\begin{array}{l} C\dot{v}_{x} ={\alpha v_{y} }/R-{i_{B} }/R \\ C\dot{v}_{y} ={\beta v_{y} }/R-{(v_{x} v_{z} \cdot 0.1/V)}/{PR} \\ C\dot{v}_{z} ={f(x)}/R-{\gamma v_{z} }/R \\ C\dot{v}_\varphi ={v_{x} }/R \\ \end{array}} \right. . \end{aligned}$$
(16)

where \(v_{x}, v_{y}, v_{z},\) and \(v_{\varphi }\) are the voltages on capacitor, and \(i_{B}\) is the current input from the memristor. By comparing (16) with (6), the values of the capacitors and resistors of the circuit in Fig. 10 may be taken as follows: \(C_{x}=C_{y}=C_{z}=C, R_{2}=R/\alpha , R_{3}=R/\beta , R_{4}=0.1 PR, R_{5} =R/\gamma ,R_{6}=R_{7}=R_{8}=R\). Let us take \(R=100\,\hbox {k}\Omega \) and \(C= 100\) nF. When \(\alpha =36, \beta = 20, \gamma = 3\), and \(P=0.05\), we have \(R_{2}=2.78\,\hbox {k}\Omega , R_{3}=5\,\hbox {k}\Omega , R_{4}=0.5\,\hbox {k}\Omega , R_{5}=33.3\,\hbox {k}\Omega , R_{6}=R_{7}=R_{8}=100\,\hbox {k}\Omega \).

A simple memristor with classical components proposed in Ref. [23] is shown in the dashed box in Fig. 10.

It can be obtained that

$$\begin{aligned} i_{B} =\frac{v_{x} }{R_{a}}+\frac{v^{2}_{\varphi } v_{x} }{R_{b} }\cdot 0.1/\hbox {V}\cdot 0.1/\hbox {V}. \end{aligned}$$
(17)

In the memristor, if we take \(C_{w}=C\) and \(R_{w}=R\), then it is not hard to see that

$$\begin{aligned} R_{a} =\frac{R}{\rho a} \quad R_{b} =\frac{R}{300\rho b}. \end{aligned}$$
(18)

When \(a=4, b=0.01\), and \(\rho =6\), we can easily obtain \(R_{a}=4.16\,\hbox {k}\Omega , R_{b}=5.55\,\hbox {k}\Omega \). When \(a=4, b=0.01\), and \(\rho =6.2\), we can easily get \(R_{a}=4.03\,\hbox {k}\Omega , R_{b}=5.376\,\hbox {k}\Omega \). When \(a=4, b=0.01\), and \(\rho =9\), we can easily acquire \(R_{a}=2.78\,\hbox {k}\Omega , R_{b}=3.7\,\hbox {k}\Omega \).

Figure 11 shows the oscilloscope traces from the memristive circuit in Fig. 10. Except for a few transients originating from different initial conditions, the results are in agreement with Fig. 3.

5 Conclusion

In this paper, a novel hyperchaotic multi-wing system has been introduced by replacing resistor in multi-wing chaotic circuit with flux-controlled memristor. It is very interesting that the new system is not only hyperchaos but also multi-wing. In addition, this method of replacing resistor with memristor can be extended to design and implement other new continuous hyperchaotic systems. The hyperchaotic property is verified by theoretical analysis, numerical simulation. And we carry out the circuit implementation of new memristive system. Since the new hyperchaotic multi-wing systems have more complex dynamical behaviors than the normal chaotic systems, it is believed that the proposed memristive systems will have broad applications in various chaos-based information technologies such as secure communication and encryption.