Generalization of combination–combination synchronization of chaotic n-dimensional fractional-order dynamical systems

Abstract

The generalization of combination–combination (C–C) synchronization of chaotic n-dimensional (nD) fractional-order $(0<\alpha \le 1)$ dynamical systems is studied. Firstly, we replace arbitrary four chaotic nD ordinary dynamical systems by four chaotic nD fractional-order dynamical systems which have unique solutions. Secondly, we extend the scheme of a recent paper (Sun et al. in Nonlinear Dyn 73: 1211–1222, 2013) to study the generalization of C–C synchronization among four nD fractional-order dynamical systems. Examples of combination–combination synchronization among four identical or different of 6D chaotic fractional-order systems are discussed. The analytical formula of the control functions is tested numerically to achieve C–C synchronization, and good agreement is found.

1 Introduction

The theory of fractional-order derivatives can be dated back to the 17th century as described by Podlubny [1]. In the last few decades, fractional-order differential systems have appeared naturally in many fields such as engineering, quantum and biological phenomena [2–6]. Chaotic motions have also been found in fractional systems, as for instance in the fractional versions of Chua system [7], Lorenz system [8], Chen system [9], Lü system [10], Rössler system [11] and Liu system [12].

Chaos synchronization introduced for the first time in [13], which is an important topic in nonlinear science. In the literature, synchronization of fractional-order dynamical systems has been widely studied. It has many types of manifestations such as complete synchronization [13], phase and anti-phase synchronization [14], projective synchronization [15] and lag synchronization [16].

Sun et al. [17] defined the two drive systems and the two response systems of ordinary autonomous differential equation, respectively, as follows:

$$\begin{aligned}&\dot{x}_i=f_i(x_i), \quad i=1,2, \end{aligned}$$

(1)

$$\begin{aligned}&\dot{y}_i=g_i(y_i)+u_i, \quad i=1,2, \end{aligned}$$

(2)

where $x_1, x_2, y_1, y_2 \in R^n$.

Definition 1

[17] If there exist four constant matrices C, D, E , $F \in R^n\times R^n$ and $E\ne 0$ or $F\ne 0$ such that:

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty } \Vert Cx_1 +Dx_2 - Ey_1 - Fy_2\Vert =0, \end{aligned} \end{aligned}$$

(3)

the drive systems (1) are said to express combination–combination (C–C) synchronization with the response systems (2), where $\Vert \cdot \Vert$ is the matrix norm.

Fractional calculus can be developed through various definitions of derivatives such as Riemann-Liouville, Caputo and Grünwald differential operators. In this work, we will use Caputo’s linear differential operator which is defined as [18]:

$$\begin{aligned}&\begin{aligned}&^c{\!}D^\alpha f(t)=J^{n-\alpha }f^{(n)}(t), \quad \alpha \in (n-1, n),\\&J^{\beta }g(t)=\frac{1}{\Gamma (\alpha )}{\int _0}^t(t-s)^{\beta -1}g(s)\mathrm{d}s, \end{aligned} \end{aligned}$$

(4)

$$\begin{aligned}&\begin{aligned}&^c{\!}D^\alpha (af(t)+g(t))=a ^c{\!}D^\alpha f(t)+ ^c{\!}D^\alpha g(t),\\&\quad a=constant. \end{aligned} \end{aligned}$$

(5)

In this paper, we aim at investigating the C–C synchronization of chaotic nD fractional-order dynamical systems with two drive and two response systems, respectively, as:

$$\begin{aligned}&{^c{\!}D}^\alpha x_i(t)=A_ix_i+f_i(x_i(t)),\quad i=1,2, \end{aligned}$$

(6)

$$\begin{aligned}&{^c{\!}D}{^\alpha } y_i(t)=B_iy_i+g_i(y_i(t))+w_i, \quad i=1,2, \end{aligned}$$

(7)

where $^c{\!}D^\alpha$ is Caputo differential operator $( 0<\alpha \le 1)$, $x_1 = (x_{11}, x_{12}, \ldots , x_{1n})^T$, $x_2 {\,=\,} (x_{21}, x_{22},\ldots , x_{2n})^T$, $y_1 {\,=\,} (y_{11}, y_{12}, \ldots , y_{1n})^T$ and $y_2{\,=\,}(y_{21}, y_{22}, \ldots , y_{2n})^T$ are the state vectors of systems (6), (7), $A_i, B_i\in {R}^{n\times n}$, $i=1,2$ are constant matrices of systems parameters, $f_1, f_2, g_1, g_2: R^n \rightarrow R^n$ are four continuous vector functions, $w_1,w_2: R^n \times R^n \times R^n \times R^n \rightarrow R^n$, $w_1=(u_1, u_2, \ldots , u_n)^T$, $w_2=(v_1, v_2,\ldots , v_n)^T$ are two control functions of the response systems (7) which are functions of $x_1, x_2$, $y_1$, $y_2$ and T denotes the transpose. Systems (6), (7) have unique solution [19]. As an example of systems (6) and (7), we consider the complex form of the fractional-order Lorenz, Chen, Lü and Liu systems which are six-dimensional real systems. These complex systems appear in several important applications in physics and engineering, for example, detuned lasers [20] and secure communications [21]. The C–C synchronization has advantages over the other types of synchronization since it can provide good security in secure communications.

Our paper is organized as follows: The scheme of C–C synchronization of chaotic nD fractional-order systems (6) and (7) is introduced in Sect. 2. In Sect. 3, the scheme of Sect. 2 is applied to obtain theoretical forms of control functions. These control functions are used to achieve complete C–C synchronization of four identical 6D fractional-order Lorenz systems as an example. In the numerical treatment, we used Adam–Bashforth–Moluton method [22] for the case $\alpha =0.99$. In Sect. 4, we consider another example of four different 6D fractional-order systems, which are Lorenz, Lü, Chen and Liu systems for the case $\alpha =0.99$. Section 5 contains our concluding remarks.

2 The scheme of C–C synchronization of four chaotic n-dimensional fractional-order dynamical systems

In this section, we firstly lay out the scheme of C–C synchronization of chaotic nD fractional-order dynamical systems (6) and (7). The error system (synchronization error) is defined as [17]:

$$\begin{aligned} \begin{aligned} e= Cx_{1}+Dx_{2}- Ey_{1}-Fy_{2}, \quad e=(e_1,e_2,\ldots ,e_n)^T. \end{aligned} \end{aligned}$$

(8)

Chao et al. [23] defined drive, response and error systems, respectively, as:

$$\begin{aligned}&^c{\!}D^\alpha x(t)= Ax+f(x),\end{aligned}$$

(9)

$$\begin{aligned}&^c{\!}D^\alpha y(t)= Ay+f(y)+u,\end{aligned}$$

(10)

$$\begin{aligned}&e=y(t)-x(t), \end{aligned}$$

(11)

where $x(t),y(t),e\in R^5$ and $u: R^5 \times R^5 \rightarrow R^5$.

Theorem 1

[23] Synchronization in two identical fractional-order complex Lorenz (5D) systems in the form (9), (10) and the error in form (11) will be achieved, if the control functions are designed as:

$$\begin{aligned} u=f(x)-f(y)-Ke, \end{aligned}$$

(12)

where K is the control gain matrix, which satisfies $|\mathrm{arg}(\lambda _i(A-K))|>\alpha \pi /2$ for all eigenvalues of (A−K).

Here, we generalize Theorem 1 to study synchronization among four different chaotic nD fractional dynamical systems (C–C synchronization), in Theorem 2 as:

Theorem 2

C–C synchronization among four different chaotic n-dimensional (6) and (7) fractional-order dynamical systems will be achieved if the control functions are designed as follows:

$$\begin{aligned} \begin{aligned} U&=Ew_1+Fw_2=Cf_{1}(x_1)+Df_{2}(x_2)\\&\quad -\,Eg_{1}(y_1)-Fg_2(y_2) +(DA_2-DA_1)x_{2}\\&\quad -\,(EB_1-EA_1)y_{1}-(FB_2-FA_1)y_{2}+ K e, \end{aligned} \end{aligned}$$

(13)

where K in (13) is the control gain matrix and satisfies $|\mathrm{arg}(\lambda _i(A_1-K))|> \alpha \pi /2$ for all eigenvalues of $(A_1-K)$ and $U=(U_1, U_2,\ldots , U_n)^T$.

Proof

Differentiating Eq. (8) by Caputo sense, we obtain

$$\begin{aligned} \begin{aligned} ^c{\!}D^\alpha e=C ^c{\!}D^\alpha x_{1}+D ^c{\!}D^\alpha x_{2}-E ^c{\!}D^\alpha y_{1}-F ^c{\!}D^\alpha y_{2}. \end{aligned} \end{aligned}$$

(14)

Using Eqs. (6), (7), (8) and (13) then,

$$\begin{aligned} \begin{aligned} ^c{\!}D^\alpha e=(A_1-K)e. \end{aligned} \end{aligned}$$

(15)

From stability theory of fractional order and since $|\mathrm{arg}(\lambda _i(A_1-K))|> \alpha \pi /2$, then $e(t)\rightarrow zero$ as $t\rightarrow \infty$. $\square$

Remark

The C–C synchronization may be considered as a generalization of several kind of synchronization in the literature, for example, if $C=F=0$ and $D=E=I$, the C–C synchronization will be reduced to the complete synchronization (one drive and one response systems), where 0 is null matrix and I is identity matrix. If $C=F=0$, $D=I$ and $E=-I$, the C–C synchronization will be reduced to the anti-synchronization and if $C=F=0$ and $E=I$, the C–C synchronization will be reduced to the projective synchronization.

3 Synchronization among four chaotic 6D identical fractional-order dynamical systems

The fractional-order real Lorenz system (3D) is [8]:

$$\begin{aligned} ^c{\!}D^\alpha x= & {} a_1(y-x),\nonumber \\ ^c{\!}D^\alpha y= & {} c_1x-y-xz ,\nonumber \\ ^c{\!}D^\alpha z= & {} xy-b_1z, \end{aligned}$$

(16)

where $a_1, b_1$ and $c_1$ are real constant parameters. In this section, we consider the complex version of (16) as:

$$\begin{aligned} ^c{\!}D^\alpha (x_1+ix_2)= & {} a_1(x_3+ix_4-(x_1+ix_2)), \nonumber \\ ^c{\!}D^\alpha (x_3+ix_4)= & {} c_1(x_1+ix_2)-(x_3+ix_4)\nonumber \\&-\,(x_1+ix_2)(x_5+ix_6), \nonumber \\ ^c{\!}D^\alpha (x_5+ix_6)= & {} (x_1+ix_2)(x_3+ix_4)\nonumber \\&-\,b_1(x_5+ix_6). \end{aligned}$$

(17)

In the literature, other complex systems are introduced and studied in [24–26]. We study in this section complete C–C synchronization among four identical 6D fractional-order Lorenz systems. The real form of (17) is:

$$\begin{aligned} ^c{\!}D^\alpha x_{1}= & {} a_1(x_{3}-x_{1}),\nonumber \\ ^c{\!}D^\alpha x_{2}= & {} a_1(x_{4}-x_{2}),\nonumber \\ ^c{\!}D^\alpha x_{3}= & {} c_1x_{1}-x_{3}-x_{1}x_{5}+x_{2}x_{6},\nonumber \\ ^c{\!}D^\alpha x_{4}= & {} c_1x_{2}-x_{4}-x_{2}x_{5}-x_{1}x_{6},\nonumber \\ ^c{\!}D^\alpha x_{5}= & {} -b_1x_{5}+x_{1}x_{3}-x_{2}x_{4},\nonumber \\ ^c{\!}D^\alpha x_{6}= & {} -b_1x_{6}+x_{1}x_{4}+x_{2}x_{3}. \end{aligned}$$

(18)

Fig. 1

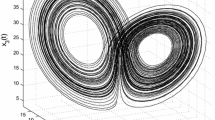
The chaotic 6D Lorenz system (18) for $a_1=10, b_1=8/3, c_1=28$ and $\alpha =0.99$ in $(x_5, x_1, x_3)$ space

To show that system (18) has chaotic behavior, we solve it using Adam–Bashforth–Moluton method [22] for $a_1=10, b_1=8/3, c_1=28$, $\alpha =0.99$ and the initial state vector $x_0=(8.4818,0.0001$, $-8.4819, -0.0001, 26.9954, 0.0001)^T$. It can be seen from Fig. 1 that system (18) has chaotic behavior. In Fig. 1, we plot $(x_5, x_1, x_3)$ space, and other spaces can be similarly plotted.

We can write the two drive systems as follows:

$$\begin{aligned} ^c{\!}D^\alpha x_{11}= & {} a_1(x_{13}-x_{11}),\nonumber \\ ^c{\!}D^\alpha x_{12}= & {} a_1(x_{14}-x_{12}),\nonumber \\ ^c{\!}D^\alpha x_{13}= & {} c_1x_{11}-x_{13}-x_{11}x_{15}+x_{12}x_{16},\nonumber \\ ^c{\!}D^\alpha x_{14}= & {} c_1x_{12}-x_{14}-x_{12}x_{15}-x_{11}x_{16},\nonumber \\ ^c{\!}D^\alpha x_{15}= & {} -b_1x_{15}+x_{11}x_{13}-x_{12}x_{14},\nonumber \\ ^c{\!}D^\alpha x_{16}= & {} -b_1x_{16}+x_{11}x_{14}+x_{12}x_{13}, \end{aligned}$$

(19)

$$\begin{aligned} ^c{\!}D^\alpha x_{21}= & {} a_2(x_{23}-x_{21}), \nonumber \\ ^c{\!}D^\alpha x_{22}= & {} a_2(x_{24}-x_{22}), \nonumber \\ ^c{\!}D^\alpha x_{23}= & {} c_2x_{21}-x_{23}-x_{21}x_{25}+x_{22}x_{26}, \nonumber \\ ^c{\!}D^\alpha x_{24}= & {} c_2x_{22}-x_{24}-x_{22}x_{25}-x_{21}x_{26},\nonumber \\ ^c{\!}D^\alpha x_{25}= & {} -b_2x_{25}+x_{21}x_{23}-x_{22}x_{24},\nonumber \\ ^c{\!}D^\alpha x_{26}= & {} -b_2x_{26}+x_{21}x_{24}+x_{22}x_{23}, \end{aligned}$$

(20)

and we can write the two response systems as follows:

$$\begin{aligned} ^c{\!}D^\alpha y_{11}= & {} a_3(y_{13}-y_{11})+u_1, \nonumber \\ ^c{\!}D^\alpha y_{12}= & {} a_3(y_{14}-y_{12})+u_2, \nonumber \\ ^c{\!}D^\alpha y_{13}= & {} c_3y_{11}-y_{13}-y_{11}y_{15}+y_{12}y_{16}+u_3, \nonumber \\ ^c{\!}D^\alpha y_{14}= & {} c_3y_{12}-y_{14}-y_{12}y_{15}-y_{11}y_{16}+u_4,\nonumber \\ ^c{\!}D^\alpha y_{15}= & {} -b_3y_{15}+y_{11}y_{13}-y_{12}y_{14}+u_5,\nonumber \\ ^c{\!}D^\alpha y_{16}= & {} -b_3y_{16}+y_{11}y_{14}+y_{12}y_{13}+u_6, \end{aligned}$$

(21)

$$\begin{aligned} ^c{\!}D^\alpha y_{21}= & {} a_4(y_{23}-y_{21})+v_1, \nonumber \\ ^c{\!}D^\alpha y_{22}= & {} a_4(y_{24}-y_{22})+v_2, \nonumber \\ ^c{\!}D^\alpha y_{23}= & {} c_4y_{21}-y_{23}-y_{21}y_{25}+y_{22}y_{26}+v_3, \nonumber \\ ^c{\!}D^\alpha y_{24}= & {} c_4y_{22}-y_{24}-y_{22}y_{25}-y_{21}y_{26}+v_4,\nonumber \\ ^c{\!}D^\alpha y_{25}= & {} -b_4y_{25}+y_{21}y_{23}-y_{22}y_{24}+v_5,\nonumber \\ ^c{\!}D^\alpha y_{26}= & {} -b_4y_{26}+y_{21}y_{24}+y_{22}y_{23}+v_6, \end{aligned}$$

(22)

where $u_i$ and $v_i \,(i=1,2,\ldots ,6)$ are control functions. We obtain the complete C–C synchronization if we choose $C=D=E=F=I$ and I is $(6\times 6)$ identity matrix in (13) (other choices of C, D, E, F can be similarly studied). For the case $a_1=a_2=a_3=a_4=10$, $b_1=b_2=b_3=b_4=8/3$ and $c_1=c_2=c_3=c_4=28$ and applying Theorem 2 as $n=6$ , we get the control functions as (other cases of $a_j$, $b_j$ and $c_j$, $j=1,2,3,4$ can be similarly studied):

$$\begin{aligned}&\left( \begin{array}{c} U_1 \\ U_2 \\ U_3 \\ U_4 \\ U_5 \\ U_6 \\ \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \\ -x_{11}x_{15}+x_{12}x_{16}-x_{21}x_{25}+x_{22}x_{26} \\ -x_{11}x_{16}-x_{12}x_{15}-x_{21}x_{26}-x_{22}x_{25} \\ -x_{12}x_{14}+x_{11}x_{13}-x_{22}x_{24}+x_{21}x_{23} \\ x_{12}x_{13}+x_{11}x_{14}+x_{22}x_{23}+x_{21}x_{24} \\ \end{array} \right) \nonumber \\&\quad +\,\left( \begin{array}{c} 0 \\ 0 \\ -(-y_{11}y_{15}+y_{12}y_{16})-(-y_{11}y_{15}+y_{12}y_{16}) \\ (y_{11}y_{16}+y_{12}y_{15})+(y_{11}y_{16}+y_{12}y_{15}) \\ -(-y_{12}y_{14}+y_{11}y_{13})-(-y_{22}y_{24}+y_{21}y_{23}) \\ -(y_{12}y_{13}+y_{11}y_{14})-(y_{22}y_{23}+y_{21}y_{24}) \\ \end{array} \right) \nonumber \\&\quad +\,\left( \begin{array}{c} 10(x_{13}+x_{23}-y_{13}-y_{23}) \\ 10(x_{14}+x_{24}-y_{14}-y_{24}) \\ 28(x_{11}+x_{21}-y_{11}-y_{21}) \\ 28(x_{12}+x_{22}-y_{12}-y_{22})\\ 0 \\ 0\\ \end{array} \right) . \end{aligned}$$

(23)

Fig. 2

Complete C–C synchronization when $\alpha =0.99$ of the a two drive systems (19), (20) and b two response systems (21), (22)

Fig. 3

Synchronization errors when $\alpha =0.99$: a $(e_1, t)$ diagram, b $(e_2, t)$ diagram, c $(e_3, t)$ diagram, d $(e_4, t)$ diagram, e $(e_5, t)$ diagram, f $(e_6, t)$ diagram

In our numerical studies, we used Adam–Bashforth–Moluton method [22] to find the numerical solution of systems (19), (20), (21) and (22) with the control functions (23). As an example, we consider the case $\alpha =0.99$ and the initial values of the two drive and the two response systems, respectively, as: $x_{10}=(7.8789, 0.0037, 4.7321$, $-0.0032, 29.9767, 0.0110)^T$, $x_{20}=(8.6056, 0.1035, 8.9812$, $0.0588, 26.6472, 0.1911)^T$, $y_{10}=(-8.2735,-0.0369$, $-6.4666, -0.0429$, $-86.7662,0.2909)^T$ and $y_{20}=(24.7574, 0.1440, 20.1183,0.0950$, $-28.4489, -0.0886)^T$. The results are displayed in Figs. 2 and  3. Figure 2 shows the complete C–C synchronization of systems (19), (20), (21) and (22). The 3D plane portraits in drive and response systems (19), (20) and (21), (22) are plotted in Fig. (2a) $(x_{14}+x_{24}, x_{11}+x_{21}, x_{12}+x_{22})$ space and $(y_{14}+y_{24}, y_{11}+y_{21}, y_{12}+y_{22})$ space in Fig. (2b) which show that the complete C–C synchronization is indeed achieved. In Fig. 3, on the other hand, it can be seen that the synchronization errors $e_i, i=1, 2,\ldots ,6$ converge to zero, as expected from the above analytical consideration of Theorem 2.

4 Synchronization among four different chaotic 6D fractional-order systems

In this section, we study complete C–C synchronization among four 6D fractional-order Lorenz (18), Lü, Chen and Liu systems. The 3D fractional-order Lü, Chen and Liu systems, respectively, are [9, 10, 12]:

$$\begin{aligned} ^c{\!}D^{\alpha } x= & {} a_2(y-x),\nonumber \\ ^c{\!}D^{\alpha } y= & {} -xz+c_2y,\nonumber \\ ^c{\!}D^{\alpha } z= & {} xy-b_2z, \end{aligned}$$

(24)

$$\begin{aligned} ^c{\!}D^{\alpha } x= & {} a_3(y-x),\nonumber \\ ^c{\!}D^{\alpha } y= & {} -xz+c_3y+(c_3-a_3)x,\nonumber \\ ^c{\!}D^{\alpha } z= & {} xy-b_3z, \end{aligned}$$

(25)

$$\begin{aligned} ^c{\!}D^{\alpha } x= & {} -a_4x-\gamma y^2,\nonumber \\ ^c{\!}D^{\alpha } y= & {} -\delta xz+b_4y,\nonumber \\ ^c{\!}D^{\alpha } z= & {} \epsilon xy-c_4z, \end{aligned}$$

(26)

where $a_i, b_i, c_i\,(i=2, 3, 4), \gamma , \delta$ and $\epsilon$ are real constant parameters. As we did for 3D fractional-order Lorenz system (16) to obtain the 6D system (18), we can write the 6D fractional-order Lü, Chen and Liu systems, respectively, as:

$$\begin{aligned} ^{c}{\!}{D^{\alpha }} x_{1}= & {} a_2(x_{3}-x_{1}), \nonumber \\ ^c{\!}D^\alpha x_{2}= & {} a_2(x_{4}-x_{2}), \nonumber \\ ^c{\!}D^\alpha x_{3}= & {} c_2x_{3}-x_{1}x_{5}+x_{2}x_{6}, \nonumber \\ ^c{\!}D^\alpha x_{4}= & {} c_2x_{4}-x_{2}x_{5}-x_{1}x_{6},\nonumber \\ ^c{\!}D^\alpha x_{5}= & {} -b_2x_{5}+x_{1}x_{3}-x_{2}x_{4},\nonumber \\ ^c{\!}D^\alpha x_{6}= & {} -b_2x_{6}+x_{1}x_{4}+x_{2}x_{3}, \end{aligned}$$

(27)

$$\begin{aligned} ^c{\!}D^\alpha y_{1}= & {} a_3(y_{3}-y_{1}), \nonumber \\ ^c{\!}D^\alpha y_{2}= & {} a_3(y_{4}-y_{2}), \nonumber \\ ^c{\!}D^\alpha y_{3}= & {} (c_3-a_3)y_{1}+c_3y_{3}-y_{1}y_{5}+y_{2}y_{6}, \nonumber \\ ^c{\!}D^\alpha y_{4}= & {} (c_3-a_3)y_{2}+c_3y_{4}-y_{2}y_{5}-y_{1}y_{6},\nonumber \\ ^c{\!}D^\alpha y_{5}= & {} -b_3y_{5}+y_{1}y_{3}-y_{2}y_{4},\nonumber \\ ^c{\!}D^\alpha y_{6}= & {} -b_3y_{6}+y_{1}y_{4}+y_{2}y_{3}, \end{aligned}$$

(28)

$$\begin{aligned} ^c{\!}D^\alpha y_{1}= & {} -a_4y_{1}-\gamma (y_{3}^2-y_{4}^2), \nonumber \\ ^c{\!}D^\alpha y_{2}= & {} -a_4y_{2}-2\gamma y_{3}y_{4}, \nonumber \\ ^c{\!}D^\alpha y_{3}= & {} b_4y_{3}-\delta (y_{1}y_{5}-y_{2}y_{6}),\nonumber \\ ^c{\!}D^\alpha y_{4}= & {} b_4y_{4}-\delta (y_{2}y_{5}+y_{1}y_{6}),\nonumber \\ ^c{\!}D^\alpha y_{5}= & {} -c_4y_{5}+\epsilon (y_{1}y_{3}-y_{2}y_{4}),\nonumber \\ ^c{\!}D^\alpha y_{6}= & {} -c_4y_{6}+\epsilon (y_{1}y_{4}+y_{2}y_{3}). \end{aligned}$$

(29)

It is easy to show that the above systems (27), (28) and (29) possess chaotic behavior by solving them as we did in Sect. 3. In Fig. 4, system (27) has chaotic behavior for $a_2=36, b_2=1, c_2=20$, $\alpha =0.99$ and the initial state vector $x_0=(-13,-1, -14, 1, 22, -1)^T$ in $(x_5, x_1, x_3)$ space. The chaotic behavior of system (28) is depicted in Fig. 5 $(y_1, y_2, y_5)$ space for $a_3=35, b_3=3, c_3=28$, $\alpha =0.99$ and the initial state vector $y_0=(-9,0.09,-12,0.09,15,-0.03)^T$. The chaotic behavior of system(29) is shown in Fig. 6 for $a_4=1, b_4=5/2, c_4=5, \gamma =1, \delta =4, \epsilon =4$, $\alpha =0.99$ and the initial state vector $y_0=(2.75,1,1,-3,-0.1,-2)^T$ in ($y_5, y_3, y_1)$ space.

Fig. 4

The chaotic 6D Lü system (27) for $a_2=36, b_2=1, c_2=20$ and $\alpha =0.99$ in $(x_5, x_1, x_3)$ space

Fig. 5

The chaotic 6D Chen system (28) for $a_3=35, b_3=3, c_3=28$ and $\alpha =0.99$ in $(y_1, y_2, y_5)$ space

We can write the two drive (6D fractional-order Lorenz and Lü) systems as follows:

$$\begin{aligned} ^c{\!}D^\alpha x_{11}= & {} a_1(x_{13}-x_{11}), \nonumber \\ ^c{\!}D^\alpha x_{12}= & {} a_1(x_{14}-x_{12}), \nonumber \\ ^c{\!}D^\alpha x_{13}= & {} c_1x_{11}-x_{13}-x_{11}x_{15}+x_{12}x_{16}, \nonumber \\ ^c{\!}D^\alpha x_{14}= & {} c_1x_{12}-x_{14}-x_{12}x_{15}-x_{11}x_{16},\nonumber \\ ^c{\!}D^\alpha x_{15}= & {} -b_1x_{15}+x_{11}x_{13}-x_{12}x_{14},\nonumber \\ ^c{\!}D^\alpha x_{16}= & {} -b_1x_{16}+x_{11}x_{14}+x_{12}x_{13}, \end{aligned}$$

(30)

$$\begin{aligned} ^c{\!}D^\alpha x_{21}= & {} a_2(x_{23}-x_{21}), \nonumber \\ ^c{\!}D^\alpha x_{22}= & {} a_2(x_{24}-x_{22}), \nonumber \\ ^c{\!}D^\alpha x_{23}= & {} c_2x_{23}-x_{21}x_{25}+x_{22}x_{26}, \nonumber \\ ^c{\!}D^\alpha x_{24}= & {} c_2x_{14}-x_{22}x_{25}-x_{21}x_{26},\nonumber \\ ^c{\!}D^\alpha x_{25}= & {} -b_2x_{25}+x_{21}x_{23}-x_{22}x_{24},\nonumber \\ ^c{\!}D^\alpha x_{26}= & {} -b_2x_{26}+x_{21}x_{24}+x_{22}x_{23}. \end{aligned}$$

(31)

We can write the two response (6D fractional-order Chen and Liu) systems as follows:

$$\begin{aligned} ^c{\!}D^\alpha y_{11}= & {} a_3(y_{13}-y_{11}), \nonumber \\ ^c{\!}D^\alpha y_{12}= & {} a_3(y_{14}-y_{12}), \nonumber \\ ^c{\!}D^\alpha y_{13}= & {} (c_3-a_3)y_{11}+c_3y_{13}-y_{11}y_{15}+y_{12}y_{16}, \nonumber \\ ^c{\!}D^\alpha y_{14}= & {} (c_3-a_3)y_{12}+c_3y_{14}-y_{12}y_{15}-y_{11}y_{16},\nonumber \\ ^c{\!}D^\alpha y_{15}= & {} -b_3y_{15}+y_{11}y_{13}-y_{12}y_{14},\nonumber \\ ^c{\!}D^\alpha y_{16}= & {} -b_3x_{16}+y_{11}y_{14}+y_{12}y_{13}, \end{aligned}$$

(32)

$$\begin{aligned} ^c{\!}D^\alpha y_{21}= & {} -a_4y_{21}-\gamma (y_{23}^2-y_{24}^2), \nonumber \\ ^c{\!}D^\alpha y_{22}= & {} -a_4y_{22}-2\gamma y_{23}y_{24}, \nonumber \\ ^c{\!}D^\alpha y_{23}= & {} b_4y_{23}-\delta (y_{21}y_{25}-y_{22}y_{26}),\nonumber \\ ^c{\!}D^\alpha y_{24}= & {} b_4y_{24}-\delta (y_{22}y_{25}+y_{21}y_{26}),\nonumber \\ ^c{\!}D^\alpha y_{25}= & {} -c_4y_{25}+\epsilon (y_{21}y_{23}-y_{22}y_{24}),\nonumber \\ ^c{\!}D^\alpha y_{26}= & {} -c_4y_{26}+\epsilon (y_{21}y_{24}+y_{22}y_{23}). \end{aligned}$$

(33)

We obtain complete C–C synchronization if we choose $C=D=E=F=I$ and $I is (6\times 6)$ identity matrix in (13) (other choices of C, D,E, F can be similarly studied). Applying Theorem 2 for the case $a_1=10, b_1=8/3, c_1=28$, $a_2=36, b_2=3, c_2=20$, $a_3=35, b_3=3, c_3=28$, $a_4=1, b_4=5/2, c_4=5, \gamma =1,\delta =4$ and $\epsilon =4$, we get the control functions as:

$$\begin{aligned}&\left( \begin{array}{c} U_1 \\ U_2 \\ U_3 \\ U_4 \\ U_5 \\ U_6 \\ \end{array} \right) \nonumber \\&\quad =\left( \begin{array}{c} -26(x_{23}-x_{21})+(y_{13}-y_{11})+35(y_{23}-y_{21})+y_{23} \\ -26(x_{24}-x_{22})+(y_{14}-y_{12})+35(y_{24}-y_{22})+y_{24} \\ 27x_{13}+35x_{21}-x_{23}-28y_{13}-9.5y_{23}\\ 27x_{14}+35x_{22}-x_{24}-28y_{14}-9.5y_{24} \\ 1/3x_{25}+2y_{25} \\ 1/3x_{26}+2y_{26}\\ \end{array} \right) \nonumber \\&\qquad + \left( \begin{array}{c} (y_{23}^2-y_{24}^2) \\ 2y_{23}y_{24} \\ -x_{11}x_{15}+x_{12}x_{16}-x_{21}x_{25}+x_{22}x_{26} \\ -x_{11}x_{16}-x_{12}x_{15}-x_{21}x_{26}-x_{22}x_{25} \\ -x_{12}x_{14}+x_{11}x_{13}-x_{22}x_{24}+x_{21}x_{23} \\ x_{12}x_{13}+x_{11}x_{14}+x_{22}x_{23}+x_{21}x_{24} \\ \end{array} \right) \nonumber \\&\qquad +\left( \begin{array}{c} 0 \\ 0 \\ 36(x_{11}+x_{21}-y_{11}-y_{21}) \\ 36(x_{12}+x_{22}-y_{12}-y_{22})\\ 0 \\ 0\\ \end{array} \right) \nonumber \\&\qquad + \left( \begin{array}{c} 0 \\ 0 \\ -(-y_{11}y_{15}+y_{12}y_{16})-4(-y_{11}y_{15}+y_{12}y_{16}) \\ (y_{11}y_{16}+y_{12}y_{15})+4(y_{11}y_{16}+y_{12}y_{15}) \\ -(-y_{12}y_{14}+y_{11}y_{13})-4(-y_{22}y_{24}+y_{21}y_{23}) \\ -(y_{12}y_{13}+y_{11}y_{14})-4(y_{22}y_{23}+y_{21}y_{24}) \\ \end{array} \right) .\quad \end{aligned}$$

(34)

Fig. 6

The chaotic 6D Liu system (29) for $a_4=1, b_4=5/2, c_4=5, \gamma =1, \delta =4, \epsilon =4$ and $\alpha =0.99$ in $(y_5, y_3, y_1)$ space

Fig. 7

Complete C–C synchronization when $\alpha =0.99$ of the a two drive systems (30), (31) and b two response systems (32), (33)

Fig. 8

Synchronization errors when $\alpha =0.99$: a $(e_1, t)$ diagram, b $(e_2, t)$ diagram, c $(e_3, t)$ diagram, d $(e_4, t)$ diagram, e $(e_5, t)$ diagram, f $(e_6, t)$ diagram

In our numerical studies, we use the control functions from (34), $\alpha =0.99$ and the initial values of the two drive and the two response systems, respectively, as $x_{10}=( 13.1645, -0.0001, 13.9264, 0.0066, 22.4827$, $-0.0136)^T$, $x_{20}=( 8.0478, -0.1$, 7.6223, 0.0487, $26.9620, -0.3009)^T$, $y_{10}=(-0.4084, 0.0492$, $-1.8907$, 0.1506, 49.2122, $-0.2999)^T$ and $y_{20}=( 21.5257$, $-0.1541, 23.3017$, $-0.1031, -0.1057, -0.0135)^T$. The results are displayed in Figs. 7 and  8. Figure 7 shows the complete C–C synchronization of systems (30), (31), (32) and (33). The 3D plane portraits in drive and response systems (30), (31) and (32), (33) are plotted in Fig. (7a) $(x_{14}+x_{24}, x_{11}+x_{21}, x_{12}+x_{22})$ space and in Fig. (7b) $(y_{14}+y_{24}, y_{11}+y_{21}, y_{12}+y_{22})$ space which show that the complete C–C synchronization is indeed achieved. In Fig. 8, on the other hand, it can be seen that the synchronization errors $e_i, i=1, 2, \ldots , 6$ converge to zero, as expected from the above analytical consideration of Theorem 2.

5 Conclusion

In this paper, we investigated the generalization of C–C synchronization of four chaotic n-dimensional fractional-order dynamical systems. We introduced the scheme for this investigation and studied a number of examples characterized by C–C synchronization of chaotic 6D fractional-order Lorenz, Lü, Chen and Liu systems. The analytical expressions for the control functions (23) have been tested numerically, leading to the conclusion that complete C–C synchronization is achieved for the case $\alpha =0.99$. The synchronization errors approach zero fast as shown in Figs. 3, 8. Other examples can be similarly studied. The C–C synchronization has advantages over the other types of synchronization since it can provide good security in secure communications. This investigation may be considered as a kind of generalization of different types of synchronization in the literature.