An efficient image encryption scheme using lookup table-based confusion and diffusion

Abstract

This paper presents a solution to satisfy the increasing requirement of real-time secure image transmission over public networks. The main advantage of the proposed cryptosystem is high efficiency. The confusion and diffusion operations are both performed based on a lookup table. Therefore, the time-consuming floating point arithmetic in chaotic map iteration and quantization procedures of traditional chaos-based image cipher can be avoided. Besides, this cryptosystem possesses satisfactory resistance to noise perturbation and loss of cipher data, which are inevitable and unpredictable in real-world channels. The channel disturbance and the deliberate damage from the opponents are both tolerated. The recovered image from the damaged cipher data has satisfactory visual perception. Simulations prove the advantages of the proposed scheme, which render it a good candidate for real-time secure image applications.

1 Introduction

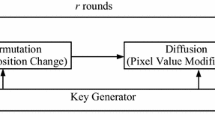
The confidentiality of multimedia content which have bulk data volume and high correlation among adjacent pixels has drawn much attention in recent years. Most of the traditional block ciphers such as DES, Triple-DES and AES that are originally developed for textual information have been found poorly fit for image encryption [1]. On the other hand, chaotic systems have been employed for image encryption, due to the fact that the fundamental features of chaotic systems can be considered analogous to some ideal cryptographic properties [2, 3]. In [4], Fridrich firstly proposed general chaos-based image encryption architecture, as shown in Fig. 1. In the first stage, pixels are shuffled by a two-dimensional area-preserving chaotic map, such as standard map, baker map and cat map. Then, pixel values are modified sequentially in the diffusion phase. During the past decades, Fridrich’s architecture has become the most popular structure, and improvements to this architecture have been extensively developed in various aspects [5–30], such as novel pixel-level confusion strategies [5–8], bit-level permutation approaches [9–13], improved diffusion techniques [14–16], combined compression and encryption methods [17–21] and enhanced key stream generators [22–30].

Fig. 1

Architecture of typical chaos-based image cryptosystems

Security and efficiency are the most important issues of image ciphers, especially the operation efficiency for real-time applications. For chaos-based image cryptosystems, the time consumption mainly derives from the floating arithmetic in the chaotic map iteration and quantification operations [6, 31]. Therefore, when satisfying the security requirements, reducing the volume of the chaotic map iteration and quantification plays critical role for promoting the encryption efficiency. In [31], an efficient diffusion scheme using simple table lookup and swapping techniques was proposed as a lightweight replacement of the chaotic map iteration for image diffusion. As the table lookup and entry swapping operations are more efficient than floating point arithmetic operations, the diffusion strategy in [31] leads to a substantial acceleration of traditional image diffusion approaches. However, pixel number counts of two-dimensional chaotic map iterations also have to be implemented so as to shuffle the plain image and simultaneously construct the lookup table, which leaves the potential for further improvement. In [32], a block cipher using Latin square-based lookup table is proposed. In this algorithm, the lookup table is independently constructed and will be used in both the confusion and diffusion procedures. However, eight substitution–permutation sub-rounds are required to achieve a satisfactory security level, which brings about unbearable computation complexity for real-time secure image applications. Besides the security and efficiency, the robustness of cipher image against noise, loss of cipher data or other external disturbances are also important to ensure the transmission of digital images [33]. This is because various kinds of disturbances are inevitable and unpredictable when the ciphertext is transmitted in real-world channels. The cipher data may be perturbed by the noise in the communication channels, and it may also be occluded deliberately by the opponents. In traditional image ciphers using plain image-related key stream generators [26–30], even a tiny disturbance in the cipher image will bring about complete incorrectness in the deciphered image. A noise-like and unrecognizable image is always generated. According to Shannon’s principle [34], difference of the plain image should spread out to the whole cipher data, whereas the variation of the cipher data should not affect the decryption process to a very large scale.

In this paper, an efficient image encryption scheme based on lookup table concept is proposed. Based on the Latin square and chaos theories, we build a novel cipher for digital image encryption. In the remainder of this paper, we denote LUT as the lookup table that is used in our scheme. As to an image of $N \times N$, totally $2N$ times iterations of chaotic system are sufficient to construct the LUT that will be used for not only pixel permutation but also image diffusion. In traditional chaos-based image cipher, at least two chaotic state variables are required for encrypting one plain pixel, in permutation and diffusion stages, respectively [35], whereas an average of $2/N$ chaotic state variables is enough in our scheme. This property brings about speed superiority accordingly. Besides, our scheme also owns outstanding robustness against noise perturbation or loss of cipher data. The distortion of the cipher image, both the noise perturbation and data missing, is tolerated in the decryption process. The decrypted image is also recognizable even if 50 % of the cipher data are lost. Simulations and security analyses prove the advantages of the proposed scheme, which render it a good candidate for real-time secure image applications.

The rest of the paper is organized as follows. In the next section, the proposed image encryption scheme is described in detail. Simulations and security analyses are reported in Sect. 3, while the conclusions are reported in Sect. 4.

2 The proposed image encryption scheme

2.1 Construction of LUT

The LUT used in our scheme is a kind of orthogonal Latin square [36]. For encrypting an image with size $N \times N$, LUT of the same size should be firstly constructed. It is an array filled with numbers from 0 to $N-1$, with each occurring exactly once in each row and exactly once in each column. Such kind of array can be obtained via a number of approaches, and the algorithm introduced in [32] and the chaotic sorting algorithm in [37] are jointly employed in our scheme. Chaotic logistic map is also introduced, which is mathematically described in Eq. (1), where $\mu$ and $x_{n}$ are the control parameter and state value, respectively. If one chooses $\mu \in [3.57, 4]$, the system is chaotic. According to the previous achievements [5, 12], there exist some periodic (non-chaotic) windows of logistic map, where such parameter $\mu$ will cause the encryption failure. Considering this, a Lyapunov exponent-based parameter selection strategy is introduced [12]. In this strategy, control parameter $\mu$ with positive Lyapunov exponent should be selected, so as to ensure the chaotic property of logistic map.

$$\begin{aligned} x_{n+1} =\mu x_n (1-x_n ). \end{aligned}$$

(1)

The following two functions are defined for LUT construction.

In PSG function, $N_{0}$ is a constant used to iterate a chaotic map $N_{0}$ times to avoid the harmful effect of transitional procedure, and $sort\_desc(X)$ is a function to obtain the descending version (ascending order is also effective) of a sequence $X$. At the end of the function, a pseudorandom sequence whose elements are 0 to $N-1$, with each occurring exactly once is produced.

In Function 2, two $N$_length pseudorandom sequences are firstly generated using different control parameters with the help of Function 1. The function $cyc\_shift(Q, q)$ cyclic shifts the sequence $Q$ with $q$ elements toward left (or right).

Several LUTs are produced using functions 1 and 2, as shown in Fig. 2. Figure 2a, b, d shows LUTs generated with coefficients $(\mu _{1}=3.9993, x\_init_{1}=0.234, \mu _{2}=3.9997, x\_init_{2}=0.567)$, whereas Fig. 2c shows the table produced by $(\mu _{1}=3.9995, x\_init_{1}=0.123, \mu _{2}=3.9999, x\_init_{2}=0.267)$. Obviously, for a given size, (1) the LUT may have different versions and (2) different parameters of the functions will result in distinct LUTs.

Fig. 2

Lookup table examples: a LUT with size $4\times 4$; b LUT with size $6\times 6$; c another LUT with size $6\times 6$; d LUT with size $9\times 9$

Now, let us investigate some interesting intrinsic features of the LUT of size $N \times N$. As mentioned before, the most important property is that each of the elements occurs once and exactly once in each row or column. Assume that there is a sequence $P=(0, 1, 2, {\ldots }, N-1)$. Then, we can obtain two sequences from the LUT, as expressed in Eq. (2), from which one could see that $C_{1}$ may be any row of the LUT, while $C_{2}$ is a column.

$$\begin{aligned} \left\{ {{\begin{array}{l} {C_1 =Table(r,:)} \\ {C_2 =Table(:,c)} \\ \end{array} }} \right. . \end{aligned}$$

(2)

• (1) As the sequence $C_{1}$ is a row of the LUT, its elements are the full set of 0 to $N-1$, with each of them occurs exactly once. Accordingly, there is a bijective transformation from $P(i)$ to $C_{1}(i)$, and it is nonlinear and secret. The $C_{1}(i)$ can be directly used as the confusion vector for pixel shuffling within a row.

• (2) Similarly, the mapping from $P(i)$ to $C_{2}(i)$ is also bijective, secret and nonlinear. The $C_{2}(i)$ also could be used as the confusion vector for shuffling pixels within a column.

• (3) When $N \ge 256$, it means no less than 8 bits should be used to precisely represent each element of the LUT. Considering the rightmost 8 bits of the elements, it can represent the values from 0 to 255, with each of the numbers uniformly distributed, whereas randomly located in all the positions. In other words, the rightmost 8 bits of the elements of LUT are uniformly distributed random values from 0 to 255.

2.2 LUT-based image permutation

From the first two intrinsic properties above-mentioned, an effective and efficient image permutation approach is subsequently obtained. It can be implemented by two steps.

• Step 1: For each row of the plain image, shuffle the positions of all the pixels according to the corresponding row vector of the LUT. As to the plain pixel at $(x, y)$, it will be shuffled to $(x, Table\,(x, y)$) in the permutated image.

• Step 2: For each column of the resultant image after the first step, shuffle all the pixels according to the corresponding column vector of the LUT. That means, after the pixel is shuffled to $(x, Table\,(x, y))$, it will be further moved to $(Table\,(x, Table\,(x, y)), Table\,(x, y))$.

The above two procedures are drawn to illustrate the concept in a simply understandable way, and one can directly combine the two stages as one step to reduce the image-scanning counts and then accelerate the operation speed [38]. In other words, we can directly construct the permutation matrix (PM) [39, 40] as Eq. (3) for all $x \in (0, 1, 2, {\ldots }, N-1)$ and $y \in (0, 1, 2, {\ldots }, N-1)$.

$$\begin{aligned} PM(x,y)=(Table(x,Table(x,y)),Table(x,y)). \end{aligned}$$

(3)

It is interesting to note that if we implement the two steps in reverse order, a totally different permutation matrix will be obtained. Analogously, we can infer the second permutation matrix (PM2) from the LUT, as described in Eq. (4).

$$\begin{aligned} PM2(x,y)=(Table(x,y),Table(Table(x,y),y)). \end{aligned}$$

(4)

The confusion results of PM and PM2 are different from each other. Supposed that we use the LUT in Fig. 2c to shuffle a $6\times 6$ image, pixel at (0, 0) will be moved to (1, 5) if we use PM as the permutation matrix, whereas it will be confused to (5, 4) when using PM2.

A numbers of simulations have been performed to evaluate the image permutation effect of PM and PM2, compared with Arnold cat map. The cat map is a well-known two-dimensional area-preserving chaotic map, and it has been widely employed to shuffle the plain image and weaken the relationship between adjacent pixels. The generalized mathematical formula of the cat map is given by Eq. (5), where $(x', y')$ are the permutated position of $(x, y)$, and $p$ and $q$ are the control parameters of the cat map. It always has to be iteratively performed three times to obtain a satisfactory confusion effect.

$$\begin{aligned} \left[ {{\begin{array}{l} {x^{\prime }} \\ {y^{\prime }} \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} 1&{}\quad p \\ q&{}\quad {pq+1} \\ \end{array} }} \right] \left[ {{\begin{array}{l} x \\ y \\ \end{array} }} \right] \hbox {\ mod} N. \end{aligned}$$

(5)

Table 1 lists the results of the proposed permutation strategies and cat map, where the standard 256 grayscale Lena image with size $512\times 512$ is adopted. The corresponding confused images are shown in Fig. 3. The consumption time is measured by running the standard C program on our computing platform, a personal computer with an Intel E5300 CPU (1.19 GHz), 2 GB memory and 320 GB hard-disk capacity, and the compile environment is Code Blocks 10.05. The LUT is generated with coefficient $(\mu _{1}=3.9993, x\_init_{1}=0.234, \mu _{2}=3.9997, x\_init_{2}=0.567)$. Figure 3a shows the plain image, while Fig. 3b–d shows the confused images using PM, PM2 and cat map, respectively.

Table 1 Simulation results of various permutation approaches

Fig. 3

Confusion effects of various strategies: a plain image, b the shuffled image using PM, c the shuffled image using PM2, d the shuffled image using cat map

As shown in Fig. 3, the confused images are all unrecognizable, and the pixel correlation coefficients of the plain image have also been significantly downgraded to a satisfactory level. The effectiveness of the image permutation approaches using LUT is thus revealed. As achieved in the previous work [27, 35], the cat map is the most efficient one among traditional image permutation techniques. However, our approaches also own tremendous efficiency advantages. The promotion of operation efficiency lies in the reduction of chaotic map iterations. In traditional image permutation approaches, the chaotic map has to be iterated once for each pixel’s relocation. Accordingly, a total number of $N^{2}$ iterations have to be implemented for an $N \times N$ image. However, only $2N$ iterations are sufficient for LUT construction in our scheme and consequently enough for image permutation. Accordingly, the saving of the chaotic iterations brings about operation efficiency superiority [6, 31]. Besides, the LUT is used not only in the permutation stage but also for image diffusion, no extra chaotic iteration has to be performed in the diffusion stage, and the operation efficiency of the cryptosystem can thus be further promoted.

2.3 Image diffusion using LUT

It is well known that a strong cryptosystem must include two phases: permutation and diffusion, a permutation-only cryptosystem is vulnerable to various attacks [39, 40]. To enhance the security of the cryptosystem, we introduce a diffusion procedure to collaborate with the LUT-based image permutation strategy. In the diffusion stage, pixel values are modified sequentially according to Eq. (6), where $p(n)$, $k(n)$, $c(n)$ and $c(n-1)$ are the current operated pixel, key stream element, output cipher-pixel and the previous cipher-pixel, respectively.

$$\begin{aligned} c(n)=k(n)\oplus \left\{ \left[ {p(n)+k(n)} \right] \hbox {\ mod} L \right\} \oplus c(n-1). \end{aligned}$$

(6)

In a traditional image diffusion module, $k(n)$ is usually produced using a 1-D chaotic map. For each pixel, the chaotic map will be iterated once to get a state variable, and then, the variable has to be further quantized to the required key stream element. The workload of floating point arithmetic of chaotic map iteration and quantization is the highest cost of the diffusion phase [6, 31].

Fig. 4

Schematic of the proposed cryptosystem

In our scheme, we use the LUT to generate pseudorandom key stream elements for each pixel encryption. As mentioned before, when the width or length of the image satisfies $N \ge 256$, no less than 8 bits are required to represent each element of the LUT. As to gray image encryption, the valid value of the key stream element $k(n)$ ranges from 0 to 255, which can be preciously represented with 8 bits. Considering this, we can consequently obtain valid key stream elements from the LUT.

• (1) The size of the LUT is the same as that of the plain image. In other words, the number of the LUT elements is identical with that of the plain pixels.

• (2) If we choose the rightmost 8 bits of the LUT elements, it can represent the values from 0 to 255. Each value is uniformly distributed, but randomly located in the LUT.

• (3) In order to further enhance the security and disturb the correspondence between the LUT and the selected key stream elements, the permutation matrix PM2 is introduced. That is, for ciphering pixel at $(x, y)$, the rightmost 8 bits of the LUT element at $PM2(x, y)$ will be chosen as the key stream element.

Note that, if $N \le 256$, the LUT is not suitable for image diffusion as the elements of the table cannot cover all the possible gray values. In this case, we suggest computing an extra $256\times 256$ LUT. One can use part of the table for image diffusion. Accordingly, $2\times 256=512$ more than the required numbers of chaotic iterations have to be implemented, and the operation efficiency is thus influenced. Otherwise, one can also choose to enlarge the original image to $256\times 256$ by padding random extra pixels. In our opinion, with the dramatic development of communication technology and the advancements of imaging instruments, digital images in the true life are always with high resolution, and there are fewer requirements for encrypting images with size less than $256\times 256$. The practicability of our scheme is almost not restricted.

2.4 The complete cryptosystem

Based on the above achievements, a complete cryptosystem is constructed based on the Fridrich architecture, as sketched in Fig. 4. The key operation procedures are described as follows.

• Step 1: Construct the LUT using functions 1 and 2.

• Step 2: Perform one-round image permutation using the permutation matrix PM, as shown in Eq. (3).

• Step 3: Perform one-round image diffusion using Eq. 6. For pixel at $(x, y)$, the key stream element for masking is the extraction of the rightmost 8 bits of the LUT element at $PM2(x, y)$.

• Step 4: Repeat the above steps $n$ times to satisfy the security requirements.

The decryption process is in a reverse order, whereas the decryption of the diffusion formula is

$$\begin{aligned} p(n)=[k(n)\oplus c(n)\oplus c(n-1)+N-k(n)] \hbox {\ mod} N. \end{aligned}$$

(7)

3 Simulations and security analyses

The chief advantages of our scheme lie in two aspects: (1) high operation efficiency and (2) the robustness against noise disturbance or loss of cipher data. In order to guarantee the noise resistance performance, we do not use plain pixel-related key stream generation mechanism. Hence, at least two overall rounds have to be implemented so as to resist known/chosen plaintext attack. In the following analyses, cipher images after two-round encryption are adopted.

Fig. 5

Histogram analysis: a plain image, b histogram of a, c cipher image, d histogram of c

3.1 Histogram analysis

An image histogram illustrates how pixels are distributed by plotting the number of pixels at each gray level. Ideally, the histograms of the encrypted image should be uniformly distributed and significantly different from those of the plain image. The histograms of the plain image and its cipher image are shown in Fig. 5b, d, respectively. Its uniformity is further verified by the chi-square test [41], as described by Eq. (8), where $k$ is the number of gray levels (256 in our scheme), and $o_{i}$ and $e_{i}$ are the observed and expected occurrence frequencies of each gray level, respectively.

$$\begin{aligned} \chi _\mathrm{test}^2 =\sum _{i=1}^k {\frac{(o_i -e_i )^{2}}{e_i }} . \end{aligned}$$

(8)

With a significance level of 0.05, it is found that $(\chi _{test}^2 =252)< (\chi _{256,0.05}^2 =293)$, which implies that the null hypothesis that the distribution is uniform cannot be rejected at 5 % significance level. In this circumstance, redundancy of the plain image is successfully hidden and does not provide any clue for applying statistical attack.

3.2 Pixel correlation analysis

As to a natural image with meaningful visual perception, the correlation among adjacent pixels is always high as their values are very close to each other. The following method can be used to evaluate an image’s correlation property. (1) 3000 pixels are randomly selected as samples and (2) calculate the correlation coefficient between two adjacent pixels in horizontal, vertical and diagonal directions according to Eqs. (9)–(11), where $x_{i}$ and $y_{i}$ are gray-level values of the ith pair of the selected adjacent pixels, while $N$ represents the total number of the samples.

$$\begin{aligned}&r_{xy}=\frac{E(x-E(x))(y-E(y))}{\sqrt{D(x)}\sqrt{D(y)}}, \end{aligned}$$

(9)

$$\begin{aligned}&E(x)=\frac{1}{N}\sum _{i=1}^N {x_i } , \end{aligned}$$

(10)

$$\begin{aligned}&D(x)=\frac{1}{N}\sum _{i=1}^N {(x_i -E(x))^{2}} . \end{aligned}$$

(11)

Table 2 Correlation coefficients of adjacent pixels

Fig. 6

Correlation of horizontal adjacent pixels: a plain image and b cipher image

For an effective encrypted image, the pixel correlation should be sufficiently low. The correlation coefficients of adjacent pixels in the plain image and its cipher image are listed in Table 2. As an example, the correlation of two horizontally adjacent pixels in the plain image and the encrypted image is shown in Fig. 6a, b, respectively. Both the calculated coefficients and figures demonstrate the pixel correlation de-correlation effect of the proposed scheme.

3.3 Key space analysis

Key space size of an image cipher is the total number of different keys that can be used. In the proposed scheme, the initial values $(x\_init_{1}, x\_init_{2})$ and control parameters $(\mu _{1}, \mu _{2})$ of the logistic map that are used for LUT construction consist of the secret key. According to the IEEE floating point standard [42], the computational precision of the 64-bit double-precision number is about $10^{-15}$. Due to the fact that $(x\_init_{1}, x\_init_{2})$ can be any one of those $10^{15}$ possible values within (0, 1)and $(\mu _{1}, \mu _{2})$ are valid within [3.9, 4], the total key space of the proposed scheme is thus calculated by Eq. (12), which is large enough to resist brute-force attack [2].

$$\begin{aligned} Key=(10^{15}\times 0.1\times 10^{15})^{2}=10^{58}\approx 2^{193}. \end{aligned}$$

(12)

3.4 Key sensitivity analysis

A number of tests have been performed to evaluate the key sensitivity of the proposed cryptosystem in two aspects: (i) completely different cipher images should be produced when slightly different keys are applied to encrypt the same plaintext and (ii) the cipher image cannot be correctly decrypted even if a tiny difference exists between the encryption and decryption keys.

To evaluate the key sensitivity of the first case, the encryption is firstly carried out with randomly selected secret key $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$. Then, a slight change $10^{-14}$ is introduced to one of the parameters with all others remain unchanged. Then, the encryption process repeats. The corresponding cipher images and differential images are shown in Fig. 7. The differences between the corresponding cipher images are computed and given in Table 3. The results obviously show that the cipher images exhibit no similarity one another and there is no significant correlation that could be observed from the differential images.

Fig. 7

Key sensitivity test 1: a plain image; b cipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$; c cipher image $(x\_init_{1} = 0.234+10^{-14}, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$; d differential image between (b) and (c); e cipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993+10^{-14}, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$; f differential image between (b) and (e); g cipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567+10^{-14}, \mu _{2}= 3.9997)$; h differential image between (b) and (g); i cipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.999+10^{-14})$; j differential image between (b) and (i)

Table 3 Differences between cipher images produced by slightly different keys

Fig. 8

Key sensitivity test 2: a cipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$; b decipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$; c decipher image $(x\_init_{1} = 0.234+10^{-14}, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$; d decipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993+10^{-14}, x\_init_{2}= 0.567, \mu _{2}= 3.9997)$; e decipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567+10^{-14}, \mu _{2}= 3.9997)$; f decipher image $(x\_init_{1} = 0.234, \mu _{1}= 3.9993, x\_init_{2}= 0.567, \mu _{2}= 3.9997+10^{-14})$

In addition, decryption using keys with slight change as described above is also performed so as to evaluate the key sensitivity of the second case. The deciphering images are shown in Fig. 8. The differences between incorrect deciphering images (Fig. 8c–f) and the plain image (Fig. 8b) are 99.60, 99.60, 99.59 and 99.59 %, respectively.

3.5 Differential attack and speed analysis

In general, opponents may make a slight change in the plain image and then compare the cipher images to extract some meaningful clues about the secret key. This is the so-called differential attack. In order to make differential attack infeasible, a minor modification in the plain image should cause substantial difference in the cipher image. Two common measures, NPCR (number of pixels change rate) and UACI (unified average changing intensity), are usually employed to test the influence of one-pixel change on the cipher image encrypted by certain cryptosystem. Suppose that $P_{1}(i, j)$ and $P_{2}(i, j)$ be the $(i, j)$ th pixel of two images $P_{1}$ and $P_{2}$, NPCR and UACI are defined in Eqs. (13)–(15), where $W$ and $H$ are the width and length of $P_{1}$ and $P_{2}$.

Table 4 NPCR and UACI performance

$$\begin{aligned}&NPCR=\frac{\sum \nolimits _{i=1}^W {\sum \nolimits _{j=1}^H {D(i,j)} } }{W\times H}\times 100\,\% , \end{aligned}$$

(13)

$$\begin{aligned}&D(i,j)=\left\{ {{\begin{array}{lll} 0 &{} \quad \hbox {if}&{} {P_1 (i,j)=P_2 (i,j)} \\ 1 &{} \quad \hbox {if}&{} {P_1 (i,j)\ne P_2 (i,j)} \\ \end{array} }} \right. , \end{aligned}$$

(14)

$$\begin{aligned}&UACI=\nonumber \\&\quad \frac{1}{W\times H}\left[ {\sum _{i=1}^W {\sum _{j=1}^H {\frac{\left| {P_1 (i,j)-P_2 (i,j)} \right| }{L-1}} } } \right] \!\times \! 100\,\% .\nonumber \\ \end{aligned}$$

(15)

Two test images are adopted. The first one is the standard Lena image of size $512\times 512$, while another one is the slightly modified version obtained by changing the lower-right pixel value from 108 to 109. The two plain images are encrypted for several rounds, and the NPCR and UACI results are listed in Table 4. The BLP algorithm proposed in [9] is introduced for comparison.

As shown in Table 4, the NPCR and UACI of the proposed scheme can reach a satisfactory level, such as $NPCR > 99.60\,\%$ and $UACI > 33.4\,\%$, in the second-round encryption. In other words, a small difference (one-bit modification) in a plain image would lead to substantially different cipher image after the second-round encryption, the differential attack is thus invalid. In comparison with BLP, our scheme has a better ability to resist differential attack.

Once the security requirement is fulfilled, the running speed becomes an important factor for practical applications. From Table 4, one can see that the proposed cryptosystem can reach a satisfactory security level in the second round, and the corresponding operation time is 20.2 ms in our computational platform. On the other hand, three-round encryption should be performed when using BLP, whereas the time consumption is 60.3 ms. The time consumption of BLP mainly derives from the real number arithmetic, which is required for chaotic systems iteration in both the permutation and diffusion phases. On the other hand, only $2\times N$ chaotic variables are sufficient for constructing the LUT that will be used throughout the encryption in our scheme. The permutation and diffusion operations are both performed based on table lookup mechanism, which is much efficient than chaotic iteration. This property brings the speed superiority of the proposed cryptosystem. Together with the noise resistance and robustness to loss of cipher data, the proposed scheme is suitable for real-time secure image transmission applications over public networks.

3.6 Information entropy

Information entropy proposed by Shannon in 1949 is a mathematical property that reflects the randomness and the unpredictability of an information source [34]. The entropy $H(s)$ of a message source $s$ is defined as

$$\begin{aligned} H(s)=-\sum _{i=0}^{2^{N}-1} {P(s_i )\log _2 P(s_i )} . \end{aligned}$$

(16)

Here, $s$ is the source, $N$ is the number of bits to represent the symbol $s_{i}$ and $P(s_{i})$ is the probability of the symbol $s_{i}$. For a truly random source consists of $2^{N}$ symbols, the entropy is $N$. Therefore, as to an effective cryptosystem, the entropy of the cipher image with 256 gray levels should ideally be 8. The BLP algorithm in [9] is also employed for comparison. According to the results in Sect. 3.5, two-round cipher images of the proposed cryptosystem and three-round encrypted data of BLP are used in this section. Eight 256 grayscale standard test images of size $512\times 512$ are encrypted and the information entropies are then calculated, as listed in Table 5, with the higher entropy for each test image shown in bold.

Table 5 Entropies of plain images and cipher images

Table 6 Local entropy test of the cipher images

The results demonstrate that the entropies of the encrypted images of both ciphers are very close to the theoretical value of 8. Both of the ciphers lead to the higher entropy in half of all the samples. Though there is no evident superiority of the proposed scheme, we will show that the cipher images of the proposed scheme own satisfactory randomness and should be considered secure against entropy attack. The local entropy measurement [43] is employed. Local entropy is the average entropy of several randomly selected non-overlapping blocks from the information source. It can overcome several weaknesses of the conventional Shannon entropy measure for evaluating the information randomness, and it is both quantitative and qualitative [43]. The local entropy tests are implemented under the case that 30 non-overlapping blocks are randomly selected with 1936 pixels in each block, just as the preferred cases in [43]. The results are listed in Table 6, where $h_{left}^{l*\alpha }$ and $h_{right}^{l*\alpha }$ are directly obtained from [43] without any modification, which represents the $\alpha$-significance acceptance intervals of the local entropy test when 30 non-overlapping blocks are randomly selected, with each of the block contains 1936 pixels.

Fig. 9

Decrypted images when the cipher data are affected by salt-and-pepper noise with various densities: a the density is 0.01; b the density is 0.05; c the density is 0.10; d the density is 0.25

Fig. 10

Tolerance against loss of cipher data: a encrypted image with 10 % occlusion; b the decrypted image of (a); c encrypted image with 25 % occlusion; d the decrypted image of (c); e encrypted image with 50 % occlusion; f the decrypted image of (e)

From Table 6, one can observe that all of the local entropies of the cipher images fall within the acceptance interval at 5 % significance level, which implies that the null hypothesis that the cipher images are random signals cannot be rejected at 5 % significance level. The results prove the randomness of the encrypted images and accordingly indicate that the proposed cryptosystem is secure against entropy analysis.

3.7 Robustness against noise

In real-world communication channels, various kinds of noise perturbation are inevitable and unpredictable. The noise will bring about disturbance to the cipher data. Therefore, the robustness against noise is also an important issue for evaluating the practicability of a cryptosystem. However, it is always neglected in the previous image encryption literature, and most of the traditional cryptosystems are very sensitive to noise. A small disturbance in the cipher image may induce tremendous distortion in the recovered image. In this section, simulation results will be given to prove the noise resistance of our scheme. We pollute the cipher data using salt-and-pepper noise with different densities and then decrypt them with correct secret key. Figure 9a–d shows the corresponding decipher images when the cipher data are distorted by the salt-and-pepper noise with densities 0.01, 0.05, 0.10 and 0.25, respectively. From visual perception, the decrypted images are all recognizable. The proportions of the incorrect pixels in the decrypted images are 3.89, 13.45, 34.6 and 67.97 %, respectively. It is well revealed that the noise disturbance of the cipher data has been tolerated.

3.8 Robustness against loss of cipher data

Except for the noise perturbation, loss of cipher data is another threat during its transmission. It may be caused by the packet loss in congestion network, or it may be deliberately brought about by opponents. Therefore, an effective cryptosystem should also gain outstanding robustness against loss of cipher data. In the following simulation, the tolerance against loss of cipher data is investigated. Figure 10b, d, f shows the recovered images when 10, 25 and 50 % of the encrypted data are occluded, respectively. It is convincing that our scheme is immune against loss of cipher data. If less than 25 % of the cipher data are occluded, the recovered image is with satisfactory resolution, and the decrypted image is also recognizable even when 50 % of the cipher data are lost.

4 Conclusions

In this paper, an efficient image encryption scheme using lookup table-based confusion and diffusion is proposed. In comparison with the traditional chaos-based block ciphers, much less chaotic map iteration and no quantification operation are required in the proposed algorithm. Hence, our scheme has higher operation efficiency and fast encryption speed. Besides, our scheme has satisfactory resistance to noise disturbance and robustness to loss of the cipher data. All these advantages make the proposed scheme suitable for real-time secure image transmission applications in real-world networks.