1 Introduction

Airship is a new kind of lighter than air (LTA) aircraft. The ascending lift is mainly from the buoyancy of low-density gas in the airship envelope [1–3]. The engine, propeller, and control vane can be installed on the hull, so the airship has a better control performance than the traditional balloon. By right of this advantage, the airship is applied to the civil and military fields widely [4–6].

The research on the control of airship dynamics at present mainly aim at the linear model of the airship after small disturbance linearization to the design controller [7–9]. The linear model only applies to the condition of the airship flying along a straight line at a constant speed. But when the airship flies slowly, the accuracy of this method will greatly reduce. [10–12] did a lot of research on the issues of trajectory tracking control of airship using the backstepping method. In [13], sliding mode variable structure control (SMC) was applied to trajectory tracking control. Two sliding mode controllers were designed for the vertical and horizontal model of the airship, respectively. [14] adopted the method of a neural network inverse system to compensate the velocity and attitude of the airship at real time, which achieved some effects. In [15], a control algorithm using Lyapunov theory and Sontag’s universal stabilizing feedback was proposed. The designed control rate was robust against uncertainty and unknown parameters of the airship model. But these methods usually require high accuracy on the model and the design of the controller is relatively complex. There are some limitations in an actual application.

Active disturbance rejection control (ADRC) is a new control algorithm, which is independent of an accurate model of system [16]. The system error will be eliminated through process error. The real time action of internal and external disturbances of the model is obtained through the extended state observer (ESO) and the dynamic feedback compensation proceeds at real time. Nonlinear state error feedback (NLSEF) is adopted to compensate error, so as to improve control performance. In recent years, the ADRC controller is applied widely to the field of aircraft control [17].

Because of the special flight characteristics of the airship, the theory of ADRC has not been applied in this field hitherto. In this paper, aiming at the control problem of nonlinear and coupling system, ADRC is adopted to design the trajectory tracking controller. Through observing and compensating the states in each channel using ESO, the decoupling control for each channel based on ADRC is achieved.

This paper is organized as follows. In Sect. 2, the six Degree of Freedom (DOF) dynamic model of the airship is introduced briefly. In Sect. 3, the model of the airship is simplified in a horizontal plane. In Sect. 4, the standard form of the model is obtained after input output (I/O) linearization. In Sect. 5, regarding the two-input and two-output (TITO) system as two single-input and single-output (SISO) subsystems, the ADRC controller for each channel is designed separately. In Sect. 6, simulation experiments are carried out to verify the performance of controller. In the last section, the research work is summarized and some existing problems are indicated.

2 Airship dynamic model

As for the airship dynamic model, most research focuses on the six DOF dynamic model [6, 7, 18]. The research in this paper is launched on the basis of the six DOF dynamic model of the airship, which has been derived in [18]. The concrete process of derivation and the meaning of expression are presented in the reference.

The forces acting on the airship in flight mainly include fluid inertia force, aerodynamic, gravity, buoyancy, and thrust that are provided by the engine. The resultant force and moment can be represented as follows:

$$\begin{aligned} &F = F_{I} + F_{at} + F_{G} + F_{B} + F_{t} \end{aligned}$$
(1)
$$\begin{aligned} &M = M_{I} + M_{at} + M_{G} + M_{B} + M_{t} \end{aligned}$$
(2)

where F denotes force, M denotes moment, subscript I denotes fluid inertia force, at denotes aerodynamic, G denotes gravity, B denotes buoyancy, and t denotes thrust.

According to the theorems of momentum and moment of momentum, the above equations can be transformed to the matrix form.

$$ M_{m}\left [ \begin{array}{c} \dot{V} \\ \dot{W} \end{array} \right ] = \left [ \begin{array}{c} F_{I} + F_{at} + F_{G} + F_{B} + F_{t} \\ M_{I} + M_{at} + M_{G} + M_{B} + M_{t} \end{array} \right ] $$
(3)

So, the dynamic equations of airship can be represented as

$$ \left [ \begin{array}{c} \dot{V} \\ \dot{W} \end{array} \right ] = M_{m}^{ - 1}\left [ \begin{array}{c} F_{I} + F_{at} + F_{G} + F_{B} + F_{t} \\ M_{I} + M_{at} + M_{G} + M_{B} + M_{t} \end{array} \right ] $$
(4)

where M m denotes mass matrix, including real mass and added mass; V=[v x  v y  v z ]T, W=[p q r]T denote velocity and angle velocity vectors of the system, respectively; F f and M f denote dynamic force and moment, respectively.

3 Simplified airship dynamic model

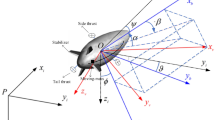
In this paper, only trajectory tracking in the horizontal plane is studied without considering the attitude motion of pitch and roll at the vertical plane. So, for the three Euler angles, i.e., yaw angle ψ, pitch angle θ, and roll angle ϕ, only yaw angle is considered. The propulsion system is assembled at the tail of airship to provide the forward power for airship. T denotes thrust and φ denotes the direction of thrust. Let T x =Tcosφ,T y =Tsinφ denote the two components of thrust along the two directions at horizontal plane. So, we can get w=0, p=0, q=0, θ=0, ϕ=0, h=0. The model [18] can be simplified as

$$ \left \{ \begin{array}{l} \dot{v}_{x} = a_{1}v_{y}r + b_{1} ( X_{a}\cos \beta + Y_{a}\sin \beta ) + b_{1}T_{x} \\ \dot{v}_{y} =a_{2}v_{x}r + b_{2} ( - X_{a}\sin \beta + Y_{a}\cos \beta ) + b_{2}T_{y}\!\! \\ \dot{r} = a_{3}N_{a} + b_{3}T_{y} \\ \dot{l}_{x} = v_{x}\cos \psi - v_{y}\sin \psi \\ \dot{l}_{y} = v_{x}\sin \psi + v_{y}\cos \psi \\ \dot{\psi} = r \end{array} \right . $$
(5)

where l x , l y denote position in a horizontal plane, the coefficients \(a_{1} = \frac{m + m_{22}}{m + m_{11}}\); \(a_{2} = \frac{m + m_{11}}{m + m_{22}}\); \(a_{3} = \frac{1}{I_{z} + m_{66}}\); \(b_{1} = \frac{1}{m + m_{11}}\); \(b_{2} = \frac{1}{m + m_{22}}\), m is the real mass of the airship and m ii (i=1,2,…,6) is the added mass, X a ,Y a are the components of aerodynamics in horizontal plane, and N a is the yawing moment, β is the sideslip angle.

Take the states variables as x=[v x  v y  r l x  l y  ψ]T, output variables as y=[l x  l y ]T, control input u=[u 1 u 2]T=[T x  T y ]T. Equation (5) can be expressed as a multiple input multiple output (MIMO) nonlinear system as follows:

$$ \left \{ \begin{array}{l} \dot{x} = f(x) + g(x)u \\ y = h(x) \end{array} \right . $$
(6)

where

$$\begin{aligned} & f(x) = \left [ \begin{array}{c} a_{1}v_{y}r + b_{1}(X_{a}\cos \beta + Y_{a}\sin \beta ) \\ a_{2}v_{x}r + b_{2}( - X_{a}\sin \beta + Y_{a}\cos \beta ) \\ a_{3}N_{a} \\ v_{x}\cos \psi - v_{y}\sin \psi \\ v_{x}\sin \psi + v_{y}\cos \psi \\ r \end{array} \right ], \\ & g(x) = \left [ \begin{array}{c@{\quad }c} b_{1} & 0 \\ 0 & b_{2} \\ 0 & b_{3} \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right ], \qquad h(x) = \left [ \begin{array}{c} l_{x} \\ l_{y} \end{array} \right ] \end{aligned}$$

4 Standard form transformation of nonlinear system

In order to get the direct relation between inputs and outputs to facilitate the design of controller, the derivative of output y about time is obtained and then arranged through introducing the operation of the Lie derivative [19–21].

$$ \dot{y} = \frac{\partial h}{\partial x} \bigl[ f(x) + g(x)u \bigr] = L_{f}h(x) + L_{g}h(x)u $$
(7)

Repeat the above operation, until

$$ y^{(r)} = L_{f}^{r}h(x) + L_{g}L_{f}^{r - 1}h(x)u $$
(8)

where \(L_{g}L_{f}^{r - 1}h(x_{0}) \ne 0\), r denotes the relative degree of system.

Letting ξ 1=l x , ξ 3=l y , the standard form of system can be transformed as followed.

$$ \left \{ \begin{array}{l} \dot{\xi}_{1} = \xi_{2} \\ \dot{\xi}_{2} = f_{1}(x) + b_{1}\cos \psi \cdot u_{1} - b_{2}\sin \psi \cdot u_{2}\\ \dot{\xi}_{3} = \xi_{4} \\ \dot{\xi}_{4} = f_{2}(x) + b_{1}\sin \psi \cdot u_{1} + b_{2}\cos \psi \cdot u_{2}\\ \dot{\eta}_{1} = q_{1}(\xi,\eta ) \\ \dot{\eta}_{2} = q_{2}(\xi,\eta ) \end{array} \right . $$
(9)

The variables η 1,η 2∈R 4 denote the internal dynamics of the system and they satisfy the constrained condition as follows:

$$ L_{g}\eta (x) = 0 $$
(10)

In this way, the states ξ(x) are transformed to a controllable and observable linear system. So, the original system is linearized partly.

5 Design of ADRC trajectory tracking controller

5.1 Decoupling control of multivariable system based on ADRC

For the TITO system shown as (9), let

$$\left [ \begin{array}{c} U_{1} \\ U_{2} \end{array} \right ] = B\left [ \begin{array}{c} u_{1} \\ u_{2} \end{array} \right ], \qquad B = \left [ \begin{array}{c@{\quad }c} b_{1}\cos \psi & - b_{2}\sin \psi \\ b_{1}\sin \psi & b_{2}\cos \psi \end{array} \right ], $$

the system can be transformed as

$$ \left \{ \begin{array}{l} \ddot{\xi}_{1} = f_{1}(x) + U_{1} \\ \ddot{\xi}_{3} = f_{2}(x) + U_{2} \\ y_{1} = \xi_{1} \\ y_{2} = \xi_{3} \end{array} \right . $$
(11)

det(B)=b 1 b 2, so B is a nonsingular matrix. Regard the dynamic coupling term f of system as external disturbance, which can be observed through ESO and then be compensated. The static decoupling is only used to the coupling matrix B. The above system can be treated as two SISO subsystems. Controllers are designed for the decoupled channels separately and the virtual control values U 1 and U 2 can be obtained. The practical control inputs u can be calculated by the following formula:

$$ u = B^{ - 1}\left [ \begin{array}{c} U_{1} \\ U_{2} \end{array} \right ] $$
(12)

Figure 1 is the control block diagram of the system.

Fig. 1
figure 1

Block diagram of ADRC decoupling control

Full size image

5.2 ADRC controller design for each channel

Traditional ADRC consists of a tracking differentiator (TD), extended state observer (ESO), and nonlinear state error feedback (NLSEF). The core part is disturbance estimation and dynamic compensation. The structural diagram of channel i (i=1,2) is shown in Fig. 2.

Fig. 2
figure 2

The structural diagram of ADRC in i channel

Full size image

The third-order observer is constructed for each channel separately. The action of acceleration f acting on the open loop system is extended to be a new state. The sum of disturbances that act on the system is estimated and compensated at real time. The concrete algorithm is as follows:

$$ \left \{ \begin{array}{l} e = z_{i1} - y_{i} \\ \dot{z}_{i1} = z_{i2} - \beta_{i1}e \\ \dot{z}_{i2} = z_{i3} -\beta_{i2}\mathop {\mathit {fal}}(e,\alpha_{i01},\delta ) + U_{i} \\ \dot{z}_{i3} = -\beta_{i3}\mathop {\mathit {fal}}(e,\alpha_{i02},\delta ) \end{array} \right . $$
(13)

where β ij (j=1,2,3) is a positive adjustable parameter, fal is a saturation function which effect is to restrain the signal oscillation, and can be represented as follows:

$$ \mathop {\mathit {fal}}(e,\alpha,\delta ) = \left \{ \begin{array}{l@{\quad }l} e / \delta^{1 -\alpha}, & |e| \le \delta \\ |e| ^{\alpha} \operatorname {sign}(e), & |e| > \delta \end{array} \right . \quad \delta > 0 $$
(14)

The state variables of ESO z i1,z i2 track the output variable y i and its differential. z i3 is the extended state and used to inhibit external disturbance and uncertainty of the controlled object. So, (13) achieves the observations on position, velocity, and unknown part of the controlled system.

Using the nonlinear combination of the PD form, the NLSEF control rate can be obtained.

$$ u_{i0} = \mathit{kp}_{i}\mathop {\mathit {fal}}(e_{1},\alpha_{i1}, \delta ) + \mathit{kd}_{i}\mathop {\mathit {fal}}(e_{2},\alpha_{i2},\delta ) $$
(15)

kp,kd are the coefficients of PD, e 1 is the difference of desired signal and observation of position, and e 2 is the difference of differential of desired signal and observation of velocity.

Considering the compensation of disturbance estimation z i3, the control signal is generated as follows:

$$ U_{i} = u_{i0} - z_{i3} $$
(16)

6 Simulation analysis

Use Matlab software to carry out the simulation experiment on the airship horizontal model and designed trajectory tracking controller. The parameters of modeling are derived in [18].

For the uncertain factors of the airship model, assuming that the uncertainty is about 15 % of certainty, the system (6) can be represented as follows:

$$ \left \{ \begin{array}{l} \dot{x} = f(x) + \Delta f(x) + (g(x) + \Delta g(x))u \\ y = h(x) \end{array} \right . $$
(17)

where Δf(x) and Δg(x) are the uncertainties of the system, which can be regarded as the perturbing terms of f(x) and g(x), and Δf(x), Δg(x) are bounded, shown as follows:

$$ \bigl\Vert \Delta f(x) \bigr\Vert \le 15~\% \cdot f(x); \qquad \bigl\Vert \Delta g(x) \bigr\Vert \le 15~\% \cdot g(x) $$
(18)
  1. (1)

    The desired trajectory is a circle

The center is set at the origin of geodetic coordinate system and the radius is 100 m, namely: y 1=l xd =Rsinωt, y 2=l yd =Rcosωt, R=100 m, ω=0.02π.

For the method of parameter tuning of ADRC, refer to [22]. Combining with the trial-and-error method, the parameters of ADRC can be obtained as follows:

For Channel 1, ESO::

β 11=110, β 12=100, β 13=80, α 101=0.5, α 102=0.5, δ=0.01.

NLSEF::

kp 1=0.8, kd 1=1.6, α 11=0.7, α 12=0.9, δ=0.01.

For Channel 2, ESO::

β 21=120, β 22=80, β 23=30, α 201=0.3, α 202=0.3, δ=0.01.

NLSEF::

kp 2=2.5, kd 2=3, α 21=0.5, α 22=0.8, δ=0.01.

In an atmosphere environment, wind is an important factor, which affects the flight performance of an airship. The main working environment of the airship is at the stratosphere where the airflow changes weakly and the wind speed and direction change very slowly [23]. In this paper, wind is considered relative to the geodetic coordinate system and regarded as an external disturbance to act on the airship model. The speed and direction of wind are unchanged.

The original states of system are \(v_{x0} = 10~\mathrm{m/s}\), v y0=0, r 0=0, l x0=80 m, l y0=30 m, ψ 0=0. The wind speed \(v_{f} = 20~\mathrm{m/s}\), direction is along the positive x axis of the geodetic coordinate system. The simulation time is 100 s and simulation step Δt=0.01 s. At last, the control effects of ADRC are compared with SMC, which is a common method in aircraft control. The simulation results are shown as Figs. 3–6.

Fig. 3
figure 3

The change curves of airship states

Full size image

Figure 3 shows the change curves of airship states. It can be seen that the states become stable after about 12 s. Driven by the thrust of T, the velocities of airship along x axis and y axis are stabilized at 6.28 m/s and 0.23 m/s, respectively. Because of the influences of factors of disturbance of wind and the uncertainty of the model parameters, the velocities of the airship will fluctuate slightly. After stabling, the airship will do circular motion along the setting reference trajectory. At this point, the yaw rate is a fixed value about 0.063 rad/s and the yaw angle increases linearly. These accord with practical flight law approximately. Figure 4 shows the curves of airship trajectory tracking at the horizontal plane.

Fig. 4
figure 4

The change curves of trajectory tracking in horizontal plane

Full size image

Figure 5 shows the comparisons of tracking error between ADRC and SMC. The tracking accuracy of ADRC is better than SMC obviously. Figure 6 shows the comparisons of control variables. Because of the influence of disturbance of wind along the positive x axis, the variable range of the component of thrust along the x axis is larger than that along y axis. But the holistic change is comparatively smooth. Table 1 shows the average performance index of the two controllers of 5 simulation experiments, including the mean and variance of steady-state error and total energy consumption. Let e lx , e ly represent the steady-state error of l x and l y , respectively. The total energy consumption s is defined as the sum of the control variable of thrust, shown as the following formula:

$$ s = \int_{t_{0}}^{t_{f}} \bigl\vert u(t) \bigr\vert \,dt $$
(19)

where t 0,t f denote the starting and ending time, respectively.

Fig. 5
figure 5

The change curves of tracking error

Full size image
Fig. 6
figure 6

The change curves of thrust

Full size image
Table 1 Comparison of performance index
Full size table

From Table 1, the mean and variance of steady-state errors of ADRC are both less than SMC, so the precision and stability of ADRC are better. And at the same time, the total energy consumption of ADRC is lower.

  1. (2)

    The desired trajectory is a sine curve

The amplitude of the sine signal is 50 m and the cycle is 100 s, namely: y 1=l xd =t, y 2=l yd =Asinωt, A=50 m, ω=0.02π.

The parameters of controllers are kept unchanged. The original state l x0=0 and other conditions are unchanged.

According to Fig. 7, because of the desired trajectory is a sine curve, the change of the states presents the trend of sine and cosine waves approximately after stabling. Figure 8 shows the change curves of trajectory tracking the sine wave in horizontal plane. Figures 9 and 10 are the comparisons of tracking error and control variables, respectively, between ADRC and SMC. Table 2 still shows the average performance index of the two controllers of 5 simulation experiments. It is seen that ADRC processes better control accuracy and consumes lower energy.

Fig. 7
figure 7

The change curves of airship states

Full size image
Fig. 8
figure 8

The change curves of trajectory tracking in a horizontal plane

Full size image
Fig. 9
figure 9

The change curves of tracking error

Full size image
Fig. 10
figure 10

The change curves of thrust

Full size image
Table 2 Comparison of performance index
Full size table

Combining the two simulations, ADRC avoids the frequent manipulation of thrusts when turning (shown as Fig. 6(b) and Fig. 10(b)), which is beneficial to the practical applications. In the second simulation, ADRC still processes better control performance under the condition of unchanging the parameters of controllers. This shows that ADRC has strong robustness.

7 Conclusion

Aiming at the airship horizontal model, the nonlinear system was transformed to a standard form of the TITO system using the method of I/O linearization. By combining the ESO and NLSEF, the ADRC trajectory tracking controllers were designed for each decoupled channel separately. This control algorithm is independent of accurate controlled model, designed simply and easy to realize. According to the special working environment of the airship, the disturbance of wind with constant speed and direction was added to the simulation as the external disturbance. The simulation results showed that the designed control scheme could overcome the influence of the uncertainties of the model and external disturbance, and it had strong stability and robustness.

The airship is a complicated nonlinear system, so it is difficult to calculate and analyze the internal dynamics of the system. And there are too many parameters and tuning difficulties in the design of the ADRC controller. How to improve the control project, simplify parameters, and make it more beneficial to practical engineering applications are the issues that need to be resolved in the future research.