1 Introduction

This work is based on the well-known phenomenon that when an undamped nonlinear conservative system, such as Duffing’s equation

$$ \ddot{x}+x+x^{3}=0 $$
(1)

is driven by a periodic forcing function Fcosωt, in the presence of small damping \(\epsilon \dot{x}\),

$$ \ddot{x}+x+x^{3}=F\cos \omega t-\epsilon \dot{x}, $$
(2)

the resulting periodic motion exhibits hysteresis and associated jump phenomenon. The usual explanation of this phenomenon [1, 2] involves comparing the response of the unforced Eq. (1) with the response of the forced Eq. (2) (see Fig. 1). The response of the unforced Eq. (1) is viewed as a graph representing the relationship between frequency and amplitude a, known as a backbone curve. The response of the forced Eq. (2) may be viewed as a modification of the backbone curve (Fig. 1). Also shown in Fig. 1 is the hysteresis and jump phenomenon associated with slowly varying (increasing or decreasing) the forcing frequency ω.

Fig. 1
figure 1

A sketch of the characteristic amplitude-frequency response curve of the damped, forced Duffing oscillator with hysteresis and jump phenomenon

Full size image

Now it may happen that in an engineering application, the system in question is exposed to repeated changes in forcing frequency so that the system is exposed to repeated jumps. Each of these jumps is not periodic and repeated exposure to such a loading situation may be objectionable (see, for example, [3]).

It is in such a scenario that an engineering designer could wish for a nonlinear system which does not exhibit jump phenomenon. One scheme for attaining such a goal would be if the associated backbone curve was a vertical straight line. This is of course the situation for a linear oscillator, which leads to the following definition: Isochronicity/isochrony is the characteristic of oscillatory systems which have a fixed, amplitude-independent frequency/period [4]. The simple harmonic oscillator (SHO) with the Lagrangian

$$ L_{\mathrm{SHO}}=\frac{\dot{X}^{2}}{2}-\frac{X^{2}}{2}, $$
(3)

and the equation of motion

$$ \ddot{X}+X=0 $$
(4)

is the archetypal example of the system displaying this characteristic. The SHO is said to have an isochronous center as the period is constant in the neighborhood of the center.

First results in the field of isochronous oscillators are believed to date back to Galileo Galilei and Christian Huygens [5]. Although Galileo did not live to complete his design, he had thought that a pendulum is isochronous in the sense that the time it takes to complete one full swing is the same regardless of the size of the swing. Huygens, however, pushed this matter further, noting that this is true for pendulums that swing only a few degrees. He pursued the question of achieving perfect isochronicity and showed that it can be realized in a simple pendulum that wraps around the cycloid [6, 7] (see Example 5 (Sect. 4.2) below).

More recent investigations of isochronicity have been directed toward nonlinear oscillators, which are in general known to have a frequency that depends on their amplitude. Thus, some Liénard-type equations

$$ \ddot{x}+u( x) \dot{x}+v( x) =0 $$
(5)

are found to exhibit the isochronicity characteristic. Sabatini [8] gave necessary and sufficient mathematical conditions for isochronicity of the differential equation (5) in terms of the coefficient functions u(x) and v(x): Let u(x), v(x) be analytic, v(x) odd, u(0)=v(0)=0, v′(0)>0. Then the origin O is a center if and only if u(x) is odd, and O is an isochronous center if and only if

$$ \biggl( \int_{0}^{x}su( s) \,ds\biggr)^{2}-x^{3} \bigl( v(x) -v^{\prime }( 0) x\bigr) \equiv 0. $$
(6)

He illustrated the existence of this behavior in the system (5) with

$$ u( x) =( 2n+3) x^{2n+1},\qquad v( x) =x+x^{4n+3}, $$
(7)

where n is a nonnegative integer. Iacono and Russo showed that this system can be explicitly solved [9]. Necessary and sufficient mathematical conditions for the isochronicity of the differential equation (5) have also been provided by Christopher and Devlin [10]: the system (5) with u(x) and v(x) being analytic, has an isochronous center at the origin if and only if

$$ v( x) =ww^{\prime }\biggl( 1+\frac{1}{w^{4}}\biggl( \int _{0}^{x}w( s) u( s) \,ds\biggr) ^{2}\biggr) , $$
(8)

where w(x) solves the functional equation in \(F(x) =\int_{0}^{x}u( s) \,ds\):

$$F\bigl( x-2w( x) \bigr) =F( x) ,\quad w( 0) =0,\quad w^{\prime }( 0) =1. $$

Chandrasekar et al. [11] investigated in detail the so-called modified Emden equation, which is a Liénard-type nonlinear oscillator (5) with

$$ u( x) =kx,\qquad v( x) =\lambda _{1}x+\frac{k^{2}}{9}x^{3}, $$
(9)

and determined the conditions under which it can yield isochronous oscillations. Chandrasekar et al. [12] found a class of coupled Liénard-type equations that exhibit the isochronicity property.

It should be noted that Liénard-type equations (5) have a term linear in the generalized velocity. Sabatini [13] studied the equation analogous to (5), but with \(\dot{x}\) replaced by \(\dot{x}^{2}\)

$$ \ddot{x}+p( x) \dot{x}^{2}+q( x) =0, $$
(10)

deriving a sufficient condition for its solution to be oscillatory, i.e., for the origin to be a center:

$$ xq( x) >0. $$
(11)

Based on his previous results [8], Sabatini also proved in [13] that when p(x) and q(x) are odd and analytic, and Eq. (11) is satisfied for small values of x≠0, the origin is an isochronous center if and only if the following expression is equal to zero in the whole domain:

$$ x\bigl[ q( x) \varPhi ^{\prime }( x) -\varPhi ( x) q^{\prime }( x) -\varPhi ( x) q( x) p( x) \bigr] \equiv 0, $$
(12)

where

$$ \varPhi ( x) =\int_{0}^{x}{\exp }\bigl( P( s) \bigr) \,ds,\quad P( x) =\int_{0}^{x}p( s) \,ds. $$
(13)

Sabatini further gave a characterization of isochronous centers: when p(x) and q(x) are polynomials and the condition (11) is satisfied, the origin represents a global isochronous center if and only if both p(x) and q(x) have an odd degree and p(x) has a positive leading coefficient [13].

The existing theory related to the oscillators modeled by Eq. (10) neither links the equation of motion with mechanical models, nor provide general solution for their isochronous motion. The study proposed in this paper resolves this shortage by presenting a family of conservative oscillators whose equation of motion has the form (10), which is interpreted here in a new way as the consequence of the position-dependent mass or geometrical (kinematic) constraints. In addition, the solution for a phase trajectory and time response of isochronous motion is also provided. Several examples are given to illustrate the findings.

2 Oscillators with position-dependent mass

Let us consider conservative oscillators whose Lagrangian has the form

$$ L=\frac{1}{2}m( x) {\dot{x}}^{2}-V(x), $$
(14)

where m(x) is a mass that changes with the displacement x and V(x) is the potential energy that is required to be positive definite and to yield the amplitude-independent frequency.

Lagrange’s equation corresponding to the Lagrangian (14) is

$$ \ddot{x}+\frac{m^{\prime }}{2m}{\dot{x}}^{2}+\frac{V^{\prime }}{m}=0, $$
(15)

where m′=dm/dx.

Now, putting the requirement of the equivalence between the Lagrangian of the oscillator under consideration (14) and the Lagrangian of the SHO with the isochronous center at the origin (3), we conclude that the following should be satisfied:

(16)
(17)

Equation (16) gives

$$ X=\int_{0}^{x}\sqrt{m(s)}\,ds, $$
(18)

and Eq. (17) defines the potential energy, so that the equation of motion (15) becomes

$$ \ddot{x}+\frac{m^{\prime }}{2m}{\dot{x}}^{2}+\frac{1}{\sqrt{m}}\biggl[ \int _{0}^{x}\sqrt{m(s)}\,ds\biggr] =0. $$
(19)

Given the fact that classical mechanical systems are such that m>0, the denominators in Eq. (19) are not zero and the radicand is always positive. Equation (19) can be related to Eq. (10) by identifying

$$ p( x) =\frac{m^{\prime }}{2m},\qquad q( x) =\frac{1}{\sqrt{m}} \biggl[ \int_{0}^{x} \!\sqrt{m(s)}\,ds\biggr] {=}\,\frac{X}{\sqrt{m}}, $$
(20)

where the latter term plays the role of the restoring force F r (x)≡q(x).

Comparing (20) and (13), we obtain that \(P=\ln \sqrt{m}\) and that \(\varPhi ( x) =\int_{0}^{x}\sqrt{m( s) }\,ds=X\) from Eq. (18). Then the condition derived by Sabatini in (12) is satisfied, since the expression in square brackets in Eq. (12) becomes:

$$ \frac{X}{\sqrt{m}}\sqrt{m}-X\frac{\sqrt{m}\sqrt{m}-X\frac{m^{\prime }}{2\sqrt{m}}}{m}-X\frac{X}{\sqrt{m}} \frac{m^{\prime }}{2m}\equiv 0. $$
(21)

In addition, the form of m(x) should be such that p(x) and q(x) are odd and analytic. To determine the form of m(x), we analyze p(x) in Eq. (20): the ratio of m′(x) and m(x) needs to be odd. Given the properties of mass in classical mechanical systems, one concludes that m(x) should be even.

Noting that \(m^{\prime }/( 2m) =( \sqrt{m}) ^{\prime }/ \sqrt{m}\), Eq. (19) can be expressed as

$$ \ddot{x}+\frac{M^{\prime }}{M}{\dot{x}}^{2}+\frac{1}{M}\biggl[ \int_{0}^{x}M(s)\,ds\biggr] =0, $$
(22)

where \(M( x) =\sqrt{m( x) }\). So, by choosing M(x) as an even analytic function, and performing its differentiation and integration with respect to x, one can find the differential equation (22) with an isochronous center. Thus, Eq. (22) and its other version (19) yield a family of conservative isochronous oscillators.

Since the solution for motion of the SHO (4) has a general form Acos(t+α), Eq. (18) also defines how x changes with time

$$ X=\int_{0}^{x}\sqrt{m(s)}\,ds =A\cos ( t+\alpha ) , $$
(23)

where A and α can be found from the initial conditions x(0) and \({\dot{x}}(0) \). So, not only does this approach yield mechanical and mathematical models of isochronous oscillators, but it also enables one to find their isochronous motion (note that this solution can be implicit). In addition, in case when the isochronous motion exists and when the corresponding initial energy level is h, the energy-conservation law can be used

$$ \frac{1}{2}m( x) {\dot{x}}^{2}+V(x)=\frac{1}{2}m( x){\dot{x}}^{2} +\frac{[ \int_{0}^{x}\sqrt{m(s)}\,ds] ^{2}}{2}=h, $$
(24)

to define this motion in the phase plane, i.e., to obtain the phase trajectory

$$ {\dot{x}}^{2}=\frac{2h-[ \int_{0}^{x}\sqrt{m(s)}\,ds] ^{2}}{m(x) }. $$
(25)

3 Examples

A few following examples illustrate potential use and benefits of the theoretical findings presented above.

3.1 Example 1: oscillators with a known mass-displacement law

The first example is related to the problem in which the form of the mass-displacement law is known, and the corresponding potential energy and the equation of motion that result in isochronous oscillations are obtained. Let the mass change in accordance with

$$ m( x) {=\exp }\bigl( x^{2k}\bigr) , $$
(26)

where k is a positive integer. This position-dependent mass will result in an odd-powered monomial term in front of \({\dot{x}}^{2}\) in Eq. (19).

To find the restoring force, the expression (18) is solved in terms of the lower incomplete gamma function γ [14]

$$ X=\int_{0}^{x}\exp \biggl(\frac{s^{2k}}{2} \biggr)\,ds =\frac{(-1)^{-\frac{1}{2k}}2^{\frac{1}{2k}}}{2k}\gamma \biggl( \frac{1}{2k},-\frac{x^{2k}}{2} \biggr) . $$
(27)

The associated potential energy (17) is

$$ V( x) =\frac{[\frac{(-1)^{-\frac{1}{2k}}2^{\frac{1}{2k}}}{2k}\gamma ( \frac{1}{2k},-\frac{x^{2k}}{2}) ]^{2}}{2}. $$
(28)

Equation (19) now transforms to a closed-form differential equation:

$$ \begin{aligned} &\ddot{x}+kx^{2k-1}{\dot{x}}^{2}+\frac{(-1)^{-\frac{1}{2k}}2^{\frac{1}{2k}}}{2k} \\ &\quad {}\times \gamma \biggl( \frac{1}{2k},-\frac{x^{2k}}{2}\biggr) \exp \biggl(-\frac{x^{2k}}{2}\biggr)=0. \end{aligned} $$
(29)

Based on Eq. (23), the isochronous oscillations are found to be defined by

$$ \frac{(-1)^{-\frac{1}{2k}}2^{\frac{1}{2k}}}{2k}\gamma \biggl( \frac{1}{2k},-\frac{x^{2k}}{2}\biggr) =A\cos ( t+\alpha ) . $$
(30)

Further, using the series representation for the lower incomplete gamma function [14, 15]

$$ \begin{aligned} &\gamma \biggl( \frac{1}{2k},-\frac{x^{2k}}{2}\biggr) =\exp \biggl( \frac{x^{2k}}{2}\biggr) \biggl( -\frac{x^{2k}}{2}\biggr) ^{\frac{1}{2k}}\\ &\quad {}\times \varGamma \biggl( \frac{1}{2k}\biggr) \sum _{n=0}^{\infty }\frac{( -\frac{x^{2k}}{2}) ^{n}}{\varGamma ( \frac{1}{2k}+n+1) }, \end{aligned} $$
(31)

the restoring force can be expressed in a polynomial form, so that the equation yielding isochronous oscillations (29) becomes

$$ \ddot{x}+kx^{2k-1}{\dot{x}}^{2}+\frac{\varGamma ( \frac{1}{2k}) }{2k}\sum_{n=0}^{\infty }\frac{( -1) ^{n}x^{2k\cdot n+1}}{2^{n}\quad \varGamma ( \frac{1}{2k}+n+1) }=0. $$
(32)

Now, it is easy to compare Eq. (32) with Eq. (10) and to recognize that p(x) and q(x) are polynomials with odd degree and that p(x) has a positive leading coefficient because k>0. Therefore, the isochronous center is global.

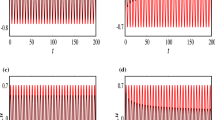
To illustrate these results, the mass variation (26) is plotted in Fig. 2a for k=2. The associated potential energy (28) is shown in Fig. 2b, from which it is seen that the potential energy is single-welled. The solution for time response obtained numerically by integrating directly Eq. (29) for x(0)=1 and \(\dot{x}( 0) =0\) is plotted in Fig. 2c in red dots. The analytical solution corresponding to these initial conditions is given by Eq. (30) with A=1.1156579646, α=0 and is plotted as a solid black line. These two types of solutions coincide. In addition, phase trajectories obtained numerically from Eq. (29) and based on Eq. (25) for h=0.622346347 are plotted in Fig. 2d and demonstrate perfect matching. Figure 2c also contains the solutions shown for two additional pairs of the initial conditions x(0)=0.1;0.5 and \(\dot{x}( 0) =0\). As it can be seen, all the resulting time histories have the same, constant period.

Fig. 2
figure 2

Example 1 for k=2: (a) mass variation (26); (b) potential energy (28); (c) time response obtained numerically from Eq. (29) for x(0)=0.1;0.5;1, \(\dot{x}( 0) =0\) (red dots), and the analytical solution Eq. (30) with A=0.100001;0.503152;1.1156579646, α=0 (solid black line); (d) phase trajectories obtained numerically from Eq. (29) (red dots) and based on Eq. (25) for h=0.622346347 (solid black line)

Full size image

It is interesting to note that when k=1, the lower incomplete gamma function turns into the imaginary error function [16], i.e.,

$$\begin{aligned} X =&\int_{0}^{x}\exp \biggl(\frac{s^{2}}{2}\biggr)\,ds =\frac{-i}{\sqrt{2}}\gamma \biggl( \frac{1}{2},-\frac{x^{2}}{2}\biggr) \\ =&\sqrt{\frac{\pi }{2}}\mbox{~erfi}\biggl( \frac{x}{\sqrt{2}}\biggr) , \end{aligned}$$
(33)

with the potential energy

$$ V( x) =\frac{\pi }{4}\mbox{~erfi}^{2}\biggl( \frac{x}{\sqrt{2}}\biggr) , $$
(34)

and the equation of motion

$$ \ddot{x}+x{\dot{x}}^{2}+\sqrt{\frac{\pi }{2}} \exp \biggl(-\frac{x^{2}}{2}\biggr) \mbox{~erfi}\biggl( \frac{x}{\sqrt{2}}\biggr)=0. $$
(35)

Given Eq. (31), the expression for the restoring force can be written down as

$$\begin{aligned} F_{r} =&\frac{\varGamma ( \frac{1}{2}) }{2}\sum_{n=0}^{\infty } \frac{( -1) ^{n}x^{2n+1}}{2^{n}\quad \varGamma ( \frac{1}{2}+n+1) } \\ =&\sum_{n=0}^{\infty } \frac{(-1)^{n}x^{2n+1}}{(2n+1)!!}, \end{aligned}$$
(36)

and the corresponding equation of motion becomes

$$ \ddot{x}+x{\dot{x}}^{2}+\sum_{n=0}^{\infty } \frac{(-1)^{n}x^{2n+1}}{(2n+1)!!}=0. $$
(37)

The results (34)–(37) agree with the results obtained in [17] by using a perturbation method.

3.2 Example 2: oscillators with a fixed restoring force

Equations (19) and (22) can be used to find the mass-displacement characteristic of an isochronous oscillator with a fixed nonlinearity, i.e., with the known form of the restoring force. To illustrate this, let us assume that the restoring force has the following form:

$$ F_{r}( x) \equiv q( x) =x+{x}^{2k+1}, $$
(38)

where k is a positive integer.

Identifying from Eq. (22) that

$$ \frac{1}{M}\biggl[ \int_{0}^{x}M(s)\,ds \biggr] =x+x^{2k+1}, $$
(39)

and solving this for M(x), one can obtain

$$ M( x) =\bigl({1+x}^{2k}\bigr)^{-\frac{2k+1}{2k}}. $$
(40)

Equation (22) gives:

$$ \ddot{x}-(2k+1)\frac{x^{2k-1}}{1+x^{2k}}{\dot{x}}^{2}+{x+x}^{2k+1}=0. $$
(41)

When k=1, the restoring force (38) is of the Duffing hardening type. The mass should change in accordance with

$$ m( x) =\frac{1}{({1+x}^{2})^{3}}, $$
(42)

and the potential energy should be

$$ V( x) =\frac{{x}^{2}}{2({1+x}^{2})}. $$
(43)

Then, the equation of motion is

$$ \ddot{x}-\frac{3x}{1+x^{2}}{\dot{x}}^{2}+{x+x}^{3}=0, $$
(44)

with the isochronous oscillations being defined by

$$ \frac{{x}}{\sqrt{{1+x}^{2}}}=A\cos ( t+\alpha ) . $$
(45)

Figures 3a and 3b show respectively the mass-displacement expression (42) and the potential energy (43). Note that for larger |x|, mass decreases considerably and becomes very small. A numerically obtained time response from Eq. (44) is plotted in Fig. 3c in red dots for x(0)=1 and \(\dot{x}(0) =0\), while the analytical solution given by Eq. (45) with A=1/\(\sqrt{2}\), α=0 is depicted by a solid black line. Phase trajectories obtained numerically from Eq. (44) and based on Eq. (25) for h=1/4 and plotted in Fig. 3d. Both Figs. 3c and 3d validate the analytical results derived. Figure 3c also includes the analytical and numerical solutions shown for two additional pairs of the initial conditions x(0)=0.1;0.5 and \(\dot{x}( 0) =0\). All these time histories have the same, constant period. This confirms that the period/frequency are amplitude-independent.

Fig. 3
figure 3

Example 2: (a) the mass-displacement expression (42); (b) potential energy (43); (c) numerically obtained time response from Eq. (44) for x(0)=0.1;0.5;1 and \(\dot{x}( 0) =0\) (red dots), and the analytical solution given by Eq. (45) with \(A=0.0995037;0.447214;1/\sqrt{2}\), α=0 (black solid line); (d) phase trajectories obtained numerically from Eq. (44) and based on Eq. (25) for h=1/4

Full size image

3.3 Example 3: oscillators with prescribed motion

The results presented in Sect. 2 can also be used to determine if there is an isochronous oscillator having the motion of the given form and, if there is, to find its mechanical and mathematical model. Such situation arises, for example, if the prescribed motion is given by

$$ x=\sinh \bigl( \cos ( t) \bigr) . $$
(46)

Based on Eq. (23), one follows

$$ X=\text{arc}\sinh ( x) . $$
(47)

The mass-displacement law is obtained first by differentiating the right-hand side of Eq. (47) and then squaring what has been obtained

$$ m( x) =\frac{1}{1+x^{2}}, $$
(48)

while the potential energy should be

$$ V( x) =\frac{( \text{arc}\sinh ( x) ) ^{2}}{2}. $$
(49)

The corresponding equation of motion is

$$ \ddot{x}-\frac{x}{1+x^{2}}{\dot{x}}^{2}+\sqrt{1+x^{2}} \text{arc}\sinh ( x) =0. $$
(50)

The time response obtained numerically by integrating directly Eq. (50) for x(0)=sinh1=1.1752011936 and \(\dot{x}(0) =0\) is shown in Fig. 4a in red dots, while the analytical solution (46) is plotted as a solid black line. A perfect match is seen. Figure 4b shows how the mass (48) changes with time, illustrating that it corresponds to periodically varying, i.e., pulsating mass with a period twice smaller than the one of the response.

Fig. 4
figure 4

Example 3: (a) time response obtained numerically from Eq. (50) for x(0)=1.1752011936 and \(\dot{x}( 0) =0\) (red dots), and the analytical solution (46) (solid black line); (b) time-varying mass plotted based on Eq. (48)

Full size image

4 On some other oscillators with position-dependent coefficient of the kinetic energy

Besides conservative oscillators with the position-dependent mass analyzed in Sect. 2, there is another family of conservative oscillators that can be considered in the same context as above. Their Lagrangian has the form

$$ L=\frac{1}{2}\tilde{T}( x) {\dot{x}}^{2}-V(x), $$
(51)

where \(\tilde{T}( x) \) is the coefficient of the kinetic energy \(T(x,{\dot{x})}=\frac{1}{2}\tilde{T}( x) {\dot{x}}^{2}\). Note that here we do not associate \(\tilde{T}( x) \) with the mass of the system under consideration, but assume that it exists due to the geometry of motion.

The Lagrange’s equation corresponding to the Lagrangian (51) is

$$ \ddot{x}+\frac{\tilde{T}^{\prime }}{2\tilde{T}}{\dot{x}}^{2}+\frac{V^{\prime }}{\tilde{T}}=0. $$
(52)

The form of this equation can directly be related to Eq. (10) and Sabatini’s results [13], as well as to the considerations given in Sect. 2. Thus, the cases with \(\tilde{T}\) and V being even functions in x are seen as leading to the equation of motion with an isochronous solution. The following examples are to illustrate two cases with such properties and to demonstrate some further benefits.

4.1 Example 4: a mechanism with two sliders and a spring

Let us consider the mechanism shown in Fig. 5: the sliders A and B of equal mass m are connected by a light rigid bar of length L and move with negligible friction in the slots shown, both of which are in a horizontal plane; the slider A is also connected with a spring. The kinetic energy of this system is given by

$$ T(x,{\dot{x})}=\frac{1}{2}\tilde{T}( x) {\dot{x}}^{2},\qquad \tilde{T}( x) =\frac{mL^{2}}{L^{2}-x^{2}}. $$
(53)

Assuming that the spring is linear and has a stiffness k, and introducing the nondimensional variables \(\bar{x}=x/L\), \(\bar{t}=\sqrt{k/m}t\), the corresponding equation of motion is

$$ \frac{d^{2}\bar{x}}{d\bar{t}^{2}}+\frac{\bar{x}}{1-\bar{x}^{2}}\biggl( \frac{d\bar{x}}{d\bar{t}}\biggr) ^{2}+\bar{x}-\bar{x}^{3}=0. $$
(54)

This equation can be related to Eq. (44) considered in Example 2, but here we deal with the softening Duffing nonlinearity. For \(\bar{x}\neq 1\), Eq. (54) satisfies the conditions for the existence of isochronous oscillations. However, the restoring force and the coefficient in front of the square of the generalized velocity do not match the form (22) with the solution (23). Here, we can pose a question of the form of the potential energy and the restoring force for which the equation of motion will correspond to Eq. (22). Thus, by calculating \(M(\bar{x})\) from \(M^{\prime }/M=\bar{x}/(1-\bar{x}^{2})\), Eq. (22) leads to

$$ \frac{d^{2}\bar{x}}{d\bar{t}^{2}}+\frac{\bar{x}}{1-\bar{x}^{2}}\biggl( \frac{d\bar{x}}{d\bar{t}}\biggr) ^{2}+\sqrt{1-\bar{x}^{2}}\arcsin \bar{x}=0. $$
(55)

Equation (23) yields its isochronous solution

$$ \arcsin \bar{x}=A\cos ( \bar{t}+\alpha ) . $$
(56)

It should be noted that the restoring force in Eq. (55) can be approximated as follows:

$$ \sqrt{1-\bar{x}^{2}}\arcsin \bar{x}\approx \bar{x}-\frac{\bar{x}^{3}}{3}, $$
(57)

so that Eq. (55) becomes

$$ \frac{d^{2}\bar{x}}{d\bar{t}^{2}}+\frac{\bar{x}}{1-\bar{x}^{2}}\biggl( \frac{d\bar{x}}{d\bar{t}}\biggr) ^{2}+\bar{x}-\frac{\bar{x}^{3}}{3}=0. $$
(58)

Comparing Eq. (58) with Eq. (54) one concludes that in case of small oscillations, the isochronous solution of the former can be taken as a good approximate solution of the latter. To confirm this, Eqs. (54) and (58) are solved numerically for \(\bar{x}(0) = 0.1\) and \(\frac{d\bar{x}}{d\bar{t}}( 0) =0\) and plotted in Fig. 6. In addition, the solution of Eqs. (56) with A=arcsin(0.1), α=0 is also shown. It is seen that these solutions agree well.

Fig. 5
figure 5

The mechanism considered in Example 4

Full size image
Fig. 6
figure 6

Example 4: (a) time response obtained numerically from Eq. (58) for \(\bar{x}( 0) = 0.1\) and \(\frac{d\bar{x}}{d\bar{t}}( 0) =0\) (red dots) and from Eq. (54) (green stars); analytical solution (56) with A=arcsin(0.1), α=0 (solid black line)

Full size image

4.2 Example 5: Huygens’ isochronous pendulum

It was Huygens [6, 7] who showed that if a pendulum of length L and mass m wraps around a cycloid [18]

$$\begin{aligned} x =&\frac{L}{4}( \theta -\sin \theta ) , \\ y =&-\frac{L}{4}( \cos \theta -1) , \end{aligned}$$

it performs isochronous oscillations. The corresponding parametric equations of motion of the bob are [18]

$$\begin{aligned} X =&\frac{L}{4}( \theta +\sin \theta ) , \end{aligned}$$
(59)
$$\begin{aligned} Y =&-\frac{L}{4}( 3+\cos \theta ) . \end{aligned}$$
(60)

Both of these cycloids are shown in Fig. 7 for L=4 and for −π≤θ≤π.

Fig. 7
figure 7

Huygens’ isochronous pendulum in motion

Full size image

The corresponding kinetic energy

$$ T=\frac{1}{2}m\bigl(\dot{X}^{2}+\dot{Y}^{2}\bigr), $$
(61)

is

$$ T=\frac{1}{2}m\biggl(\frac{L}{2}\cos \frac{\theta }{2} \biggr)^{2}\dot{\theta}^{2}. $$
(62)

It is seen that the kinetic energy (62) of Huygens’ pendulum has a position-dependent coefficient.

Its potential energy

$$ V=mgY $$
(63)

has the form

$$ V=-mg\frac{L}{4}(3+\cos \theta ). $$
(64)

On the other hand, a simple pendulum (SP) of the same length and the same mass has a constant period if it performs small oscillations. Its kinetic energy is of the form

$$ T_{\mathrm{SP}}=\frac{1}{2}m(L\dot{\varphi})^{2}, $$
(65)

and the potential energy is

$$ V_{\mathrm{SP}}=-mgL\biggl(1-\frac{\varphi ^{2}}{2}\biggr). $$
(66)

The equality between two expressions for the kinetic energy (62) and (65) yields

$$ \dot{\varphi}=\frac{1}{2}\dot{\theta}\cos \frac{\theta }{2}. $$
(67)

This is satisfied for

$$ \varphi =\sin \frac{\theta }{2}. $$
(68)

By using (68), the expression for the potential energy V (64) becomes

$$ V=-mgL\biggl(1-\frac{1}{2}\sin ^{2}\frac{\theta }{2} \biggr)=-mgL\biggl(1-\frac{\varphi ^{2}}{2}\biggr), $$
(69)

i.e., it transforms to the potential energy of the simple pendulum (66), which confirms that Huygens’ pendulum belongs to a wide class of isochronous oscillators discussed in Sect. 2 that can be transformed into simple harmonic oscillators by establishing the equivalence between their Lagrangians or the kinetic and potential energies.

Let us now define the problem in a deductive way: find the form of X and Y for which the system described by (61) and (63) performs isochronous oscillations. To that end, we make (63) equal to (66), which leads to

$$ Y=L\biggl(\frac{\varphi ^{2}}{2}-1\biggr). $$
(70)

Knowing that the solution for motion of the simple pendulum has the form

$$ \varphi =A\sin \biggl(\sqrt{\frac{g}{L}}t+\varphi \biggr)=A\sin \psi , $$
(71)

we have

$$ Y=L\biggl(\frac{( A\sin \psi ) ^{2}}{2}-1\biggr). $$
(72)

We also make (61) equal to (65), deriving

$$ \dot{X}^{2}=L^{2}\dot{\varphi}^{2}- \dot{Y}^{2}=L^{2}\dot{\varphi}^{2}\bigl( 1-\varphi ^{2}\bigr) , $$
(73)

or

$$ X=L\int_{0}^{\varphi }\sqrt{1-\varphi ^{2}}\,d\varphi . $$
(74)

Integrating (74), one obtains

$$ X=\frac{L}{2}\bigl( \varphi \sqrt{1-\varphi ^{2}}+\arcsin \varphi \bigr) . $$
(75)

This is a conditional expression for which −1≤A≤1. Taking, A=1, one follows

$$ X=\frac{L}{2}\bigl( \sin \psi \sqrt{1-( \sin \psi ) ^{2}}+ \arcsin ( \sin \psi ) \bigr) , $$
(76)

so that the solutions for X and Y become equal to Eqs. (59) and (60) with 2ψ=θ. Thus, this transformation approach presented in this paper obviously gives the same results as derived in [18].

5 Conclusions

This study has been concerned with conservative nonlinear oscillators that have isochronous orbits around the origin. Their mechanical and mathematical models have been proposed as having the Lagrangian of the analogous form to the simple harmonic oscillator, but with the kinetic energy whose coefficient is position-dependent. Such coefficient can stem from the position-dependent mass or it can be the consequence of geometric/kinematic constraints. The class of oscillators with the position-dependent mass has been considered in detail. It has been found that such systems have an isochronous center in the origin if the mass is an even function in the displacement and the potential energy is related to it in a specific way. The corresponding equation of motion has been derived, as well as its exact isochronous solutions for motion and for a phase trajectory. It has also been demonstrated how certain systems can be adjusted to exhibit isochronous oscillations the form of which has been derived in this study, and how one can find approximations for isochronous oscillations.