1 Introduction

Strong earthquakes in mountainous areas, such as the 2008 Wenchuan earthquake (Qi et al. 2010; Yin et al. 2009) and the 1999 Chi–Chi Earthquake (Huang et al. 2001; Liao and Lee 2000), can trigger considerable landslides that can cause a devastating number of deaths and property loss. Many factors can control these slope failures, including the engineering geology, hydrogeology and seismic ground acceleration (Jibson 1993; Jibson et al. 2000; Keefer 1984). Among these factors, the ground acceleration is commonly considered one of the most important (Meunier et al. 2007, 2008). However, the ground acceleration fluctuates strongly within tens of seconds during an earthquake, so the peak ground acceleration (PGA, the absolute maximum value on an accelerogram) is usually taken as the most important parameter in the study of earthquake-induced landslides (Yuan et al. 2013).

Since the end of the nineteenth century, a large number of seismic stations have been built around the world, and tens of thousands of ground acceleration records have been collected during different earthquakes. Combined with these records, some theoretical and empirical methods, such as the finite-fault model (Beresnev and Atkinson 1999), stochastic point-source model (Gillespie 1976), Green’s function method (Hartzell 1978) and empirical regression methods (Abrahamson and Silva 1997; Boore et al. 1997; Campbell 1997; Chiou et al. 2008), have been proposed to estimate the ground acceleration as well as the PGA. Among them, because of their simplicity and convenience, empirical methods are the most commonly employed to predict the PGA distribution of an earthquake and are used extensively (Power et al. 2012).

Empirical methods use a large amount of ground-motion data to fit an empirical mathematical expression and consider many factors that influence the PGA, such as the source, path and site conditions (Douglas 2003). However, these models consider only the spatial distribution of the fault. Because the seismic source is too complex, these empirical models simply assume the source to be a point source (where energy is both concentrated and released), a line source with a uniform energy distribution or a plane source. Some scholars have proposed models considering the spatial distribution of ruptures (Ohno et al. 1993; Thompson and Baltay 2018). However, the energy of a seismic source is distributed unevenly in three-dimensional (3D) space, especially that of a strong earthquake. For example, the energy of the 2008 Wenchuan earthquake was unevenly distributed on an inclined plane, with a length of 300 km and a width of 40 km (Shen et al. 2009). In addition, these models usually contain tens of constants to be regressed by thousands of earthquake records in similar regions. Thus, it is difficult to use these ready-made empirical methods to other areas without enough records. Therefore, it is necessary to study how to build an empirical attenuation model considering a nonuniform spatial distribution of seismic source energy and its 3D scale with as few parameters as possible.

This paper is structured as follows. Section 1 reviews the current work on the main empirical attenuation models of ground motion. Section 2 presents the empirical attenuation model and computation process proposed in this paper. Section 3 takes the 2008 Wenchuan earthquake as an example to calculate its PGA distribution. Then, the resulting near-field PGA of the 2008 Wenchuan earthquake is compared with those of other methods and discussed in Sect. 4. Our conclusions are given in Sect. 5.

2 Methods

2.1 Empirical attenuation model of the near-field PGA

As mentioned in Sect. 1, seismic source of a strong earthquake is a 3D-plane with an uneven distribution of seismic energy. The fault plane is usually divided into a large number of rectangles to estimate the rupture process through geophysical inversion methods (Beresnev and Atkinson 1999; Wang et al. 2008). During the rupture process, these rectangles can be taken as many sub-sources with the same size but different energies (Fig. 1). These sub-sources are triggered successively from the hypocentre to the fault boundary during the earthquake. Hence, for a site on the Earth’s surface (site A), its acceleration is the result of contributions from many relevant sub-sources. Each sub-source has a different start time and propagation time to site A (Douglas 2003, 2011), so each sub-source has a different contribution to site A. In total, the PGA at site A is a complex consequence of different sub-sources.

Fig. 1
figure 1

Seismic fault model on a 3D scale. Point A is a site on the Earth’s surface. Sub-sources inside the yellow line affect the PGA at site A

Full size image

Because of the complexity of the earthquake process, we assume that the seismic source can be totally divided into n sub-sources. Each sub-source is an independent process and has an effect on the PGA at site A. The energy and scale of each sub-source are much smaller than those of the whole source and can be taken as a point source. Based on the attenuation equation for a point source (Abrahamson and Silva 1997; Boore et al. 1997; Campbell 1997; Chiou et al. 2008), the PGA value due to the ith (i ≤ n) sub-source releasing at site A, yi can be calculated by

$$\lg y_{i} = a + b\lg M_{i} + c\lg (R_{i} + h)$$
(1)

where a, b, c and h are constants to be regressed; yi is the PGA value to be calculated, cm/s2; Mi is the energy of the ith sub source, here given as the seismic moment, dyn cm(1 dyn cm = 10−7 N m); Ri is the distance from the midpoint of the ith sub source to site A, km; and lg returns the base-10 logarithm to a number.

Equation (1) is commonly used to express the attenuation of the PGA (Abrahamson and Silva 1997; Boore et al. 1997; Campbell 1997; Chiou et al. 2008). Here, we use this formula to express the attenuation of sub-sources. Usually, the constant b is a positive value and relates to the attenuation of seismic energy, while the constant c is a negative value and represents the effect of distance attenuation, and lg(Ri + h) represents the effect of the distance to the hypocentre. Because unrealistically high values of ground motion are predicted for small Ri, the constant h is positive and is introduced to avoid the near-field saturation effect (Douglas 2003; Hansen 1970).

Usually, the rupture process of a seismic fault starts from the hypocentre. We assume that the rupture of the sub-sources begins from the hypocentre and transfers successively to adjacent sub-sources until the fault boundary is reached. Because the sub-sources are not all triggered at the same time, not all sub-sources contribute to the PGA value at site A. It is assumed that m sub-sources affect the PGA at site A, and m is smaller than n (0 < m ≤ n). Here, Eq. (2) is used to regress the range of sub-sources and express each sub-source’s effect:

$$Y = \sum\limits_{i = 1}^{m} {y_{i} \, \frac{{R_{\min } }}{{R_{i} }}}^{{{{R_{0} } \mathord{\left/ {\vphantom {{R_{0} } e}} \right. \kern-\nulldelimiterspace} e}}}$$
(2)

where Y is the PGA value at site A released by a total of m sub-sources, cm/s2; yi and Ri have the same meaning as Eq. (1); Rmin is the minimum value of Ri, km; R0 is the distance from site A to the epicentre, km; m is a positive integer; and e is a constant to be regressed as a positive integer.

In Eq. (2), m is a parameter that needs to be determined by discriminant (3).

$$m = {\text{Num}}\left[ {\frac{{R_{i} }}{{R_{\min } }} \le f} \right]$$
(3)

where Num[condition] denotes the number of total sub-sources under the condition in brackets; f is a constant to be regressed, and it is positive and larger than 1; and the other symbols have the same meaning as in Eqs. (1) and (2).

This model divides the seismic fault into n parts with different energies and considers the fault size and a nonuniform energy distribution. Each part of these equations has an explicit physical meaning, rather than the equation being completely empirical. The propagation velocity of a seismic wave is usually faster than the rupture velocity of the fault (Xia et al. 2005). Moreover, sub-sources have different hypocentral distances to site A. These sub-sources are not triggered simultaneously but are triggered successively (like firecrackers). Hence, there are time and phase differences when the waves from the different sub-sources reach site A. For a site near the fault, when its acceleration reaches the PGA, the rupture on the fault has usually travelled a short distance along the fault, so only some sub-sources near the site affect the PGA at this site. For a site far from the fault, most of the fault has been ruptured, so more sub-sources will affect the PGA at the site. The PGA is expected to be influenced by fewer sub-sources when the site is close to the fault than when the site is far from the fault. Discriminant (3) can ensure that the PGA at site A is affected by part of the seismic fault: the value of m is smaller when site A is closer to the seismic fault and larger when site A is far from the seismic fault.

Because these m sub-sources have different distances to the hypocentre and are not triggered at the same time, the vibrations produced by these m sub-sources do not reach site A simultaneously. What is more important is that the PGA value at site A cannot be simply taken as the sum of these m sub-sources simply. When the time taken for the wave from one sub-source to reach site A is not equal to the time required for site A to reach the PGA of its accelerogram, then the effect of this sub-source will decrease sharply. Based on the assumption that the hypocentral distance from a sub-source to site A has an important influence, \(\frac{{R_{\min } }}{{R_{i} }}^{{{{R_{0} } \mathord{\left/ {\vphantom {{R_{0} } e}} \right. \kern-\nulldelimiterspace} e}}}\) is included in Eq. (2) to consider this situation, where R0/e represents the sub-source near hypocentre whose effect on the PGA is much more than the effects of other sub-sources far from the hypocentre.

2.2 Computation process

There are four steps in the computational process, as shown in Fig. 2. The first step is to obtain the spatial and slip displacement distribution of the seismic source. The sub-sources are divided in the second step. According to the records of aftershocks, the parameters in Eq. (1) will be iteratively regressed in the third step. Then, parameters in Eqs. (2) and (3) are also iteratively regressed in the fourth step.

Fig. 2
figure 2

Flowchart of the computation process

Full size image

In the first step, the spatial and slip displacement distribution on seismic source plane should be obtained accurately. At present, the spatial distribution of the seismic source can be determined through aftershock positioning, field surveys, geophysical measurements and GPS (global positioning system) and InSAR (interferometric synthetic aperture radar) measurements (Shen et al. 2009). Based on the spatial distribution of the rupture, the distribution of the slip displacement can be inverted by the finite-fault method using far-field body waveform records (Wang et al. 2008). Sometimes, the slip displacement distribution is rapidly obtained by official organizations or other scholars after a strong earthquake occurs. Then, based on Eq. (4) (Hanks and Kanamori 1979), we can obtain the seismic moment distribution:

$$M_{0} = \mu DS$$
(4)

where M0 is the seismic moment, dyn cm; μ is the shear modulus, which is 3 × 1010 Pa; D is the fault slip displacement; and S is the seismic fault area.

In the second step, the seismic fault is reasonably divided into many sub-sources (each with a rectangular shape) with the same size. To ensure the size of each sub-source, we use aftershock records. Strong earthquakes usually trigger many aftershocks with different magnitudes and depths. These aftershocks are usually triggered under similar stress and structural conditions, but the amount of energy released differs. Equation (5) (Hanks and Kanamori 1979) can transform the aftershock magnitude into the seismic moment

$$M = \frac{2}{3} \times \lg M_{{0}} - 10.7$$
(5)

where M0 is the seismic moment, dyn cm; M is uniformly valid with respect to 3 < ML < 7, 5 < MS < 7.5, and Mw at larger magnitude, MS is the surface-wave magnitude, ML is the local magnitude, and Mw is the moment magnitude. Using Eq. (5) and the aftershock magnitude, the moment range of aftershocks can be determined.

Then, an iterative process is needed to divide the seismic source into sub-sources with the same size, which have the same moment range as the aftershocks. Given the dimensions of a rectangle, the fault plane is divided into sub-planes accordingly, the moment of each sub-plane is calculated by the slip displacement distribution and Eq. (4), and the moment range of the sub-plane is obtained. The above process is repeated until the moment range of the sub-planes has the same range as that of the aftershocks. The final sub-planes and their moments can be taken as the sub-sources.

In the third step, the constants in Eq. (1) are regressed based on the collected aftershock data. Because the sub-sources have the same energy range as the aftershocks, a large number of aftershock records following this strong earthquake can compose a database and satisfy the required quantity of data to regress Eq. (1). Aftershock records often have different magnitudes and a wide range of hypocentral distances, and their distribution is extremely uneven (Campbell 1981). Moreover, the seismic moment and hypocentral distance are correlated. It is very important to consider this nonuniform distribution and correlation when regressing this empirical attenuation model (Campbell 1981; Huo and Hu 1992; Joyner and Boore 1981). Liu and Luo (2014) proposed a weighted two-step regression method that considers nonuniform distributions. This paper modifies the regression method presented by Liu and Luo (2014) and applies it to calculate the constants in Eq. (1), i.e. a, b, c and h.

To avoid ambiguity among the constants, we introduce a new equation:

$$\lg y_{af} = a + b\lg M_{af} + c\lg (R_{af} + h)$$
(6)

where a b c and h have the same meanings in Eq. (1), \(y_{af}\) is the PGA value in the aftershock database, cm/s2; Maf is the seismic moment in this database, dyn cm; and Raf is the hypocentral distance to site A in this database, km.

  1. 1.

    Assuming there are N records and NE earthquakes in this database, a new Eq. (7) is used to replace a + blgMaf in Eq. (6) by linear regression (Joyner and Boore 1981)

    $$a + b\lg M_{af} = \sum\limits_{o = 1}^{{N_{E} }} {F_{o} E_{o} }$$
    (7)

    where o is the number of earthquakes in the aftershock database; Eo is a dummy variable (where Eo = 1 for earthquake o and Eo = 0 otherwise); \(M_{af}\) is the seismic moment of the oth earthquake; and Fo (F1, F2, …, \(F_{{N_{E} }}\)) is the constant to be regressed.

  2. 2.

    The aftershock records are divided into q levels according to the hypocentral distance with the logarithm base 10. For a record within a certain distance level, the weight of each record is:

    $$\omega_{pq}^{{\prime}} = 1/\left( {n_{p} n_{q} } \right)$$
    (8)

    where nq is the number of earthquakes in this distance level and np is the number of records with this magnitude in this distance level. For example, if a record is located at one distance level, there are 5 aftershocks at this level, and there are 2 earthquakes of the same magnitude at this level \(\omega^{{\prime}}_{pq}\) of 1/(2 × 5).

    To ensure the same degree of freedom, the weights of all records are normalized by Eq. (9):

    $$\omega_{pq} = \omega^{{\prime}}_{pq} /q$$
    (9)

    where q is the number of distance levels.

    A weighted diagonal matrix is obtained by:

    $$W = {\text{diag}}\left[ {\begin{array}{*{20}c} {W_{1} } & {W_{2} } & \cdots & {W_{N} } \\ \end{array} } \right]$$
    (10)

    where the value of WN is equal to \(\omega_{pq}\), and W is an N × N diagonal matrix.

  3. 3.

    Eqs. (6) and (7) are linearized according to the nonlinear regression method proposed by Draper and Smith (1998) to obtain matrices Z2 and X2:

    $$Z_{1} = \left[ {\begin{array}{*{20}c} {\lg y_{af1} } & {\lg y_{af2} } & \cdots & {\lg y_{afN} } \\ \end{array} } \right]^{{\mathrm{T}}}$$
    (11)

    where N is the number of total records, and \(\lg y_{afN}\) is the record value with the logarithm base 10

    $$X_{1} = \left[ {\begin{array}{*{20}c} {\lg \left( {R_{11} + h} \right)} & {E_{11} } & {E_{12} } & {E_{13} } & \cdots & {E_{{1N_{E} }} } \\ {\lg (R_{21} + h)} & {E_{21} } & {E_{22} } & {E_{23} } & \cdots & {E_{{2N_{E} }} } \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\lg (R_{N1} + h)} & {E_{N1} } & {E_{N2} } & {E_{N3} } & \cdots & {E_{{NN_{E} }} } \\ \end{array} } \right]$$
    (12)

    where RN1 is the hypocentral distance of the Nth record, and \(E_{{NN_{E} }}\) can be obtained with Eq. (7).

  4. 4.

    The values of c F1, F2, …, \(F_{{N_{E} }}\) can be calculated by Eq. (13)

    $$B_{1} = \left[ {\begin{array}{*{20}c} c & {F_{1} } & {F_{2} } & {F_{3} } & \cdots & {F_{{N_{E} }} } \\ \end{array} } \right]^{{\mathrm{T}}} = (X_{1}^{{\mathrm{T}}} WX_{1} )^{ - 1} X_{1}^{{\mathrm{T}}} WZ_{1}$$
    (13)
  5. 5.

    The aftershock records are divided into k levels by their magnitude. The weight of each record is

    $$v_{k}^{\prime } = 1/n_{k}$$
    (14)

    where nk is the number of earthquakes in the magnitude level where the record is located.

    To ensure the same degree of freedom, the weights of all records are normalized by Eq. (15):

    $$v_{k} = v_{k}^{\prime } /k$$
    (15)

    where k is the number of magnitude levels.

    A weighted diagonal matrix is obtained:

    $$V = {\text{diag}}\left[ {\begin{array}{*{20}c} {V_{1} } & {V_{2} } & \cdots & {V_{{N_{E} }} } \\ \end{array} } \right]$$
    (16)

    where \(V_{{N_{E} }}\) is equal to \(v_{k}\) and V is an NE × NE diagonal matrix.

  6. 6.

    Equation (6) and the values obtained by Eq. (13) are linearized according to the nonlinear regression method proposed by Draper and Smith (1998) to obtain matrices Z2 and X2:

    $$Z_{2} = \left[ {\begin{array}{*{20}c} {F_{1} } & {F_{2} } & \cdots & {F_{{N_{E} }} } \\ \end{array} } \right]^{{\mathrm{T}}}$$
    (17)
    $$X_{2} = \left[ {\begin{array}{*{20}c} 1 & {M_{1} } \\ \vdots & \vdots \\ 1 & {M_{{N_{E} }} } \\ \end{array} } \right]$$
    (18)

    where \(M_{{N_{E} }}\) is the magnitude value of the NEth magnitude.

  7. 7.

    The values of a and b can be determined by Eq. (19).

    $$B_{2} = \left[ {\begin{array}{*{20}c} a & b \\ \end{array} } \right]^{{\mathrm{T}}} = (X_{2}^{{\mathrm{T}}} VX_{2} )^{ - 1} X_{2}^{{\mathrm{T}}} VZ_{2}$$
    (19)
  8. 8.

    An unbiased variance estimate can be calculated by:

    $$\hat{\sigma }^{2}_{1} = \frac{{(Z_{1} - X_{1} B_{1} )^{{\mathrm{T}}} W(Z_{1} - X_{1} B_{1} )}}{{N - N_{E} - 2}} + \frac{{(Z_{2} - X_{2} B_{2} )^{{\mathrm{T}}} V(Z_{2} - X_{2} B_{2} )}}{{N_{E} - 2}}$$
    (20)
  9. 9.

    The constant h cannot be resolved directly; it needs to be iterated from 0 to 10 until the minimum value of \(\hat{\sigma }^{2}_{1}\) is obtained.

    In the fourth step, the constants in Eqs. (2) and (3) need to be regressed, where a, b, c and h are obtained with Eqs. (6)–(20). Substituting these constants into Eq. (1), several iterations are needed to obtain the constants in Eqs. (2) and (3). Based on the moments and hypocentral distances of the sub-sources, a group of orthogonal values of e and f are adopted to regress the estimated PGA values of the earthquake stations, and the least square errors between the estimated and true values are calculated by Eq. (21) until the value of \(\hat{\sigma }_{2}\) reaches its minimum, after which the values of e and f can be determined:

    $$\hat{\sigma }_{2} = \sum {\left( {\lg Y_{{{\text{est}}}} - \lg Y_{{\mathrm{tru}}} } \right)^{2} }$$
    (21)

    where Yest is the estimated PGA value and Ytru is the true PGA value.

3 Applying this model to compute the PGA distribution of the Wenchuan earthquake

The Wenchuan earthquake was an immense and catastrophic event (Yin et al. 2009). The Chinese National Strong Motion Observation Network System (CNSMONS) obtained thousands of acceleration records during the mainshock and aftershocks. In addition, many scholars have studied the landslides triggered by this shock (Qi et al. 2010; Xu et al. 2014), fault rupture process (Shen et al. 2009; Wang et al. 2008) and other characteristics of this earthquake (Xu et al. 2009), which provide the data foundation for this section. Taking the 2008 Wenchuan earthquake as an example, its PGA distribution was computed using the methodology presented in Sect. 2.

3.1 Database

After the Wenchuan earthquake, many seismic fault models were constructed. Among them, the model presented by Shen et al. (2009) which was inferred from GPS and InSAR data and fit well with field investigation and measurement data (Xu et al. 2009) was adopted in this paper. This fault model has two parts, i.e. the Beichuan fault (BCF) and the Pengguan fault (PGF), as shown in Fig. 3. The BCF dips to the northwest with a moderate angle of ∼ 43° at the southwest end, and the fault plane gradually becomes steeper northeastward along the strike direction, reaching ∼ 50° at Nanba (see Fig. 3); the dip angle jumps to ∼ 56° across the Nanba step-over and increases progressively to become nearly vertical at the northeastern end of the rupture. The PGF dips at ∼ 28°, suggesting a common root shared with the Yingxiu–Beichuan segment of the BCF at a depth of ∼ 18 km (Shen et al. 2009). The fault model of the Wenchuan earthquake is made of 673 rectangles, each with a length of approximately 3 km and a width of approximately 5 km, and each part is inverted for the strike-slip and thrust-slip displacements (Shen et al. 2009). As these 673 rectangles are based on post-earthquake GPS and InSAR measurements, which were observed with some delays (from days to weeks), in this study, the first 599 rectangles were used as the fault sub-sources of the Wenchuan earthquake. These rectangles are located within a subsurface depth of 20 km, which represents the lower limit of the aftershock depth range (Chen et al. 2009). Based on the fault model presented by Shen et al. (2009, the BCF consists of two parts: one part contains 85 sub-sources located at a depth of 20 km, and the other part contains 423 sub-sources. The PGF consists of the remaining 91 sub-sources. Using a shear modulus of 3 × 1010 Pa, the moment of these rectangles ranges from 1.62 × 1017 N m to 4.49 × 1018 N m. These sub-sources amount to moment magnitudes of 5.44 to 6.40 based on the transform Eqs. (4) and (5). The summed moment of these three parts is 7.71 × 1020 N m, equivalent to an event of Mw7.89 based on Eq. (5), and this value is close to the magnitude of Mw7.9 reported by the USGS in 2008.

Fig. 3
figure 3

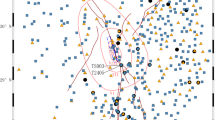
Map showing the study area. Green boxes are seismic stations. Orange lines are the surface ruptures of the 2008 Wenchuan earthquake. The star is the mainshock. Circles are aftershocks, and the colours represent different magnitudes. Points are sub-sources, and the colours represent different moments; red points represent the highest moments, and blue points represent the lowest moments. Pink triangles represent the names of key places

Full size image

The 2008 Wenchuan earthquake had a great effect on a vast region. The study area selected for this research extends 130 km from the seismic fault in the hanging wall and ~ 20 km away in the footwall, both of which are ~ 300 km in the strike direction (see Fig. 3). To keep the hanging wall and footwall in entirely mountainous areas, the southeastern boundary of the study area is irregular.

Since 2002, CNSMONS has constructed more than 1600 permanent free-field strong-motion observation stations (Lu et al. 2010). During the Wenchuan earthquake, 1208 components of strong-motion records of the mainshock and 6153 components of strong-motion records of aftershocks were recorded by nearly 380 digital strong-motion accelerographs managed by CNSMONS (Chen et al. 2009; Huang et al. 2008). Because the site condition has an obvious effect on the PGA (Boore and Bommer 2005; Douglas 2003), we selected stations with similar site conditions to reduce these effects based on V20 (the average shear-wave velocity within 20 m of the surface) and V30 (the average shear-wave velocity within 30 m of the surface) of these stations (see Fig. 3 and Table 1). Only 12 seismic stations satisfy this requirement in the study area. These stations all rest on soil, and the V20 and V30 velocities of these stations are similar (Feng 2013). The station names are 51WCW, 51LXS, 51LXM, 51LXT, 51MXN, 51SFB, 51HSD, 51HSL, 51MXD, 51MZQ, 51SPA, 51JYH. Each record from these stations has three components, which are labelled EW (east–west), NS (north–south) and UD (up–down). Considering the PGA values of the ground motions parallel and perpendicular to the earthquake fault (Douglas 2003), the EW and NS component records were converted into the FP direction (parallel to the earthquake fault) and FH direction (perpendicular to the earthquake fault) by Eqs. (22) and (23). As shown in Table 1, the maximum PGA value was recorded in the EW direction by station 51WCW, and this maximum value is significant in all records. Hence, to compare the maximum PGA value between our model and those of other models in Sect. 4, this paper took EW component records as an example to regress the parameters of Eqs. (1)–(3):

$$a(t)_{FP} = a(t)_{NS} \sin \theta + a(t)_{EW} \cos \theta$$
(22)
$$a(t)_{FH} = a(t)_{NS} \cos \theta - a(t)_{EW} \sin \theta$$
(23)

where a(t)EW is the horizontal ground acceleration in the EW direction; a(t)NS, a(t)FP and a(t)FH are those in the NS, FP and FH directions, respectively; and θ is the angle between the surface fault and east direction. (θ is 42° for the 2008 Wenchuan earthquake.)

Table 1 Ground-motion stations used in this paper and their PGA values of the 2008 Wenchuan earthquake
Full size table

Based on the sub-source division of the fault model, 13 aftershocks located within the main seismic plane were selected (Table 2). A total of 111 acceleration records were collected by these stations during the mainshock and aftershocks, and each record has three components. Among these 111 records, 99 are from aftershocks and 12 are from the mainshock. The magnitudes and hypocentral distances of these records are shown in Fig. 4.

Table 2 Aftershock events used in this model
Full size table
Fig. 4
figure 4

Magnitude and hypocentral distance distribution of aftershock records

Full size image

Records from strong-motion accelerographs, especially those collected by analogue instruments, invariably contain noise that can mask and distort the ground-motion signal at both high and low frequencies. Our data were gathered by modern digital instruments, so the records are reliable and robust (Boore 2001; Boore and Bommer 2005; Douglas and Boore 2011) and do not require a baseline correction or filtering. The maximum values from the accelerogram were directly picked as the PGA value.

3.2 Results

According to Eqs. (4)–(21) in Sect. 2, the constants in Eqs. (1)–(3) were regressed in this subsection.

First, we calculated the hypocentral distances (in m) of 99 aftershock records and obtained the values with the logarithm base 10. These records were divided into 7 classifications: 0–4.36, 4.36–4.52, 4.52–4.67, 4.67–4.835, 4.835–4.97, 4.97–5.12 and more than 5.12. The range of aftershock magnitudes is shown in Table 2. These magnitudes were divided into 7 classifications: 5.4 (Ms), 5.5 (Ms), 5.8 (Ms), 5.9 (Ms), 6.1 (Ms), 6.3 (Ms) and 6.4 (Ms). We set different values of h from 1 to 10 and substituted them into Eqs. (6)–(21) in Sect. 2. Therefore, a group of constants in Eq. (6) and an unbiased variance estimate were acquired. The values of a, b, c and h were taken as suitable values once the unbiased variance estimate reached its minimum. The results are shown in Table 3. Then, we obtained Eq. (24).

$$\lg y_{i} = - \,3.0050 + 0.2855 \times \lg M_{i} - 1.4929 \times \lg (R_{i} + 3)$$
(24)
Table 3 Regression results of Eq. (6)
Full size table

Subsequently, we replaced Eq. (1) with Eq. (24) and used a group of orthogonal values of e and f to regress the estimated PGA values at the 12 stations. Each of the three parts of the fault model was calculated separately. There PGA values were obtained at each station by a pair of e and f values, and we took the maximum PGA among these three as the estimated value at this station. For the 12 stations and a pair of e and f values, we obtained the estimated PGA values and calculated the least square errors between the estimated and true values by using Eq. (21). We performed the regression with different pairs of e and f values until the value of \(\hat{\sigma }_{2}\) reached its minimum. Finally, e was equal to 2, f was equal to 1.088, and \(\hat{\sigma }_{2}\) reached 0.4696. We obtained Eqs. (25) and (26) as a result. A comparison between the estimated and true values is shown in Table 4.

$$Y = \sum\limits_{i = 1}^{m} {y_{i} \, \times \frac{{R_{\min } }}{{R_{i} }}}^{{{{R_{0} } \mathord{\left/ {\vphantom {{R_{0} } 2}} \right. \kern-\nulldelimiterspace} 2}}}$$
(25)
$$m = {\text{Num}}\left[ {\frac{{R_{i} }}{{R_{\min } }} \le 1.088} \right]$$
(26)
Table 4 Estimated values and errors for the 12 stations obtained by the model in this study
Full size table

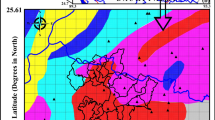
Then, we calculated the PGA distribution of the Wenchuan earthquake in the EW direction for the study area (Fig. 5). The estimated PGA distribution shows attenuation. The PGA attenuates with increasing distance to the surface rupture. Because of the uneven moment distribution on the fault surface, the degree of attenuation differs along the fault from southwest to northeast. There are four places on the seismic fault where the PGA is obviously higher than in other places, i.e. Dujiangyan city, Wenchuan County, Mianzhu County and Beichuan County. There is a wide blue area between Dujiangyan city and Wenchuan County (see Fig. 5), where the PGA reaches its maximum value of 1638.51 cm/s2. With increasing distance from the seismic rupture, the blue area decreases and fades. The area between the BCF and PGF also has relatively high PGA values.

Fig. 5
figure 5

Map of the estimated PGA distribution during the Wenchuan earthquake in the EW direction

Full size image

4 Discussion

4.1 Error analysis

In this section, we will continue to take the Wenchuan earthquake as an example to discuss the accuracy and applicability of the proposed model in detail. To compare the precision of our model, we obtained an interpolated map of the PGA during the Wenchuan earthquake using the records in the EW direction for the entire study area (see Fig. 6). Another estimated PGA distribution map (see Fig. 7) for the Wenchuan earthquake was presented by the United States Geological Survey (USGS); this map was produced by a finite-fault model of the 2008 Wenchuan earthquake motion, and a bias correction and spatial interpolation were applied to the recorded values. However, the USGS model assumes that faults of the Wenchuan earthquake are two planes with an even energy distribution, and the range of the map covers only a part of our study area.

Fig. 6
figure 6

Interpolated PGA map of the Wenchuan earthquake in the EW direction

Full size image
Fig. 7
figure 7

Map of the estimated PGA during the Wenchuan earthquake published by the USGS

Full size image

The three PGA distribution maps presented in Figs. 5, 6, and 7 all show similar attenuation characteristics with increasing distance from the faults. Along the fault zones, there are several individual regions with high PGA values, including Wenchuan County, Beichuan County, Dujiangyan city and Mianzhu County. It is obvious that Figs. 5 and 7 provide more details on the PGA distribution, which indicates that empirical methods can overcome the shortage of stations and make the PGA distribution more continuous. Because the USGS empirical model assumes the seismic fault to be a rectangle plane, the PGA distribution looks like buffer zones with a rectangle. The model presented in this paper considers a much more accurate fault model with an uneven energy distribution, and thus, the resulting PGA distribution seems smoother.

Taking records from the 12 stations, the errors related to our method are shown in Table 4. Because the PGA distribution map obtained from the USGS spans a smaller area and shows a PGA interval of 200 cm/s2, we linearly interpolated its PGA values for the 8 stations within its area. In addition, the errors of the USGS model related to the true records are shown in Table 5. The errors of the two models are both plotted and compared in Fig. 8, in which the stations on the horizontal axis are arranged with increasing distance from the fault from left to right. It can be clearly seen that the model presented in this paper has a higher accuracy than the USGS model in the near field. For example, at station 51SFB, the nearest station to the PGF (at a distance of 0.7 km) and situated at a distance of 20 km from the BCF, our model has an error of 20.71%, which is far less than the error of 44.47% reached by the USGS model; at station 51WCW, the nearest station to the hypocentre and 16 km from the BCF, our model has a very small error of 0.06%, which is much smaller than the error of 4.28% reached by the USGS model; at station 51MZQ, only 4 km from the BCF, our model has an error of 18.99%, which is much less than the error of 37.00% reached by the USGS model; finally, at station 51JYH, 12 km from the BCF and 126 km from the hypocentre, our model has an error of − 21.72%, which is also relatively small and acceptable. However, as the hypocentral distance and fault distance increase, the error of our model fluctuates more than that of the USGS model (see Fig. 8). In addition, the error range of our model in the far field is also consistent with that of other empirical methods (Abrahamson and Silva 1997; Boore et al. 1997; Campbell 1997; Chiou et al. 2008; Douglas 2003). That is, our model provides a much more accurate estimate of the near-field PGA distribution than that achieved by the USGS model.

Table 5 Estimated values and errors of the 12 stations by the USGS model
Full size table
Fig. 8
figure 8

Error comparison between the two models. The distance from each station to the fault increases from left to right on the horizontal axis

Full size image

The PGA is usually taken as one of the most important parameters in the study of earthquake-induced landslides, especially in the near field, and there is a strong correlation between the PGA distribution and landslide distribution according to many studies such as Keefer (1984), Jibson (1993) and Yuan et al. (2013).

A detailed landslide inventory (including 196,007 landslides within a total area of 1150.8 km2) was adopted herein. The total volume of the landslides is 1 × 1010 m3 (Xu et al. 2016). We used the same study area as shown in Sect. 3 to clip the landslide inventory and obtained a new inventory containing 186,147 landslides. A map showing the new landslide distribution from this new inventory is shown in Fig. 9. It can be seen that the landslides are mostly distributed along the seismic faults, and the dependence of the landslide probability density on the landslide area shows a three-parameter inverse-gamma distribution, which proves that the landslide inventory adopted is relatively complete (Malamud et al. 2004).

Fig. 9
figure 9

Landslide inventory map in the study area. a Landslide inventory map. b Dependence of the landslide probability density on the landslide area, which shows a three-parameter inverse-gamma distribution

Full size image

To study the relation between the PGA and landslide distribution, the PGA was divided into 9 classes, namely 0–30 cm/s2, 30–100 cm/s2, 100–300 cm/s2, 300–500 cm/s2, 500–700 cm/s2, 700–900 cm/s2, 900–1100 cm/s2, 1100–1300 cm/s2 and more than 1300 cm/s2, and the area of each PGA class in the study area is 58.62 km2, 6237.72 km2, 18,061.06 km2, 6072.03 km2, 4187.64 km2, 2876.15 km2, 1607.03 km2, 788.06 km2 and 171.30 km2, respectively. Evidently, the distribution area decreases with increasing PGA. The landslide was divided into 7 groups by size, including 0–0.1 × 104 m2, 0.1 × 104–0.5 × 104 m2, 0.5 × 104–2.5 × 104 m2, 2.5 × 104–12.5 × 104 m2, 12.5 × 104–62.5 × 104 m2, 62.5 × 104–312.5 × 104 m2 and more than 312.5 × 104 m2. The distribution of the number of landslides is shown in Table 6, and the landslide density related to the total area of each PGA class is counted under each class (see Fig. 10).

Table 6 Number of landslides in different PGA classes
Full size table
Fig. 10
figure 10

Histogram of the landslide density related to the area in each PGA class. The horizontal axis is the PGA class (× 1000 cm/s2), and the vertical axis is the landslide density (1/km2)

Full size image

Both Table 6 and Fig. 10 indicate that landslides can be triggered when the PGA exceeds 30 cm/s2. Keefer (1984) studied a large number of earthquake inventories and pointed out that M4.0 is the minimum magnitude that may trigger landslides. Using Eqs. (5) and (24), it can be calculated that the PGA is 37.95 cm/s when the magnitude is M4.0 with a focal depth of 11 km. That is, the result according to Keefer (1984) is similar to that reached in this paper. Moreover, the numbers of landslides in different size groups show that a large landslide is triggered by a larger PGA (see Table 6), which indicates the reliability of the model presented in this paper.

Figure 10 shows a clear tendency that landslides with an area of less than 2.5 × 104 m2 occur in a wide region, and the landslide density increases with increasing PGA in this area range; the maximum landslide area is presented in the area with the highest PGA (greater than 1500 cm/s2). In addition, landslides area in the range from 2.5 × 104 m2 to 62.5 × 104 m2 occurs once the PGA exceeds 30 cm/s2; furthermore, the landslide density gradually increases and then sharply increases at a PGA of 900 cm/s2, and landslides mainly occur in the region where the PGA exceeds 900 cm/s2. Additionally, landslides area over 62.5 × 104 m2 occurs in regions where the PGA is above 700 cm/s2, and the density is relatively low. Because the PGA reached by the model in this paper is related only to coseismic faults, the PGA attenuates with increasing distance from the coseismic fault. Thus, the relationship between the PGA and the coseismic landslides mentioned above reflects the controlling effect of coseismic activity on coseismic landslides. From this aspect, the results mentioned above are in accordance with many studies on landslides triggered by the 2008 Wenchuan earthquake, such as Huang and Li (2008), Qi et al. (2010), Qi et al. (2011), Xu et al. (2014) and Huang and Fan (2013), which further confirms the reliability of our model.

4.2 Limitations

The model in this paper shows better estimation results than other methods in the near field. The relationship between the landslide distribution and PGA shown by our model is also consistent with the findings of previous studies. Nevertheless, there are limitations of this model that deserve further discussion.

First, unlike other models, our model requires the ground-motion records of mainshocks and aftershocks to regress its parameters. Due to the sparsity of stations in the near field, the number of records used in this model is not large. Hence, with the increase in the numbers of stations and records in the near field for another strong earthquake in the future, our model is expected to be further developed and optimized.

Second, because there are few stations in the near field and the station distribution is uneven, it is difficult to give an exact range of the near field for the 2008 Wenchuan earthquake. The estimation error increases as the distance from the station to the fault increases within 20 km. However, there are no stations or records within the distance range of 20–50 km. The error distribution within this range cannot be obtained in detail, and the most applicable scope of this model cannot be obtained exactly.

Third, there are limitations in the application of our model. Each part of our model has an explicit physical meaning. The parameters a, b, c, h, e and f are affected by the geophysical conditions along the propagation path and the characteristics of the seismic source. In other words, the parameters a, b, c, h, e and f cannot be applied directly to another region when the geophysical conditions and source characteristics change. With increasing numbers of ground-motion records during strong earthquakes in a region, the model of this paper can be continuously developed in this region; then, the proposed model can eventually be developed into an empirical model for this region, and the model and its parameters can subsequently be applied directly to this area for another strong earthquake.

5 Conclusion

In this paper, an empirical attenuation model further considering an uneven distribution of energy on the fault plane is proposed. The main characteristic of this model is that it takes the fault as a certain number of sub-sources that are triggered in succession, and thus, the uneven energy distribution of a strong earthquake can be considered more accurately than in other empirical models. Based on this assumption, this paper establishes an attenuation model including three equations. These equations consider the fault size, energy distribution and spatial distribution. Each part of this model has an explicit physical meaning. In addition, the computation processes of this model are formulated in this paper. Among these processes, a weighted two-step regression method is developed to consider both the nonuniform energy distribution and the correlation between the magnitude and hypocentral distance. Compared with the results obtained by a finite-fault model developed by the USGS, the proposed model can provide more details and give more precise results in the near field of the 2008 Wenchuan earthquake. Analysis of the 2008 Wenchuan earthquake-induced landslides indicates that the PGA distribution estimated by our model is able to validate other scholars’ findings, which indicates that this empirical model is relatively reliable from another perspective.