1 Introduction

Flood, a natural disaster that brings disruption to services, causes damages to crops and properties and sometimes loss of human lives. Flood risk assessment is required for the planning, design, and construction of engineering infrastructure projects and in various environmental, insurance, development, and ecological studies (Caballero and Rahman 2014a). Flood damage can be minimized by ensuring optimum capacity to drainage structures so that flood water is drained quickly. An over- and under design of these structures causes increased capital cost and flood damage, respectively. The optimum design of water infrastructures depends largely on the reliable estimation of design floods, which is a flood discharge associated with a given annual exceedance probability or average recurrence interval (ARI).

To estimate design flood, at-site flood frequency analysis is ideally adopted, which however needs a long period of recorded streamflow data (Charalambous et al. 2013). These data at many locations are often limited or completely absent (i.e., ungauged situation). Under these circumstances, regional flood frequency analysis (RFFA) methods are adopted. The commonly used RFFA methods include rational method (I.E. Aust. 1987), index flood method (IFM) (Hosking and Wallis 1993; Zaman et al. 2012), and quantile regression technique (QRT) (Thomas and Benson 1970; Haddad et al. 2012). The rational method is a simple technique for estimating a design discharge from a small watershed, which was developed by Kuichling (1889) for small drainage basins in urban areas. In Australian rainfall and runoff (ARR), the national standard for design flood estimation, probabilistic form of the rational method known as probabilistic rational method has been recommended (I.E. Aust. 1987, 2001). In Australia, the probabilistic rational method has been examined by Pilgrim and McDermott (1982), Weeks (1991), Rahman et al. (2008, 2011), and Pirozzi et al. (2009). There has been limited independent validation of the probabilistic rational method, and the user has little knowledge about the uncertainty in the estimated flood quantiles generated by this method (Rahman et al. 2011). The IFM has been adopted by many countries. This relies on the identification of homogeneous regions (Hosking and Wallis 1993; Bates et al. 1998; Rahman et al. 1999; Kjeldsen and Jones 2010; Ishak et al. 2011). As Australia is extremely diverse in hydrology, there exists a great heterogeneity among catchments, and the use of IFM in Australia has been found to be of little success (Bates et al. 1998). The QRT, proposed by the United States Geological Survey, has been applied by many researchers using either an ordinary least square (OLS) or generalized least square (GLS) regression techniques (Thomas and Benson 1970; Stedinger and Tasker 1985; Bayazit and Onoz 2004; Rahman 2005; Griffis and Stedinger 2007; Ouarda et al. 2008; Kjeldsen and Jones 2009; Haddad and Rahman 2011; Haddad et al. 2012, 2013, 2014). Some of the recent developments in regional flood estimation in Australia include L moment-based IFM (Bates et al. 1998; Rahman et al. 1999), various forms of regression-based techniques (Rahman 2005; Haddad et al. 2012; Hackelbush et al. 2009; Micevski et al. 2014), and regional Monte Carlo simulation technique (Rahman et al. 2002; Rahman and Carroll 2004; Caballero and Rahman 2014b).

Most of the hydrologic processes are nonlinear and exhibit a high degree of spatial and temporal variability, and a simple log-transformation cannot often guarantee the achievement of linearity in modeling. Most of the above RFFA methods assume linear relationship between flood statistics and predictor variables in log domain while developing the regional prediction equations. With the use and reliance on increased computing techniques, a notable trend can be observed toward the application of model-free techniques especially during the past few decades in various fields on water resources engineering. These techniques include artificial neural networks (ANN), adaptive neuro fuzzy inference system (ANFIS), genetic expression modeling (GEP), genetic algorithm (GA), and GA-based artificial neural networks (GAANN). These techniques could provide good alternatives to the linear techniques such as QRT and IFM (Aziz et al. 2011). These nonlinear techniques have been widely applied to a variety of complex nonlinear problems in finance, medicine, and engineering. These techniques can provide a model structure that can easily account for nonlinearity between the model input and output and their complex interactions. These techniques do not need any fixed pre-defined model structure. These nonlinear techniques have been applied in streamflow forecasting and rainfall–runoff modeling but their application to RFFA problems is rather limited.

This paper seeks to focus on the development and testing of GAANN-based RFFA methods using the most extensive and comprehensive database that has become available in Australia as a part of the ongoing revision of the ARR—the national guide to flood estimation (I.E. Aust. 1987, 2001). The paper has the following objectives: (a) to test the applicability of the GAANN to RFFA problem using an extensive data set in eastern Australia; (b) to compare the performances of the GAANN-based RFFA models with an RFFA model based on BPANN (results obtained from Aziz et al. (2014) using same data set); and (c) to compare the performance of GAANN-based RFFA model with traditional approach such as QRT.

2 Overview of GAANN and its application in RFFA

GA was developed in 1960s–1980s (Holland 1975; Goldberg 1989). The concept of GA evolved from the biological evolutionary process. The major difference between GA and the classical optimization search techniques is that the GA works with a population of possible solutions, whereas the classical optimization techniques such as quasi-Newton method work with a single solution (Jain et al. 2005) to find the optimum solution through an iterative process. Here, optimization means a mathematical process of selecting the best available solution of a problem based on some criteria. GA is based on the Darwinian-type survival of the fittest strategy, whereby potential solutions to a problem compete and mate with each other in order to produce increasingly stronger individuals.

ANN was initially developed in 1940s (McCulloch and Pitts 1943) with a desire to understand the human brain and emulate its functioning. Application of ANN in hydrologic modeling was inspired by the work on forecasting mapping (predictors) for chaotic dynamic systems (Farmer and Sidorowich 1987). Since early 90s, ANNs have been applied to many hydrologic problems such as rainfall–runoff modeling, streamflow forecasting, groundwater modeling, water quality, rainfall forecasting, hydrologic time series modeling, and reservoir operations (e.g., Govindaraju 2000; Luk et al. 2001; Dawson and Wilby 2001; Zhang and Govindaraju 2003; Abrahart et al. 2004; Abrahart et al. 2007; Chen et al. 2008; Chokmani et al. 2008; Wu et al. 2008; Turan and Yurdusev 2009; Besaw et al. 2010; Tiwari and Chatterjee 2010; Gao et al. 2010; Hou et al. 2012).

In the fields of hydrology and water resources, although the GA techniques have been used widely to solve a number of water resource problems (Wang 1991; Franchini 1996; Franchini and Galeati 1997; Savic et al. 1999; Khu et al. 2001; Cheng et al. 2002), however, the combined use of GA and ANN, i.e., GAANN, could not attract much attention of researchers as yet. The probable reason might be that the algorithm of back-propagation (BP) is much simpler and easy to understand than GA; hence, most of the ANN applications in the literature used BP algorithm. The few GA and ANN hybrid applications in water resource field include Jain and Srinivasulu (2004), who demonstrated that GA is better than BP for training an ANN model to predict daily flows more accurately.

Morshed and Kaluarachchi (1998) conducted experiments to compare GA and BP in flow and transport simulations. They reported better performance of BP over GA and concluded that their results were based on a single set of simulations, and therefore, more research is needed to prepare alternative GA as a complementary to BP for situations where BP may fail. See and Openshaw (1999) recombined a series of neural networks via a rule-based fuzzy logic model that has been optimized using a GA. Abrahart et al. (1999) also used a GA to optimize the inputs to an ANN model used to forecast runoff from a small catchment. Rao and Jamieson used hybrid neural network and GA approach to investigate the minimum-cost design of a pump-and-treat aquifer remediation scheme. In the field of RFFA, there are few studies using BPANN (Dawson et al. 2006; Aziz et al. 2014) but to the best of author’s knowledge, there has been no notable application of GAANN in RFFA especially using the Australian conditions and the data.

3 Working structure of GAANN and QRT

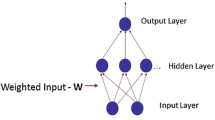
The basic working of GAANN can be understood concisely by looking at Figs. 1 and 2. An initial population of individuals (also called chromosomes) is created, and according to an objective function in focus, the fitness values of all chromosomes are evaluated. From this initial population, parents are selected who mate together to produce offsprings (also called children). The genes of parents and children are mutated. The fittest among parents and children are sent to a new pool. The whole procedure is carried over until any of the two stopping criteria is met, i.e., the required number of generations has been reached or convergence has been achieved. Chromosomes, which are the basic unit of population, represent the possible solution vector and are assembled from a set of genes that are generally binary digits, integers, or real numbers. A chromosome can be thought of as a vector x consisting of l genes g l.

Fig. 1
figure 1

Flowchart showing steps in GAANN model

Full size image
Fig. 2
figure 2

a Real-value genes and b an example of assigning gene values of a chromosome to the respective synaptic weights of ANN architecture during GAANN model

Full size image
$$x \, = \, \left( {g_{1} , \, g_{2} , \ldots , \, g_{l} } \right), \quad g_{l} \in G$$
(1)

l is referred to as the length of the chromosome. The “g” represents the binary genes (G = {0,1}), or integer genes (G = {…−2,−1,0,1,2…}) or real-value genes (G = R). In the last case, the real values are stored in a gene by means of a floating point representation (Rooji et al. 1996).

The three genetic operators such as selection, crossover (mating), and mutation in GA are primary force to produce new and unique offsprings having the same number of genes as that of parents. The selection operator is used to select parents from the pool. A number of selection techniques have been developed by various researchers (e.g., Holland 1975; Baker 1987; Goldberg 1989; de la Maza and Tidor 1993); however, their success and utility depends upon the nature of problem in hand. Crossover (mating) operator is used to produce offsprings from the selected parents. The parent chromosomes are mated to produce new offsprings representing new solution vectors. The mutation operator is used to introduce changes in genes of a chromosome. The mutation keeps the diversity in the genes of a population and stops it from a premature convergence (Bowden et al. 2005).

The flowchart of the GAANN model is shown in Fig. 1. An initial population is crowded with “n” number of chromosomes where “n” is referred to as the population size. An objective function comprising of feed forward ANN model with complete description of its architecture is defined. It reads training patterns once at the start of model and stores them in memory for applying to each chromosome. The total number of genes l of each chromosome represents the total synaptic weights of ANN model.

$$\left\{ {g_{1} , \, g_{2} , \ldots \ldots g_{l} } \right\} \, = \, \left\{ {w_{(if \to hr)} , \, w_{(ib \to hr)} , \, w_{(hf \to or)} , \, w_{(hb \to or)} } \right\}$$
(2)

where “w” represents the value of a synaptic weight; subscript “i” represents a node of input layer; “h” is a node of hidden layer and “o” represents the output layer node; “f” is the serial number of node, which forwards the information (i.e., f = 1, 2, 3,…); “r” is the serial number of node, which receives information (i.e., r = 1, 2, 3,…); “ib” represents the bias node of input layer; and “hb” is the bias node of hidden layer.

At the start of model, the fitness values of all the chromosomes of population are evaluated by ANN function. The real values stored in the genes of chromosome are read as the respective weights of ANN model. The ANN performs feed forward calculations with the weights read from genes of forwarded chromosome as per Eq. 2 and calculates mean squared error (MSE). No backward calculations are performed in GAANN like in the BP artificial neural network (BPANN) in which the weights are optimized by performing backward calculations. In GAANN, only the feed forward calculations are carried out for all the chromosomes, and MSE is calculated for each chromosome. The inverse of MSE is regarded as the fitness value of chromosome. By this way, the fitness values of all chromosomes of initial population are calculated by ANN function. Later on, the selection operator selects two parent chromosomes randomly. The selected parents are mated to produce two children having the same number of genes.

The GAANN is coded in C language, and some subroutines of LibGA package (Arthur and Rogers 1995) for evolutionary operators of GA have been used with alterations to read and process the negative real values.

In QRT, flood quantiles (Q T ) from the set of gauged catchments are generally regressed against catchment characteristics (predictor variables) (X) using the power form equation (Thomas and Benson 1970; Stedinger and Tasker 1985; Haddad and Rahman 2012):

$$Q_{T} = \beta_{0} X_{1}^{{\beta_{1} }} X_{2}^{{\beta_{2} }} \ldots$$
(3)

where regression coefficient βs is generally obtained by using an OLS or GLS regression. In developing the QRT, both the dependent and independent variables are generally log-transformed to linearize Eq. 3. In this study, an OLS regression was adopted to develop a prediction equation for each of the six flood quantiles separately using two predictor variables [catchment area (A) and design rainfall intensity for a given ARI and duration equal to time of concentration (tc) (I tc_ARI)]. The data sets for building and independent testing of the QRT model were the same as with the ANN models. The MINITAB 14 software was used to develop the QRT models.

4 Study area and data selection

This study focuses on eastern Australia consisting of New South Wales (NSW), Victoria (VIC), Queensland (QLD), and Tasmania (TAS). This region has the highest density of streamflow gauging stations with good-quality data as compared to other parts of Australia. For RFFA study, streamflow data (annual maximum series) and climatic and catchment characteristics data are needed. As a part of catchment selection and data preparation, the following criteria were considered

  • Study catchments have been minimally affected by the land-use change and artificial storage such as dam.

  • Study catchments have a relatively long period of quality-controlled streamflow record. The criteria used for this purpose include data quality, record length, catchment size, land use, regulations, gap filling, and rating curve extrapolation. Stations with poor- or low-quality data were excluded from the study.

  • A scarcity of stream gauging stations with long records requires a compromise between maximizing the number of stations (which provides a greater spatial coverage) and maximizing the record length (which enhances the accuracy of RFFA models). For this study, the stations having a minimum record length of 25 years were selected. As far as a catchment size is concerned, the priority was given to small-/medium-sized catchments with an upper limit of 1,000 km2; however, an upper limit of 1,900 km2 was adopted for Tasmania due to the limited availability of the number of small/medium catchments in Tasmania.

  • In the case of land use, each selected catchment was examined by going through the topographic and aerial photographic maps, and catchments that had undergone major land-use changes over the period of streamflow records were excluded.

  • Additionally, major regulation undermines the purpose of RFFA and hence gauging stations with significant regulation or diversion were excluded. Streams with minor regulation, such as small farm dams and small storage diversion weirs, were included because this type of regulation is unlikely to have a significant effect on AM floods.

  • In preparing the streamflow data, gaps in the annual maximum flood series data were filled by two methods (Ishak et al. 2013): (1) comparison of the monthly instantaneous maximum data with monthly maximum mean daily data at the same station for years with data gaps; if a missing month of instantaneous maximum flow corresponded to a month of very low maximum mean daily flow, then that was taken to indicate that the annual maximum did not occur during that missing month; and (2) regression of annual maximum mean daily flow series against the annual instantaneous maximum series of the same station. Moreover, the stations having AM flood data associated with a high degree of rating curve extrapolation were identified by using a “rating ratio.” The AM flood series data point for each year (estimated flow) was divided by the maximum gauged flow for that station to define the rating ratio. Any station with a “very high rating ratio” was excluded from the database as explained in Haddad et al. (2010) and Haddad and Rahman (2012). These data were prepared as part of ARR (2012) update project.

Based on above criteria, a total of 452 stations were selected for this study. The selected stations are shown in Fig. 5, which include 96, 131, 172, and 53 stations from NSW, VIC, QLD, and TAS, respectively. The catchment sizes of the selected 452 stations range from 1.3 to 1,900 km2 with the median value of 256 km2. For the stations of NSW, VIC, and QLD, the upper limit of catchment size was 1,000 km2; however, for Tasmania, there were four catchments in the range of 1,000–1,900 km2. Overall, there are about 12 % catchments in the range of 1–50 km2, about 11 % in the range of 50–100 km2, 53 % in the range of 100–500 km2, and 24 % >1,000 km2. The annual maximum flood record lengths of the selected stations range from 25 to 75 years (mean 33 years). The Grubbs and Beck (1972) method was adopted in detecting high and low outliers (at the 10 % level of significance) in the annual maximum flood series data. The detected low outliers were treated as censored flows in flood frequency analysis. Only a few stations had a high outlier, which was not removed from the data set as no data error was detected for these high flows. The annual maximum flood series data in the selected stations did not show any trend (at the 5 % level of significance) based on Mann–Kendall test (Kendall 1970).

In estimating the flood quantiles for each of the selected stations, log-Pearson III (LP3) distribution was fitted to the annual maximum flood series using Bayesian method as implemented in FLIKE software (Kuczera 1999). According to ARR, LP3 is the recommended distribution for at-site flood frequency analysis in Australia (I. E Aust., 1987), and hence, it was adopted. In previous applications (e.g., Haddad and Rahman 2011, 2012), it has been found that LP3 distribution provides an adequate fit to the Australian annual maximum flood data.

In developing the prediction equations for flood quantiles, initially a total of five explanatory variables were adopted (Aziz et al. 2014) using the same 452 catchments. These variables are (1) catchment area expressed in km2 (A); (2) design rainfall intensity values in mm/h I tc, ARI (where ARI = 2, 5, 10, 20, 50, and 100 years, and tc = time of concentration (hour), estimated from tc = 0.76A 0.38); (3) mean annual rainfall expressed in mm/y (R); (4) mean annual areal evapotranspiration expressed in mm/y (E); and (5) main stream slope expressed in m/km (S). It should be noted that to estimate time of concentration (tc), a number of alternative equations are available (I.E. Aust. 1987); however, for the present study area (i.e., eastern Australia), tc = 0.76A 0.38 has been recommended for general application (I.E. Aust 1987; Weeks 1991; Rahman et al. 2011). Hence, this equation is adopted in this study to estimate tc.

In the study by Aziz et al. (2014) where the ANN and Gene Expression programming techniques were used to develop the prediction equation, it was found that two variables (A and I tc, ARI ) model outperformed other models. Based on this finding, two predictor variables, i.e., A and I tc, ARI, are selected for this study (Fig. 3)

Fig. 3
figure 3

Location of study catchments (Red color indicates selected test catchments)

Full size image

The summary of the selected predictor variables is provided in Table 1.

Table 1 Exploratory data analysis of different explanatory variables
Full size table

5 Adopted methodology

Models were developed for six flood quantiles separately being 2-, 5-, 10-, 20-, 50-, and 100-year ARIs. Total data set was randomly split into 80 % (for training) and 20 % (for model validation) as shown in Fig. 3. Moreover, the results from GAANN were compared with the BPANN- and QRT-based RFFA models. In both the cases of BPANN and QRT, 80 % (randomly selected) of the available data set was used for model development and the remaining 20 % were used for model validation.

Optimum regions were identified as part of the study conducted by Aziz et al. (2014) for ANN-based RFFA models in the eastern Australia using these 452 catchments where the best results can be obtained when all the 452 stations are combined to form one region. Hence, in this paper, all the 452 stations were combined to form one region.

In the case of GAANN, at the start of modeling, the fitness values of all the chromosomes of population are evaluated by ANN function. The real values stored in the genes of chromosome are read as the respective weights of ANN model. Figure 2 shows an example of translation of the genes of a chromosome into the respective synaptic weights of an ANN model. The ANN performs feed forward calculations with the weights read from genes of forwarded chromosome as per Eq. 4 and calculates MSE. The inverse of MSE is regarded as the fitness value of chromosome. By this way, the fitness values of all chromosomes of initial population are calculated by ANN function.

Later on, the selection operator selects two parent chromosomes randomly. The roulette wheel operator with elitism is used in this model. Elitism is a scheme in which the best chromosome of each generation is carried over to the next generation in order to ensure that the best chromosome does not get lost during the calculations. The selected parents are mated to produce two children having the same number of genes. The uniform crossover operator is used with a crossover rate of p c  = 1.0. In uniform crossover, a toss is done at each gene position of an offspring, and depending upon the result of toss, the gene value of first parent or second parent is copied to the offspring. The genes of children are then mutated with the swap mutation operator with a mutation rate of p m  = 0.8. The mutated children are then evaluated by ANN function to know their fitness values. The fitness values of all the four chromosomes (two parents and two children) are compared, and the two chromosomes of highest fitness values are then sent to a new population and the other two are abolished.

The evolutionary operators continue this loop of selection, crossover, mutation, and replacement until the population size of new pool is same as old pool. One generation cycle completes at this stage, and process is repeated until any of two stopping criterion is fulfilled, i.e., maximum number of generations are reached or the convergence has been achieved. And the best chromosome which is tracked so far through the number of generations is sent to the ANN function. The genes of best chromosome are read as weights of ANN model and represent the optimized weights of ANN model. With these weights, the model is said to be fully trained. Finally, the training and test sets are simulated by using these weights. In the model, a population size of 100 is used and the model is run for 100 generations or till the model is converged. The sigmoid function is used, and the data are normalized in the range of 0.05 and 0.95. The learning rate of 0.15 and the momentum factor of 0.075 are used in the model. Different models were tried, and finally, the model with architecture of 2:5:1 (i.e., two inputs, five hidden, and one output node) was selected. The MSE was used to determine the fitness of the ANN models. The best optimized GAANN models in terms of RMSE and the coefficient of efficiency (CE) was selected for prediction equation.

6 Assessment of model performance

For the assessment of model performance, the following statistical measures were used

  • Coefficient of efficiency:

    $$\text{CE} \, = \, 1 \, - \frac{{\sum\limits_{i = 1}^{n} {(Q_{i} - \hat{Q}_{i} )^{2} } }}{{\sum\limits_{i = 1}^{n} {(Q_{i} - \bar{Q}_{i} )^{2} } }}^{{}}$$
    (4)

  • Ratio between predicted and observed flood quantiles:

    $$\text{Ratio} \, = r = \frac{{Q_{{\text{predicted}}} }}{{Q_{{\text{observed}}} }}$$
    (5)

  • Relative error (RE):

    $$\text{RE} \, \left( \% \right) \, = \, \text{Abs}\left[ {\frac{{\left( {Q_{{\text{pred}}} - Q_{{\text{obs}}} } \right)}}{{Q_{{\text{obs}}} }} \times 100} \right]$$
    (6)

where Q pred is the flood quantile estimate from the GAANN-based or QRT-based models, and Q obs is the at-site flood frequency estimate obtained from LP3 distribution using a Bayesian parameter fitting procedure (Kuczera 1999). The CF, median relative error, and median ratio values were used to measure the relative accuracy of a model.

7 Results

The predicted and observed flood quantiles for the 90 independent test catchments were used to assess the relative performances of the three different RFFA models as described below. Median ratio (r) values for the GAANN-, BPANN-, and QRT-based RFFA models are presented in Table 2. The median r values for the GAANN and BPANN are both closer to 1. In the case of GAANN, an underestimation is noted for all the ARIs except for 2 and 100 years, but all of these values are within acceptable range in the RFFA modelling. However, GAANN-based model provides an overall value as 1 in case of median ratio values. The QRT shows an overestimation for all the ARIs, in particular for 10 and 100 years. Overall, GAANN and BPANN both provide the most plausible r values ranging from 0.89 to 1.17 for the six ARIs.

Table 2 Median Q pred /Q obs ratio (r) values for GAANN-, BPANN-, and QRT-based RFFA models
Full size table

Table 3 shows the median RE values for GAANN-, BPANN-, and QRT-based RFFA models. For all the ARIs, BPANN-based RFFA technique outperforms the GAANN and QRT. For higher ARIs (20–100 years), GAANN-based RFFA method provides reasonably acceptable results. When comparing GAANN with QRT, it is found that QRT-based RFFA method performs better than GAANN, with overall RE value of 51.9 % (QRT), as compared to 58.4 % for GAANN. Hence, in terms of median RE value, BPANN-based RFFA model outperforms the remaining two techniques. This can also be seen in Fig. 4 where RE values of the ANN-based method is consistently smaller than GAANN and QRT.

Table 3 Median relative error (RE) values (%) for GAANN-, BPANN-, and QRT-based RFFA models
Full size table
Fig. 4
figure 4

Comparison of RE values between BPANN-, GAANN-, and QRT-based RFFA models

Full size image

Table 4 compares the CE values for GAANN-, BPANN-, and QRT-based RFFA methods. For all ARIs, GAANN and BPANN provide the comparable results except for 5- and 100-year ARIs, where GAANN outperforms BPANN. Both the BPANN and GAANN provide the similar CE values for 10-year ARI (0.63) and for 20-year ARI (0.71). When compared with QRT-based technique, both GAANN and BPANN perform better than the QRT. Although GAANN and BPANN both provide the CE values close to each other (except for 50-year ARI) and within acceptable range, overall BPANN outperforms the GAANN.

Table 4 Coefficient of efficiency (CE) values for GAANN, BPANN, and QRT RFFA models
Full size table

The observed and predicted flood quantiles for the 90 test catchments were plotted for all the ARIs for the three methods (example shown in Figs. 5, 6, 7 for 20-year ARI). It was found that BPANN-based RFFA models provide the best fit with the observed flood quantiles.

Fig. 5
figure 5

Plot of observed (target) and predicted (output) quantiles for Q 20 (GAANN-based model) for 90 independent test catchments

Full size image
Fig. 6
figure 6

Plot of observed (target) and predicted (output) quantiles for Q 20 (BPANN-based model) for 90 independent test catchments

Full size image
Fig. 7
figure 7

Plot of observed (target) and predicted (output) quantiles for Q 20 (QRT-based model) for 90 independent test catchments

Full size image

Considering the above results, it can be concluded that, although for eastern Australia, BPANN-based RFFA models outperform the GAANN and QRT methods but GAANN-based RFFA model can also be recommended for this region of Australia as both BPANN and GAANN perform very similarly.

8 Conclusion

In RFFA, use of nonlinear models is not as common as the linear models such as regression-based methods. This paper compares two nonlinear models in RFFA with the traditional QRT. The adopted nonlinear models are GA optimized for artificial neural network (ANN) called GAANN and BP algorithm optimized for ANN (BPANN). This study uses data set from 452 natural catchments from eastern states of Australia. Based on an independent testing, it has been found that both the nonlinear models outperform the linear QRT-based RFFA model. Overall, BPANN-based RFFA model provides the best prediction, with a relative error of about 40 % and coefficient of efficiency of 0.65. The finally selected BPANN-based RFFA model needs two predictor variables (catchment area and design rainfall intensity), which are easy to obtain, and hence, the developed model can be used in practice with sufficient ease. The method developed in this study can be adapted to other countries to develop nonlinear RFFA models.