1 Introduction

Recordings obtained in recent earthquakes (1989 Loma Prieta, 1994 Northridge, 1995 Kobe 1999 Kocaeli, and 1999 Chi–Chi) revealed that seismic ground motions recorded within the near-fault region are quite different from the usual far-fault ground motions observed at large distance in many respects such as the period of earthquake continuity, peak ground acceleration, velocity and displacement, rupture directivity, fling step and pulse properties(Chopra and Chintanapakdee 2001). Forward directivity and fling effects have been identified by seismologists as the primary characteristics of near-fault ground motions (Mavroeidis and Papageorgiou 2003). Fault-normal components of ground motions often contain large displacement and velocity pulses, which expose the structure to high input energy in the beginning of the earthquake. The pulses are strongly influenced by the rupture mechanism, the slip direction relative to the site and the location of the recording station relative to the fault which is termed as “directivity effect” due to the propagation of the rupture toward the recording site (Bray and Rodriguez-Marekb 2004; Liao et al. 2004). Because of the unique characteristics of near-fault ground motions, the ground motions recorded in the near-fault region have the potential to cause considerable damage to structures. Therefore, structural response to near-fault ground motions has received much attention in recent years. The effects of near-fault ground motions on many civil engineering structures such as buildings and bridges have been investigated in many recent studies (Sehhati et al. 2011; Champion and Liel 2012; Chioccarelli and Iervolino 2012; Ruiz-García and Negrete-Manriquez 2011; Farid Ghahari et al. 2010; Trifunac 2009; Adanur et al. 2012; Jalali et al. 2012; Liu et al. 2012; Mortezaeia et al. 2010; Çavdar 2012; Mazza and Vulcano 2012; Taflanidis 2011; Karalar et al. 2012). It can be clearly seen from these studies that the near-fault ground motion has a significant influence on the nonlinear dynamic response of structures. Structures located within the near-fault region suffered more severe damage than those located in the far-fault zone. The related study is therefore a very important topic for the structural engineering.

It should be noted that available research on nonlinear dynamic response and seismic damage of concrete gravity dams to near-fault strong ground motions is fairly limited. Akköse and Şimşek (2010) studied the seismic response of a concrete gravity dam subjected to near-fault and far-fault ground motions, including dam–water–sediment–foundation rock interaction. They found that the linear and nonlinear seismic response of the selected concrete gravity dam subjected to near-fault ground motions are affected greater than those subjected to far-fault ground motion. Bayraktar and his co-workers (Bayraktar et al. 2008, 2009, 2010) examined the effects of near-fault and far-fault ground motions on the nonlinear response of gravity dams. The results revealed that the earthquake record of the near-fault ground motion has a remarkable effect on the earthquake response of the dams. Zhang and Wang (2013) evaluated the near-fault and far-fault ground motion effects on nonlinear dynamic response and seismic damage of concrete gravity dams, including dam-reservoir-foundation interaction. Although previous studies provided some information on the near-fault ground motions effects on dynamic response of dams, there is no sufficient research about the near-fault ground motion effects on the seismic performance and accumulated damage of concrete gravity dams.

It is known that seismic performance assessment of concrete gravity dams has become significantly important in view of the observed lack of seismic resistance of dams during strong earthquakes. Due to the severe damage effects of impulsive type motions on structures, satisfactory seismic performance of concrete gravity dams located in the near-fault region is necessary because the release of the impounded large quantities of water can cause considerable amount of devastation in the downstream populated areas. The state-of-the-art for evaluating seismic response of concrete gravity dams has progressively moved from elastic static analysis to elastic dynamic, nonlinear static and finally nonlinear dynamic analysis. The traditional seismic performance evaluation method is based on linear theory. It is assumed that the tensile stresses should be less than the dynamic tensile strength of the concrete material. However, in practice, up to five stress excursions above the tensile strength of the concrete material have been considered acceptable based on engineering judgment and other considerations (USACE 2003). To overcome the above shortcomings, a new performance evaluation approach mainly based on the demand-capacity ratio (DCR) and the cumulative overstress duration, was proposed by Ghanaat (2002, 2004). Yamaguchi et al. (2004) used this method to evaluate the seismic performance of concrete gravity dams. Sevim (2011) investigated the effect of material properties on the seismic performance of arch dam-reservoir-foundation interaction systems based on the Lagrangian approach using DCR.

In order to consider the reservoir effect on the behavior of the dam under strong ground motions, three approaches are generally used in the analyses of fluid–structure interaction problems. The simplest one is the added mass approach initially proposed by Westergaard (1933) (with added masses on the dam). Another approach is the Eulerian approach (Maity and Bhattacharyya 2003), in which the displacements are the variables in the structure and the pressures or velocity potentials are the variables in the fluid. Since these variables in the structure and fluid are different in the Eulerian approach, a special-purpose computer program is required for the solution of coupled systems. The third way to represent the fluid-structure interaction is the Lagrangian approach (Wilson and Khalvati 1983; Calayir and Dumanoǧlu 1993), where the displacements are the variables for both the fluid and the structure. For that reason, Lagrangian displacement-based fluid elements can be easily incorporated into a general-purpose computer program for structural analysis, because special interface equations are not required. Dynamic response of fluid–structure systems using the Lagrangian approach has been investigated by many researchers (Bilici et al. 2009; Calayir and Karaton 2005a; Zhang and Wang 2013).

The main objective of the present study is to investigate the near-fault and far-fault ground motion effects on seismic performance of concrete gravity dams with considering the influence of dam-reservoir-foundation interaction. For this purpose, an approach based on the stress DCR, the cumulative overstress duration and the spatial extent of overstressed regions is selected for the seismic performance evaluation of concrete gravity dams by using linear analysis results. Nonlinear analysis of dams is performed by using the concrete damage plasticity (CDP) model, which includes the strain hardening or softening behavior. Koyna gravity dam is employed as a numerical application. The 1979 Imperial Valley, 1989 Loma Prieta, 1994 Northridge and 1999 Kobe earthquake records that display ground motions with an apparent velocity pulse are selected to represent the near-fault ground motion characteristics. The earthquake ground motions recorded at the same site from other events that the epicenter far away from the site serve as the far-fault ground motions, which are used to compare with near-fault ground motions. Lagrangian approach is used for the finite element modeling of the dam-reservoir-foundation interaction problem. Nonlinear seismic damage analyses of the selected concrete dam subjected to both near-fault and far-fault ground motions are performed. The influence of near-fault ground motions on seismic performance of concrete gravity dams is discussed.

2 Seismic performance evaluation methods

A systematic and rational methodology for seismic performance assessment and qualitative damage estimation using standard results from linear time-history analysis is presented. The performance evaluation and assessment of the probable level of damage are formulated based on the DCR for stresses, the cumulative duration of stress excursions beyond the tensile strength of the concrete and the spatial extent of overstressed regions. This evaluation is applied to the damage control range of strains shown in Fig. 1.

Fig. 1
figure 1

Illustration of seismic performance and damage criteria (Ghanaat 2004)

Full size image

2.1 Demand-capacity ratio

The DCR for concrete gravity dams is defined as the ratio of the calculated maximum principal stress to tensile strength of the concrete. The tensile strength of the plain concrete used in this definition is the static tensile strength characterized by the uni-axial splitting tension tests or from

$$f_{t} = 1.7f_{c}^{{{\prime }2/3}}$$
(1)

proposed by Raphael (1984), where \(f_{c}^{{\prime }}\) is the compressive strength of the concrete. The maximum permitted DCR for the linear analysis of dams is two. This corresponds to a stress demand twice the static tensile strength of the concrete. As illustrated in the stress–strain curve in Fig. 1c, the stress demand associated with a DCR of two corresponds to the so-called “apparent dynamic” tensile strength of the concrete, a quantity proposed by Raphael for evaluation of the results of linear dynamic analysis.

2.2 Cumulative inelastic duration

The cumulative inelastic duration of stress excursions is defined as the total duration of the stress excursions above a stress level associated with a DCR ≥ 1. The higher the cumulative duration, the higher is the possibilities for more damage. The sinusoidal stress history with five stress cycles is shown in Fig. 1a. The sinusoidal cycle duration of the stress excursion above the tensile strength is equal to T/3, where T is the period of the sinusoid. The total inelastic duration for all five stress excursions (shaded area) amounts to 5T/3. Considering that the period of the signal is 0.24 s, and the cumulative inelastic duration of stress excursions is 0.4 s. The cumulative duration for a DCR of two is assumed zero. For gravity dams, a lower cumulative duration of 0.3 s (in Fig. 2) is assumed, mainly because gravity dams resist loads by cantilever mechanism only, as opposed to arch dams that rely on both the arch and cantilever actions.

Fig. 2
figure 2

Seismic performance threshold curves for concrete gravity dams (Ghanaat 2004)

Full size image

2.3 Performance criteria for concrete gravity dams

The seismic performance and probable level of damage of concrete gravity dams are evaluated on the basis of the DCR, the cumulative inelastic duration and the spatial extent of overstressed regions described above. Three performance levels are considered (Ghanaat 2004):

  1. 1.

    Minor or no damage: The dam response is assumed to be elastic if the DCR ≤ 1. The dam is considered to behave in the elastic range with little or no possibility of damage.

  2. 2.

    Acceptable level of damage: If the estimated DCR > 1, the dam will exhibit nonlinear response in the form of cracking and joint opening. If the estimated DCR < 2, the overstressed regions are limited to 15 % of the dam cross-section surface area, the cumulative duration of stress excursion also falls below the performance curve given in Fig. 2, and the level of nonlinear response or cracking can be considered acceptable with no possibility of failure.

  3. 3.

    Severe damage: The damage is considered as severe if the DCR > 2 or the cumulative overstress duration for all DCR values between 1 and 2 falls above the performance curves as shown in Fig. 2. In these situations, nonlinear time-history analysis may be required to further investigate the performance of the dam.

3 Concrete damaged plasticity (CDP) model

In order to describe the complex mechanical behavior of concrete material under earthquake conditions, a number of constitutive models have been developed, including the isotropic damage models (Lubliner et al. 1989; Lee and Fenves 1998), the anisotropic damage models (Dragon and Mróz 1979; Murakami and Ohno 1981) and the damage models (Cervera et al. 1995, 1996; Yazdchi et al. 1999; Hatzigeorgiou et al. 2001) for concrete gravity dams under seismic loads. In this section, a basic constitutive model developed by Lubliner et al. (1989) and modified by Lee and Fenves (1998) is presented. The model describing the nonlinear behavior of each compounding substance of a multiphase composite material is commonly used for seismic cracking analysis of concrete dams. In this model, the uniaxial strength functions are factorized into two parts to represent the permanent (plastic) deformation and degradation of stiffness (degradation damage).

3.1 Damage evolution

In the incremental theory of plasticity, the total strain tensor, ε, is decomposed into the elastic part, ε e, and the plastic part, ε p, which for linear elasticity is given by

$$\varepsilon = \varepsilon^{\text{e}} + \varepsilon^{\text{p}}$$
(2)

The state of the local nonlinear problem with variables {ε e, ε p, κ} is assumed to be known at time t. With this information, the stress tensor is given by

$$\sigma = (1 - d)\bar{\sigma } = (1 - d){\mathbf{E}}_{0} (\varepsilon - \varepsilon^{\text{p}} )\quad {\text{and }}\,d{ = }d (\kappa )$$
(3)

where E 0 is the initial (undamaged) elastic stiffness of the material; d is the scalar stiffness degradation variable, which can take values in the range from 0 (undamaged material) to 1 (fully damaged material). The damage associated with the failure mechanisms of the concrete (cracking and crushing) therefore results in a reduction in the elastic stiffness, which is assumed to be a function of a set of the internal variable κ consisting of tensile and compressive damage variables, i.e., κ = {κ t, κ c}. Damage functions in tension d t and in compression d c are nonlinear functions calculated by comparison of the uniaxial response with experimental data. Following the usual notions of continuum damage mechanics, the effective stress \(\bar{\sigma }\) is defined as

$$\bar{\sigma } = \frac{\sigma }{1 - d} = {\mathbf{E}}_{0} (\varepsilon - \varepsilon^{\text{p}} )$$
(4)

Similarly, the first effective stress invariant \(\bar{I}_{1}\) and the second effective deviatoric stress invariant \(\bar{J}_{2}\) are defined in terms of the effective stress tensor.

$$\bar{I}_{1} = \bar{\sigma }_{ii}$$
(5)
$$\bar{J}_{2} = \frac{1}{2}\bar{S}_{ij} \bar{S}_{ij}$$
(6)

where \(\bar{S}_{ij}\) is the effective deviatoric stress tensor.

3.2 Yield criterion

The yield function proposed by Lubliner et al. (1989) and modified by Lee and Fenves (1998) is adopted. The concrete damaged plasticity model uses the yield condition to account for different evolution of strength under tension and compression. In terms of effective stresses, the yield function takes the following form.

$$F = \frac{1}{1 - \alpha }\left( {\bar{q} - 3\alpha \bar{p} + \beta (\tilde{\varepsilon }^{p} )\left\langle {\hat{\bar{\sigma }}_{\hbox{max} } } \right\rangle - \gamma \left\langle { - \hat{\bar{\sigma }}_{\hbox{max} } } \right\rangle } \right) - \bar{\sigma }_{c} (\tilde{\varepsilon }_{c}^{p} ) \le 0$$
(7)

With

$$\alpha = \frac{{{{\sigma_{b 0} } \mathord{\left/ {\vphantom {{\sigma_{b 0} } {\sigma_{c0} - 1}}} \right. \kern-0pt} {\sigma_{c0} - 1}}}}{{{{2\sigma_{b0} } \mathord{\left/ {\vphantom {{2\sigma_{b0} } {\sigma_{c0} - 1}}} \right. \kern-0pt} {\sigma_{c0} - 1}}}};\;\;\;0 \le \alpha \le 0.5$$
(8)
$$\beta = \frac{{\bar{\sigma }_{c} (\tilde{\varepsilon }_{c}^{p} )}}{{\bar{\sigma }_{t} (\tilde{\varepsilon }_{t}^{p} )}}(1 - \alpha ) - (1 + \alpha )$$
(9)
$$\gamma = \frac{{3(1 - K_{c} )}}{{2K_{c} - 1}}$$
(10)
$$\bar{p} = - \frac{{\bar{\sigma }}}{3} :{\mathbf{I}}$$
(11)
$$\bar{q} = \sqrt {\frac{ 3}{2}{\bar{\mathbf{S}}} :{\bar{\mathbf{S}}}}$$
(12)

where α and β are dimensionless material constants, \(\hat{\bar{\sigma }}_{\hbox{max} }\) is the algebraically maximum eigenvalue of \(\bar{\sigma }\), \(\sigma_{b 0}\) is the initial equibiaxial compressive yield stress, \(\sigma_{c 0}\) is the initial compressive yield stress, \(\bar{\sigma }_{c}\) and \(\bar{\sigma }_{t}\) are the effective compressive and tensile cohesion stresses, respectively, \(\tilde{\varepsilon }_{c}^{p}\) and \(\tilde{\varepsilon }_{t}^{p}\) are the equivalent compressive and tensile plastic strains, respectively, K c is the strength ratio of concrete under equal biaxial compression to triaxial compression, \(\bar{p}\) is the effective hydrostatic pressure, \(\bar{q}\) is the Mises equivalent effective stress and \({\bar{\mathbf{S}}}\) is the deviatoric part of the effective stress tensor\(\bar{\sigma }\).

Typical yield surfaces in the deviatoric plane are shown in Figs. 3, 4 shows the initial shape of the yield surface in the principal plane stress space.

Fig. 3
figure 3

Yield surfaces in the deviatoric plane

Full size image
Fig. 4
figure 4

Initial yield function in plane stress space

Full size image

3.3 Flow rule

The plastic strain rate is evaluated by the flow rule, which is defined by a scalar plastic potential function, G. During plasticity, the normality plastic flow rule is applied as

$$\dot{\varepsilon }^{p} = \dot{\lambda }\frac{{\partial G(\bar{\sigma })}}{{\partial \bar{\sigma }}}$$
(13)

where \(\dot{\lambda }\) is a non-negative function referred to as the plastic consistency parameter. A Drucker–Prager hyperbolic function is used as the plastic potential function:

$$G = \sqrt {( \mathrel\backepsilon \sigma_{t0} \tan \psi )^{2} + \bar{q}^{2} } - \bar{p}\tan \psi$$
(14)

where \(\psi\) is the dilation angle measured in the p–q planes at high confining pressure; \(\sigma_{t0}\)is the uniaxial tensile stress at failure; and \(\mathrel\backepsilon\) is a parameter, referred to as the eccentricity, that defines the rate at which the function approaches the asymptote defined by \(\psi\)(the flow potential tends to a straight line as the eccentricity tends to zero). This flow potential, which is continuous and smooth, ensures that the flow direction is defined uniquely. The material parameters in this analysis are shown in Table 1.

Table 1 Material parameters used in the CDP model for concrete
Full size table

4 Lagrangian formulation for dynamic interaction of dam-reservoir-foundation systems

The formulation of the fluid system based on Lagrangian approach is given according to Refs (Wilson and Khalvati 1983; Calayir and Dumanoglu 1993). In this approach, displacements are selected as the variables in both fluid and structure domains. Fluid is assumed to be linearly elastic, inviscid and irrotational. Some details of Lagrangian formulation for dynamic interaction of dam-reservoir-foundation systems can be found in Ref Zhang and Wang (2013).

5 Near-fault and far-fault ground motion records considered in this study

A total of 8 records are selected as the input ground motion from 1979 Imperial Valley, 1989 Loma Prieta, 1994 Northridge and 1995 Kobe earthquakes in the magnitude (M w) range of 6.5–6.9. The assembled database can be investigated in two sub-data sets. The first set, which displays ground motions with an apparent velocity pulse, is selected to represent the near-fault ground motion characteristics. The velocity pulse duration in the near-fault ground motions is larger than 1.0 s. In addition, the ratio of the peak ground velocity (PGV) to the peak ground acceleration (PGA) of the near-fault ground motions is larger than 0.1 s. On the contrary, the second set of four ordinary ground motion records, recorded at the same site condition from the same earthquake events with epicenter far away from the site, is employed to represent the characteristics of far-fault ground motion. Informations pertinent to the ground motion data sets, including closest fault distance, station, component of earthquake and PGA, PGV and the ratio of PGV to PGA, are presented in Tables 2 and 3. The ground motion records are obtained from the databases of the COSMOS (2013) and PEER (2013).

Table 2 Properties of selected near-fault ground motions considered in this investigation
Full size table
Table 3 Properties of selected far-fault ground motions considered in this investigation
Full size table

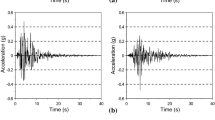
The near-fault and far-fault ground motion records are normalized to have the PGA equal to 0.30 g. In this analysis, only the first 15 s of the earthquake records is considered. Two different levels of PGA are considered for the input motions: 0.20 and 0.30 g. As a typical example, Fig. 5 shows the acceleration, velocity and displacement time histories of the fault-normal component of the near-fault and far-fault ground motions with a PGA of 0.30 g. As shown in Fig. 5, it can be seen from that there is a distinct difference between the velocity pulse of ground motions recorded at near-fault and far-fault regions. The near-fault ground motion possesses significantly long period pulse in the acceleration time history that is consistent with velocity and displacement histories. The long period response of the near-fault ground motion is more excessive than that of the far-fault ground motion. Figure 6 shows the acceleration response spectrum with damping ratio 5 % for selected near-fault and far-fault ground motion records.

Fig. 5
figure 5

Sample of acceleration, velocity and displacement time histories for a near-fault ground motion recorded at Jensen Filtration Plant station and b far-fault ground motion recorded at Warm Springs station in Northridge earthquake

Full size image
Fig. 6
figure 6

Acceleration response spectrum with damping ratio 5 % for selected near-fault and far-fault ground motions

Full size image

6 Seismic performance evaluation of Koyna dam under Koyna earthquake

6.1 Description of model of Koyna gravity dam used for evaluation

Koyna concrete gravity dam in India, 103 m high and 70.2 m wide at its base, is one of a few concrete dams that have experienced a destructive earthquake. The Koyna earthquake of magnitude 6.5 on the Richter scale on December 11, 1967, with maximum acceleration measured at the foundation gallery of 0.49 and 0.34 g in horizontal and vertical direction, has caused very serious structural damage to the dam, including horizontal cracks on the upstream and downstream faces of a number of non-overflow monoliths around the elevation at which the slope of the downstream face changes abruptly (Chopra and Chakrabarti 1973). Leakage was observed in some of these monoliths near the changes in the slope of the downstream face, implying complete penetration from the upstream face to the downstream face.

This problem has been extensively analyzed by a number of investigators (Zhang et al. 2013b, c; Pan et al. 2011; Calayir and Karaton 2005b; Das and Cleary 2013; Omidi et al. 2013). In this paper, the dynamic response analysis of Koyna dam is performed by using the CDP model for the concrete material made in ABAQUS program. The time histories of Koyna earthquake are shown in Fig. 7. The finite element model of the dam-reservoir-foundation interaction system, which consists of 5,553 elements and 5,813 nodes, is given in Fig. 8a, and the dimensions of the dam are given in Fig. 8b. The mesh of the dam is adequately refined at the base and near the changes in the slope of the downstream face, in which crack propagations are expected. The reason is that damage due to tensile stresses is expected to initiate near stress concentrations in those zones.

Fig. 7
figure 7

Koyna earthquake on December 11, 1967. a Horizontal component, b vertical component

Full size image
Fig. 8
figure 8

Finite element discretization for the dam-reservoir-foundation system of Koyna dam: a dam-reservoir-foundation system and b concrete gravity dam

Full size image

The material parameters for Koyna dam concrete are as follows: the elasticity modulus E = 3.1 × 104 MPa, the Poisson’s ratio ν = 0.2, the mass density ρ = 2643 kg/m3, the fracture energy is 250 N/m. The tensile and compressive strength of the dam are 2.9 and 24.1 MPa, respectively. Since the presented research aims at comparing the near-fault and far-fault ground motion effects on the seismic damage of concrete gravity dams, the foundation rock is assumed to be linearly elastic. In order to avoid reflection of the outgoing waves, the foundation rock is assumed to be massless. The elasticity modulus and Poisson’s ratio of the foundation rock are taken as 21.6 GPa and 0.20, respectively. The fluid is assumed to be linearly elastic, inviscid and irrotational. The bulk modulus and mass density of the fluid are taken as 2.07 GPa and 1,000 kg/m3. A dynamic magnification factor of 1.2 is considered for the tensile strength to account for strain rate effects. The energy dissipation of the dam and foundation is considered by the Rayleigh damping method with 5 % damping ratio. The maximum reservoir water level of 96.5 m is considered. Applied loads include self-weight of the dam, hydrostatic, uplift, hydrodynamic and earthquake forces. The static solutions of the dam due to its gravity loads and hydrostatic loads are taken as initial conditions in the dynamic analyses of the system.

6.2 Seismic performance evaluation of Koyna dam

As mentioned, the seismic performance evaluation method based on the DCR and the cumulative overstress duration is used to assess the seismic performance of Koyna gravity dam under the 1967 earthquake. The linear time-history analysis of Koyna dam is performed. The Hilber-Hughes-Taylor time integration is used to calculate the dynamic response. The integration time step used in the analysis is 0.005 s.

The time history of maximum principle tensile stresses at the change in downstream slope is plotted by displaying the DCR in Fig. 9. It can be seen from Fig. 9 that the maximum principal stress peaks in excess of the tensile strength of the concrete (2.9 MPa) are 8 cycles. Some values of the maximum principal stresses are over than DCR = 2 (3 cycles). Using this information, the performance curve shown in Fig. 10 is constructed to illustrate application of the proposed damage criteria to Koyna dam. The results in Fig. 10 show that the stress DCR exceed 2, and the cumulative inelastic duration is substantially greater than the acceptance level. It means that the 1967 Koyna earthquake will cause significant damage on the dam body. Therefore, a nonlinear time-history analysis might be required to estimate the damage more accurately.

Fig. 9
figure 9

Maximum stress history for Koyna dam

Full size image
Fig. 10
figure 10

Performance assessment curve for Koyna dam

Full size image

According to the proposed performance criteria, the Koyna earthquake causes significant nonlinear deformation in Koyna dam. It can be stated that the linear time-history analysis of the dam is insufficient, and nonlinear analysis is required to further investigate the performance of the dam. To validate this aspect of the proposed damage criteria, nonlinear dynamic response analysis of Koyna gravity dam under the 1967 earthquake is conducted employing the CDP model. The seismic response of the dam is investigated by comparison of the linear with non-linear dynamic procedures.

The accumulated damage process of Koyna dam during the Koyna earthquake at four selected times is shown in Fig. 11. The damage of a crack at an element integration point is indicated by shading the related area with red color. As shown, the crack propagation process and failure modes are obtained. It can be seen that a crack initially progressed a long way from the upstream side to the downstream side at the dam heel (Fig. 11a), which may be due to stress concentration. Furthermore, an initial crack in the dam near the discontinuity in the slope of the downstream face is observed at this time and then extends deeper inside of the dam. The initial crack at the downstream face is approximately in a horizontal region (Fig. 11a). At t = 4.21 s, cracks begin to initialize near the middle of the upstream face (Fig. 11b) due to the vibration characteristics. As the dam oscillates during the earthquake, these previously formed cracks at the upstream and downstream faces extend into the dam, penetrating the whole section of the dam (Fig. 11d). This means that the Koyna earthquake causes serious structural damage to Koyna dam. By comparing the current results with the previous research results (Zhang et al. 2013b, c; Pan et al. 2011; Calayir and Karaton 2005b; Das and Cleary 2013; Omidi et al. 2013), it can be noted that the occurring damage profile match reasonably well with the previous researches, the CDP model can predict effectively the cracking profile and the crack propagation process in concrete gravity dams under seismic conditions.

Fig. 11
figure 11

Crack propagation process of Koyna dam at four selected times. a Time A (t = 3.92 s), b Time B (t = 4.21 s), c Time C (t = 4.67 s), d Time D (t = 5.56 s)

Full size image

7 Seismic performance assessment of concrete gravity dams under near-fault ground motions

Due to the unique characteristics of the near-fault ground motions and their potential to cause severe damage to structures, the interest of the near-fault effects on structural response has increased. Earthquake engineers have been considering methods to incorporate near-fault effects in engineering design (Mavroeidis and Papageorgiou 2003). The seismic safety evaluation of high dams subjected to near-fault ground motions remains a crucial problem in dam construction. In this study, a set of selected near-fault and far-fault ground motion records is used to examine the near-fault ground motion effects on seismic performance of concrete gravity dams with considering the influence of dam-reservoir-foundation interaction. Only the horizontal component of the seismic input is considered in this analysis. A 5 % damping ratio has been assumed in all dynamic analyses. The integration time step used in the time-history analysis is 0.005 s.

7.1 Seismic performance evaluation

The seismic performance of Koyna dam is firstly evaluated by using the linear time-history analysis results for both near-fault and far-fault ground motions scaled to 0.20 and 0.30 g. The response of the dam has been determined in terms of the response parameters such as the DCR, the cumulative overstress duration and overstressed areas.

The maximum principle tensile stress histories at the change in downstream slope for both near-fault and far-fault earthquake records with a PGA level of 0.20 g are plotted by displaying the DCR in Figs. 12, 13, 14 present the corresponding performance evaluation curves for both near-fault and far-fault earthquakes at the 0.20 g level. Figure 15 shows the overstressed regions of the dam in terms of the DCR values for near-fault ground motions scaled to 0.20 g. The shaded areas indicated that the concrete material regions where the computed DCR values exceeded 1.0. It is clear from Figs. 12 and 14a that the dam subjected to far-fault ground motions with a PGA level of 0.20 g is considered to behave in the elastic range with little or no possibility of damage, because the maximum principle tensile stresses are almost less than the tensile strength of the concrete material (2.9 MPa).

Fig. 12
figure 12

Time histories of maximum principal tensile stresses for far-fault ground motions with a PGA level of 0.20 g

Full size image
Fig. 13
figure 13

Time histories of maximum principal tensile stresses for near-fault ground motions with a PGA level of 0.20 g

Full size image
Fig. 14
figure 14

Performance assessment curves for Koyna dam subjected to near-fault and far-fault earthquakes with a PGA level of 0.20 g

Full size image
Fig. 15
figure 15

Overstressed regions for Koyna dam under near-fault ground motions with a PGA level of 0.20 g

Full size image

It can be seen from Fig. 13 that the maximum principal stress peaks in excess of the tensile strength of the concrete material vary from 4 to 7 cycles for different near-fault earthquake records with a PGA level of 0.20 g. Figure 14b shows that the cumulative overstress duration for DCR = 1 is higher than 0.3 s for all cases, but most of the resulting cumulative duration curves are located within the zone of acceptable performance, and the areas of overstressed regions associated with DCR > 1 represent only 2.5, 2.0, 5.5, and 1.2 % of the total section area (Fig. 15). It is therefore concluded that the actual seismic performance of the dam subjected to near-fault ground motions at the 0.20 g level is likely to exhibit some tensile cracking but the global consequences of the resulting damage are expected to be minor. The damage is considered as acceptable level. Based on these results, it can be concluded that the results from the linear time-history analysis still provide sufficient information to characterize the response of the dam for both near-fault and far-fault ground motions with a PGA level of 0.20 g.

Figures 16 and 17 display the maximum principle tensile stress histories for both near-fault and far-fault earthquake records with a PGA level of 0.30 g. The corresponding performance evaluation curves are shown in Fig. 18. The overstressed regions computed using the linear time-history analyses in terms of the DCR values for near-fault ground motions scaled to 0.30 g are shown in Figs. 19 and 20. The shaded areas indicated that the concrete material regions where the computed DCR values exceeded 1.0.

Fig. 16
figure 16

Time histories of maximum principal tensile stresses for far-fault ground motions with a PGA level of 0.30 g

Full size image
Fig. 17
figure 17

Time histories of maximum principal tensile stresses for near-fault ground motions with a PGA level of 0.30 g

Full size image
Fig. 18
figure 18

Performance assessment curves for Koyna dam subjected to near-fault and far-fault earthquakes with a PGA level of 0.30 g

Full size image
Fig. 19
figure 19

Overstressed regions for Koyna dam under far-fault ground motions with a PGA level of 0.30 g

Full size image
Fig. 20
figure 20

Overstressed regions for Koyna dam under near-fault ground motions with a PGA level of 0.30 g

Full size image

It can be seen from Figs. 16, 18a and 19 that the dam subjected to far-fault earthquake records with a PGA level of 0.30 g suffers an acceptable level damage with no possibility of failure as the estimated DCR < 2, most of the resulting cumulative duration curves are located within the zone of acceptable performance, and the overstressed regions associated with DCR > 1 are <15 % of the total section area. Therefore, some tensile cracking damage around the neck of the dam is expected but it will not drastically affect the resulting dynamic behavior.

It is clear from Fig. 17 that the maximum principal stress peaks in excess of the tensile strength of the concrete material vary from 7 to 13 cycles for different near-fault earthquake records with a PGA level of 0.30 g. Some values of the maximum principal stress are over than DCR = 2 (3–5 cycles) for all near-fault earthquakes. Results in Fig. 18b show that the stress DCR exceed 2 and the cumulative inelastic duration are substantially greater than the acceptance level. It means that the near-fault ground motions with a PGA level of 0.30 g will cause a considerable damage on the dam body as the performance curve is above the acceptance curve. Therefore, it can be stated that the linear time-history analysis of the dam is insufficient, and the nonlinear time-history analysis is required to estimate the performance more accurately.

Based on these results, it can be concluded that there are more seismic performance demands for the dam subjected to near-fault ground motions. The nonlinear analysis is required for near-fault ground motions at the 0.30 g level to further assess the dam damage.

7.2 Nonlinear dynamic response and seismic damage analysis

According to the proposed performance criteria, the results corresponding to the 0.30 g PGA level clearly indicated significant nonlinear deformation should be expected for near-fault ground motions. The nonlinear analysis must be carried out for seismic performance assessment of the dam. To validate this aspect of the proposed damage criteria, nonlinear dynamic damage analyses of the selected concrete dam under near-fault ground motions are conducted employing the CDP model with the strain hardening or softening behavior. In order to study the influence of near-fault ground motions on the seismic performance of concrete gravity dams, nonlinear seismic analyses of concrete gravity dams subjected to far-fault ground motions are also performed.

The seismic damage profiles of Koyna gravity dam during the real near-fault and far-fault ground motions with a PGA of 0.3 g are shown in Figs. 21 and 22, respectively. The shaded areas related with red color indicate those elements that experienced some level of tensile damage. The figures depict the damage predicted for real ground motions considered in this study. From the cracking profiles shown in Figs. 21 and 22, it can be observed that the failure mechanism is formed of two main damage zones one at the base and one in the upper parts of the dam (downstream face or upstream face). Two damage zones are clearly identified, and they correspond to the areas associated with the maximum tensile demands predicted by the previous linear analyses. It can be also seen from Figs. 21 and 22 that as-recorded near-fault ground motions have significant influence on the seismic damage of concrete gravity dams. For the far-fault ground motions associated with a PGA level of 0.30 g, some moderate damage is identified (Fig. 22) but it does not seem to reach a level that could compromise the integrity of the section. On the other hand, the results corresponding to the input near-fault ground motions associated with a PGA level of 0.30 g clearly show indications of significant strength degradation in the dam, with a cracking pattern that completely extends across the upper section.

Fig. 21
figure 21

Cracking profiles for Koyna dam under near-fault ground motions with a PGA level of 0.30 g

Full size image
Fig. 22
figure 22

Cracking profiles for Koyna dam under far-fault ground motions with a PGA level of 0.30 g

Full size image

Figure 23 shows the time histories of horizontal displacements at the dam crest obtained from nonlinear analyses for both near-fault and far-fault ground motions, with positive displacement in the downstream direction. It is clear from Fig. 23 that the non-linear response obtained from near-fault ground motions has a substantially different displacement history than that obtained from far-fault ground motions. The crest horizontal displacement values for near-fault ground motions are greater than those for far-fault ground motions although the peak ground acceleration of near-fault and far-fault records are the same.

Fig. 23
figure 23

Time histories of horizontal displacements at the crest of the dam subjected to near-fault and far-fault ground motions from the (a) Northridge, (b) Imperial Valley, (c) Loma Prieta and (d) Kobe earthquakes. For ground motion information see Tables 2 and 3.

Full size image

Comparison of the dam crest horizontal displacement histories from the nonlinear analyses of the concrete gravity dam subjected to near-fault and far-fault ground motions indicates that a remarkable upstream deviation appears in the dam response under some near-fault ground motion cases, and there is a little, if any, residual deformation of the dam under far-fault ground motions compared with the initial displacement when imposing the seismic load. The maximum residual displacement of about 1.98 cm occurs under the near-fault ground motion recorded at Corralitos, CA #57007 station in Loma Prieta earthquake, with respect to the equivalent deformation caused by the static loads. It is also seen from Fig. 23 that plastic deformations in the dam subjected to near-fault ground motions are larger than those subjected to far-fault ground motions.

8 Conclusions

The study summarized in this paper is intended to evaluate the seismic performance of dam-reservoir-foundation systems subjected to near-fault earthquakes. For that purpose, a systematic approach for seismic performance evaluation and assessment of the probable level of damage using standard results from linear time-history analyses are presented. The performance evaluation method is proposed based on the DCR, the cumulative overstress duration and the spatial extent of overstressed regions. A total of eight records for both near-fault and far-fault ground motions are selected as the input ground motion from 1979 Imperial Valley, 1989 Loma Prieta, 1994 Northridge and 1995 Kobe earthquakes. Koyna gravity dam is chosen for analyses. The reservoir water is modeled using two-dimensional fluid finite elements by the Lagrangian approach. Nonlinear seismic analyses of concrete gravity dams under earthquake conditions are performed according to the CDP model including the strain hardening or softening behavior.

The performance evaluation of Koyna dam shows that the 1967 Koyna earthquake will cause significant damage on the dam body as the performance curve is above the acceptance curve. The results from the nonlinear time-history analysis also show that the Koyna earthquake causes a severe damage on the dam body, with a cracking pattern that completely extends across the upper section.

The selected near-fault and far-fault ground motions at the 0.20 g level cause an acceptable level damage on the dam. The damages are considered as moderate damage and little or no possibility of damage, respectively. It can be concluded that the results from the linear time-history analysis still provide sufficient information to characterize the response of the dam for both near-fault and far-fault ground motions with a PGA level of 0.20 g. The seismic performance of the dam subjected to far-fault ground motions at the 0.30 g level is likely to exhibit some tensile cracking but the global consequences of the resulting damage are expected to be minor. But the near-fault ground motions with a PGA level of 0.30 g will cause a considerable damage on the dam body. It can be concluded that there are more seismic performance demands for the dam subjected to near-fault ground motions. The nonlinear analysis is required for near-fault ground motions at the 0.30 g level to further assess the dam damage.

The performed seismic damage analyses show that accumulated damage of dams under consideration is found to be significantly affected by near-fault ground motion. The crest horizontal displacement values for near-fault ground motions are greater than those for far-fault ground motions. A remarkable upstream deviation appears in the dam response under some near-fault ground motion cases. Near-fault ground motions have the potential to cause more seismic performance demands in concrete gravity dams due to their impulsive effects. Therefore, the effects of near-fault ground motions on seismic performance of concrete gravity dams should be taken into account to obtain more realistic results.