1 Introduction

Liquefaction of saturated granular soil induced by earthquakes is a major concern because of the potential severity of damage to civil engineering structures (Goh and Goh 2007). Therefore, the precise determination of liquefaction potential of soils is primary component of the geotechnical site investigation (Kayadelen 2011). Over the past 30 years, various researchers have been performed the studies to develop the relationship between liquefaction resistance and seismic parameter of soils (Goh 1995; Boulanger et al. 1997; Juang et al. 2003; Robertson and Wride 1998; Seed et al. 1983; Liao et al. 1988; Law et al. 1990; Seed and Idriss 1971). Among them, standard penetration tests (SPT), cone penetration tests (CPT), flat dilatometer tests (DMT), the shear wave velocity technique (SWV) and self-boring pressure meter (SBPT) are the most commonly used in situ tests for liquefaction potential prediction. In addition, several alternative computer-aided pattern recognition approaches have emerged with the pervasive developments in computational software and hardware. Among them, artificial neural networks (ANNs) are the most widely used pattern recognition procedures that have been introduced for determination of liquefaction occurrence based on both SPT and CPT field data (e.g., Cetin et al. 2004; Hanna et al. 2007; Hashash 2007; Kayadelen 2011; Mohammad et al. 2010; Oommen and Baise 2010; Pal 2006; Samui et al. 2008; Shuh et al. 2008; Thomas et al. 2010). These black-box models have the ability to operate on large quantities of data and learn complex model functions from examples, i.e., by training on sets of input and output data. The greatest advantage of ANNs over traditional modeling techniques is their ability to capture nonlinear and complex interaction between variables of the system without having to assume the form of the relationship between input and output variables. In the context of determination of liquefaction occurrence, ANNs can be trained to learn the relationship between the soil and earthquake characteristics with the liquefaction potential, requiring no prior knowledge of the form of the relationship. However, at the same time, the main disadvantages of the ANNs approach is the large complexity of the network structure, as it represents the knowledge in terms of a weight matrix together with biases which are not accessible to user (Xue and Yang 2013). These methods, more importantly, consider all soil parameters to be deterministic, i.e., having fixed values. In actual fact, there also exists a form of uncertainty of non-statistical nature, i.e., vagueness, associated with these as well as other variables. The effects of these fuzzy variables are usually defined in linguistic terms, often reflecting the subjective judgment of experts. Fuzzy systems are used to handle uncertainty from the data that cannot be handled by classical methods. It uses the fuzzy set to represent a suitable mathematical tool for modeling of imprecision and vagueness. The pattern classification of fuzzy classifiers provides a means to extract fuzzy rules for information mining that leads to comprehensible method for knowledge extraction from various information sources. Therefore, this form of uncertainty can be handled in a rational framework of fuzzy set theory.

Fuzzy comprehensive evaluation method is a synthetical assessment method that applies fuzzy mathematical principles to evaluate things and phenomenon affected by variety of factors. It regards evaluation objectives as a fuzzy set (named the factor set) composed of variety of factors with different assessment levels selected. Another fuzzy set named the evaluation set is employed to calculate the membership degree of each individual factor in the evaluation set to establish a fuzzy matrix. The quantitative evaluation value of each factor is finally determined by calculating the weight distribution of each factor in evaluation goal. It applies the fuzzy transformation theory and maximum membership degree law and makes a comprehensive evaluation to various factors. This study investigates the feasibility of using fuzzy comprehensive evaluation model for predicting soil liquefaction during earthquake. In the fuzzy comprehensive evaluation model of soil liquefaction, the following factors, such as earthquake intensity, standard penetration number, mean diameter and groundwater table, are selected as the evaluating indices. In order to demonstrate the rationality and effectiveness of the fuzzy comprehensive evaluation model, this technique is applied to 23 practical examples. The results show that the fuzzy comprehensive evaluation model of soil liquefaction is feasible and valuable.

2 Brief review of soil liquefaction

In common usage, liquefaction refers to the loss of strength in saturated, cohesionless soils due to the buildup of pore pressures during dynamic loading. A more precise definition of soil liquefaction is given as follows (Sladen et al. 1985): “Liquefaction is a phenomenon wherein a mass of soil loses a large percentage of its shear resistance, when subjected to monotonic, cyclic or shock loading and flows in a manner resembling a liquid until the shear stresses acting on the mass are as low as the reduced shear resistance.” In a more general manner, soil liquefaction has been defined as the transformation “from a solid state to a liquefied state as a consequence of increased pore pressure and reduced effective stress.”

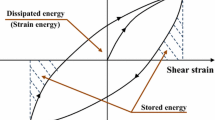
Liquefaction results from the tendency of soils to decrease in volume when subjected to shearing stresses. When loose, saturated soils are sheared, the soil grains tend to rearrange into a more dense packing, with less space in the voids, as water in the pore spaces is forced out. If drainage of pore water is impeded, pore water pressure increases progressively with the shear load. This leads to the transfer of stress from the soil skeleton to the pore water precipitating a decrease in effective stress and shear resistance of the soil. If the shear resistance of the soil becomes less than the static, driving shear stress, the soil can undergo large deformations and is said to liquefy (Fig. 1). By the narrowest definition (Castro 1987), true liquefaction refers only to the flow of soil under a static shear stress that exceeds the undrained, residual shear resistance of a contractive soil. Liquefaction of loose, cohesionless soils can be observed under both monotonic and cyclic shear loads (Xue and Yang 2013).

Fig. 1
figure 1

Schematic of saturated sand liquefaction process (Xue and Yang 2013). a Before earthquake, b during liquefaction, c after eqrthquake

Full size image

3 Basic theory of fuzzy comprehensive evaluation

Fuzzy comprehensive evaluation refers to the decision-making or comprehensive evaluation of an object or phenomenon, which is affected by multiple factors. It is easy to conduct an evaluation or decision of a certain object or phenomenon if only a single factor is taken into consideration. However, in fact, multiple factors should be considered and identified in the evaluation process. As it is difficult to make a decision by applying an ordinary mathematic method, fuzzy comprehensive evaluation of fuzzy mathematics is able to handle the issues of making decisions or evaluations with multiple factors. It is an evaluation method based on existing evaluation standards and fuzzy conversion of the actual measured data or estimated data. Compared to other methods, it is a comprehensive, objective and integrated method for results evaluation. Specific steps are as follows:

  1. 1.

    Determine the factors set of the evaluated object: factors sets are composed of the elements of various factors that can affect the evaluated object, and are denoted by U, that is

    $$ U = \left\{ {U_{1} ,U_{2} , \ldots ,U_{m} } \right\} $$
    (1)

    Each element U i denotes the corresponding influencing factor. These factors usually have certain degree of fuzziness.

  2. 2.

    Determine the evaluation set: evaluation sets are composed of the elements of various comprehensive evaluation results of the evaluated object, as set by the evaluators. It is denoted by V, that is

    $$ V = \left\{ {V_{1} ,V_{2} , \ldots ,V_{n} } \right\} $$
    (2)

    Each element denotes the corresponding possible comprehensive evaluation result.

  3. 3.

    Construct single-factor evaluation matrix: evaluate single factor and then get vector R i . A single-factor evaluation matrix R is constituted by numbers of single-factor evaluation vector put together. There are some commonly used membership degree calculation function of single factor, such as “linearity lower semi-ladder-shaped” distribution function and so on.

    $$ R = \left[ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \vdots \\ {R_{m} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {r_{11} } & {r_{12} } & \cdots & {r_{1n} } \\ {r_{21} } & {r_{22} } & \cdots & {r_{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {r_{m1} } & {r_{m2} } & \cdots & {r_{mn} } \\ \end{array} } \right] $$
    (3)

    In Eq. (3), R is a fuzzy relationship matrix composed of evaluation factor set U and the evaluation set V.

  4. 4.

    Determine evaluation factors weight vector \( w = \{ w_{1} ,w_{2} , \ldots ,w_{m} \} \). To fuzzy comprehensive evaluation model, how to select an appropriate weight calculation method for your research fields for the model has been one of the difficulties (Ma et al. 2010). Commonly used weighting methods are over standard weighting method (Ma et al. 2009), biasing weighting method (Ben et al. 2006), analytic hierarchy process (AHP) (Liu et al. 2009), and so on. Among them, over standard weighting method is commonly used in articles about all kinds of fuzzy comprehensive evaluation, which is calculated as follows:

    $$ w_{i} = \frac{{x_{i} }}{{a_{i} }} $$
    (4)

    In Eq. (4), x i is the practice measure value of the i factor in distinguishing samples and a i states the statistical average value of the i factor in distinguishing standard. As the weight of fuzzy comprehensive evaluation method, it needs normalize, that is:

    $$ w_{i} = (x_{i} /a_{i} )/\sum\limits_{i = 1}^{m} {(x_{i} /a_{i} )} $$
    (5)
  5. 5.

    Comprehensive evaluation: the last results of comprehensive evaluation can be got by doing complex operations calculation between single factor weight vector w and fuzzy relationship matrix R, that is:

    $$ B = w \cdot R = \left\{ {b_{1} ,b_{2} , \ldots ,b_{m} } \right\}. $$
    (6)

In Eq. (6), b i is the membership degree value of evaluation samples to each evaluation standard. The determination results are usually defined according to the maximum membership degree law.

4 Case study

4.1 Studied samples

The susceptibility of soil deposits to liquefaction is determined by a combination of various factors to which they may be subjected, such as soil properties, geological conditions and ground motion characteristics. Therefore, it is widely recognized that the determination of liquefaction potential is a complex geotechnical engineering problem and has attracted considerable attention of geotechnical researchers in the past three decades. Note that soil properties and geological conditions determine the resistance of the deposit to liquefaction, while earthquake characteristics control the seismic loading conditions. Among the factors listed herein, the three most important ones are the following: (1) the ground is loose sandy deposit; (2) the ground water table is high and the ground is saturated; and (3) the earthquake intensity is sufficiently large and the duration of shaking is sufficiently long. Rather than employing complex calculation methods, this study obtained data related to the factors that influence liquefaction potential from the direct measurements of field experiments and observational instruments. The purpose was to simplify the assessment model and computational procedures. After referring to previous studies, the following factors, such as earthquake intensity M, standard penetration number N 63.5, mean diameter d 50 and groundwater table d w, are selected as the evaluating indices. The database used in this study is from the 1975 Haicheng earthquake and the 1976 Tangshan earthquake (Ren 2002). A few of the original records were omitted because of incomplete data, as shown in Table 1.

Table 1 Studied samples
Full size table

4.2 Derivation of membership functions of indices

The membership function of a fuzzy set is a generalization of the indicator function in classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy truth represents membership in vaguely defined sets, not likelihood of some event or condition. There are many forms of membership functions. The most commonly used form of membership function includes: normal type, partial large-scale, partial small, triangular fuzzy numbers, lower semi-trapezoidal, trapezoidal and ridge et al. A good choice of membership functions and aggregation operators is crucial to the behavior of fuzzy systems. However, in many cases, there are no theoretical criteria that would justify the use of one or another function, and they are selected based on their goodness of fit to empirical data. The choice of these membership functions is a problem by itself and will not be discussed here. Based on the distribution characteristic of input data, this study selected a trapezoidal membership function for the fuzzy system.

According to Ref. (Ministry of Construction of the People’s Republic of China 2002), soil liquefaction consequences can be classified as four classes, which are expressed as V = {no liquefaction, mild liquefaction, medium liquefaction, serious liquefaction} = {V 1, V 2, V 3, V 4}. Therefore, the membership functions of indices are derived as follows:

For earthquake intensity M:

$$ U_{\text{I}} (x) = \left\{ {\begin{array}{*{20}c} 1 \hfill & {x \le 6.5} \hfill \\ {7.5 - x} \hfill & {6.5 < x \le 7.5} \hfill \\ 0 \hfill & {x > 7.5} \hfill \\ \end{array} } \right. $$
(7)
$$ U_{\text{II}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 6.5} \hfill \\ {x - 6.5} \hfill & {6.5 < x \le 7.5} \hfill \\ 1 \hfill & {7.5 < x \le 7.9} \hfill \\ {\frac{8.1 - x}{8.1 - 7.9}} \hfill & {7.9 < x \le 8.1} \hfill \\ 0 \hfill & {x > 8.1} \hfill \\ \end{array} } \right. $$
(8)
$$ U_{\text{III}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 7.9} \hfill \\ {\frac{x - 7.9}{8.1 - 7.9}} \hfill & {7.9 < x \le 8.1} \hfill \\ 1 \hfill & {8.1 < x \le 8.6} \hfill \\ {\frac{9.3 - x}{9.3 - 8.6}} \hfill & {8.6 < x \le 9.3} \hfill \\ 1 \hfill & {x > 9.3} \hfill \\ \end{array} } \right. $$
(9)
$$ U_{\text{IV}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 8.6} \hfill \\ {\frac{x - 8.6}{9.3 - 8.6}} \hfill & {8.6 < x \le 9.3} \hfill \\ 1 \hfill & {x > 9.3} \hfill \\ \end{array} } \right. $$
(10)

For standard penetration number N 63.5:

$$ U_{\text{I}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 9} \hfill \\ {\frac{x - 9}{11 - 9}} \hfill & {9 < x \le 11} \hfill \\ 1 \hfill & {x > 11} \hfill \\ \end{array} } \right. $$
(11)
$$ U_{\text{II}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 6.5} \hfill \\ {\frac{x - 6.5}{7.5 - 6.5}} \hfill & {6.5 < x \le 7.5} \hfill \\ 1 \hfill & {7.5 < x \le 7.9} \hfill \\ {\frac{11 - x}{11 - 9}} \hfill & {9 < x \le 11} \hfill \\ 0 \hfill & {x > 11} \hfill \\ \end{array} } \right. $$
(12)
$$ U_{\text{III}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 1} \hfill \\ {\frac{x - 1}{3 - 1}} \hfill & {1 < x \le 3} \hfill \\ 1 \hfill & {3 < x \le 6.5} \hfill \\ {\frac{7.5 - x}{7.5 - 6.5}} \hfill & {6.5 < x \le 7.5} \hfill \\ 0 \hfill & {x > 7.5} \hfill \\ \end{array} } \right. $$
(13)
$$ U_{\text{IV}} (x) = \left\{ {\begin{array}{*{20}c} 1 \hfill & {0 < x \le 1} \hfill \\ {\frac{x - 1}{3 - 1}} \hfill & {1 < x \le 3} \hfill \\ 0 \hfill & {x > 3} \hfill \\ \end{array} } \right. $$
(14)

For groundwater table d w:

$$ U_{\text{I}} (x) = \left\{ {\begin{array}{*{20}c} 1 \hfill & {0 < x \le 0.2} \hfill \\ {\frac{0.25 - x}{0.25 - 0.2}} \hfill & {0.2 < x \le 0.25} \hfill \\ 0 \hfill & {x > 0.25} \hfill \\ \end{array} } \right. $$
(15)
$$ U_{\text{II}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 0.2} \hfill \\ {\frac{x - 0.2}{0.25 - 0.2}} \hfill & {0.2 < x \le 0.25} \hfill \\ 1 \hfill & {0.25 < x \le 0.65} \hfill \\ {\frac{0.75 - x}{0.75 - 0.65}} \hfill & {0.65 < x \le 0.75} \hfill \\ 0 \hfill & {x > 0.75} \hfill \\ \end{array} } \right. $$
(16)
$$ U_{\text{III}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 0.65} \hfill \\ {\frac{x - 0.65}{0.75 - 0.65}} \hfill & {0.65 < x \le 0.75} \hfill \\ 1 \hfill & {0.75 < x \le 1.4} \hfill \\ {\frac{1.6 - x}{1.6 - 1.4}} \hfill & {1.4 < x \le 1.6} \hfill \\ 0 \hfill & {x > 1.6} \hfill \\ \end{array} } \right. $$
(17)
$$ U_{\text{IV}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 1.4} \hfill \\ {\frac{x - 1.4}{1.6 - 1.4}} \hfill & {1.4 < x \le 1.6} \hfill \\ 1 \hfill & {x > 1.6} \hfill \\ \end{array} } \right. $$
(18)

For mean diameter d 50:

$$ U_{\text{I}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 0.25} \hfill \\ {\frac{0.31 - x}{0.31 - 0.25}} \hfill & {0.25 < x \le 0.31} \hfill \\ 1 \hfill & {x > 0.31} \hfill \\ \end{array} } \right. $$
(19)
$$ U_{\text{II}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 0.18} \hfill \\ {\frac{x - 0.18}{0.22 - 0.18}} \hfill & {0.18 < x \le 0.22} \hfill \\ 1 \hfill & {0.22 < x \le 0.25} \hfill \\ {\frac{0.31 - x}{0.31 - 0.25}} \hfill & {0.25 < x \le 0.31} \hfill \\ 0 \hfill & {x > 0.31} \hfill \\ \end{array} } \right. $$
(20)
$$ U_{\text{III}} (x) = \left\{ {\begin{array}{*{20}c} 0 \hfill & {x \le 0.1} \hfill \\ {\frac{x - 0.1}{0.15 - 0.1}} \hfill & {0.1 < x \le 0.15} \hfill \\ 1 \hfill & {0.15 < x \le 0.18} \hfill \\ {\frac{0.22 - x}{0.22 - 0.18}} \hfill & {0.18 < x \le 0.22} \hfill \\ 0 \hfill & {x > 0.22} \hfill \\ \end{array} } \right. $$
(21)
$$ U_{\text{IV}} (x) = \left\{ {\begin{array}{*{20}c} 1 \hfill & {x \le 0.1} \hfill \\ {\frac{0.15 - x}{0.15 - 0.1}} \hfill & {0.1 < x \le 0.15} \hfill \\ 0 \hfill & {x > 0.15} \hfill \\ \end{array} } \right.. $$
(22)

Figures 2, 3, 4 and 5 show the membership function curves of earthquake intensity M, standard penetration number N 63.5, groundwater table d w and mean diameter d 50, respectively.

Fig. 2
figure 2

Membership function of earthquake intensity

Full size image
Fig. 3
figure 3

Membership function of standard penetration number

Full size image
Fig. 4
figure 4

Membership function of groundwater table

Full size image
Fig. 5
figure 5

Membership function of mean diameter

Full size image

4.3 Weight calculation by over standard weighting method

Compared to other methods, such as biasing weighting method, AHP, etc., the over standard weighting method is both easy and effective, and it is suitable for areas such as environmental assessment, geotechnical engineering projects, and so on. Therefore, it is commonly used in articles about all kinds of fuzzy comprehensive evaluation. In this study, the over standard weighting method is also selected for the calculation of the fuzzy weights. Among all the factors that affect the occurrence of liquefaction during earthquake, the standard penetration number N 63.5 and mean diameter d 50 play an obvious role. Therefore, the weights w can be derived as follows:

$$ w = \left\{ {w_{M} ,w_{{N_{63.5} }} ,w_{{d_{\text{w}} }} ,w_{{d_{50} }} } \right\} = \left\{ {0.15,0.4,0.2,0.25} \right\}. $$
(23)

4.4 Calculation results

Based on the above theories, the 23 studied samples of soil liquefaction can be calculated. Taking group 2 as an example, the detailed evaluation procedures are as follows:

  1. 1.

    Determine the factors set of soil liquefaction, that is \( U = \{ 7,3,0.166,0.5\} . \)

  2. 2.

    Construct single-factor evaluation matrix. The evaluation matrix for U using Eqs. (7)–(22) is as follows:

    $$ R = \left[ {\begin{array}{*{20}c} {0.5} \hfill & {0.5} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ \end{array} } \right]. $$
  3. 3.

    Choose a weighting method and then calculate the weights for the index subsets. The weights for U are as follows:

    $$ w = \{ 0.15,0.4,0.2,0.25\}. $$
  4. 4.

    Comprehensive evaluation. The last results of comprehensive evaluation can be got by doing complex operations calculation between single factor weight w and fuzzy relationship matrix R, that is:

    $$ B = w \cdot R = \{ 0.075,0.275,0.65,0\}. $$

    According to the maximum membership degree law, the comprehensive evaluation result is medium liquefaction, which agrees well with the actual result. By analogy, all the other forecasted and actual liquefaction results are listed in Table 2.

    Table 2 Calculation results
    Full size table

It can be seen that the predictions using the fuzzy comprehensive evaluation method have a high success rate (95.65 %), and it can meet the practical demand in engineering very well. The results indicate that the method presented in this paper seems to be a good tool to predict the liquefaction potential of soils.

5 Conclusions

In this paper, we propose a fuzzy comprehensive evaluation model to assess the soil liquefaction potential. The over standard weighting method is selected for the calculation of the fuzzy weights. Some factors that affect the soil liquefaction, such as earthquake intensity, standard penetration number, mean diameter and groundwater table, are selected as the evaluating indices. The results show that it is a useful tool to assess the potential of soil liquefaction. However, there are still some drawbacks in selecting membership functions and classification criteria in the evaluation model. In order to achieve more reliable results, lots of practical testing and improvements should be done in the future.