1 Introduction

Tsunami waves often experience abnormal amplification in the nearshore region leading to unexpectedly high runup. Quite often such situations are the result of the specific bathymetry of the basin and coastal topography (Pelinovsky 1996; Levin and Nosov 2008). One of the most recent examples is the 2009 tsunami in American Samoa (Okal et al. 2010; Roeber et al. 2010; Fritz et al. 2011; Gelfenbaum et al. 2011; Tonini et al. 2011). On the island of Tutuila, the maximum runup height reached 17.6 m in the village of Poloa and in the city of Leone; the inundation reached an impressive 500 m along the bed of the Leafu River (Okal et al. 2010). As it has been previously pointed out (Gelfenbaum et al. 2011), many of these inundated locations can be schematically presented as narrow bays with a gradual decrease in water depth along the bay.

The capital city Pago Pago, which is located at the toe of a narrow 4-km-long bay and represents the most characteristic example of a narrow bay, was also considerably damaged (destroyed infrastructures, boats and shipping containers carried inland into commercial areas, etc.) The runup height there reached 8 m over an inundation of 538 m at its toe, while the tsunami wave height measured by the tide gauge at the entrance of the bay was at most 3 m (Okal et al. 2010).

Anomalous amplification of tsunami in the Pago Pago harbour has been underlined by many authors (Okal et al. 2010; Roeber et al. 2010; Fritz et al. 2011; Gelfenbaum et al. 2011) and explained by wave trapping and focusing (Okal et al. 2010; Fritz et al. 2011), resonant effects in the bay (Roeber et al. 2010) and the impact of fringing coral reefs (Gelfenbaum et al. 2011). In this study, we demonstrate that the significant tsunami amplification in Pago Pago was caused by wave focusing at the specific bay geometry (decrease in water depth and bay cross-section in the direction normal to the coast). It is shown that runup formulas for narrow bays give a reasonable forecast for Pago Pago, while plane beach formulas underestimate runup. It is suggested to use formulas for narrow bays in such bay geometries and to incorporate them into tsunami early warning systems.

2 Samoa 2009 tsunami in Pago Pago

Pago Pago is an example of a harbour, whose geometry is very vulnerable to tsunami inundation. It amplified the tsunami from just a few metres at the entrance to 8 m at the head, causing extensive flooding and structural damage up to 538 m inland (Okal et al. 2010; Fritz et al. 2011). Several large boats and tens of vehicles were swept inland. The geometry of the harbour is shown in Fig. 1. It can be seen that the bay has a parabolic shape with narrowing cross-section and decreasing depth in the direction normal to the shore. The field survey data demonstrate that the inundation zone also had a parabolic shape (Fritz et al. 2011). This justifies the use of linearly inclined bay with a parabolic cross-section, performed below for modelling tsunami runup in Pago Pago.

Fig. 1
figure 1

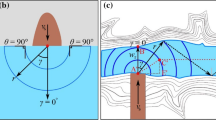
Geometry of Pago Pago harbour, American Samoa, the location of the tide gauge (14°16′38.12″S, 170°41′22.67″W) is marked by the star (a); cross-section of the Pago Pago harbour at the location of the tide gauge (b) and longitudinal projection of the bay from the location of the tide gauge to the shore (c). Red dashed lines correspond to the parabolic approximation of the bay cross-section (b) and linear approximation of the bay longitudinal projection (c), respectively

Full size image

The action of tsunami in Pago Pago was described by the NOAA employee Gordon Yamazaki. “By this time, a river of water was running down highway 1 moving very rapidly inland. When I returned the water was over 10 feet deep and a couple of feet below the floor. The water started receding back to the bay with all kinds of debris, vehicles and boats included. I stayed upstairs taking pictures and watching for anyone floating by in case we could try to make an attempt at rescue. There were a total of four waves that we saw in the span of about an hour after the quake with each one smaller than the other. The last one I saw did not reach the building we are in…”

Y. Gordon also took numerous photos, which clearly demonstrate the arrival of the first four waves; some of them are shown in Fig. 2. It can be seen in Fig. 2b that tsunami runup has a surging character. The water flow inundates the coast smoothly, without breaking.

Fig. 2
figure 2

Tsunami in Pago Pago: a the first wave receding back to the harbour; b the second wave at Pago Plaza; c the third wave coming into Pago Plaza parking lot; d the Park Service building and Pago harbour during the third wave impact (photo credits: Gordon Yamazaki, NOAA)

Full size image

At the same time, Fig. 2c demonstrates strong currents during wave runup and the violence of the water flow. Overland flow speeds of the tsunami front were estimated from security camera footage to be 2.5 m/s about 200 m inland (Fritz et al. 2011).

3 Runup characteristics in theoretical models

In order to understand the physics of extreme amplification and runup observed in Pago Pago and to study the influence of the bay geometry, two different runup formulations will be applied to Pago–Pago case: the model of wave runup on 1D beach of constant slope (Carrier and Greenspan 1958; Synolakis 1987) and the model of an inclined bay with a parabolic cross-section (Choi et al. 2008; Didenkulova and Pelinovsky 2009, 2011a). Both problems allow finding an analytical solution for wave runup in the nonlinear shallow water framework.

In the case of 1D runup on a plane beach (or an inclined channel of rectangular cross-section), the governing equations are classical shallow water equations

$$ \frac{\partial H}{\partial t} + u\frac{\partial H}{\partial x} + H\frac{\partial u}{\partial x} = 0,\quad \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + g\frac{\partial H}{\partial x} = g\frac{\partial h}{\partial x}, $$
(1)

where H(x, t) = h(x) + η(x, t) is total water depth, η(x, t) is water displacement, u(x, t) is depth-averaged velocity, h(x) = αx is unperturbed water depth, α is bottom slope, g is gravity acceleration, x is coordinate directed offshore and t is time. After the pioneer work by (Carrier and Greenspan 1958) who applied the hodograph transformation to Eq. (1), solutions for the runup of waves of different shapes have been obtained (Pedersen and Gjevik 1983; Synolakis 1987; Tadepalli and Synolakis 1994; Brocchini and Gentile 2001; Kânoğlu 2004; Tinti and Tonini 2005; Didenkulova et al. 2006; Antuono and Brocchini 2007; Madsen and Fuhrman 2008).

Here, in order to estimate the runup in the city of Pago Pago, a two-step concept suggested in (Didenkulova et al. 2008) is used. It is based on a Fourier representation of the wave approaching the coast. It is assumed that the incident wave at a fixed point \( \left| x \right| = L \) (located far away from the shoreline) at a water depth h 0 is specified by the Fourier integral:

$$ \eta_{0} (t) = \int\limits_{ - \infty }^{ + \infty } {A(\omega )\exp (i\omega {\text{t}}){\text{d}}\omega } , $$
(2)

where A(ω) is an incident wave spectrum

$$ A(\omega ) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\eta_{0} (t)\exp (i\omega t){\text{d}}t} . $$
(3)

In this case, the dynamics of the moving shoreline r and the shoreline velocity u can be found as a Riemann time transformation of the corresponding solutions for runup height R and velocity U of the linearized Eq. (1):

$$ u(t) = U\left( {t + \frac{u}{\alpha g}} \right),\quad r\left( t \right) = R\left( {t + \frac{u}{\alpha g}} \right) - \frac{{u^{2} }}{2g}, $$
(4)

where R and U are given by the following Fourier series:

$$ R(t) = \sqrt {2\pi \tau_{1} } \int\limits_{ - \infty }^{ + \infty } {\sqrt {|\omega |} } A(\omega )\exp \left\{ {i\left( {\omega (t - \tau_{1} ) + \frac{\pi }{4}{\text{sign(}}\omega )} \right)} \right\}{\text{d}}\omega , $$
(5)
$$ U\left( t \right) = \frac{{\sqrt {2\pi \tau_{1} } }}{\alpha }\int\limits_{ - \infty }^{ + \infty } {\sqrt {|\omega |^{3} } } A(\omega )\exp \left\{ {i\left( {\omega \left( {t - \tau_{1} } \right) + \frac{\pi }{4}{\text{sign}}(\omega ) + \frac{\pi }{2}} \right)} \right\}{\text{d}}\omega . $$
(6)

Here, \( \tau_{1} = 2L/\sqrt {gh_{0} } \) represents a travel time to the shore.

The wave runup in an inclined bay of parabolic cross-section is described in Choi et al. (2008), Didenkulova and Pelinovsky (2011a). In the assumption of a narrow bay, where the velocity component along the bay is much larger than the cross-section velocity component, the nonlinear shallow water equations have a similar form as Eq. (1) with the difference lying in the 2/3 coefficient multiplied to \( \partial u/\partial x \) in the first equation:

$$ \frac{\partial H}{\partial t} + u\frac{\partial H}{\partial x} + \frac{2H}{3}\frac{\partial u}{\partial x} = 0,\quad \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + g\frac{\partial H}{\partial x} = g\frac{\partial h}{\partial x}. $$
(7)

Here, h and H are the unperturbed and total water depth along the main longitudinal axis of the bay, respectively, and u is the flow velocity averaged over a bay cross-section.

Nonlinear shallow water Eq. (7) can also be solved analytically with the use of the hodograph transformation. This approach generalizes the Carrier-Greenspan transformation for long wave runup on a plane beach. In the case of an inclined bay of a parabolic cross-section, it leads to the associated spherical, symmetrical, linear wave equation (Didenkulova and Pelinovsky 2009, 2011b). As a result, the solution of the Cauchy problem can be expressed in terms of elementary functions and dynamics of the moving shoreline, and the shoreline velocity can simply be found as the time derivative of the incident wave η 0(t)

$$ R(t) = 2\tau_{2} \frac{{d\eta_{0} (t - \tau_{2} )}}{{{\text{d}}t}},\quad U(t) = \frac{{2\tau_{2} }}{\alpha }\frac{{d^{2} \eta (t - \tau_{2} )}}{{{\text{d}}t^{2} }}, $$
(8)

where \( \tau_{2} = \sqrt 6 L/\sqrt {gh_{0} } \) is the travel time of tsunami wave to the shore of the narrow bay. Nonlinear solution for r and u in the bay can be found by the same Riemann time transformation as for a plane beach Eq. (4).

It should be noted that both Eqs. (1) and (7) are limited to the case of non-breaking waves, which are characterized by the breaking parameter, which characterizes the moments of the first wave breaking in shallow water, to be <1:

$$ Br = \frac{{\hbox{Max}} ({{{d}}U/{{d}}t})}{\alpha g} < 1. $$
(9)

Below, all described characteristics are calculated for Samoa 2009 tsunami runup in Pago Pago.

4 Estimates of wave runup in Pago Pago harbour

In order to estimate the tsunami runup characteristics in Pago Pago, we use the tide gauge record measured in Pago Pago harbour (Fig. 3).

Fig. 3
figure 3

Tide gauge record of Samoa 2009 tsunami in Pago Pago; the time is shown in minutes after the earthquake (provided by Vasily Titov)

Full size image

The main problem here is related to the definition of the incident wave from the tide gauge data. However, to the first approximation for calculating tsunami runup, it is possible to use the tide gauge record as an incident wave.

The results of these calculations are shown in Fig. 4. The distance from the tide gauge to the shore is L = 1.1 km, and the initial water depth is taken at the deepest point in the cross-section, which is h 0 = 37 m. So the bottom slope used in calculations is about 0.03. The fact that the location of the tide gauge is shifted to the side of the bay is not so important from narrow bay view point, when it is assumed that waves propagate in the longitudinal direction of the channel and have the same structure all over the cross-section.

Fig. 4
figure 4

Runup estimates for Samoa 2009 tsunami in Pago Pago made by the assumption of the plane beach (black dashed line) and an inclined bay (red solid line); the thick solid blue line reflects 8 m level of runup measured in Pago Pago during the field survey (Okal et al. 2010)

Full size image

It can be seen in Fig. 4 that runup values calculated for a plane beach (Eqs. 4–6), and inclined bay (Eq. 8) have similar shapes, but an inclined bay gives larger values of runup and rundown heights (Table 1). The maximum runup height for a plane beach reaches 7.2 m, which slightly underestimates the measured value of tsunami runup by 0.8 m. At the same time, the inclined bay model overestimates the runup height by 0.9 m.

Table 1 Calculated runup characteristics for a plane beach and an inclined bay
Full size table

It takes about 2 min for the tsunami to propagate from the tide gauge location to the coast, and this value differs slightly between the plane beach and inclined bay models. Tsunami in the bay arrives 26 s later than at the plane beach, but, as it can be seen from Fig. 4, although the first wave arrives later when the wave propagates in the bay, the arrival time of the largest wave front for both models coincides.

The flow velocity at the coast also has a similar shape (most of the main peaks coincide) for a plane beach and an inclined bay, but there are some deviations in their values (Fig. 5). The maximum flow velocity in the inclined bay reaches 5.3 m/s (Table 1). However, when tsunami passes the security camera (200 m onshore, approximately 4 m high above the sea level), the flow velocities are about 3 m/s for both models, which is consistent with the estimated value of 2.5 m/s (Fritz et al. 2011).

Fig. 5
figure 5

Flow velocity at the coast for Samoa 2009 tsunami in Pago Pago calculated for a plane beach (black dashed line) and an inclined bay (red solid line)

Full size image

The last comment here is about the wave breaking, which is proportional to the wave height and therefore differs for the two models (Table 1). What is important is that in both cases, it remains less than 1, which corresponds to non-breaking wave propagation and justifies the use of nonlinear shallow water theory. The surging character of tsunami runup in Pago Pago is also confirmed by observations seen in Fig. 2.

5 Conclusion

The anomalous amplification and runup in Pago Pago (Tutuila, American Samoa) during the Samoa tsunami of 29 September 2009 is studied using two models of bottom bathymetry of Pago Pago harbour: the plane beach model and the narrow bay model. Both formulations result in equally good estimates of runup, having approximately the same difference with the field measurements. However, the later model (narrow bay model) presents more wave amplification and, consequently, runup, which is the main observation of the field survey. The character of tsunami runup and the speed of the water flow inland estimated by the corresponding formulas for narrow bays are also in a good agreement with observations. It is suggested to use these formulas to forecast tsunami runup in narrow bays and to incorporate them in tsunami early warning systems. These formulas require only time differentiation of an incident wave that can be done instantly after the tide gauge registers the wave or by using a pre-computed tsunami records and can lead to a reduction of computation time for tsunami runup forecast.