1 Introduction

Despite a great deal of attention paid to hubs in spatial networks, it appears that there are unexplored issues in the analysis of flows within the hub itself. This paper outlines a simple typology, notation, and analytical framework for routing traffic at transfer nodes. The fundamental idea is that flows between network nodes interconnect at various types of hubs. Transfer aspects of hub and spoke systems are widely recognized as a hindrance to efficient completion of transit trips. For example, time-consuming delays at transfer points for bus passengers are a major reason for poor levels of service between some nodes when the origin and destination are on different network spokes. In discussing models for this situation, this paper adapts ideas from diverse types of transportation situations, such as subway systems, internet backbone peering and connectivity, logistics facilities, and border crossings. The ideas here are flexible enough to suggest a framework for further research on a variety of interesting optimization problems that might arise in connection with a hub: the minimization of transfer delay, the design of strong surveillance schemes, or the decision to link certain paths directly.

By focusing attention on intra-hub connectivity, some new aspects of hub network efficiency may be realized. There is a precedent for this scale of analysis in Koopmans and Beckmann (1957), who looked at interdependent flow and location decisions in plant layout and showed that they lead to quadratic programs. Their work inspired further exploration of internal economies of scale (Reiter and Sherman 1962). By analyzing internal linkages at hubs, this paper opens a series of questions about network efficiency, in the same way that internal economies of scale are studied in industrial economics.

Three approaches to this issue are apparent: a descriptive (and data intensive) study could be carried out to recover historical data from the operational records of the throughput conditions at a hub. A second approach would be to derive generalized models of the flows from spatial interaction theory (Fotheringham and O’Kelly 1989; O’Kelly 1986). A third approach, and the main one adopted in the present paper, is to combine the expected flows with a network design problem to potentially optimize certain aspects of the operational management of the transport system (see also Campbell 1994; Crainic and Kim 2007). This paper deals with a relatively simple case where lines come into the hub at distinct points, and there the flows (passengers, packages, etc.) are either passed through on that same line or are switched to another line.

2 Typology of related transfer problems

In the present paper it is assumed that exogenously given interactions flow from origins to destinations, via hubs which act as switching points. Focusing on the hub facility itself, note that the spokes that come to the facility can be regarded as either (1) terminating at the hub or (2) part of a line passing through the hub. In both cases however, exogenously given flows may pass through the facility, either after making a transfer (Case 1), or on the same line (Case 2). These types of interchange and transfer problems give rise to two different analytical cases which are discussed next.

Case 1: Hub Terminus

The first case is exemplified by spokes that terminate at a hub; i.e. doors at a cross-dock, airline gates at an airport, or transit routes that enter an urban area and stop at a terminus. In these cases the flows need to transfer to a connecting segment to continue their journey. The facility in each of these examples is the cross-dock, the airport, or the city center. Assuming that several terminating spokes connect at the facility, one then has the problem of optimizing the organization of flows from one door/gate/terminal to another. To emphasize the need to connect stages of the trip at the facility, these intra-facility connections will be referred to as “links” and distinguished from lines and spokes. The problem in this case is typically one of minimizing transaction costs.

Case 2: Hubs with through connections

The second case is exemplified by transfer hubs on bus, train, or subway lines where several lines (e.g. red, green, blue etc.) pass through the station. These lines meet at the common facility, perhaps occurring at various levels (i.e. a third dimension). Someone on a red line destined for another red line station stays on the train and makes no transfer and has a “through” connection. On the other hand a red line passenger needing to transfer to the blue line, exits the red train at the station, moves to the other platform (which may be some distance away) and then boards the blue train. The questions that arise in this case tend to involve the volume of required transfers and decisions about connections.

Although the two cases and the literatures that relate to them are perhaps rather separate, a number of useful cross-fertilizations occur when the problems are juxtaposed. The paper poses a variety of optimization problems for making efficient joins between incoming and outgoing flows at the hub. One particular optimization problem occurs when deciding which spokes may be bridged together allowing for a smoother transfer or more favorable connection from one spoke to another; in essence this converts two (or more) terminating spokes (Case 1) into linked or connected lines (Case 2). In a planning context this might be the problem of deciding which inbound and outbound spokes should be given a favored path through the terminal. Operationally, there are of course logical and physical limitations on the spokes that can be joined: sharp changes in line direction or level being impossible. Spokes, by definition, terminate at the hub (just like wire spokes attached to a hub on a bicycle wheel). However, whenever spokes can be interconnected to form continuous lines, the decision problem would be to select pairs of spokes to join. One variant, with special relevance for Case 2, is whether the spokes contain multiple nodes: invariably such feeder lines have multiple station stops on either side of the transfer station. The distinction between independent and interdependent nodes (such as might occur on regular spokes and feeders respectively) and a distinction between terminating and through lines gives rise to as many as four special cases, of which two are considered here in detail, as shown below.

 

Terminating spokes

Through lines

Independent nodes

Case 1

See Case 1

Interdependent nodes (feeders)

See Case 2

Case 2

The two instances that are not explicitly dealt with (single nodes on through lines, and feeders arriving at terminals) are both useful potential extensions, though they would seem to be readily handled as parts of the two cases that are dealt with. The nodes on through lines for example, lead to expected inter-gate flows, and it seems that whether this is a feeder blending several flows, or a single node, the analysis is basically the same. The case of feeders arriving at terminals is in fact similar to Case 1 so long as the feeder flows are bundled/aggregated appropriately.

Thus, while terminating spokes can have independent nodes and several interdependent nodes (as on a feeder line), the primary focus here is on the problem of terminating spokes with single nodes (Case 1). Through lines can also have independent nodes and feeder lines, and in this paper the focus is on the essential problem (Case 2) of through lines with multiple feeder nodes.

3 Related literature

While this paper is not a review of the voluminous research on network routing, some existing papers that have examined parts of the problems outlined above are cited here as an introductory guide to further conceptual development. Kleinrock (1964) simulates the flows in communications networks between lines that join at a central node; the primary focus of his approach is to emphasize stochastic models for queuing. He develops considerable numerical insight into the impact of network structure on the throughput of flows. Kara and Tansel’s (2001) and Yaman et al.’s (2007) work on the ‘latest arrival’ problem is a merger of the hub flow problem and the earlier communications network ideas of Kleinrock. When there are multiple destinations for flows in each inbound vehicle, one cannot dispatch an outbound vehicle until the latest arrival containing material for that destination occurs. In a related case airlines also hold departures to accommodate late incoming connections (Lim et al. 2005). In distinction to this however, one notes that the waves of transit vehicle departures have to adhere to a schedule and so cannot usually wait for the last inbound passenger (i.e. in bus or train networks). The idea of optimally pulsing or organizing the waves of interconnecting paths is beyond the scope of this paper though clearly there is ample opportunity for further research to combine the network concepts here with the large body of literature on optimal transit scheduling (see Chang and Hsu (2001) and Chowdhury and Chien (2002) for representative samples). A recent detailed treatment of the synchronization of flows is in Bobzin (2005).

In many models of hub and spoke networks, the links to the hub are typically just a single path from an origin. However, Kuby and Gray (1993) expand this idea to include hub networks with feeders, especially for air freight, where the useful notion of feeder is introduced to allow multiple pick-up points along a spoke entering a hub. While this is clearly too inconvenient for most air passenger applications, it does make a great deal of sense for the amalgamation of flows in surface transportation networks. It also gives rise to the kind of flow aggregation problem that could potentially strain the capacity of the link and the terminal. Although this present paper does not focus on capacity or flow estimation per se, it is important to note that in modeling the flows arriving at a hub from a spoke, one needs to be cognizant of the volume of aggregated flows.

A hub node can also be used to represent an intermodal facility such as a connection between ground and air transportation (Hall 2001; Crainic and Kim 2007). In the area of logistics and facility layout, cross-dock facility planning is very relevant to the present situation. When flows meet at a location it is often required to optimize assignments to particular gates to minimize intra-facility costs. Researchers on this topic derive a special type of quadratic assignment problem called the dock-door assignment problem (Tsui and Chang 1992; see also review of assignment problems in general by Pentico 2007). The typical cross-docking system occurs for example in a mail distribution center with receiving doors and shipping doors (Oh et al.’s 2006). “The assignment of destinations to shipping doors, clustering of destinations to form groups, and determination of the number of groups are major operational problems directly related with the efficiency of the center.” While there are strong similarities between the goals of the present paper and Oh et al.’s (2006) objective of minimizing travel within the center, the present paper suggests variations on the model that might be adapted to intra-hub movements of a more general nature. One distinction between the typical cross-dock model and the present case is that it is envisioned that multiple origins and destinations connect to each of the terminal gates. These multiple spokes can arise either from the feeder functionality, or the hub-like amalgamation of multiple incoming flows through a particular gate.

Finally, a series of developments in the hub location literature (Campbell 1994) guide solution procedures for network optimization involving hub activity levels: these include simply enumerating the levels of activities at the hub (O’Kelly 1986), to a quadratic assignment-type problem, where a variety of optimization techniques have been applied to provide a heuristic driven approach to what can be an unwieldy problem (Skorin-Kapov et al. 1996).

In summary then, the literature suggests that this kind of problem domain will entail integer programs, probably with quadratic objective functions. In fact the full complexity of the interdependent strategic and operational decisions on clustering and linking paths is likely to require some variants of the classical quadratic assignment or generalized assignment problem. Along with these challenges, the routing of flows is expected to give rise to some substantively interesting problems.

4 Case 1: Optimal allocation and matching

In considering Case 1 (optimization of connections), the important decision variables are (1) the ways in which the incoming and outgoing spokes are connected at the hub gates, (2) which spokes (representing nodes) connect to the same gates, and (3) the arrangement of these allocations to minimize the amount of inter-gate costs. The scale or distance between gates at the terminal varies somewhat by application. When the gates are separated and require longer walks between stations (e.g. St. Pancras to King’s Cross in London), there is simply a larger intervening movement between the facilities, but the connection between the lines is still appropriately represented as a form of movement between lines or stations. It is not clear from the literature what if any impact the length of the intra-facility linkage might have other than the obvious one that longer links pose greater costs and delays.

The optimal allocation and matching problem is related to the task of selecting improved interline connections. As will be seen in this section, many location and optimization issues that arise under the topic of this paper are variants on the quadratic assignment problem; the organization of connections at the hub play a key role in the throughput. Imagine a set of origins connected to one side of the facility (IN), and the destinations connected on the other side (OUT). The flow connects through inbound and outbound gates at the central hub. Each origin and each destination needs to be handled by a particular pair of hub gates, k and m respectively. The material is transferred between the gates without intervening storage, but with a cost of movement. That cost is assumed to be small relative to the total cost of accessing the hub from the originating point; the flow is presumed to have arrived at the exterior of the hub, and ready for assignment to a gate.

Although the feeder problem could be applied to this part of the paper also (a la Kuby and Gray 1993), here we focus on a simple version of the problem, as all the nodes are considered to be independent, and thus each spoke has one associated node; this further leads to the fact that one can refer interchangeably to node or spoke i (as each spoke has just one unique node). The issue of combining these ideas with a more complete treatment of feeders, realistic flows, and so on, is left for future research.

A question arises then as to the optimal allocation of nodes to gates. The merit of assigning node i to gate k and node j to gate m depends on whatever else is assigned to those same gates, especially if each node is assigned to a unique gate. This is a key similarity to the so-called single-gate assignment constraint in the hub literature. The ultimate assignment of node i to k will of course depend on the components of its interactions, and the assignment of the nodes with which it interacts: once the material reaches the hub at gate k it is then routed through the facility to the connections for node j etc. It is this interdependence of the routing decision variable for the inbound and outbound gates that make this a fundamentally quadratic problem (routing depends on the product of X ik and X jm ). However, the product of the two assignment variables is sometimes represented as a linear term with four subscripts: these routes are defined by R ijkm which is the routing variable from i to k and from m to j.

In very broad terms, the objective is to assign the incoming node or spoke to a gate, and assign the outgoing node or spoke to a gate, to minimize the total movement of the transfer operation. Unlike some prior research, this model simultaneously assigns the inbound and outbound spokes under a variety of protocols, noting the fact that an incoming flow from an origin can contain items for multiple destinations [see other examples applied to less-than-truckload shipping by Bartholdi and Gue (2000, 2004) and Oh et al. (2006)].

Assuming a desire to optimize the allocation of origin node i to gate k and the allocation of destination node j to gate m, the following integer program chooses {\(X_{ik}^O \), \(X_{jm}^D \), R ijkm } to

$${\text{Minimize}}\;\sum\nolimits_{i \in O} {\sum\nolimits_{j \in D} {\sum\nolimits_{k \in {\text{I}}N} {\sum\nolimits_{m \in {\text{OUT}}} {W_{ij} \;R_{ijkm} } } } } \left[ {C_{ik}^O + C_{km}^H + C_{jm}^D } \right]$$
(1)

Subject to:

$$\sum\nolimits_{k \in {\text{IN}}} {X_{ik}^O } = 1\quad \quad \quad \quad {\text{for all }}i \in O$$
(2)
$$\sum\nolimits_{m \in {\text{OUT}}} {X_{jm}^D } = 1\quad \quad \quad {\text{for all }}j \in D$$
(3)
$$\sum\nolimits_{m \in {\text{OUT}}} {R_{ijkm} } - X_{ik}^O = 0\;\;{\text{for all }}i \in O,{\text{ }}j \in D,{\text{ }}k \in {\text{IN}}$$
(4)
$$\sum\nolimits_{k \in {\text{IN}}} {R_{ijkm} } - X_{jm}^D = 0\quad {\text{for all }}i \in O,{\text{ }}j \in D,{\text{ }}m \in {\text{OUT}}$$
(5)
$$X_{ik}^O ,{\text{ }}X_{jm}^D ,{\text{ }}R_{ijkm} \in \left\{ {0,1} \right\}.$$
(6)

The data associated with the problem are primarily driven by W ij , the pre-specified flows between the origins and destinations. The variables to describe these decisions are as follows:

\(X_{ik}^O \) :

the allocation of origin node i to inbound gate k; every unique origin is assigned to one gate; O is the set of origin nodes.

\(X_{jm}^D \) :

the allocation of destination node j to outbound gate m; D is the set of destination nodes.

Constraint (2) ensures that every unique origin is assigned to one gate. Constraint (3) ensures that every unique destination is assigned to one gate. In constraints (4) and (5) the routing variables R ijkm are constrained by the allocation variables, following a formulation in O’Kelly et al. (1995).

The unit cost coefficients associated with these movements are as follows: \(C_{ik}^O \) is the cost to assign origin i to inbound dock gate k; \(C_{jm}^D \) is the cost to assign destination j to outbound dock gate m; and \(C_{km}^H \) is the inter-gate cost between gates k and m at the hub.

The objective can then be re-written as follows (O’Kelly 1987) where the range of summation of i, j, k, m is simplified (e.g. Σ i ∈O is written as Σ i )

$$\begin{array}{*{20}c} {\sum\nolimits_i {\sum\nolimits_j {\sum\nolimits_k {\sum\nolimits_m {W_{ij} \;R_{ijkm} \left[ {C_{ik}^O } \right]} } } } + \sum\nolimits_i {\sum\nolimits_j {\sum\nolimits_k {\sum\nolimits_m {W_{ij} \;R_{ijkm} } } } } \left[ {C_{jm}^D } \right] + } \\ {\sum\nolimits_i {\sum\nolimits_j {\sum\nolimits_k {\sum\nolimits_m {W_{ij} \;R_{ijkm} \;\left[ {C_{km}^H } \right] = } } } } } \\ \end{array} $$
(7)
$$\begin{array}{*{20}c} {\sum\nolimits_i {} \sum\nolimits_k {C_{ik}^O } \;\sum\nolimits_j {W_{ij} } \;\sum\nolimits_m {R_{ijkm} } + \sum\nolimits_j {} \sum\nolimits_m {C_{jm}^D } \;\sum\nolimits_i {W_{ij} } \;\sum\nolimits_k {R_{ijkm} } + } \\ {\sum\nolimits_i {\sum\nolimits_j {\sum\nolimits_k {\sum\nolimits_m {W_{ij} \;R_{ijkm} \;\left[ {C_{km}^H } \right] = } } } } } \\ \end{array} $$
(8)
$$\sum\nolimits_i {\sum\nolimits_k {} } O_i \;X_{ik}^O \;C_{ik}^O + \sum\nolimits_j {\sum\nolimits_m {} } D_j \;X_{jm}^D \;C_{jm}^D + \sum\nolimits_i {\sum\nolimits_j {\sum\nolimits_k {\sum\nolimits_m {} } } } W_{ij} \;R_{ijkm} \;C_{km}^H $$
(9)

and the three components in Eq. (9) are referred to as P1 (the inbound cost of moving materials from the terminal entrance to the assigned gates), P2 (the outbound cost of moving materials from the assigned gates to the terminal exit), and P3 (the inter-gate costs or distances) respectively. Note that O i  = Σ j W ij , and D j  = Σ i W ij are outflows from origins and inflows to destinations respectively. It is assumed that the costs of getting from the origin and destination to the hub are calculated outside the model, and in terms of orders of magnitude they are likely to be much larger than the intra-facility costs.

Depending on the number and configuration of incoming and outgoing lines, the potential gate locations may or may not all be active in a solution. The decision as to the active subset of the gates to use could result in some gates getting no assignment. This suggests a generalized form of quadratic assignment where the active gates and the flows between them are determined, thereby producing a configuration for the intra-hub flows and linkages. If one wished to force the use of all the available gates, for reasons of balance, the following constraints could be added:

$$\sum\nolimits_i {X_{ik}^O \geqslant 1} \quad \quad \quad \quad \quad {\text{for all }}k \in {\text{IN}}$$
(10)
$$\sum\nolimits_j {X_{jm}^D \geqslant 1} \quad \quad \quad \quad \quad {\text{for all }}m \in {\text{OUT}}$$
(11)

Adding constraints (10) and (11) gives rise to an interesting variant on the problem, where we might explore the increased cost associated with forcing gates to have an assignment. It also turns out in the numerical examples to be essential to enforce the binary restriction on the allocation variables X O and X D.

5 Case 2: Optimal interline connection

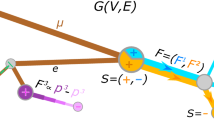
To consider Case 2 (interline connections), examine a network with a number of spokes entering a central switching point (see Fig. 1), so the flows from the nodes on the spokes reach nodes on other spokes by traversing the hub at the center of the network. If permitted by the network protocol, which pairs of spokes should be joined so as to have “through” connections? One simple optimization rule would be to join the busiest pairs, assuming a feasible connection. However, from the point of view of interaction through a switch or a border crossing, the apparent simplicity of the calculations hides many nuances which need to be considered in more detail [as a simplifying assumption, the flows proceed from left to right (i.e. from set O to set D) and so in this case, the nodes in O cannot interact with each other; this is not a major limitation however as the sets O and D can be expanded to include all interacting places].

Fig. 1
figure 1

Example for Cases 1 and 2: lines meet at the central hub. (a) Case 1. (b) Case 2

Full size image

Transit routes coming into a terminal usually have many stops. Each of those various stations gives rise to potential interactions with nodes along the other lines, as well as with the central terminus. The terminating point for the portion of the journey on one line links to the origination for the other line: in essence then the transfer appears to occur within one facility. It is primarily the traffic flow through the hub that is the subject of the analysis. The interactions are weighted by the amount of flow between nodes on spokes and the flows on intra-hub links are then the accumulation of all the traffic that crosses those connections.

An interesting problem is to decide if any spokes ought to be bridged together so that the passengers transiting the hub can stay at a brief station stop and then continue on the same line to their destination, (such as might occur at Union Station in Toronto). In a related area, route choice in a subway system with transfers (Lee and Lee 1998) is considered for quite complex subway systems (such as in Seoul South Korea) where dozens of interconnected rail lines provide regional coverage and connection. A comprehensive atlas of such systems has recently been provided by Ovenden (2007). Estimating travel time in these networks typically requires some measure of the probable number of transfers. Optimizing connectivity in such systems is equivalent to eliminating the necessity for a transfer between some in and outbound lines. One simple ad hoc way to decide these joins would be to mesh together the segments that have the highest interaction (not necessarily the largest numbers of pairs of interactions). For example if lines 2 and 5 in Case 2 of Fig. 1 were to be designated the ‘green’ line all five stations could have easier access to each other through the hub. It is the model problem to decide if other pairs of lines could produce a better pairing—for example the three stops on spoke 5 could be better joined to the five stops on spoke 3 depending on the flows.

The interline improvement problem can then be seen as an application of this measurement scheme. Suppose that there is a fixed budget for upgrading interline connections. A simple knapsack problem would be suited to the task of selecting the subset of the activities that maximizes return subject to a cost constraint for the improvements. If the link between the spokes terminating at k and m respectively, is modeled as having benefit or flow W km and cost C km , the decision problem might be to choose {X km } to

$${\text{Max}}\quad \quad \quad \;\quad \quad \sum\nolimits_k {\sum\nolimits_m {X_{km} \;W_{km} } } $$
(12)
$${\text{Subject to}}\quad \quad \quad \sum\nolimits_k {\sum\nolimits_m {X_{km} \;C_{km} \leqslant C} } $$
(13)
$$\quad \quad \quad \quad \quad \quad \quad X_{km} \in \left\{ {0,1} \right\}$$
(14)

As this is a simple variant of the knapsack problem (X binary), we could essentially rank the interlink flows in terms of their ratios of W km /C km and progress through these in a greedy fashion to add the improvements with the greatest “bang for the buck.” Infeasible connections could be blocked by setting a large cost coefficient. As is usual with knapsack problems, ranking flows in order of these ratios does not usually produce an optimal solution, so the task would have to be completed with some branch and bound steps (Nemhauser and Wolsey 1988). The knapsack problem is a well studied subroutine in many optimization texts and will be simply incorporated here by reference (Martello and Toth 1990).

The problem with this knapsack is that it does not deal with matching or assignment constraints, and these are needed to ensure that each gate is paired with at most one other gate. Disregarding intra-facility costs and capacity, one sees that a feeder arriving at a hub contains all the traffic that originated on the feeder nodes destined for other nodes on other feeders. Thus a simple aggregation of all the flows gives the expected interaction between gate k and m. A direct approach is to pre-process the W ij flows such that all flows from the spokes assigned to gates k and m are found by summing

$$W_{km} = \sum\nolimits_{i \in {\text{spoke }}k} {\sum\nolimits_{j \in {\text{spoke }}m} {W_{ij} } } $$
(15)

Then, the following assignment problem could be solved to determine the best links to connect:

$${\text{Max}}\quad \quad \quad \;\quad \quad \sum {_k } \;\sum {_m } \;X_{km} \;W_{km} $$
(16)
$${\text{Subject to}}\quad \quad \quad \sum {_k } \;X_{km} = 1$$
(17)
$$\quad \quad \quad \quad \quad \quad \quad \sum {_m } \;X_{km} = 1$$
(18)
$$\quad \quad \quad \quad \quad \quad \quad X_{km} \in \left\{ {0,1} \right\}$$
(19)

6 Solution methods

Generally, for small test cases, the models can be explored with commercial software such as CPLEX. However, because the problems outlined above (especially for Case 1) can become large for practical instances, it is important to devise some additional solution techniques (see also Oh et al. 2006). Lower bounding is a common device in optimization. It is used to set a floor under the objective function: while we have no interest in an underestimate of the true cost per se, we do benefit from knowing that the optimal solution must be greater than the lower bound.

One possible heuristic approach is to work out a decoupled version of the allocation variables, using modified coefficients. Having solved by inspection for those allocations, the original objective can be evaluated, and a bound on its accuracy established. Details of this substitution follow from exploiting the triangle inequality (for the relationship between C ik and C km for example). This leads to two substitutions for the inter-gate assignment cost, leading in turn to a lower bound.

Let \(C_{im}^M \) = distance from origin i to the outbound gate. It is clear from the triangle inequality that \(C_{im}^M \leqslant C_{ik}^O + C_{km}^H \). This observation leads to the first substitution

$$C_{km}^H \geqslant C_{im}^M - C_{ik}^O .$$
(20)

Let \(C_{jk}^K \) = distance from destination j to inbound gate. Again, it is clear from the triangle inequality that \(C_{jk}^K \leqslant C_{km}^H + C_{jm}^D \). This observation leads to the second substitution

$$C_{km}^H >C_{jk}^K - C_{jm}^D .$$
(21)

Since there are two alternative sets of substitutions leading to two contenders for the lower bound, the larger resulting objective function becomes the largest lower bound. Solving the problem (to be derived below) with these artificial substitutions for the inter-gate costs can lead to a new set of allocations. To distinguish these from the primal variables, use \(Z_{ik}^O \) which is an allocation variable from origin to gate k (decision variable in relaxation) and \(Z_{jm}^D \) an allocation variable from destination to gate m (decision variable in relaxation).

Approaching the objective from the first substitution (20) into P3 we obtain the following result: \({\text{LB}}1 = \sum {_j \sum {_m } } \;Z_{jm}^D \sum {_i } \;W_{ij} \left[ {C_{jm}^D + C_{im}^M } \right]\)

Proof

From (20) \(C_{km}^H >C_{im}^M - C_{ik}^O \) and inserting in the objective:

$$\begin{aligned} & {\text{P}}3 >\sum {_i \sum {_j \sum {_k } } \sum {_m } } \;W_{ij} \;Z_{ik}^O \;Z_{jm}^D \left[ {C_{im}^M - C_{ik}^O } \right] \\ & = \sum {_i \sum {_j } \sum {_m } } \;W_{ij} \;Z_{jm}^D \left[ {C_{im}^M } \right] - {\text{P}}1 \\ \end{aligned} $$

combining P1, P2, and lower bound estimate of P3, noting the ability to cancel P1:

$$\begin{aligned} & {\text{LB}}1 = \sum {_j } \sum {_m \sum {_i } } \;W_{ij} \;Z_{jm}^D \;C_{jm}^D + \sum {_i \sum {_j } \sum {_m } } \;W_{ij} \;Z_{jm}^D \left[ {C_{im}^M } \right] \\ & \quad \quad \quad \quad \quad \quad \quad \quad = \sum {_j \sum {_m } } \;Z_{jm}^D \;\sum {_i } \;W_{ij} \left[ {C_{jm}^D + C_{im}^M } \right]\quad \quad \blacksquare \\ \end{aligned} $$
(22)

Define \(C_{jm}^J = \sum {_i } \;W_{ij} \left[ {C_{jm}^D + C_{im}^M } \right]\). The first lower bound based allocation can be found from setting \(Z_{jm * }^D = 1\) for m such that m* is the index with \(C_{jm*}^J + C_{jm}^J \) over all m, and repeated for each j. This provides a feasible allocation of the destination nodes to outbound gates.

Approaching the objective from the second substitution (21) into P3 we obtain the following result (similar proof omitted):

$${\text{LB}}2 = \sum {_i \sum {_k } } \;Z_{ik}^O \;\sum {_j } \;W_{ij} \left[ {C_{ik}^O + C_{jk}^K } \right].$$
(23)

Define \(C_{ik}^I = \sum {_j } \;W_{ij} \left[ {C_{ik}^O + C_{jk}^K } \right]\). The second lower bound based allocation can thus be found from setting \(Z_{ik*}^O = 1\) for k such that k* is the index with \(C_{ik*}^I <C_{ik}^I \) over all k, and repeated for each i. This provides a feasible allocation of the origin nodes to the inbound gates.

Having assigned the \(Z_{jm}^D \) and \(Z_{ik}^O \) variables according to the lower bound coefficients, it is possible to evaluate the primal objective from the Z variables. Of course this solution provides an initial solution (labeled as a BKS), but may still leave a gap between the BKS and the lower bound. It remains then to gauge the quality of the lower bound in comparison to the BKS.

7 Numerical results

7.1 Case 1

The flow matrix illustrated in Table 1 has ten basic origins treated separately, and eight destinations. There are four inbound hub gates, and four outbound hub gates. The problem is to determine the allocation of the nodes or spokes to the gates at the hub.

Table 1 Sample input data for 10 × 8 problem
Full size table

In the present context the models are solved to optimality using CPLEX. Some comparative bounds are also discussed briefly later in this section.

The numerical solutions are interesting because the assignments provide a routing solution for each OD pair. A sample optimal solution for this 10 × 8 problem is shown in Fig. 2. Note that the gate assignments of the ten origins may be denoted [1 1 2 2 3 3 4 4 4 4] and of the eight destinations may be denoted [1 1 2 2 3 4 4 4]. The resulting inter-gate flows are easily found by adding up the interactions and are shown on Fig. 2. Examining the resulting solution shown in Fig. 2, note that all four inbound and outbound gates are used. Note that the four incoming spokes and the four outgoing spokes might be joined to form through connections, one possible solution would be to solve a small assignment problem [as in Eqs. (16), (17), (18), and (19) above]. In this case joining 1 to 1, 2 to 3, 3 to 2 and 4 to 4 is shown to be the solution that maximizes flows on the connections and those flows (5, 9, 24, 184) are emphasized on the diagram.

Fig. 2
figure 2

10 × 8 Node example. Notes: The thicker lines represent upgraded inter-gate linkages. The 4 × 4 table shows the interactions between the gates, with the upgraded inter-gate linkages highlighted

Full size image

Once the model is set up as an optimization task in standard software, experiments can be performed to test the result of adding extra constraints (like the added generalized assignment constraints) or modified data. Two added variants on the test data set are now introduced. The problems are set up to consider a number of variants on the location and clustering of the spokes and variations on the inter-facility distance.

First, various spatial clusters of the ten inbound and eight outbound nodes are taken into consideration: bundling the ten origins and eight destinations into groups, as shown in Fig. 3 where there are two, three, and four clusters respectively. Flows are regarded as arriving from separate originating sources, but they arrive near the hub at the same physical location (like having north and south regions send their component flows to the hub through a north and south entrance). From that entrance or arrival point the nodal flows are assigned to gates to minimize intra-facility distances. Unlike the nodes on feeders, considered below in Case 2, these flows may have distinct allocations.

Fig. 3
figure 3

Case 1 results for 2, 3, and 4 clusters of flows

Full size image

Second, the fact that the intra-facility distances may be more or less important is simulated by considering the in- and out-bound sides of the facility to be progressively closer together: i.e. at a distance of 1.0, 0.8, 0.6, 0.4, 0.2, and 0.0 units apart with this last case obviously signifying a long narrow linear facility. A total of 18 cases are therefore considered [three node cluster configurations × six facility layouts], and these are run without and with the gate-usage restriction. Numerical results for the 18 test runs are shown in Table 2. These show that the objective function is somewhat higher (of course) as a result of the added gate-usage restrictions, but more interesting is the explicit routing instructions that emerge as needed to force certain gate assignments.

Table 2 Case 1 for 18 test data instances
Full size table

The models are run for a variety of intra-facility distance parameter choices, one of which (intra-facility distance of 0.4) is shown in Fig. 3. In the top panel (i.e. results for two clusters) because the base model solution leaves several gates unused, the imposition of a gate usage rule requires at least a minimal amount of shifting of the allocations to insure that gates 2 and 3 are used. This also occurs in the middle panel which shows the results for three clusters; since every gate is not used, some adjustments are needed to accommodate constraints (10) and (11). Finally, in the bottom panel of that figure which shows results for four clusters, and because the model allocations actually use all the gates the extra constraint has no effect.

Comparative empirical results for the bounds on the objective functions are shown in Table 3 for the basic 10 × 8 example. Knowing the optimal solution in the present case allows us to gauge the quality of the lower bound, as well as determining if a reasonably good solution was derived as a by product of the Z variables. The interesting result of this small example experiment is that the lower bound quantity is tight compared to the initial BKS (ranging from 2.8% to 6.8%). However as the result of evaluating the primary objective function, note that an improved solution is found in many cases (i.e. a better solution is found between the BKS and the LB). These comparative bounds are given below in Table 3.

Table 3 Case 1 model runs for 10 × 8 system, with lower bound for comparison
Full size table

7.2 Case 2

When the ten and eight nodes are clustered the resulting aggregate inter-gate flows are obtained from Eq. (9). The model is solved for the aggregated flows data (see Table 1) and produces new gate assignments. Considering these inter-gate flows the optimal allocation of the improved linkages are shown in the colored boxes corresponding to the colored lines on the diagram (Fig. 4). The 2 × 2 case has a very high level of flow aggregation basically taking place on a pair of through lines, and a criss-cross pattern for the red to green line interchanges, as shown to the right of the diagram. below: For example, in the 3 × 3 case, the interactions between nodes 4,5,6 and a,b,c account for a total of 35 units of flow, and these are connected in the diagram on the “green” line. Clearly 7,8,9,10 to f,g,h is a very large flow (blue line) and this might require some capacity balance in a more elaborate case. When the system is organized into four incoming and outgoing feeder lines, the optimal organization of red, green, blue, and grey lines shown to the lower right of the figure. This chart shows which pairs of gates might be connected or given improved service capability. To be clear, the remaining inter-gate interactions still take place, but need to connect by movement from one gate area to another, in a manner akin to “walking from one platform to another” in the transit example.

Fig. 4
figure 4

Case 2 results for 2, 3, and 4 feeder lines. Notes: the connections between the colored lines are not shown for clarity, but it should be clear that the x and y gates are fully interconnected

Full size image

8 Conclusions and future work

The paper has suggested a class of problems that may have been overlooked in the literature: i.e. the handling of intra-facility flows at a hub or switching point. Handling such flows has been shown to give rise to a number of interesting matching and optimization problems. Among these, the idea of adapting the dock-door assignment problem to the hub flow issue, and the idea of selectively joining pairs of spokes to form through connections are especially ripe for further realistic modeling. Some simplifications adopted here would need to be expanded in an application: one would be a much larger scale of the number of nodes. As suggested in the review, subway and cross-dock problems pose considerable complex challenges in the real world. Secondly, the results and conclusions in this paper are dependent on the very simple numerical set up of the sample problem, but even within that framework a reasonable range of results is found and these are expected to be easy to generalize: depending on the spatial arrangement of the flows and the location of the gates relative to the inbound and outbound spokes, the actual usage and levels of flow between gates reflects intuitive levels of spatial organization.

The two special cases that are modeled here also seem to encompass the major representative problems. Variants on these problems are potential topics for further work, and would depend on the particular protocols that govern the network: a lot might depend for example on whether all the incoming flows on a feeder are permitted to disperse to the most suitable gates for the completion of their journeys, or if some kind of single allocation to a transfer node is a more fitting protocol.

For future expansion of these ideas, more realistic situations will need to be examined. Synchronizing and organizing the timing of arrivals and departures at hubs in a type of pulsed arrival and departure pattern is quite difficult (Bobzin 2005). Airlines manage this interdependence by organizing a set of inbound and outbound flights (Trietsch 1993). The difficulty of making those connections work in a very small time window (with the consequence of possible missed connections and the delay of outbound flights to accommodate the late arriving inbound passengers) has led to more relaxed timing. Recently, the idea has been modified to provide more slack between waves of arrivals to make sure that the time is sufficient to make the connections even if there are inbound delays. Also it is clear that a choreographed arrival and departure rate might be very sensitive to random disruption, and in a sense impossible to “get it right” all the time.

Future work such as the question of the optimal number of lines to switch at the same hub, the sensitivity of these issues to the basic number and interaction patterns of the underlying network nodes and the potential for the system to create a second or third hub will be dealt with in follow-up papers on particular extensions and applications.

A two hub version of this problem is similar to a single hub network except that the nodes can have interactions through a high capacity connector.

A security version of this problem would be to model the inter-terminal flows and to maximize the time spent in scrutiny—in other words to delay the traversal of the flows for the longest possible time. This is likely to be an inconvenient level of intervention however, and so the best practice might be to delay the highest risk material and permit the fastest passage for the least threat. As a contemporary and relevant security extension for the paper, note that the flows at a hub intermingle a variety of components. The inbound flows to a particular gate (or freight dock in logistics) comprise many elements that need to be dispersed to other nodes, and so traverse the hub to reach the appropriate outgoing gates. Suppose the components have varying densities of potential threat levels. The inter-gate flows are then a blend of a variety of rates and intensities: scrutiny might be targeted most intensively where the flows have the highest probability of intercepting a threat. Among the previously understudied aspects of this problem are the pairs of interactions to be provided with especially favored flow. This aspect of the problem has potential applications to security issues where certain through flows receive heightened scrutiny while others are given an automated clear path (EZ Pass, Clear Path, Electronic Data Exchange; these are various methods to assure a quicker passage through a check point). Because terrorist attacks often target busy transport facilities, the ideas here have relevance for the detection of vulnerable links; i.e. ones that involve a high amount of transfer from one line to another.

Future applications are also likely for planning bus routes. For example a realistic application was studied for the LakeTran bus system in Lake Co. Ohio where the towns spread out along a linear network served as the hub collection points for the local communities. In planning transfers for this Dial-a-Ride bus system the goal was to assess the probable impact on the expected number of stops and waits for a flexible on demand system feeding into a main line or backbone route; the convenience vs efficiency trade off was of great concern to the system operators.