Introduction

Heat transfer of any system can be enhanced by changing the flow geometry, boundary conditions, or by enhancing thermal conductivity of the fluid. In this direction, various techniques have been proposed to enhance the heat transfer characteristics of fluids. Researchers have also tried to increase the thermal conductivity of base fluids by suspending micro- or larger-sized solid particles in fluids, since the thermal conductivity of solid is typically higher than that of liquids. Numerous theoretical and experimental studies of suspensions containing solid particles have been conducted since Maxwell’s theoretical work was published more than 100 years ago (Yu et al. 2008). However, it has not been very successful for a system where settling of solid particles of suspension due to large size and high density of the particles occur.

Nanofluids are solid–liquid composite materials consisting of nanometer-sized solid particles, rods, or tubes suspended in different base fluids and they provide a promising solution for enhancing heat transfer because of improved stability compared with conventional fluids added with micrometer- or millimeter-sized solid particles. With such ultra-fine nanoparticles, nanofluids can flow smoothly in a system without clogging, and the size of the heat transfer system can be reduced considerably for the use of nanofluids with high heat transfer efficiency. Lee et al. (1999) and Wang et al. (1999) have demonstrated high heat transfer capabilities of nanofluids. They showed that alumina and copper oxide nanoparticles suspended in water and ethylene glycol significantly enhance the fluid thermal conductivity.

Hong et al. (2005) found non-linear enhancement of thermal conductivity of nanofluids with the volume fraction of iron nanoparticles. From the results of Xie et al. (2002), it is observed that effective thermal conductivity ratio increases with volume fraction of alumina nanoparticles. However, still there is a controversy toward enhancement of thermal conductivity of nanofluids. Putnam et al. (2006) reported no significant enhancement of thermal conductivity of Au/ethanol nanofluids. Liu et al. (2006) concluded that the enhancement of thermal conductivity may be due to higher thermal conductivity and difference in morphology between the particles. Shou and Chen (2006) found that the thermal conductivity of nanofluids increases significantly with temperature for different types of nanofluids. The same was also observed by Patel et al. (2003) and Das et al. (2003). Zhu et al. (2006) found that the abnormal and nonlinear increase of thermal conductivity of Fe3O4/H2O nanofluids was attributed to the nanoparticles clustering and alignment. The same was also accepted by Hong et al. (2005, 2006). They found that the nanofluids containing Fe nanoparticles showed a more effective thermal transport property than nanofluids containing Cu nanoparticles dispersed with little agglomeration.

During the current decade, several efforts have been undertaken to model the thermal conductivity of nanofluids. Keblinski et al. (2002) assessed various mechanisms of heat transfer at nano-scale; however, they indicated that none of the mechanisms could justify the anomalous enhancement of thermal conductivity. In fact, many factors such as particle shape and size, volume fraction, thermal conductivity of the nanoparticles, viscosity, temperature and thermal conductivity of base fluids, interface between liquid and nanoparticles, membrane of liquid molecules around the nanoparticles, and others may influence the thermal conductivity of nanofluids, and it is very difficult to predict the proportion of the influence of these factors. Many experimental investigations on the factors influencing thermal conductivity of nanofluids have been reported. However, these factors were not considered while deriving the models.

Yu and Choi (2003) proposed a modified Maxwell’s model based on the effective medium theory by considering the effect of nano-layer. The same effect was also considered by them in case of non-spherical particles (Yu and Choi 2004). Xue (2003) developed a model based on Maxwell’s theory and average polarization theory to predict effective thermal conductivity of nanofluids by considering the effect of interface between the solid particles and the base fluid. Xue and Xu (2005) derived an equation based on Bruggeman model where they considered the effect of interfacial shells between the nanoparticles and the base fluids. Xie et al. (2005) proposed an effective thermal conductivity of nanofluids by considering the effect of different factors such as nano-layer thickness, particle size, volume fraction, etc. Xuan et al. (2003) considered the Brownian motion of the nanoparticles and proposed a modified equation to calculate effective thermal conductivity of nanofluids. Wang et al. (2003) proposed a model based on the effective medium approximation and the fractal theory to predict thermal conductivity of nanofluids. Jang and Choi (2004) considered four modes of energy transport in the nanofluids such as (i) collision between base fluid molecules, (ii) thermal diffusion of nanoparticles in fluids, (iii) collision between nanoparticles due to Brownian motion, and (iv) thermal interaction of dynamic nanoparticles with the base fluid molecules to calculate a new theoretical model to predict thermal conductivity of nanofluids. Koo and Kleinstreuer (2004) proposed a model by considering Brownian motion of the particles. Hemanth et al. (2004) applied kinetic theory approach to model the effective conductivity where they considered the dependence of thermal conductivity on particle size and temperature. However, the limitation of their model was that they considered an empirical constant “c” which depends of particle–fluid combination for different concentrations and conditions which is required to be determined experimentally. Prasher et al. (2006) have presented a model based on the fractal theory using Monte Carlo simulation. They have shown the effect of aggregation structure on prediction of thermal conductivity of nanofluids and the rapid increase in thermal conductivity of nanofluids at lower concentrations. Evans et al. (2006) concluded that thermal conductivity of nanofluids can be described by the effective medium theory based on molecular dynamics simulation. They found no significant enhancement of thermal conductivity of nanofluids due to the effects associated with Brownian motion of the particles in the fluid. Keblinski et al. (2008) concluded that the effective medium theories for composite materials were capable of explaining the experimental data without considering the Brownian motion induced by the micro-convection. Nie et al. (2008) have explained different anomalies for the high-thermal conductivity enhancement of nanofluids. A detailed survey on the available experimental results and theoretical models on thermal conductivity of nanofluids is provided by Li et al. (2009). Although different experimental phenomenon and theoretical analysis were reported, there is no accepted conclusion on thermal conductivity enhancement of nanofluids. Thus, more theoretical and experimental works are required to be carried out.

From the above discussion, it is observed that a lot of effort has gone into the modeling of thermal conduction in nanofluids; however, none has been very successful in correctly satisfying the experimental results obtained by different researchers. All the available models have successfully validated for their own experimental results. However, an attempt was not made to develop a single model which could satisfy the available published results from different literatures. In this direction, an attempt was made to predict thermal conductivity of nanofluids and validated with published results. Most of the models predict a linear dependence of thermal conductivity enhancement with respect to the particle concentration. On the contrary, the recent experimental data such as those by Hong et al. (2005), Liu et al. (2006), Ponmozhi et al. (2010), and many other experiments confirmed that there is a non-linear dependence of conductivity enhancement on the particle concentration over a wide range of volume fractions.

It is known that Maxwell’ model on thermal conductivity of composite materials (Yu et al. 2008) considers the effect of particle concentration, particle and fluid conductivity. The effect of particle shape was considered by Hamilton and Crosser (1962), which is a modified version of Maxwell’s equation. However, both Maxwell’s model and Hamilton’s model have not considered the effect of particle size and temperature on thermal conductivity of the nanofluids. It is, therefore, important to look into the mechanism of thermal conduction in nanofluids more closely and form a suitable model to predict the thermal behavior of nanofluids. Since Maxwell’s model for thermal conductivity gives accurate predictions for macro particles, any model predicting thermal conductivity of nanoparticles should also give matching results with Maxwell’s model for macro particles.

Description of model

In the present model, the particles are assumed to be spherical and mono-dispersed, without agglomeration in a liquid. The particles have low concentration (approx. <2%), in which, inter-particle interactions are assumed to be negligible. The thermal conductivity given by Maxwell’s model and the micro-convective heat transfer of the nanoparticles due to their Brownian motion in the liquid are coupled in order to derive a model in which thermal conductivity is a function of temperature, viscosity, and particle size. Thermal conductivity of the nanofluids is estimated by coupling the heat conduction given by Maxwell with heat transfer coefficient due to micro-convection of the particles. In order to develop a model for thermal conductivity, three modes of heat transfer are assumed to be prevalent in nanofluid viz., conduction through liquid, conduction through particles, and micro-convection around particles moving in a liquid as suggested by Jang and Choi (2004). The proposed model has been validated against a wide range of experimental results available in the literatures.

The heat transfer in nanofluids is due to two prominent factors, which are as follows:

  1. 1.

    Conduction through nanoparticles and base fluid.

  2. 2.

    Micro-convection due to Brownian motion of nanoparticles.

The relative velocity between the particles, the fluid arises from the Brownian motion, and the random movement of nanoparticles can be considered as being akin to the eddy motion in turbulent flow. As the statistically random velocity fluctuations caused by turbulent eddies enhance the rate of transport in nanofluids, the random Brownian motion of particles in nanofluids enhances the rate of heat transport. The prominent factors mentioned above were incorporated in two different steps. In a first step, it is assumed that initially the particles are at rest in the base fluid. Since there is no Brownian motion, there will be no heat transfer due to micro-convection in the nanofluids. The thermal conductivity of the nanofluid will be equal to that of the results given by Maxwell equation and it is given by Eq. 1.

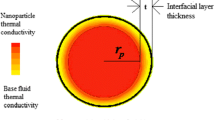
$$ k_{\text{m}} = \left[ {{\frac{{k_{\text{p}} + 2k_{\text{f}} + 2(k_{\text{p}} - k_{\text{f}} )v_{\text{f}} }}{{k_{\text{p}} + 2k_{\text{f}} - (k_{\text{p}} - k_{\text{f}} )v_{\text{f}} }}}} \right]k_{\text{f}} . $$
(1)

In the second step, the Brownian motion and heat transfer due to micro-convection were incorporated. It is assumed that there is a unit cell of liquid having Maxwell’s thermal conductivity (k m) inside which there is a single nanoparticle. The particle is located at middle of the unit cell having the dimensions of ‘l’. The particle diameter is ‘d p’. A similar approach was used by Patel et al. (2008). The volume of the cell is equal to the suspension volume (liquid + particle) per nanoparticle, which is calculated from the volume fraction ratio and the particle size for a homogeneous suspension, and the method of calculation is given below:Number of nanoparticles per unit volume of suspension

$$ n = {\frac{{v_{\text{f}} }}{{{\frac{\pi }{6}}d_{\text{p}}^{3} }}} $$
(2)

Volume of nanofluid suspension per nanoparticle

$$ l^{3} = \frac{1}{n}, $$

where

$$ l \; = \;{\text{length of cubical cell}}\; = \;\left( {{\frac{\pi }{{6\,v_{\text{f}} }}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} d_{\text{p}} . $$
(3)

As discussed above, the heat transfer between two faces of the unit cell is possible by:

  1. 1.

    the thermal conductivity of fluid (k m) and

  2. 2.

    the convective heat transfer due to particle motion.

The convective resistance between the liquid and the nanoparticle can be expressed in terms of the particle interfacial heat transfer coefficient (h), which depends on the particle velocity. The above discussed heat transfer modes in a nanofluid can be represented by thermal resistance form, which can be represented by Fig. 1.

Fig. 1
figure 1

Two modes of heat transfer in a thermal resistance form. R c the thermal resistance due to convection in a nanofluid, R m the Maxwell’s thermal resistance

Full size image

The effective thermal resistance of the circuit is given by

$$ {\frac{1}{{R_{\text{eff}} }}} = {\frac{1}{{R_{\text{m}} }}} + {\frac{1}{{R_{\text{c}} }}}, $$
(4)

where \( R_{\text{m}} = {l \mathord{\left/ {\vphantom {l {k_{\text{m}} A_{\text{m}} ,}}} \right. \kern-\nulldelimiterspace} {k_{\text{m}} A_{\text{m}} ,}} \) k m, and A m represent the thermal conductivity and cross-sectional area of the liquid medium participating in heat conduction through path I. The convective heat resistance can be expressed by \( R_{\text{c}} = {1 \mathord{\left/ {\vphantom {1 {hA_{\text{s}} }}} \right. \kern-\nulldelimiterspace} {hA_{\text{s}} }} \) and thus the effective thermal resistance of the circuit is given by

$$ {\frac{1}{{R_{\text{eff}} }}} = {\frac{{k_{\text{m}} A_{\text{m}} }}{l}} + hA_{\text{s}} , $$
(5)

where \( A_{\text{s}} = \pi d_{\text{p}}^{2} \), \( A_{\text{m}} = {\frac{{(l^{3} - {\frac{\pi }{6}}d_{\rm p}^{3} )}}{l}} \approx l^{2} . \)

The total heat flux through the cell under consideration can be given as: \( q_{\text{eff}} = {{\Updelta T} \mathord{\left/ {\vphantom {{\Updelta T} {R_{\text{eff}} }}} \right. \kern-\nulldelimiterspace} {R_{\text{eff}} }} \). Assuming that q f is the heat transfer through a unit cell when there are no nanoparticles used

$$ q_{\text{f}} = {\frac{\Updelta T}{{R_{\text{f}} }}} = {\frac{{k_{\text{f}} A_{\text{f}} }}{l}}\Updelta T = {\frac{{k_{\text{f}} A_{\text{m}} }}{l}}\Updelta T $$
(6)

since \( A_{\text{f}} = l^{2} \approx A_{\text{m}} \). Therefore, heat flux ratio is given by

$$ {\frac{{q_{\text{eff}} }}{{q_{\text{f}} }}} = {\frac{{R_{\text{f}} }}{{R_{\text{eff}} }}} = {\frac{l}{{k_{\text{f}} A_{\text{m}} }}}\left[ {{\frac{{k_{\text{m}} A_{\text{m}} }}{l}} + hA_{\text{s}} } \right]. $$

Thus,

$$ {\frac{{q_{\text{eff}} }}{{q_{\text{f}} }}} = {\frac{{k_{\text{m}} }}{{k_{\text{f}} }}} + {\frac{{hA_{\text{s}} l}}{{k_{\text{f}} A_{\text{m}} }}}, $$
(7)

where \( h = {{k_{\text{p}} Nu} \mathord{\left/ {\vphantom {{k_{\text{p}} Nu} {d_{\text{p}} }}} \right. \kern-\nulldelimiterspace} {d_{\text{p}} }}. \)

The Nusselt number in case of the convective heat transfer over a spherical particle at low Peclet number is given by (White 1991):

$$ Nu = 2 + 0.5Pe + f(Pe^{2} ). $$
(8)

The Nusselt number correlation given in Eq. 8 is applicable for spherical particles exchanging heat convectively with a liquid medium at very low Reynolds numbers, i.e., Re ≪ 1 and Pe ≪1. Here, the size of the particles is in the order of 10−7 to 10−8 m and the Brownian motion velocity is also very low (≈10−3 to 10−4 m/s); hence Pe 2 is negligible compared to that of Pe. Since the heat conduction through the liquid and the particles is already accounted separately using Maxwell’s thermal conductivity, only the advection part in the convection correlation needs to be considered additionally. Thus, the first term “2,” which corresponds to the conduction, is omitted and the heat transfer coefficient h is evaluated from a simplified expression of the form

$$ Nu = 0.5Pe. $$
(9)

Peclet number is given by \( Pe = {{u_{\text{p}} d_{\text{p}} } \mathord{\left/ {\vphantom {{u_{\text{p}} d_{\text{p}} } {\alpha_{\text{m}} }}} \right. \kern-\nulldelimiterspace} {\alpha_{\text{m}} }} \)

$$ h = {\frac{{k_{\text{p}} Pe}}{{2d_{\text{p}} }}} = {\frac{{k_{\text{p}} u_{\text{p}} }}{{2\alpha_{\text{m}} }}}. $$

In the present model, u p is proposed to be the Brownian motion velocity of particles given by Keblinski et al. (2002):

$$ u_{\text{p}} = {\frac{{2k_{\text{b}} T}}{{\pi \mu d_{\text{p}}^{2} }}},\quad h = {\frac{{k_{\text{p}} Pe}}{{2d_{\text{p}} }}} = {\frac{{k_{\text{p}} u_{\text{p}} }}{{2\alpha_{\text{m}} }}} = {\frac{{k_{\text{p}} k_{\text{b}} T}}{{\pi \alpha_{\text{m}} \mu d_{\text{p}}^{2} }}}. $$

Thus, Eq. 7 can be written as:

$$ \begin{aligned} {\frac{{q_{\text{eff}} }}{{q_{\text{f}} }}} &= {\frac{{k_{\text{m}} }}{{k_{\text{f}} }}} + {\frac{{k_{\text{p}} k_{\text{b}} T}}{{\pi \alpha_{\text{m}} \mu d_{\text{p}}^{2} }}}{\frac{{A_{\text{s}} l}}{{k_{\text{f}} A_{\text{m}} }}} \hfill \\ &= {\frac{{k_{\text{m}} }}{{k_{\text{f}} }}} + {\frac{{k_{p} k_{b} T}}{{\pi \alpha_{\text{m}} \mu d_{\text{p}}^{2} }}}{\frac{{\pi d_{\text{p}}^{2} l}}{{k_{\text{f}} l^{2} }}}\quad ({\text{since}}\;A_{\text{m}} \approx l^{2} ) \hfill \\ \end{aligned} $$
$$ {\frac{{q_{\text{eff}} }}{{q_{\text{f}} }}} = {\frac{{k_{\text{m}} }}{{k_{\text{f}} }}} + {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}}{\frac{{k_{\text{b}} T}}{{\alpha_{\text{m}} \mu }}}\left( {\frac{1}{l}} \right) $$
$$ {\frac{{q_{\text{eff}} }}{{q_{\text{f}} }}} = {\frac{{k_{\text{m}} }}{{k_{\text{f}} }}} + {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}}{\frac{{k_{\text{b}} T}}{{\alpha_{\text{m}} \mu d_{\text{p}} }}}\left( {{\frac{{6v_{\text{f}} }}{\pi }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} . $$

Thus, the heat transfer ratio becomes

$$ {\frac{{q_{\text{eff}} }}{{q_{\text{f}} }}} = \left[ {{\frac{{k_{\text{p}} + 2k_{\text{f}} + 2(k_{\text{p}} - k_{\text{f}} )v_{\text{f}} }}{{k_{\text{p}} + 2k_{\text{f}} - (k_{\text{p}} - k_{\text{f}} )v_{\text{f}} }}}} \right] + {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}}{\frac{{k_{\text{b}} T}}{{\alpha_{\text{m}} \mu d_{\text{p}} }}}\left( {{\frac{{6v_{\text{f}} }}{\pi }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} . $$
(10)

Although the present model has considered the thermal resistances in parallel configuration appropriately, the actual representation of the resistances in the form of equations can only be considered approximate; this is in view of the fact that the heat flow in the neighborhood of the spherical particle is strictly not one dimensional.

Results and discussion

The present model has been validated against a variety of experimental data available in the literature. Figure 2 shows the comparison of upper and lower limits of experimental results and the values of thermal conductivity enhancement predicted from the theoretical model for alumina and titanium oxide-based nanofluids for different concentration of nanoparticles. It is observed that the values predicted from the model are within the range of experimental results as suggested by Pak and Cho (1998).

Fig. 2
figure 2

Comparison of predicted values and experimental results of Al2O3 and TiO2 (Pak and Cho 1998)

Full size image

Figure 3 shows the comparison of the experimental results of Chon and Kihm (2005) with the proposed model for Al2O3 at 294 and 344 K for the variation of particle diameter. It is observed that with an increase in size of nanoparticles, the thermal conductivity decreases exponentially and then it becomes nearly constant at higher size of nanoparticles, at 150 nm. This is the range for which it satisfies with Maxwell’s results. It is also observed that thermal conductivity ratio is found to increase with an increase of temperature. The same trend was also observed for the experimental results. Both the temperature and particle size effect were not considered by the Maxwell’s model, whereas the influence of these parameters were confirmed experimentally. The effect of size was strongly observed in the thermal conductivity of nanofluids where high-specific surface area of nanoparticles facilitates large heat transfer between the liquid and the particles, thereby increasing the effective heat transfer capacity of the suspension. Both the predicted values and experimental results are found to be the same trend, and the results predicted by the model lie within ±5% of experimental values. However, the Maxwell’s’ equation predicts that thermal conductivity remains constant with change in the size of the nanoparticles but the proposed model correctly predicts the trend observed from the experimental results as suggested by Chon and Kihm (2005).

Fig. 3
figure 3

Effect of particle size and temperature on thermal conductivity of alumina-based nanofluids

Full size image

The Brownian motion velocity is found to be higher for the lower particle size, which results in larger heat transfer by virtue of micro-convection. In the literature, very little experimental data are available for a particular system with particle size variation. Figure 4 shows the experimental data of Cu–water-based nanofluid solution (Liu et al. 2006). It is noteworthy to mention that the increase in thermal conductivity is higher for metallic powder-based nanofluid as compared to metallic oxides because of the higher thermal conductivity of base metal. The Maxwell’s model gives nearly no increase in thermal conductivity at this low concentration, whereas the results obtained from the proposed model matches with experimental results of Liu et al. (2006). The nature of graph obtained from the proposed model is exactly same as in case of Liu et al. (2006) for the Cu-based nanofluid. Figure 4 also shows the comparison of experimental and predicted values of thermal conductivity for Al2O3 and CuO as suggested by Lee et al. (1999). In both cases, the results obtained from the proposed model are well within the experimental results, i.e., ±5%, which justified the selection of the proposed model.

Fig. 4
figure 4

Nanofluid enhancement study for different concentration and different particles

Full size image

Figure 5 shows the thermal conductivity of Al2O3 for different concentrations of particle size, e.g., 10, 50, and 150 nm. The following observations can be derived from the results: firstly, thermal conductivity of nanofluids increases by increase in both particle concentration and particle size. This observation has already been confirmed by the experimental results. Secondly, with an increase of the particle size, i.e., above 150 nm, the predicted results match with Maxwell’s model. This proves that the proposed model satisfies the Maxwell’s results for macro particle, i.e., the developed model also satisfies classical model for predicting thermal conductivity for macro-sized particles.

Fig. 5
figure 5

Variation of thermal conductivity with volume fraction and particle size for alumina-based nanofluids

Full size image

Conclusions

A theoretical model has been proposed to predict the thermal conductivity enhancement of nanofluids. The heat transfer contributions from liquid–solid conduction and micro-convection around particles are considered separately using thermal resistance modeling. The diffusion velocities of particles due to Brownian motion are used for the modeling of micro-convection around the nanoparticles.

It is concluded that the predicted results from the proposed model lie within ±5% of the experimental results. This slight variation can be attributed to the fact that the properties such as viscosity and thermal diffusivity of the fluid will have slight variations, which are not available in the literatures.

The dependence of thermal conductivity of nanofluids on particle concentration follows a combination of Maxwell’s law and one-third power law. The predicted values are reasonably accurate over a wide range of parameters like particle volume fraction, temperature, and particle size, and the model is also found to be working well for different nanofluid systems like suspension of insulating particles (oxides), conducting particles (like copper) suspended in conducting liquid (water). The present model is able to clearly bring out the non-linear dependence of thermal conductivity of nanofluids at low volume fraction of particles. The developed model successfully predicts the strong temperature dependence on the thermal conductivity of nanofluids where higher dependence on thermal conductivity was observed at nanolevel particle size.