Introduction

Molecular dynamics is becoming an increasingly important tool in gaining a better understanding about numerous heat transfer research problems. Many problems in this field require modeling the fluid–solid wall boundary condition across which the heat transfer takes place. Numerous models have been proposed and developed in literature.

Abraham (1978), in a pioneering study, used four wall models to study the interfacial fluid density profile of solid/liquid interface systems using Monte Carlo simulations: (a) Lennard-Jones (L-J) atoms were placed and constrained to remain at the lattice sites of first two planes of an fcc solid termed L-J (100) wall, (b) discrete centers of interaction in each solid plane were replaced by a continuous distribution of Lennar-Jones atoms with uniform planar density leading to the L-J 10-4 wall model, (c) proposed “Boltzmann weighted” wall whose potential is proportional to the probability that a single molecule is at a distance z from the (100) wall irrespective of its x, y coordinates, (d) the “Hard wall” whose potential is infinite if an atom penetrates the wall structure, and zero otherwise.

Xu and Li (2007), Thompson and Troian (1997), Priezjev (2007), Voronov et al. (2006) arranged the solid wall atoms in a crystalline structure and remained fixed during the whole computation process. The fluid atoms were coupled with a thermostat to assign a specific temperature to the fluid. Koplik et al. (1989), to study microscopic aspects of slow viscous flows past a solid wall, set the wall atoms into an initial fcc lattice structure and assigned them a heavy mass m H = 1010m allowing them to move according to the equations of motion. The walls would retain their integrity during the course of the simulation as well as conserve energy in collisions, but eventually disintegrate theoretically.

Xu and Zhou (2004) studied Poiseuille flow in a nanoscale channel using a thermal wall model. The wall atoms are arranged in a fcc structure and remain fixed during the simulation. According to the model, when a liquid particle strikes the wall, all three components of velocities are reset to a biased Maxwellian distribution and the direction of the z-component velocity is set away from the wall; the criteria for liquid atom ‘striking’ the wall was not mentioned.

Markvoort et al. (2005) looked into the dependence of wetting on solid–gas interface for different density gases. The walls were constructed in a different simulation by randomly placing the wall atoms, governed by L-J potential, in a simulation box and giving them a high temperature. The domain was then cooled down and the system was crystallized, which was placed in a wider box forming a wall. None of the wall atoms were fixed or restricted. However, it was seen that as the mass of the wall was so large compared to a single gas particles that a single collision hardly affected the wall and the wall atoms keeps their positions.

Drazer et al. (2005) used molecular dynamics simulation to study the behavior of closely fitting spherical and ellipsoidal particles moving through a fluid-filled nanoscale cylinder. The cylindrical wall was composed of atoms of mass m w = 100 tethered to fixed lattice sites by a stiff linear spring. Heat transfer between wall and fluid was not considered in the model.

Spijker et al. (2008) developed a new particle wall boundary condition to replace solid walls. The new condition is based on averaging the contributions of an explicit solid wall and allows for different crystal lattices to be included. Wemhoff and Carey (2005) replaced the solid wall by deriving a wall potential to bind a liquid argon film to the imaginary wall, in order to reduce computational cost. The wall potential depends on the approximated values of Hamaker constant for metal–metal and fluid–fluid interaction. The system pressure was adjusted to an equilibrium value using a flux boundary. The model did not include heating/cooling of fluid by the wall atoms.

Yang (2006) simulated a plane wall where the wall atoms were anchored to their respective lattice sites by a harmonic restoring force. The wall atoms interacted by the L-J potential, and a Gaussian isokinetic thermostat was used to adjust the wall temperature to a constant value at each time step. Ziarani and Mohamad (2008) used a similar method of spring force but used velocity rescaling to achieve constant wall temperature instead of a thermostat. In addition, the first five molecules at the two end of each layer were completely frozen to avoid walls being washed away by fluid molecules.

Maruyama and Kimura (1999), Ohara and Suzuki (2000), Yi et al. (2002), Nagayama and Cheng (2004) modeled the solid wall as (111) fcc structure made up of three layers of solid atoms governed by a harmonic potential. Outside the three layers, ‘phantom’ molecules were used to maintain the solid atoms at a specified mean temperature resembling a Langevin thermostat.

The reason that such various models have been introduced in the past is that no one particular model has been accepted by all researchers; the biggest concern is that the actual physics of the any heat transfer model may not be properly depicted. Wall models need to be thoroughly validated to show their physical soundness. Maroo and Chung (2008) proposed a novel ‘fluid–wall thermal equilibrium model’ in a recent work. Validations were done by evaluating physical properties of thermal conductivity and change in internal energy of fluid between two walls and comparing them to thermodynamic tabulated values; these validations were state-dependent and time independent. In this work, the proposed model is tested against the time-dependent analytical solution of 1-D heat equation. The physical soundness of the model is shown along with new insight into heat transfer in nanochannels. The model allows for simulations of constant wall temperature and heat flux problems, and partial wall heating/cooling and is less computationally demanding.

Molecular dynamics simulation method

The basis of the molecular dynamics (MD) simulation can be stated as follows: as every substance is made from elementary particles (atoms/molecules) and if the basic dynamic parameters of these molecules (i.e. position, velocity and interaction force) can be determined, the physical properties of the substance, like temperature, pressure, etc. can be obtained from those dynamic parameters using statistical methods. All MD simulations follow Newton’s second law in its simple form for simple atomic systems or in a more generalized form (Lagrangian/Eulerian formulation) for complex geometry systems. The force on each molecule by all other molecules in the system can be determined by using the molecular interaction potential function. From this force, the equation of motion can be integrated over time to obtain the new positions and velocities of each molecule. This information can be statistically analyzed by space/time averaging to provide macroscopic physical properties, and thus the evolution of the system can be studied.

Simulation models and algorithms

The computational domain is a cuboid expressed in Cartesian coordinates with the z-direction denoting the height of the domain. The domain consists of a platinum (Pt) wall and argon (Ar) fluid. Pt atoms, arranged in fcc (111) structure as shown in Fig. 1, constitute the Pt wall. The distance between the argon atoms was calculated as follows: knowing the volume occupied by liquid argon, the saturation density at the equilibration temperature (from argon thermodynamic tables) is used to obtain the total mass of liquid argon, which divided by the mass of an argon atom gives the total number of liquid (or vapor) argon atoms. The interatomic distance between the atoms is then obtained assuming they are arranged in a simple cubic structure. The argon atoms are arranged by this interatomic distance thus defining the initial structure of the domain. The atomic interaction is governed by the modified Lennard-Jones potential as defined by Stoddard and Ford (1973):

$$ U_{\text{MLJ}} (r) = 4\varepsilon \left[ {\left\{ {\left( {{\frac{\sigma }{r}}} \right)^{12} - \left( {{\frac{\sigma }{r}}} \right)^{6} } \right\} + \left\{ {6\left( {{\frac{\sigma }{{r_{\text{cut}} }}}} \right)^{12} - 3\left( {{\frac{\sigma }{{r_{\text{cut}} }}}} \right)^{6} } \right\}\left( {{\frac{r}{{r_{\text{cut}} }}}} \right)^{2} - \left\{ {7\left( {{\frac{\sigma }{{r_{\text{cut}} }}}} \right)^{12} - 4\left( {{\frac{\sigma }{{r_{\text{cut}} }}}} \right)^{6} } \right\}} \right] .$$
(1)
Fig. 1
figure 1

Arrangement of Pt wall atoms in fcc(111) structure. a 3-D view of the first three layers. b X–Y projection (top view) of the wall atoms

Full size image

The above potential form is employed for both Ar–Ar and Ar–Pt interaction with the following values [6]: σ Ar–Ar = 3.4 × 10−10m, ɛ Ar–Ar = 1.67 × 10−21J, σ Ar–Pt = 3.085 × 10−10m,  ɛ Ar–Pt = 0.894 × 10−21J. The cutoff radius is set as r cut = 4σ Ar–Ar. The force of interaction can be calculated from the potential function as follows: \( \vec{F} = - \nabla U \). The argon atoms are subjected to six boundaries, two in each of the x, y, and z-directions. The boundaries in the x and y-directions are periodic. The boundaries in the z-direction are the Pt walls. Dimensionless parameters are used in this work. The use of dimensionless parameters in molecular dynamics is very helpful due to several reasons (Rapaport 1995).

The force interaction for Ar–Ar and Ar–Pt can be deduced to the following equations:

$$ \begin{gathered} {\text{Ar-Ar}}\;{\text{interaction}} \hfill \\ \ddot{r}_{i}^{\ast} = 48\sum\limits_{j( \ne i)} {\left( {r_{ij}^{\ast\, - 14} - 0.5\,r_{ij}^{\ast\, - 8} - r_{\text{cut}}^{\ast\, - 14} + 0.5\,r_{\text{cut}}^{\ast\, - 8} } \right)} \,\vec{r}_{ij}^{\ast} \hfill \\ \end{gathered} $$
(2)
$$ \begin{gathered} {\text{Ar-Pt}}\;{\text{interaction}} \hfill \\ \ddot{r}_{i}^{\ast} = 48\left( {{\frac{{\varepsilon_{\text{Ar-Pt}} }}{{\varepsilon_{\text{Ar}} }}}} \right)\sum\limits_{j( \ne i)} {\left( {\left[ {{\frac{{\sigma_{\text{Ar-Pt}} }}{{\sigma_{\text{Ar}} }}}} \right]^{12} r_{ij}^{\ast\, - 14} - 0.5\,\left[ {{\frac{{\sigma_{\text{Ar-Pt}} }}{{\sigma_{\text{Ar}} }}}} \right]^{6} r_{ij}^{\ast\, - 8} - \left[ {{\frac{{\sigma_{\text{Ar-Pt}} }}{{\sigma_{\text{Ar}} }}}} \right]^{12} r_{\text{cut}}^{\ast\, - 14} + 0.5\left[ {{\frac{{\sigma_{\text{Ar-Pt}} }}{{\sigma_{\text{Ar}} }}}} \right]^{6} \,r_{\text{cut}}^{\ast\, - 8} } \right)} \,\vec{r}_{ij}^{\ast} \hfill \\ \end{gathered}. $$
(3)

The algorithm used to calculate the atomic force interactions is the linked-cell algorithm which is a cell-based method and involves data organization (Allen and Tildesley 1987). The equations of motion need to be integrated in order to obtain the positions and velocities of the atoms at every time step. Thus, after calculating the force of interaction from the potential function, Newton’s second law is used to determine the acceleration:

$$ \vec{F}_{i} = m_{i} \vec{a}_{i} \Rightarrow {\frac{{{\text{d}}^{2} \vec{r}_{i} }}{{{\text{d}}t^{2} }}} = {\frac{{\vec{F}_{i} }}{{m_{i} }}} $$
(4)

where \( \vec{F} \) is the force acting on atom i, and m and \( \vec{a} \) are its mass and acceleration, respectively. Using the acceleration, the position and velocities are obtained via the integrator method. The integrator method used here is the Velocity-Verlet method:

$$ r(t + \Updelta t) = r(t) + \Updelta t\;v(t) + {\frac{{\Updelta t^{2} \,a(t)}}{2}} $$
(5a)
$$ v(t + {{\Updelta t} \mathord{\left/ {\vphantom {{\Updelta t} {2)}}} \right. \kern-\nulldelimiterspace} {2)}} = v(t) + {\frac{\Updelta t\,a(t)}{2}} $$
(5b)
$$ v(t + \Updelta t) = v(t + {{\Updelta t} \mathord{\left/ {\vphantom {{\Updelta t} {2)}}} \right. \kern-\nulldelimiterspace} {2)}} + {\frac{\Updelta t\,a(t + \Updelta t)}{2}}. $$
(5c)

The advantage of this method is that the calculation of velocities is in phase with that of the positions. Also, this method calculates the velocities more accurately than the Verlet and leap-frog methods (Sadus 1999).

Fluid–wall thermal equilibrium model

The heat transfer from the heated wall to the fluid is simulated with the following wall–fluid interaction mechanism. The wall–fluid thermal energy transfer interaction is constituted of two parts: (1) interaction potential model (LJ potential), and (2) proposed ‘fluid–wall thermal equilibrium model’ (to numerically simulate heat transfer between wall and fluid atoms). The interaction potential model, using the LJ potential, is a standard method as it has been used by many researchers in molecular dynamics approach. The fluid–wall thermal equilibrium model is presented in details below.

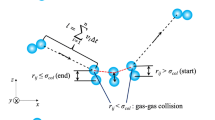
Figure 2 shows the schematic of the fluid-heated wall thermal equilibrium model. The Pt atoms constituting the heated wall are assumed to be fixed in space, and do not move at any time during the simulation since for a solid, their range of movement is relatively much restricted than those of the fluid atoms. The fluid–wall thermal energy exchange is simulated as follows: the Pt wall is specified a constant temperature, and an argon atom reaches this temperature (i.e. the atom is assigned a corresponding velocity by instantaneous velocity scaling; direction of the atom is not changed) by “coming in thermal equilibrium with” the temperature of the wall. The force due to the wall atoms on the fluid atoms is either attractive or repulsive depending on the distance between the two due to the nature of the Lennard-Jones potential. A distance r cr, less than r cut, is defined as the neutral position of wall influence. Accordingly, any fluid atom on the z = r cr, as shown in Fig. 2, would experience a zero force from the first layer wall atom that is located at the shortest distance from this fluid atom. It is noted that this fluid atom would experience only attractive forces from other wall atoms as the distance between this fluid atom and other wall atoms are all larger than that shortest distance Therefore, any fluid atom will has to get below z = r cr (i.e., in region 3) to have any chance of experiencing a repulsive force from the wall atoms. On the basis of the above scenarios, the fluid atoms can be divided into three groups based on their locations in the respective regions near the wall as shown in Figure 2.

Fig. 2
figure 2

Constant wall-temperature boundary condition

Full size image

  • Region 1: z > rcut: The fluid atoms which are above the cutoff radius do not experience any force from the wall atoms.

  • Region 2:z < rcut and z > rcr: In this region, the fluid atoms only experience an attractive force by the wall atoms due to the nature of the L-J potential.

  • Region 3: z < rcr: In this region, the fluid atoms can experience either an attractive force or a repulsive force due to the wall atoms.

The physical mechanism of a fluid receiving heat from a solid wall is composed of a two-stage force interaction that results in an energy transfer from the hot wall to the fluid atoms. During the first stage, the fluid atom is accelerated toward the wall atoms by the attractive force. The fluid atom would then reach a zero force point before being bounced back by a repulsive force. Therefore, a fluid atom is considered to be heated up to the wall temperature only when: (a) the atom is in region 3 as it can only experience a repulsive force from wall atoms in this region and the repulsive force is the indispensible second stage of the heat exchange interaction mentioned above (b) the magnitude of the z-component force due to the wall atoms \( \left| {\ddot{r}_{\text{{\it z}-fluid-wall}} } \right| \)is greater than the z-component of the attractive/repulsive force due to the neighboring fluid atoms, \( \left| {\ddot{r}_{\text{{\it z}-fluid-fluid}} } \right| .\) This condition is based on the concept that the fluid atom must be primarily dominated by the wall force in order to satisfy the requirement that it is receiving energy from the wall atoms. These proposed criteria allow us to numerically simulate the energy exchange due to collisions between the fluid atoms and the wall. The criteria are summarized below:

$$ {\text{Thus, if }}\left\langle \begin{aligned} &{\text{fluid atom is in region 3}} \hfill \\ &{\text{and}} \hfill \\ &\left| {\ddot{r}_{\text{{\it z}-fluid-wall}} } \right| > \left| {\ddot{r}_{\text{{\it z}-fluid-fluid}} } \right| \hfill \\ \end{aligned} \right. \, \left. \begin{aligned} \hfill \\ \hfill \\ \hfill \\ \end{aligned} \right\}\;\;{\text{fluid atom is heated up to the wall temperature}} . $$

At each time step, the fluid atoms which meet the above criteria are identified and randomly assigned temperatures within ±1 K of the wall temperature such that the mean value of the temperatures for these atoms equals the wall temperature.

The step-change in wall temperature incorporated in this model theoretically corresponds to a wall with an infinite thermal conductivity, and the heating time period of the wall is neglected. This was again taken as a reasonable assumption for highly conductive metallic materials since the heating time period for three-molecular layers of platinum would be in the order of 1–10 ps or less. Thus, it is reasonable to neglect the wall heating time and not to affect the physical conclusions. Maruyama and Kimura (1999) concluded that the solid wall temperatures “quickly respond” to the temperature change, which strengthens our assumption of neglecting the heating time period for platinum.

Model validation

Maroo and Chung (2008), in a previous work, have attempted to validate the model by having liquid argon between two platinum walls initially at 100 K. The lower wall temperature was changed to 110 K while that of the upper wall to 90 K. The final steady-state heat flux and temperature gradient was calculated in liquid argon layer, and thermal conductivity values were deduced. The change in internal energy was also evaluated as the difference between initial and final energy averages of liquid argon. These properties matched well with those from thermodynamic tables of argon for two cases of wall–fluid heating/cooling. Thin film evaporation mechanism was simulated and a non-evaporating film was obtained. An equation was derived to evaluate the Hamaker constant from the MD simulations, which has not been attempted before. The Hamaker constant was calculated for the non-evaporating film and the value fell between the typical range of the order of 10−20 and 10−21 J.

Although the previous validation effort provides us with physical soundness of the proposed model, both the thermal conductivity and the change in internal energy are state-dependent but time independent. Thus to further validate our model, we perform a similar simulation but now compare the temperature gradients in liquid argon, at different time intervals, with that of the 1-D analytical solution obtained from the heat equation. A 1-D problem, as shown in Figure 3, can be defined as:

$$ {\frac{{\partial T\left( {z,t} \right)}}{\partial t}} = {\frac{1}{\alpha }}\,{\frac{{\partial T^{2} \left( {z,t} \right)}}{{\partial z^{2} }}}.$$
(6)
Fig. 3
figure 3

1-D heat problem

Full size image

Initial condition: \( T(z,t = 0) = T_{i} .\)

Boundary conditions: \( \begin{gathered} T(z = 0,t) = T_{\text{low}} \hfill \\ T(z = h,t) = T_{\text{upp}} \hfill \\ \end{gathered} .\)

The solution to the above equations can be shown to be:

$$ T(z,t) = T_{\text{low}} + \left( {T_{\text{up}} - T_{\text{low}} } \right){\frac{z}{H}} + \sum\limits_{n = 1}^{\infty } {{\frac{2}{n\pi }}} \left[ {\left( {T_{\text{up}} - T_{i} } \right)\left( { - 1} \right)^{n} - \left( {T_{\text{low}} - T_{i} } \right)} \right]\sin \left( {{\frac{n\pi }{H}}z} \right)e^{{ - \alpha \left( {{\frac{n\pi }{H}}} \right)^{2} t}} $$
(7)

where H is the nanochannel height and α is the thermal diffusivity of fluid.

Equation 7 will be used to find the analytical solution of temperature gradient in liquid argon at different time intervals. To the best of our knowledge, there has been no mention, in the published literature so far, of comparing time-varying temperature gradient in liquid at nanoscale using molecular dynamics simulations to analytical solution of the heat equation.

Results and discussion

The simulation process is divided into three parts: velocity-scaling period, equilibration period and the heating period. During the velocity-scaling period (0–500 ps), the velocity of each argon atom is scaled at every time step so that the system temperature remains constant. This is followed by the equilibration period (500–1,000 ps) in which the velocity-scaling is removed and the argon atoms are allowed to move freely and equilibrate. The wall temperature during these two steps is the same as the initial system temperature. At the start of the heating period (1,000–2,500 ps), the wall temperatures are step-changed to desired temperatures, and the heating and/or cooling process of liquid argon is observed.

The computational domain is a cuboid with dimensions of 5.939 nm × 5.939 nm × 23.657 nm. The domain comprises of 16,384 argon atoms at liquid saturation density of 100 K. The Pt walls are placed at z = 0 and z = 23.657 nm and are made up of a total of 3,224 Pt atoms. The initial system temperature is 100 K. The domain, at an intermediate time step, is shown in Figure 4. The time step is 5 fs. At the end of equilibration period (i.e., t = 1,000 ps), the upper wall temperature is increased to 110 K and the lower wall temperature is decreased to 90 K.

Fig. 4
figure 4

Computational domain at intermediate timestep

Full size image

Figure 5 shows the variation of average system temperature and energy with time. The system temperature fluctuates about a mean value of 100.43 K, and the system mean energy is −0.041164 eV/atom during the equilibration period. The average system temperature and energy evaluated in the final 500 ps is 99.60 K and −0.041374 eV/atom.

Fig. 5
figure 5

Average temperature and energy variation with time of liquid argon

Full size image

In order to evaluate the temperature gradient, the domain was divided into 70 equal slices along the height of the channel (i.e., in z-direction) and the average temperature of each slice was evaluated at every timestep. The temperature gradient was then averaged over 100 ps (20,000 timesteps) to obtain good statistical averages. Hence, if the temperature gradient is averaged from time t ps to t + 100 ps, the statistical average can be said to hold at t + 50 ps and the analytical solution is calculated at that timestep. The simulation values are compared to the heat equation’s analytical solution (Eq. 7) in Fig. 6. As it can be seen, the results match quite well thus validating the proposed ‘fluid–wall thermal equilibrium model’ on a temporal basis.

Fig. 6
figure 6

Temperature gradient along z-direction at different timesteps for T i = 100 K, T up = 110 K, and T low = 90 K (smooth lines represent analytical solutions)

Full size image

Liquid argon heating from both platinum walls

An additional case was simulated by heating liquid argon from both walls. The computational domain is similar to previous simulation: 5.939 nm × 5.939 nm × 23.657 nm, 16,384 argon atoms, and 3,224 Pt atoms constituting the walls. The initial system temperature is 100 K. The upper and lower wall temperatures are increased to 120 K at the end of equilibration period (i.e. t = 1,000 ps). The temperature gradient is averaged over 100 ps, and the simulation results are compared to analytical solution in Fig. 7. It can be seen that heat transfer occurs at a faster rate in the nanochannel than evaluated from heat equation’s analytical result. This occurrence can be attributed to the length scale of the current case as the heat equation is usually applied at a continuum scale. Hence, faster heating rate at nano length scale is not unexpected. The results compared well in the previous case (with heating/cooling at the walls) since higher heating rate at the upper wall is matched with higher cooling rate at the lower wall. It is fairly easy to imagine that heat transfer across a nanochannel of an even smaller height (say about 5–10 molecular diameters) would happen at a much higher rate. Also from this conclusion, it should be expected that with an increasing nanochannel height, the error between molecular dynamics simulation result and analytical result would keep decreasing up to a particular channel height, beyond which the results would perfectly match. To verify this point of view, another simulation in conducted with increased nanochannel height as explained below.

Fig. 7
figure 7

Temperature gradient along z-direction at different timesteps for h = 23.657 nm, T i = 100 K, T up = 120 K, and T low = 120 K (smooth lines represent analytical solutions)

Full size image

The dimensions of computational domain are 5.939 nm × 5.939 nm × 44.357 nm. The height is about ~1.9 times the previous case. The domain now consists of 30,720 argon atoms and 3,224 Pt atoms. The initial system temperature is 100 K. Similar to previous run, the upper and lower wall temperatures are increased to 120 K at the end of equilibration period (i.e., t = 1,000 ps). Figure 8 shows the comparison between simulation and analytical results. It can be seen that the results match better than previous simulation of shorter nanochannel (Figure 7). In order to find the error, the average temperature of the domain is obtained from the temperature gradients of simulation and analytical results and plotted in Figure 9 at intervals of 100 ps. It can be noticed from the initial error (at 50 ps) that for a shorter channel height, liquid argon gets heated up faster as pointed out earlier. The maximum error for the shorter nanochannel occurs at 1,350 ps (analytical temperature = 109.14 K) and the value is 5.01 K. For the larger nanochannel, the error remains nearly the same ~3.4 K during the final 1,000 ps of simulation. The simulations were only run till 2,500 ps due to computational limitations and final steady state is not obtained in either case. This justifies that the error between MD simulation and heat equation’s analytical result depends on length scale of the problem.

Fig. 8
figure 8

Temperature gradient along z-direction at different timesteps for h = 44.357 nm, T i = 100 K, T up = 120 K, and T low = 120 K (smooth lines represent analytical solutions)

Full size image
Fig. 9
figure 9

Average domain temperatures from MD simulation and analytical equation with heating from both platinum walls for different nanochannel heights

Full size image

Conclusion

A novel ‘fluid-heated wall thermal equilibrium model’ for numerically simulating heating/cooling of fluid atoms by wall atoms is proposed. The model was initially validated in a previous work by Maroo and Chung (2008) by comparing thermal conductivity and change in internal energy of argon from molecular dynamics simulation to tabulated thermodynamic values; but since these two properties are state-dependent only, additional validation cases are presented in this work which tests the time-dependent nature of the model. Liquid argon is placed between two platinum walls with an initial equilibrium temperature of 100 K. The upper wall temperature is then changed to 110 K and the lower wall temperature to 90 K. The temperature gradient, along the height of the channel, is evaluated and compared to the analytical solution obtained by solving 1-D heat equation and good agreement was found between the predicted and theoretical results.

Additional simulations are conducted with heating at both walls by increasing the wall temperatures to 120 K for two different nanochannel heights. It is concluded that heat transfer occurs at a faster rate than predicted by the heat equation at nanoscale. The error between the MD simulation and the heat equation’s analytical result depends on the length scale of the problem and reduces with the increase in channel height. The results compared well in the previous case (with heating and cooling at the walls) since higher heating rate at the upper wall is matched with higher cooling rate at the lower wall. These comparisons show the physical soundness of the proposed model. In addition, the proposed model is less computationally demanding and enables partial wall heating/cooling. This model can be applied to fluid–solid systems which follow the Lennard-Jones potential for interaction. Future work includes extending this concept to more complex molecular systems.