DOA and phase error estimation using one calibrated sensor in ULA

Abstract

A new method is presented to effectively estimate the direction-of-arrival of a source signal and the phase error of a uniform linear array. Assuming that one sensor (except the reference one) has been calibrated, the proposed method appropriately reconstructs the data matrix and establishes a series of linear equations with respect to the unknown parameters through eigenvalue decomposition. The unknown parameters can be determined directly by the least squares method. Unlike the conventional methods, the proposed method only requires one calibrated sensor, which may not be consecutively spaced to the reference one. The computational complexity analysis is given and the effectiveness of the proposed method is validated by simulation results.

1 Introduction

The problem of direction-of-arrival (DOA) estimation using sensor arrays plays an important role in various areas such as wireless communication, radar and radio astronomy (Krim and Viberg 1996; Schmidt 1986; Ng and See 1996; Zhang et al. 2017; Liao et al. 2016). In general, an accurate knowledge of the array characteristics is required to determine the unknown DOA of the incoming signal. However, the array systems in practical applications usually suffer from various kinds of imperfections and hence, the array manifold is only imprecisely known. In this situation, the performance of direction finding techniques may be significantly degraded due to the mismatch between the actual and nominal array manifolds.

During the past few decades, the problems of array calibration and DOA estimation in the presence of array uncertainties have received extensive attention (Friedlander and Weiss 1988; Liu et al. 2011; Cao et al. 2013; Liao and Chan 2012, 2015; See and Gershman 2004; Zhang et al. 2015; Roy and Kailath 1989). Assuming that a series of calibration sources are located with exactly known DOAs, the array can be effectively calibrated. In practice, however, the calibration sources are not always available. In order to deal with this problem, some methods are proposed to calibrate arrays in the absence of the exact knowledge of DOAs (Friedlander and Weiss 1988; Liu et al. 2011; Cao et al. 2013). In particular, Weiss and Friedlander proposed an alternative iterative method (named as WF method), which can estimate the DOAs and gain-phase error of each sensor element simultaneously (Friedlander and Weiss 1988). However, this method may be considerably deteriorated in the presence of relatively large phase uncertainties due to the ambiguity in estimating the phase uncertainties and DOAs. The eigenstructure based methods in Liu et al. (2011) and Cao et al. (2013) can work well when the phase error is large. Nevertheless, both of these methods suffer from heavy complexity.

Recently, great interest has been shown in partly calibrated arrays by the research community; see the literature Liao and Chan (2012, 2015), See and Gershman (2004) and the references therein. It has been shown in Liao and Chan (2015) and See and Gershman (2004) that if each subarray is calibrated, the ESPRIT-like algorithm (Liao and Chan 2015) or spectral rank-reduction algorithm (See and Gershman 2004) can be utilized to determine the DOAs. For a partly calibrated uniform linear array (ULA) where some sensors have been calibrated, i.e. the gains/phases of these sensors are known as prior, the shift-invariant property can be employed to estimate the DOAs as well as the gains/phases. It should be noted that the approaches in Liao and Chan (2012, 2015) and See and Gershman (2004) require at least one pair of consecutive calibrated sensors.

In this paper, the problem of DOA estimation and phase error calibration in a ULA is addressed. We develop a new method to estimate DOA of a single signal and phase error of sensor array provided that one sensor, which is different from the reference one, is calibrated. The proposed method in this paper constructs a series of data matrices and estimates the unknown DOA together with phase errors by LS minimization. Analysis on the computational complexity is contained and simulation results comparing the performance of the proposed method to MUSIC method (Schmidt 1986) and WF method (Friedlander and Weiss 1988) demonstrate its superiority.

2 Problem formulation

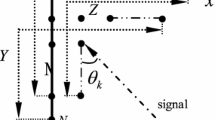
Consider a ULA comprising M omnidirectional sensors labeled $1,2,\ldots ,M$, and inter-element spacing is half a wavelength as shown in Fig. 1. The reference sensor, whose label is ${(M+1)}/{2}$, is located at origin. It is assumed that a signal impinges on the array with DOA $\theta$. In the presence of phase error, the steering vector can be written as

$$\begin{aligned} {\widetilde{\mathbf{a}}}(\theta )={\varvec{\Phi }}{} \mathbf{a}(\theta ) \end{aligned}$$

(1)

where $\mathbf{a}(\theta )$ is the steering vector under ideal condition, which is given by

$$\begin{aligned} \mathbf{a}(\theta )= \left[ e^{j\frac{(1-M)}{2}\pi \mathrm{sin}(\theta )},e^{j\frac{(3-M)}{2}\pi \mathrm{sin}(\theta )},\ldots ,1,\ldots ,e^{j\frac{(M-3)}{2} \pi \mathrm{sin}(\theta )},e^{j\frac{(M-1)}{2}\pi \mathrm{sin}(\theta )}\right] \end{aligned}$$

(2)

where ${\varvec{\Phi }}=\mathrm{diag}{\left[ e^{j{\varphi }_1},\ldots ,e^{j{\varphi }_M}\right] }$, ${\varphi }_m(m=1,2,\ldots ,M)$ denotes the phase error of the mth sensor. The presence of the mismatch between the actual and nominal array manifolds significantly degrades the performance of some classical subspace-based direction finding method, such as MUSIC (Schmidt 1986), ESPRIT (Krim and Viberg 1996; Weiss and Gavish 1991), etc.

Fig. 1

ULA with one calibrated sensor

In this paper, we consider the problem of estimating the DOA and phase error in a partly calibrated array. We take the sensor locates at origin as the reference one, and assume that one of other sensors whose label is c has been calibrated. In other words, it can be assumed that ${\varphi }_r=0$ and ${\varphi }_c$ is known, where r is the label of the reference sensor. For the array configuration described above, we have ${\varphi }_{\frac{M+1}{2}}=0$ (i.e. $r={\frac{M+1}{2}}$). The received vector of array is thus given by

$$\begin{aligned} \mathbf{x}(t)={\widetilde{\mathbf{a}}}(\theta )s(t)+\mathbf{n}(t)={\varvec{\Phi }}{} \mathbf{a}(\theta )s(t)+\mathbf{n}(t) \end{aligned}$$

(3)

where s(t) contains the complex envelope of the signal, $\mathbf{n}(t)$ is a complex Gaussian additive noise vector of $M\times 1$ dimension. The snapshot data matrix composed of L snapshots can be written as

$$\begin{aligned} \mathbf{X}=[\mathbf{x}(1),\mathbf{x}(2),\ldots ,\mathbf{x}(L)]={\varvec{\Phi }}{} \mathbf{a}(\theta )\mathbf{S}+\mathbf{N} \end{aligned}$$

(4)

where $\mathbf{S}=[s(1),s(2),\ldots ,s(L)]$ and $\mathbf{N}=[n(1),n(2),\ldots ,n(L)]$. Then the covariance matrix of the array output can be derived as

$$\begin{aligned} {\mathbf{R}}={\mathbf{E}}\{{\mathbf{x}}{{\mathbf{x}}}^{\mathrm{H}}\}={{\sigma }_s^2}{\varvec{\Phi }}{\mathbf{a}}(\theta ) \mathbf{a}^{\mathrm{H}}(\theta ){{\varvec{\Phi }}}^{\mathrm{H}}+{{\sigma }_n^2}{\mathbf{I}} \end{aligned}$$

(5)

where ${{\sigma }_n^2}$ is noise power and signal power is defined by ${{\sigma }_s^2}=\mathbf{E}\{s(t)s^{\mathrm{H}}(t)\}$. In practice, the covariance matrix $\mathbf{R}$ is often estimated by $\widehat{\mathbf{R}}= \frac{1}{L}{} \mathbf{X}{} \mathbf{X}^{\mathrm{H}}$. Thus our objective is to simultaneously estimate the DOA and phase errors from array output $\mathbf{X}$ or covariance matrix $\widehat{\mathbf{R}}$.

3 Proposed method for ULA

Without loss of generality, it is assumed that the first sensor has been calibrated, i.e. $c=1$ in the following text.

3.1 Phase-error calibration

Before presenting the proposed phase error calibration method, we first construct some selection matrices as follow

$$\begin{aligned} \mathbf{J}_1&= \left[ \begin{array}{cc} \mathbf{O}_{\frac{{(M+1)}}{2}\times \frac{{(M-1)}}{2}}&\mathbf{I}_{\frac{{(M+1)}}{2}} \end{array} \right] \end{aligned}$$

(6)

$$\begin{aligned} \mathbf{J}_2&= \left[ \begin{array}{cc} \mathbf{O}_{\frac{{(M-1)}}{2}\times \frac{{(M+1)}}{2}}&\mathbf{I}_{\frac{{(M-1)}}{2}} \end{array} \right] \end{aligned}$$

(7)

$$\begin{aligned} \mathbf{J}_3&= \left[ \begin{array}{ccc} \mathbf{O}_{\frac{{(M-1)}}{2}\times \frac{{(M-1)}}{2}}&\mathbf{I}_{\frac{{(M-1)}}{2}}&\mathbf{0}_{\frac{{(M-1)}}{2}} \end{array} \right] \end{aligned}$$

(8)

where $\mathbf{O}_{m\times n}$, $\mathbf{I}_{m}$ and $\mathbf{0}_m$ denote $m\times n$ zeros matrix, $m\times m$ identity matrix and $m\times 1$ zero vector, respectively. We give the following formula in (9), which can be used to derive to the proposed method.

$$\begin{aligned} e^{jA}+e^{jB}=2{\mathfrak {R}}\left( e^{j\frac{A-B}{2}}\right) e^{j\frac{A+B}{2}} \end{aligned}$$

(9)

where ${\mathfrak {R}}(\cdot )$ returns the real part of a complex number, A and B are arbitrary real numbers.

From (9), we construct the following extracted output data using selection matrices

$$\begin{aligned} \mathbf{X}_1&=\mathbf{J}_1\mathbf{X} \end{aligned}$$

(10)

$$\begin{aligned} {} \mathbf{X}_2&=\mathbf{J}_1\mathrm{flipud}(\mathbf{X}) \end{aligned}$$

(11)

where $\mathrm{flipup}(\cdot )$ is the operator that flips matrices up to down, for an arbitrary $p\times l$ matrix $\mathbf{C}$, we have $\mathrm{flipud}(\mathbf{C})={\mathbf{P}}{\mathbf{C}}$, where $\mathbf{P}$ is the $p\times p$ exchange matrix with ones on its anti-diagonal and zeros elsewhere.

Fig. 2

Sum output from symmetrical sensors

For ease of illustration, we denote $\varTheta =\pi \mathrm{sin}(\theta )$. Now considering the sum of $\mathbf{X}_1$ and $\mathbf{X}_2$ as Fig. 2 shows, we can obtain

$$\begin{aligned} \mathbf{X}_{12}=\mathbf{J}_1\mathbf{X}+\mathbf{J}_1\mathrm{flipud}(\mathbf{X}) ={\varGamma }_{12}{\mathbf{b}}_{12}{} \mathbf{S}+\mathbf{N}_{12} \end{aligned}$$

(12)

where $\mathbf{N}_{12}$ denotes the compound noise, $\mathbf{\varGamma }_{12}$ is a real diagonal matrix which can be written as the following expression by using (9),

$$\begin{aligned} {\varGamma }_{12}=2{\mathrm{diag}}\left\{ \left[ 1,{\mathfrak {R}}\left( e^{j\frac{2{\varTheta }+ {{\varphi }_{{(M+3)}/{2}}-{\varphi }_{{(M-1)}{2}}}}{2}}\right) ,\ldots ,{\mathfrak {R}}\left( e^{j\frac{{(M-1)}{\varTheta }+{{\varphi }_{M}-{\varphi }_{1}}}{2}}\right) \right] \right\} \end{aligned}$$

(13)

and $\mathbf{b}_{12}$ is a complex vector containing the sum information of phase errors of symmetric sensors, we have:

$$\begin{aligned} {\mathbf{b}}_{12}=\left[ 1,e^{j\frac{{\varphi }_{{(M+3)}/{2}}+{\varphi }_{{(M-1)}/{2}}}{2}},\ldots ,e^{j\frac{{\varphi }_M+{\varphi }_1}{2}}\right] ^{\mathrm{T}} \end{aligned}$$

(14)

According to the subspace methodology, we know that ${\varGamma }_{12}{\mathbf{b}}_{12}$ spans the same subspace as the principal eigenvector of $\mathbf{R}_{12}$ does, which can be described as

$$\begin{aligned} {\mathrm{span}}({\varGamma }_{12}{\mathbf{b}}_{12})={\mathrm{span}}({\gamma }_{12}) \end{aligned}$$

(15)

where $\mathbf{R}_{12}$ is the covariance matrix of $\mathbf{X}_{12}$, ${\gamma }_{12}$ is the principal eigenvector of $\mathbf{R}_{12}$ and has been normalized by its first element. It is necessary to note that the signs of elements in ${\varGamma }_{12}$ remain uncertain, leading to a $\pi$-ambiguity problem between ${\varGamma }_{12}$ and the phases of ${\mathbf{b}}_{12}$. Based on reasonable hypothesis that the phases of ${\mathbf{b}}_{12}$ distributed on the range $(-{\frac{\pi }{2}},{\frac{\pi }{2}})$. Then the following equation holds

$$\begin{aligned} \angle {\mathbf{b}}_{12}=\angle {\gamma }_{12} \end{aligned}$$

(16)

where $\angle [\star ]={\mathrm{arctan}}\left[ \frac{Im(\star )}{Re(\star )}\right]$ returns a phase value on the range $(-{\frac{\pi }{2}},{\frac{\pi }{2}})$. From Eq. (16), we can establish a series of equations about $\varphi _m$. Obviously, the number of equations is less than that of unknown parameters, so it is required to establish more equations to get a solution of $\varphi _m$. Similar to (10) and (11), we construct the following two sets data using selection matrices

$$\begin{aligned} \mathbf{X}_3&=\mathbf{J}_2\mathbf{X} \end{aligned}$$

(17)

$$\begin{aligned} \mathbf{X}_4&=\mathbf{J}_3\mathrm{flipud}(\mathbf{X}) \end{aligned}$$

(18)

$$\begin{aligned} {} \mathbf{X}_5&=\mathbf{J}_3\mathbf{X} \end{aligned}$$

(19)

$$\begin{aligned} {} \mathbf{X}_6&=\mathbf{J}_2\mathrm{flipud}(\mathbf{X}). \end{aligned}$$

(20)

We sum up $\mathbf{X}_3$ and $\mathbf{X}_4$, $\mathbf{X}_5$ and $\mathbf{X}_6$, respectively, as Fig. 3 shows. The obtained sum data can be derived by

$$\begin{aligned} \mathbf{X}_{34}&=\begin{bmatrix}{\mathbf{x}}^{\mathrm{T}}_{0}\\\mathbf{X}_3+\mathbf{X}_4\end{bmatrix} ={\varGamma }_{34}{\mathbf{b}}_{34}{} \mathbf{S}+\mathbf{N}_{34} \end{aligned}$$

(21)

$$\begin{aligned} \mathbf{X}_{56}&=\begin{bmatrix}{\mathbf{x}}^{\mathrm{T}}_{0}\\\mathbf{X}_5+\mathbf{X}_6\end{bmatrix} ={\varGamma }_{56}{\mathbf{b}}_{56}{} \mathbf{S}+\mathbf{N}_{56} \end{aligned}$$

(22)

where ${\mathbf{x}}^{\mathrm{T}}_{0}=\mathbf{X}({\frac{M+1}{2}},:)$ means the $\frac{M+1}{2}$th row of $\mathbf{X}$. Both ${\varGamma }_{34}$ and ${\varGamma }_{56}$ are diagonal real matrices, and $\mathbf{N}_{34}$ and $\mathbf{N}_{56}$ denote the terms of compound noise. The complex vector ${\mathbf{b}}_{34}$ and ${\mathbf{b}}_{56}$ can be written as

$$\begin{aligned} {\mathbf{b}}_{34}&=\left[ 1,e^{j\frac{{{\varTheta }}+{\varphi }_{(M+3)/ 2}+{\varphi }_{ (M+1)/ 2 }}{2}},\ldots ,e^{j\frac{{\varTheta }+{\varphi }_{M}+{\varphi }_{2}}{2}}\right] ^{\mathrm{T}} \end{aligned}$$

(23)

$$\begin{aligned} {\mathbf{b}}_{56}&=\left[ 1,e^{j\frac{-{\varTheta }+{\varphi }_{(M+1)/ 2 }+{\varphi }_{(M-1)/ 2 }}{2}},\ldots ,e^{j\frac{-{\varTheta }+{\varphi }_{(M-1)}+{\varphi }_{1}}{2}}\right] ^{\mathrm{T}}. \end{aligned}$$

(24)

Denote the covariance matrix of $\mathbf{X}_{34}$ and $\mathbf{X}_{56}$ as $\mathbf{R}_{34}$ and $\mathbf{R}_{56}$, respectively, then the following two equations hold

$$\begin{aligned} \angle {\mathbf{b}}_{34}= & {} \angle {\gamma }_{34} \end{aligned}$$

(25)

$$\begin{aligned} \angle {\mathbf{b}}_{56}= & {} \angle {\gamma }_{56} \end{aligned}$$

(26)

where ${\gamma }_{34}$ and ${\gamma }_{56}$ are the principal eigenvector of $\mathbf{R}_{34}$ and $\mathbf{R}_{56}$, respectively. From (23) and (24) we know that new parameter ${\varTheta }$, which contains the information of DOA, has been introduced.

Fig. 3

Sum outputs from malposed sensors

Then equations can be established using (16), (25) and (26) by the expression

$$\begin{aligned} \mathbf{C}_1{\mathbf{u}}&={\mathbf{d}}_1 \end{aligned}$$

(27)

$$\begin{aligned} \mathbf{C}_2{\mathbf{u}}&={\mathbf{d}}_2 \end{aligned}$$

(28)

$$\begin{aligned} \mathbf{C}_3{\mathbf{u}}&={\mathbf{d}}_3 \end{aligned}$$

(29)

respectively, or equivalently expressed as

$$\begin{aligned} \mathbf{B}{\mathbf{u}}=\mathbf{d}. \end{aligned}$$

(30)

In the above equations, $\mathbf{u}$ is the unknown parameter vector containing the information of phase errors and DOA, which can be described as

$$\begin{aligned} \mathbf{u}=\left[ \varphi _1,\ldots ,\varphi _m,\ldots ,\varphi _M,{\varTheta }\right] ^{\mathrm{T}} \end{aligned}$$

(31)

$\mathbf{d}$ is a vector constructed by the phases of the principal eigenvectors

$$\begin{aligned} \mathbf{d}=\left[ \begin{array}{lll} {\mathbf{d}}_1\\ {\mathbf{d}}_2\\ {\mathbf{d}}_3 \end{array} \right] = \left[ \begin{array}{lll} \angle \gamma _{12} \left( 2:\frac{{(M+1)}}{2}\right) \\ \angle \gamma _{34} \left( 2:\frac{{(M+1)}}{2}\right) \\ \angle \gamma _{56} \left( 2:\frac{{(M+1)}}{2}\right) \end{array} \right] \end{aligned}$$

(32)

$\mathbf{C}_1$, $\mathbf{C}_2$, $\mathbf{C}_3$ are $M_1\times (M+1)$ coefficient matrices extracted from the phase of $\mathbf{b}_{12}$, $\mathbf{b}_{34}$, $\mathbf{b}_{56}$, respectively, and $M_1=\frac{{(M-1)}}{2}$. A short analysis yields

(33)

In (33), $M_1\triangleq {{(M-1)}}/{2}$, $\mathbf{0}_{M_1}$ and $\mathbf{1}_{M_1}$ denote $M_1\times 1$ vector with all zeros and ones, respectively. $\mathbf{P}_{M_1}$ is ${M_1}$dimension exchange matrix with ones on its anti-diagonal and $\mathbf{I}_{M_1}$ is ${M_1}$ dimension identity matrix. We can prove that (see “Appendix” for detail)

$$\begin{aligned} {} {\mathrm{rank}}\left( \mathbf{C}_{12}\right) = {\mathrm{rank}}\left( \mathbf{C}_{13}\right) ={\mathrm{rank}}\left( \mathbf{C}_{23}\right) =M-1 \end{aligned}$$

(34)

where , , and , respectively. Similarly, we denote ${\mathbf{d}_{12}}$, ${\mathbf{d}_{13}}$ and ${\mathbf{d}_{23}}$ as , , and , respectively. From (34), we know that $\mathbf{C}_{ij}$($i=1,2$, $j=2,3$ and $i\ne j$) is a matrix of full row rank.

Provided that $\varphi _{{(M-1)}/ 2}=0$ and the value of $\varphi _c$ has been known, we have

$$\begin{aligned} {} \widetilde{\mathbf{C}}_{ij}\widetilde{\mathbf{u}}={\mathbf{d}}_{ij}-{\varphi }_c\mathbf{C}_{ij}(:,c) \end{aligned}$$

(35)

where $\widetilde{\mathbf{C}}_{ij}$ is a $(M-1)\times (M-1)$ modified coefficient matrix which can be obtained by rejecting the $\frac{M+1}{2}$th and cth columns from $\mathbf{C}_{ij}$ ($i=1,2$, $j=2,3$ and $i\ne j$).

Without loss of generality, we assume that $c<\frac{M+1}{2}$, then $\widetilde{\mathbf{u}}$ can be described as

$$\begin{aligned} \widetilde{\mathbf{u}}=\left[ \varphi _1,\ldots ,{\varphi }_{c-1},{\varphi }_{c+1},\ldots ,{\varphi }_{\frac{M-1}{2}},{\varphi }_{\frac{M+3}{2}},\ldots ,\varphi _M,{\varTheta }\right] ^{\mathrm{T}}. \end{aligned}$$

(36)

Because the property of full row rank of $\mathbf{C}_{ij}$, the rows of $\mathbf{C}_{ij}$ are linearly independent, either are the rows of $\widetilde{\mathbf{C}}_{ij}$. The following equation hold

$$\begin{aligned} \mathrm{rank}\left( \widetilde{\mathbf{C}}_{ij}\right) =M-1. \end{aligned}$$

(37)

Then for any given M, $\widetilde{\mathbf{C}}_{ij}$ is a matrix of full column rank. In other words, Eq. (35) must have an unique least squares solution, which can be given by

$$\begin{aligned} {} {\widehat{\widetilde{\mathbf{u}}}}_{LS}={\widetilde{\mathbf{C}}}^{\dagger }_{ij}\left[ {\mathbf{d}}_{ij}- {\varphi }_c\mathbf{C}_{ij}(:,c)\right] \end{aligned}$$

(38)

where ${\widetilde{\mathbf{C}}}^{\dagger }_{ij}$ is the pseudoinverse of ${\widetilde{\mathbf{C}}}_{ij}$.Then the DOA and phase error can be simultaneously obtained from (38).

3.2 Method to improve practicality

The method proposed above has a limitation which can be expressed by the following mathematical expression

$$\begin{aligned} {} {\mathrm{max}(\mathrm{abs}(\angle \mathbf{b}))}\le \frac{\pi }{2} \end{aligned}$$

(39)

where $\mathbf{b}=\left[ {\mathbf{b}}_{12}^{\mathrm{T}},\ {\mathbf{b}}_{34}^{\mathrm{T}},\ {\mathbf{b}}_{56}^{\mathrm{T}}\right] ^{\mathrm{T}}$. To improve the maneuverability, we apply a rotational factor $\varOmega$ to the array response if the rough direction of signal is prior known. The prior information of DOA can be obtained beforehand by using a direction finding method with low resolution. Once we have known that the direction of a signal or a calibration source locates in the range of $[\theta _0-\delta ,\theta _0+\delta ]$, where $\delta$ is a positive number which is expected to be as small as possible. Under the assumption that $\theta _0-\delta$ and $\theta _0+\delta$ have the same signs, we can choose the rotational factor $\varOmega$ as

$$\begin{aligned} \varOmega =\frac{\pi \left[ \mathrm{sin}(\theta _0-\delta )+\mathrm{sin}(\theta _0+\delta )\right] }{2}. \end{aligned}$$

(40)

Construct a diagonal rotational matrix $\varXi$ as

$$\begin{aligned} {\varvec{\Xi }}=\mathrm{diag}\left\{ \left[ e^{j\frac{(M-1)\varOmega }{2}},\ldots ,1,\ldots ,e^{j\frac{(1-M)\varOmega }{2}}\right] \right\} . \end{aligned}$$

(41)

We use ${\varvec{\Xi }}$ to compensate received vector of array $\mathbf{x}(t)$, and then the modified received vector $\mathbf{y}$ can be derived as

$$\begin{aligned} \mathbf{y}(t)={\varvec{\Xi }}{} \mathbf{x}(t)={\varvec{\Phi }}\mathbf{a}(\widetilde{\varTheta })s(t)+{\mathbf{n}}_y(t) \end{aligned}$$

(42)

where $\widetilde{\varTheta }={\varTheta }-\varOmega$ is a modified inter-element delay difference that distributed around zero and its estimation $\widehat{\widetilde{\varTheta }}$ can be obtain if we exert the proposed method on $\mathbf{y}(t)$ instead of $\mathbf{x}(t)$. In this case, the applied condition (39) is much easier to be satisfied and DOA can be obtained by

$$\begin{aligned} \widehat{\theta }=\mathrm{arcsin}\left( \frac{\widehat{\widetilde{\varTheta }}+\varOmega }{\pi }\right) . \end{aligned}$$

(43)

As the phase errors are direction-independence, so the rotational factor $\varOmega$ does not affect the estimation of $\varphi _m$.

4 Computational complexity and simulations

To the best of our knowledge, there are no state of the art methods which are based on partly calibrated arrays can estimate phase error and DOA under the above conditions, especially when the calibrated sensor is not consecutively spaced to the reference one. In addition, references Liu et al. (2011) and Cao et al. (2013) have concluded that their methods have high complexity as compared to the WF method in Friedlander and Weiss (1988). Therefore, we will compare the performance of our proposed method with the classical phase calibration method which proposed by Friedlander and Weiss (1988). This WF method simultaneously estimates DOA and phase error in an iterative approach. To be specific, the DOA is first be estimated by assuming that the phase parameters are known. Given estimates of the phase parameters, the DOA is again obtained according to the theory of eigenstructure subspace. The WF algorithm iteratively performs the two-step procedure until convergence. This method may suffer from suboptimal convergence because of the joint iteration between DOA estimation and array parameter estimation, and they are based on the assumption that the array perturbations are small. Nevertheless, it can be applied to an arbitrary array, so in the subsections below we will test the WF method for performance comparison, including the computational complexity and the estimated accuracy.

4.1 Computational complexity analysis

The computational complexity of the WF method mainly comes from the EVD and the peak search of the spatial spectrum. For every iteration, it implements a $M\times M$ EVD, requiring on the order of $15M^3$ operations (Weiss and Gavish 1991; Golub and Loan 1996). Then the total operations of WF method is $K(15M^3+D)$, where K is the number of iteration, D is the operation number of peak search process.

The proposed method implements $(\frac{M+1}{2})\times (\frac{M+1}{2})$ EVD twice, which requires $\frac{15}{4}(M+1)^3$ operations totally. In addition, it computes the inverse of a $(M-1)\times (M-1)$ matrix, which has the same order of $15(M-1)^3$.

For any $M \ge 2$, we have $15M^3>\frac{15}{4}(M+1)^3$. Then as long as the iteration number K is slightly greater than 1, the proposed method exhibits significant computational advantages as compared to the WF method.

4.2 Simulations and results

In this subsection, numerical experiments are provided to explore different aspects of proposed method and make comparisons with other techniques. Specifically, performance comparison with the MUSIC method (Schmidt 1986) and the WF method (Friedlander and Weiss 1988) is made in the terms of the root mean square error (RMSE) of DOA estimates and the RMSE phase error estimates.

In the next simulations, the phase error $\{\varphi _m\}_{m=1}^{M}$ of sensors are generated by

$$\begin{aligned} \varphi _m=\sqrt{12}\sigma _{\varphi }\eta _m \end{aligned}$$

(44)

where $\eta _m$ is independent and identically distributed random variable which is distributed uniformly in the range of $[-0.5,0.5]$, $\sigma _{\varphi }$ is the standard deviation of $\varphi _m$.

Fig. 4

Spatial spectrums of different methods

We use a ULA with element number $M=15$ as shown in Fig. 1. A signal impinging on the array from direction $\theta =12^{\circ }$, and we have known it is located at $[\theta _0-\delta ,\theta _0+\delta ]$ with $\theta _0=9^{\circ }$ and $\delta =8^{\circ }$. The number of samples is 512. It is assumed that the accurate value of phase error of the first sensor has been known. In addition, comparison with MUSIC method is made to illustrate the performance improvement of the proposed method.

Figure 4 shows the spatial spectrums of different methods when $\sigma _{\varphi }=30^{\circ }$ and SNR is 15 dB. Figure 5 shows the RMSE curves of DOA estimates versus the standard deviation of the phase error $\sigma _{\varphi }$ and the RMSE curves of phase error estimates versus $\sigma _{\varphi }$, respectively. The performance of estimation versus SNR is shown in Fig. 6.

We observe from Fig. 4 that when the MUSIC algorithm has partly knowledge of phase parameters, no reliable estimate of the DOAs can be extracted from the plot. For WF method, it converges to suboptimal solution and results in the degradation of its performance. The spatial spectrum generated by the proposed method gets its peak value when the direction is $12^{\circ }$, which is exactly the true value of DOA. In other words, the accuracy of DOA has been greatly improved by using the propose algorithm.

It can be seen from Fig. 5 that the WF method performs slightly better than MUSIC algorithm using partly calibrated sensors, and that the propose method outperforms the WF method. All methods degrade as $\sigma _{\varphi }$ increases. Moreover, it can be noted that when $\sigma _{\varphi }$ is no larger than $40^{\circ }$, which is reasonable in most engineering applications, the proposed methods are significantly better than the WF method. This result is consistent with the analysis in Sect.  3 and verifies the effectiveness of the proposed method.

Fig. 5

Estimation performance versus $\sigma _{\varphi }$. a RMSE of DOA estimates versus $\sigma _{\varphi }$. b RMSE of phase error estimates versus $\sigma _{\varphi }$

Fig. 6

Estimation performance versus SNR. a RMSE of DOA estimates versus SNR. b RMSE of phase error estimates versus SNR

Figure 6 shows the RMSE curves of DOA estimates versus SNR and the RMSE curves of phase error estimates versus SNR, respectively. All methods perform better as $\sigma _{\varphi }$ increases. It can be noted that when SNR is larger than 0 dB, the proposed methods are better than the WF method. But when SNR is lower than 0 dB, the performance of the proposed method is poor. This is because when SNR is low, the accurate estimation of the subspace of signal becomes difficult, and that leads to a poor estimation of the DOA and phase error.

5 Conclusion

In this paper, we address the estimation of DOA and phase error for a ULA with one calibrated sensor. Under some reasonable assumptions, a novel error calibration method is presented. The proposed method constructs equations by modified received data matrix and solves DOA and unknown phase error by LS method. The proposed method is computationally attractive and has the capability to calibrate the phase error of array sensor without deploying a calibration source at accurately known location. At the same time, it does not require consecutive calibrated sensors. In this paper, method to improve practicality is also considered, and simulation results confirmed the high performance of the proposed method.

Additionally, it is worth noting that although this paper addresses the problem of direction finding and phase error estimation for a partly calibrated ULA, the application of the proposed method can also be extended to array with an arbitrary geometry. Array shape calibration can also be applied by using the same idea mentioned in the paper. All those are included in our further study.

Appendix

The proof of (34).

(1)

where $\begin{array}{*{20}{c}} r\\ {\widetilde{\quad \quad }} \end{array}$ and $\begin{array}{*{20}{c}} c\\ {\widetilde{\quad \quad }} \end{array}$ denote elementary row operation and elementary column operation, respectively, and they does not change the rank of a matrix. From the analysis above, we conclude that

(2)

So, we have

(3)

We have

From the proof above, we can conclude that

This completes the proof.