1 Introduction

Under the circumstances of a harmonic vibration, the vibrated bodies usually exhibit plenty of puzzling phenomena [1–8], for which the underlying mechanism still remains unknown. Despite the clear physical picture that these intriguing phenomena essentially originate from the complex interactions between bodies, the dynamics of contacts and impacts therein still consists of various difficult issues in modeling, such as the relative kinematics between bodies, stick-slip transitions in friction, energy dissipation and dispersion in impacts, and transitions among contact states.

Generally, a system with contacts/impacts and friction will experience a nonsmooth process, in which the state of every individual contact/impact set manifests different properties related to the physical interactions induced by the relative motion between two bodies. The corresponding mechanism should strictly adhere to the material behaviors, thus a priori knowledge is necessary for reflecting the constitutive relationships between load and deformation. To reduce the complexity in modeling, however, contact/impact dynamics often needs to be analyzed based on some assumptions and empirical laws that come from physical intuition or phenomenological analysis.

Rigid body dynamics is a commonly used framework in treating contact/impact phenomena where deformation in bodies is considered to be very small and negligible. Under the framework, the most common approaches used to study contact/impact problems involve a constraint or compliance-based method. A constraint-based method assumes the following: (1) a sustained contact admits a weaken interaction to be modeled as constraint equations in association with the geometries of contacting bodies [9, 10], and (2) collision triggers a strong interaction governed by an impact law, e.g., one employing a coefficient of restitution to characterize the sudden changes of velocity before and after impacts [11–13]. The compliance-based method takes into account the local behaviors of materials in modeling, in which a stiffness parameter is adopted to reflect the local elasticity, and a damping coefficient to mimic the energy dissipation [14–17]. The first method requires a model with a hierarchical structure to deal with contact and impact dynamics separately, while the second one can result in a simple mathematical structure to be easily programmed.

In the field of multibody system dynamics, compliance-based methods have proved successes in industrial applications [14, 15]. Their usage, however, often requires parameters that have to be determined via a fitting process to find out the values satisfying the practical requirements. This is usually unavailable in real physics, and thus causes relatively large discrepancies between the scenarios in prediction and reality. Moreover, as numerical solutions mix with information on different scales, the inherent system characteristics are consequently confusing, especially in the case of long-term behaviors [18].

Pfeiffer and Glocker [9, 19] systematically solved contact and impact problems using constraint-based methods. To describe the interactions on interfaces, they introduced complementary relationships, and/or the assumption about impact that compression and restitution finish simultaneously to form a uniform framework as a linear complementarity problem (LCP). Following their work, a number of LCP-based methods, accompanying the modification in numerical implementation, were introduced to deal with multi-rigid-body dynamics [20, 21]. Because of the unrealistic assumption that impacts synchronize in compression and restitution [11, 12], an LCP formulation does not correspond to fundamental physical properties. Moreover, the discontinuity in Coulomb’s friction, together with the absence of material behaviors, may generate no solution, e.g., the problem of Painlevé paradox [22–25], or multiple ones, as in the indeterminacy of rigid body dynamics [13]. In addition, some special contact state transitions, such as in the scenario of a sequence of impacts converging to one contact state [18], essentially cannot be attributed to an LCP formulation.

Even though impacting bodies can be approximately assumed as rigid, the material behaviors adjacent to impacting points play a dominant role in transferring the momentum and energy between the bodies. Therefore, it seems inevitable to take into account the material behaviors during impact. To satisfy some rigid requirements in physics and to restrict impact solutions without resorting to the small-scaled deformation, our previous work presented a framework for multiple impacts in multibody systems [26, 27]. The work deals with such as impact problem as a set of first-order differential equations with regard to a “time-like” independent normal impulse. Energetic coefficients of restitution and friction coefficients are applied to individual impacts, each of which may go through multiple compression-restitution phases and may undergo stick-slip transition due to friction. Energy dispersions are attributed to impulse ratios, and determined by the relative contact stiffness as well as the corresponding contact potential energies. This method has been successfully applied to solve a number of problems, including the problem of Newton’s cradle [27], a column of particles [28], a disc-ball system [29, 30], a rocking block [31, 32], etc.

This paper aims at inserting the new theory in multiple impacts into the constraint-based approaches for developing a uniform framework for dealing with contact/impact phenomena. Aside from the complexity in impact processes, this framework also takes into account to miscellaneous difficult issues, including the relative kinematics between bodies, transitions among the states in every contact set, and system singularities due to the absence of material behaviors. For illustration, our study will focus on a 3D body with the shape of a dumbbell bouncing on a harmonically vibrating plate. This system in a 2D situation was first experimentally investigated in [6] with motions limited in a vertical plane, and was further theoretically analyzed in [33] by introducing the theory of multiple impacts into the system. In particular, when specifying the vibration of the plate with certain parameters, both the results obtained from simulations and experiments demonstrated that such a simple object can exhibit periodic behaviors in its gross motion. Their agreement implies that the contact/impact model can match the physical properties. This may be beneficial for discovering the underlying mechanism governing the global self-ordered phenomena in complex systems, which essentially depend on the deterministic process in contacts and impacts.

For a common case in reality, the 3D dynamics of the bouncing dumbbell is somewhat complex with miscellaneous issues that need to be resolved in modeling. Meanwhile, one may wonder how the same system behaves in a 3D situation, and whether the vibration of the plate can excite similar periodic phenomena as discovered in a 2D system. To answer these questions, this paper presents a full description for the underlying dynamics of a 3D rigid body, including a general theory for solving the systems with multiple frictional contact/impacts, resolution of system singularities, and identification of transitions of contact states.

The organization of the paper is as follows. In Sect. 2, a three-dimensional bouncing dumbbell system is described, following by an analysis of the relative kinematics and the governing equations. Section 3 presents an LCP formulation of the contact dynamics under Coulomb friction, and solves the impact dynamics using the theory of multiple impacts proposed in [26]. A hierarchical structure is conducted into the model to associate the physical law with the corresponding state in every individual contact sets. In Sect. 4, transitions of the states in contact sets are traced by binary identifiers, and the system mode of dumbbell motion is distinguished by a set vector with elements whose values can be evaluated. System singularities are also treated here. In Sect. 5, we justify the model by investigating the planar motion of the bouncing dumbbell, in combination with a comparison of the numerical results and the existing findings. Then, numerical simulations are performed to identify the periodic behaviors of a 3D rigid body. We give a summary and discuss the future research directions in Sect. 6.

2 Relative kinematics and governing equations of the bouncing dumbbell system

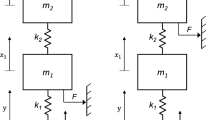
Figure 1 depicts the system of a rigid dumbbell bouncing upon a harmonically vibrating plate. The dumbbell has mass m and consists of two identical solid balls with radius r rigidly connected by a light-weight rod with diameter D r , length l−2r (l is the distance between the centers of the two balls). The harmonic motion of the plate is

$$ z_{p}=A_z\sin{(\omega t+\phi_{0})}, $$
(1)

where A z denotes the amplitude, ω signifies the angular frequency, and ϕ 0 is the initial phase angle related with the releasing time of the dumbbell.

Fig. 1
figure 1

The system of a dumbbell bouncing on plate in a harmonic vibration z p =A z sin(ωt+ϕ 0). (a) The front view for the system and (b) for the top view

Full size image

Let (O,i,j,k) represent an inertial frame fixed on a space plane related to the equilibrium position of the vibrating plate. To give an attitude representation for the dumbbell, a translational coordinate system (O′,i′,j′,k′) is equipped at the mass center of Ball 1. With regard to the translational frame, we perform three consecutive rotations, following a sequence of the 3−2−1 set of Euler’s angles [34], to establish a body-fixed coordinate frame (O′,e 1,e 2,e 3). The angles in the three consecutive rotations are respectively (π/2+θ), −β and γ, such that the unit vector e 1 is along the direction of the rod axis. In terms of the above definition, the rotation matrix R between frames (O′,i′,j′,k′) and (O′,e 1,e 2,e 3) is given by

$$\begin{aligned}{} [ \boldsymbol{e}_1,\boldsymbol{e}_2, \boldsymbol{e}_3 ] = \bigl[ \boldsymbol{i^{\prime}}, \boldsymbol{j^{\prime}},\boldsymbol{k^{\prime}} \bigr] \left [ \begin{array}{c@{\quad}c@{\quad}c} -s_{\theta}c_{\beta} \ & -c_{\theta}c_{\gamma}+s_{\theta}s_{\beta }s_{\gamma} \ & c_{\theta}s_{\gamma}+s_{\theta}s_{\beta}c_{\gamma}\\ c_{\theta}c_{\beta} \ & -s_{\theta}c_{\gamma}-c_{\theta}s_{\beta }s_{\gamma} \ & s_{\theta}s_{\gamma}-c_{\theta}s_{\beta}c_{\gamma}\\ s_{\beta} \ & c_{\beta}s_{\gamma} \ & c_{\beta}c_{\gamma} \end{array} \right ] = \bigl[ \boldsymbol{i^{\prime}}, \boldsymbol{j^{\prime}},\boldsymbol{k^{\prime}} \bigr]\boldsymbol{R} \end{aligned}$$
(2)

where symbols s (⋅) and c (⋅) are the abbreviations for trigonometric functions sin(⋅) and cos(⋅), respectively.

Likewise, the angular velocity vector can be constructed from the changing rate of the rotation matrix R, and expressed as

$$ \boldsymbol{\omega}= \dot{\theta}\boldsymbol{k^{\prime}} - \dot{\beta } \boldsymbol{e}_2^{\prime} + \dot{\gamma}\boldsymbol{e}_1 $$
(3)

where vector \(\boldsymbol{e}_{2}^{\prime}\) corresponds to the generated vector of j ′ owing to the first rotation (π/2+θ) around axis k ′. In the body-fixed coordinate system (O′,e 1,e 2,e 3) the inertia tensor of the dumbbell at its mass center C is

$$\begin{aligned} \boldsymbol{I}=\left [ \begin{array}{c@{\quad}c@{\quad}c} J_2 & 0 & 0\\ 0 & J_1 &0\\ 0 & 0 & J_1 \end{array} \right ] \end{aligned}$$
(4)

where J 2 is the principal moment of inertia of the body with respect to e 1, and J 1 is the same inertia for principal axes e 2 and e 3. Let us select the generalized coordinates of the system as \(\mathbf {q}={(x_{1},y_{1},z_{1},\theta,\beta,\gamma)^{T}}\in\mathbb{R}^{6}\), where (x 1,y 1,z 1) are the coordinates of the mass centers of Ball 1 in inertial frame (O,i,j,k). The kinetic energy of the dumbbell has a form as follows:

$$\begin{aligned} T =&\displaystyle\frac{1}{2}m|\boldsymbol{\upsilon }_{C}|^2+\displaystyle\frac{1}{2}\boldsymbol{\omega}^{T}\cdot \boldsymbol{I}\cdot\boldsymbol{\omega} \\ =&\displaystyle\frac{1}{2}m(\dot{x}_{1}^{2}+\dot {y}_{1}^{2}+\dot{z}_{1}^{2}+\frac{1}{4}l^2\dot{\beta }^{2}+\displaystyle\frac{1}{4}l^{2}c^2_{\beta}\dot{\theta }^{2}+ls_{\theta}s_{\beta}\dot{x}_{1}\dot{\beta}-lc_{\theta}c_{\beta }\dot{x}_{1}\dot{\theta}-lc_{\theta}s_{\beta}\dot{y}_{1}\dot{\beta} \\ &{}-ls_{\theta}c_{\beta}\dot{y}_{1}\dot{\theta}+lc_{\beta}\dot {z}_{1}\dot{\beta})+\displaystyle\frac{1}{2}J_1(c^{2}_{\beta}\dot {\theta}^{2}+\dot{\beta}^{2}) +\displaystyle\frac{1}{2}J_{2}(s_{\beta}\dot{\theta}+\dot{\gamma})^{2} \end{aligned}$$
(5)

where υ C is the velocity of the mass center. The potential energy with respect to the zero-value surface designated on the (O−ij) plane is expressed as

$$ U=mg \biggl(z_{1}+\displaystyle\frac{1}{2}ls_{\beta} \biggr) $$
(6)

Let A and B be the points on the surfaces of Ball 1 and Ball 2, at which contacts or impacts between the dumbbell and the plate possibly occur. Correspondingly, we earmark respectively A′ and B′ for the corresponding points on the vibrating plate. So, there are contact sets {A,A′} and {B,B′} in the dumbbell system.

To satisfy the requirements in Coulomb’s friction law, the contact forces in every individual contact set are mandatorily decomposed into the components along the normal and tangential directions with regard to the corresponding common tangential plane between the surfaces on which the contact points are located separately. Note that the two points in each contact set satisfy the condition that the distance between them should be of minimum value between the plate and the corresponding ball. The two contact sets in the dumbbell system have the same direction along unit vector k.

The normal and tangential components of the contact forces can be represented by \(\boldsymbol {F}^{n}=[F_{A}^{n},\,F_{B}^{n}]^{T}\) and \(\boldsymbol{F}^{\tau }=[F_{Ax}^{\tau},\,F_{Bx}^{\tau},\,F_{Ay}^{\tau},\,F_{By}^{\tau}]^{T}\), respectively. Defining a Lagrangian function L=T−U, and then using the Euler–Lagrange equations, the motion of the dumbbell is governed by the dynamics

$$ \boldsymbol{M}(\mathbf{q})\ddot{\mathbf{q}}-\boldsymbol{h}(\mathbf {q}, \dot{\mathbf{q}},t)=\boldsymbol{Q}+\boldsymbol{W}\boldsymbol {F}^{n}+ \boldsymbol{N}\boldsymbol{F}^{\tau} $$
(7)

where the matrices M(q), \(\boldsymbol{h}(\mathbf {q},\dot{\mathbf{q}},t)\), Q, W, and N are given in Appendix.

To determine the physical laws applied in the contact forces F n and F τ, the relative kinematics needs to be established to detect the state in every individual contact set. Points A and B always follow the relationships:

$$ \left \{ \begin{array}{l} \mathbf{r}_{O^{\prime}A}=-r\boldsymbol{k}^{\prime}\\ \mathbf{r}_{O^{\prime}B}=-lc_{\beta}s_{\theta}\boldsymbol{i}^{\prime }+lc_{\beta}c_{\theta}\boldsymbol{j}^{\prime}+(ls_{\beta}-r)\boldsymbol {k}^{\prime} \end{array} \right . $$
(8)

Considering that A and B are the moving points on the rigid body of the dumbbell, the instantaneous velocities at points A and B are expressed as

$$ \left \{ \begin{array}{l} \boldsymbol{\upsilon}_{A}(\mathbf{q},\dot{\mathbf{q}})=\boldsymbol{\upsilon}_{O^{\prime }}+\boldsymbol{\omega}\times\mathbf{r}_{O^{\prime}A}\\ \boldsymbol{\upsilon}_{B}(\mathbf{q},\dot{\mathbf{q}})=\boldsymbol{\upsilon}_{O^{\prime }}+\boldsymbol{\omega}\times\mathbf{r}_{O^{\prime}B} \end{array} \right . $$
(9)

Let δ=(δ A (q),δ B (q))T denote the relative normal displacements in the two contact sets. We easily have

$$ \left \{ \begin{array}{l} \delta_{A}(\mathbf{q})=(\mathbf{r}_{OA}- \mathbf{r}_{OA^{\prime }})\cdot\boldsymbol{k}=z_{1}-r-z_{p}\\ \delta_{B}(\mathbf{q})=(\mathbf{r}_{OB}- \mathbf{r}_{OB^{\prime }})\cdot\boldsymbol{k}=z_{1}+ls_{\beta}-r-z_{p} \end{array} \right . $$
(10)

The time rates of change of δ A and δ B are

$$\begin{aligned} \dot{\boldsymbol{\delta}}=[\boldsymbol{W}_A, \boldsymbol{W}_B]^{T} \dot{\mathbf {q}}-\dot{\mathbf{z}}_p=\boldsymbol{W}^{T}( \mathbf{q})\dot{\mathbf {q}}-\dot{\mathbf{z}}_p \end{aligned}$$
(11)

where \(\dot{\boldsymbol{\delta}}=(\dot{\delta}_{A},\dot{\delta}_{B})^{T}\), \(\dot {\mathbf{z}}_{p}=(\dot{z}_{p},\dot{z}_{p})^{T}\). Obviously, Eq. (11) also corresponds to the normal components of the instantaneous relative velocities between the two points in each contact set.

Since the plate only vibrates in vertical direction while keeping still in the horizontal plane (O−ij), by Eq. (9), the tangential components of the relative velocities for the points in contact sets are given by

$$\begin{aligned} \boldsymbol{\upsilon}^{\tau}=[\boldsymbol{N}_{Ax},\boldsymbol {N}_{Bx},\boldsymbol{N}_{Ay},\boldsymbol{N}_{By}]^T \dot{\mathbf {q}}=\boldsymbol{N}^{T}(\mathbf{q})\dot{\mathbf{q}} \end{aligned}$$
(12)

where \(\boldsymbol{\upsilon}^{\tau}=(\upsilon^{\tau}_{Ax},\upsilon^{\tau }_{Bx},\upsilon^{\tau}_{Ay},\upsilon^{\tau}_{By})^{T}\), and \(\upsilon ^{\tau}_{Ax}=\boldsymbol{\upsilon}_{A}\cdot\boldsymbol{i}\), \(\upsilon^{\tau }_{Ay}=\boldsymbol{\upsilon}_{A}\cdot\boldsymbol{j}\), and so on.

By differentiating Eqs. (11) and (12) with respect to time, the evolution of the relative motion for the points in contact sets is governed by the relationships

$$ \left \{ \begin{array}{l} \ddot{\boldsymbol{\delta}}=\boldsymbol{W}^{T}(\mathbf{q})\ddot{\mathbf {q}}+\boldsymbol{S}^{n}-\ddot{\mathbf{z}}_p\\ \dot{\boldsymbol{\upsilon}}^{\tau}=\boldsymbol{N}^{T}(\mathbf{q})\ddot {\mathbf{q}}+\boldsymbol{S}^{\tau} \end{array} \right . $$
(13)

where \(\ddot{\mathbf{z}}_{p}=(\ddot{z}_{p},\ddot{z}_{p})^{T}\), \(\boldsymbol {S}^{n}=\dot{\boldsymbol{W}}^{T}(\mathbf{q})\dot{\mathbf {q}}=(0,-ls_{\beta}\dot{\beta}^{2})^{T}\), and \(\boldsymbol{S}^{\tau}=\dot {\boldsymbol{N}}^{T}(\mathbf{q})\dot{\mathbf{q}}\), whose concrete expression is given in Appendix.

Because the points in each contact set move on body surfaces, it is worth noting that the instantaneous accelerations between each pair of points in contact sets do not agree with the differential relationships in Eq. (13). This has been illustrated in [42], and corresponds to a reminiscence of nonholonomic constraints in rigid body dynamics, in which the differentiation of a velocity constraint cannot be directly related to the second derivatives of the position vectors in configurations.

3 Local contact/impact dynamics in the bouncing dumbbell

3.1 Contact dynamics

Clearly, an open contact set with δ i (t)>0 admits \(F_{i}^{n}(t)=0\). Nevertheless, δ i (t)=0 does not necessitate \(F_{i}^{n}(t)> 0\) because contact force vanishes when the contact set is just separated with nonzero velocity. To detect a contact state, therefore, the following two complementary conditions are required:

$$ \delta_{i}(t)\cdot F_{i}^{n}(t)=0,\quad \delta_{i}(t)\geq0,\ F_{i}^{n}(t)\geq0,\ i=A,B $$
(14)

and

$$ \dot{\delta}_{i}(t)\cdot F_{i}^{n}(t)=0,\quad \dot{ \delta}_{i}(t)\geq0,\ F_{i}^{n}(t)\geq0,\ i=A,B $$
(15)

The combination of (14) and (15) means that if δ i (t)>0, or if δ i (t)=0 together with \(\dot{\delta }_{i}(t)>0\), then \(F_{i}^{n}=0\), while the case of \(\dot{\delta }_{i}(t)<0\) with δ i (t)=0 corresponds to an impact triggered at the point. Contact is established only if both conditions δ i (t)=0 and \(\dot{\delta}_{i}(t)=0\) exist simultaneously in the contact set.

Once a contact state is built, we can use constraint equations to reflect the interactions between bodies without resorting to the concrete physical mechanism on the interfaces. To determine contact forces in a sustained contact process, an LCP formulation has to be established at the acceleration level

$$ \ddot{\delta}_{i}(t)\cdot F_{i}^{n}=0,\quad \ddot{ \delta}_{i}(t)\geq0,\ F_{i}^{n}(t)\geq0,\ i=A,B $$
(16)

To reflect tangential interactions on a rough surface, we introduce Coulomb’s friction law into the contact set. The tangential and normal forces then satisfy

$$ \left \{ \begin{array}{l} \left\{ \begin{array}{l} F_{ix}^{\tau}=-\mu_i\cos\vartheta F_{i}^{n},\\ F_{iy}^{\tau}=-\mu_i\sin\vartheta F_{i}^{n}, \end{array} \right.\quad \hbox{if}\ \sqrt{ {\upsilon^{\tau}_{ix}}^{2}+ {\upsilon^{\tau}_{iy}}^{2}} \neq0,\ \hbox{sliding\ state} \\ \sqrt{{F_{ix}^{\tau}}^2+{F_{iy}^{\tau}}^2} \leq\mu_{i}^sF_{i}^{n},\quad \hbox{if}\ \sqrt{{\upsilon^{\tau}_{ix}}^{2}+ {\upsilon^{\tau }_{iy}}^{2}}=0,\ \hbox{stick\ state} \end{array} \right . $$
(17)

where ϑ represents the sliding direction following the definition of \(\cos\vartheta=\upsilon^{\tau}_{ix}/ \sqrt{{\upsilon^{\tau}_{ix}}^{2}+{\upsilon^{\tau}_{iy}}^{2}}\), μ i , \(\mu_{i}^{s}\) are respectively the slip and static friction coefficients at the corresponding point.

Symmetrical to the normal interaction in contact sets, condition \(\dot {\boldsymbol{\upsilon}}^{\tau}=0\) (\({\boldsymbol{\upsilon}}_{i}^{\tau}= {{\upsilon }}_{ix}^{\tau}\boldsymbol{i} +{{\upsilon}}_{iy}^{\tau}\boldsymbol{j}\)) can be applied to the stick state of friction to determine the relationship between normal and tangential forces. Therefore, to measure the tangential and normal interactions between bodies, the kinematical relationships of the relative motion mapping at the acceleration level are required. They can be obtained from the combination of Eqs. (7) and (13)

$$ \left \{ \begin{array}{l} \ddot{\boldsymbol{\delta}}=\boldsymbol{W}^{T} \boldsymbol{M}^{-1}\boldsymbol {W}\boldsymbol{F}^{n}+\boldsymbol{W}^{T} \boldsymbol{M}^{-1}\boldsymbol {N}\boldsymbol{F}^{\tau}+\boldsymbol{W}^{T} \boldsymbol {M}^{-1}(\boldsymbol{Q}+\boldsymbol{h})+\boldsymbol{S}^{n}-\ddot{\mathbf {z}}_p\\ \dot{\boldsymbol{\upsilon}}^{\tau}=\boldsymbol{N}^{T}\boldsymbol {M}^{-1}\boldsymbol{W}\boldsymbol{F}^{n}+\boldsymbol{N}^{T}\boldsymbol {M}^{-1}\boldsymbol{N}\boldsymbol{F}^{\tau}+\boldsymbol {N}^{T}\boldsymbol{M}^{-1}(\boldsymbol{Q}+\boldsymbol{h})+\boldsymbol {S}^{\tau} \end{array} \right . $$
(18)

Physically, no real rigid body exists actually, such that contact deformation is inevitable, at least in the adjacent region of every individual contact set. Basically, Eq. (18) represents an internal dynamics with the decomposition in the normal and tangential directions, confined in a thin layer of the elastic boundary. In the normal direction, for a sustained contact point i, the internal dynamics in the boundary layer is stable, and evolves quickly within an extremely small scale in time and size, thus it can be neglected by the global motion of the system. The solution of the internal dynamics at its equilibrium state can thus be used to reflect contact forces. We refer to [35] for the proof of this property in contact dynamics of rigid body systems. Note that the physical property of a contact set cannot admit the solution with a value \(F_{i}^{n}<0\), so the complementary condition shown in Eq. (16) exists in a mathematical sense.

For the relative tangential motion in contact sets, the occurrence of \(\boldsymbol{\upsilon_{i}^{\tau}}=0\) corresponds to an equilibrium state that may be maintained in the tangential direction, such that the stick state is equivalent to a tangential constraint defined at the velocity level. This constraint allows the relationship between normal and tangential forces to be determined from \(\dot{\upsilon}^{\tau}_{{ix}}=\dot{\upsilon }^{\tau}_{{iy}}= 0\). Nevertheless, the tangential equilibrium state is limited by an upper bound \(\mu_{i}^{s}\) in the empirical law of Coulomb’s friction. Therefore, a transition from a stick state to a slip state occurs once the solutions violate the upper bound \(\mu_{i}^{s}\). Detailed discussion was given in [33, 36] on identifying the stick-slip transitions of friction.

In most cases, the contact forces can be uniquely determined using the relationships shown in Eqs. (14), (15), (16), (17), and (18). In some peculiar situations, however, the absence of the response of the internal dynamics in contact sets may result in difficulties in solving the problems of contacts/impacts with friction. This will be further discussed in Sect. 4.

3.2 Impact dynamics

An impact occurs at the instant when condition \(\dot{\delta}_{i}(t)<0\) with δ i (t)=0 exists. Unlike a contact process, impact triggers a small-time-scaled process during which the strong interactions between bodies cannot be just modeled via solution of the internal dynamics at its normal equilibrium state. Therefore, the presence of local deformation is basically indispensable for impact dynamics. Nevertheless, the small-scaled time and deformation triggered in a common scenario of impacts often results in difficulties in simulations, especially in dealing with multiple impacts with friction [37–39].

To solve the problem of impact in a simple way without resorting to local deformation, our previous work [26] presented a theoretical framework for multiple impacts, established based upon several hypotheses of shock dynamics. These assumptions include that the configuration of system in impact is invariant, non-impulsive forces are all neglected, and the dissipation of energy induced by the normal motion can be separated from the tangential motion at contact points. Under those assumptions, Eq. (7) can be simplified as

$$ \boldsymbol{M}\,d\dot{\mathbf{q}}=\boldsymbol{W}\,d\boldsymbol {P}^{n}+ \boldsymbol{N}\,d\boldsymbol{P}^{\tau} $$
(19)

where d P n=F n  dt and d P τ=F τ  dt are the vectors for the increments of normal and tangential impulses at contact points, respectively.

To reflect the transformation between the work done by contact forces and the potential energy accumulated at the corresponding contact points, we designate an elastic constitutive relationship for the normal contact force with a form as follows:

$$ F_{i}^{n}=f_{i}(\delta_i)=k_i(- \delta_i)^{\eta_i} $$
(20)

where k i is the contact stiffness at contact point i. Based on the definition above, δ i is always negative when the local normal deformation is in compression. η i is an exponent depending on contact mechanics.

The variation of the elastic potential energy dE i in contact set i induced by the work done by normal force \(F_{i}^{n}\) through a normal deformation dδ i can be expressed as \(dE_{i}=-F_{i}^{n}\cdot d\delta_{i}\), which is equally rewritten as \(dE_{i}=-\dot{\delta}_{i}\,dP_{i}^{n}\). Let us denote E i (0)=0 while \(P_{i}^{n}=0\). The potential energy corresponding to the impulse \(P_{i}^{n}\) is as follows:

$$ E_i \bigl(P_i^n \bigr)=-\int _0^{P_i^n} \dot{\delta}_i \,dP_i^n $$
(21)

To get a relationship between the normal force \(F_{i}^{n}\) and the potential energy E i , let us differentiate for the elastic constitutive relationship

$$ \displaystyle\frac{dF_i^n}{dt}=\frac{\partial f_i(\delta_i)}{\partial\delta_i}\frac{d\delta_i}{dt}=- \eta_ik_i(-\delta_i)^{(\eta _i-1)}\dot{\delta_i} , $$
(22)

then we get

$$ F_i^n=(\eta_i+1)^{\frac{\eta_i}{\eta_i+1}}k_i^{\frac{1}{\eta_i+1}}E_i^{\frac{\eta_i}{\eta_i+1}} $$
(23)

Obviously, the distribution of potential energies among different contact sets determines the correlations of normal differential impulses in space. Denoting point j with the maximal potential energy, that is, E j =max{E i ,i=A,B}, and defining \(dP_{^{j}}^{n}\) as a primary differential impulse, we can obtain

$$ \frac{dP_i^n}{dP_j^n}=\frac{F_i^n}{F_j^n}=\frac{(\eta _i+1)^{\frac{\eta_i}{\eta_i+1}}k_i^{\frac{1}{\eta_i+1}} E_i^{\frac{\eta_i}{\eta_i+1}}}{(\eta_{_j}+1)^{\frac{\eta _{j}}{\eta_{j}+1}}k_j^{\frac{1}{\eta_{j}+1}}E_j^{\frac{\eta _{j}}{\eta_{j}+1}}} $$
(24)

Equation (24) corresponds to the distributing rule in multiple impacts, as discovered in [26]. For the system studied in this paper, Hertz contact [40] with η i =3/2 admits the relationship between \(F_{i}^{n}\) and E i with a form as follows:

$$ F_i^n=k_i^{\frac{2}{5}} \biggl( \dfrac{5}{2}E_i \biggr)^{\frac{3}{5}} $$
(25)

The same material property at each pair of contact points admits k i /k j =1, such that the concrete values for the material parameters in contact interfaces are unnecessary if impact forces are not cared in simulations. Thus, Eq. (24) can be further simplified as

$$ \dfrac{dP_i^n}{dP_j^n}= \biggl(\frac{E_i}{E_j} \biggr)^{\frac {3}{5}}= \varLambda_{i,j}^{n},\quad \hbox{and}\quad \varLambda_{j,j}^n=1 $$
(26)

To reflect the friction effects in impact processes, it is necessary to provide the relationships between tangential impulse \(dP_{i}^{\tau}\) with primary normal impulse \(dP_{j}^{n}\). Incorporating the Coulomb’s friction law into contact dynamics yields the equivalent relationship between infinitesimal normal and tangential impulses, depending on the tangential state in an individual contact set. By considering that the normal differential impulse has been linked with the primary impulse \(dP_{j}^{n}\), the governing equations in Eq. (19) become

$$ \boldsymbol{M}\,d\dot{\mathbf{q}}= \bigl(\boldsymbol{W}\boldsymbol{\varLambda }^{n}+\boldsymbol{N}\boldsymbol{\varLambda}^{\tau} \bigr)\,dP_j^n $$
(27)

where \(\boldsymbol{\varLambda}^{n}=[\varLambda_{A,j}^{n}, \varLambda_{B,j}^{n}]^{T}\) and \(\boldsymbol{\varLambda}^{\tau}=[\varLambda_{Ax,j}^{\tau}, \varLambda _{Bx,j}^{\tau}, \varLambda_{Ay,j}^{\tau}, \varLambda_{By,j}^{\tau}]^{T}\) are the ratio matrices of the normal and tangential differential impulses relative to the primary impulse \(dP_{^{j}}^{n}\). These values depend on the current potential energy and the current tangential states in an individual contact set when primary normal impulse is \(P_{j}^{n}\).

To advance a numerical procedure in simulations, the initial values for Λ n(0) and Λ τ(0) must be provided since, at the start of an impact, there exists no potential energy at any point. Refer to [26] for the detailed discussion for Λ n(0) and Λ τ(0). Here, the initial values of Λ n(0) can be expressed by \(\varLambda_{i,j}^{n}(0)=({\dot{\delta }_{i}(0)}/\dot{\delta}_{j}(0))^{\frac{3}{2}}\), and Λ τ(0) can be obtained in terms of the friction relationship in each contact set.

Due to strong interaction and other factors, energy dissipation in impacts is inevitable. Suppose that energy dissipation only occurs in an expansion phase, and define ε i as the transition efficiency between potential energy dE i and the work dw i done by the contact forces. Then we have

$$ dw_i=-\varepsilon_i\,dE_i,\quad \varepsilon_i(\dot{\delta_i})=\left \{ \begin{array}{l@{\quad }l} 1 & \hbox{if}\ \dot{\delta}\le0\\ e^2_i & \hbox{if}\ \dot{\delta}> 0 \end{array} \right . $$
(28)

where e i is a macroscopic parameter to encapsulate the loss of energy induced by various factors confined in a single compression-expansion cycle. Clearly, the integral form of Eq. (28) can reflect the variation of the potential energy even though the contact set may go through a multiple compression-expansion cycle.

As indicated in [26], the parameter e i agrees with the definition of the energetic coefficient of restitution [11]. For a fully elastic impact, in which e i =1, the energy absorbed in the contact set can be completely released through the expansion phase without dissipation. If 0<e i <1, part of the energy is dissipated during the impact process. For the specific case e i =0, which corresponds to a fully plastic impact in the contact set, the limitation of \(E_{i}(P_{j}^{n})\ge0\) implies that all the energy absorbed in compressional phases will suddenly disappear when the compressional phase is completed. Then the impact at that point finishes with a conglutinate state.

The end of an impact is identified by the condition E i =0, corresponding to a physical picture that no potential energy exists in an open contact set. Generally, the potential energy at the impacting points cannot disappear simultaneously. Therefore, a two-point impact evolved in the dumbbell system will be first transferred into a single impact, followed by continuous changing of the dumbbell velocity until the potential energy at the impact-retained point is completely released.

4 Classification and transitions of contact/impact modes and system singularities

To determine the interaction between the vibrating plate and the dumbbell, it is necessary to correctly distinguish the state in every individual contact set and timely update it along with the dynamical evolution. In this section, we use binary identifiers to classify the states in contact sets, and specify a set vector to identify the system mode of the dumbbell. In addition, the system singularities are also discussed.

4.1 Contact/impact modes and solutions for constraints

Although only two contact sets are involved in this system, its motion consists of plenty of modes due to the variations of contact states. To clarify this point, we number contact points A and B as i=1, 2, respectively, and quantify the states of contact set i as follows:

$$ a_i({\delta_i})=\left \{ \begin{array}{l@{\quad}l} 1 & \hbox{if}\ {\delta_i}= 0,\\ 0 & \hbox{if}\ {\delta_i}> 0, \end{array} \right . \qquad b_i(\dot{\delta_i})=\left \{ \begin{array}{l@{\quad}l} 1 & \hbox{if}\ {\dot{\delta}_i}< 0,\\ 0 & \hbox{if}\ {\dot{\delta}_i}\ge0, \end{array} \right . \qquad c_i \bigl(|{\boldsymbol{ \upsilon}_i^{\tau}}| \bigr) = \left \{ \begin{array}{l@{\quad}l} 1 & \hbox{if}\ |{\boldsymbol{\upsilon}_i^{\tau}}|\ne0\\ 0 & \hbox{if}\ |{\boldsymbol{\upsilon}_i^{\tau}}|= 0 \end{array} \right . $$
(29)

Variable a i (δ i ) distinguishes whether contact i is closed or not, \(b_{i}(\dot{\delta_{i}})\) identifies the occurrence of an impact event, and \(c_{i}({|{\boldsymbol{\upsilon}_{i}^{\tau }}|})\) for the stick-state identification in its tangential direction. Since the values of \(b_{i}(\dot{\delta_{i}})\) and \(c_{i}({|{\boldsymbol{\upsilon }_{i}^{\tau}}|})\) make sense only if a i (δ i )=1, the contact state can be demarcated by defining a set as follows: \(s_{i}=\{ s_{i}^{1},s_{i}^{2},s_{i}^{3}\}=\{a_{i}, a_{i} \wedge b_{i}, a_{i}\wedge c_{i}\}\). After Boolean operation, set s i has five possible values, including s i ={0,0,0};{1,0,0};{1,0,1};{1,1,0};{1,1,1}. Therefore, there are 25 system modes that may be triggered in the dumbbell motion.

To classify the system modes in the dumbbell, we construct a set vector S i : S i =2i−1∧s i , such that S 1=s 1 if i=1. While i=2, the elements in S 2 have two bits ended by 0. For example, if s 2={1,0,1}, bit operation S 2={10}∧s 2 admits S 2={10,00,10}. Define \(\boldsymbol {\mathcal{M}}=\sum_{i=1}^{n}\mathbf{S}_{i}\) (n is the number of potential contact points), in which the elements are evaluated obeying Boolean conjunction operation. Therefore, set vector \(\boldsymbol {\mathcal{M}}\) can be in general expressed as: \(\boldsymbol{\mathcal {M}}=\{ s_{n}^{1} s_{n-1}^{1} \ldots s_{1}^{1}, s_{n}^{2} s_{n-1}^{2} \ldots s_{1}^{2}, s_{n}^{3} s_{n-1}^{3} \ldots s_{1}^{3}\}\), whose values can be used to distinguish the system mode related to the motion of the dumbbell.

Note that Eq. (18) in a matrix notation is expressed as

$$ \left [ \begin{array}{c} \ddot{\boldsymbol{\delta}}\\ \dot{\boldsymbol{\upsilon}}^{\tau} \end{array} \right ]_{3n\times1}= \left [ \begin{array}{c@{\quad}c} \mathbf{A} & \mathbf{B}\\ \mathbf{C} & \mathbf{D} \end{array} \right ]_{3n\times3n} \left [ \begin{array}{c} \boldsymbol{F}^{n}\\ \boldsymbol{F}^{\tau} \end{array} \right ]_{3n\times1}+\left [ \begin{array}{c} \mathbf{R}\\ \mathbf{H} \end{array} \right ]_{3n\times1} $$
(30)

For the dumbbell with a impact-free mode, we can reconstruct Eq. (30), based on the value of \(\boldsymbol{\mathcal{M}}\) and Coulomb’s friction law, to determine the equalities satisfied by the contact forces

$$ \left [ \begin{array}{c@{\quad}c} \mathbf{\widehat{A}} & \mathbf{\widehat{B}} \\ \mathbf{\widehat{C}} & \mathbf{\widehat{D}} \end{array} \right ]_{3n\times3n} \left [ \begin{array}{c} \boldsymbol{F}^{n}\\ \boldsymbol{F}^{\tau} \end{array} \right ]_{3n\times1}+\left [ \begin{array}{c} \mathbf{\widehat{R}}\\ \mathbf{\widehat{H}} \end{array} \right ]_{3n\times1}\triangleq\mathbf{L} \boldsymbol{F}+\mathbf{V}=\mathbf{0} $$
(31)

If the coefficient matrix L is of full rank and positive, contact forces can be uniquely determined [41]. Clearly, the mathematical property in matrix L can expose the system singularities that may be triggered in the system.

The dumbbell will be in an impact mode once an event of impact is triggered at one single point, while the other point is either airborne or in a contact state, or both the two contact sets simultaneously participate in the impact. Based on the theory of multiple impacts, we should examine the friction state and the potential energy at every individual contact set to establish the relationships of differential impulses d P n and d P τ with respect to a “time-like” independent impulse, say, \(dP_{j}^{n}\), the primary normal impulse.

For the dumbbell-suffered impacts, we use a unit matrix I n×n , then set the element \(\boldsymbol{\varLambda }(i,j)=-(E_{i}/E_{j})^{\frac{3}{5}}\). Using Coulomb’s friction law to reflect the relationships among the tangential and normal impulses, together with a column vector R a with zero entries except the jth one of value 1, we can construct a set of algebraic equations expressed as

$$ \left [ \begin{array}{c@{\quad}c} \boldsymbol{\varLambda} & \mathbf{0} \\ \mathbf{\widehat{C}} & \mathbf{\widehat{D}} \end{array} \right ]_{3n\times3n} \left [ \begin{array}{c} d\boldsymbol{P}^{n}\\ d\boldsymbol{P}^{\tau} \end{array} \right ]_{3n\times1}\triangleq \mathbf{K}\,d\boldsymbol{P}=\mathbf{R}_a(j) $$
(32)

If matrix K is of full rank, Eq. (32) can provide the ratios of d P n/dP j and d P τ/dP j needed by the impulsive differential equations (27).

4.2 Transitions among various contact states

The entries of \(\boldsymbol{\mathcal{M}}\) should be timely updated to reflect the variation of the contact states. To enhance the accuracy in numerical simulations, we adopt the following approach to zero-value checking related with δ i , \(\dot{\delta}_{i}\), and \(\boldsymbol{\upsilon}_{i}^{\tau}\).

If the value of δ i or \(\dot{\delta}_{i}\) in the subsequent numerical step changes its sign, then the step will repeat with half of the current length until the target value (δ i or \(\dot{\delta}_{i}\)) reaches the interior of a specified scope Ω adjacent to zero. The search process for the zero-value checking of \(\boldsymbol{\upsilon}_{i}^{\tau}\), starts only if the signs of both \({\upsilon}_{ix}^{\tau}\) and \({\upsilon}_{iy}^{\tau}\) are simultaneously altered, because \(\boldsymbol{\upsilon}_{i}^{\tau}\) is impossible to pass through the zero point in all other cases. Basically, the search process is required mandatorily in simulation because the occurrence of those zero values may excite new physical mechanisms that need to be employed in dealing with the dynamics.

Note that the entries of \(\boldsymbol{\mathcal{M}}\) are also influenced by some limitations in physics, including the upper bound \(\mu _{i}^{s}\) on the coefficient of friction, and nonpenetration of contacts. For example, if a negative value of \({F_{i}^{n}}\) is found in the solutions of Eq. (31), or the ratio between \({F_{i}^{n}}\) and \({F_{i}^{\tau}}\) is larger than \(\mu_{i}^{s}\), then the current state of a contact set is in violation of the physical law previously specified. In principle, these cases also require a search process until solutions are found to comply with all the constraints. An efficient way in simulation is that, once the solutions violate the prescribed relationships in physical laws, the alternative relationships in these physical laws are directly applied to simulations.

The existence of gravity and energy dissipation in an impact admits the transition of a sequence of impacts into a contact state during a finite time interval. The transition can be roughly quantified by a legible condition expressed as [29]

$$ \dfrac{\dot{\delta}_{i}^{+}}{gT_c} \le1 $$
(33)

where T c is a time scale related to the period of single impact, and \(\dot{\delta}_{i}^{+}\) is the post-impact velocity of the contact point. The value of T c can be estimated based on relevant theories in contact mechanics [11].

4.3 Singularities appearing in the dumbbell system

The mode \(\boldsymbol{\mathcal{M}}=\{11,00,00\}\) with \(\dot{\delta}_{A}=\dot {\delta}_{B}=0\) corresponds to the dumbbell either resting or rotating around its spinning axis on the plate. This system mode is related with conditions \({\upsilon^{\tau}_{{Ax}}}^{2}+{\upsilon^{\tau }_{{Ay}}}^{2}=0\), \({\upsilon^{\tau}_{{Bx}}}^{2}+{\upsilon^{\tau }_{{By}}}^{2}=0\). Using these conditions, after performing elementary row operations, we can express Eq. (31) as

(34)

where \(\xi_{1}= ({J_{1}^{2}+(2J_{1}-J_{2})mr^{2}} )/({J_{1}l})\).

Obviously, the matrix before the vector of contact forces, the so-called constrained Delassus’s matrix [31, 43] is not of full rank and asymmetric. Thus, singularity appears in the mathematical model. This is related to a common problem of indeterminacy in rigid body dynamics, in which the contact forces are uncertain [41]. To reveal the property of the singularity, we adopt the condition, \(\dot{\theta}^{2}+\dot{\beta}^{2}=0\) in Eq. (34) implying \(\dot{\theta}= \dot{\beta}=0\) and perform algebraic operation then easily get the relationships satisfied by the contact forces

$$ \left \{ \begin{array}{l@{\quad}l} F_{Ax}^{\tau}c_{\theta}+F_{Ay}^{\tau}s_{\theta}=0\\ F_{Ax}^{\tau}+F_{Bx}^{\tau}=F_{Ay}^{\tau}+F_{By}^{\tau}=0\\ F_A^n=F_B^n=\frac{1}{2}m(g+\ddot{z}_p) \end{array} \right . $$
(35)

It is clear that there exists a one-dimensional set of solutions for the tangential forces, although the normal forces can be uniquely determined. Therefore, the singularity is induced by the absence of the tangential compliance in Coulomb’s friction law.

Substitution of Eq. (35) into the governing equation (7) yields

$$ \ddot{x}_1=0,\qquad \ddot{y}_1=0,\qquad \ddot{\theta}=0,\qquad \ddot{ \beta}=0,\qquad \ddot {\gamma}=0 $$
(36)

Under this mode, \(\dot{\theta}=0\), \(\dot{\beta}=\beta=0\), and \(\boldsymbol{\upsilon }_{A}^{\tau}=\boldsymbol{\upsilon}_{B}^{\tau}=0\) always hold. These conditions, together with Eq. (36), admit the following kinematical equations:

$$ \left \{ \begin{array}{l} \dot{x}_{1}s_{\theta}-\dot{y}_{1}c_{\theta}=0\\ \dot{x}_{1}c_{\theta}+\dot{y}_{1}s_{\theta}=r\cdot C_1\\ \dot{\theta}=0,\quad \dot{\beta}=0,\quad \dot{\gamma}=C_1 \end{array} \right . $$
(37)

where C 1 is an integral constant depending on the kinematics when the motion mode \(\mathbf{\mathcal{M}}=\{11,00,00\}\) starts. The solution presented in Eq. (37) agrees with the physical picture that the motion of the dumbbell may either statically rest or purely roll on the plate when the mode is maintained in the system.

As the system evolves, its mode \(\boldsymbol {\mathcal{M}}=\{11,00,00\}\) may be destroyed and then transferred into others. To predict a transition from this singular mode into a slip state, introduce the following condition:

$$ \sqrt{ \bigl({F_{Ax}^{\tau}+F_{Bx}^{\tau}} \bigr)^2+ \bigl({F_{Ay}^{\tau}+F_{By}^{\tau}} \bigr)^2}\ge\hbox{min} \bigl\{\mu_i^s \bigr \} \cdot \bigl(F_A^n+F_B^n \bigr) $$
(38)

Inequality (38) can be understood as a representative of a generalized friction law for a rigid body with two points contacting within a flat face. The transition of the body from a stick state into a slip state is distinguished by the ratio between the respective summations of the tangential and normal forces at the two points. By Eq. (38), the body will immediately start to slip once any point shakes off the limitation of the static friction. However, for the case investigated here, the relationships of the tangential contact forces shown in Eq. (35) mean that the breaking of the stick is impossible unless a detachment occurs.

Because the normal contact forces at each contact point are unique, the transition from the mode \(\boldsymbol{\mathcal{M}}=\{11,00,00\}\) going for a detachment motion can be easily predicted using the values of \(F_{A}^{n}\) and \(F_{B}^{n}\). Since \(F_{A}^{n}=F_{B}^{n}\) always holds in this mode, the two points will simultaneously detach from the plate, followed by a sequence of double impacts, when the vibration intensity of the plate is large enough.

The absence of the tangential compliance in Coulomb’s friction law also results in a singularity when the dumbbell is in the mode \(\boldsymbol {\mathcal{M}}=\{11,11,00\}\), where both the relative tangential velocities at the two contact points vanish in double impacts [38, 39]. Similar to the analysis above, the singularity can be distinguished by the mathematical property of matrix K. Based on the stick condition \(\boldsymbol{\upsilon}_{A}^{\tau}=\boldsymbol{\upsilon }_{B}^{\tau}=0\), the following kinematical relationship is always satisfied by the dumbbell in the mode \(\boldsymbol{\mathcal{M}}=\{11,11,00\}\)

$$ \left \{ \begin{array}{l} \dot{x}_{1}\cos{\theta}+\dot{y}_{1}\sin{\theta}=r\cdot C_2\\ \dot{\theta}=0,\quad \dot{\gamma}=C_2 \end{array} \right . $$
(39)

Likewise, the transition from the mode \(\boldsymbol{\mathcal{M}}=\{ 11,11,00\}\) into other modes can be distinguished using the same methodology as in the mode \(\boldsymbol{\mathcal{M}}=\{11,00,00\}\).

5 Numerical investigation for the motion of the 3D dumbbell

To validate the 3D model, we adopt the physical parameter values shown in Table 1 mainly from [6] to revisit the experimental results. We first set the 3D dumbbell in an initial state to generate a 2D scenario in which the motion of the dumbbell is limited in a vertical plane where the rod axis (e 1) lies, and then to predict numerically how dumbbell system behaves in a 3D situation. An aspect ratio A r =(l+2r)/(2r) describes the geometry of the dumbbell, and Γ=4π 2 f 2 A z /g (f=2πω) for the representation of the intensity of the vibration.

Table 1 Physical parameters in the dumbbell
Full size table

The dynamics of the dumbbell is sensitive to the initial state. This phenomenon has been experimentally discovered in [6] and also numerically demonstrated in our simulation. Nevertheless, both the experimental findings and our simulation results indicate that the elements densely occupy in the set of initial states to agitate the dumbbell in a periodic mode. In particular, once a periodic motion is formed, its global property appears to be insensible to the initial states. In this paper, the numerical investigation focuses only on the periodic behaviors of the dumbbell.

5.1 Periodic behaviors in planar dynamics

The experiments in [6] demonstrated that a stable drift mode can be easily excited for a dumbbell with its shape described by A r =3.9 under the vibration with Γ=0.9 and f=25 Hz. In this mode, the dumbbell during every cycle of the vibration experiences a sequence of single impacts that alternate between the contact modes {00,00,00} and {01,01,01}, and a single contact with one ball staying on the plate while the other free in air (the dumbbell in the mode \(\boldsymbol{\mathcal{M}}=\{01,00,01\}\)), followed by double impacts \(\boldsymbol{\mathcal {M}}=\{11,10,11\}\) related to the activated impact involving the free ball. In particular, in this mode, the trajectory of the dumbbell’s mass center projected on a horizontal plane approaches a straight line that lies in the vertical plane containing e 1.

To represent the dumbbell in a drift mode, we present the numerical results obtained from an initial state with q(0)=(0,0,r,0,100,0)T and \(\dot{\mathbf {q}}(0)=(0,0,0,0,0,0)^{T}\). This corresponds to a scenario that the dumbbell contacts the plate at point A, inclines at an angle β(0)=10∘, then falls down under gravity at the moment when the plate is at its equilibrium position (ϕ 0=0). The dumbbell in a drift mode takes a period as long as that of a vibration. Figure 2 plots the normal displacements versus time, and Fig. 3 shows the tangential velocities at contact point A, compared with the experimental curve from [6]. The double impacts change the direction of the friction force, which accounts for an asymmetric structure in the curve of \(\upsilon_{A}^{\tau}\) (see Fig. 3) that yields a drift motion on a horizontal plane.

Fig. 2
figure 2

Time histories of the normal motions in Ball 1 (red circle symbol), Ball 2 (black solid line) and the vibrating plate (blue dashed line) in a drift mode

Full size image
Fig. 3
figure 3

Tangential velocity at contact point A in a drift mode

Full size image

The next interesting phenomenon found in [6] is related to a jump mode (see Fig. 4), in which the dumbbell moves like a particle bouncing on the plate with the same period of the vibration. The jump mode is easily excited by setting an initial state to the dumbbell as follows: q(0)=(0,0,r,0,0,0)T, \(\dot{\mathbf{q}}(0)=(0,0,2g/f,0,0,0)^{T}\), related with a scenario that the dumbbell in a configuration parallel to the horizontal plate (β(0)=00), vertically bounces off the plate at a velocity (\(\dot{y}_{1}(0)=2g/f\)). Under the initial condition, the dynamics consists of a singular mode \(\mathbf{\mathcal{M}}=\{11,11,00\} \), during which the two balls simultaneously collide against the plate.

Fig. 4
figure 4

Normal motions of Ball 1 (red circle symbol), Ball 2 (black solid line) and the vibrating plate (blue dashed line) in the jump mode with β 0=0∘

Full size image

While the phenomenon of a jump mode can be simulated by setting the dumbbell in a stringent configuration parallel to the horizontal plate, the real occurrence of the phenomenon should be checked in association with a small perturbation in the special initial state. Figure 5 presents the results obtained from the same initial conditions except a slight change in the inclined angle to β(0)=1∘. A comparison of Figs. 5 and 4 shows good robustness of the jump mode, although the small perturbation results in two subsequent single impacts (see Fig. 6), instead of double impacts.

Fig. 5
figure 5

Normal motions of Ball 1 (red circle symbol), Ball 2 (black solid line) and the vibrating plate (blue dashed line) in the jump mode with β 0=1∘

Full size image
Fig. 6
figure 6

Normal velocity of the contact point A in the jump mode with β 0=1∘

Full size image

The third interesting phenomenon defined in [6] is a flutter mode, in which the two ends collide alternately against the plate within the double periods of the vibration. Obviously, more energy needs to be input into the system to sustain a flutter mode. Our numerical results demonstrate that the dumbbell in a shape A r =3.9 cannot admit a stable flutter mode no matter which initial state is selected. Meanwhile, if the parameters of the vibration remain unchanged (f=25 Hz and Γ=0.9), the achievement of a flutter mode will require an enlarged coefficient of restitution. To represent the dumbbell motion in a flutter mode, we just alter the length of the rod to admit an aspect ratio A r =5.7, and set the coefficient of restitution to be e=0.8. The dumbbell motion in a flutter mode is triggered by an initial condition as follows: q(0)=(0,0,r+A z sin(π/6),0,110,0)T, \(\dot{\mathbf{q}}(0)=(0,0,0.4~\mbox{m/s}, 0,-9.6~\mbox{rad/s},0)^{T}\). In this mode, both tips take turns to impact against the plate with the same time interval equal to the double period of the vibration (see Fig. 7).

Fig. 7
figure 7

Normal motions of Ball 1 (red circle symbol), Ball 2 (black solid line) and the vibrating plate (blue dashed line) in a flutter mode

Full size image

5.2 3D periodic behaviors

The 3D motion of the dumbbell can be realized by setting an initial state with non-zero spinning angular velocity or non-zero horizontal velocity along the direction perpendicular to e 1. Interestingly, numerical simulations demonstrate that the periodic behaviors in a 3D case can be triggered with the same normal motions as in a 2D case just by adding a nonzero horizontal velocity to the initial state. The 3D case exhibits more novel phenomena related to the horizontal motions due to frictional impacts. More specifically, the energy related to the periodically normal motion is principally influenced by the relative normal velocity in impacts, while friction at contact points plays a role of mainly adjusting the horizontal motion. For simplicity, the numerical results presented below are obtained by adopting all the parameters used in 2D simulations except a change in the horizontal velocity to \(\dot{x}_{1}(0)=1m/s\). In the following, we plot the phase portraits to expose their intrinsic structures in order to help understand the periodic patterns agitated in the 3D motion of the dumbbell.

In Fig. 8, the curves of θ versus \(\dot{\theta}\) are given for the three different patterns: In the drift mode, the sign of \(\dot{\theta}\) attracts broad attention, as it often remains negative, this makes the dumbbell continually rotate around a vertical axis. In the phase plane of θ–\(\dot{\theta}\), the jump mode is related to a fixed point (an asterisk point), while the flutter mode corresponds to a closed curve symmetric with respect to the origin (0,0). Obviously, the structures in the phase portraits of the last two modes cannot support a sustained rotation of the dumbbell.

Fig. 8
figure 8

Phase portraits of \(\dot{\theta}\)–θ in drift, flutter and jump modes. Arrows along the orbits demonstrate the evolution of phase trajectories with time. In (a), the black solid lines in the curve indicating a drift mode represent a composite phase mixed with a free and a single impact mode, the blue dashed lines are for a singe contact at point A, and the red circles correspond to double impacts. As shown in (b), the jump mode has just one point represented by a black asterisk. For the flutter mode, the red diamond marks a single impact at point A, the black circle signs a single impact at point B, and a red solid line denotes free motion followed by a single impact at point A, and the black dashed line signifies another free motion stage. The same marks will be used in the upcomming phase portraits (Color figure online)

Full size image

The curves of β versus \(\dot{\beta}\) are plotted in Fig. 9 using the same markers as in Fig. 8 for the three different modes in its 3D motion of the dumbbell. Due to the periodicity in the normal motion of the dumbbell, it is clear that the phase trajectories are closed in all three different patterns. Inversely, the phase trajectories for the curves of γ versus \(\dot{\gamma}\) are unclosed as shown in Fig. 10, Consequently, the motion of the dumbbell in all three different patterns has horizontal transport, depending on the initial value specific for \(\dot{x}_{1}(0)\).

Fig. 9
figure 9

Phase portraits of \(\dot{\beta}\)–β in drift, flutter, and jump modes (Color figure online)

Full size image
Fig. 10
figure 10

Phase portraits of \(\dot{\beta}\)–β in drift, flutter, and jump modes (Color figure online)

Full size image

To reveal the transport behaviors of the dumbbell in the three different periodic patterns, a simple way is to project the position of the mass center of the dumbbell on the horizontal plane (O–ij). As plotted in Fig. 11, the drift mode corresponds to a circle trajectory, the flutter mode to a dog-leg path, and the jump mode to a straight line perpendicular to the vertical plane where e 1 lies.

Fig. 11
figure 11

The trajectories of the mass center of the dumbbell projected on a horizontal plane (O–ij) in drift, jump, and flutter modes. Arrows positioned in the orbits signify velocities of the mass center at the corresponding instants

Full size image

The energy of the dumbbell in periodic modes varies within every individual period, and can be timely compensated and adjusted through the physical mechanism of frictional collisions between the dumbbell and the vibrating plate. Obviously, the driving conditions in vibration and the parameters of impact and friction, as well as the shape of the dumbbell, have a rather important influence on the formation of persistent motions. Despite the complexity of the global property in the dumbbell system, the model proposed in this paper may provide a usefull tool for understanding the effects of these factors on the transport behavior of the bouncing dumbbell.

6 Conclusions and future work

This work studies the dynamics of a three-dimensional dumbbell bouncing on a vibrating plate. Modeling the interactions between the dumbbell and the plate faces several difficult, including the relative kinematics, contact and impact dynamics with stick-slip transition owing to friction, transition from one contact state to another, as well as the singularities often appearing while using rigid body model.

In order to incorporate physical mechanisms (friction and impact laws, LCP formulation) into contact sets, the relative displacement and the relative velocity in each contact set are mandatorily decomposed along the normal and tangential directions with respect to the common tangential plane. Differential forms of the relative velocities also need to be conducted into the relative kinematics. Note that the two points in each contact set vary on the surfaces of the corresponding contacting bodies, and the instantaneous accelerations between every two points in general do not agree with the differential forms in the relative kinematics.

Due to the possible variation of the states in each contact set, the dynamics of the dumbbell requires a model with a hierarchical structure. In an impact-free process, the absence (open contact sets) or the ignorance (closed contact sets) of compliances allows the interaction between the dumbbell and the plate to be measured using the Coulomb’s friction law together with the LCP formulation. To deal with an impact with one or both active contact sets, the method developed in [26] can be applied, in which the velocities of the contacting bodies can be governed by a set of impulsive differential equations associated with the distribution of the potential energy accumulated in each contact set. In particular, the local deformation does not need to be conducted into simulations although the model still strictly adheres to the physical properties of compliance. In addition, the dissipation of energy is directly governed by the energetic coefficient of restitution and the Coulomb’s friction law at each contact set, such that the whole physical process in impacts can be accurately described.

The hierarchical structure in the integrated model requires precisely distinguishing of transitions among the different states in each contact set. By specifying legible conditions to these transitions, the state of the dumbbell motion can be traced using a set vector \(\boldsymbol{\mathcal{M}}\) with elements that can be evaluated by binary identifiers. In association with the combination of the states in the two contact sets, \(\boldsymbol{\mathcal{M}}\) describes 25 possible modes of the dumbbell’s motion. Among these modes, there are two singular modes where the tangential components of the contact forces (or impulses) have nonunique solutions. While the tangential forces (impulses) cannot be uniquely determined in simulation, the kinematical relationships degenerated from the singularities still make the dumbbell motion solvable. To give a resolution for the transitions from these singular modes into another, a supplementary condition needs to be imposed on the dynamics.

The experimental findings in [6] are revisited for comparison with our numerical results, which are obtained by specifying initial states to trigger planar motions. Corresponding to the three types of periodic behaviors in the planar dynamics, the 3D scenario of the dumbbell presents more novel physical phenomena surrounding the trajectory of the dumbbell’s mass center projected onto the horizontal plane. They include a closed circle orbit formed in a drift mode, a dog-leg path generated in a flutter mode, and a straight line in a jump mode.

In summary, this paper presents a general methodology for modeling the nonsmooth dynamics of a simple object. Further investigation needs to be conducted to study the local properties of the energetic coefficient of restitution and friction, to develop the uniform formulation for the relative kinematics between the contacting bodies in complex shapes, as well as to build the general formulation that admits realistic resolutions to different kinds of singularities existing in rigid body dynamics.

This study also brings out some hints for deeper understanding of the fundamental properties of the systems with strong nonlinearity, such as the sensitive dependence of dynamics responses on initial states, and bifurcation behaviors related to different types of periodic motions. These typically nonlinear characteristics of the dumbbell system are dominated by the determinant dynamics related to the contacts/impacts with friction. Connecting the physical parameters with the underlying mechanisms of the global properties may have implications in revealing the intrinsic properties of complex systems, thus it is worthy of exploration in the future work.