1 Introduction

Dynamics modeling of mechanical systems has been applied to different engineering branches and has attracted attention of many researchers. Many solutions for solving the dynamical equations of motion have been proposed. When multi-body systems are considered, the quality of system modeling and solution of its related equations are important. Parallel and serial robots are some of the multi-body systems which require knowledge of their dynamic models. This information, for example, can be used for design and selection of the robot components, control and simulation.

Generally, solving kinematics problem of a multi-body system is necessary for the dynamics analysis. In [1–11], the common dynamics methods such as Newton–Euler method, Lagrangian formulation and the principle of virtual work are used. Many researchers have considered kinematics and dynamics analysis of parallel robots. In [12], the direct kinematics of parallel robots with revolute joints is presented. The direct kinematics of parallel robots is usually more difficult than its serial counterpart. For parallel robots, obtaining solution to the direct kinematics is commonly challenging and most of the times results in a high degree polynomial with multiple answers [13–15]. Numerical methods are commonly employed to obtain the multiple solutions. Still additional methods are required to identify the one correct solution among the multiple solutions. These make obtaining the direct kinematics problem challenging [16]. Direct dynamics problem requires solution of the direct kinematics. This requirement further introduces challenges for direct dynamic applications of parallel robots. Therefore, dynamical solution methods that are independent of directly obtaining kinematics solution are certainly more desirable. One method with such characteristic is the natural orthogonal complement (NOC) method. The NOC was first introduced by Angeles and Lee [17]. The NOC dynamic modeling was found to have certain advantageous in [18] and others. This method defines natural orthogonal complement for Cartesian velocity-constraint matrix. The velocity constraint matrix may also be defined in joint space in which case the form of natural orthogonal complement will be different. The NOC generally leads to elimination of non-working constraint wrenches. Furthermore, using the NOC, the number of driven dynamic equations becomes minimum and separated. The NOC uses the Newton–Euler dynamic equations and incorporates the kinematics constraint equations. This eliminates the need to directly solve the kinematics.

In [1], kinematics and dynamics of a parallel robot with a 3UPS-PU (where U, P and S, represent universal, prismatic and spherical joints, respectively) architecture is investigated. To obtain the dynamical equations of motion for this robot, the Newton–Euler method and the NOC approach are used. In [2], a formulation of inverse dynamics for Stewart platform using Newton–Euler method is presented. Gravity effects and viscous friction in joints are considered. Additionally, it is shown that to obtain actuated forces a proper elimination method can lead to a fast and economic algorithm which is useful for real time control.

The decoupled natural orthogonal complement (DeNOC) method was first introduced in [5]. Unlike the NOC, the DeNOC method allows one to write expressions of the elements of the matrices and vectors associated with the dynamic equations of motion in analytical and recursive form. In this reference, DeNOC method is used to obtain the dynamics analysis of a hexaglide parallel robot. The concept of DeNOC is applied to a 3-RRR planar parallel manipulator to develop dynamics formulation that is both recursive and modular. An algorithmic approach to the development of both forward and inverse dynamics is demonstrated [6]. Recently, application of DeNOC was extended to obtain a recursive forward dynamics algorithm for serial robots with flexible links. The algorithm is applied to a two flexible link arm and is shown to be computationally more efficient and numerically more stable than other algorithms present in the literature [19]. Additional studies on DeNOC for both serial and parallel mechanism as well as other dynamic systems may be found in [5, 20–24]. In [4], the dynamics of non-holonomic mechanical system is derived using the NOC.

References [7–9] used the principle of virtual work and introduced a new recursive matrix method which is useful for dynamic modeling of parallel robots. Recursive matrix method is used to obtain the dynamics analysis of the Agile Wrist [25]. Additionally, actuated powers in two states, full and simplified dynamic models are compared.

In [14], a new spherical star-triangle parallel robot, called SST, is introduced. In [10] and [11], inverse and direct dynamics of this robot is presented using virtual work method. However, the virtual work method requires solution of the direct kinematics problem for obtaining the direct dynamics. Therefore, an algorithm for selecting the admissible solution among eight possible solutions for the SST robot is also presented [11]. However, time to obtain direct kinematics solution can negatively affect the performance of the system. With the NOC, the system kinematics is integrated with its dynamics as a set of differential equations. This potentially can aid in lowering the computation time.

In this paper, first geometry of the SST parallel manipulator and the NOC are briefly described. Next, the constraint equations and other necessary equations for dynamics analysis of the SST parallel robot using the NOC are formulated. Finally, two examples, direct and inverse dynamics, are presented. In the first example, a robot trajectory is given and inverse dynamics using the NOC is solved to obtain required motor torques. Results are next verified with inverse dynamics using the virtual work method [10]. In the second example, motor torques, obtained from the inverse dynamics of the first example, are used as input for the direct dynamics solution using the NOC. The output of the direct dynamics is compared with the input of the inverse dynamics.

2 Introducing the SST parallel robot

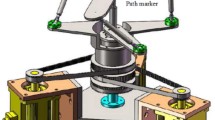
The SST parallel manipulator [14] consists of a fixed virtual spherical triangular base, P, and a moving platform which is shaped like a spherical star, S. The fixed base and the moving platform are connected via three legs. Each of the three moving legs is made of RRP (revolute-revolute-spherical slider [26]) joints. The isotropic model of this manipulator is shown in Fig. 1. To develop the mathematical model of the manipulator, first a sphere with center at O and a fixed spherical triangle, P1P2P3, on its surface is considered. The unit vector v k is defined along OP k . The revolution axis of each actuated joint is along unit vector e k (k=1,2,3). This unit vector is perpendicular to plane OP k P k+1. Rotation about axis of the unit vector e k is defined by angle γ k . See Fig. 2.

Fig. 1
figure 1

Isotropic model of the SST manipulator with motors

Full size image
Fig. 2
figure 2

Parameters description of kth leg

Full size image

The moving spherical star (MSS), S, is next considered. The MSS is made of three arcs which are located on surface of a second sphere. The three arcs of MSS intersect at point E. The angle between these arcs (α 1, α 2 and α 3) can be manually selected by the robot designer to obtain the desired performance. Position of point E defines end-effector position. Direction OE can be defined by unit vector s. See Figs. 1 and 2. The arcs of the moveable star platform ER k intersect the line which is along the actuator links at the point R k . Angular position of the actuators are defined by the unit vector e k+3 (k=1,2,3). Direction of this unit vector is defined along OR k . Additionally, there exist two more joints. The second joint is also a revolute joint with its axis along e k+3. The third joint is referred to as spherical slider joint with its axis along e k+6. The axes of all three joints pass through center of the sphere, point O. See Fig. 2. Rotation about axis of the unit vector e k+3 is defined by angle μ k .

Finally, the motion of the spherical slider joint can also be viewed as a revolute joint with an axis that passes through the origin of the sphere. This axis is defined by a unit vector, e k+6 (k=1,2,3). See Fig. 2. This unit vector is perpendicular to the plane OER k and passes through origin. Therefore

$$ \mathbf{e}_{k+6}=\frac{\mathbf{s}\times\mathbf{e}_{k+3}}{\Vert \mathbf{s}\times\mathbf{e}_{k+3}\Vert} \quad \mbox{for } k=1,2,3 $$
(1)

Finally, rotation about axis of the unit vector e k+6 is defined by angle β k .

3 The Natural Orthogonal Complement (NOC)

Dynamic models developed using the NOC offer many advantages such as being structurally algorithmic, computationally efficient and numerically robust. The method leads to the elimination of the non-working kinematic-constraint wrenches and also to the derivation of the minimum number of equations. Additionally, the dynamics model is in the form of the Euler–Lagrange equations without involving constraint forces, moments or Lagrange multipliers. The resulting equations of motion for the manipulator are in terms of the actuated joint coordinates [24].

Any formulation of equations of motion requires characterization of the role of the physical restrictions that are imposed on a system’s movement. These restrictions lead to constraint equations between joint variables (generalized coordinates), which include both passive and active joints. In dynamics analysis of parallel manipulator using the NOC, obtaining the constraint equation is an important stage. If we describe the joint variables with q i (i=1,2,…,m), then we can write an independent constraint equations in general form as

$$ \mathbf{f}(\mathbf{q})=\mathbf{0} $$
(2)

If the degrees of freedom of the robot number n, then the number of dimensions of the constraint vector equation f(q) will be equal to (m−n). The time derivative of the constraint equations can be written as

(3)

in which Φ is (m−n)×m matrix and is called Jacobian matrix of both active and passive joints. Additionally, \(\dot{\mathbf{q}}\) is the time derivative of the joint variables and is called joint-velocity vector. Therefore, we can write

(4)

We can separate Φ and q with respect to actuated and unactuated parts as

(5)
$$ \dot{\mathbf{q}}=\left[\begin{array}{c} {}[\dot{\mathbf{q}}^{a}]_{n \times 1}\\ {}[\dot{\mathbf{q}}^{u}]_{(m-n)\times 1} \end{array}\right]_{m\times 1} $$
(6)

where the trailing superscript “a” and “u” designate “actuated joints” and “unactuated joints”, respectively. Dimensions of the matrices Φ a and Φ u are equal to (m−n)×n and (m−n)×(m−n), respectively. Additionally, the \(\dot{\mathbf{q}}^{a}\) and \(\dot{\mathbf{q}}^{u}\) are vectors of the actuated and unactuated joint rates, respectively. By placing Eqs. (5) and (6) into Eq. (3), we will have

(7)

The above equation can be rewritten as

(7a)

By taking time derivative of the above equation, we can write

(7b)

or

(7c)

Using Eqs. (5) and (6), we can write

(8)

where and . In the NOC, the twist vector, t i , and its derivative, \(\dot{\mathbf{t}}_{i}\), of ith rigid body can be defined as

(9)

In which r is number of rigid bodies in a system. Therefore, the twist vector and its time derivative for all rigid bodies existing in the system can be written as

$$ \mathbf{t}=\left[\begin{array}{c} \mathbf{t}_{1}\\ \mathbf{t}_{2}\\ \vdots \\ \mathbf{t}_{r} \end{array} \right]_{6r\times 1},\qquad \dot{\mathbf{t}}=\left[\begin{array}{c} \dot{\mathbf{t}}_{1}\\ \dot{\mathbf{t}}_{2}\\ \vdots \\ \dot{\mathbf{t}}_{r} \end{array}\right]_{6r\times 1} $$
(10)

The twist vector of the ith rigid body can be written as a linear transformation of the joint-velocity vector as follows:

(11)

where \(\mathbf{K}_{i}=\frac{\partial \mathbf{t}_{i}}{\partial \dot{\mathbf{q}}}\) is a (6×m) matrix and is called Jacobian matrix of ith rigid body. Equation (11) is also used in the direct kinematics of a serial type multi-body system to express the twist of the ith rigid body as a linear transformation of the joint velocities. Equation (11), for i=1,2,…,r, can be assembled and expressed in compact form as

$$ \mathbf{t}=\mathbf{K}\dot{\mathbf{q}},\quad \mathbf{K}=\left[\begin{array}{c} \mathbf{K}_{1}\\ \vdots\\ \mathbf{K}_{r}\end{array}\right]_{6r\times m} $$
(12)

where K represents Jacobian matrix of all rigid bodies existing in a system. Additionally, the K matrix can be divided into two parts K a and K u as

$$ \mathbf{K} = \left[\begin{array}{c@{\quad}c} [\mathbf{K}^{a}]_{6r\times n} & [\mathbf{K}^{u}]_{6r\times (m-n)}\end{array} \right] = \left[\begin{array}{c@{\quad}c} \frac{\partial \mathbf{t}}{\partial \mathbf{q}^{a}} & \frac{\partial \mathbf{t}}{\partial \mathbf{q}^{u}}\end{array}\right]_{6r\times m} $$
(13)

Therefore, Eq. (12) can be rewritten as

$$ \mathbf{t}=\mathbf{K}^{a}\dot{\mathbf{q}}^{a} +\mathbf{K}^{u}\dot{\mathbf{q}}^{u} $$
(14)

The time derivative of Eq. (12) leads to the twist vector differentiation as

$$ \dot{\mathbf{t}}=\mathbf{K}\ddot{\mathbf{q}} +\dot{\mathbf{K}}\dot{\mathbf{q}} $$
(15)

Using Eqs. (3), (5), (6), and (7), we can obtain the joint-velocity vector as a function of independent the joint-velocity vector as

$$ \dot{\mathbf{q}}=\mathbf{L}\dot{\mathbf{q}}^{a} $$
(16)

where the L matrix is defined as

(17)

The L matrix is called joint orthogonal complement and shows the relation between the independent and dependent joint velocities. Multiplying the two sides of Eq. (16) by the Φ matrix and using Eq. (3), we will have

(18)

Since the \(\dot{\mathbf{q}}^{a}\) vector represents array of independent and arbitrary joint rates, we can write

(19)

The time derivative of Eq. (16) can be written as

$$ \ddot{\mathbf{q}} = \mathbf{L}\ddot{\mathbf{q}}^{a}+\dot{\mathbf{L}}\dot{\mathbf{q}}^{a} $$
(20)

By substitution Eq. (16) into Eq. (12), we will have

$$ \mathbf{t}=\mathbf{K}\dot{\mathbf{q}}=\mathbf{K}\mathbf{L}\dot{\mathbf{q}}^{a} =\mathbf{T}\dot{\mathbf{q}}^{a} $$
(21)

where

$$ \mathbf{T} = \mathbf{K}\mathbf{L} $$
(22)

where T is a (6r×n) matrix and is called the NOC matrix. The T matrix is defined as the linear transformation which maps the independent joint velocities into the generalized twist of the system. Substituting the K matrix from Eq. (13) and the L matrix from Eq. (17) into above equation leads to

(23)

Additionally, the time derivative of Eq. (21) leads to

$$ \dot{\mathbf{t}}=\mathbf{T}\ddot{\mathbf{q}}^{a}+\dot{\mathbf{T}}\dot{\mathbf{q}}^{a} $$
(24)

where

(25)

Equations (17), (23), and (25) allows obtaining the L, T and \(\dot{\mathbf{T}}\) matrices when the constraint equations of a multi-body system are supplied. These matrices will be used in dynamics analysis of the multi-body system.

4 Constraints equations for the SST parallel manipulator

Consider the joint variables γ k , μ k and β k , for k=1,2,3, as shown in Fig. 2. Additionally, consider Fig. 3 in which the moving coordinate frame {E}, xyz, is attached to the MSS and the base coordinate frame {B}, x 0 y 0 z 0, is attached to the robot fixed base. To write the constraint equations between joint variables of the SST robot, for each branch, we must place the x 0 y 0 z 0 frame on the xyz frame. Another words, we must obtain a rotation matrix between these two frames. For this purpose, we need to define four additional coordinate frames for each branch as

  • A fixed, non moving, coordinate frame for each leg, {0k} or x 0k y 0k z 0k .

  • A moving coordinate frame for each leg, {1k} or x 1k y 1k z 1k , attached to the actuated link.

  • A moving coordinate frame for each leg, {2k} or x 2k y 2k z 2k , attached to the intermediate passive link.

  • A moving coordinate frame for each leg, {3k} or x 3k y 3k z 3k , attached to the MSS.

Next, consider the coordinate frames in Fig. 4 for kth branch as well as Figs. 5, 6 and 7 for each branch. Using rotation matrices, we can place the coordinate frame x 0k y 0k z 0k on the moving coordinate frame x 3k y 3k z 3k by

$$ {}_{3k}^{0k}\mathbf{R} = {}_{1k}^{0k}\mathbf{R} {}_{2k}^{1k}\mathbf{R} {}_{3k}^{2k}\mathbf{R} \quad \mbox{for } k=1,2,3 $$
(26)

where

(27)
(28)
(29)

Consider the first branch in Fig. 5. The coordinate frame x 01 y 01 z 01 coincides with the base coordinate frame {B}. Additionally, the coordinate frame x 31 y 31 z 31 also coincides with the moving coordinate frame {E}. Therefore, we can write

$$ {}_{\mathrm{E}}^{\mathrm{B}}\mathbf{R}={}_{31}^{01}\mathbf{R} $$
(30)

Consider the second branch in Fig. 6. We can place the coordinate frame x 32 y 32 z 32 on the moving coordinate frame {E} using rotation about the x 32 axis by angle (−α 2). Therefore, we can write

$$ {}_{\mathrm{E}}^{32}\mathbf{R}={}_{31}^{32}\mathbf{R} =\mathit{Rot}(x_{32},-\alpha_{2}) =\mathit{Rot}(\mathbf{s},-\alpha_{2}) $$
(31)

Additionally, the rotation matrix between the coordinate frames x 01 y 01 z 01 and x 02 y 02 z 02 can be written as

$$ {}_{02}^{\mathrm{B}}\mathbf{R}={}_{02}^{01}\mathbf{R} =\left[\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{array}\right] $$
(32)

Using Eqs. (26), (31), and (32), we can write

$$ {}_{\mathrm{E}}^{\mathrm{B}}\mathbf{R}={}_{02}^{01}\mathbf{R} \ {}_{32}^{02}\mathbf{R} \ {}_{31}^{32}\mathbf{R} ={}_{02}^{\mathrm{B}}\mathbf{R}\ {}_{32}^{02}\mathbf{R} \ {}_{\mathrm{E}}^{32}\mathbf{R} $$
(33)

Similarly, for the third branch (see Fig. 7), we can obtain

$$ {}_{\mathrm{E}}^{\mathrm{B}}\mathbf{R}={}_{03}^{01}\mathbf{R}\ {}_{33}^{03}\mathbf{R}\ {}_{31}^{33}\mathbf{R} ={}_{03}^{\mathrm{B}}\mathbf{R}\ {}_{33}^{03}\mathbf{R}\ {}_{\mathrm{E}}^{33}\mathbf{R} $$
(34)

where

$$ {}_{\mathrm{E}}^{33}\mathbf{R}={}_{31}^{33}\mathbf{R} =\mathit{Rot}\bigl(x_{31},-(\alpha_{2}+\alpha_{3})\bigr) =\mathit{Rot}\bigl(\mathbf{s},-(\alpha_{2}+\alpha_{3})\bigr), $$
(35)
$$ {}_{03}^{\mathrm{B}}\mathbf{R}={}_{03}^{01}\mathbf{R} =\left[\begin{array}{c@{\quad}c@{\quad}c} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{array} \right] $$
(36)

Finally, the three rotation matrices, obtained from each branch, are equated in order to obtain the constraint equations. Therefore, we can write

$$ {}_{\mathrm{E}}^{\mathrm{B}}\mathbf{R} ={}_{31}^{01}\mathbf{R}={}_{02}^{01}\mathbf{R}\ {}_{32}^{02}\mathbf{R}\ {}_{31}^{32}\mathbf{R} ={}_{03}^{01}\mathbf{R}\ {}_{33}^{03}\mathbf{R}\ {}_{31}^{33}\mathbf{R} $$
(37)

By equating corresponding terms of the above equation, six independent constraint equations can be obtained. The six equations also represent the constraint Eq. (2), f(q)=0, which is utilized to obtain the L matrix.

Fig. 3
figure 3

The moving and base coordinate frames

Full size image
Fig. 4
figure 4

Coordinate frame description of kth leg

Full size image
Fig. 5
figure 5

Coordinate frames for the first branch

Full size image
Fig. 6
figure 6

Coordinate frames for the second branch

Full size image
Fig. 7
figure 7

Coordinate frames for the third branch

Full size image

5 Computing the K matrix of the SST robot

To write the K matrix, we must write the twist vector, t, for every one of the system rigid bodies. Then, using Eq. (11), the matrix K i and consequently matrix K can be determined. Consider Figs. 3 and 4. To obtain the twist vector, t, several steps are taken. First, extension of the robot joints are defined by vectors e i as

(38)
(39)
(40)
(41)
(42)
(43)
(44)

These unit vectors were earlier defined in Sect. 2. Additionally, consider Figs. 1 and 2. The actuated links of the branches 1, 2, and 3 are called rigid bodies 1, 2, and 3, respectively. The intermediate passive links of the branches 1, 2, and 3 are called rigid bodies 4, 5, and 6, respectively. The MSS is called rigid body 7.

In the next step, position vectors r ij are defined. Here indices i and j represent the joint number and rigid body number, respectively. The vector r ij connects joint number i to center of mass of the rigid body j. Consider Fig. 8. Using the simple assumption of having mass center of the actuated link being located in the middle of the rigid body, we can write

(45)
(46)
(47)

Additionally, we assume that the mass centers of the intermediate passive links are at a distance of R, radius of sphere, from center of the sphere.

(48)
(49)
(50)

The mass centers of the passive revolute joints are located on their respective axis of rotation. Therefore

(51)
(52)
(53)

The mass center of the MSS may help define the other vectors as

$$ \mathbf{r}_{17} = (2R/\pi) {}_{02}^{01}\mathbf{R}\ {}_{32}^{02}\mathbf{R}\ {}_{31}^{32}\mathbf{R} \left[\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0\end{array} \right]^{T} $$
(54)

We can then write

$$ \mathbf{r}_{47} = -\mathbf{r}_{14} + \mathbf{r}_{17} $$
(55)
Fig. 8
figure 8

The position vectors r ij

Full size image

The twist vectors of the rigid bodies 1 to 7 can now be written as

(56)
(57)
(58)
(59)
(60)
(61)
(62)

Therefore, using Eq. (12) the K matrix representing Jacobian of all rigid bodies can be obtained. Upon obtaining the K and L matrices, Eq. (22) can be used to obtain the NOC matrix T.

6 Dynamics modeling

Consider a multi-body system consisting of r rigid bodies. The wrench acting on the ith rigid body can be represented as

$$ \mathbf{w}_{i}^{*} = \left[\begin{array}{c@{\quad}c} \mathbf{n}_{i}^{*} & \mathbf{f}_{i}^{*} \end{array} \right]^{\mathrm{T}} \quad \mbox{for } i=1,2,\ldots,r $$
(63)

where \(\mathbf{n}_{i}^{*}\) and \(\mathbf{f}_{i}^{*}\) represent the D’Alembert’s resultant inertia force and torque exerted at the center of mass, respectively. Therefore, we can write

(64)
(65)

where m i is the body mass, \(\ddot{\mathbf{c}}_{i}\) is acceleration of the ith mass center, I i is moment of inertia of the ith body about ith mass center, ω i is angular velocity of the ith body and is angular acceleration of the ith body. The Newton–Euler equations for each individual body can be written as

(66)

where M i and Ω i are defined as

(67)

When all r rigid bodies in a multi-body system are considered, Eq. (66) can be written as

(68)

where

(69)
(70)

and w ∗ is called the dissipate wrench vector and is defined as

$$ \mathbf{w}^{*} = \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} (\mathbf{w}_{1}^{*})^{\mathrm{T}} & (\mathbf{w}_{2}^{*})^{\mathrm{T}} & \cdots & (\mathbf{w}_{r}^{*})^{\mathrm{T}} \end{array} \right]^{\mathrm{T}} $$
(71)

The vector of generalized forces of the actuated joints, τ a, that includes forces and moments of actuated joints is defined as

(72)

where n is the number of actuated joints. Therefore, we can obtain powers of the actuated joints as

(73)

Additionally, the powers related to the inertia (π ∗), gravity (π g) and friction (π f) can be written as

(74)
(75)
(76)

where w g and w f represent the gravity and friction wrenches, respectively. We can write

(77)
(78)

Using the natural orthogonal complement T, Eqs. (74), (75), and (76) can be written as

(79)
(80)
(81)

In a dynamics system, if we apply the D’Alembert’s resultant inertia forces and torques, we can say that the sum of the above powers is zero. Therefore, we have

$$ \pi^{a} + \pi^{*} + \pi^{g} + \pi^{f} = 0 $$
(82)

Substituting Eqs. (79), (80), and (81) into the above equation will yield

(83)

Factoring actuated velocity vector will yield

(84)

Since the above equation is valid for any \(\dot{\mathbf{q}}^{a}\), it follows that

(85)

or

(86)

Furthermore, we can write the power dissipated by friction in another form as

(87)

Substituting Eq. (16) into the above equation will yield

(88)

Therefore, Eq. (86) can be rewritten as

(89)

If we substitute w ∗ from Eq. (68) into the above equation, it will yield

(90)

Substituting Eqs. (21) and (24) into the above equation will yield

(91)

This equation represents system dynamical model in terms of the actuated joints. Finally, the dynamics equation of motion can be represented as

(92)

where

(93)
(94)
(95)
(96)

From the foregoing discussion, then, it becomes apparent that Eq. (92) represents the system’s Euler–Lagrange dynamical equations, free of non-working generalized constraint forces.

6.1 Inverse dynamics analysis

For the inverse dynamics problem, a desired trajectory of the MSS is given and the problem is to determine the input torques required to produce the desired motion. The solution process first requires solving the inverse kinematics problem, which calculates the required values of the actuated joint-trajectories, q a, \(\dot{\mathbf{q}}^{a}\) and \(\ddot{\mathbf{q}}^{a}\). Next, the K, L and T matrices are used to evaluate Eqs. (93) to (96). The dynamic Eq. (92) can now be used to obtain the necessary actuated torques.

A possible advantage of the NOC for the inverse dynamics calculations may be its lower computation time. As will be shown in Sect. 7.2, inverse dynamics computation time using the NOC is approximately 37 % lower than the virtual work method. Clearly, this statement should be taken with great care as a true scientific comparison requires counting and comparing exact number of additions and multiplications for each method.

6.2 Direct dynamics analysis

The direct dynamics problem aims to find the response of a robot arm corresponding to given applied moments and/or forces. That is, given the vector of joint moments or forces, it computes the resulting motion of the manipulator as a function of time. In the direct dynamics problem, the vector of initial actuated joint positions and vector of initial actuated joint velocities are given. Therefore, we need to formulate the dynamics equations in terms of the generalized coordinates of joints and their time derivatives. Unlike other common dynamics methods such as principle of virtual work [10], solution of the direct dynamics problem does not require directly solving the direct kinematics problem. Additionally, the dynamics equations are formulated in terms of only the actuated joints [11]. However, using the NOC kinematics, the equations are integrated with its dynamics as a set of differential equations. Furthermore, the L matrix allows obtaining the unactuated joint velocities given the actuated joint velocities. This eliminates the need to obtain the dynamics equations in terms of only the actuated joints. These advantages can potentially simplify the direct dynamics problem.

The direct dynamics problem may be solved using Eqs. (7) and (92), a state space for q and \(\dot{\mathbf{q}}\). Now having q, the position at the middle of MSS (point E) can be computed at any time using the unit vector s that is defined as

$$\mathbf{s} = {}_{02}^{01}\mathbf{R}\ {}_{32}^{02}\mathbf{R}\ {}_{31}^{32}\mathbf{R} \left[\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0\end{array}\right]^{T} $$

7 Numerical simulation

The solution outlined in this paper is applied to an isotropic model of the SST robot [14]. See Fig. 1. Based on the previous sections, a computer program is developed using MATLAB software for both direct and inverse dynamics solutions. For inverse dynamics simulation, a trajectory for the MSS is supplied and required motor torques are calculated. Results are verified with another reference [10] using a different method. For direct dynamics simulation, output of the inverse dynamics simulation is used. Results are confirmed with input trajectory used in the inverse dynamics simulation.

7.1 Specification of the SST manipulator

  1. (a)

    Architecture parameters—fixed base: Assume that the radius is 0.35 meters and that the planes OP1P2, OP2P3 and OP3P1 of SST manipulator are located in x–y, y–z and z–x of base coordinate frame, respectively. See Fig. 1. Therefore

    $$\mathbf{v}_{1}=\left[\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0\end{array} \right]^{\mathrm{T}}, \qquad \mathbf{v}_{2}=\left[\begin{array}{c@{\quad}c@{\quad}c} 0 & 1 & 0\end{array} \right]^{\mathrm{T}}, \qquad \mathbf{v}_{3}=\left[\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 1\end{array} \right]^{\mathrm{T}} $$
  2. (b)

    Architecture parameters—MSS: Assume radius is 0.4 meters and that the angle between the planes OER k and OER k+1 is 120 degree. See Figs. 1 and 3. Therefore

    $$\alpha_{1}=\alpha_{2}=\alpha_{3}=120^{\circ} $$
  3. (c)

    Mass properties of MSS:

    $$m_{s}=2.6\mbox{ kg} $$
    $${}^{\mathrm{E}}\mathbf{I}_{\mathrm{s}}=\left[\begin{array}{c@{\quad}c@{\quad}c} 0.224 & 0 & 0\\ 0 & 0.224 & 0\\ 0 & 0 & 0.150\end{array} \right]\mbox{~kg}{\cdot}\mbox{m}^{2} $$
  4. (d)

    Equal mass properties for each actuator link, k=1,2,3:

    $$m_{a}=0.3\mbox{~kg} $$
    $${}^{1k}\mathbf{I}_{a}=\left[\begin{array}{c@{\quad}c@{\quad}c} 0.0001 & 0 & -0.0001\\ 0 & 0.008 & 0\\ -0.0001 & 0 & 0.008\end{array} \right]\mbox{~kg}{\cdot}\mbox{m}^{2} $$
  5. (e)

    Equal mass properties for each intermediate passive link, k=1,2,3:

    $$m_{ipl}=0.06\mbox{~kg} $$
    $${}^{2k}\mathbf{I}_{ipl}=\left[\begin{array}{c@{\quad}c@{\quad}c} 0.00001 & 0 & 0\\ 0 & 0.005 & 0\\ 0 & 0 & 0.005\end{array} \right]\mbox{~kg}{\cdot}\mbox{m}^{2} $$

7.2 Example-1: simulation of inverse dynamics

For the inverse dynamics simulation, the trajectory of MSS is specified as follow

$$\theta=\tan^{-1}(s_{y}/s_{x}) $$
$$\varphi =\cos^{-1}s_{z} $$
$$\psi =0 $$

where

$$s_{x}=\frac{1}{71}\biggl( 4\sqrt{6}\cos(12t)-12\sqrt{2}\sin(12t)+\frac{\sqrt{13395}}{3}\biggr) $$
$$s_{y}=\frac{1}{71} \biggl(4\sqrt{6}\cos(12t)+12\sqrt{2}\sin(12t)+\frac{\sqrt{13395}}{3}\biggr) $$
$$s_{z}=\frac{1}{71}\biggl(-8\sqrt{6}\cos(12t)+\frac{\sqrt{13395}}{3}\biggr) $$

where 0≤t≤π/6. Angles θ, φ and ψ are shown in Fig. 4. This implies that position of point E, moves along a circular path on the surface of the sphere while MSS does not rotate about the unit vector s. See Fig. 9. Results of this simulation are calculated as function of time and are plotted in Fig. 10. The output of the inverse dynamics problem using virtual work [10] and commercial software for this example is also plotted in Fig. 10. As can be seen the required torques are nearly identical. These results verify the correctness of the mathematical model. Additionally, simulation time using the virtual work method is slightly lower than the NOC. The CPU time, for virtual work and the NOC methods, using a 2 GHz processor with 2 GB RAM memory, are 2.7612 and 1.7316 seconds, respectively.

Fig. 9
figure 9

Inverse dynamics input: circular path followed by point E on MSS

Full size image
Fig. 10
figure 10

Required input torques for circular path using both the NOC and virtual work [10]

Full size image

7.3 Example-2: simulation of direct dynamics

For the direct dynamics simulation, the output of the inverse dynamics problem given in previous subsection is used. The input torques, Fig. 10, are applied as a function of time. Additionally, the initial conditions of actuators are assumed as

$$\gamma_{1}=\frac{\pi}{4}\mbox{~rad},\qquad \gamma_{2}=0.5549\mbox{~rad},\qquad \gamma_{3}=1.0159\mbox{~rad} $$
$$\dot{\gamma}_{1}=4.2096 \ \frac{\mathrm{rad}}{\mathrm{s}},\qquad \dot{\gamma}_{2}=-0.6918 \ \frac{\mathrm{rad}}{\mathrm{s}},\qquad \dot{\gamma} _{3}=-0.6918 \ \frac{\mathrm{rad}}{\mathrm{s}} $$

Simulation result is plotted in Fig. 11. Results show that the trajectory of point E moves along a circular path. Figure 11 also shows that the simulated path and real path are very close. This result verifies the correctness of our mathematical model.

Fig. 11
figure 11

Direct dynamics output: three-dimensional trajectory of point E

Full size image

8 Conclusion

The application of the Natural Orthogonal Complement for the inverse and direct dynamic analysis of SST spherical parallel manipulators for the first time is presented. The method uses joint orthogonal complement which indirectly incorporates the kinematics model. Several other advantages of NOC are pointed out. Using this method, the direct and inverse kinematics problems are indirectly solved. Furthermore, there is no need to obtain the velocity and acceleration inversions in order to solve the inverse and the direct dynamics problems. Using the NOC, the solution for both direct and inverse dynamics problems of the SST parallel robot is presented. The derived formulations can be used to compute the required actuator torques for a given trajectory of the moving platform or to obtain the resulting trajectory for a given actuator torques. The developed formulations are implemented and simulated using two examples. First, inverse kinematics solution is verified using another dynamical method as well as a commercial multi-body dynamical package. Next, direct dynamics results are verified using the inverse dynamics results. The study presented in this paper provides a framework for our future research in the areas of SST manipulator control.