1 Introduction

Data mining is a procedure that pulls previously unknown patterns or information from databases. It is also characterised as a descriptive analytics approach known as clustering, which discovers patterns based on specified dissimilarity criteria [9]. Due to extensive applicability, clustering has captured the attention of research communities who have worked to develope several evolutionary metaheuristic algorithms to solve clustering problems (Dorigo et al. [5]; Cura [4]; Kumar and Sahoo [18,19,20]; Karaboga and Ozturk [16]; Hatamlou et al. [13]; Hatamlou [11]). Clustering methods optimally divide a set of data objects and retain them in clusters (Nanda and Panda [26]; Mat et al. [22]). The clustering process is carried with the help of some dissimilarity measures. The Euclidean distance given in Eq. (1) is an extensively accepted similarity measure in the partitional clustering techniques. It is described as a sum of the square root of the difference between data objects and the cluster centres. The data objects are tailored into the clusters according to the distance values.

$$ D\left({Z}_i,{C}_j\right)=\sqrt{\sum \limits_{i=1}^n\sum \limits_{k=1}^d{\left({Z}_{ik},{C}_{jk}\right)}^2} $$
(1)

where Zi symbolizes the ith data instance/object, Cj represents the jth cluster centre/centroid, whereas n and d denote the number of instances/data objects and dimension/attribute in the dataset, respectively.

In this study, an enhanced version of the whale optimization algorithm (WOA) is proposed to find optimized cluster centres. The WOA is a nature-inspired method that simulates the foraging behaviour of humpback whales (Mirjalili and Lewis [24]). The original WOA suffers from various issues such as the ones listed below:

  • Convergence rate: The convergence rate is concentric around the search space mechanism and the coordination among exploration and exploitation processes is lacking (Kumar and Sahoo [19]).

  • Local optima: It is a situation when the candidate solution is not getting an update and primarily occurs due to the absence of a population divarication mechanism. It is observed that the original WOA suffers from local optima (Kumar and Kaur [17]).

To overcome these and other problems that are inherent in the original WOA, this study proposes an improved algorithm called the Enhanced Whale Optimization Algorithm (EWOA). The EWOA is adapted from the original WOA and enhanced with two additional operational procedures to accelerate the convergence rate and overcome the local optima situation. To accelerate the convergence rate, position update equations from the water wave optimization algorithm are incorporated into the algorithm to improve the search space, while the tabu and neighbourhood search mechanisms were incorporated to overcome the local optima situation. The efficiency of the proposed EWOA is measured using a simulation-based experiment conducted on eight benchmark datasets, namely the Iris, Cancer, CMC, Wine, Glass, Thyroid, LR and ISOLET datasets, and the results obtained are then compared to seven existing clustering algorithms/techniques, namely the Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Cat Swarm Optimization (CSO), Genetic Algorithm (GA), Advanced Chemical Reaction Optimization (ACRO), WOA, and K-means algorithms. The performance of each algorithm is compared and analyzed using the average intra-cluster distance and f-measure parameters. The applicability and feasibility of the proposed algorithm is demonstrated via the experimental study that has been carried out in this paper. The experimental results highlighted the enhancements that were made and proved the superiority of the proposed EWOA clustering algorithm.

The core contributions of this study are summarized as follows:

  1. i).

    Introduced the EWOA as an improvement to the original WOA by incorporating some key enhancements to overcome the problems that are inherent in the the original WOA.

  2. ii).

    Incorporate tabu and neighbourhood strategy to handle local optima situations.

  3. iii).

    Incorporate the position update equations from the water wave optimization algorithm to improve the search space, minimize the intra-cluster distance and accelerate the convergence rate.

  4. iv).

    Demonstrate the feasibility and applicability of the proposed EWOA model by implementing the algorithm in solving cluster analysis problems using eight experimental benchmark datasets.

  5. v).

    Proved the superiority of the proposed EWOA model by comparing the results of the experimental study obtained via the proposed EWOA model and seven other well-known clustering algorithms.

This paper is divided into 6 sections. The literature review and related works is presented in Section 2, while Section 3 describes the background details of the algorithms and methods that are employed in this paper. The improvements and enhancements that were done to the algorithm are detailed in Section 4, while the experimental study and the results that were obtained are presented in Section 5. Concluding remarks and the future scope of this study is presented in Section 6, followed by the list of declarations, acknowledgments and the list of references.

2 Literature review

Several algorithms have been developed, hybridized, and improved in the past few decades to solve clustering problems. Some of them are expounded in this section. Premalatha and Natarajan [27] proposed a PSO algorithm with an enhanced discrete binary PSO, where the model was tested using three datasets and compared with the K-means clustering algorithm, and the outcome was an improved execution and more diversity in the swarm. Kao et al. [15] studied partitional clustering problems using a hybrid optimization solution, while Chang et al. [3] eliminated the local optima and premature convergence problems of the standard genetic algorithm with their proposed gene rearrangement strategy. Jiang and Wang [14] presented a cooperative coevolution framework for BPSO algorithms, in which cooperative coevolution was used to decompose the problem into K subproblems, while PSO was used to solve these problems. Wang et al. [38] proposed a chaotic KH hybridized clustering method which had a better convergence speed. Kumar and Sahoo [18] proposed a hybrid data clustering algorithm by combining CSO and K-harmonic means algorithms, tested it against various existing algorithms, and concluded that the proposed hybrid model has improved convergence speed. Kumar and Sahoo [19] introduced another hybrid algorithm that combined the PSO and MCSS algorithms, in which this hybrid model employed the neighbourhood technique to improve the search process. Menéndez et al. [23] proposed a multi medoid-based ACO clustering algorithm that automatically determines the optimum number of clusters and works without predetermined criteria, i.e. the number of clusters. Hatamlou [12] hybridized the PSO and the big bang-big crunch (BB-BC) algorithms to overcome the local optima and premature convergence problems.

Zhang et al. [41] and Karaboga and Ozturk [16] studied the use of the ABC algorithm that simulated the intelligent foraging behaviour of honey bee swarms in clustering problems and proved that the ABC algorithm is indeed efficient for solving multivariate data clustering problems. Yan et al. [40] introduced a hybrid variant of the ABC algorithm for solving clustering problems, in which the crossover operator of GA is integrated with the ABC algorithm to accelerate its convergence speed and achieve optimality in the solution faster. Alshamiri et al. [2] integrated the extreme learning machine (ELM) model into the ABC algorithm, in which the ELM model will project the input data into a high-dimensional feature space, while the ABC algorithm will perform the partitions. Kumar and Sahoo [20] proposed an efficient two-step ABC algorithm, in which the K-means algorithm is used to identify the initial seed points or food sources for the ABC algorithm.

Senthilnath et al. [31] implemented the firefly algorithm that simulates the social insects’ behaviour and flash pattern of fireflies in solving clustering problems. Hatamlou [11] introduced a black hole (BH) phenomenon-based algorithm for clustering, in which the search space is defined in terms of the black hole, stars, and their absorption mechanism. The efficiency of the BH-based method was tested using standard datasets and was proven to be an effective clustering technique. Wang et al. [39] proposed a bee pollinator with a flower pollination algorithm to improve searchability and achieve faster convergence. Siddiqi et al. [32] introduced a new hybrid model that integrated the GA and SimE algorithms to automate the partitional clustering process. A greedy method is first applied to select the initial seed points, and optimization methods are then implemented to optimize them. Kushwaha et al. [21] proposed a magnetic force-based clustering algorithm in which a magnetic force-based search mechanism is implemented to find the optimal cluster centres. The data points are considered as particles and get rendered due to magnetic forces. The optimum position for the centroid particles is said to be achieved when the magnetic force applied by the data points approaches zero.

To automate the clustering process, Zhou et al. [43] projected the simplex method in the social spider algorithm. The simplex method is used to estimate and update the positions of the spiders. This stochastic variant strategy enhanced the population diversity and improved the local search ability of the traditional algorithm. Han et al. [10] hybridized the birds flock and gravitational search algorithm (BFGSA) to develop an efficient algorithm for partitional clustering that uses neighbourhood strategies to explore a broader range of search space. This hybrid model managed to overcome the local optima, handling of multidimensional data, and premature convergence problems. Ganguly [6] proposed a neighbour heuristic-based algorithm for cluster analysis, in which a function was introduced to avoid the direct distance vectors computation and get the topmost similar vectors in this work. Singh et al. [35] introduced an artificial chemical reaction-based algorithm for partitional clustering problems, whereby neighbourhood and position-based operators were taught to overcome the deficiencies of traditional chemical reaction algorithms resulting in a more efficient clustering algorithm. Singh and Kumar [33] hybridized the ACRO algorithm with genetic operators, whereas Singh and Kumar [34] introduced a neighborhood search based on the CSO algorithm and applied this to solve clustering problems. Motwani et al. [25] developed three methods to generate the initial centroids for initial cluster selection and concluded that the farthest distributed centroid clustering algorithm produces quality clusters.

Santana-Velásquez et al. [30] focused on applying Machine Learning (ML) techniques as an alternative to DRG’s traditional classification methods. The primary goal is to determine if ML techniques can categorize patients according to the DRGs criteria using information available during discharge. This data served as the foundation for subsequent research on the prediction of DRGs in the early phases of patients’ hospitalization episodes. Stephan et al. [36] applied the HAW technique in an ANN model concurrently with feature selection (FS) and parameter optimization algorithms. Backpropagation learning was used to develop HAW in this study, which comprises robust backpropagation (HAW-RP), Levenberg–Marquart (HAW-LM), and momentum-based gradient descent (HAW-GD) methods. The accuracy, complexity, and computation time of this hybrid model was studied using several breast cancer datasets. Goyal et al. [8] applied various optimization algorithms such as the particle swarm optimization (PSO), cat swarm optimization (CSO), BAT, cuckoo search algorithm (CSA) optimization algorithm, and whale optimization algorithm (WOA) for load balancing, energy efficiency, and better resource scheduling to create an efficient cloud environment. The study found that the WOA beat all the other algorithms in response time, energy consumption, execution time, and throughput in the scenario of seven servers and eight server configurations.

Stephan et al. [37] proposed a novel hybrid Artificial Bee Colony (hybrid ABC) optimization algorithm where the strong explorative capabilities of the chemotaxis phase of the bacterial foraging optimization were integrated with a spiral model-based exploitative phase of the ABC algorithm. This enabled the proposed hybrid ABC algorithm to overcome the demerits of poor exploration procedures in the standard ABC algorithm and outperform the corresponding standalone ABC algorithm. Rahnema and Gharehchopogh [29] proposed an improved version of the ABC algorithm based on the swarm intelligence characteristic of whales and found that random memory and elite memory enhanced the convergence speed of the improved algorithm. Ghany et al. [7] combined the WOA with the tabu search method. The tabu search enabled the WOA to store multiple best solutions and utilize them to explore the solution space more effectively. Purushothaman et al. [28] combined the Gray wolf optimization and grasshopper algorithms for clustering. This hybridization improved reliability and reduced computational time. Ahmadi et al. [1] modified the Gray wolf optimization algorithm by introducing a balanced approach to exploration and exploitation and centers around the best solution, and showed that the proposed algorithm produced state-of-the-art results with a higher accuracy rate. Kumar and Kaur [17] introduced three new variants of the bat algorithm that managed to resolve problems related to initial cluster selection, convergence rate, and local optima with the help of enhanced cooperative evolution, elitist, and neighbourhood search strategies. These enhancements resulted in a robust partitional clustering algorithm.

All these innovations to the existing bio-inspired algorithms were proven to have improved efficiency, faster convergence rate, shorter computation time, and higher accuracy when compared to the corresponding standard, standalone bio-inspired algorithms.

3 Methodology

This section gives the background description of the algorithms and methods that have been implemented in this work. The Enhanced Whale Optimization Algorithm (EWOA) has been successfully utilized in the field of clustering to produce optimal cluster centres. The dataset is first put into memory, and the fundamental parameters are then configured. Following that, other sequential processes, such as sampling or cluster centre selection, goal function computation, assignment of data items to appropriate clusters, and updating of points are performed.

3.1 Whale optimization algorithm

The whale optimization algorithm is a nature-inspired algorithm that simulated the foraging behaviour of humpback whales [24]. Although it was initially designed to solve numerical problems, it was soon applied to several other domains such as clustering, due to its self-explorative nature and ability to achieve convergence at a faster rate. The formulated mathematical model stimulated the prey identification and hunting strategies of humpback whales. The prey finding and encircling processes are modelled using Eqs. (2) and (3):

$$ \overrightarrow{D}=\left|\overrightarrow{C_{cv}}\overrightarrow{Z^{\ast }}(t)-\overrightarrow{Z}(t)\right| $$
(2)
$$ \overrightarrow{Z}\left(t+1\right)=\overrightarrow{Z^{\ast }}(t)-\overrightarrow{A_{cv}}.\overrightarrow{D} $$
(3)

where \( \overrightarrow{A_{cv}}=2\overrightarrow{a}.r-\overrightarrow{a} \), \( \overrightarrow{C_{cv}}=2r \). The terms \( \overrightarrow{Z} \) and \( \overrightarrow{Z^{\ast }} \) denote the current position vector and global best position vector, respectively, \( \overrightarrow{C_{cv}} \) and \( \overrightarrow{A_{cv}} \) are coefficient vectors, r is a rand (0, 1) function, a is linearly decreased from 2 to 0 over the iterations.

The bubble-net attacking process is a combination of shrinking encircling, and spiral position update methods. In shrinking encircling, the coefficient vectors get varied to simulate the humpback whale behaviour. At the same time, in the spiral position update method, the formulated spiral equation is trailed to find the helix-shaped movement of whales as denoted by Eqs. (4) and (5). The humpback whales perform shrinking encircling or spiral movements that can be calculated using Eq. (6).

$$ {\overrightarrow{D}}^{\prime }=\left|\overrightarrow{Z^{\ast }}(t)-\overrightarrow{Z\ }(t)\right|\kern0.5em $$
(4)
$$ \overrightarrow{Z}\left(t+1\right)={\overrightarrow{D}}^{\prime }.{e}^{bl}.\cos \left(2\pi l\right)+\overrightarrow{Z^{\ast }}(t) $$
(5)
$$ \overrightarrow{Z}\left(t+1\right)=\left\{\begin{array}{c}\overrightarrow{Z^{\ast }}(t)-\overrightarrow{A_{cv}}.\overrightarrow{D}\kern4.75em if\ p<0.5\ \\ {}{\overrightarrow{D}}^{\prime }.{e}^{bl}.\cos \left(2\pi l\right)+\overrightarrow{Z^{\ast }}(t), ifp\ge 0.5\ \end{array}\right. $$
(6)

Here, \( \overrightarrow{D} \) is a distance vector, b is a constant vector, and l is a rand [−1,1], and p is a rand (0,1) function. The humpback whale search preys randomly in search space. The movements of the whale results in the change in vector location as denoted by Eqs. (7) and (8).

$$ \overrightarrow{D}=\left|\overrightarrow{C_{cv}.}\overrightarrow{Z_{rand}}-\overrightarrow{Z}\right| $$
(7)
$$ \overrightarrow{Z}\left(t+1\right)=\overrightarrow{Z_{rand}}-\overrightarrow{A_{cv}}.\overrightarrow{D} $$
(8)

The term \( \overrightarrow{Z}\left(t+1\right) \) represents a new position vector, while the term \( \overrightarrow{Z_{rand}} \) denotes a randomly chosen vector.

3.2 Water wave optimization algorithm (WWOA)

Recently, a water wave theory-based optimization algorithm was introduced for solving global optimization problems (Zheng [42]). This algorithm inherits the propagation, refraction, and breaking phenomena of water waves for searching and optimization. In water wave propagation operations, the new water waves are generated using Eq. (9) while the wavelength, λ is calculated using Eq. (10).

$$ \overrightarrow{Z}\left(t+1\right)=\overrightarrow{Z}+\mathit{\operatorname{rand}}\left(-1,1\right)\times \lambda \times {L}_d $$
(9)
$$ \lambda =\lambda \times {\alpha}^{\frac{\left(f(x)- fmin+\varepsilon \right)}{\left( fmax- fmin+\varepsilon \right)}} $$
(10)

Here, Ld is the length of the search space (1 ≤ d ≤ n), λ is the wavelength, fmin and fmax are the minimum and maximum fitness values, respectively, α is the wavelength dropping factor, and ε is a fixed constraint.

3.3 Tabu search

Tabu search is an elite list-based global optimization technique. The starting solutions are stored in the list and iteratively compared with the upcoming solutions. If an improved solution is obtained, the previous/starting solution is updated/ replaced with a better solution. The implementation of tabu search avoids re-entering previously explored regions and uses a single point for exploration [42].

3.4 Neighbourhood strategy

The neighbourhood strategy is used to enhance the searchability of the algorithm and increases the probability of finding a new solution. This primary centers around the neighbouring solutions and uses them to generate new solutions [30].

4 Proposed work: An enhanced whale optimization algorithm (EWOA) for partitional clustering

This section detailed the EWOA for solving partitional clustering problems. In this study, two improvements are proposed: (i) The propagation method is incorporated into the whale optimization algorithm; (ii) An integrated strategy is proposed to handle the local optima situation. A detailed description is given below.

4.1 Improvements in search space mechanism

The whale optimization algorithm is incorporated with an additional exploration mechanism to enhance searchability. The random prey search operation of the whale optimization algorithm is replaced with the propagation method of the water wave optimization algorithm given in Eqs. (9) and (10). The explorative search mechanism of the water wave algorithm is utilized to generate the new location vector and diversify the solution.

4.2 Integration of tabu and neighbourhood search strategies

In the second improvement, an integrated strategy based on tabu, and neighbourhood search is designed and implemented to solve local optima and nullify premature convergence problems. Here, the tabu list is extended to store N number of global best ZN, gbest positions in it. These ZN, gbest best positions are used as neighbouring points in the neighbourhood search strategy. Afterward, to generate a single point, the harmonic means of ZN, gbest point is calculated. To understand in a better way, assume that, Ztabu, gbestare a tabus list that stores (N) number of global best data points (ZN, gbest). These data points are used as neighbouring points Zi, neigh = {Z1, gbest, Z2, gbest, ……ZN, gbest}, where N = 1, 2, …, 9, and the harmonic mean of these neighbouring data points is calculated, Znew=Harmonic mean of(ZN, neigh) is used to generate a new data point.

4.3 Proposed EWOA model in solving clustering problems

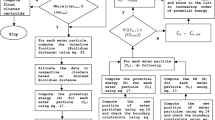
The enhanced whale optimization algorithm is successfully implemented in the clustering field to achieve the optimal cluster centres. Initially, the dataset is loaded in memory, and basic parameters are initialized. Afterward, the different consecutive operations, sampling or cluster centre selection, objective function computation, assignments of data objects to respective clusters, updates, and others are followed. The pseudo-code of the proposed algorithm is detailed in Algorithm 1 and graphically presented in Fig. 1.

Fig. 1
figure 1

Flow chart of EWOA

Full size image
figure a

4.4 Toy example

The working of EWOA algorithm in the clustering field is exemplified using an artificial dataset. The artificial dataset (9,3,4) contains 9 data instances, 3 classes, and 4 attributes.

  1. Step 1.

    Load dataset and specify number of clusters (K = 3), total population = 9, no of iterations = 10.

5.1

3.5

1.4

0.2

4.9

3

1.4

0.2

4.7

3.2

1.3

0.2

7

3.2

4.7

1.4

6.4

3.2

4.5

1.5

6.9

3.1

4.9

1.5

6.3

3.3

6

2.5

5.8

2.7

5.1

1.9

7.1

3

5.9

2.1

  1. Step 2.

    Randomly selected initial cluster centres.

4.7000

3.2000

1.3000

0.2000

6.9000

3.1000

4.9000

1.5000

5.8000

2.7000

5.1000

1.9000

  1. Step 3.

    Evaluate the objective function.

0.5099

4.1641

4.2083

0.3000

4.2367

4.1809

0.0000

4.4159

4.3347

4.2767

0.2646

1.4491

3.8497

0.6481

1.063

4.4159

0.000

1.253

5.4727

1.6155

1.3342

4.3347

1.253

0.000

5.529

1.1874

1.5684

  1. Step 4.

    Assign data objects to clusters according to minimum objective function values.

0.5099

4.1641

4.2083

0.3000

4.1809

4.2367

0.0000

4.3347

4.4159

0.2646

1.4491

4.2767

0.6481

1.063

3.8497

0.0000

1.253

4.4159

1.3342

1.6155

5.4727

0.0000

1.253

4.3347

1.1874

1.5684

5.529

The index values of the clusters are:

1

2

3

1

3

2

1

3

2

2

3

1

2

3

1

2

3

1

3

2

1

3

2

1

2

3

1

  1. Step 5.

    Generated cluster centres in 9th iteration.

5.1000

3.5000

1.4000

0.2000

6.3000

3.3000

6.0000

2.5000

7.1000

3.0000

5.9000

2.1000

  1. Step 6.

    Check for local optima.

  2. Step 7.

    Update the candidate solution.

  3. Step 8.

    Check the ‘Stop’ criteria. If requirements are met, ‘Stop’, else repeat steps 3–8.

  4. Step 9.

    Optimal solution.

5.1000

3.5000

1.4000

0.2000

6.3000

3.3000

6.0000

2.5000

7.1000

3.0000

5.9000

2.1000

5 Experimental results and analysis

This section provides a detailed description of simulation results and parameter settings for the EWOA. The simulation is performed in the MATLAB 2016 environment, configured on a Windows 10 OS, processor intel i3, 8 GB RAM equipped machine. The performance of the proposed EWOA is measured on eight datasets, and the characteristics are detailed in Table 1. The results are compared with seven clustering algorithms, namely the PSO, ACO, CSO, GA, ACRO, WOA, and K-means clustering algorithms. The user-defined parameters setting of EWOA are defined as population = K × d, number of clusters or groups =K, A = [−1, 1], random function (0,1) and length of search space (1 ≤ d ≤ n), iterations = 200. The algorithms run thirty times individually, and the results are evaluated as an average case of performance parameters (intra-cluster distance and f-measure).

Table 1 Description of datasets
Full size table

5.1 Results and discussion

This subsection presents a comparative analysis and convergence behaviour of EWOA and other clustering algorithms. Table 2 presents the performance comparison of K-means, GA, PSO, ACO, CSO, ACRO, WOA, and EWOA using average intra-cluster distance and f-measure parameters. From simulation outcomes, it is observed that the EWOA obtain minimum intra-cluster distance values except for the CMC datasets. Further, the f-measure is also computed to assess the classification of data objects to corresponding clusters. The EWOA attained a healthy f-measure rate except for CMC and LR datasets. For the CMC dataset, ACRO algorithm, and LR dataset, GA has superior results.

Table 2 Performance comparison of EWOA and other well-known clustering algorithms
Full size table

The convergence behavior of AWOA, WOA, ACRO, CSO, ACO, PSO, GA, and K-means clustering algorithms are depicted in Fig. 2a-h. The x-axis shows the number of iterations, and the y-axis shows the intra-cluster distance. From graphs, it is revealed that EWOA converges on a minor level except for the CMC dataset. Although in most aspects, the EWOA provides a better convergence rate.

Fig. 2
figure 2

a Convergence on Iris dataset b Convergence on Cancer Dataset c Convergence on CMC dataset d Convergence on Wine Dataset e Convergence on Glass Dataset f Convergence on Thyroid Dataset g Convergence on LR Dataset h Convergence on ISOLET Dataset

Full size image

Except for the CMC and LR datasets, the EWOA achieved a better f-measure rate. GA outperforms the CMC dataset, the ACRO method, and the LR dataset.

Figure 2a-h shows the convergence behavior of EWOA and other clustering algorithms. The convergence on ISOLET dataset is described with the Number of Iterations v/s Intra Cluster Distance, compared with the EWOA, WOA, ACRO, CSO, ACO, PSO, GA & K-means.

5.2 Statistical analysis

The Friedman statistical test is carried out to prove the significance of the results and verify the feasibility of the newly proposed algorithm. Here two hypotheses (null hypothesis (H0) and alternative hypothesis (H1)) are projected; the H0 expresses that the algorithms have similar performance; the H1 expressese that algorithms have dissimilar performance. Table 3 shows the statistical analysis using the intra-cluster distance parameter. The test shows that the critical value is 14.067144, and the p value is 7.12E-07 at a significance level from 0.5. These values are consistent with the test which showed that the null hypothesis (H0) is rejected, hence proving that the algorithms have dissimilar performances. The EWOA was also found to have significantly distinct performances compared to the other algorithms that are compared in this study.

Table 3 Statistical analysis using intra-cluster distance
Full size table

Table 4 shows the statistical analysis using the f-measure parameter. The EWOA gets the first rank except for CMC and LR datasets. However, for cancer, wine and balance, it is approximately equal to the ACRO algorithm. The critical value is 14.0671 that shows the significant difference among algorithms.

Table 4 Statistical analysis using F-measure
Full size table

Table 4 shows the statistical analysis using the f-measure parameter. The EWOA gets the first rank for all the datasets except for the CMC and LR datasets. However, for the cancer, wine and balance datasets, the results obtained from the EWOA was found to be approximately equal to the results from the ACRO algorithm. The critical value of 14.0671 indicates that there is a significant difference in the performance of the algorithms.

6 Conclusion and future work

In this study, an improvement to the original WOA called the Enhanced Whale Optimization Algorithm (EWOA) has been developed for solving clustering problems. This improved algorithm has proven to be able to overcome the problems that are inherent in the original WOA, namely the slower convergence rate due to the convergence being concentric around the search space mechanism and the local optima situation. To overcome the problems that are inherent in the WOA, the EWOA is enhanced with two additional operational procedures to accelerate the convergence rate and overcome the local optima situation. Minimum intra-cluster distance and an accelerated convergence rate was achieved through the implementation of position update equations from the water wave optimization algorithm that were incorporated into the algorithm to improve the search space, whereas the local optima situation was overcome by implementing the tabu and neighbourhood search strategies into the algorithm. The efficiency of the proposed EWOA was measured using a simulation-based experimental study that was conducted on eight benchmark datasets, namely the Iris, Cancer, CMC, Wine, Glass, Thyroid, LR and ISOLET datasets. The results obtained were then compared to the results obtained via seven existing clustering algorithms/techniques, namely the PSO, ACO, CSO, GA, ACRO, WOA, and K-means algorithms. The performance of each algorithm was compared and analyzed using the average intra-cluster distance and f-measure parameters. The results obtained clearly showed the applicability and feasibility of the enhancements that were made to the EWOA and the superiority of the proposed EWOA model in solving clustering problems compared to the existing models/methods. The future scope of this work involves the application of the proposed EWOA model in solving problems related to vehicular networks for cluster head formation and load balancing.