1 Background

Vascular related diseases have become one of the most common diseases with high mortality, high morbidity and high medical risk in the world. According to World Health Organization (WHO), cardiovascular disease has become the world’s number one killer of human health [32]. Vessel segmentation is a key step toward accurate diagnosis. Although algorithms on image segmentation have become increasingly mature, vessel segmentation is still a challenging problem. Many factors influence the segmentation result including vessel geometrical appearances, imaging quality, characteristics of nearby tissues, and etc.

Numerous researches have been done on vessel segmentation. The existing methods can be divided into three categories [13]. The first type is the region-growing algorithms, including traditional region-growing methods [2, 30, 39] and wave propagation methods [4, 22]. These algorithms are usually fast and easy to implement. However, region-growing based algorithms can hardly include geometrical information and this leads to bad results on low-contrast images. The second category consists of centerline-based algorithms [9, 16, 31]. These techniques are able to extract vessel skeleton accurately. The shortcoming of these methods is that solution on extraction of the vessel surface is not offered. The third category contains active contour based methods. These methods use parametrical (snake) [27, 40] or implicit [18, 20, 23] (level set) active contours to model vascular walls. Under acting of internal forces and external forces, the active contour will settle at the vessel surface after a number of iterations.

Although classical active contour based models [12, 27, 33, 40] have good efficiency in feature segmentation, it cannot handle topological changes that are required in some applications. Level set based models can handle complex boundaries by regarding the boundary as the zero level set in a higher dimension. The level set method was first proposed by Osher and Sethian in [21]. It was then used in shape recovery and isolation of shapes from background by Malladi et al. in [19]. Existing level set methods are generally classified into edge-based and region-based methods. Edge-based methods utilize edge indicators like image gradient to constrain the evolution of level set [5, 6]. But the performance of the edge indicators is often limited in the case of weak boundaries, which is a common phenomenon for vessel images. Region-based methods aim to identify regions of interest by using a certain region descriptor to guide the motion of the active contour. One well-known region-based model is the Chan-Vase (CV) model proposed in [7]. This model utilizes the average intensity inside and outside curve as the region indicator. This model performs well when the desired region has similar intensity. However, CV model did not take intensity inhomogeneity into consideration. Li et al. proposed a Region-Scalable Fitting (RSF) model to alleviate the influence of intensity inhomogeneity [15]. The RSF model utilizes local intensity average instead of the global average used in CV model. The RSF model has shown powerful capability for segmenting images with intensity inhomogeneity [15].

Derived from active contour theory, level set methods can also be used for vessel extraction. In [18], Lorigo et al. proposed an approach termed Curve Evolution for Vessel Segmentation (CURVES) by utilizing the information of local intensities and smoothness. Nain et al. applied level set methods to vessel extraction by adding a shape prior in [20]. J. Brieva et al. applied the CV model to extract vessel structures in coronary angiography [3]. Sum and Cheung proposed a CV based model to extract vessel structures with non-uniform illumination [25]. In [15], Li et al. validated the effectiveness of the RSF model using Magnetic Resonance Imaging (MRI) vessel images. However, most of these level set based models suffer from two problems. The first is called the leakage problem (or over-segmentation in some literatures), which is related to the wrong inclusion of those non-vessel structures with high contrast. The second one is the initial condition problem, which presents itself as the sensitivity of the evolution result to the initialization condition. More recently, Wang and Jiang proposed a non-parametric shape prior constrained active contour model to segment coronary arteries [28]. This model utilizes histogram information to determine the appropriate window size. Tian et al. [26] proposed an active contour method based on a vessel vector field deriving from vesselness measure. Wang et al. [29] also utilize a level-set based algorithm for cerebral vessel segmentation problems.

In this paper, we propose an algorithm termed centerline constrained level set (CC-LS) by incorporating a centerline based constraint into the level set evolution. This CC-LS approach overcomes the above two problems by constraining the unstable level set evolution using the pre-extracted centerline information. The rest of this paper is organized as follows. In section II, we review previous level set models for vessel segmentation. In section 3, the proposed CC-LS approach is explained in detail, and we validate the proposed algorithm on 2D&3D coronary artery data in section 4. Experiment result in section 5 shows that the proposed approach leads to improved efficiency and accuracy. Some analyses and discussions are given in section 6.

2 Previous works

In this section, we review the CV and RSF models for vessel extraction.

2.1 Chan-vase model

Chan and Vase proposed a model for active contours to detect objects in a given image using level set in [7]. In this model, the image domain and the original image are defined as Ω and I. C is the evolving curve in Ω as the boundary of an image subset ω(ω ⊂ Ω, C = ∂ω). In what follows, inside(C) and outside(C) denote the region ω and region Ω\ω, respectively. The fitting term in CV model is defined as follow:

$$ {\displaystyle \begin{array}{r}{E}_{fit}^{CV}\left({c}_1,{c}_2,C\right)={E}_1^{CV}+{E}_2^{CV}={\lambda}_1^{CV}{\int}_{inside(C)}{\left|I\Big(x,y\Big)-{c}_1\right|}^2 dxdy\\ {}+{\lambda}_2^{CV}{\int}_{outside(C)}{\left|I\left(x,y\right)-{c}_2\right|}^2 dxdy\end{array}} $$
(1)

where c1 and c2 are two variables calculated as the mean intensities in inside(C) and outside(C). \( {\lambda}_1^{CV} \) and \( {\lambda}_2^{CV} \) are two balancing parameters used to modulate the influence of inside error and the outside error. The CV based method is in fact a clustering algorithm built based on the simplified consumption that the pixels within the target region have intensities close to c1 while the intensities in the background take values around c2. When the current curve reaches the target boundary C0, the minimal energy can be attained:

$$ \underset{C}{\operatorname{inf}}\left\{{E}_1^{CV}(C)+{E}_2^{CV}(C)\right\}\approx 0\approx {E}_1^{CV}\left({C}_0\right)+{E}_2^{CV}\left({C}_0\right) $$
(2)

Here, when the curve C is outside the object, \( {E}_1^{CV}(C)>0 \) and \( {E}_2^{CV}(C)\approx 0 \), and in case of the curve C is inside the object,\( {E}_1^{CV}(C)\approx 0 \) but \( {E}_2^{CV}(C)>0 \). \( {E}_1^{CV}(C)>0 \) or \( {E}_2^{CV}(C)>0 \) corresponds to the case that the curve C lies inside or outside the object, respectively. Finally, the fitting energy is minimized when C = C0. The final energy functional ECV(c1, c2, C) in CV model is composed of a weighted sum of fitting term \( {E}_{fit}^{CV}\left({c}_1,{c}_2,C\right) \), a curve length term Length(C) and an area term Area(inside(C)):

$$ {\displaystyle \begin{array}{c}{E}_{CV}\left({c}_1,{c}_2,C\right)={\mu}_{CV} Length(C)+{\upsilon}_{CV} Area\left( inside(C)\right)\\ {}+{E}_{fit}^{CV}\left({c}_1,{c}_2,C\right)\end{array}} $$
(3)

where μCV and υCV are the parameters to balance different energy terms. The vessel segmentation problem is solved via minimizing the total energy in different image partitions [3].

2.1.1 Region-scalable-fitting model

In CV model, the mean intensities in the entire regions inside(C) and outside(C) are used in the fitting function energy. However, such mean intensities often deviate from the local intensity values because in most cases the intensities within inside(C) and outside(C) are inhomogeneous. This also means that local intensity information is not fully considered in this CV model, which often leads to lowered segmentation accuracy for those images with intensity inhomogeneity [15].

The RSF model was proposed by Li et al. in [5] to deal with this intensity inhomogeneity by using the intensity information in local regions at a controllable scale. In this RSF method, a local intensity fitting energy is proposed by applying a Gaussian weighting kernel Kσ. The local intensity fitting energy is defined as follow:

$$ {\displaystyle \begin{array}{r}{E}_{fit}^{RSF}\left(C,{f}_1,{f}_2\right)={\lambda}_1^{RSF}\int {K}_{\sigma}\left(\overrightarrow{x}-\overrightarrow{y}\right){\left|I\left(\overrightarrow{y}\right)-{f}_1\left(\overrightarrow{x}\right)\right|}^2{M}_I\left(\phi \left(\overrightarrow{y}\right)\right)d\overrightarrow{y}\\ {}+{\lambda}_2^{RSF}\int {K}_{\sigma}\left(\overrightarrow{x}-\overrightarrow{y}\right){\left|I\left(\overrightarrow{y}\right)-{f}_2\left(\overrightarrow{x}\right)\right|}^2{M}_O\left(\phi \left(\overrightarrow{y}\right)\right)d\overrightarrow{y}\end{array}} $$
(4)
$$ {M}_O(x)=\frac{1}{2}\left[1+\frac{2}{\pi}\arctan \left(\frac{x}{\varepsilon}\right)\right] $$
(5)
$$ {M}_I(x)=1-{M}_O(x) $$
(6)

Where, the two terms MI and MO are the Heaviside functions used to define regions inside(C) and outside(C), respectively. ε is the parameter to adjust the smoothness of the step function. ϕ(x) is the level set function. Term Kσ is a scaled Gaussian filter which should be modulated based on the size of local region centered at the point \( \overrightarrow{x} \):

$$ {K}_{\sigma}\left(\overrightarrow{u}\right)=\frac{e^{-{\overrightarrow{u}}^2/2{\sigma}^2}}{{\left(2\pi \right)}^{n/2}{\sigma}^n} $$
(7)

Instead of using the average values c1and c2 in CV model, the local weighted average \( {f}_1\left(\overrightarrow{x}\right) \) and \( {f}_2\left(\overrightarrow{x}\right) \) is used in the RSF model. The definition can be expressed as

$$ {f}_i\left(\overrightarrow{x}\right)=\frac{K_{\sigma}\left(\overrightarrow{x}\right)\ast \left[{M}_i\left(\phi \left(\overrightarrow{x}\right)\right)I\left(\overrightarrow{x}\right)\right]}{K_{\sigma}\left(\overrightarrow{x}\right)\ast {M}_i\left(\phi \left(\overrightarrow{x}\right)\right)},i=1,2 $$
(8)

where ∗ is the convolution operator. Then, following the definition in [14], the final energy function ERSF is calculated as the weighted sum of the length term C, the penalty term PRSF and the local intensity fitting energy \( {E}_{fit}^{RSF} \):

$$ {E}_{RSF}={E}_{fit}^{RSF}+{\upsilon}_{RSF}C+{\mu}_{RSF}{P}_{RSF} $$
(9)

where μRSF and υRSF are the weighting parameters to balance the influence of different terms.

2.2 Shortcomings of CV and RSF

Most level set based models suffer from two problems: the leakage problem and the initialization problem. The leakage problem presents as the error inclusions of some non-vessel structures in level set evolutions. The initialization problem corresponds to the problem that the segmentation is sensitive to the initial level set condition. Both the two problems are attributed to the unstable evolution caused by the intensity inhomogeneity and intensity variation.

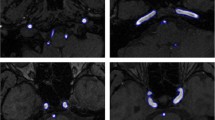
We use the illustrations in Fig. 1 and Fig. 2 to depict these two problem. Here, the CV model uses different initial conditions under parameters μCV = 0.1, υCV = 0, \( {\lambda}_1^{CV}={\lambda}_2^{CV}=1 \) referring to [7]. The RSF model uses different initial conditions under parameters:μRSF = 2, υRSF = 0.001 × 255 × 255, \( {\lambda}_1^{RSF}={\lambda}_2^{RSF}=1 \), σRSF = 2.5, εRSF = 1.0 referring to [15].

Fig. 1
figure 1

Results of the CV approach with different initial zero level sets after 500 iterations. The first row shows the initial zero level sets (marked out using red rectangles), and the images in the second row include the corresponding results of the CV approach with parameters \( {\lambda}_1^{CV}={\lambda}_2^{CV}=1.0 \), μCV = 1.0, υCV = 0. Note the leakage problem is depicted using blue arrows in the second row

Full size image
Fig. 2
figure 2

Results of RSF model with different initial conditions of zero level sets after 500 iterations. For each column, the first row shows the initial zero level set (red rectangles). The second row is the result of RSF model with the parameters \( {\lambda}_1^{RSF}={\lambda}_2^{RSF}=1.0 \), μRSF = 2, υRSF = 0.001 × 255 × 255, σRSF = 2.5, εRSF = 1.0

Full size image

The segmentation of CV model suffers greatly from the leakage problem (see the arrows in Fig. 1). This problem becomes worse for those images with more high contrast noise and artifacts. We can see in Fig. 1 that the result of CV method tends to be seriously degraded by the leakage problem, resulting in many error inclusions of non-vessel structures presented as the leaked small regions (see the arrows in Fig. 1). The first column in Fig. 2 shows that the RSF method can alleviates this leakage problem by incorporating adaptive local intensity information. Nevertheless, some evidence also shows that the RSF methods still suffer from the leakage problem (to be seen in the Fig. 10 below). The reason is that the evolutions in CV and RSF models work by clustering intensities with close intensities values, which might result in leakages into those non-vessel regions with similar intensities.

Figures 1 and 2 also provide the results of CV and RSF algorithms when using different initialization conditions. Note the results in the second rows were obtained by using the same parameter settings for the CV and RSF algorithms, respectively. It is also observed in Figs. 1 and Fig. 2 that the results of the CV and RSF methods vary greatly when different initial zero level set conditions are used. Some unpredictable evolutions are observed comparing different columns in Figs. 1 and 2.

3 Method

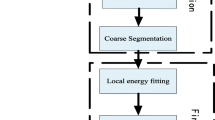
From above we can see that both the RSF and CV approaches suffer from the leakage problem and the initialization sensitivity problem. These two problems are actually caused by the locally unstable level set evolution caused by the non-vessel regions with intensities close to those in the vessel branches. An instinct observation of vascular structures is the tube-shaped structures around the centerlines, and this is used to build centerline constraint to constrain the evolution to proceed along the centerlines. A method termed Centerline constrained level set (CC-LS) is thus developed, and CC-LS method utilizes the centerline information in the following two aspects: 1, the initial level set condition is derived from the extracted centerlines to improve extraction efficiency and accuracy; 2, a new centerline modulated velocity term in the level set evolution. Figure 3 shows the fhowchart of the proposed method.

Fig. 3
figure 3

Flowchart of the proposed method

Full size image

3.1 Initialization

Level set methods use a distance field function φ to represent the segmented surface. For each pixel p, ∣φ(p)∣ is the distance from p to current surface. The relation φ(p) < 0 holds when p lies inside the curve, and φ(p) > 0 otherwise.

The Narrowband technique in [11] is used here for acceleration. The main idea of the Narrowband technique is to build an adaptive mesh around the propagating interface (in our method, the zero level set), that is, a thin band of neighboring level sets, and the computation is only performed on these grid points [1].

An operation of morphological dilation was applied on the extracted centerline and contour of the result is used as the initial zero level set. The size of the morphological operator can be set according to the vessel radius. The region representing this initial zero condition distributes equally along the vessel topology, and contributes to the final segmentation accuracy and efficiency.

The morphological dilation on centerline gives a rough estimation of vessel lumen, which contributes to saving iterations of level set evolution in fitting the zero level set to real vessel lumen.

3.2 Energy function

The energy function in the proposed CC-LS model can also be expressed by eq. (10):

$$ {E}_{CCLS}={E}_{fit}^{RSF}+{\upsilon}_{CCLS}C+{\mu}_{CCLS}{P}_{DR} $$
(10)

Note the format of this energy function is the same as eq. (9) in RSF model. The term of local intensity fitting energy \( {E}_{fit}^{RSF} \) can be calculated using eq. (4). The main difference between the energy function in the CC-LS method and the original RSF method is that we use the distance regularization term in [17] instead of the penalty term in RSF. This distance regularization term is able to keep the flatness of ϕ outside the narrowband by regularizing the distance field property inside the narrowband, and is calculated as follows:

$$ {P}_{DR}\left(\phi \right)=\int p\left(\nabla \phi \right)d\overrightarrow{x} $$
(11)
$$ p(s)=\Big\{{\displaystyle \begin{array}{c}\frac{1}{{\left(2\pi \right)}^2}\left(1-\cos \left(2\pi s\right)\right),s\le 1\\ {}\frac{1}{2}{\left(s-1\right)}^2,s\ge 1\end{array}} $$
(12)

3.3 Curve evolution

With the energy function defined in 3.2, the evolution equation can be derived by applying gradient descent method:

$$ \frac{\partial \phi }{\partial t}=-\frac{\partial E}{\partial \phi } $$
(13)

where \( \frac{\partial E}{\partial \phi } \) is the Gâteaux derivative of E

$$ {\displaystyle \begin{array}{r}\frac{\partial E}{\partial \phi }={\delta}_{\varepsilon}\left(\phi \right)\left({\lambda}_1^{CCLS}{e}_1-{\lambda}_2^{CCLS}{e}_2\right)-{\upsilon}_{CCLS}{\delta}_{\varepsilon}\left(\phi \right)\mathit{\operatorname{div}}\left(\frac{\nabla \phi }{\mid \nabla \phi \mid}\right)\\ {}-{\mu}_{CCLS}\Big({\nabla}^2\phi -\mathit{\operatorname{div}}\left(\frac{p^{\hbox{'}}\left(\nabla \phi \right)}{\nabla \phi }-\nabla \phi \right)\end{array}} $$
(14)

Due to the leakage problem, some high contrast non-vessel structures lying away from centerline still tend to be extracted in the evolution. The proposed CC-LS approach solves this problem by multiplying a velocity term in eq. (12), leading to a new evolution equation as below.

$$ \frac{\partial \phi }{\partial t}=-v\frac{\partial E}{\partial \phi } $$
(15)

The velocity term v is defined as

$$ v(p)=\Big\{{\displaystyle \begin{array}{c}1,d(p)<D+1\\ {}\frac{1}{{\left(d(p)-D\right)}^2},d(p)\ge D+1\end{array}} $$
(16)

Where d(p) is the Euclidean distance from point p to the centerline topology and D is a user-set parameter which approximates the vessel radius. The velocity term restricts the values of ∂ϕ/∂t on those points far away from centerline to zero, which means a significantly decreased v(p) on the positions far away from centerline points. In this way, the level set curve will evolve normally in the target vessel area around the centerline, and the evolution on distant non-vessel points will get suppressed.

3.4 Centerline extraction

The centerline extraction algorithm used in this paper is the minimal path propagation with backtracking (MPP-BT) algorithm proposed in [9]. This MPP-BT method is used in this study to provide efficient extraction of curve-like structures without the requirement of setting start points for each branch.

3.4.1 Potential function in the MPP-BT method

The MPP-BT algorithm calculates the potential values by applying the “Symmetric Convexity” metric which is a combination of “Symmetry” and “Convexity” metrics for vessel structures [9]. For each searched point p, the medialness measure Mc(p, θ) and the potential Pc are calculated as follow:

$$ {M}_c\left(p,\theta \right)=\frac{\kappa +c{\left(p,\theta \right)}^2}{\gamma +1/s{\left(p,\theta \right)}^2}=\frac{\left(\kappa +c{\left(p,\theta \right)}^2\right)\ast s{\left(p,\theta \right)}^2}{\gamma^{\ast }s{\left(p,\theta \right)}^2+1} $$
(17)
$$ {P}_c(p)=\frac{1}{\prod \limits_{n=1}^N{M}_c\left(p,{\theta}_n\right)} $$
(18)

where θi denotes the i-th traversal direction. As illustrated in Fig. 4, medialness measure is calculated upon the four directions for 2D images, and the thirteen directions for 3D condition. κ and γ are the parameters to balance the magnitudes of the convexity c(p, θ)2 and symmetry 1/s(p, θ)2. The potential Pc is calculated by multiplying the inverse of the N largest Mc for all the directions. It is found in [21] that this medial measure gives an effective centerline characterization.

Fig. 4
figure 4

Four directions in 2D image (left) and thirteen directions in 3D image (right) for calculating the centerline potential function

Full size image

3.4.2 Minimal path based tracking algorithm

The Dijkstra algorithm is used to find the minimal path in MPP-BT algorithm. The Dijkstra algorithm is a greedy algorithm to find the minimal path between a single source point and multiple terminal points. A priority queue Q is used in the algorithm to find a neighbor pn with minimum sum weight on the path. Each unsearched neighbor p'n of pn will be inserted into the queue Q and the path sum weight of p'n will be updated. Connection information is stored for further use. The greedy search will not stop until the queue Q is empty or stopping criterion is satisfied.

.

Backtracking operation is applied to eliminate the influence of the geometric distance between start point ps and reached point p. With connection information stored, we can easily backtrack from p to the start point ps. In MPP-BT algorithm, after the backtracking process with fixed step lbk, point \( {p}_{bk}^E \) is reached, and the summed weight between p and \( {p}_{bk}^E \) is used as the priority of point p in Dijkstra algorithm.

3.4.3 Stopping criterion

A normalized backtracking speed metric \( N\overline{S}(p) \) is used as the stop criterion in MPP-BT method. Considering that the centerline points are always preferably visited in the backtracking process, the cost difference will increase significantly when the propagation starts reaching a non-centerline point. The normalized backtracking speed is defined as follow:

$$ N\overline{S}(p)=\frac{\overline{S}\left(p,{l}_{AVE}\right)}{S_{\mathrm{max}}(p)} $$
(19)
$$ S(p)=\frac{l{}_{bk}}{U(p)-U\left({p}_{bk}^E\right)} $$
(20)

where p is current point, lbk is backtracking step, \( {p}_{bk}^E \) is end point in the backtracking path, U(p) is the sum weight on the path from ps to p

$$ U(p)=\sum \limits_{p\in path\left({p}_s,p\right)}{P}_c(p) $$
(21)

\( \overline{S}\left(p,{l}_{AVE}\right) \) is the average S(p) over the last lAVE points recently reached and Smax(p) is the maximum value of all S(p) calculated. A dynamically varying parameter \( N{\overline{S}}^{\mathrm{min}} \) is used here. \( N{\overline{S}}^{\mathrm{min}} \) is initialized to an input parameter \( N{\overline{S}}_0^{\mathrm{min}} \) and will update to \( N\overline{S}(p) \) when a point p is reached with \( N\overline{S}(p)<N{\overline{S}}^{\mathrm{min}} \). The search stops when there are lE successive points reached with \( N\overline{S}(p)<N{\overline{S}}^{\mathrm{min}} \).

3.4.4 Centerline extraction

A centerline feature map IBK is built for centerline extraction using the MPP-BT approach based on the observation that the points on the backtracking path are often centerline points. This feature map IBK is first initialized to zero for all points at first. In the MPP-BT approach, the accumulation is applied upon the end point \( {p}_{bk}^E \) in the backtracked path. The algorithm adds \( 1/\left(\eta +P\left({p}_{bk}^E\right)\right) \) to \( {I}_{BK}\left({p}_{bk}^E\right) \) when a point p is reached. Parameter η here is a small positive number used to avoid zero division. After the minimal path propagation quits when the stopping criterion is met, the algorithm calculates a threshold which is the α quantile of all non-zero value in IBK and segments IBK using the threshold. An additional backtracking operation from each extracted centerline point is performed to ensure the connectivity which labels all points on the backtracking path as centerline points. An example of the final centerline extraction result is depicted in Fig. 5.

Fig. 5
figure 5

Centerline extraction result on a 2D vessel image. Parameters are set based on [9] (lbk = 15,lAVE = 1000,lE = 1500, κ = 1,γ = 100, \( N{\overline{S}}_0^{\mathrm{min}}=0.05 \), α = 0.7, Rmin = 3, Rmax = 20 as listed Table 1). (a) Original image with start point ps. (b) Extracted centerline using MPP-BT

Full size image

4 Experiment

.

We test the proposed CC-LS algorithm using 2D and 3D coronary images. Four 2D coronary artery angiogram images were collected from a GE rotational angiography system (Cardiology Department of the University Hospital of Rennes, .

France). The 3-D coronary artery datasets include nine sets of CT angiography (CTA) data acquired from a Siemens dual-source CT system (Somatom Definition Flash) in the Radiology Department of the First Hospital of Nanjing, China. All experiments were performed on the same PC with Intel® Core™ i7–4790 CPU and NVidia GTX 970 GPU. Compute Unified Device Architecture (CUDA) is used in the centerline extraction part for 2D images and level set evolution part for 3D images to accelerate computation.

Table 1 lists the parameter setting for the proposed method. For the centerline part, all parameters are set according to [9]. In our experiments, we apply 5 × 5 sized morphological operator for 2D images and 3 × 3 × 3 sized operator for 3D images on the extracted centerline to acquire the initial zero level set. For the level set step, most parameters are set as proposed in [15]. The distance parameter D reflects vessel radius, and is set to 1 and 3 for the studies on 2D and 3D images respectively. The parameters for the experiment on 3D images are listed in Table 1.

Table 1 Parameter setting for the method
Full size table

The illustrations from Fig. 6, 7, 8 and 9 are used to provide some guidance on the parameter setting. Parameter D contributes to the velocity term. When D is too small, the level set evolution stops too early while unconnected parts get involved when D comes too large. Parameter \( {\lambda}_1^{CCLS} \) and \( {\lambda}_2^{CCLS} \) decide the balance between internal force and external force. Nothing will get segmented when external force dominates. Parameter σCCLS contributes to the calculation of image energy, which also has great impact on the result. From the experiments, we suggest that parameters in Table 1 are able to give proper results.

Fig. 6
figure 6

Vessel segmentation result after 50 iterations level set evolution with different D settings. (a) D = 1, (b) D = 3, (c) D = 13, (d) No distance restriction. Other parameters are set according to Table 1.

Full size image
Fig. 7
figure 7

Vessel segmentation results after 50 iterations level set evolution with different \( {\lambda}_1^{CCLS} \) settings. (a) \( {\lambda}_1^{CCLS}=0.5 \), (b) \( {\lambda}_1^{CCLS}=1.0 \), (c) \( {\lambda}_1^{CCLS}=1.5 \). The other parameters are set according to Table 1

Full size image
Fig. 8
figure 8

Vessel segmentation results with different \( {\lambda}_2^{CCLS} \) settings. (a) \( {\lambda}_2^{CCLS}=0.5 \). (b) \( {\lambda}_2^{CCLS}=1.0 \). (c) \( {\lambda}_2^{CCLS}=1.5 \). The other parameters are set according to Table 1

Full size image
Fig. 9
figure 9

Vessel segmentation results with different σCCLS settings. (a) σCCLS = 1. (b) σCCLS = 3. (c) σCCLS = 5. The other parameters are set according to Table 1

Full size image

5 Results

Figure 10 compares the RSF evolution with centerline-based initialization (the second row) and the traditional RSF with a properly selected initial condition specified by the red rectangle in Fig. 10 (a1) (the first row). The corresponding parameters are given in the caption below. The result in Fig. 10 shows that the centerline-based initialization can lead to improved result in much less iterations. This advantage of iteration saving will be more remarkable for 3D images.

Fig. 10
figure 10

The RSF evolution with different initial condition. The first row contains the results of original RSF while the second row contains the result of results of centerline-initialized RSF, the green line in (a2) represents the extracted centerline. Each column represents results after different iteration times. The first column contains the initial zero level set. The second column gives zero level set after 50 iterations. The third column shows zero level set after 100 iterations. The fourth column gives zero level set after 200 iterations. The fifth column gives zero level set after 400 iterations for the two methods. \( {\lambda}_1^{RSF}={\lambda}_2^{RSF}=1.0 \),μRSF = 2, υRSF = 0.001 × 255 × 255, σRSF = 2.5, εRSF = 1.0

Full size image

Figure 11 compares the RSF evolution with centerline-based initialization and the proposed CC-LS method, in which the centerline-initialized level set function is used with parameter \( {\lambda}_1^{RSF}={\lambda}_1^{CCLS}=1.5 \), \( {\lambda}_2^{RSF}={\lambda}_2^{CCLS}=1.0 \), μRSF = μCCLS = 2, νRSF = νCCLS = 0.001 × 255 × 255. The evolved curve of zero level .

Fig. 11
figure 11

Illustration of the effect of the velocity term in the CC-LS method. (a) The original image. (b) Initial zero level set built based on the centerline. (c) Zero level set after 50 iterations without using the velocity term (same as RSF with centerline-based initialization). (c) Zero level set after 50 iterations using our velocity term. \( {\lambda}_1^{RSF}={\lambda}_1^{CCLS}=1.5 \), \( {\lambda}_2^{RSF}={\lambda}_2^{CCLS}=1.0 \),μRSF = μCCLS = 2, υRSF = υCCLS = 0.001 × 255 × 255, σRSF = σCCLS = 2.5, εRSF = εCCLS = 1.0

Full size image

.

set after 50 iterations is depicted in Fig. 11(c), in which some wrongly included non-vessel structures (pointed by blue arrows) can be observed. This shows that well-initialized RSF based evolution still suffers from leakages. As to the result of the proposed CCLS method, we can see that the centerline based velocity term works well to overcome the wrongly inclusion of the non-vessel structures (in Fig. 11(d)). Figure 12 depicts the segmentation results of 2D images for the RSF method and the.

Fig. 12
figure 12

Comparison of the segmentations between RSF model and the proposed CC-LS method on 2D coronary images. The first row and the second row contains the initial zero level set for RSF model along with the vessel segmentation result using RSF model after 1500 iterations. \( {\lambda}_1^{RSF}={\lambda}_2^{RSF}=1.0 \), μRSF = 2, υRSF = 0.001 × 255 × 255, σRSF = 2.5, εRSF = 1.0. Several undesired parts are labeled out using blue arrows. The third row and the fourth row contains the initial zero level set constructed using centerline along with the segmentation result using proposed CC-LS method after 30 iterations with parameters in Table 1. \( {\lambda}_1^{CCLS}=1.5 \), \( {\lambda}_2^{CCLS}=1.0 \), D = 1, σCCLS = 2.5, εCCLS = 1, μCCLS = 2, υCCLS = 0.001 × 255 × 255. Start points for centerline extraction are marked out using yellow points

Full size image

CC-LS method. A 5 × 5 morphological dilation was applied on the extracted centerline to get initial level set. The result of proposed method after 30 iterations is compared with the result of original RSF method. The size of the morphological operator is set according to the vessel radius. For the RSF model, we iterate 1500 times on each image. Although the zero level set does not stabilize after 1500 iterations, the result of RSF model does not get better with a larger iteration number. The centerline-based initialization and the velocity term work well in improving the evolution efficiency and guiding the level set evolution to avoid the inclusion of non-vessel tissues (several examples are marked as blue arrows in Fig. 12).

.

We also did some evaluations on the 2-D results. Metrics including precision, recall and dice were calculated and shown in Table 2. As we can see in the table, the proposed method performs better than other methods listed for comparison. The original RSF performs badly as the algorithm tries to segment the background rather than the target vessel in areas far away from the initial zero level set (shown in Fig. 12). The performance of CC-LS without the velocity term is much better than that of the original RSF which shows the significance of the centerline based initialization. However, the CC-LS without velocity term does not perform as well as the complete CC-LS method in precision metric. This is because leakages appear in the results of CC-LS without velocity term. The performance of the proposed algorithm is also compared with CCMPP algorithm proposed in [8], whose code is available online. The propose algorithm also outperforms the CCMPP method.

Table 2 Performance evaluation on 2-D vessel images
Full size table

However, it is also found that the centerline extraction suffers from some tiny structure missing (pointed by the arrow in Fig. 13(b)) when the velocity term is used. Figure 13(c) and Fig. 12(d) gives the result without and with the velocity term, respectively. We can see that the velocity term constrains the evolution around the extracted centerlines, but the missing part in the extracted centerlines leads to vessel ending missing in the final segmentation result (pointed by the arrow in Fig. 13(d)).

Fig. 13
figure 13

(a) The original image. (b) Extracted centerline. (c) The result without using the velocity term. (d) The result using the velocity term. Note the vessel ending is not segmented due to the missing part (pointed by the yellow arrow in (c)) in the centerline constraint

Full size image

Figure 14 depicts the vessel segmentation results under different start point settings. We tested start points on different positions and got the same result. This example shows that the proposed CC-LS algorithm is quite robust to setting of the start point.

Fig. 14
figure 14

Illustration of the influence of start point setting. The first row gives different start point settings on the same image. For (a1) and (d1), the start points are set outside the target vessel (marked out using blue rectangle). The orange spots represent the start points for centerline extraction. The green lines represent the extracted centerline. The red lines represent the initial zero level set. The second row gives the segmentation results of the proposed CC-LS method after 100 iterations. \( {\lambda}_1^{CCLS}=1.5 \), \( {\lambda}_2^{CCLS}=1.0 \), D = 1, σCCLS = 2.5, εCCLS = 1, μCCLS = 2, υCCLS = 0.001 × 255 × 255

Full size image

Figure 16 illustrates the results on 3D data. Start points were set to the center positions in the origin regions of left coronary arteries (LCA) (Note that the segmentation is not sensitive to the start point positions). For 3D images, the extracted centerline dilated by a 3 × 3 × 3 sized filter is used as the initial condition. It is found in Fig. 16 that the proposed method is able to extract vessel lumen without including non-vessel structures. However, similar problem with 2D images still exists. Figure 15 depicts the same image as Fig. 16(d4) with a different view spot. We can see that the thin vessel endings (pointed by yellow arrow in Fig. 15) are not extracted because of the centerline distance term.

Fig. 15
figure 15

A 3D example of algorithm’s shortcoming. Unsegmented vessel ending is marked as yellow arrow

Full size image
Fig. 16
figure 16

Segmentation results on different 3D coronary images. For each row, one 3D coronary image is tested using proposed CC-LS method. The first column gives the original coronary images. Bone structures are removed manually to attain a better view. The second column gives the centerline extraction results using method introduced in 3.2. The third column gives the vessel segmentation results after 50 iterations with parameters in Table 1. In the fourth column, we overlap the segmentation results to the original images

Full size image

The computational cost of the proposed method on the 2D images in Fig. 13 is listed in Table 3 in unit of milliseconds. The computational cost of the segmentation task in Fig. 13(a1) is much smaller than others because the size of this image has 256 × 256 pixels while the other images contain 512 × 512 pixels. The computational cost for 3D data in Fig. 16 is listed in Table 4 (in seconds). It is found that the computational cost varies within a certain range even for images in the same size. The total computational cost is slightly larger than the sum of computational cost in centerline extraction and total computational cost for all iterations due to the operations like image loading and centerline dilation. The computational cost for each iteration is also slightly higher than the computational cost of the original RSF method. It is also found that this increased computational cost can be well compensated by the reduced iteration number in the CC-LS method.

Table 3 Computational cost for CC-LS (in milliseconds) on 2-D image data
Full size table
Table 4 Computational cost for CC-LS (in seconds) on 3-D image data
Full size table

Parameter sensitivity is analyzed using the results in Fig. 7, 8, 9 and 10. Parameters \( {\lambda}_1^{CCLS} \) and \( {\lambda}_2^{CCLS} \) are used to modulate the balance between internal and external forces, and should be suitably set to provide reasonable results. It is also found that the segmentation is also dependent on the setting of the parameters D and parameters σCCLS. Also, the segmentation performance is found much less sensitive to parameters μCCLS and υCCLS. For this CC-LS method, it is found that the same parameter setting can be used for the same type of data.

6 Discussion

In this paper, we propose a new algorithm for vessel segmentation. The proposed algorithm applies centerline information to level set evolution, and is able to achieve better performance than traditional level set algorithms. The segmented vessel can provide direct help to diagnosis of vascular diseases including stenosis and calcification. Moreover, the segmentation is a prior for hemodynamic analysis. The application of proposed algorithm is not limited to the realm of vessel. It has potential to segment all crack-like structures in 2-D images and tubular objects in 3-D images.

The algorithm still has a lot of space for lifting. Firstly, the algorithm itself includes two separated steps named centerline extraction and level-set evolution. As both steps are iterative, it might be possible to merge the steps into one. The level-set can grow with centerline tracking. Secondly, the property of centerline is not fully utilized in the proposed algorithm. The vessel displays symmetric features around the centerline, and the symmetric feature can be applied in the level-set function. Thirdly, one roughly set start point is needed in the algorithm which makes it a semi-automatic segmentation. The start-point-setting step might be eliminated in the future.

7 Conclusion

In this paper, we developed an algorithm called CC-LS to extract vessel structures. A minimal path tracking algorithm is applied for vessel centerline extraction. The extracted centerline is later used for zero level set initialization. A velocity term is calculated using the distance to centerline in order to constrain the evolution of level set. We applied the proposed algorithm on both 2D and 3D coronary data and obtained satisfactory results. Moreover, the proposed algorithm has potential to segment other curve-like objects such as cracks [9] and some special kinds of text [36, 37], once centerlines can be extracted from the objects.

However, we notice that our proposed algorithm is not able to extract narrow endings in vascular structures. The reason is that the backtracked centerline extraction cannot achieve vascular endings and distance constraint velocity term limits the growth of level set. In our future work, we are going to concentrate on improving our velocity term to eliminate this side-effect without reducing restrict effect. We also take deep learning based algorithms [10, 24, 38, 41] into consideration which are proved to have superior performance on image segmentation problems. Additionally, level set evolution costs unbearably long time on 3D images which needs further acceleration. The time cost problem may be solved by using better GPUs or some new parallel frameworks [34, 35] in the future.