1 Introduction

The problem of automatic classification of normal/pathological subjects is of great importance in clinical medicine [33]. Magnetic resonance imaging (MRI) is concerned with soft tissue anatomy and generates a large information set and details about the subject’s brain condition. There exists a large body of work on using brain MR images for automatic diagnosis [12, 34].

A promising approach for analyzing the obtained images is the wavelet transform which offers the capability of simultaneous feature localization in the time and frequency domains [8, 16]. By applying a single-level wavelet transform to an image, four subbands are usually defined as the low-low (LL), low-high (LH), high-low (HL), and high-high (HH) subbands. The LL provides an approximation to the image, and the other three provide high-frequency coefficients for finer-scale image details representation. The wavelet transform have already been applied successfully in many areas related to computer vision.

In the last decade, scholars have applied wavelet transform and other techniques to detect abnormal brain images. Chaplot, et al. [3] used the approximation coefficients obtained by discrete wavelet transform (DWT), and employed the self-organizing map (SOM) neural network and support vector machine (SVM). Maitra and Chatterjee [17] employed the Slantlet transform, which is an improved version of DWT. Their feature vector of each image is created by considering the magnitudes of Slantlet transform outputs corresponding to six spatial positions chosen according to a specific logic. Then, they used the common back-propagation neural network (BPNN). El-Dahshan, et al. [9] extracted the approximation and detail coefficients of 3-level DWT, reduced the coefficients by principal component analysis (PCA), and used feed-forward back-propagation artificial neural network (FP-ANN) and K-nearest neighbor (KNN) classifiers. Zhang, et al. [29] proposed using DWT for feature extraction, PCA for feature reduction, and FNN with scaled chaotic artificial bee colony (SCABC) as classifier. Based on it, Zhang, et al. [30] suggested to replace SCABC with scaled conjugate gradient (SCG) method. Ramasamy and Anandhakumar [23] used fast-Fourier-transform based expectation-maximization Gaussian mixture model for brain tissue classification of MR images. Zhang and Wu [28] proposed to use kernel SVM (KSVM), and they suggested three new kernels as homogeneous polynomial, inhomogeneous polynomial, and Gaussian radial basis. Saritha, et al. [24] proposed a novel feature of wavelet-entropy (WE), and employed spider-web plots (SWP) to further reduce features. Afterwards, they used the probabilistic neural network (PNN). Das, et al. [7] proposed to use Ripplet transform (RT) + PCA + least square SVM (LS-SVM), and the 5 × 5 CV shows high classification accuracies. Kalbkhani, et al. [15] modelled the detail coefficients of 2-level DWT by generalized autoregressive conditional heteroscedasticity (GARCH) statistical model, and the parameters of GARCH model are considered as the primary feature vector. Their classifier was chosen as KNN and SVM models. Zhang, et al. [31] suggested to use particle swarm optimization (PSO) to train the KSVM, and their result on a 90 image database achieved 97.11 % accuracy. Padma and Sukanesh [21] used combined wavelet statistical texture features, to segment and classify AD benign and malignant tumor slices. El-Dahshan, et al. [10] used the feedback pulse-coupled neural network for image segmentation, the DWT for features extraction, the PCA for reducing the dimensionality of the wavelet coefficients, and the FBPNN to classify inputs into normal or abnormal. Zhang, et al. [35] used discrete wavelet packet transform (DWPT), and harnessed Tsallis entropy to obtain features from DWPT coefficients. Then, they used a generalized eigenvalue proximal SVM (GEPSVM) with RBF kernel.

All abovementioned methods achieved promising results; however, there are two problems. (1) Most of them used DWT, the coefficients of which require a large storage memory and (2) The classifier training is not stable, and the accuracy can be improved.

To address these two problems, we gave two potential contributions in this study. First we introduced the wavelet energy (WE), which is a rather novel feature-extraction technique that calculates the energy from the wavelet coefficients. It has already been applied to many academic and industrial fields [1, 6, 22]. Next, we proposed to use the biogeography-based optimization (BBO) method to train the classifier, with the aim of improving its classification performance.

2 Feature extraction

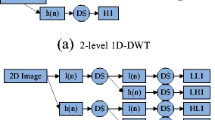
2.1 2D-DWT

The two-dimensional DWT (2D-DWT) decomposes an image into several sub-bands according to a recursive process [20, 32]. The 1-level decomposition obtains two kinds of coefficients. One contains LH1, HL1, and HH1, which represent details of the original images. The other is LL1 that corresponds to the approximation of original image [11]. The approximation LL1 is then decomposed into second-level approximation and detail coefficients, and the process is repeated to achieve the desired level of resolution.

The obtained coefficients for the approximation and detail subbands are useful features for texture categorization. The 2D-DWT decomposes an image into spatial frequency components that describe the image texture. In practical, the coefficients are obtained by convolving the image with a bank of filters. Afterwards, selected features are extracted from the coefficients for further processing.

2.2 Wavelet-energy

After wavelet transformation is applied on the image, wavelet coefficients from the detail subbands of all the decomposition levels are used to formulate the local wavelet energy feature [16]. The wavelet energy in LL, HL, LH, and HH subbands can be, respectively, defined as:

$$ E\left(\mathrm{L}\mathrm{L}\right)={\displaystyle \sum_x{\displaystyle \sum_y\mathrm{L}\mathrm{L}{\left(x,y\right)}^2}} $$
(1)
$$ E\left(\mathrm{L}\mathrm{H}\right)={\displaystyle \sum_x{\displaystyle \sum_y\mathrm{L}\mathrm{H}{\left(x,y\right)}^2}} $$
(2)
$$ E\left(\mathrm{H}\mathrm{L}\right)={\displaystyle \sum_x{\displaystyle \sum_y\mathrm{H}\mathrm{L}{\left(x,y\right)}^2}} $$
(3)
$$ E\left(\mathrm{H}\mathrm{H}\right)={\displaystyle \sum_x{\displaystyle \sum_y\mathrm{H}\mathrm{H}{\left(x,y\right)}^2}} $$
(4)

where E represents the wavelet-energy. These energies reflect the strength of the images’ details in different subbands. Suppose a 3-level decomposition, the final extracted features are the energies from the 10 subbands including (LL3, LH3, HL3, HH3, LH2, HL2, HH2, LH1, HL1, HH1).

3 Classifier

The introduction of support vector machine (SVM) is a landmark of the field of machine learning. The advantages of SVMs include high accuracy, elegant mathematical tractability, and direct geometric interpretation. Recently, multiple improved SVMs have grown rapidly, among which the kernel SVMs are the most popular and effective. Kernel SVMs have the following advantages [27]: (1) they work very well in practice and have been remarkably successful in such diverse fields as natural language categorization, bioinformatics and computer vision; (2) they have few tunable parameters; and (3) their training often involves convex quadratic optimization. Hence, solutions are global and usually unique, thus avoiding the convergence to local minima exhibited by other statistical learning systems, such as neural networks.

3.1 SVM

Suppose some prescribed data points each belong to one of two classes, and the goal is to classify which class a new data point will be located in. Here a data point is viewed as a p-dimensional vector, and our task is to create a (p-1)-dimensional hyperplane. Many possible hyperplanes might classify the data successfully [2]. One reasonable choice as the best hyperplane is the one that represents the largest separation, or margin, between the two classes, since we could expect better behavior in response to unseen data during training, i.e., better generalization performance [26]. Therefore, we choose the hyperplane so that the distance from it to the nearest data point on each side is maximized. Figure 1 shows the geometric interpolation of linear SVMs, here H1, H2, H3 are three hyperplanes which can classify the two classes successfully, however, H2 and H3 does not have the largest margin, so they will not perform well to new test data. The H1 has the maximum margin to the support vectors (S11, S12, S13, S21, S22, and S23), so it is chosen as the best classification hyperplane.

Fig. 1
figure 1

The geometric interpolation of linear SVMs (H denotes for the hyperplane, S denotes for the support vector)

Full size image

Given a p-dimensional N-size training dataset of the form

$$ \left\{\left({x}_n,{y}_n\right)\Big|{x}_n\in {R}^p,{y}_n\in \left\{-1,+1\right\}\right\},n=1,\dots, N $$
(5)

where y n is either −1 or +1 corresponds to the class 1 or 2. Each x n is a p-dimensional vector. The maximum-margin hyperplane that divides class 1 from class 2 is the desired SVM. Considering that any hyperplane can be written in the form of

$$ \mathbf{w}\mathbf{x}-b=0 $$
(6)

We choose the w and b to maximize the margin between the two parallel hyperplanes as large as possible while still separating the data. Hence, we define the two parallel hyperplanes by the equations as

$$ \mathbf{w}\mathbf{x}-b=\pm 1 $$
(7)

Therefore, the task can be transformed to an optimization problem. That is, we want to maximize the distance between the two parallel hyperplanes, subject to prevent data falling into the margin. Using simple mathematical knowledge, the problem can be finalized as

$$ \begin{array}{l}\underset{\mathbf{w},b}{ \min}\left\Vert \mathbf{w}\right\Vert \\ {}s.t.\ {y}_n\left(\mathbf{w}{x}_n-b\right)\ge 1,\ n=1,\dots, N\end{array} $$
(8)

In practical situations the ||w|| is usually be replace by

$$ \begin{array}{l}\underset{\mathbf{w},b}{ \min}\frac{1}{2}{\left\Vert \mathbf{w}\right\Vert}^2\\ {}s.t.\ {y}_n\left(\mathbf{w}{x}_n-b\right)\ge 1,\ n=1,\dots, N\end{array} $$
(9)

The reason leans upon the fact that ||w|| is involved to a square root calculation. After it is superseded with formula (9), the solution will not change, but the problem is altered into a quadratic programming optimization that is easy to solve by using Lagrange multipliers and standard quadratic programming techniques and programs.

3.2 Soft margin

In practical applications, there may is no hyperplane that splits the samples perfectly. In such case, the “soft margin” method will choose a hyperplane that splits the given samples as cleanly as possible, while still maximizing the distance to the nearest cleanly split samples.

Positive slack vector ξ = (ξ 1, …, ξ n , …, ξ N ) are introduced to measure the misclassification degree of sample x n (the distance between the margin and the vectors x n that lying on the wrong side of the margin). Then, the optimal hyperplane separating the data can be obtained by the following optimization problem.

$$ \begin{array}{l}\underset{\mathbf{w},\xi, \mathbf{b}}{ \min}\frac{1}{2}{\left\Vert \mathbf{w}\right\Vert}^2+c{e}^T\boldsymbol{\upxi} \\ {}s.t.\ \left\{\begin{array}{c}\hfill {y}_n\left({\mathbf{w}}^T{x}_n-\mathbf{b}\right)\ge 1-{\xi}_n\hfill \\ {}\hfill {\xi}_n\ge 0\hfill \end{array}\right.,\ n=1,\dots, N\end{array} $$
(10)

where c is the error penalty (i.e., box constraint in some other literatures) and e is a vector of ones of N-dimension. Therefore, the optimization becomes a trade-off between a large margin and a small error penalty. The constraint optimization problem can be solved using “Lagrange multiplier” as

$$ \underset{\mathbf{w},\xi, \mathbf{b}}{ \min}\underset{\alpha, \beta }{ \max}\left\{\frac{1}{2}{\left\Vert \mathbf{w}\right\Vert}^2+c{e}^T\boldsymbol{\upxi} -{\displaystyle \sum_{n=1}^N{\alpha}_n\left[{y}_n\left({\mathbf{w}}^T{x}_n-\mathbf{b}\right)-1+{\xi}_n\right]-{\displaystyle \sum_{n=1}^N{\beta}_n{\xi}_n}}\right\} $$
(11)

The min-max problem is not easy to solve, so dual form technique is commonly proposed to solve it as

$$ \begin{array}{l}\underset{\alpha }{ \max }{\displaystyle \sum_{n=1}^N{\alpha}_n}-\frac{1}{2}{\displaystyle \sum_{n=1}^N{\displaystyle \sum_{m=1}^N{\alpha}_m{\alpha}_n{y}_m{y}_n{x}_m^T{x}_n}}\\ {}s.t.\left\{\begin{array}{c}\hfill 0\le {\alpha}_n\le c\hfill \\ {}\hfill {\displaystyle \sum_{n=1}^N{\alpha}_n{y}_n}=0\hfill \end{array},\kern0.5em n=1,\dots, N\right.\end{array} $$
(12)

The key advantage of the dual form function is that the slack variables ξ n vanish from the dual problem, with the constant c appearing only as an additional constraint on the Lagrange multipliers. Now, the optimization problem (12) becomes a quadratic programming (QP) problem, which is defined as the optimizing a quadratic function of several variables subject to linear constraints on these variables. Therefore, numerous methods can solve formula (10) within milliseconds, such as Sequential Minimal Optimization (SMO), least square, interior point method, augmented Lagrangian method, conjugate gradient method, simplex algorithm, etc.

3.3 Kernel SVM

Linear SVMs have the downside due to linear hyperplanes, which cannot separate complicated distributed practical data. In order to generalize it to nonlinear hyperplane, the kernel trick is applied to SVMs. The resulting algorithm is formally similar, except that every dot product is replaced by a nonlinear kernel function. In another point of view, the KSVMs allow to fit the maximum-margin hyperplane in a transformed feature space. The transformation may be nonlinear and the transformed space higher dimensional; thus though the classifier is a hyperplane in the higher-dimensional feature space, it may be nonlinear in the original input space. For each kernel, there should be at least one adjusting parameter so as to make the kernel flexible and tailor itself to practical data. RBF kernel is chosen due to its excellent performance with the form of

$$ k\left({x}_m,{x}_n\right)= \exp \left(-\frac{\left\Vert {x}_m-{x}_n\right\Vert }{2{\sigma}^2}\right) $$
(13)

where σ represents the scaling factor. Put formula (13) into formula (12), and we got the final SVM training function as

$$ \begin{array}{l}\underset{\alpha }{ \max }{\displaystyle \sum_{n=1}^N{\alpha}_n}-\frac{1}{2}{\displaystyle \sum_{n=1}^N{\displaystyle \sum_{m=1}^N{\alpha}_m{\alpha}_n{y}_m{y}_n \exp \left(-\frac{\left\Vert {x}_m-{x}_n\right\Vert }{2{\sigma}^2}\right)}}\\ {}s.t.\left\{\begin{array}{c}\hfill 0\le {\alpha}_n\le C\hfill \\ {}\hfill {\displaystyle \sum_{n=1}^N{\alpha}_n{y}_n}=0\hfill \end{array},\kern0.5em n=1,\dots, N\right.\end{array} $$
(14)

It is still a quadratic programming problem, and we chose interior point method to solve the problem. However, there is still an outstanding issue, i.e., to determine the values of parameter C and σ in Eq. (14).

4 Optimization method

To determine the best parameters of C and σ, traditional method used either trial-and-error or grid-searching methods. They will cause heavy computation burden, and cannot guarantee to find the optimal or even near-optimal solutions. In this study, we used BBO.

4.1 Biogeography

Biogeography-based optimization (BBO) was inspired by biogeography, which describes speciation (i.e., the formation of new and distinct species in the course of evolution) and migration of species between isolated habitats (such as islands), and the extinction of species [5]. Habitats friendly to life are termed to have a high habitat suitability index (HSI), and vice versa. Features that correlate with HSI include land area, rainfall, topographic diversity, temperature, vegetative diversity, etc. Those features are called suitability index variables (SIV). Like other bio-inspired algorithms, the SIV and HSI are considered as search space and objective function, respectively [14].

Habitats with high HSI have not only a high emigration rate, but also a low immigration rate, because they already support many species. Species that migrate to this kind of habitat will tend to die even if it has high HSI, because there is too much competition for resources from other species. On the other hand, habitats with low HSI have both a high emigration rate and a low immigration rate; the reason is not because species want to immigrate, but because there is a lot of resources for additional species [25].

To illustrate, Fig. 2 shows the relationship of immigration and emigration probabilities, where the λ and μ represents the immigration and emigration probability, respectively. I and E represents the maximum immigration and emigration rate, respectively. S max is the maximum number of species the habitat can support, and S 0 the equilibrium species count. Following common convention, we assumed a linear relation between rates and number of species, and gave the definition of the immigration and emigration rates of habitats that contains S species as follows:

Fig. 2
figure 2

Model of immigration λ and emigration μ probabilities

Full size image
$$ {\lambda}_S=I\left(1-\frac{S}{S_{\max }}\right) $$
(15)
$$ {\mu}_S=\frac{ES}{S_{\max }} $$
(16)

The emigration and immigration rates are used to share information between habitats. Consider the special case E = I, we have λ S  + μ S  = E.

4.2 Biogeography-based optimization

Emigration and immigration rates of each habitat are used to share information among the ecosystem. With modification probability P mod, we modify solutions H i and H j in the way that we use the immigration rate of H i and emigration rate of H j to decide some SIVs of H j be migrated to some SIVs of H i .

Mutation was simulated in the SIV level. Very high and very low HSI solutions are equally improbable, nevertheless, medium HSI solutions are relatively probable. Above idea can be implemented as a mutation rate m, which is inversely proportional to the solution probability P S .

$$ m(H)={m}_{\max}\left(\frac{1-{\mathbf{P}}_S}{{\mathbf{P}}_{\max }}\right) $$
(17)

where m max is a user-defined parameter, representing the maximum mutation rate. P max is the maximum value of P(∞).

Elitism was also included in standard BBO, in order to retain the best solutions in the ecosystem. Hence, the mutation approach will not impair the high HSI habitats. Elitism is implemented by setting λ = 0 for the p best habitats, where p is a predefined elitism parameter. In closing, the pseudocodes of BBO were listed as follows.

  1. Step 1

    Initialize BBO parameters, which include a problem-dependent method of mapping problem solutions to SIVs and habitats, the modification probability P mod, the maximum species count S max, the maximum migration rates E and I, the maximum mutation rate m max, and elite number p.

  2. Step 2

    Initialize a random set of habitats.

  3. Step 3

    Compute HSI for each habitat.

  4. Step 4

    Computer S, λ, and μ for each habitat.

  5. Step 5

    Modify the whole ecosystem by migration based on P mod, λ and μ.

  6. Step 6

    Mutate the ecosystem based on mutate probabilities.

  7. Step 7

    Implement elitism.

  8. Step 8

    If termination criterion was met, output the best habitat, otherwise jump to Step 3.

5 Experiments

The experiments were carried out on the platform of P4 IBM with 3.2GHz processor and 8GB RAM, running under Windows 7 operating system. The algorithm was in-house developed based on the wavelet toolbox of 64bit Matlab 2014a (The Mathworks ©). The programs can be run or tested on any computer platforms where Matlab is available.

5.1 Materials

The datasets brain consists of 90 T2-weighted MR brain images in axial plane and 256x256 in-plane resolution, which were downloaded from the website of Harvard Medical School (URL: http://www.med.harvard.edu/aanlib/home.html). The abnormal brain MR images of the dataset consist of the following diseases: Glioma, Metastatic adenocarcinoma, Metastatic bronchogenic carcinoma, Meningioma, Sarcoma, Alzheimer, Huntington, Motor Neuron disease, Cerebral Calcinosis, Pick’s disease, Alzheimer plus visual agnosia, Multiple sclerosis, AIDS dementia, Lyme encephalopathy, Herpes encephalitis, Creutzfeld-Jakob disease, and Cerebral Toxoplasmosis. The samples of each disease are illustrated in Fig. 3. Note that all diseases are treated as abnormal brains, and our task is a binary classification problem, i.e., distinguish abnormal brains from normal brains.

Fig. 3
figure 3

Sample of brain MRIs: (a) Normal Brain; (b) Glioma, (c) Metastatic adenocarcinoma; (d) Metastatic bronchogenic carcinoma; (e) Meningioma; (f) Sarcoma; (g) Alzheimer; (h) Huntington; (i) Motor Neuron disease; (j) Cerebral Calcinosis; (k) Pick’s disease; (l) Alzheimer plus visual agnosia; (m) Multiple sclerosis; (n) AIDS dementia; (o) Lyme encephalopathy; (p) Herpes encephalitis; (q) Creutzfeld-Jakob disease; and (r) Cerebral Toxoplasmosis

Full size image

5.2 Cross validation setting

We randomly selected 5 images for each type of brain. Since there are 1 type of normal brain and 17 types of abnormal brain in the dataset, 5*(1 + 17) = 90 images was selected to construct the brain dataset, consisting of 5 normal and 85 abnormal brain images in total.

The setting of the 5-fold cross validation was shown in Fig. 4. In this study, we divided the dataset into 5 equally distributed subgroups, each subgroups contain one normal brain and 17 abnormal brains. We perform five experiments. In each experiment, four groups were used for training, and the left group was used for validation. Each group was used once for validation.

Fig. 4
figure 4

Illustration of 5-fold Cross Validation of Brain Dataset

Full size image

Further, the 5-fold CV was repeated 5 runs, i.e., a 5 × 5-fold CV was implemented, with the aim or reducing randomness. The confusion matrices of 5 runs were combined to form the final confusion matrix, with the ideal results of 425 abnormal instances and 25 normal instances perfectly recognized.

5.3 Feature extraction

The 3-level 2D-DWT of Haar wavelet decomposed the input image into 10 subbands as shown in Fig. 5. Symmetric padding method [18] was utilized to calculate the boundary value, with the aim of avoiding border distortion. After decomposition, 10 features were obtained from calculating the energy of those 10 subbands (LL3, HL3, LH3, HH3, HH2, HL2, LH2, HH1, HL1, and LH1).

Fig. 5
figure 5

The results of a 3-level 2D DWT: (a) a normal brain MR image; (b) decomposition result

Full size image

The wavelet-energy can reduce the dimension of DWT coefficients. For a 256x256 image, the 3-level DWT did not reduce the dimension, but the 3-level wavelet-energy can reduce the feature dimension from 65,536 to only 10.

5.4 Algorithm comparison

The wavelet-energy features were fed into different classifiers. We compared the proposed BBO-KSVM method with Back Propagation Neural Network (BP-NN) [4], KSVM [19], and PSO-KSVM [31]. The results were shown in Table 1. The kernel function was set to RBF.

Table 1 Classifier comparison based on WE features (WE = Wavelet-energy)
Full size table

Two images of Lyme Encephalopathy are shown in Fig. 6. The left image was incorrectly classified as normal, and the right image was correctly predicted as abnormal. The reason is the left image did not fully capture the focus and deformed region. This gives us a hint that the proposed method may be improved by using multi-slices.

Fig. 6
figure 6

Two images of Lyme Encephalopathy: (a) Incorrectly classified; (b) Correctly classified

Full size image

6 Discussion

Results in Table 1 are the main contribution of this study. It showed that BP-NN [4] correctly matched 390 cases with 86.67 % classification accuracy. KSVM [19] correctly matched 413 cases with accuracy of 91.78 %. The PSO-KSVM [31] correctly matched 437 brain images with accuracy of 97.11 % classification accuracy. Finally, the proposed BBO-KSVM correctly matched 440 cases with accuracy of 97.78 %.

Therefore, the proposed method had the most excellent classification performance. In addition, the proposed method achieved the sensitivity of 98.12 %, specificity of 92.00 %, and precision of 99.52 %. This validated the effectiveness of the proposed method. It may be applied in practical use.

Why the proposed BBO-KSVM performs the best? Because it is combined on two successful components: the KSVM and the BBO. KSVM is widely used for pattern-recognition problems, and it achieves excellent results. On the other hand, BBO is a rather novel method, which included mutation and elitism mechanisms. The importance of introducing BBO is to determine the optimal values of parameters C and σ in KSVM, otherwise it is hard to get the optimal weights for KSVM. Therefore, the BBO is an effective means to find the optimal values. Integrating BBO to KSVM enhances the classification capability of KSVM. The comparison in the experiment also shows BBO excels PSO.

We choose the Haar wavelet, although there are other outstanding wavelets. We will compare the performance of different families of wavelet in future work.

The contributions of this paper lie in following aspects: (i) A new approach for automatic classification of MR Images as normal or abnormal using Wavelet-Energy, SVM, and BBO was proposed. (ii) Our experiments demonstrated the proposed method performed better than BP-NN, KSVM, and PSO-KSVM. (iii) Wavelet-Energy was validated as effective feature for MR brain image classification.

7 Conclusions and future research

In this study, we proposed a new approach for automatic classification of MR Images as normal or abnormal using Wavelet-Energy, SVM, and BBO. The results showed that the proposed method gave better results than latest methods. This automated CAD system, could be further used for classification of image with different pathological condition, types and disease status.

In the future, we may focus on following regards: (i) we try to increase the decomposition level of 2D-DWT, in order to test whether higher level can lead to better classification performance. (ii) we may replace wavelet-energy with more efficient feature descriptors, such as scale-invariant features. (iii) Some advanced pattern recognition techniques may be used, such as deep learning and RBFNN [13]. (iv) Multiple slices can be used to improve the classification performance.