1 Introduction

Digital watermarking is an important technique for copyright protection in recent years. In general, the watermarking in frequency domain [4, 5, 11, 15, 16, 21, 24–28] has better performance than watermarking in airspace domain [1, 2, 7, 9, 12, 18, 20]. Hence most watermarking scheme are implemented in frequency domain such as discrete Fourier transform method [24], discrete cosine transform method [15, 26], and discrete wavelet transform method [4, 5, 11, 16, 21, 25, 27, 28].

In [7], Chen et al. introduced a framework for solving the inherent tradeoffs between the robustness, the degradation of the host image, and the embedding capacity. They adjusted the tradeoffs optimally between rate, distortion, and robustness in an information embedding system, namely quantization index modulation. In [18], the authors proposed a novel hiding data scheme with distortion tolerance. The proposed scheme not only can prevent the quality of the processed image from being seriously degraded, but also can simultaneously achieve distortion tolerance. But the associated embedding system is implemented in the single-bit spatial domain which fails to take the advantages offered by wavelet-based transform or other transform. Therefore, this study utilizes DWT low-frequency coefficients to embed one watermark bit in the host image. Besides, the proposed optimization technique is complicated. To improve the efficiency of their optimization technique, this study optimizes the tradeoff between peak signal to noise ratio (PSNR) and bit error ratio (BER) by using Lagrange Principle.

First, the PSNR and the amplitude quantization equation are rewritten as a performance index in matrix form and a constraint with embedding state. Then, an optimization equation is then proposed to connect the performance index and the constraint. Second, the Lagrange Principle is used to derive the optimal solution. The optimal result is then applied to embed the watermark. In other words, this study proposes an optimization-based formula for the modification of low-frequency amplitude. Finally, the performance of the proposed scheme is evaluated by PSNR and BER. Simulation results indicate that the proposed scheme has good image quality under high embedding capacity and robust to JPEG compression.

The rest of this paper is organized as follows. Section II reviews some mathematical preliminaries. Section III rewrites the PSNR and the amplitude quantization equation as a performance index in matrix form and a constraint with embedding state. Moreover, an optimization-based equation that connects the performance index and amplitude-quantization constraint is proposed. Finally, the Lagrange Principle is used to solve the optimization-based problem and the associated optimal solution is then applied to embed the watermark. In detection, watermark can be extracted without original image. Section IV does some experiments to test the performance of the proposed scheme. Conclusions are finally drawn in Section V.

2 Mathematical preliminaries

Before introducing the proposed optimization-based image watermarking, DWT, SNR, matrix operations, and Lagrange Principle are reviewed in this section.

2.1 Discrete-time wavelet transform (DWT)

In conventional discrete cosine transform or Fourier transform, sinusoids are used for basis functions. It can only provide the frequency information. Temporal information is lost in this transformation process. In some applications, we need to know the frequency and temporal information at the same time, such as a musical score, we want to know not only the notes (frequencies) we want to play but also when to play them. Fast Fourier transform (FFT) efficiently do the decomposition of signal into uniform-resolution analysis. It is suitable to analyze the wide-sense-stationary condition but not in non-stationary condition. Unlike conventional Fourier transform or Fast Fourier transform, wavelet transforms are based on small waves, called wavelets. It can be shown that we can both have frequency and temporal information by this kind of transform using wavelets even in non-stationary condition. The wavelet transform maps a function which belongs to functional space L 2(ℝ) onto a scale-space plane. The wavelets are obtained by a single prototype function ψ(x) which is regulated with a scaling parameter and shift parameter [22]. In any dicretised wavelet transform, there are only a number of wavelet coefficients for each bounded rectangular region. Still, each coefficient requires the evaluation of an integral. To avoid this numerical complexity, one need one auxiliary function, the basic scaling function φ(⋅). The basic scaling function and the wavelet basis function are as follows.

$$ {\varphi}_{j,n}(t)={2}^{\raisebox{1ex}{$j$}\!\left/ \!\raisebox{-1ex}{$ 2$}\right.}\varphi \left({2}^jt\mathit{\hbox{-}}n\right) $$
(1)
$$ {\psi}_{j,n}(t)={2}^{\raisebox{1ex}{$j$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\psi \left({2}^jt-n\right) $$
(2)

where t ∈ ℝ, n ∈ ℤ. From these two functions, one can construct two subspaces as follows.

$$ {V}_j=\mathrm{span}\left({\varphi}_{j,n}:n\ \in \mathbb{Z}\right) $$
(3)
$$ {W}_j=\mathrm{span}\left({\psi}_{j,n}:n\ \in \mathbb{Z}\right) $$
(4)

where j and n are the dilation and translation parameters; From this, one can require that the sequence

$$ \left\{0\right\}\subset \cdots \subset {V}_1\subset {V}_0\subset {V}_{-1}\subset \cdots \subset {L}^2\left(\mathbb{R}\right) $$
(5)

form a mutiresolution analysis of L 2(ℝ) and that the subspaces ⋯, W 1, W 0, W − 1, ⋯ are the orthogonal differences of the above sequence, that is, W j is the orthogonal complement of V j inside the subspace V j − 1. Then, the orthogonality relations follow the existence of sequences h = {h n } n ∈ ℤ and g = {g n } n ∈ ℤ that satisfy the following identities:

$$ {h}_n=\left\langle {\varphi}_{0,0},{\varphi}_{-1,n}\right\rangle \mathrm{and}\varphi (t)=\sqrt{2}{\displaystyle \sum_{n\in \mathbb{Z}}{h}_n\varphi \left(2t-n\right)} $$
(6)
$$ {g}_n=\left\langle {\psi}_{0,0},{\varphi}_{-1,n}\right\rangle \mathrm{and}\psi (t)=\sqrt{2}{\displaystyle \sum_{n\in \mathbb{Z}}{g}_n\varphi \left(2t-n\right)} $$
(7)

where h = {h n } n ∈ ℤ and g = {g n } n ∈ ℤ are respectively the sequence of low-pass and high-pass filters [10, 19, 23].

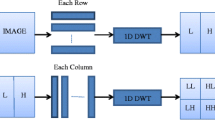
In this paper, we use the wavelet bases in (1) and (2) to transform the host image into the orthogonal DWT domain by four-level decomposition. A method to implement DWT is a filter bank that provides perfect reconstruction. DWT has local analysis of frequency in space and time domain and it gets image multi-scale details step by step. If the scale becomes smaller, every part gets more accurate and ultimately all images details can be focalized accurately. If DWT is applied to an image, it will produce high-frequency parts, middle-frequency parts, and a lowest-frequency part which is a square coefficient matrix. Figure 1 shows the one-level decomposition of 2D DWT.

Fig. 1
figure 1

One-level decomposition of 2D DWT

Full size image

2.2 Mathematical definitions and theorems

To find the extreme of the matrix function, some optimization methods for matrix function are introduced in [3, 6, 8, 17]. First of all, operations of the matrix function are reviewed in Theorem 1 and Theorem 2.

Theorem 1.

If W is an n × n matrix, and \( \tilde{\mathbf{C}} \) is an n × 1 column vector, then

$$ \frac{\partial \mathbf{W}\tilde{\mathbf{C}}}{\partial \tilde{\mathbf{C}}}=\mathbf{W} $$
(8)

Theorem 2.

If \( \tilde{\mathbf{C}} \) is an n × 1 column vector, and C is an n × 1 constant vector, then

$$ \frac{\partial {\left(\tilde{\mathbf{C}}-\mathbf{C}\right)}^T\left(\tilde{\mathbf{C}}-\mathbf{C}\right)}{\partial \tilde{\mathbf{C}}}=2\left(\tilde{\mathbf{C}}-\mathbf{C}\right) $$
(9)

In order to apply the Lagrange Principle, we have to introduce the gradient of a matrix function \( f\left(\tilde{\mathbf{C}}\right) \) as follows.

Definition 2.

Suppose that \( \tilde{\mathbf{C}}={\left[{\tilde{c}}_1,{\tilde{c}}_2,\cdot \cdot \cdot, {\tilde{c}}_n\right]}^T \) is an n × 1 matrix and \( f\left(\tilde{\mathbf{C}}\right) \) is a matrix function. Then the gradient of \( f\left(\tilde{\mathbf{C}}\right) \) is

$$ \nabla f\left(\tilde{\mathbf{C}}\right)=\frac{\partial f}{\partial \tilde{\mathbf{C}}}={\left[\frac{\partial f}{\partial {\tilde{c}}_1},\frac{\partial f}{\partial {\tilde{c}}_2},\cdots, \frac{\partial f}{\partial {\tilde{c}}_n}\right]}^T $$
(10)

Now we consider the problem of minimizing (or maximizing) the matrix function \( f\left(\tilde{\mathbf{C}}\right) \) subject to a constraint \( g\left(\tilde{\mathbf{C}}\right)=0 \). This problem can be described as follows

$$ \begin{array}{cc}\hfill minimize\hfill & \hfill f\left(\tilde{\mathbf{C}}\right)\hfill \end{array} $$
(11a)
$$ \begin{array}{cc}\hfill subject\;to\hfill & \hfill g\left(\tilde{\mathbf{C}}\right)=0\hfill \end{array} $$
(11b)

In order to solve (11), Lagrange Principle is applied as follows.

Theorem 3.

Suppose that g is a continuously differentiable function of \( \tilde{\mathbf{C}} \) on a subset of the domain of a function f. Then if \( {\tilde{\mathbf{C}}}_0 \) minimizes (or maximizes) \( f\left(\tilde{\mathbf{C}}\right) \) subject to the constraint \( g\left(\tilde{\mathbf{C}}\right)=0 \), \( \nabla f\left({\tilde{\mathbf{C}}}_0\right) \) and \( \nabla g\left({\tilde{\mathbf{C}}}_0\right) \) are parallel. That is, if \( \nabla g\left({\tilde{\mathbf{C}}}_0\right)\ne 0 \), then there exists a scalar λ such that

$$ \nabla f\left({\tilde{\mathbf{C}}}_0\right)=\lambda \nabla g\left({\tilde{\mathbf{C}}}_0\right) $$
(12)

Based on Theorem 3, if we let

$$ J\left(\tilde{\mathbf{C}},\lambda \right)=f\left(\tilde{\mathbf{C}}\right)+{\lambda}^Tg\left(\tilde{\mathbf{C}}\right), $$
(13)

then the original problem (12) becomes a matrix function \( J\left(\tilde{\mathbf{C}},\lambda \right) \) which has no constraint. The necessary conditions for existence of the extreme of J are

$$ \frac{\partial J}{\partial \lambda }=0, $$
(14)

and

$$ \frac{\partial J}{\partial \tilde{\mathbf{C}}}=0. $$
(15)

Finally, we use Theorem 3 and the techniques in (13)-(15) to propose an optimization-based image watermarking in next section.

3 Proposed watermarking technique

Since a tradeoff exists between image quality measured by PSNR and robustness measured by BER, the scalar parameter λ is introduced to connect the performance index obtained from PSNR and amplitude quantization equation. Finally, the Lagrange Principle in Theorem 3 is applied to find the optimal solution and then this optimal solution is used to embed watermark. This section also introduces the extraction techniques.

3.1 Proposed embedding technique

Before the proposed embedding technique is implemented, the watermark bits B = {b i } are randomly generated by using binary code. Accordingly, the values in the watermark belong to the set {0, 1}. The watermark is embedded into the coefficients of DWT middle-frequency sub-band LH2. Unlike the traditional single-coefficient quantization, the proposed embedding technique is as follows.

  • If the embedded bit “b i  = 1” is embedded into k consecutive coefficients {|c 1|, |c 2|, ⋅ ⋅ ⋅ ⋅⋅, |c k |}, then amplitude \( {\displaystyle \sum_{i=1}^k\left|{c}_i\right|} \) is modified to

    $$ {A}_1=\left\lfloor \raisebox{1ex}{${\displaystyle \sum_{i=1}^k\left|{c}_i\right|}$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right\rfloor S+\frac{3}{4}S $$
    (16)

  • If the embedded bit “b i  = 0” is embedded into k consecutive coefficients {|c 1|, |c 2|, ⋅ ⋅ ⋅ ⋅⋅, |c k |}, then amplitude \( {\displaystyle \sum_{i=1}^k\left|{c}_i\right|} \) is modified to

    $$ {A}_0=\left\lfloor \raisebox{1ex}{${\displaystyle \sum_{i=1}^k\left|{c}_i\right|}$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right\rfloor S+\frac{1}{4}S $$
    (17)

where {c i } are the LH2 coefficients in DWT; ⌊⌋ indicates the floor function; the number of consecutive coefficients k is adopted as the first secret key KY 1 and S is the quantization size (QS) which is adopted as the secret key KY 2. To combine Eqs. (16) and (17) into a single equation, all k absolute values of the middle-frequency LH2 coefficient are input into a vector form which will be used in optimization procedure.

$$ {\mathbf{C}}_k={\left[\left|{c}_1\right|,\left|{c}_2\right|,\cdot \cdot \cdot \cdot, \left|{c}_k\right|\right]}^T $$
(18)

Based on Eqs. (16), (17) and (18), the embedding can be rewritten as an equation that incorporates an embedding state, that is

$$ \mathbf{W}{\tilde{\mathbf{C}}}_k=\alpha {A}_1+\left(1-\alpha \right){A}_0 $$
(19)
$$ \mathbf{W}{\tilde{\mathbf{C}}}_k-\left[\alpha {A}_1+\left(1-\alpha \right){A}_0\right]=0 $$
(20)

where \( {\tilde{\mathbf{C}}}_k \): \( {\tilde{\mathbf{C}}}_k={\left[\left|{\tilde{c}}_1\right|,\left|{\tilde{c}}_2\right|,\cdot \cdot \cdot \cdot \cdot, \left|{\tilde{c}}_k\right|\right]}^T \) is the watermarked (unknown) wavelet-coefficient vector that corresponds to C k .

W: \( \mathbf{W}=\left[\begin{array}{cccc}\hfill {w}_1\hfill & \hfill {w}_2\hfill & \hfill \cdots \hfill & \hfill {w}_k\hfill \end{array}\right] \) is a weighting matrix whose scalar entries can be arbitrarily determined by an encoder. To avoid any entry from being arbitrarily large, without loss of generality, the summation of all the scalar entries is assumed to equal to k. For example, \( \mathbf{W}=\left[\begin{array}{cccc}\hfill 0.7\hfill & \hfill 1.1\hfill & \hfill \cdots \hfill & \hfill 0.8\hfill \end{array}\right] \).

α: the embedding state; If binary bit “1” is embedded then the state of α is “1”; otherwise, the state of α is “0”.

To have the best image quality under the embedding Eq. (20), we discuss the calculation of PSNR and the corresponding optimization problem for modifying the amplitude in (20). Since we implement the DWT with orthogonal wavelet bases, PSNR is rewritten in the following form.

$$ PSNR=-10{ \log}_{10}\left(\frac{{{\left\Vert \tilde{\mathbf{P}}\left(i,j\right)-\mathbf{P}\left(i,j\right)\right\Vert}_2}^2}{255^2MN}\right) $$
(21)
$$ =-10{ \log}_{10}\left(\frac{{{\left\Vert {\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right\Vert}_2}^2}{255^2MN}\right) $$
(22)

where MN is the size of the image, respectively. For the optimization of the watermarked image quality, Eq. (22) is rewritten as a performance index.

$$ f\left({\tilde{\mathbf{C}}}_k\right)=\frac{{{\left\Vert {\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right\Vert}_2}^2}{255^2MN} $$
(23)

or

$$ f\left({\tilde{\mathbf{C}}}_k\right)=\frac{{\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)}^T\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)}{255^2MN} $$
(24)

Since 2552 MN is a constant, Eq. (24) can be rewritten as a more simple form for the performance index of optimization.

$$ f\left({\tilde{\mathbf{C}}}_k\right)={\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)}^T\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right) $$
(25)

Based on the performance index \( f\left({\tilde{\mathbf{C}}}_k\right) \) in (25) and the constraint \( g\left({\tilde{\mathbf{C}}}_k\right) \) in (20), the optimization-based quantization problem is in the following form.

$$ \begin{array}{cc}\hfill minimize\hfill & \hfill f\left({\tilde{\mathbf{C}}}_k\right)={\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)}^T\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)\hfill \end{array} $$
(26a)
$$ \begin{array}{cc}\hfill subject\;to\hfill & \hfill g\left({\tilde{\mathbf{C}}}_k\right)=\mathbf{W}{\tilde{\mathbf{C}}}_k-\left[\alpha {A}_1+\left(1-\alpha \right){A}_0\right]=0\hfill \end{array} $$
(26b)

To embed the watermark B, we need to solve the optimization problem (26). By Theorem 3, we set Lagrange multiplier λ to combine (26a) and (26b) into the following matrix function.

$$ J\left({\tilde{\mathbf{C}}}_k,\lambda \right)=f\left({\tilde{\mathbf{C}}}_k\right)+{\lambda}^Tg\left({\tilde{\mathbf{C}}}_k\right) $$
(27)

or

$$ J\left({\tilde{\mathbf{C}}}_k,\lambda \right)={\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)}^T\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)+{\lambda}^T\left\{\mathbf{W}{\tilde{\mathbf{C}}}_k-\left[\alpha {A}_1+\left(1-\alpha \right){A}_0\right]\right\} $$
(28)

The necessary conditions for existence of the minimum of \( J\left({\tilde{\mathbf{C}}}_k,\lambda \right) \) are

$$ \frac{\partial J}{\partial {\tilde{\mathbf{C}}}_k}=2\left({\tilde{\mathbf{C}}}_k-{\mathbf{C}}_k\right)+{\mathbf{W}}^T\lambda =0 $$
(29a)
$$ \frac{\partial J}{\partial \lambda }=\mathbf{W}{\tilde{\mathbf{C}}}_k-\left[\alpha {A}_1+\left(1-\alpha \right){A}_0\right]=0 $$
(29b)

Multiply (2a) by W, we have

$$ 2\left(\mathbf{W}{\tilde{\mathbf{C}}}_k-\mathbf{W}{\mathbf{C}}_k\right)+\mathbf{W}{\mathbf{W}}^T\lambda =0 $$
(30)

Since \( \mathbf{W}{\tilde{\mathbf{C}}}_k=\alpha {A}_1+\left(1-\alpha \right){A}_0 \) from (29b), Eq. (30) is rewritten as

$$ 2\left[\alpha {A}_1+\left(1-\alpha \right){A}_0-\mathbf{W}{\mathbf{C}}_k\right]+\mathbf{W}{\mathbf{W}}^T\lambda =0 $$
(31)

Hence the optimal solution for vector parameter λ is

$$ {\lambda}^{*}=-2{\left(\mathbf{W}{\mathbf{W}}^T\right)}^{-1}\left[\alpha {A}_1+\left(1-\alpha \right){A}_0-\mathbf{W}{\mathbf{C}}_k\right] $$
(32)

Replacing (32) to (29a), the optimal solution of modified coefficients is

$$ {{\tilde{\mathbf{C}}}_k}^{*}={\mathbf{C}}_k+{\mathbf{W}}^T{\left(\mathbf{W}{\mathbf{W}}^T\right)}^{-1}\left[\alpha {A}_1+\left(1-\alpha \right){A}_0-\mathbf{W}{\mathbf{C}}_k\right] $$
(33)

According to Eq. (33), if binary bit “1” is embedded then the state of α is “1”. If binary bit “0” is embedded then the state of α is “0”. Therefore, the encoder can arbitrarily construct the scaling matrix W to obtain the optimal modified coefficients \( {{\tilde{\mathbf{C}}}_k}^{*} \) and then the embedding process can be completed. Figure 2 shows the proposed embedding process.

Fig. 2
figure 2

Watermark embedding

Full size image

This study chooses k = 3 to be an example of detail embedding process. Every three consecutive coefficients in DWT level four is grouped into the vector form C 3 = [|c 1|, |c 2|, |c 3|]T. If the weighting matrix W is

$$ \mathbf{W}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right], $$
(34)

then the embedding process is

$$ \left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{c}\hfill \left|{\tilde{c}}_1\right|\hfill \\ {}\hfill \left|{\tilde{c}}_2\right|\hfill \\ {}\hfill \left|{\tilde{c}}_3\right|\hfill \end{array}\right]=\alpha {A}_1+\left(1-\alpha \right){A}_0 $$
(35)

Substituting C 3 into (33) yields the optimal coefficient vector \( {{\tilde{\mathbf{C}}}_3}^{*}={\left[\begin{array}{ccc}\hfill \left|{{\tilde{c}}^{*}}_1\right|\hfill & \hfill \left|{{\tilde{c}}^{*}}_2\right|\hfill & \hfill \left|{{\tilde{c}}^{*}}_3\right|\hfill \end{array}\right]}^T \).

3.2 Extraction technique

Because of the nature of quantization, our extraction process is blind. To extract the hidden watermark, we group every k (the first secret key KY 1) consecutive coefficients into \( {{\tilde{\mathbf{C}}}^{*}}_k=\left\{\left|{{\tilde{c}}^{*}}_1\right|,\left|{{\tilde{c}}^{*}}_2\right|,\cdot \cdot \cdot, \left|{{\tilde{c}}^{*}}_k\right|\right\} \), where \( {\tilde{c}}^{*} \) denote the watermarked coefficient which is optimized. Then, the decoder can use the second secret key KY 2 to extract the watermark by using the following rules:

  • If the summation of \( {{\tilde{\mathbf{C}}}^{*}}_k=\left\{\left|{{\tilde{c}}^{*}}_1\right|,\left|{{\tilde{c}}^{*}}_2\right|,\cdots, \left|{{\tilde{c}}^{*}}_k\right|\right\} \) satisfies

    $$ {\displaystyle \sum_{i=1}^k\left|{{\tilde{c}}_i}^{*}\right|}-\left\lfloor \raisebox{1ex}{${\displaystyle \sum_{i=1}^k\left|{{\tilde{c}}_i}^{*}\right|}$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right\rfloor S\ge \frac{S}{2}, $$
    (36)

  • then the extracted value \( {\widehat{b}}_i=1 \).

  • If the summation of \( {{\tilde{\mathbf{C}}}^{*}}_k=\left\{\left|{{\tilde{c}}^{*}}_1\right|,\left|{{\tilde{c}}^{*}}_2\right|,\cdot \cdot \cdot, \left|{{\tilde{c}}^{*}}_k\right|\right\} \) satisfies

    $$ {\displaystyle \sum_{i=1}^k\left|{{\tilde{c}}_i}^{*}\right|}-\left\lfloor \raisebox{1ex}{${\displaystyle \sum_{i=1}^k\left|{{\tilde{c}}_i}^{*}\right|}$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right\rfloor S<\frac{S}{2}, $$
    (37)

  • then the extracted value \( {\widehat{b}}_i=0 \).

By repeating the rules (36) and (37), all hidden watermarks can be extracted as \( \widehat{B}=\left\{{\widehat{b}}_i\right\} \) . The detail process of the proposed extraction technique is shown in Fig. 3.

Fig. 3
figure 3

Watermark extraction

Full size image

4 Experimental results

This section describes some experiments to evaluate the performance of the proposed image watermarking method. As the examples of weighting matrix, this study considers the matrices \( {\mathbf{W}}_1=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right] \) and \( {\mathbf{W}}_2=\left[\begin{array}{cccc}\hfill 0.7\hfill & \hfill 1.2\hfill & \hfill 1.3\hfill & \hfill 0.8\hfill \end{array}\right] \). In the experiments, 100 images including Lena, Jet, Peppers, and Cameraman of size 512 × 512 are adopted [13, 14]. Each host image is decomposed into three levels using a DWT transform and then the watermark is embedded into the middle-frequency LH2 coefficients. Since the Lagrange Principle specifies the optimal quantization of the LH2 amplitude, the PSNR can exceed 40 dB for high embedding capacity when the entries of the weighting matrix are all one. Figure 3 presents the original images. Figures 4, 5, 6 and 7 display the watermarked images with different NCC, QS and weighting matrices. Table 1 presents the average PSNR and embedding capacity under different numbers of consecutive coefficients (NCC), quantization sizes (QS) and weighting matrices.

Fig. 4
figure 4

Original images

Full size image
Fig. 5
figure 5

Watermarked images with k = 2, S = 30

Full size image
Fig. 6
figure 6

Watermarked images with k = 4, S = 60, W 1

Full size image
Fig. 7
figure 7

Watermarked images with k = 4, S = 60, W 2

Full size image
Table 1 Number of Consecutive Coefficients (NCC), Quantization Sizes (QS), average psnr, and embedding capacity
Full size table

To better illustrate the effect of scaling factors adjustment on PSNR, a case k = 4, S = 60, W 1 with w 1 + w 2 = 2, w 3 = 1, w 4 = 1 and their relationship are shown in Figs. 8 and 9. It is clear that the PSNR drops as w 2 decreases and is maximized when w 2 = 1, which corresponds to w 1 = 1 as well. In other words, huge variation of coefficients reduces PSNR.

Fig. 8
figure 8

Watermarked images with k = 8, S = 120, W 1

Full size image
Fig. 9
figure 9

The relation between weight and PSNR for image Lena

Full size image

Following the embedding process, some attacks are made against the image to test the robustness of the embedded watermark. The robustness is measured using the bit error ratio (BER).Fig. 10.

Fig. 10
figure 10

The relation between weight and PSNR for image Jet

Full size image
$$ \mathrm{B}\mathrm{E}\mathrm{R}=\frac{B_{error}}{B_{total}}\times 100\% $$
(38)

where B error and B total denote the number of error bits and the number of total bits, respectively. Based on the same technique of quantization, we contrast our technique against the one proposed by Lin et al. [18]. Besides, we also contrast our technique against the traditional method which used single-coefficient quantization index modulation, i.e., k = 1, S = 15. The test of robustness supports the following conclusions.

  1. (1)

    Additive noise: Table 2 presents the experimental results of adding Gaussian noise. This table also indicates that different parameters k, S and weighting matrices have similar BER. Lin et al. [18] has slightly lower robustness than ours.

    Table 2 Average ber after gaussian noise
    Full size table
  2. (2)

    JPEG compression: As shown in Table 3, the watermarked image is compressed by JPEG compression with different quality factors. The proposed method is robust against this compression. Compare to the method proposed by Lin et al. [18], our method has much better robustness than their method. Accordingly, the developed method clearly improves the robustness against this attack. This table also shows that different weighting matrices W 1 and W 2 have similar BER. However, with the increase of the parameters k and S, BER decreases rapidly.

    Table 3 Average ber after jpeg compression
    Full size table
  3. (3)

    Median filtering: Table 4 presents the effects of adopting a circular median filter with radii 3 and 4. The results also indicate that the proposed method is better than the one proposed by Lin et al. [18]. The results in this table also present that different parameters k, S and weighting matrices have similar BER.

    Table 4 Average ber after median filter
    Full size table
  4. (4)

    Rotation: A rotation attack with different angles is applied to the watermarked image. The experimental results in Table 5 show that our method has much better robustness than the method proposed by Lin et al. [18]. These results also show that different parameters k, S and weighting matrices have similar BER.

    Table 5 Average ber after rotation
    Full size table
  5. (5)

    Scaling: The scaling attack with different amounts is applied to the watermarked image. Table 6 shows the experimental results. The BER is around 38 %. The results also indicate that the proposed method is better than the one proposed by Lin et al. [18]. Moreover, they also show that different parameters k, S and weighting matrices have similar BER.

    Table 6 Average ber after scaling
    Full size table

This study uses the Lagrange Principle to optimize tradeoff efficiently. It only uses the differentiation of a function to obtain the optimal solution. The experimental results shown in Tables 1, 2, 3, 4, 5 and 6 indicate better performance.

5 Conclusion

This paper presents an optimization-based amplitude quantization technique for image watermarking. To enhance the robustness, the watermark is embedded in the middle-frequency LH2 coefficients in DWT. Based on an equation that connects the watermarking performance index and the amplitude-quantization constraint, we obtained an optimization-based formula for image watermarking. The experimental results show that the proposed method has high PSNR and embedding capacity. In the proposed optimization-based formula, the weight matrix W affects algorithm performance, for example, huge variation of coefficients reduces PSNR. In as a future work, the problem to decide W of improving performance will be considered.