Introduction

Tropical maize represents one of the most diverse sources of germplasm used in several plant breeding programs (Fan et al. 2015; Teixeira et al. 2015; Laborda et al. 2005). Recently, high-density single-nucleotide polymorphisms (SNPs) have been used to characterize the heterotic pools via genetic diversity (Oyekunle et al. 2015) and population structure analysis (da Silva et al. 2015; Nelson et al. 2016). Moreover, the applicability of such diversity information extends to association studies (Chen and Lipka 2016; Crossa et al. 2007), genomic prediction (Yu et al. 2016), and germplasm architecture (Bernardo and Thompson 2016).

Population structure (PS) in maize could arise from local adaptation or diversifying selection (Orozco-Ramirez et al. 2016; Navarro et al. 2017; Bedoya et al. 2017). For the temperate maize, several subpopulations/groups (flint, dent, stiff stalk, and non-stiff stalk) were described according to morphological, genetic, and environmental adaptability characteristics (Rincent et al. 2014; Schaefer and Bernardo 2013). However, the tropical materials are not as organized as the temperate, which can be due to the stronger divergence of heterotic groups by long-term selection (Wu et al. 2016). For instance, at the International Maize and Wheat Improvement Center (CIMMYT), the development of Lowland Tropical and Subtropical/Midaltitude subgroups began in the mid-1980s (Braun et al. 1996); nonetheless, temperate materials started around 100 years ago (Unterseer et al. 2016; Wu et al. 2016). A detailed description of PS in maize lines of Brazil was reported by Laborda et al. (2005) and Lanes et al. (2014). In the last study, 81 microsatellite loci were screened concerning 90 maize parental inbreds of tropical hybrids in order to identify three heterotic pools (tropical flint, semi-flint, and semi-dent), which agreed with what has been used by Brazilian maize seed companies.

Different ways to investigate PS can be classified into either non-model-based (or non-parametric) or model-based approaches. Non-parametric methods include principal component analysis (Patterson et al. 2006; Price et al. 2006), discriminant analysis of principal components (Jombart et al. 2010), and non-metric multidimensional scaling (Zhu and Yu 2009). For model-based clustering, the algorithm in ADMIXTURE v.1.23 (Alexander et al. 2009), similar with STRUCTURE v.2.3.4, is an ordinarily used approach. Also, the recently developed ChromoPainter/fineSTRUCTURE v.2 (Lawson et al. 2012) considers linkage disequilibrium (LD) patterns in the genome, aiming to make use of haplotype structure and extracting more information from the data. Furthermore, to identify the optimal number of clusters, methods such as k-means clustering (Cros et al. 2015; Jan et al. 2016; Reif et al. 2003), ADMIXTURE cross-validation (Alexander et al. 2009), and ∆K Evanno criteria (Evanno et al. 2005) are the well-known ones in practice.

Accounting for the population structure has been proven very useful for many different applications in plant breeding, especially in association and prediction analyses. In the genomic prediction methods, one strategy is to consider PS in the design of the cross-validation scheme, for example ensuring that each subpopulation is equally represented in the training and validation sets (Albrecht et al. 2014; Guo et al. 2014). Also, several optimization criteria of the calibration set can be applied to maximize predictive ability in highly diverse panels (Isidro et al. 2015; Rincent et al. 2017, 2012). Another option is using PS as covariates in models aiming to control potential confounding factors and improve statistical power by reducing residual variance (Aschard et al. 2015). For instance, principal components (PCs) and admixture coefficients have been successfully used as fixed effects (covariates) in mixed-model equations for association studies (Price et al. 2010; Tucker et al. 2014; Yu et al. 2006) and genomic prediction (Azevedo et al. 2017; Daetwyler et al. 2012; Roorkiwal et al. 2016). On the other hand, using PCs in genomic best linear unbiased prediction (GBLUP) model may result in an ill-posed model because the PCs enter both as fixed effects and implicitly through the random effect (de los Campos and Sorensen 2014). Hence, Janss et al. (2012) proposed a reparameterized Bayesian whole-genome random regression (WGRR) model to handle this problem, drawing inferences based on all or some PCs, allowing a natural separation of across- and within-subpopulation genetic variance. In plant breeding, Guo et al. (2014) applied this model in maize and rice populations to control PS and found that within-subpopulation genetic variance contributed the majority of genomic heritability.

Furthermore, the presence of hidden or known structure and family relatedness within a breeding population is critical when evaluating genomic estimated breeding values (GEBVs), genomic heritability, and predictive ability, because it could lead to biased estimations (Isidro et al. 2015; Lehermeier et al. 2014; Spindel et al. 2015; Unterseer et al. 2014; Windhausen et al. 2012). Therefore, a standard approach to prediction analysis is partitioning the genomic variability into within- and across-group components (Technow et al. 2012). In animal breeding, within-group estimates of GEBV can be more accurate than across-group (Saatchi et al. 2011; Ventura et al. 2016), which can be due to non-persistent associations or inconsistent LD between SNPs and QTL across populations (Hayes et al. 2009; Iheshiulor et al. 2016). However, in plant breeding, exploiting within-group analyses may not always improve predictive ability (Cros et al. 2015; Schulz-Streeck et al. 2012). It has been shown that splitting the breeding population into subgroups could lead to a reduction of population size, loss of diversity, and besides that, no correlation between marker effects is assumed in the subpopulations (Albrecht et al. 2014; Huang et al. 2016; Riedelsheimer et al. 2013). In order to overcome this last drawback, Lehermeier et al. (2015) applied a multi-group (MG-GBLUP) analysis to control heterogeneity of marker effects between subpopulations and found promising results depending on the genetic architecture of the trait. Previous reports have shown the superiority of the multi-group over within-group prediction based on predictive ability and genomic heritability (Karoui et al. 2012; Olson et al. 2012; Porto-Neto et al. 2015; Wientjes et al. 2017; Zhou et al. 2014).

In a typical maize hybrid breeding program, inbred lines from two heterotic groups are mated. However, depending on the strategy, more than two groups are used in the crossing. In this case, although two alleles may share a common genetic background in hybrids, it is essential to find patterns of PS and apply this information in genome-based predictions, as an attempt to identify high performing hybrids (Albrecht et al. 2014; Lehermeier et al. 2015). Therefore, our objectives were (i) to investigate PS in a set of tropical maize inbreds and their derived hybrids, and (ii) to control PS in genomic predictions of single-crosses considering two scenarios: applying (1) the traditional GBLUP (GB) and four adjustment methods of PS in the whole group, and (2) homogeneous- (A-GB), within- (W-GB), multi- (MG-GB), and across-group (AC-GB) analysis in stratified groups.

Materials and methods

Phenotypic data

We used 452 maize single-crosses (hybrid dataset) provided by Helix Sementes®, São Paulo, Brazil. The hybrids represent a partial diallel mating design between 128 tropical inbred lines (inbred dataset). No heterotic group information was available. The field design used was a randomized complete block with two replications. Experimental trials were carried out in five sites in southern, southeastern, and west-central regions of Brazil during the first growing season of 2014/2015. For more details about the sites, see Sousa et al. (2017). The hybrids analyzed in each location varied, thus creating an unbalanced experiment. Two-row plots of 5 m spaced 0.70 m were used. Sowing density was about 63,000 kernels per hectare, under conventional fertilization, weed, and pest control. The traits evaluated were grain yield (GY, t ha−1) and plant height (PH, cm). Plots were mechanically harvested and converted to 13% moisture, and plant height measured from soil surface to the flag leaf collar on one representative plant within each plot (company criteria). We used a linear mixed model to calculate the BLUPs for hybrids, including site as a fixed effect, and hybrid and interaction as random effects. We used a factor analytic of order 1 (FA1) structure for the genotype effects across sites, and for the residual term, an unstructured (US) covariance matrix across sites. Variance components and entry-mean based heritability were obtained for GY and PH, and the significance of the random effects of hybrids was assessed by the likelihood ratio test (LRT) at 5% probability, using ASReml-R (Butler et al. 2009).

Genotypic data

The genotyping of the inbreds was performed by Affymetrix® platform, containing 614,000 SNPs (Unterseer et al. 2014). Markers with low call rate (< 95%) and with at least one heterozygous combination were removed. Imputation was done based on Wright equilibrium using snpReady-R (Granato et al. 2018). Polymorphic SNP markers were used to build the hybrid genotype dataset, deduced by combining the genotypes from its two parents. Afterwards, minor allele frequency was conducted over hybrid markers considering the threshold of 0.05, resulting in a total of 52,700 high-quality SNPs distributed in the ten maize chromosomes as follows: (1) 7015, (2) 6020, (3) 6072, (4) 5953, (5) 6431, (6) 4736, (7) 5197, (8) 4436, (9) 3529, and (10) 3311.

Linkage disequilibrium (LD) among markers may lead to unstable estimates of PS (Campoy et al. 2016; Galinsky et al. 2016). Therefore, we thinned both datasets using PLINK v.1.9 (Purcell et al. 2007) by removing SNPs that were in LD, with a pairwise r2 value higher than 0.7 within a 50-SNP sliding window which was advanced by 10 SNPs each time. The final genomic data was 32,838 SNPs for the inbred dataset and 26,210 SNPs for the hybrid dataset, which was used as input to perform PS analysis and genomic prediction.

Inference of population structure

Inbred dataset

We used four approaches to detect PS: (a) principal component analysis (PCA), (b) non-metric multidimensional scaling (nMDS), (c) ADMIXTURE, and (d) ChromoPainter/fineSTRUCTURE. PCA was performed using SNPRelate-R (Zheng et al. 2012) in the pruned SNP data (32,838 SNPs), and the results were presented as two- and three-dimensional principal component scores plots. For nMDS analysis, labdsv-R (Roberts 2016) was used in the Rogers’ distance matrix, with three dimensions, and the first two dimensions were plotted.

ADMIXTURE was used to perform a maximum likelihood estimation of individual ancestries, and ChromoPainter and fineSTRUCTURE were used to find patterns of haplotype similarity. Firstly, we applied the ChromoPainter unlinked model on haplotypes, with ten expectation maximization (EM) steps. Secondly, fineSTRUCTURE was used to perform Markov chain Monte Carlo (MCMC) analysis with 100,000 burn-in iterations and sample iterations with a thinning interval of 100. Normalization parameter c was calculated following the unlinked case, c = 1/(N − 1), where N is the number of individuals. Visualization of the posterior distribution of clusters was performed using the tree-building algorithm, and the number of clusters was inferred by, arbitrarily setting a cutoff in the tree.

To estimate the optimal number of clusters, we used two approaches, the cross-validation errors analyzed in ADMIXTURE, and the Bayesian information criterion (BIC) values in k-means clustering, implemented in adegenet 2.0.1-R (Jombart et al. 2015). Furthermore, to visualize the genetic differences between inbred lines, a neighbor-joining tree (NJT) was generated based on the modified Rogers’ distance. We also investigated the LD structure within 70 kb of distance among all pairs of markers (32,838 SNPs), using PLINK v.1.9, and the values were reported as the average r2 across ten chromosomes.

Hybrid dataset

We used PCA, nMDS, and fineSTRUCTURE to detect PS following the same procedure as the inbred dataset. In addition, we built an artificial ADMIXTURE coefficient for the hybrids, following the equation: ADM12 = (ADMP1 + ADMP2)/2, where ADM is the admixture coefficient of each parent, ranging from 0 to 1.

In order to visualize and describe related individuals, we used discriminant analysis of principal components (DAPCs) (Jombart et al. 2010), using the inferred groups of fineSTRUCTURE. The number of principal components to be retained in the discriminant analysis was set to 15 following alpha-score optimization, a method that finds a trade-off between discriminative power and model overfitting. We also plotted the genomic relationship matrix (GRM) by a network graph, in which two hybrids were linked when their relationship coefficient was ≥ 0.6. The networks were visualized using the igraph-R (Csardi and Nepusz 2006) with the Fruchterman Reingold layout.

Statistical models

Traditional GBLUP model

We used the additive-dominance GBLUP in the whole group (452 hybrids) ignoring the population structure by fitting the following model:

$$ \widehat{\boldsymbol{y}}=\boldsymbol{X}\boldsymbol{\beta } +{\boldsymbol{Z}}_{\boldsymbol{a}}\boldsymbol{a}+{\boldsymbol{Z}}_{\boldsymbol{d}}\boldsymbol{d}+\boldsymbol{\varepsilon}, $$
(1)

where \( \widehat{\boldsymbol{y}} \) is a vector of hybrid BLUPs, β is a vector of fixed effects, a is a vector of additive genetic effects on the individuals considered as random, d is the vector of dominance random effects, and ε is a vector of random residuals. X, Za, and Zd are the incidence matrices for β, a, and d, respectively. The distributions were assumed as \( \boldsymbol{a}\sim N\left(\mathbf{0},{\sigma}_a^2{\boldsymbol{G}}_{\boldsymbol{a}}\right) \), \( \boldsymbol{d}\sim N\left(\mathbf{0},{\sigma}_d^2{\boldsymbol{G}}_{\boldsymbol{d}}\right) \), and \( \boldsymbol{\varepsilon} \sim N\left(\mathbf{0},{\sigma}_e^2{\boldsymbol{I}}_{\boldsymbol{n}}\right) \). Ga and Gd are the additive and dominance GRM, following the equations: \( {\boldsymbol{G}}_{\boldsymbol{a}}=\frac{{\boldsymbol{W}}_{\boldsymbol{A}}{\boldsymbol{W}}_{\boldsymbol{A}}^{\prime }}{tr\left({\boldsymbol{W}}_{\boldsymbol{A}}{\boldsymbol{W}}_{\boldsymbol{A}}^{\prime}\right)/m} \) and \( {\boldsymbol{G}}_{\boldsymbol{d}}=\frac{{\boldsymbol{W}}_{\boldsymbol{D}}{\boldsymbol{W}}_{\boldsymbol{D}}^{\prime }}{tr\left({\boldsymbol{W}}_{\boldsymbol{D}}{\boldsymbol{W}}_{\boldsymbol{D}}^{\prime}\right)/m} \), where m is the number of markers. The incidence matrices WA and WD were designed following VanRaden (2008) and Da et al. (2014). To build the WA matrix, we used a genotypic incidence matrix (SA) coded as 2 for homozygote A1A1, 1 for heterozygote A1A2, and 0 for homozygote A2A2. For WD, the genotypic incidence matrix (SD) was coded as 0 for both homozygotes and 1 to the heterozygote.

PS covariates

We applied the Q+K model (Yu et al. 2006) on the genomic prediction of hybrids for both traits, using the PS-related variables as fixed covariates in the GBLUP (GB) model. Hence, we used four contrasting Q approaches that includes (a) first three PCs (GB+PC), (b) three dimensions of non-metric multidimensional scaling (GB+nMDS), (c) artificial admixture coefficients (GB+ADM), and (d) a matrix of zeros and ones based on fineSTRUCTURE group clustering (GB+FINE). Furthermore, to select the top PCs (Patterson et al. 2006), we evaluated the number of statistically significant principal components, measured by the Tracy-Widom test using LEA-R (Frichot and Francois 2015) and added a varied number of PCs (3, 5, 10, 14) in GBLUP.

For the whole-group GB and GB plus PS covariates models, we evaluated the predictive ability (r). The r was measured as the Pearson’s correlation of the adjusted values and predicted phenotypic values of the hybrids, obtained from 50 replications. In each replication, 75% of the single-crosses were randomly sampled to form the training set (TS) whereas the remaining hybrids constituted the validation set (VS). We used the T2 validation scenario proposed by Technow et al. (2012), in which both parents (female or male) of a single cross participate in the validation set. Also, reliability (REL) (Gorjanc et al. 2015) was used to compare the model performance. REL was calculated according to the formula: \( REL=1-\left( PEV/{\sigma}_g^2\right) \), where PEV is the variance of prediction errors of the GEBV of the hybrid (\( {\widehat{g}}_i \)). Note \( PEV= SD{\left({\widehat{g}}_i\right)}^2=\mathit{\operatorname{var}}\left({g}_i-{\widehat{g}}_i\right) \), where SD is the standard deviation. The model with the highest REL value presented the best precision in earlier studies (He et al. 2016; Gorjanc et al. 2015). The mean values of r and REL estimated from 50 replications in the independent validation were used in the overall model performance comparison. We applied Fisher’s Z transformation in the predictive abilities from all models, and the means were compared by Scott-Knott’s test at 5% significance. All variance components were determined using Bayesian generalized linear regression (BGLR) (Perez and de los Campos 2014) for the five mixed-models. We used a total of 30,000 MCMC iterations, 5000 for burn-in, and 5 for thinning. We also reported posterior mean estimates and standard deviations (SDs) of the broad sense genomic heritability [\( {H}_g^2=\left({\sigma}_a^2+{\sigma}_d^2\right)/\left({\sigma}_a^2+{\sigma}_d^2+{\sigma}_e^2\right) \)], where \( {\sigma}_a^2 \), \( {\sigma}_d^2 \), and \( {\sigma}_e^2 \) are the additive, dominance, and residual variances, respectively.

Homogeneous-, within-, multi-, and across-group analysis

We used the stratified groups (subgroups) to make inferences of hybrid prediction using four main approaches, detailed in Lehermeier et al. (2015). The first is a homogeneous-group (A-GB) approach, which assumes constant marker effects across groups, which means that we use all available data (whole group), but evaluating the accuracy within subpopulations (in each group the marker effects are identical). A second method is a stratified within-group analysis (W-GB), estimating marker effects and variance components within each K separately, with a specific GRM. A third scheme is a multivariate approach (MG-GB) that uses multi-group data and accounts for heterogeneity, with population-specific marker effects that can be correlated between subpopulations. The last approach used was the across-group prediction (AC-GB), where individuals from one group were used to build the training set to predict the performances of individuals from a different group (validation set). For example, if we used K1 to predict K2 (K1→K2) subpopulation, we randomly sampled 75% of the hybrids to form the TS with K1 individuals and the rest of VS from K2.

For the homogeneous-group approach, we used the additive-dominance A-GBLUP by fitting the following model:

$$ \widehat{{\boldsymbol{y}}_{\boldsymbol{k}}}={\boldsymbol{X}}_{\boldsymbol{k}}{\boldsymbol{\beta}}_{\boldsymbol{k}}+{\boldsymbol{Z}}_{{\boldsymbol{a}}_{\boldsymbol{k}}}{\boldsymbol{a}}_{\boldsymbol{k}}+{\boldsymbol{Z}}_{{\boldsymbol{d}}_{\boldsymbol{k}}}{\boldsymbol{d}}_{\boldsymbol{k}}+{\boldsymbol{\varepsilon}}_{\boldsymbol{k},} $$
(2)

where \( \widehat{{\boldsymbol{y}}_{\boldsymbol{k}}} \) is the nk-dimensional vector of hybrid BLUPs of subpopulation k, βk is the pk-dimensional vector of fixed effects common for all k subpopulations, ak is the nk-dimensional vector of additive genetic of random effects on the individuals for subpopulation k, dk is the nk-dimensional vector of dominance random effects for subpopulation k, and εk is nk-dimensional vector of random residuals belonging to subpopulation k. Xk, Za, and Zd are the incidence matrices for βk, ak, and dk, respectively. The complete vector\( \boldsymbol{a}=\left({\boldsymbol{a}}_{\mathbf{1}}^{\prime },\dots, {\boldsymbol{a}}_{\boldsymbol{K}}^{\prime}\right) \) is assumed to follow \( \boldsymbol{a}\mid {\sigma}_a^2\sim {MVN}_{n\times n}\left(\mathbf{0},{\sigma}_a^2{\boldsymbol{G}}_{\boldsymbol{a}}\right) \), and the vector \( \boldsymbol{d}=\left({\boldsymbol{d}}_{\mathbf{1}}^{\prime },\dots, {\boldsymbol{d}}_{\boldsymbol{K}}^{\prime}\right) \) is assumed to follow \( \boldsymbol{d}\mid {\sigma}_d^2\sim {MVN}_{n\times n}\left(\mathbf{0},{\sigma}_d^2{\boldsymbol{G}}_{\boldsymbol{d}}\right) \). Ga and Gdwere built following the same parameterization as those defined in model (1). It is worth noting that the residuals are assumed to follow a normal distribution with mean 0 and subpopulation-specific variance as \( {\boldsymbol{\varepsilon}}_{\boldsymbol{k}}\sim {MVN}_{n_k\times {n}_k}\left(\mathbf{0},{\sigma}_{{\boldsymbol{\varepsilon}}_k}^2\boldsymbol{I}\right) \). We assigned a scaled inverse chi-square prior distribution with degrees of freedom (df1) and scale parameter (S1) of \( {\sigma}_a^2\sim {\upchi}^{-2}\left({df}_1,{S}_1\right) \), \( {\sigma}_d^2\sim {\upchi}^{-2}\left({df}_1,{S}_1\right) \), and \( {\sigma}_{{\boldsymbol{\varepsilon}}_k}^2\sim {\upchi}^{-2}\left({df}_0,{S}_0\right) \) for \( {\sigma}_a^2 \), \( {\sigma}_d^2 \), and \( {\sigma}_{{\boldsymbol{\varepsilon}}_k}^2 \), respectively.

For the within-group method, we used the additive-dominance W-GBLUP by fitting the following model:

$$ \widehat{{\boldsymbol{y}}_{\boldsymbol{k}}}={\boldsymbol{X}}_{\boldsymbol{k}}{\boldsymbol{\beta}}_{\boldsymbol{k}}+{\boldsymbol{Z}}_{{\boldsymbol{a}}_{\boldsymbol{k}}}{\boldsymbol{a}}_{\boldsymbol{k}}+{\boldsymbol{Z}}_{{\boldsymbol{d}}_{\boldsymbol{k}}}{\boldsymbol{d}}_{\boldsymbol{k}}+{\boldsymbol{\varepsilon}}_{\boldsymbol{k}}, $$
(3)

where \( \widehat{{\boldsymbol{y}}_{\boldsymbol{k}}} \), ak, dk, and εk are the same as those defined in model (2). However, βk is the pk-dimensional vector of fixed effects specific for subpopulation k, and the vectors of additive and dominance effects for each subpopulation are assumed to follow different independent normal distributions: \( {\boldsymbol{a}}_{\boldsymbol{k}}\mid {\sigma}_{a_k}^2\sim {MVN}_{n_k\times {n}_k}\left(\mathbf{0},{\sigma}_{a_k}^2{\boldsymbol{G}}_{{\boldsymbol{a}}_{\boldsymbol{k}}}\right) \) and \( {\boldsymbol{d}}_{\boldsymbol{k}}\mid {\sigma}_{d_k}^2\sim {MVN}_{n_k\times {n}_k}\left(\mathbf{0},{\sigma}_{d_k}^2{\boldsymbol{G}}_{{\boldsymbol{d}}_{\boldsymbol{k}}}\right) \), where \( {\boldsymbol{G}}_{{\boldsymbol{a}}_{\boldsymbol{k}}} \) and \( {\boldsymbol{G}}_{{\boldsymbol{d}}_{\boldsymbol{k}}} \) is the genomic relationship matrix among individuals of the kth subpopulation, and \( {\sigma}_{a_k}^2 \) and \( {\sigma}_{d_k}^2 \) are the additive and dominance variances of the kth subpopulation. Residuals are assumed to follow a normal distribution with mean 0 and subpopulation-specific variance as \( {\boldsymbol{\varepsilon}}_{\boldsymbol{k}}\sim {MVN}_{n_k\times {n}_k}\left(\mathbf{0},{\sigma}_{{\boldsymbol{\varepsilon}}_k}^2\boldsymbol{I}\right) \). As in A-GB, we assigned a scaled inverse chi-square prior distribution with degrees of freedom (df1) and scale parameter (S1) of \( {\sigma}_a^2\sim {\upchi}^{-2}\left({df}_1,{S}_1\right) \), \( {\sigma}_d^2\sim {\upchi}^{-2}\left({df}_1,{S}_1\right) \), and \( {\sigma}_{{\boldsymbol{\varepsilon}}_k}^2\sim {\upchi}^{-2}\left({df}_0,{S}_0\right) \) for \( {\sigma}_a^2 \), \( {\sigma}_d^2 \), and \( {\sigma}_{{\boldsymbol{\varepsilon}}_k}^2 \), respectively. Also, to each group k, marker effect based on the adjusted entry means for grain yield, and plant height was estimated, using rrBLUP-R (Endelman 2015). Besides that, LD structure was investigated within 70 kb of distance between all pairs of markers, and the values were reported as the average r2 across ten chromosomes.

For the additive-dominance MG-GBLUP approach, we used the following model:

$$ \widehat{{\boldsymbol{y}}_{\boldsymbol{k}}}={\boldsymbol{X}}_{\boldsymbol{k}}{\boldsymbol{\beta}}_{\boldsymbol{k}}+{\boldsymbol{Z}}_{{\boldsymbol{a}}_{\boldsymbol{k}}}{\boldsymbol{a}}_{\boldsymbol{k}}+{\boldsymbol{Z}}_{{\boldsymbol{d}}_{\boldsymbol{k}}}{\boldsymbol{d}}_{\boldsymbol{k}}+{\boldsymbol{\varepsilon}}_{\boldsymbol{k}}, $$
(4)

where \( \widehat{{\boldsymbol{y}}_{\boldsymbol{k}}} \), βk, ak, dk, and εk are the same as those defined in model (3). However, the model estimates population-specific marker effects allowing for correlations of effects between groups. In this case, the complete vector of the genomic values of individuals in each group is an augmented form (n. K), \( {\boldsymbol{a}}^{\ast}=\left({\boldsymbol{a}}_{\mathbf{1}}^{\ast \prime },\dots, {\boldsymbol{a}}_{\boldsymbol{K}}^{\ast \prime}\right) \) and \( {\boldsymbol{d}}^{\ast}=\left({\boldsymbol{d}}_{\mathbf{1}}^{\ast \prime },\dots, {\boldsymbol{d}}_{\boldsymbol{K}}^{\ast \prime}\right) \), with the additive and dominance effects following a multivariate normal distribution a∗ ∣ ∑a~MVNn. k × n. k(0, ∑a ⊗ Ga), and d∗ ∣ ∑d~MVNn. k × n. k(0, ∑d ⊗ Gd). ∑a and ∑d are an unstructured (US) genomic variance-covariance matrix (V-COV) among subpopulations. Differently, from A-GB and W-GB, we assumed a correlation between residuals and following a normal distribution with subpopulation-specific residual variances, \( {\boldsymbol{\varepsilon}}_{\boldsymbol{k}}\sim {MVN}_{n_k\times {n}_k}\left(\mathbf{0},{\mathbf{\sum}}_e\otimes {\boldsymbol{D}}_{\boldsymbol{e}}\right) \), where ∑e is an US V-COV of residuals. The hyperparameters of the prior distributions of the variance components were chosen according to the inverse Wishart, ∑a~W−1(Ψ, v), where the scale matrix Ψ was a diagonal with entries equal to Ψ = 0.5 × (v + k + 1), and the degrees of freedom (v) were set to v = k + 3, where k is the number of groups (Lehermeier et al. 2015). The same approach was assumed to the dominance and residual variances.

The predictive ability of A-GB, W-GB, and MG-GB were assessed with 50 replications from independent T2 validation scenario, randomly sampling 75% of the hybrids to form the TS and the rest of VS. We applied Fisher’s Z transformation in the predictive abilities from all models, and the means were compared by Scott-Knott’s test at 5% significance. A total of 30,000 MCMC iterations, 5000 for burn-in, and 5 for thinning were used to estimate the parameters using the MTM-R package. We reported posterior mean estimates and standard deviations of the \( {H}_g^2 \) for each k.

Results

Inbred PS

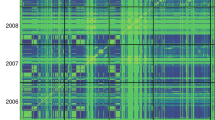
In the ADMIXTURE analysis, the optimal number of clusters was L = 7 with the smallest cross-validation error (Supplemental Fig. S1a, Fig. S2). The k-means clustering identified L = 3 with the smallest BIC value (Supplemental Fig. S1b). The fineSTRUCTURE result is a coancestry heatmap, which shows the amount of shared genetic chunks between the inbred lines (Fig. 1a). We defined a cutoff on the maximum a posteriori tree with three groups (L), each containing 100 (L1), 13 (L2), and 15 (L3) inbred lines. In within-group L1, five distinct subgroups were revealed, explaining the seven groups identified in the ADMIXTURE results (Supplemental Fig. S2a). Moreover, PCA, nMDS, and cluster (NJT) analysis also revealed levels of PS identified in both model-based clusterings (Fig. 1; Supplemental Fig. S3a). The first two PCs explained 5.36% and 4.24% of the total variance, clearly splitting the groups along the axis. However, nMDS analysis revealed that L1 and L3 were clustered together, but separated from L2. The relationship between LD and physical distance was plotted (Supplemental Fig. S3b), and the LD decayed faster with the r2 dropping to half its maximum value within 1.3 kb.

Fig. 1
figure 1

Population structure analysis in 128 tropical maize inbred lines. a Coancestry heatmap of fineSTRUCTURE unlinked model. The scale shows lower (white) to higher (black) amount of shared genetic chunks between the inbred lines. On the left and top is the maximum a posteriori (MAP) tree. The dashed red line is the cutoff threshold splitting L1, L2, and L3 groups. Dashed blue line clustered the subgroups S1, S2, S3, S4, and S5. b First two principal components. c Circular neighbor-joining tree based on modified Rogers’ distance

Full size image

Hybrid PS

The unlinked coancestry heatmap of fineSTRUCTURE clustered hybrids into three groups (K), containing 113 (K1), 121 (K2), and 218 (K3) hybrids (Fig. 2a). Three subgroups of within-group K1 were also clearly shown. In the artificial admixture coefficients (Fig. 2b), we found a mixture of groups in the hybrids. PCA and nMDS dots were color-coded based on the fineSTRUCTURE group clustering. The first two PCs explained 7.40% and 6.05% of the total variance (Fig. 2c). Furthermore, the 3-D PCA score plot (Supplemental Fig. S4a) revealed a clear separation of K1 from K2, wherein PC1, PC2, and PC3 together explained 18.3% of the data variation. The within-group individuals of K1 were spread along the axis (blue density plot), confirming the subgroups identified in fineSTRUCTURE (Fig. 2a; S4a). In addition, a pattern also was detected for nMDS analysis (Fig. 2d). Network graph revealed that individuals from K2 and K3 are more related according to the GRM (Fig. 2e). The DAPC plot (Supplemental Fig. S4b) using two discriminant functions indicated that K1 were highly discriminated from K2, with reliable separation along the principal component axes. The plot did not reveal high discrimination between K2 and K3, since overlapping existed between groups.

Fig. 2
figure 2

Population structure analysis in 452 tropical maize single-cross hybrids. a Coancestry heatmap of fineSTRUCTURE unlinked model. The scale shows lower (white) to higher (black) amount of shared genetic chunks between the individuals. On the left and top is the maximum a posteriori (MAP) tree. The dashed red line is the cutoff threshold splitting K1, K2, and K3 groups. b Artificial admixture coefficients, where each color represents a group (K1-K7). c First two principal components, applied to raw SNP data (32,838 SNPs). The percentages in parentheses in the axis titles represent the variance explained by each of the two principal components. d First two non-metric multidimensional scaling (nMDS) dimensions, applied to Rogers’ distance matrix. e Network representation of the GRM, where individuals were linked when their relationship coefficient was ≥ 0.6 (not all hybrids are shown). Colors in b, c, and e indicate three groups clustered from fineSTRUCTURE results. The number of hybrids per group is indicated in parenthesis. Density plot shows the distribution of individuals in each group

Full size image

Hybrid prediction along PS covariates

From the phenotypic analysis, it was found significant differences in the hybrids by the likelihood ratio test (P < 0.05), for GY and PH. Entry-mean based heritability was 0.77 for GY and 0.86, reflecting the good accuracy of the phenotypic evaluation. The adjusted values for GY varied from 3.39 to 9.37 t ha−1, and for PH from 185 to 277 cm.

From the prediction analysis, we did not observe significant differences from Scott-Knott’s test (P < 0.05) between the values of predictive ability (r) among all tested models for both traits (Figs. 3a; 4a). For instance, the r reached similar values of 0.74 for GY and 0.80 for PH for all models. In this case, there was no advantage of adding PS covariates in the prediction approach. However, it is important to highlight that the highest REL were observed using nMDS and FINE as covariates to predict GY (Supplemental Fig. S5a). For PH, FINE and ADM were the best models regarding REL (Supplemental Fig. S5b). Besides, estimates of broad sense genomic heritability varied slightly among models for both traits (Supplemental Fig. S6; Supplemental Fig. S7). Based on the Tracy-Widom test, the significant axes of variation to account for the genetic structure were 14 (Supplemental Fig. S8a). For both traits, the predictive ability values slightly decreased when added more than three PCs in GBLUP model (Supplemental Fig. S8b), showing that three PCs in the model could be efficient to account population structure.

Fig. 3
figure 3

Comparison of predictive ability (r) for grain yield. a GBLUP (GB) model and GB with four fixed covariates: principal components (GB+PC), non-metric multidimensional scaling dimensions (GB+nMDS), admixture coefficients (GB+ADM), and fineSTRUCTURE group clustering (GB+FINE). b GB, homogeneous- (A-GBLUP), within- (W-GBLUP), and multi-group (MG-GBLUP) analysis for K1, K2, K3, K1K2, K1K3, and K2K3 groups. c Across-group (AC-GBLUP) analysis for nine prediction schemes. Data are mean ± standard deviation (SD) estimated from 50 replications in independent validation. Letters above bars indicate significant differences between models’ predictive abilities from Scott-Knott test (P < 0.05)

Full size image
Fig. 4
figure 4

Comparison of predictive ability (r) for plant height. a GBLUP (GB) model and GB with four fixed covariates: principal components (GB+PC), non-metric multidimensional scaling dimensions (GB+nMDS), admixture coefficients (GB+ADM), and fineSTRUCTURE group clustering (GB+FINE). b GB, homogeneous- (A-GBLUP), within- (W-GBLUP), and multi-group (MG-GBLUP) analysis for K1, K2, K3, K1K2, K1K3, and K2K3 groups. c Across-group (AC-GBLUP) analysis for nine prediction schemes. Data are mean ± standard deviation (SD) estimated from 50 replications in independent validation. Letters above bars indicate significant differences between models’ predictive abilities from Scott-Knott test (P < 0.05)

Full size image

Subgroup prediction

We used within-group (K1, K2, K3, K1K2, K1K3, and K2K3 subpopulations) hybrids to investigate the predictive ability and broad sense genomic heritability for GY and PH. The highest r was observed when combining K2 plus K3 for GY (r = 0.74) and PH (r = 0.80), reaching similar values to the whole-group prediction (Figs. 3b; 4b). As expected, A-GB and MG-GB presented significantly higher values of r relative to W-GB for most of the groups. However, A-GB and MG-GB yielded similar values of r for all traits and groups, but in some cases, the MG-GB significantly outperformed the A-GB, and vice versa. For instance, the r reached values of 0.78, 0.80, and 0.84 in the K3 group using the within-, homogeneous-, and multi-group analysis for PH. We also observed that combining the subgroups K1K2+K3 and using the MG-GB model significantly improved the r for K3 (r = 0.84) compared to the whole-group prediction (r = 0.79), remaining similar values for the K1K2 group (r = 0.76) for plant height (Fig. 4b). For both traits, lower estimates of \( {H}_g^2 \) were observed from W-GB compared to A-GB and MG-GB (Supplemental Fig. S6b; Supplemental Fig. S7b). For example, the \( {H}_g^2 \) for PH using the whole-group (GB) was 0.86, and for W-GB was 0.71 while MG-GB was 0.89 for the K1 group. Moreover, MG-GB presented higher \( {H}_g^2 \) with lower SD compared to A-GB showing better model fit to the training data.

We also used eight across-group (K1 → K2, K1 → K3, K2 → K3, K2 → K1, K3 → K1, K3 → K2, K1K2 → K3, K1K3 → K2, and K2K3 → K1) prediction schemes (Figs. 3c; 4c). As expected, we observed lower r from AC-GB compared to the whole-group (traditional GBLUP), W-GB, and MG-GB for both traits. It is important to note that the r was low when predicting groups genetically distant (Fig. 2). For example, using K1 → K2 and the opposite (K2 → K1), the r for GY was 0.42 and 0.30, respectively. The significant highest r was observed when predicting K2K3 → K1 (r = 0.66) for GY, and K1K2 → K3 (r = 0.65) and K1K3 → K2 (r = 0.65) for PH.

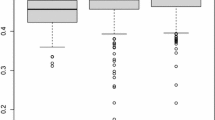
The relationship between LD and physical distance (kb) was plotted for K (452), K1 (113), K2 (121), and K3 (218) (Fig. 5a). LD (r2) rapidly decayed following the highest number of individuals inside the group. Yan et al. (2009) showed the same tendency working with a diverse global maize collection. For K, K1, K2, and K3 the LD decayed with the r2 dropping to half their maximum value within 5.5, 6.5, 10, and 11.5 kb, respectively. Additive marker effects distribution estimated across the groups were different for GY, but it was similar for PH, in all ten chromosomes (Fig. 5b, c). Pearson correlation between group SNP effect for GY was 0.27 (K1-K2), 0.46 (K1-K3), and 0.14 (K2-K3). For PH, the r was 0.33 (K1-K2), 0.38 (K1-K3), and 0.46 (K2-K3). Posterior mean estimates and posterior SD of the genomic correlations from MG-GB for GY varied among the three groups 0.34 ± 0.14 (K1-K2), 0.75 ± 0.09 (K1-K3), and 0.48 ± 0.15 (K2-K3). For PH, the values were 0.31 ± 0.16 (K1-K2), 0.74 ± 0.10 (K1-K3), and 0.51 ± 0.14 (K2-K3). Thus, the estimated genomic correlations between subpopulations K1-K3 was high for both traits, which is agreement with the GRM (Fig. 2e).

Fig. 5
figure 5

a Pattern of linkage disequilibrium (LD) within 70 kb of distance among all pairs of markers (26 K SNPs) for 452(K), 113(K1), 121(K2), and 218(K3) individuals. Values reported are the average r2 across ten chromosomes. Boxplots of additive marker effect estimates for b GY and c PH, for K1, K2, and K3 groups

Full size image

Discussion

The most common source of tropical germplasm found in the breeding programs are Tusón, Tuxpeño, Antigua Composite, Suwan-1, and Cuban Flint (also called Cateto in Brazil) (Hallauer and Carena 2014; Laborda et al. 2005), and as observed in previous studies, the number of subgroups inside tropical and subtropical still diverge (Molin et al. 2013; Reif et al. 2003; Wu et al. 2016; Ertiro et al. 2017). In the present study, 128 tropical inbred lines were characterized using k-means clustering and two model-based approaches to identify groups/clusters. Based on k-means, we classified three groups, which were consistent according to fineSTRUCTURE (Fig. 1a) and PCA (Fig. 1b). Another way to visualize the structure of populations is by the extent of linkage disequilibrium, which influences the resolution of the genome-wide analysis (Yang et al. 2011). In our study, the LD decayed within 1.3 kb (Supplemental Fig. S3b), which was consistent with the findings of Unterseer et al. (2014). These authors worked with 285 temperate and tropical maize lines genotyped with 600 K SNPs, and found L = 7 in ADMIXTURE, and observed fastest LD decay in (sub)tropical lines (70 kb) explained by the high heterogeneity inside the groups. Chia et al. (2012) and Yan et al. (2009) also found fastest LD decay within distances between 5 and 10 kb, respectively, in highly diverse tropical maize lines.

Recently, in an applied breeding scheme, Edriss et al. (2017) studied genomic prediction of tropical maize hybrids generated from 2022 diverse breeding lines from five subpopulations, demonstrating the importance of PS in genomic studies. Thus, it is common verifying PS among inbred lines to explore heterosis in divergent parental crossing (Fernandes et al. 2015; Mundim et al. 2015). However, in tropical maize breeding, hybrids could be generated from various heterotic parent groups, reflecting in high levels of structuring, confirming our results identified from fineSTRUCTURE, PC, and DAPC results (Fig. 2 and Supplemental Fig. S4). For example, within-group K1 (Fig. 2a) revealed three distinct subgrouping, which can be identified in 2-D (Fig. 2c) and 3-D (Supplemental Fig. S4) PCA graph. Also, estimates of genomic correlations based on the variance-covariance matrix between subpopulations show the extent of genetic heterogeneity between groups, corresponding to the marker effects correlations (Lehermeier et al. 2015). In our work, the estimated genomic correlations between subpopulations K1-K3 was high while the group K1-K2 was low for both traits. According to Lehermeier et al. (2015), those correlations between groups are trait-specific, being affected by the similar or contrasting values of QTL effects, epistasis, dominance, and by differences in marker-QTL LD between subgroups.

In our work, both traits showed high values of predictive ability and genomic heritability for GY (0.74; 0.79) and PH (0.80; 0.86) from traditional GBLUP (Figs. 3, 4; Supplemental Fig. S7, Supplemental Fig. S8). Similar findings were observed by Maenhout et al. (2010), Massman et al. (2013), and Santos et al. (2016). Moreover, the methods GBLUP, PC, nMDS, ADM, and FINE were compared regarding r and REL. There was no advantage of adding PS covariates in the prediction model based on r. Thus, one explanation could be the fact that the GRM implicitly captured the genetic variation from PS and admixture of the hybrids. Another reason could be the similarity in the mean performance of the traits between the subpopulation. According to Isidro et al. (2015) and Windhausen et al. (2012) traits are primarily impacted by PS. Therefore, predictive abilities depend on the interaction of trait architecture and levels of PS. On the other hand, including PS covariates reported herein showed better performance concerning reliability, which could substantially reduce the standard error of the genetic variant association and, consequently, increase the accuracy of GEBV estimation. As a consequence, possible changes of individual ranking could be observed in the models with and without PS correction, which is in agreement with Azevedo et al. (2017).

Several studies have been successfully conducted including PC as covariates in GWAS analysis (Sukumaran et al. 2015; Wang et al. 2011; Zhang et al. 2016). However, in genomic prediction studies, adding PC eigenvectors in the model have shown low r or at least the same value (Daetwyler et al. 2012; Newell and Jannink 2014). As already reported by Janss et al. (2012) and de los Campos and Sorensen (2014), the PCs added as fixed effects in the GBLUP enter twice in the model, causing misleading interpretations. On the other hand, Roorkiwal et al. (2016) studied a collection of 320 elite breeding chickpea lines including admixture coefficients (PS covariable) as fixed effect in the RR-BLUP, and found that the predictive abilities improved slightly for days to maturity (DM), days to flowering (DF), and seed dry weight (SDW). In addition, Azevedo et al. (2017) simulated four scenarios including PCs and eigenvectors into GBLUP model and found higher estimates of r compared to the model with no PS correction. In our work, even finding structuring in PC plot (Fig. 2c), including the first three PCs did not change predictive ability scenario for both traits (Figs. 3a; 4a). Furthermore, we used Tracy-Widom test to select the top principal components, but the r slightly decreased when added the first 5, 10, and 14 significant PCs in GBLUP model for both traits (Supplementary Fig. S8b). These results are in agreement with Azevedo et al. (2017), and Daetwyler et al. (2012) who observed a decline of r as an increasing number of PC was fitted into the model. Therefore, the main advantage of PS correction for long-term genomic prediction is that the estimated marker effects could potentially be valid for some generations ahead (training set), saving time, and resources in the re-estimation of new effects of markers (Crossa et al. 2007, 2010; Guo et al. 2014; Isidro et al. 2015; Lehermeier et al. 2015; Windhausen et al. 2012; Azevedo et al. 2017).

The prediction including three nMDS dimensions performed better than the others methods of GY regarding reliability. In a GWAS analysis, Zhu and Yu (2009) compared nMDS and PC and found an increase in power and a decrease in false positive rate using nMDS associated with genomic kinship. Further, Sukumaran et al. (2012) worked with PS of 300 wheat lines for ten grain quality traits and tested three mixed models including admixture coefficients, nMDS, and PCA as fixed covariates in GWAS analysis. The authors found nMDS as the best approach for the amount of phosphorus (P). On the other hand, in our results, ADM was the lowest ranked method so far according to REL for GY. In contrast, for PH showed better performance compared to GBLUP. In animal prediction, Thomasen et al. (2013) studied US and Danish Jersey cattle by including admixture coefficients estimated from STRUCTURE in genomic prediction models and did not find any improvement of prediction reliabilities.

From our findings, predictive ability was significantly higher in A-GB and MG-GB when compared with W-GB for both traits (Figs. 3b; 4b). According to Lehermeier et al. (2015), MG-GB allows subpopulation-specific marker effects, borrowing the information between subpopulations. In contrast, within-group prediction (W-GB) reduces training size, nevertheless, increases the relationship between genotypes (Iheshiulor et al. 2016; Lehermeier et al. 2015; Mendes and de Souza 2016; Riedelsheimer et al. 2012; Huang et al. 2016). Schulz-Streeck et al. (2012) found better predictive ability joining all populations derived from five biparental populations of maize. Riedelsheimer et al. (2012) also studied PS splitting the whole population in within-group of related lines and showed that population structuring reduced predictive ability in 3.6% for SNPs relative to the whole population. In our study, higher estimates of r were observed from MG-GB in K3 group, for GY (0.77) and PH (0.84) relative to the whole group from traditional GBLUP and GB plus PS covariables, showing the efficiency of the method. We also observed that combining subgroups (K1K2+K3) significantly improved the r for K3 in both traits (Figs. 3b; 4b). Another way to visualize the impact of PS in the subgroups prediction is to measure the extent of genomic heritability. In our results, the \( {H}_g^2 \) for PH using the whole group (GB) was 0.86, for W-GB was 0.71, and A-GB was 0.77 while MG-GB was 0.89 for the K1 group (Supplemental Fig. S6b; Supplemental Fig. S7b). This agrees with the results reported by Guo et al. (2014) and Lehermeier et al. (2015), in which the PS showed a significant impact on genomic heritability.

In our study, as expected, we observed a considerable decrease in predictive ability and genomic heritability by the across-group (AC-GB) prediction for both traits compared to the others approaches (Figs. 3b; 4b; Supplemental S6b; Supplemental S7b). This could be related to the non-consistent additive marker effects between the subgroups for both traits, especially for GY (Fig. 5b, c). Also, this result could be justified by the low relatedness of the individuals between training and validation and different marker effects between groups (Habier et al. 2007). Similar findings were observed by Guo et al. (2014) who reported more substantial reductions in predictive ability due to the correction for PS in across-subpopulations, and Mendes and de Souza (2016) who studied PS within and across groups from 250 tropical maize single-crosses genotyped with 614 AFLP marker, finding high accuracy estimates for within-group prediction.

Conclusion

Our results suggest that there was no advantage of adding population structure covariates in the prediction model based on predictive ability. However, using non-metric multidimensional scaling and fineSTRUCTURE group clustering increased the reliability of GEBV estimation for grain yield and plant height. Furthermore, applying the multi-group method in stratified groups may be an efficient method, significantly increasing the predictive ability and genomic heritability compared to the whole-, within-, and across-group prediction.