In [1], the results of processing experimental data on changes in the strength of threads and single filaments of a copolymer para-aramid fiber when a suspension of carbon nanotubes (CNTs) is introduced into the technological process, are presented. The average value of the tensile strength of the threads as a result of such processing increased by 30.04%, but of single filaments — by 9.76%. This is an important finding, analogous to which could not be found in the available scientific and technical publications. In this work, the results of extended processing of the same experimental data are presented. Usually, treating the surface of para-aramid fibers with various nanoparticles increases the shear characteristics of composites. In [2, 3], results for para-aramid Kevlar fibers treated with functionalized graphenes and multilayer CNTs are presented, and in [4] — for Twaron fibers treated with functionalized CNTs. No increase in the filament strength was found.

In [1], the parameters of two-parameter distributions adequate for experimental data are given, in particular, the Weibull–Gnedenko distribution, whose parameters were determined using the standard wblfit procedure of the universal mathematical Mathlab package. The wblfit procedure for estimating the parameters of the Weibull–Gnedenko two-parameter distribution implements the maximum similarity principle (MSP) developed by R. Fisher. When solving many problems in the mechanics of composites related to fracture problems, the three-parameter Weibull-Gnedenko distribution is used, with the distribution function F (x) of fiber strength determined by the equation

$$ {\displaystyle \begin{array}{c}F\left(\left.x\right|a,b,{x}_u\right)=1-\exp \left[-{\left(\frac{x-{x}_u}{a}\right)}^b\right]\dots, x\ge {x}_u,\\ {}F(x)=0\dots \dots x<{x}_m,\end{array}} $$
(1)

and the density function f (x) of fiber strength distribution

$$ f\left(\left.x\right|a,b,{x}_u\right)={\left(\frac{x-{x}_u}{a}\right)}^b\frac{b}{x-{x}_u}\exp \left[-{\left(\frac{x-{x}_u}{a}\right)}^b\right] $$
(2)

containing the so-called shear parameter xu , which is the point of beginning of failure. If the mechanical stress applied to a sample is lower than xu , the probability of failure (or the fraction of failed samples when testing a series of samples) is zero.

After determining the parameters of the theoretical distribution, it is necessary to check the correctness of its application to experimental results. For this aim, a nonparametric test of the agreement hypothesis was carried out using the Kolmogorov criterion

$$ {D}_n=\left.\sup \right|{F}_n(x)-F\left.(x)\right|. $$
(3)

Its variant, which is very convenient for engineering applications, is given in monograph [5]. For practical calculations of this statistic, the following formulas are recommended:

$$ {D}_n^{+}=\underset{1\le j\le n}{\max}\left(\frac{j}{n}-F\left({x}_j\right)\right), $$
(4a)
$$ {D}_n^{-}=\underset{1\le j\le n}{\max}\left(F\left({x}_j\right)-\frac{j-1}{n}\right), $$
(4b)
$$ {D}_n=\max \left({D}_n^{+},{D}_n^{-}\right). $$
(5)

The agreement hypothesis is not rejected if the value of Dn obtained from Eq. (5) is lower than the critical value Dn (Q) . The significance level Q in this work was assumed to be 5%. For calculating Dn (Q) , the following approximation is proposed in [5]:

$$ {D}_n(Q)=\sqrt{\frac{1}{2n}\left(y-\frac{2{y}^2-4y-1}{18n}\right)}-\frac{1}{6n},y=-\ln (0.005Q). $$
(6)

In Eqs. (3)-(6), Fn is an empirical distribution function, F is a theoretical distribution function with known parameters, n is the volume of experimental sample and x j is a j th element from an experimental sample arranged in ascending order. There is no standard procedure in the Mathlab package for estimating the three parameters of the Weibull–Gnedenko distribution. For this aim, the MSP was also used in our work. Using the standard procedure to find the extremum minsearch of the Mathlab package, we sought for the maximum similarity function L (xu , a,b) according to the distribution parameters xu , a , and b :

$$ L\left({x}_u,a,b\right)=\sum \limits_{i=1}^nf\left(\left.{x}_i\right|{x}_u,a,b\right), $$
(7)

where xi , i = 1, 2,..., n, is the vector of experimentally determined values of strength.

The processing results of experimental data for the Weibull–Gnedenko distribution are given in Table 1. As is seen, the shear parameter characterizing the onset of fracture for threads, as a result of using CNTs, increased by 59.65%, and for filaments — by 30.19%, with average values increasing by 30.04 and 9.76%, respectively. The physicochemical reason for this is clear: under the action of CNTs, changed is not only the strength of individual filaments, but also the friction between them, which obviously contributed to a more uniform tension of filaments when testing threads. The change in the theoretically maximum possible value of the parameter is also of interest. The Weibull–Gnedenko distribution does not answer this question. Theoretically, the maximum value of the parameter, as follows from formula (1), can take any value. For this purpose, it is possible to employ the distribution proposed in [6] and used to determine the extreme values of the strength of the filaments of basalt and taparan para-aramid fibers in [7]. We used the distribution function

Table 1 Estimates of Parameters of the Weibull–Gnedenko Distribution
Full size table
$$ {\displaystyle \begin{array}{c}F\left(\left.x\right|{x}_m,{x}_u,k,{n}_1,{n}_2\right)=\exp \left[-k\frac{{\left({x}_m-x\right)}^{n_1}}{{\left(x-{x}_u\right)}^{n_2}}\right],\dots {x}_u\le x\le {x}_m,\\ {}F(x)=0\dots x<{x}_u\dots \dots F(x)=1\dots x>{x}_m,\end{array}} $$
(8)

and the density function

$$ f\left(\left.x\right|{x}_m,{x}_u,k,{n}_1,{n}_2\right)=k\frac{\frac{n_1{\left({x}_m-x\right)}^{n_1-1}}{{\left(x-{x}_u\right)}^{n_2}}+\frac{n_2{\left({x}_m-x\right)}^{n_1}}{{\left(x-{x}_u\right)}^{n_2+1}}}{\exp \left[k\frac{{\left({x}_m-x\right)}^{n_1}}{{\left(x-{x}_u\right)}^{n_2}}\right]}. $$
(9)

Distribution function (8) includes five parameters. The parameters xu and xm have a physical meaning — they are the minimum and maximum possible values of strength. Along with, for example, the average value, these are parameters of the general population. They may or may not appear in the experimentally obtained sample; therefore, another method for their determination is required. The quantities k , n1 , and n2 are adjustment parameters. The MSP was also used to estimate the distribution parameters of (8). The results of processing experimental data are shown in Table 2.

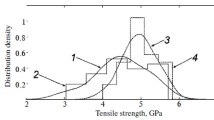
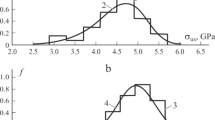
Table 2 Distribution Parameters of (8)
Full size table

As pertains, the minimum values the results for filaments are quite consistent with the results given in Table 1. For threads, the increase in the minimum value is 34.11%, which exceeds the 30.04% increase in the average value. For filaments, the increase in the minimum value is 21.41%, which by 9.76% exceeds the increase in the average value. The increase in the maximum possible value for threads is 21.48% and for the filaments — 4.39%, which is less than the increase in the corresponding average values. The histograms of experimental data and the corresponding distribution density functions calculated for the parameter values from Tables 1 and 2 are shown in Fig. 1. It is clearly seen that the share of results in the range of small values has significantly decreased.

Fig. 1
figure 1

Histograms of experimental data in relation to distribution density functions: 1-3 — processing of experimental data for the strength of original filaments; 4-6 — filaments treated with CNTs; 1 — histogram, 2 — distribution density according to Eq. (2) ( xu = 2.6305, a = 2.1749, and b = 4.1005); 3 — distribution density according to Eq. (9) ( xu = 2.8954, xm = 6.4104, k = 0.0192, n1 = 5.4969, and n2 = –0.7928); 4 — histogram, 5 — distribution density according to Eq. (2) ( xu = 3.4247, a = 1.7094, and b = 4.1628); 6 — distribution density according to Eq. (9) (xu = 3.5152, xm = 6.6917, k = 0.0437, n1 = 5.1401, and n2 = –0.6442).

Full size image

As the most important practical result of this work, apparently, it should be considered the fact that, when modifying an aramid fiber using an aqueous suspension of CNTs, the minimum values of strength, characterizing the general population, from which the sample is extracted and which are actually the characteristic point of the onset of fracture, increase to a greater extent. than the average strength.