Introduction.

Delamination [1] is one of the most dangerous and difficult to control types of damage in layered polymer composite materials (PCMs). That is why the occurrence and growth of delaminations in PCMs arouses interest of many authors.

It is known [2] that studies of the dominating fracture mode at the beginning and growth of delamination are focused on the mechanics of interlaminar fracture, within the framework of which it is required to determine, first of all, the change in the deformation energy per unit area of delamination increment. This parameter, G , is called the elastic energy release rate at the top of a crack. In order to clear up whether the delamination will grow or not at a static loading, the calculated values of G are compared with its critical values Gc . As a rule, considered are three fracture modes: mode I (opening mode), mode II (shearing mode), and mode III (tearing mode). Modes I and II are considered the most critical ones, and, therefore, the greatest attention in the development of calculation and test methods is focused exactly on them [3, 4]. Such an approach requires both computer modeling and determ ination of experimental characteristics.

Another approach consists in estimating the growth of delaminations in cyclic (fatigue) loadings. In [3, 4], equations for estimating the delamination growth rate are presented for different fracture modes. In [4], the following equation for this rate is given in the case of the mixed (I+II) fracture mode:

$$ \frac{dL}{dN}={m}_1{\left(\frac{G_I}{G_{Ic}}\right)}^{n_1}+{m}_2{\left(\frac{G_{II}}{G_{II c}}\right)}^{n_2}, $$
(1)

where \( \frac{dL}{dN} \) is the delamination growth rate in one fatigue loading cycle; GI and GII are the elastic energy release rates

in modes I and II, respectively, but GIc and GIIc are their critical values — the characteristic fracture resistances (they are determined experimentally and, as a rule, are smaller than GIc (GIIc) in static loadings); m1, m2 , n1, and n2 are material constants.

Thus, to calculate the delamination growth rate by Eq. (1), at least six parameters have to be determined experimentally.

According to [2], the procedure for estimating the delamination growth rate with the use of Eq. (1) consists of two stages.

In the first stage, the relation between the elastic energy release rates GI and GII and the delamination length L at a given stress or strain has to be found. For the initial length of a delamination, the critical values of GIc and GIIc are determined. They are compared with material delamination properties, and the number of loading cycles for initiation of the delamination is determined.

In the second stage, for some increment of the number of loading cycles, new values of GI and GII and the delamination growth rate dL / dN are determined. This process is continued until the delamination reaches the critical length at a certain number of loading cycles before the final fracture of specimen.

An analysis of this procedure for estimating the delamination growth with use of Eq. (1) reveals that it is rather complicated and requires a significant volume of preliminary experimental research, which casts some doubt on the prospects of wide use of this procedure for engineering estimations of the beginning and duration of a delamination in layered materials.

It is also necessary to note that this procedure is practically unsuitable for engineering estimations of delamination growth in layered PCMs at their cyclic tension. At the same time, it is known that such loadings and fracture modes are rather widespread and therefore deserve a separate consideratio n and analysis.

1. Physical model for delamination growth at cyclic tension of layered composites

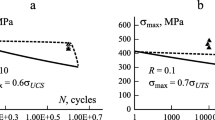
In [5,6,7], the basic propositions of the model of damage growth at cyclic loadings of layered PCMs are presented, which differ greatly from the methods of linear mechanics of interlaminar fracture described in the Introduction. In [8], as one of special cases of this model, the basics of physical modeling of delamination growth in layered PCMs at cyclic tension are presented. An illustration of the delamination mode at such a loading is given on Fig. 1. According to the data of works [5,6,7,8], the basic features of physically modeling delamination growth are as follows.

Fig. 1
figure 1

Delamination modes at tension of layered PCMs: a) — a laminate without delamination; b) — full debonding; c) — partial debonding.

Full size image

The delamination parameter D is introduced as the normalized delamination area A / A0 , where A is the actual (measured) delamination area and A0 is the total area accessible to delamination.

It is assumed that there exists a relation between the parameter D and elastic (Young’s) modulus that can be written as

$$ E={E}_0g(D), $$
(2)

where E is the current elastic modulus, E0 is the initial value of the modulus (of the intact material), and g(D) is some function.

A simple model for an estimating the decreased elastic modulus E on delamination growth is proposed, namely,

$$ E={E}_0+\left({E}^{\ast }-{E}_0\right)\frac{A}{A_0}, $$

where E* is the elastic modulus corresponding to the full delamination of composite. By processing the experimental data given in [9], it was found that E / E0 = 0.65 at A / A 0= 1 .

Thus, the function g(D) in Eq. (2) can be written as

$$ g(D)=1-0.35D $$

from which it follows that

$$ D=2.857\left(1-\frac{E}{E_0}\right) $$

and

$$ \frac{dD}{dN}=-2.857\left(\frac{1}{E_0}\frac{dE}{dN}\right). $$

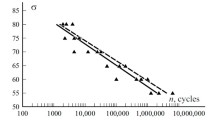
On Fig. 2, experimental data are given for the equation

$$ \frac{dD}{dN}=-2.857\left(\frac{1}{E_0}\frac{dE}{dN}\right)=f\left(\frac{\varDelta \sigma}{\sigma_{UTS}}\right). $$
(3)
Fig. 2
figure 2

Approximation of experimental data (dots) on the growth rate of delamination in the laminate considered (data of work [9]) by Eq. (4).

Full size image

In the case of laminate made of a [45/90/-45/0]S quasi-isotropic XAS/914 carbon plastic and subjected to a cyclic tension with R = 0.1, where σUTS = 550 MPa is its strength (data of [9]). Here, an example of approximation of these experimental data performed in [9] with use of the equation

$$ \frac{dD}{dN}=9.2\cdot {10}^{-5}{\left(\frac{\varDelta \sigma}{\sigma_{UTS}}\right)}^{6.4}, $$
(4)

similar in form to the known Paris equation, is also shown. The data of Fig. 2 demonstrate that the approximation of experimental data by Eq. (4) at small and great values of the parameter ∆σ / σUTS cannot be considered good enough — the discrepancy between calculations and experimental data is too great.

It is known that many researchers run into similar problems when using the Paris equation to estimate the growth rates of cracks in metal materials. It is also known that, in similar cases, instead of Paris equation, it is recommended to apply the Collipriest equation [10], which, for a cyclic loading with R = 0, can be written as

$$ \frac{da}{dN}={C}_K{\left(\frac{\log \frac{\varDelta K}{K_{th}}}{\log \frac{K_c}{\varDelta K}}\right)}^n, $$
(5)

where ∆K is the total amplitude of the stress intensity factor (SIF); Kc is the conditional critical value of SIF; Kth is the threshold (minimum) value of ∆K; CK and n are material-dependent empirical constants.

As the experience of practical application of Eq. (5) to metal materials shows, the introduction of the parameters Kc and Kth into this equation considerably raises the approximation reliability of experimental data on crack growth rates in the ranges of small and great values of SIF. Therefore, to increase the approximation reliability of the experimental data shown on Fig. 2, it is proposed to use Eq. (5) for the layered PCM considered.

Let us introduce a parameter \( \varDelta \overline{\sigma}=\frac{\varDelta \sigma}{\varDelta_{UTS}}. \) as

This parameter can be named the relative total amplitude of cyclic tensile stresses in delamination of a layered composite.

A repeated analysis of experimental data in Fig. 2 allows us to assume that they can be approximated by the equation

$$ \frac{dD}{dN}=C{\left(\frac{\log \frac{\varDelta \overline{\sigma}}{{\overline{\sigma}}_{th}}}{\log \frac{{\overline{\sigma}}_c}{\varDelta \overline{\sigma}}}\right)}^m, $$
(6)

where C , m , \( {\overline{\sigma}}_c \) , and \( {\overline{\sigma}}_{th} \) are the empirical constants dependent on the type and properties of the layered PCM.

Thus, if the empirical constants C , m , \( {\overline{\sigma}}_c \) , and \( {\overline{\sigma}}_{th} \) are known, then, to each value of \( \varDelta \overline{\sigma} \) there corresponds a certain delamination rate dD / dN , and the duration of delamination growth is found as

$$ {N}_f=A\underset{D_i}{\overset{D_f}{\int }} dD, $$
(7)

where Di and Df are the initial and final, respectively, delamination size; the parameter A is determined as

$$ A=\left(1/C\right){\left(\frac{\log \frac{\varDelta \overline{\sigma}}{{\overline{\sigma}}_{th}}}{\log \frac{{\overline{\sigma}}_c}{\varDelta \overline{\sigma}}}\right)}^{-m}. $$

From the results of Fig. 2 data processing, the empirical constants C , m , \( {\overline{\sigma}}_c \) , and \( {\overline{\sigma}}_{th} \) for Eq. (6) were found:

$$ {\overline{\sigma}}_{th}=\varDelta {\sigma}_{th}/{\sigma}_{UTS}=220/550=0.4, $$

where ∆σth = 220 MPa is the total stress amplitude at which the delamination rate is minimum,

$$ {\overline{\sigma}}_c=\varDelta {\sigma}_c/{\sigma}_{UTS}=510/550=0.927, $$

where ∆σc = 510 MPa is the total stress amplitude at which the delamination rate is maximum,

$$ C\approx 3.5\cdot {10}^{-6}\mathrm{and}\ m\approx 1.6 $$

On Fig. 3, the experimental data given in [9] and graphic relation for the laminate considered are shown together with relation (4) for comparison. Comparing Eqs. (4) and (6), it can be concluded that, in the ranges of small and great values of the parameter ∆σ / σUTS , the approximation reliability of experimental data by Eq. (6) is higher than by Eq. (4).

Fig. 3
figure 3

Approximation of experimental data (■) on the growth rate of delamination in the laminate considered by Eqs. (6) (––––) and (4) (– – –).

Full size image

In [9], the following relation, which can be used to estimate the duration of delamination growth in the case considered, was obtained:

$$ {N}_f=3.1\cdot {10}^4{\left(\frac{\varDelta \sigma}{\sigma_{UTS}}\right)}^{-6.4}\left(1-\frac{\varDelta \sigma}{0.9{\sigma}_{UTS}}\right). $$
(8)

On Fig. 4, S–N curves for the duration of delamination growth, constructed as trend lines of calculation data found using Eqs. (7) and (8), are presented. In calculations, it was assumed that Di = 0 and Df = 1 . Here, the results of experimental studies [9] into the duration of delamination growth in the same laminate are also presented.

Fig. 4
figure 4

S–N curves of duration of delamination growth in the laminate considered: experimental (×) and calculated by relations (7) (––––, ♦) and (8) (– – –, ▲).

Full size image

2. Discussion of results

Based on an analysis of Fig. 3 data, it can be asserted that, from the physical point of view, Eq. (6) in the form of the known Collipriest equation approximates experimental data on the delamination growth rate in the layered PCMs considered with a greater reliability than Eq. (4), which is su ggested in work [9] in the form of Paris equation.

Integrating Eq. (6), relation (7) for constructing the S–N curve of duration of delamination growth in PCMs under the conditions of cyclic loading considered were obtained. Taking into account the significant scatter of experimental data on the duration of delamination growth typical of layered PCMs, it is difficult to expect a highly accurate estimates by using S–N curves. Nevertheless, it can be asserted that, in the example considered, with the use of Eq. (6) and the S–N curve constructed on the basis of relation (7), reasonably accurate results were found, which were slightly more accurate than those obtained using relations (4) and (8) of work [9].

Let us note some basic features of the results found.

It is known that the use of Paris equation to calculate the duration of crack growth in metal materials rather frequently leads to overestimated estimates at high values of ∆K and to underestimated ones at low values of ∆K. These drawbacks can be eliminated using Collipriest equation (5) containing the parameters Kc and Kth , adjusting the kinetic diagram of fatigue failure in the ranges of high and low values of ∆K.

Comparing the S–N curves calculated on the basis of Eqs. (7) and (8) and using experimental data for the layered PCMs considered, which are shown on Fig. 4, similar features can be observed when Eqs. (4) and (6) in the form of Paris and Collipriest equations, respectively, were used. Thus, it can be stated that Eq. (6) in the form of Collipriest equation raises the accuracy of calculated estimates for the duration of delamination growth in the ranges of high and low stresses.

Conclusion

The basic features of physically modeling the delamination growth in layered PCMs in cyclic tension outlined in work [8] have been reported. It is noted, that these features significantly differ from propositions of the classical mechanics of interlaminar fracture of PCMs.

Within the framework of the model submitted for estimating the growth rate of delaminations at tension of layered PCMs, an equation in the form of the known Collipriest equation widely used at an estimation of growth rates of cracks in metal designs is offered.

By the example of processing experimental data on the delamination growth rate in a laminate from a quasiisotropic [45/90/–45/0]S XAS/914 carbon plastic at cyclic tension with R = 0.1, it is shown, that, with the use of the equation suggested, a high enough level of approximation reliab ility of experimental data can be achieved.

Integrating the equation suggested, a relation for constructing the S–N curve of delamination growth is obtained.

The calculated S–N curve is compared with known experimental data. It is concluded that, in the example considered, with use of Eq. (6) in the form of Collipriest equation, results of acceptable accuracy were found. These results are important for a better understanding of the process of dela mination growth in layered PCMs subjected to tension.

As a recommendation for the further research, it is necessary to for a more comprehensively verify the equations and relations offered.