Mathematical modeling and methods of analysis of generalized functionally gradient porous nanobeams and nanoplates subjected to temperature field

Abstract

Mathematical models of size-dependent porous Bernoulli–Euler nanobeams and Kirchhoff nanoplates subjected to temperature are derived. Temperature interaction is governed by a 3D (2D) heat conduction equation. And for advancements, it has been deemed necessary to find the most accurate and efficient computational technique for the application of the plates and beams materials. Thus, the Navier (NM), Bubnov–Galerkin (BGM), Kantorovich–Vlasov (KVM), Vaindiner (VaM), variational iteration (VIM) methods, as well as the finite difference method (FDM) of the second-order of accuracy, and the finite element method (FEM) are employed. We aim to investigate the convergence of these methods, depending on the size-dependent factors for the mentioned porous composite nanostructures located in the temperature field. There are no restrictions on the distribution of the temperature field interacting with nanobeams/nanoplates. The results show through the numerical and analytical solutions that KVM, VIM, and a combination of VIM and VaM are superior techniques, as they provide a higher level of accuracy and less computational time. In comparing their results to the exact solution, the difference is less than 1.2%. Thus, when studying the stress–strain state of porous nanoplates/nanobeams, preference should be given to these methods. It means that our results may have a challenging impact on the classical computational methods mainly based on FEM and FDM.

1 Introduction

Functionally graded materials (FGMs) remain one of the most attractive objects of scientific research around the world. They have been studied by authors in a number of publications (see [1,2,3] and references therein). In FGMs, the properties change in a particular direction in order to achieve required properties such as high mechanical strength, corrosion resistance, and application at high temperatures [4]. Our study is motivated by the fact that porous functionally graded (FG) micro/nanostructures (such as micro/nanofilms, micro/nanoplates, micro/nanobeams) have tremendous application potential in micro/nanoelectromechanics, micro/nanoelectronics, physics, and biology. Porous materials are used while fabricating various nanoelectromechanical systems (NEMS) and microelectromechanical systems (MEMS) [5, 6]. As a rule, FGMs are applied in flow thermal barrier systems, so a clear understanding of the mechanical behavior of FGM structures under thermal loads is essential for their optimal design.

As it is well known and documented, the classical continuum theories cannot describe the mechanical behavior of micro-/nano-sized structures. However, a few theories accounting for the various size-dependent effects have been recently developed, for example, Eringen's nonlocal theory [7], strain gradient theory [8], modified couple stress theory [9], etc.

We limit our studied literature to those works most directly related to our study. Thus, the review below covers only works dealing with beams and plates made of porous functionally gradient materials being embedded into a temperature field and in a linear formulation and the methods of their solutions.

Genao et al. [10] analyzed quasi-static bending behavior of FG porous microplates using a nonlinear FM model based on the general third-order plate theory. The FE model accounts for the von Kármán nonlinearity, the micro-structural size effects, material property variations with three types of porosity distributions, and temperature-dependent material properties. The micro-structural size-dependent effect was captured using the length scale parameter of the modified couple stress theory. Cong et al. [11] investigated the buckling and post-buckling behavior of an FGM porous plate resting on elastic foundations and subjected to thermomechanical loads. The Galerkin method was used to find a closed-form solution with buckling loads and post-buckling equilibrium paths for simply supported plates. Karami et al. [12] adopted the size-dependent analytical model to assess the influence of temperature distribution, material composition, porosity, and the phase velocities of an FG nanoplate. The properties of the material were described by a power function and depended on a single coordinate. The temperature was a function of only one coordinate and was estimated by the solution to a 1D heat conduction equation. The problem was solved analytically, based on the strong truncation, i.e., a system with one degree-of-freedom was considered. Fana et al. [13] studied the geometrically nonlinear vibrations of microplates with/without a central cutout made of a porous functionally graded material (PFGM) while incorporating the couple stress type of size dependency. To this end, a new power-law function was employed that could simultaneously match the effects of material gradient and porosity. Ghobadi et al. [14] studied the static and dynamic responses of the sandwich functionally graded porous flexoelectric nanoplate under electrical and thermal loadings, using the modified flexoelectric theory and the Kirchhoff's classical plate theory. Using Galerkin's method, the nonlinear partial differential equations (PDEs) were converted to nonlinear coupled ordinary differential equations (ODEs). Akbaş [15] investigated the thermal effects on the free vibration of functionally graded porous deep beams. Mechanical properties of the FG beams were temperature-dependent and varied across the height direction with different porosity models. The problem was solved in a linear formulation with the help of the piecewise solid continua model, and FEM was adopted to get the computational results. Moreover, the temperature field was taken into account, but a heat conduction equation was not solved. Arshid et al. [16] investigated the buckling and bending of the annular/circular micro sandwich plate with its core made of saturated porous materials (two functionally graded piezo-electro-magnetic polymeric nanocomposite layers were located on its top and bottom). The temperature was set by a certain value, but the heat conduction equation was not solved. The properties of the layers were temperature-dependent and were varied through the thickness following the given functions. The equations were solved via the method of generalized differential quadrature for various boundary conditions. Bamdad et al. [17] presented the analysis of vibration and loss of stability of a magneto-electro-elastic multilayer Timoshenko beam with a porous core. The properties of the material depended on temperature. The pore types were set by a trigonometric function. The temperature field was known, but the heat conduction equation was not solved. She et al. [18] and Ebrahimi [19] investigated the vibrational properties of porous nanobeams. The theory of the nonlocal deformation gradient in combination with a refined beam model was adopted to formulate a size-dependent model. The governing equations were derived on the basis of Hamilton's variational principle and were solved by the trigonometric series method. The influence of the nonlocal parameter, the deformation gradient parameter, temperature changes, the volume fraction of porosity, and material changes on the vibration characteristics of nanotubes was studied. However, the heat conduction equation was not solved, and the temperature field was a priori set. Hamed et al. [20] analyzed the mechanical bending behavior of functionally graded porous nanobeams. A comparison between four types of porosity was illustrated. The effect of nanoscale was described by the Eringen's differential nonlocal continuum theory. The mathematical model was solved numerically using the FEM. Ebrahimi and Jafari [21] presented a thermo-mechanical vibration analysis of a porous functionally graded Timoshenko beam in a thermal environment by employing a semi-analytical differential transform method (DTM) combined with a Navier type method. Two types of thermal loadings, i.e., the uniform and the linear temperatures rising through the beam's thickness, were considered. The mathematical model was solved numerically using FEM. Shahverdi et al. [22] performed vibration analysis of porous functional gradient nanoplates, and the model included two scale parameters. Porosity-dependent material properties of the nanoplate were determined via a modified power-law function and through the Mori–Tanaka model. The PDEs were solved for hinged nanoplates via Galerkin's method in the first approximation.

Ebrahimi and Jafari [23] proposed the theory of beams with four alternate shift deformations for thermomechanical vibration characteristics of porous, functionally modified beams exposed to various types of thermal loads via analytical approaches. Four types of thermal load: uniform, linear, nonlinear, and sinusoidal temperature growth in the direction of the z-axis were investigated. The influence of the degree index, volume fraction of porosity, different porosity distribution, and thermal effect on the vibration of porous beams FG was analyzed. Ghadiri et al. [24] studied the free vibration of a functionally graded porous cylindrical microshell subjected to a thermal environment on the basis of the first-order shear deformation and the modified couple stress theory. The material properties were considered temperature-dependent. Ebrahimi and Jafari [25] investigated the thermomechanical vibration characteristics of functionally graded Reddy's beams made from porous material subjected to various thermal loads using the analytical Navier's method. Again, four types of heat loads were considered: uniform, linear, nonlinear, and sinusoidal temperature rise in the direction of thickness. It was assumed that the thermomechanical properties of the FG beam material were temperature-dependent and varied with the direction of the thickness. Awrejcewicz et al. [26] investigated the chaotic dynamics of microbeams made of functionally graded materials taking into account the modified couple stress theory and von Kármán geometric nonlinearity. The beam properties changed along the thickness direction. The influence of size-dependent and functionally graded coefficients on the vibration characteristics, as well as the scenarios of transition from regular to chaotic vibrations were studied. Awrejcewicz et al. [27] examined the size-dependent model based on the modified couple stress theory for the geometrically nonlinear curvilinear Timoshenko beam made from functionally graded material properties. The influence of the size-dependent coefficient and the material grading on the stability of the curvilinear beams were investigated based on the setup method. The FDM of the second-order accuracy was adopted to solve the problem. Stability loss of the curvilinear Timoshenko beams was analyzed using the Lyapunov criterion based on the estimation of the Lyapunov exponents. Awrejcewicz et al. [28] presented a comprehensive review of literature on reducing nonlinear PDEs to a set of nonlinear ODEs, emphasizing their reliability, validity, accuracy, and computational efficiency. The following methods were reviewed and examined due to their state-of-the-art levels of performance and computational advantages: the Fourier methods, the Navier's method of double trigonometric series, the Galerkin- type methods, the variational methods, the variational iterational methods, the Kantorovich-Vlasov method [30, 31], the variational iterations method [32,33,34], the Vaindiner's method [35], the Agranovskii-Baglai-Smirnov method [36] with respect to the archetypal finite element and finite difference methods. The comparisons of the tested approaches (mentioned above) were carried out based on the modified Germain-Lagrange partial differential equations governing the dynamics of a nanoplate and in contrast to the exact results obtained based on the Navier's method.

The literature survey shows that when analyzing porous functionally gradient nanobeams and nanoplates located in a temperature field, in majority of the cases, the heat conduction equations were not solved and involved the temperature function depended only on one coordinate. Moreover, the solutions were mainly obtained by only one method, which was not satisfactorily validated. Basically, the technique of double trigonometric series was used in the analysis of the beams' problem. The porosity distribution of the material was studied only along the thickness of either beam or plate. Furthermore, the reported investigations included only one kind of boundary condition. The types of porosity of the material were taken into account in a limited way.

In contrast, the present work allows us to define the temperature field for beams and plates from the solution of 2D and 3D heat conduction PDEs solved by the finite element method while investigating the convergence of the solution. For the first time, a theory is proposed for the study of functionally gradient porous nanostructures, when the type of porosity varies in thickness and volume of a beam/plate. Furthermore, the properties of the porous medium materials depend on temperature. In addition, the solutions obtained are reliable since the problems were solved by different analytical, analytical–numerical, and numerical methods. Exact solutions of porous structures (nanoplates) located in a temperature field are obtained using the Navier's method.

For the first time, we addressed the problems dealing with methods of reducing PDEs to ODEs (the Kantorovich-Vlasov methods, the variational iterations method, the Vaindiner's method, the finite differences method) while solving equations governing the behavior of porous nanobeams and nanoplates. The convergence of the considered methods is investigated. It is found that the employed methods of reduction of nonlinear PDEs to ODEs are efficient, possess high-precision, and require much less computation time compared to the FEM or FDM. The latter observation may introduce a novel computational trend while solving nonlinear PDEs describing the static behavior of nanobeams and nanoplates.

The method of variational iterations developed in this work (often this method in the literature is called the generalized Kantorovich–Vlasov method [37, 38]) is used to analyze r-shaped (L-shaped) and polygonal plates for problems of dynamics.

For porous materials, there is no analysis of experimental, analytical, and numerical comparison results in the literature known to us. To analyze the free oscillations of full-sized square clamped and hinged-supported plates, the experiment was carried out in [39]. In thie latter study, a whole-field technique called amplitude-fluctuation electronic speckle pattern interferometry optical system is employed to investigate the vibration behaviour of square isotropic plates with different boundary conditions. A speckle-interferometric optical system with an amplitude-fluctuation electronic speckle structure used to study the vibrational behavior of isotropic plates was carried out. This method is very convenient to investigate vibration objects because no contact is required compared to classical modal analysis using accelerometers. High-quality interferometric fringes for mode shapes are produced instantly by a video recording system. For the finite element method, the differences with experiment are 1.9–4.9% for pinching, depending on the first to 12 modes, for hinged support 3.1% and 2.5% for the same modes [39]. These results were compared with results obtained by finite element methods and the general Kantorovich method [40]. The solution obtained using the ANSYS software package and the solution using variational iterations (the generalized Kantorovich method) almost completely coincided, but the solution obtained via the ANSYS software package required 10,201 finite elements.

The paper is organized in the following way. In Sect. 2, the mathematical models of the functionally graded nanoplates are developed. Solutions to the equations governing the static behavior of porous nanoplates subjected to 3D temperature fields are presented and discussed. Numerical results regarding nanoplates are reported in Sect. 4. Section 5 deals with the mathematical modeling of functionally graded nanobeams subjected to temperature field where the numerical results are reported and discussed. The final section includes concluding remarks.

2 Mathematical model of FG nanoplates

Consider an elastic, isotropic, inhomogeneous rectangular nanoplate with dimensions a, b, ℎ along the x, y, z axes, respectively (Fig. 1). Porosities in the plate may appear in FGMs as a result of the manufacturing process. We assume that the FG plate material is porous. The porosity distributions in FG plates can be modeled using various functions (exponential, trigonometric). Porosity is distributed along the plate's thickness and surface, while the Young's modulus E = E(x, y, z) and the Poisson's ratio $\nu = \nu (x,y,z)$ are the functions of the variables (x, y, z). The origin of coordinates is located in the upper left corner of the plate in its middle surface, whereas the x, y axes are parallel to the sides of the plate, and the z axis is directed down (see Fig. 1).

Fig. 1

The investigated plate

In the given coordinate system, the plate is treated as a 3D object, with Ω defined as follows: $\Omega = \{ x,y,z/(x,y,z) \in [0,a] \times [0,b] \times [ - h/2,h/2]\}$. The plate middle surface $z=0$ is defined by $\Gamma = \left\{ {x,y/\left( {x, y} \right) \in \left[ {0,a} \right] \times \left[ {0,b} \right]} \right\}$.

We denote plate displacements along the axes x, y, z by u, v, w respectively, where the plate deflection $w = w\left( {x,y} \right)$. All components of the displacement are assumed to be essentially smaller than the characteristic plate dimension.

In the modified couple stress theory [9], the summed energy of deformation U of an elastic body of space is governed by the following formula (it differs from the classic formula only with underlined terms)

$$ U = \frac{1}{2}\int\limits_{\Omega } {\left( {\sigma_{xx} \varepsilon_{xx} + \sigma_{yy} \varepsilon_{yy} + \sigma_{xy} \varepsilon_{xy} + \underline{{m_{xx} \chi_{xx} + m_{yy} \chi_{yy} + m_{xy} \chi_{xy} }} } \right)\,d\Omega } $$

(1)

where $\sigma_{xx} ,\sigma_{yy} , \sigma_{xy}$ denote the Cartesian components of the stress tensor; $\varepsilon_{xx} ,\varepsilon_{yy} , \varepsilon_{xy}$ are the strain components; $m_{xx} ,m_{yy} , m_{xy}$ are the components of the deviatoric part of the symmetric couple stress tensor; $\chi_{xx} , \chi_{yy} , \chi_{xy}$ are the components of the symmetric curvature tensor.

Owing to the Kirchhoff hypothesis, the following relations between the deformations in the plate middle surface $\varepsilon_{xx} ,\varepsilon_{yy} , \varepsilon_{xy}$ and displacements hold:

$$ \varepsilon_{xx} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }},\quad \varepsilon_{yy} = - z\frac{{\partial^{2} w}}{{\partial y^{2} }},\quad \varepsilon_{xy} = - 2z\frac{{\partial^{2} w}}{\partial x\partial y}. $$

(2)

The non-zeroth components of the symmetric curvature tensor are as follows

$$ \chi_{xx} = \frac{{\partial^{2} w}}{\partial x\partial y},\quad \chi_{yy} = - \frac{{\partial^{2} w}}{\partial x\partial y},\quad \chi_{xy} = \frac{1}{2}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right). $$

(3)

For a linear isotropic elastic material, the stresses imposed by kinematic parameters appearing in the equation for the density of deformation energy are defined by the following state equations [9]

$$ \begin{aligned} \sigma_{xx} & = \left( {\lambda + 2\mu } \right)\varepsilon_{xx} ,\quad \sigma_{yy} = \left( {\lambda + 2\mu } \right)\varepsilon_{yy} ,\quad \sigma_{xy} = 2\mu \varepsilon_{xy} , \\ m_{xx} & = 2\mu l^{2} \chi_{xx} ,\quad m_{yy} = 2\mu l^{2} \chi_{yy} ,\quad m_{xy} = 2\mu l^{2} \chi_{xy} , \\ \end{aligned} $$

(4)

$$ \lambda (x, \, y, \, z,e_{i} ) = \frac{E\nu }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}},\quad \mu \, (x, \, y, \, z,e_{i} ) = \frac{E}{{2\left( {1 + \nu } \right)}}, $$

(4a)

where l is the length scale parameter, and it stands for the additional length-independent material parameter coupled with the symmetric tensor of the rotation gradient; λ(x, y, z, e_i), µ(x, y, z, e_i) are the Lamè parameters; E(x, y, z) and v(x, y, z) are the Young's modulus and the Poisson coefficient, respectively; $e_{i} = \sqrt 3 /2\sqrt {\left( {\varepsilon_{xx} - \varepsilon_{yy} } \right)^{2} + \varepsilon_{yy}^{2} + \varepsilon_{xx}^{2} + 3/2 \varepsilon_{xy}^{2} }$ is the intensity of deformation.

Substitution of (2), (3), (4) into (1) yields potential energy of the system

$$ U = \frac{1}{2}\int\limits_{0}^{a} {\int\limits_{0}^{b} {\int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\left( {\lambda + 2\mu } \right)\left( { - z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} + \left( {\lambda + 2\mu } \right)\left( { - z\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)^{2} + 2\mu \left( { - z\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} + \left. {\frac{1}{2}\mu l^{2} \,\left[ { - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right]^{2} + \frac{1}{2}\mu l^{2} \,\left[ { - \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right]^{2} + \mu l^{2} \,\left[ { - \frac{{\partial^{2} w}}{\partial x\partial y}} \right]^{2} } \right\}\,dzdydx.} \right.} } } $$

(5)

The following relations are introduced

$$ \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left( {\lambda + 2\mu } \right)z^{2} \,dz} = \alpha_{1} ,\quad \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\mu z^{2} \,dz} = \alpha_{2} ,\quad \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\mu \,dz} = \alpha_{3} , $$

(6)

where $\alpha_{i} = \alpha_{i} \left( {x,y} \right)$ are the functions of coordinates and intensity of deformations. Then, the relation (5) takes the following form

$$ U = \frac{1}{2}\int\limits_{0}^{a} {\int\limits_{0}^{b} {\left\{ {\alpha_{1} \left( {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} + \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)^{2} } \right) + 2\alpha_{2} \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} + \left. {\underline{{\frac{1}{2}\alpha_{3} l^{2} \,\left( {\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right]^{2} + \,\left[ {\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right]^{2} + 2\,\left[ {\frac{{\partial^{2} w}}{\partial x\partial y}} \right]^{2} } \right)}} } \right\}\,dxdy.} \right.} } $$

(7)

The external work associated with the distributed forces has the following form

$$ \,W = \iint\limits_{\Gamma } {q\left( {x,y} \right)\,w(x,y)d\Gamma } $$

(8)

Carrying out both the variations with respect to w and the integration by parts, we get

$$ \begin{aligned} \delta U =& \iint\limits_{\Gamma } {\left\{ \begin{gathered} \alpha _{1} \frac{{\partial ^{4} w}}{{\partial x^{4} }} + 2\frac{{\partial \alpha _{1} }}{{\partial x}}\frac{{\partial ^{3} w}}{{\partial x^{3} }} + \frac{{\partial ^{2} \alpha _{1} }}{{\partial x^{2} }}\frac{{\partial ^{2} w}}{{\partial x^{2} }} + \alpha _{1} \frac{{\partial ^{4} w}}{{\partial y^{4} }} + 2\frac{{\partial \alpha _{1} }}{{\partial y}}\frac{{\partial ^{3} w}}{{\partial y^{3} }} + \frac{{\partial ^{2} \alpha _{1} }}{{\partial y^{2} }}\frac{{\partial ^{2} w}}{{\partial y^{2} }} \hfill \\ + 2\left( {\frac{{\partial ^{2} \alpha _{2} }}{{\partial x\partial y}}\frac{{\partial ^{2} w}}{{\partial x\partial y}} + \frac{{\partial \alpha _{2} }}{{\partial x}}\frac{{\partial ^{3} w}}{{\partial x\partial y^{2} }} + \frac{{\partial \alpha _{2} }}{{\partial y}}\frac{{\partial ^{3} w}}{{\partial x^{2} \partial y}} + \alpha _{2} \frac{{\partial ^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) \hfill \\ + \frac{1}{2}l^{2} \left[ \begin{gathered} \alpha _{3} \frac{{\partial ^{4} w}}{{\partial x^{4} }} + 2\frac{{\partial \alpha _{3} }}{{\partial x}}\frac{{\partial ^{3} w}}{{\partial x^{3} }} + \frac{{\partial ^{2} \alpha _{3} }}{{\partial x^{2} }}\frac{{\partial ^{2} w}}{{\partial x^{2} }} + \alpha _{3} \frac{{\partial ^{4} w}}{{\partial y^{4} }} + 2\frac{{\partial \alpha _{3} }}{{\partial y}}\frac{{\partial ^{3} w}}{{\partial y^{3} }} + \frac{{\partial ^{2} \alpha _{3} }}{{\partial y^{2} }}\frac{{\partial ^{2} w}}{{\partial y^{2} }} \hfill \\ + 2\left( {\frac{{\partial ^{2} \alpha _{3} }}{{\partial x\partial y}}\frac{{\partial ^{2} w}}{{\partial x\partial y}} + \frac{{\partial \alpha _{3} }}{{\partial x}}\frac{{\partial ^{3} w}}{{\partial x\partial y^{2} }} + \frac{{\partial \alpha _{3} }}{{\partial y}}\frac{{\partial ^{3} w}}{{\partial x^{2} \partial y}} + \alpha _{3} \frac{{\partial ^{2} w}}{{\partial x\partial y}}} \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right\}\delta w\,\,dxdy} \\ &+ \int\limits_{0}^{a} {\alpha _{1} \frac{{\partial ^{2} w}}{{\partial y^{2} }}\delta \left( {\frac{{\partial w}}{{\partial y}}} \right)|_{0}^{b} - \left( {\frac{{\partial \alpha _{1} }}{{\partial y}}\frac{{\partial ^{2} w}}{{\partial y^{2} }} + \alpha _{1} \frac{{\partial ^{3} w}}{{\partial y^{3} }}} \right)\delta \left( w \right)|_{0}^{b} - 2\left( {\frac{{\partial \alpha _{2} }}{{\partial x}}\frac{{\partial ^{2} w}}{{\partial x\partial y}} + \alpha _{2} \frac{{\partial ^{3} w}}{{\partial x^{2} \partial y}}} \right)\delta \left( w \right)|_{0}^{b} dx} \\ & + \int\limits_{0}^{b} {\alpha _{1} \frac{{\partial ^{2} w}}{{\partial x^{2} }}\delta \left( {\frac{{\partial w}}{{\partial x}}} \right)|_{0}^{a} - \left( {\frac{{\partial \alpha _{1} }}{{\partial x}}\frac{{\partial ^{2} w}}{{\partial x^{2} }} + \alpha _{1} \frac{{\partial ^{3} w}}{{\partial x^{3} }}} \right)\delta \left( w \right)|_{0}^{a} \,} - 2\left( {\frac{{\partial \alpha _{2} }}{{\partial y}}\frac{{\partial ^{2} w}}{{\partial x\partial y}} + \alpha _{2} \frac{{\partial ^{3} w}}{{\partial x\partial y^{2} }}} \right)\delta (w)|_{0}^{a} \,dy + 2\alpha _{2} \frac{{\partial ^{2} w}}{{\partial x\partial y}}\delta \left( w \right)|_{0}^{a} |_{0}^{b} , \\ \end{aligned} $$

(9)

$$ \,\delta W = \iint\limits_{\Gamma } {q\left( {x,y,t} \right)\,\delta w\,d\Gamma }. $$

(10)

Therefore, in the framework of the modified couple stress theory and variable parameters of elasticity, the PDEs governing statics of the nanoplates are as follows

$$ \left( {\alpha_{1} + \frac{1}{2}l^{2} \alpha_{3} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\left( {\alpha_{2} + \frac{1}{2}l^{2} \alpha_{3} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \left( {\alpha_{1} + \frac{1}{2}l^{2} \alpha_{3} } \right)\frac{{\partial^{4} w}}{{\partial y^{4} }} + 2\left( {\frac{{\partial \alpha_{1} }}{\partial x} + \frac{1}{2}l^{2} \frac{{\partial \alpha_{3} }}{\partial x}} \right)\frac{{\partial^{3} w}}{{\partial x^{3} }} + \left( {\frac{{\partial^{2} \alpha_{1} }}{{\partial x^{2} }} + \frac{1}{2}l^{2} \frac{{\partial^{2} \alpha_{3} }}{{\partial x^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\left( {\frac{{\partial \alpha_{1} }}{\partial y} + \frac{1}{2}l^{2} \frac{{\partial \alpha_{3} }}{\partial y}} \right)\frac{{\partial^{3} w}}{{\partial y^{3} }} + \left( {\frac{{\partial^{2} \alpha_{1} }}{{\partial y^{2} }} + \frac{1}{2}l^{2} \frac{{\partial^{2} \alpha_{3} }}{{\partial y^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} + 2\left( {\frac{{\partial^{2} \alpha_{2} }}{\partial x\partial y} + \frac{1}{2}l^{2} \frac{{\partial^{2} \alpha_{3} }}{\partial x\partial y}} \right)\frac{{\partial^{2} w}}{\partial x\partial y} + 2\left( {\frac{{\partial \alpha_{2} }}{\partial x} + \frac{1}{2}l^{2} \frac{{\partial \alpha_{3} }}{\partial x}} \right)\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} + 2\left( {\frac{{\partial \alpha_{2} }}{\partial y} + \frac{1}{2}l^{2} \frac{{\partial \alpha_{3} }}{\partial y}} \right)\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} = q(x,y), $$

(11)

and the following boundary conditions (for $[0;\,b]$) are implemented

$$ \begin{gathered} \alpha _{1} \frac{{\partial ^{2} w}}{{\partial y^{2} }}|_{0}^{b} \,\, = 0\quad {\text{or}}\quad \delta \left( {\frac{{\partial w}}{{\partial y}}} \right)|_{0}^{b} = 0, \hfill \\ \left( {\frac{{\partial \alpha _{1} }}{{\partial y}}\frac{{\partial ^{2} w}}{{\partial y^{2} }} + \alpha _{1} \frac{{\partial ^{3} w}}{{\partial y^{3} }}} \right) - 2\left( {\frac{{\partial \alpha _{2} }}{{\partial x}}\frac{{\partial ^{2} w}}{{\partial x\partial y}} + \alpha _{2} \frac{{\partial ^{3} w}}{{\partial x^{2} \partial y}}} \right)\,\, + 2\alpha _{2} \frac{{\partial ^{2} w}}{{\partial x\partial y}}|_{0}^{b} = 0\quad {\text{or}}\quad \delta \left( w \right)|_{0}^{b} = 0.\, \hfill \\ \end{gathered} $$

(12)

The distributions of porosity are given respectively by three different types of porosity [13], in which the porosity and FG of the material plate are defined using the power functions: (1) uniform porosity (U-PFGM), (2) reduced porosity from the top and bottom surfaces to the center (X-PFGM), and (3) increased porosity at the top and bottom [the surfaces shown in Fig. 2 are viewed down to the center (O-PFGM)]. In addition, we will consider three patterns in which the porosity and FG of the material plate are defined using the trigonometric functions.

Fig. 2

Schematic representation of different porosity distribution patterns in nanoplate by thickness

The Poisson ratio and Young's modulus of a porous functionally graded material (PFGM) of a nanoplate associated with different porosity distributions can be described in the following ways.

• 1. U-PFGM pattern:

$$ E(z) = \left( {E_{c} - E_{m} } \right)\left( {1/2 + z/h} \right)^{k} + E_{m} - \left( {E_{c} + E_{m} } \right)\Gamma^{*} /2\,, $$

(13a)

$$ \nu (z) = \left( {\nu_{c} - \nu_{m} } \right)\left( {1/2 + z/h} \right)^{k} + \nu_{m} - \left( {\nu_{c} + \nu_{m} } \right)\Gamma^{*} /2\,, $$

(13b)

$$ \alpha_{T} (z) = \left( {\alpha_{Tc} - \alpha_{Tm} } \right)\left( {1/2 + z/h} \right)^{k} + \alpha_{Tm} - \left( {\alpha_{Tc} + \alpha_{Tm} } \right)\Gamma^{*} /2. $$

(13c)

• 2. X-PFGM pattern:

  $$ E(z) = \left( {E_{c} - E_{m} } \right)\left( {1/2 + z/h} \right)^{k} + E_{m} - \left( {E_{c} + E_{m} } \right)\left( {1/2 - \left| z \right|/h} \right)\Gamma^{*} , $$

  (14a)
  $$ \nu (z) = \left( {\nu_{c} - \nu_{m} } \right)\left( {1/2 + z/h} \right)^{k} + \nu_{m} - \left( {\nu_{c} + \nu_{m} } \right)\left( {1/2 - \left| z \right|/h} \right)^{*} , $$

  (14b)
  $$ \alpha_{T} (z) = \left( {\alpha_{Tc} - \alpha_{Tm} } \right)\left( {1/2 + z/h} \right)^{k} + \alpha_{Tm} - \left( {\alpha_{Tc} + \alpha_{Tm} } \right)\left( {1/2 - \left| z \right|/h} \right)\Gamma^{*} . $$

  (14c)

• 3. O-PFGM pattern:

  $$ E(z) = \left( {E_{c} - E_{m} } \right)\left( {1/2 + z/h} \right)^{k} + E_{m} - \left( {E_{c} + E_{m} } \right)\left| z \right|\Gamma^{*} /h, $$

  (15a)
  $$ \nu (z) = \left( {\nu_{c} - \nu_{m} } \right)\left( {1/2 + z/h} \right)^{k} + \nu_{m} - \left( {\nu_{c} + \nu_{m} } \right)\left| z \right|\Gamma^{*} /h\,, $$

  (15b)
  $$ \alpha_{T} (z) = \left( {\alpha_{Tc} - \alpha_{Tm} } \right)\left( {1/2 + z/h} \right)^{k} + \alpha_{Tm} - \left( {\alpha_{Tc} + \alpha_{Tm} } \right)\left| z \right|\Gamma^{*} /h. $$

  (15c)

Substituting relations (13a–15c) into Lame's relations (4a), from Eq. (5), we obtain the sought differential equations describing the behavior of the functionally graded porous nanoplates. In the above, Γ represents the porosity index, $\nu_{c} \,(\,\nu_{m} )$—the Poisson ratio, $E_{c} \,\,(E_{m} )$—Young's modulus and $\alpha_{Tc} \,\,(\alpha_{Tm} )$ stands for the thermal expansion coefficients associated with the ceramic and metal phases functionally graded material (FGM). In addition, $\Gamma^{*}$ is an indicator of porosity, whereas k represents the gradient index of material property. It shows the ratio of the volumetric fractions of the material (in particular, ceramics at the top and metal at the bottom). If k = 0, then no pores appear. The power coefficient k takes the values $0.2 \le k \le 5,$ whereas $E_{c} = 210\;{\text{GPa}},$ $E_{m} = 70\;{\text{GPa}},$ $\nu_{c} = 0.24,$ $\nu_{m} = 0.35,\;\alpha_{Tc} = 23 \cdot 10^{ - 6} 1/{^\circ }{\text{C,}}\;\alpha_{Tm} = 24 \cdot 10^{ - 6} 1/{^\circ }{\text{C}}$, and we fixed $\Gamma^{*} = 0.4,$ $k = 1$ while carrying the numerical simulation.

Let the material properties of nanoplate such as the Poisson's ratio, Young's modulus, and thermal expansion coefficients be defined by using the following equations

$$ E(z) = \left[ {E_{c} + \left( {E_{m} - E_{c} } \right)\left( {1/2 + z/h} \right)^{n} } \right]\left[ {1 - \psi_{i} (z)} \right], $$

(16a)

$$ \nu (z) = \left[ {\nu_{c} + \left( {\nu_{m} - \nu_{c} } \right)\left( {1/2 + z/h} \right)^{n} } \right]\left[ {1 - \psi_{i} (z)} \right], $$

(16b)

$$ \alpha_{T} (z) = \left[ {\alpha_{Tc} + \left( {\alpha_{Tm} - \alpha_{Tc} } \right)\left( {1/2 + z/h} \right)^{n} } \right]\left[ {1 - \psi_{i} (z)} \right], $$

(16c)

where $\psi_{i} (z)$ is a porosity distribution function.

In this study, the latter functions are classified into three different types [41, 42]:

$$ {\text{Type}}\;1:\;\psi_{1} (z) = K\cos \left[ {\pi z/h} \right]; $$

(17a)

$$ {\text{Type}}\;2:\;\psi_{2} (z) = K\cos \left[ {\left( {\pi /2} \right)(z/h + 1/2)} \right]; $$

(17b)

$$ {\text{Type}}\;3:\;\psi_{3} (z) = K\cos \left[ {\left( {\pi /2} \right)(z/h - 1/2)} \right]. $$

(17c)

Type 1 corresponds to the location of symmetric porosity with respect to the midplane of plates. Type 2(3) stands for the porosity distributions enhanced on the bottom (top) surface. Figure 3 shows the types of porosity distribution along the plate thickness made of the FGMs.

Fig. 3

Three types of porosity distribution

In what follows, we consider the special case when the Young's modulus E = E(z) and the Poisson ratio $\nu = \nu (z)$ are functions only of the thickness variable z. Consequently, the Lamé parameters also depend on the variable z, i.e., we have

$$ \lambda \left( z \right) = \frac{E\left( z \right)\nu \left( z \right)}{{\left( {1 + \nu \left( z \right)} \right)\left( {1 - 2\,\nu \left( z \right)} \right)}},\quad \quad \mu \left( z \right) = \frac{E\left( z \right)}{{2\left( {1 + \nu \left( z \right)} \right)}}. $$

For a linear isotropic elastic material, with an account of (11), the following PDE governing behavior of functionally graded porous nanoplates is considered

$$ \left( {D_{1} \frac{{\partial^{4} w}}{{\partial x^{4} }} + D_{2} 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + D_{1} \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) = q, $$

(18)

where $D_{1} = \alpha_{1} + \frac{1}{2}l_{{}}^{2} \alpha_{3} ,\,\,\,\,D_{2} = \alpha_{2} + \frac{1}{2}l_{{}}^{2} \alpha_{3}$.

The following boundary conditions are applied:

• 1. simple support

$$ w\left| {_{\Gamma } = 0,} \right.\quad \left. {\frac{{\partial^{2} w}}{{\partial n^{2} }}} \right|_{\Gamma } = 0, $$

(19)

• 2. rigid clamping

  $$ w\left| {_{\Gamma } = 0,} \right.\quad \left. {\frac{\partial w}{{\partial n}}} \right|_{\Gamma } = 0, $$

  (20)

  where n is the normal to the boundary $\Gamma$ of the median plane of the plate.

The temperature components $E(z,T),$ $\alpha_{T} (z)$ must be taken into account according to the Duhamel–Neumann law. Then, the governing PDE takes the following form

$$ \left( {D_{1} \frac{1}{{\lambda^{2} }}\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2D_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + D_{1} \lambda^{2} \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) = \tilde{q}, $$

(21)

where $\tilde{q} = q - \Delta \left( {M_{T} } \right)$, $M_{T} = 2\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\frac{1}{(1 - v(z))}\alpha_{T} (z)E(z)\Delta T(x,y,z)zdz}$, $\alpha_{T} (z)$ stands for the thermal expansion coefficient, $T_{0} (x,y,z)$ is the environmental temperature, $\Delta T(x,y,z) = T(x,y,z) - T_{0} (x,y,z)$, where $T(x,y,z)$ is the temperature field determined from the solution of the 3D heat conduction Eq. (22) estimated with the help of the FEM.

The 3D conduction PDE also known as the Laplace equation, takes the following form

$$ \frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }} = 0. $$

(22)

Four types of boundary conditions are considered.

• 1. The first type of boundary conditions (Dirichlet problem).

The boundary conditions are taken in the form

$$ T\left| {_{\Gamma } = T_{w} (x,y,z)} \right., $$

(23)

where $T_{w} (x,y,z)$ is given, $\Gamma = \{ x,y,z/\left( {x, y,z} \right) \in \left[ {0,a} \right] \times \left[ {0,b} \right] \times \left[ { - h/2,h/2} \right]$.

• 2. The second type of boundary conditions (Neumann problem).

Here the value of the gradient of heat flow $q\left| {_{\Gamma } = q_{w} (x,y,z)} \right.$ is prescribed on the boundary, and the boundary conditions take the form

$$ q\left| {_{\Gamma } = q_{w} (x,y,z)} \right. $$

(24)

• 3. The (mixed) third type of boundary conditions.

It entails setting the temperature of the body surface $T_{f}$ and its environment and setting heat transfer between the surface of this body and the environment:

$$ q|_{\Gamma } = \alpha (T_{f} - T_{w} ) $$

(25)

where $\alpha$ stands for heat transfer coefficient.

• 4. The fourth type of boundary conditions.

It needs to enter equality temperature on a surface partition of two bodies or a body with the environment:

$$ q_{f} |_{z = 0} = q_{w} |_{z = 0} $$

(26)

The non-dimensional parameters are introduced in the following way

$$ \begin{gathered} \overline{w} = \frac{w}{h},\quad \overline{x} = \frac{x}{a},\quad \overline{y} = \frac{y}{b},\quad \overline{q} = \frac{{a^{2} b^{2} }}{{Eh^{4} }}q,\quad \overline{\gamma } = \frac{l}{{h^{2} }},\quad \lambda = \frac{a}{b}\,,\quad \overline{h} = \frac{h(x,y)}{{h_{0} }}, \hfill \\ \overline{E}(z) = \frac{E(z)}{{E_{0} }},\quad \overline{D}_{1} = \overline{\alpha }_{1} + \frac{1}{2}\overline{\gamma }^{2} \overline{\alpha }_{3} ,\quad \,\overline{D}_{2} = \overline{\alpha }_{2} + \frac{1}{2}\overline{\gamma }^{2} \overline{\alpha }_{3} , \hfill \\ \overline{z} = \frac{z}{h},\quad \lambda_{1} = \frac{{h^{2} }}{{a^{2} }},\quad \lambda_{2} = \frac{{h^{2} }}{{b^{2} }}, \hfill \\ \end{gathered} $$

(27)

where $\overline{\gamma } \in (0;1]$ is the non-dimensional material length parameter equal to 0 for the classical case, $h_{0}$ is the plate's thickness, and $E_{0}$ stands for the Young's modulus (here plates of constant thickness will be investigated).

Taking into account the introduced assumptions, Eqs. (21) and (22) take the following counterpart non-dimensional form

$$ \left( {D_{1} \frac{1}{{\lambda^{2} }}\frac{{\partial^{4} w}}{{\partial x^{4} }} + D_{2} 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + D_{1} \lambda^{2} \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{q} , $$

(28)

$$ \lambda_{1} \frac{{\partial^{2} T}}{{\partial x^{2} }} + \lambda_{2} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }} = 0. $$

(29)

Bars over the non-dimensional quantities are omitted in Eqs. (28), (29). PDE (21) can be presented in the operator form

$$ L(w) = \tilde{q}, $$

(30)

where

$$ L(w) = \left( {D_{1} \frac{1}{{\lambda^{2} }}\frac{{\partial^{4} w}}{{\partial x^{4} }} + D_{2} 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + D_{1} \lambda^{2} \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right). $$

(31)

Similarly, Eqs. (19), (20), and (28) can be described in a similar way, i.e., we have

$$ l(w) = f. $$

(32)

The heat conduction Eq. (29) with boundary conditions (33) is solved by FEM using "COMSOL," and the estimated function $T(x,y,z)$ obeys the following restrictions

$$ \left\{ {\begin{array}{*{20}l} {0 \le x \le 1;\;0 \le y \le 1;\; - \frac{1}{2} \le z \le \frac{1}{2};} \hfill \\ {T\left| {_{\Gamma } = 293,15\;{\text{K}},} \right.} \hfill \\ {T(0.5;0.5;0.5) = 495\;{\text{K}}.} \hfill \\ \end{array} } \right. $$

(33)

In order to get reliable results with regard to the solution of the heat conduction equation, a mesh with a number of nodes n = 16,000 has been adopted. The exemplary temperature distribution on the plate is presented in Fig. 4a, b.

Fig. 4

3D (a) and 2D (b) visualization of the temperature field of the plate

3 Solving of the equation of porous nanoplates subjected to 3D temperature fields

To analyze the stress–strain state of porous nanoplates interplaying with a temperature field while considering the dependence of material properties from temperature, both analytical and analytical–numerical methods for reducing PDEs to ODEs via nonclassical approaches are adopted for the first time, and their benefits/drawbacks are illustrated and discussed [4]. Namely, the Kantorovich-Vlasov methods (KVM), variational iteration method (VIM), Vaindiner's method (VaM), and Vaindiner's method in combination with variational iteration method (VaM + VIM), were applied.

3.1 Navier's method based on double trigonometric series (NM)

First, we considered the possibility of getting the analytical solution to the equation describing the stress–strain state of porous nanoplate (28), given the boundary conditions (19), and subjected to temperature field (29), (33). Using Navier's method of double trigonometric series [29], the external transverse load $\tilde{q}(x,y)$ is taken into account in the following form

$$ \tilde{q}(x,y) = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {B_{mn} \sin \left( {m\pi x} \right)\sin \left( {n\pi y} \right)} } , $$

(34)

while deflection function $w(x,y)$ is approximated by the form of the double trigonometric series

$$ w(x,y) = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {A_{mn} \sin \left( {m\pi x} \right)\sin \left( {n\pi y} \right)} } . $$

(35)

Then, the counterpart solution (in a general form) can be written as follows

$$ w = \frac{1}{{\pi^{4} }}\sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {B_{mn} \frac{\sin m\pi x\sin n\pi x}{{\left[ {\frac{{D_{1} }}{{\lambda^{2} }}m^{4} + 2D_{2} \left( {mn} \right)^{2} + \lambda^{2} D_{1} n^{4} } \right]}}} } , $$

(36)

where

$$ B_{mn} = 4\int_{0}^{1} {\int_{0}^{1} {\tilde{q}(x,y)\sin \left( {m\pi x} \right)\sin \left( {n\pi y} \right)dxdy} } . $$

(37)

As it can be expected, the accuracy of solving the problem depends on the number N of approximating functions in (36). The convergence of the solution for a homogeneous material (aluminum) and porous structures made from ceramics and metal embedded into temperature field (29), (33) depends on the number of terms of the series N in (36), for the fixed value $\gamma = 0$. Table 1 presents the values of deflection in the center of the plate, i.e. $w(0.5;\,0.5) \cdot 10^{3}$.

Table 1 Quantifying reliable solutions for solid and porous nanoplate by deflection w_N in the plate center versus number N of series terms

Analysis of the results given in Table 1 shows that the final reliable solution is obtained at N = 25, which is highlighted in color.

For visualization, the obtained numerical values of the deflection given in Table 1 are presented graphically. The numerical results regarding the stress–strain state of porous nanoplate located in a temperature field yielded by the NM are shown in Fig. 5.

Fig. 5

Visualization of solutions presented in Table 1 for different kinds of porosity

It can be concluded that the solutions practically become reliable for N = 9. In what follows, we will consider this as an "exact" solution and compare it with the solutions obtained numerically using other methods.

3.2 Bubnov–Galerkin method (BGM)

Further, we will apply the Bubnov–Galerkin method (BGM) [29, 43] to solve (28) by taking into account the boundary conditions (19). Displacements w are approximated by the following series

$$ w(x,y) = \sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {A_{ij} \sin (m\pi x)\sin (n\pi y)} } , $$

(38)

which yields the system of N² linear algebraic equations with unknown $A_{ij}$, i.e., we have

$$ \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left[ {\left( {\sum\limits_{m,n = 1}^{N} {\left( { - D_{1} \frac{1}{{\lambda^{2} }}m^{4} + 2D_{2} m^{2} n^{2} + D_{1} \lambda^{2} n^{4} } \right)A_{ij} \pi^{4} \sin (m\pi x)\sin (n\pi y)} } \right) - \tilde{q}} \right]} } \sin (i\pi x)\sin (j\pi y)dxdy,\quad i,j = 1,2, \ldots ,N. $$

(39)

The resulting algebraic system is solved by the Gauss method, and the accuracy of the solution depends on the number N [see (38)]. Let us examine the convergence of the outcome given by the BGM for a homogeneous material (aluminum) and porous plates made from ceramics and metal in the temperature field governed by Eqs. (29) and (33). Table 2 shows the values of deflection in the center of the plate $w(0.5;0.5) \cdot 10^{3}$ for the fixed value $\gamma = 0$.

Table 2 Quantifying reliable solutions based on BGM for solid and porous plate for various series terms N

Analysis of the results given in Table 2 shows that the final (reliable) solution is obtained by the BGM at N = 25, and it is highlighted in color.

For visualization, the obtained numerical values of the deflection given in Table 2 are presented graphically. Convergence visualization of the solution equation describing the stress–strain state of porous nanoplate located in a temperature field BGM of double rows is shown in Fig. 6. It can be concluded that the solutions obtained by the BGM practically become reliable for N = 9.

Fig. 6

Visualization of the results presented in Table 2 with regard to convergence of the BGM for a porous plate in a 3D temperature field for $\gamma = 0$

It follows that the solution obtained by the BGM completely coincided with the solutions obtained by the NM, i.e., it can be treated as an exact solution.

3.3 Kantorovich–Vlasov method (KVM)

In the next step, we will apply the Kantorovich–Vlasov Method (KVM) [29,30,31], using Eq. (28) and taking into account boundary conditions (19). In this case, displacements w are approximated by the following series

$$ w_{N} (x,y) = \sum\limits_{j = 1}^{N} {X_{j} (x)Y_{j} (y)} . $$

(40)

Observe that the weight functions $X_{j} (x)$ satisfy boundary conditions (20), and the functions $Y_{j} (y)$ are the searched functions defined by the BGM with respect to the co-ordinate $x$, i.e., we have

$$ \left( {(L(w_{j} ) - \tilde{q}),X_{k} (x)} \right) = 0,\quad k = 1,2, \ldots ,N. $$

(41)

Consequently, a system of n ODEs is obtained with respect to y. Solving the system of ODEs by FDM of the second-order accuracy with the corresponding boundary conditions, we get a set of functions $Y_{j} (y).$ Next, we substitute them into (40), and we obtain a solution to Eq. (28).

Let us study the convergence of the solution yielded by the KVM for homogeneous material (aluminum) and porous plates from ceramics and metal in the temperature field (29), (33), depending on the number of nodes $n$ on each of the axis $x,\;y$. Table 3 shows the values of deflection in the center of the nanoplate $w(0.5;0.5) \cdot 10^{3}$ for the fixed value $\gamma = 0$.

Table 3 The values of the plate deflection versus $n$ obtained by KVM

For visualization, the obtained numerical values of the displacement given in Table 3 are presented graphically (see Fig. 7).

Fig. 7

Visualization of the results presented in Table 3

It can be concluded that the solutions obtained by the KVM practically become reliable for $n = 51.$

3.4 Variational iteration method (VIM)

The subsequent technique that will be applied to solve PDE (28), taking into account boundary conditions (19), is called the variational iteration method (VIM) [29, 32,33,34] or the extended Kantorovich method (EKM) [44,45,46]. Therefore, solutions obtained by the VIM for the first iteration at $x$ coordinate and the known functions $\,X_{j}^{(0)} (x)$ are sought in the following form

$$ w_{N}^{(1)} (x,y) = \sum\limits_{j = 1}^{N} {X_{j}^{(0)} (x)Y_{j}^{(1)} (y)} . $$

(42)

Observe that though the functions $\,X_{j}^{(0)} (x)$ are a priori specified, they may not generally satisfy the given boundary conditions. Then it will take more iterations for the solution to converge. We employ the BGM with regard to coordinate $x$ and get a set of ordinary differential equations (ODEs) with respect to coordinate $y$, and by solving the ODEs, we find the functions $\,Y_{j}^{(1)} (y)$. Further, we employ the BGM with regard to coordinate $y,$ and get a set of ODEs with respect to coordinate $x$. The obtained ODEs are solved by the FDM of the second-order of accuracy with the corresponding boundary conditions. Thus, we get an iterative procedure, which ends at step $n$ after achieving a given accuracy $\varepsilon$. As a result, the solution to Eq. (28) takes the following form

$$ w_{N}^{(m)} (x,y) = \sum\limits_{j = 1}^{N} {X_{j}^{(m - 1)} (x)Y_{j}^{(m)} (y)} ,\quad m = 1,2, \ldots ,n. $$

(43)

Let us study the convergence of the solution by the VIM for homogeneous material (aluminum) and porous plates from ceramics and metal in the temperature field (29), (33), taking into account boundary conditions (20) depending on the number of grid nodes $n$ on each axis $x,y$ for $\gamma = 0$. Table 4 shows the values of displacement in the center of the plate $w(0.5;0.5) \cdot 10^{3}$.

Table 4 The values of the deflection plate center versus $n$ along the axis x and axis y, based on VIM

For visualization, the obtained numerical values of the deflection given in Table 4 are presented graphically (Fig. 8).

Fig. 8

Visualization of the results presented in Table 4

It can be concluded that the solutions obtained by the VIM practically become reliable for $n = 51.$

3.5 Vaindiner's method (VaM)

Vaindiner's method (VaM) [29, 35] can be viewed as an extension and modification of the KVM and BGM. According to this method, an approximate solution to operator Eq. (30) will be searched in the form

$$ w_{ij} (x,y) = \sum\limits_{j = 1}^{N} {\left( {X_{1j} (x)Y_{1j} (y) + X_{2j} (x)Y_{2j} (y)} \right)} ,\quad i = 1,2, $$

(44)

where weight functions $Y_{1j} (y),$ and $X_{2j} (x)$ are known, and they satisfy the boundary conditions (19), while functions $X_{1j} (x)$ and $Y_{2j} (y)$ are unknown. They are determined using the BGM in the following way

$$ \begin{gathered} \left( {L(w_{ij} ) - \tilde{q},Y_{1k} (y)} \right) = 0,\quad k = 1,2, \ldots ,N,\;i = 1,2, \hfill \\ \left( {L(w_{ij} ) - \tilde{q},X_{2k} (x)} \right) = 0,\quad k = 1,2, \ldots ,N,\;i = 1,2. \hfill \\ \end{gathered} $$

(45)

As a result, the system of 2N ordinary differential equations is obtained. The resolving system of ODEs is solved by the method of FDM of the second-order of accuracy with the corresponding boundary conditions. This allows us to find the functions $X_{1j} (x)$ and $Y_{2j} (y),$ and then substituting them in (44) yields the solutions of PDE (30).

Now, we study the convergence of the solution of the desired differential equation by the VaM for homogeneous material (aluminum) and porous plates from ceramics and metal in the temperature field (29), (33), taking into account boundary conditions (20), depending on the number of grid nodes $n$ on both axis x and axis y (for $\gamma = 0$). Table 5 presents the values of deflection in the center of the plate for a homogeneous material (aluminum) and porous plates from ceramics and metal in the temperature field (29), (33), taking into account boundary conditions (20) versus the number of grid nodes $n$ with regard to the axis x and axis y $(\gamma = 0)$. Table 5 shows the values displacement in the center of the plate $w(0.5;0.5) \cdot 10^{3}$.

Table 5 The values of the plate center deflection versus $n$ along the axis x and axis y, obtained by the VaM

For visualization, the obtained numerical values of the deflection given in Table 5 are presented graphically (Fig. 9).

Fig. 9

Visualization of the results presented in Table 5

It can be concluded that the solutions obtained by the VaM practically become reliable for $n = 51.$

3.6 Finite difference method (FDM)

We will use the FDM of the second order of accuracy to obtain numerical solutions for numerous PDEs with approximation $O\left( {h^{2} } \right)$. We get a system of linear equations $n^{2}$ for each grid node, where n stands for the number of grid nodes regarding the x and y axes. We solve this system by the Gauss method, taking into account boundary conditions.

Let us search for a solution of PDE by the FDM depending on the number of grid nodes n axis x and axis y for a homogeneous material (aluminum) and porous plates from ceramics and metal in the temperature field (29), (33), taking into account boundary conditions (19) for $\gamma = 0$. Table 6 shows the values displacement in the center of the plate $w(0.5;0.5) = A \cdot 10^{ - 3}$.

Table 6 The values of the center plate deflection versus n along the axis x and axis y, obtained by FDM

For visualization, the obtained numerical values of the deflection given in Table 6 are presented graphically (see Fig. 10).

Fig. 10

Visualization of the results reported in Table 6

It can be concluded that the solutions obtained by the VaM practically become reliable for $n = 51.$

3.7 Comparison of results obtained by different methods

Previously, the equation governing bending of nanoplates made from a homogeneous material (aluminum) and porous plates from ceramics and metal U-PFMG in the temperature field (29), (33), taking into account boundary conditions (20) depending on the number of grid nodes $n$ on axis x and axis y, at $\gamma = 0$ has been solved by various methods including the BGM, KVM, VIM, VaM, NM and FDM.

Tables 7 and 8 present the values of the maximum displacement $w(0.5;0.5)$ at the center of the plate, based on the number of grid nodes n employed on axis x and axis y, and calculated by various methods. Also, obtained results are compared with the exact solution of the problem obtained by the NM with the help of the double trigonometric series.

Table 7 Analytical and numerical solutions obtained by various methods for the estimation of the homogeneous plate center deflection depending on the number of grid nodes n along each axis x, y

Table 8 Analytical and numerical solutions obtained by various methods for the estimation of the porous plate center deflection depending on the number of grid nodes n along each axis $x,\;y$

For visualization, the obtained numerical results given in Tables 7 (Fig. 11) and 8 (Fig. 12) are presented graphically.

Fig. 11

Visualization of the results reported in Table 7

Fig. 12

Visualization of the results shows in Table 8

Let us analyze the accuracy of these methods. For this purpose, we calculate the error from the exact solution of the deflection at the center of the plate $w(0.5;0.5)$ obtained by the NM for homogeneous material and porous structures.

Thus, the maximum difference between the exact solution and solutions obtained by other methods (KVM, VIM, VaM) does not exceed 1.2%, which shows the high competitiveness of these methods. In addition, the maximum difference between solutions obtained VIM and VaM is less than 0.3%. Based on the obtained results, we can conclude that the advantage of these methods is in high accuracy and low cost of computational time. It should also be emphasized that the latter techniques are based on solving a system of n algebraic equations, while the FDM and FEM are based on solving $n^{2}$ algebraic equations. In our case, the clock frequency of the processor of the computer on which the problem was solved is 2.2 GHz. It means that in order to obtain a solution by the FDM for n = 51, the solutions of the algebraic equations by the Gauss method require 125 thousand times more time than for the KVM.

4 Numerical results and discussions

Recall that in Sect. 2 of the paper, the mathematical model of functionally graded porous nanoplates subjected to temperature field, considering the modified couple stress theory, was constructed. In Sect. 3, we employed reduction procedures of PDEs to get the counterpart ODEs by using the KVM, VIM, VaM, and FDM. In addition, the exact solution in the framework of NM for equations describing the static behavior of porous nanoplates subjected to temperature field was obtained. It has been noticed that in the case of NM, more than three members of the series were considered to attain the exact solution (36). The solutions obtained by reducing PDE (28) to ODEs coincide well with Navier's precise solution. At the same time, the solution obtained by the FDM of the second-order of accuracy converges to the exact Navier solution with a considerable amount of partitioning of the integrating plate's region. For example, by dividing the rectangular region of the isotropic metal plate into $51 \cdot 51$ intervals, the error is 3%, and for a porous plate, it achieves 7.8% (Table 9). In Table 9, the exact solution is highlighted in blue. Temperature field exhibited by plates subjected to stationary temperature field based on solving 3D heat conduction Eq. (29), (33) by the FEM has also been found. However, the exact solution is obtained by using 16 000 FEs.

Table 9 Comparison of accuracy of the employed methods of analysis of the functionally gradient porous nanoplates located embedded into temperature field

Furthermore, for the homogeneous and isotropic nanoplates (solution highlighted in yellow), and for porous nanoplates with simple support boundary conditions (19) and stiff clamping (20), under the action of a uniformly distributed load $q = 1 \cdot 10^{ - 3}$ and a temperature field (33), the effect of the size-dependent parameter $\gamma$ has also been studied (Figs. 13, 14, 15, 16). The solution is obtained by the NM based on (36) for N = 25. Dependence of the functions $w(0.5;0.5)$ and $\chi (x;y) = \frac{1}{2}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)$ in the center of the plate $(x = y = 0.5)$ from size-dependent parameter $\gamma$ has been investigated.

Fig. 13

Dependence of the functions $w(0.5;0.5)$ and $\chi (0.5;0.5)$ on the size-dependent parameter $\gamma$ taking into account, a uniformly distributed load $q = 1 \cdot 10^{ - 3}$ and a temperature field

Fig. 14

Functions $w(0.5;0.5)$ and $\chi (0.5;0.5)$ for different $\gamma$ and K subjected only to 3D temperature field

Fig. 15

The dependence of the function $w(0.5;0.5)$ versus $\gamma$ for isotropic and porous nanoplates subjected to 3D temperature field

Fig. 16

Function $w(0.5;0.5)$ versus $\gamma$ and the type of porosity for isotropic and porous nanoplates subjected to 3D temperature field

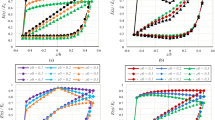
In Fig. 13, in the case of simple support (19), the dotted lines show the solutions obtained only by considering the temperature field. The solid lines show the solutions obtained by considering both the temperature field and the uniformly distributed load $q = 1 \cdot 10^{ - 3}$. Solid and dotted color line corresponds to the same pore characteristics for porous nanoplates U-PFGM (14a)–(14c) (blue curves), X-PFGM (15a)–(15c) (green curves), O-PFGM (16a)–(16c) (red curves).

For the same boundary conditions (19), only the temperature field affects the functions $w(0.5;0.5)$, $\chi (0.5;0.5)$, and depends on the pore volume K, and the size-dependent parameter $\gamma$ is studied. In this case, the ratios in Eqs. (16a)–(17c) with an account of the pore volume are employed. The following notation is used: type 1 (17a) (brown curves), type 2 (17b) (birch curves), type 3 (17c) (purple curves)—see Fig. 14. The solution is also obtained by the NM for N = 25 [for $K = 0.1$ they are shown with dotted lines and for $K = 0.5$ by solid lines (Fig. 14)].

Figure 15 presents the obtained solutions for the function $w(0.5;0.5)$ versus $\gamma$ for nanoplates using the boundary conditions (19), (20), and porous materials properties (14a)–(16c), subjected to a 3D temperature field. For boundary conditions (19) (solid lines), the solution using NM (N = 25) is obtained, and for the boundary conditions (20) (dashed lines), the result by VIM is presented (the color scale of the curves is shown in Fig. 15).

For nanoplates subjected to 3D temperature field, and for the boundary conditions (20), the influence of porosity type (17a)–(17c) on $w(0.5;0.5)$ for different $\gamma$ and K has been investigated (description of the solution given in Fig. 16 are the same as in Fig. 14). The results are obtained by using VIM.

Based on the results reported in Figs. 13, 14, 15 and 16, we can conclude that the functionally gradient porous nanoplates have a significantly lower load-carrying capacity compared to isotropic metallic nanoplates. The maximum difference in the load-carrying capacity between the metal plates and the porous structure is more than 300%. The type of porosity also significantly affects the load-carrying capacity of nanoplates. For comparing materials with the porosity distributions modeled by the power function [U-PFGM (14a)–(14c), X-PFGM (15a)–(15c), O-PFGM (16a)–(16c)], it was found that the material U-PFGM (uniform distribution of pores) has the lowest load-carrying capacity while the X-PFGM (increase number of pores in the vicinity of the median surface) has the highest. The size-dependent parameters $\gamma$ ($0 \le \gamma \le 0.7$) significantly affect the load-carrying capacity of nanoplates. Increasing the size-dependent parameters practically increases the carrying capacity by a factor of two for porous structures; three for homogeneous material. It was found that an increase in the maximum pore volume also significantly reduces the load-carrying capacity of the nanoplates.

4.1 Modelling of functionally graded porous nanobeam subjected to temperature field based on the modified couple stress theory

Consider a 2D elastic rectangular nanobeam beam occupying an area Ω, where $\Omega = \{ x \in [0;a],\,\,z \in [ - h/2;h/2]\}$. We assume that the material of the nanobeam is elastic, inhomogeneous, and isotropic, subjected to a temperature field. In contrast to many other articles, there are no restrictions on the temperature field, which is determined from the solutions of the 2D heat conduction equation.

The porosity and gradient of the nanobeam material are described by various models (14a)–(17c) [13, 14]. Porosity is distributed along the beam's thickness, while the Young's modulus E = E(z) is a function of the variable $z$.

The rectangular system of coordinates is given in the following way: a reference line, further called the middle line z = 0, is fixed in the beam, whereas the axis OX is directed from the left to the right of the center line, and the axis OZ is directed downwards (OZ⊥OX)—see Fig. 17.

Fig. 17

The computational scheme of a nanobeam rigidly clamped

A differential equation describing static behavior of a porous Euler–Bernoulli nanobeam subjected to temperature field (the influence of the temperature field on the model follows the classical Duhamel–Neumann relations) in the framework of the modified couple stress theory has the form

$$ D_{1} \frac{{d^{4} w}}{{dx^{4} }} = q - \frac{{d^{2} M_{T} }}{{dx^{2} }} $$

(46)

where $M_{T} = 2\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\alpha_{T} (z)E(z)\Delta T(x,y,z)zdz} ;\; - \frac{h}{2} \le z \le \frac{h}{2};\;0 \le x \le a$, $D_{1}$ is defined in the same way as for the plate, i.e., we have $D_{1} = \alpha_{1} + \frac{1}{2}l_{{}}^{2} \alpha_{3} ,\,\,$ and $\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left( {\lambda + 2\mu } \right)z^{2} \,dz} = \alpha_{1}$, $\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\mu \,dz} = \alpha_{3}$.

The following boundary conditions are applied:

• (1) simple support

$$ w = 0,\quad \frac{{d^{2} w}}{{dx^{2} }} = 0\quad {\text{for}}\;x = 0,\;x = a, $$

(47)

• (2) rigid clamping

  $$ w = 0,\quad \frac{dw}{{dx}} = 0\quad {\text{for}}\;x = 0,\;x = a. $$

  (48)

The 2D heat conduction PDE takes the following form

$$ \frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }} = 0, $$

(49)

and the non-dimensional parameters are introduced in the following way

$$ \overline{w} = \frac{w}{h},\quad \overline{x} = \frac{x}{a},\quad \overline{q} = \frac{{a^{4} }}{{Eh^{4} }}q,\quad \overline{\gamma } = \frac{l}{{h^{2} }}\,\,,\quad \lambda_{3} = \frac{{h^{2} }}{{a^{2} }}\,,\quad \overline{E}(z) = \frac{E(z)}{{E_{0} }}\,. $$

(50)

Then PDEs (46) and (49) take the following counterpart non-dimensional forms

$$ D\frac{{d^{4} w}}{{dx^{4} }} = \tilde{q}, $$

(51)

$$ \lambda_{3} \frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }} = 0, $$

(52)

where $\tilde{q} = q - \frac{{d^{2} M_{T} }}{{dx^{2} }}$,$M_{T} = 2\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\alpha_{T} (z)E(z)\Delta T(x,y,z)zdz}$.

PDE (52) is supplemented by the following temperature conditions

$$ \left\{ {\begin{array}{ll} {x = 0;\;x = 1;\; - \frac{1}{2} \le z \le \frac{1}{2}} \hfill \\ {T = 293,\;15\;{\text{K}}} \hfill \\ {0 < x < 1} \hfill \\ {T(0.5;\,0.5) = 495\;{\text{K}}} \hfill \\ \end{array} } \right. $$

(53)

The distribution of the temperature field of the beam and visualization of the temperature field is shown in Fig. 18 (K is the temperature measured in Kelvins).

Fig. 18

Visualization of the temperature field of the beam

4.2 Finite difference method (FDM)

We will use the FDM to obtain numerical solutions of Eq. (51) governing the behavior of the porous nanobeam subjected to temperature field (52), (53) with approximation $O\left( {h^{2} } \right)$. We obtain a system of linear equations n² for each grid node, where n is the number of grid nodes along the axis x. We solve this system by the Gauss method, considering the boundary conditions (Table 10).

Table 10 The values of the plate deflection center versus n obtained by the FDM [boundary conditions of rigid clamping (48)]

It can be concluded that the exact solution for the function deflection w can be obtained by solving Eqs. (51) through FDM of the second-order of accuracy for both metal beam and porous (U-PFMG), and for $n \ge 51$.

4.3 NM (double trigonometric series)

We consider the analytical solution to PDE associated with a porous nanobeam (51) for the boundary conditions (47) subjected to temperature field (52), (53) by using Navier's method (NM) [29]. External transverse load $\tilde{q}(x)$ is taken into account in the form of trigonometric series. The stress–strain state of porous nanobars subjected to temperature field is investigated, and the solution is obtained by the FDM.

Let us investigate the dependence of the deflection function $w(x)$ and the function of the second derivatives on the deflection $\chi (x) = \frac{{\partial^{2} w}}{{\partial x^{2} }}$ for the size-dependent parameter $\gamma$ of nanobeams made of a homogeneous material and porous silicon-metal structures with the porosity distributions (14)–(20).

For a nanobeam subjected to temperature field (52), (53), depending on the size-dependent parameter $\gamma$, the value of the deflection function $w(0.5)$ and second derivative function $\chi (0.5)$ in the beam center is obtained by the NM [boundary conditions of simple support (47)] are reported in Figs. 19, 20, and by FDM [boundary conditions stiff clamping (48)] are presented in Figs. 21, 22.

Fig. 19

The value of the deflection $w(0.5)$ in the nanobeam center subjected to temperature field depending versus the size-dependent parameter $\gamma$

Fig. 20

The value of the second derivative function $\chi (0.5)$ in the nanobeam center subjected to temperature field depending versus the size-dependent parameter $\gamma$

Fig. 21

The value of the deflection function $w(0.5)$ in the nanobeam center subjected to temperature field depending versus the size-dependent parameter

Fig. 22

The value of the second derivative function $\chi (0.5)$ in the nanobeam center subjected to temperature field depending versus the size-dependent parameter

For nanobeams subjected to temperature field, the influence of porosity type (17a)–(17c) on function $w(0.5)$ depending on the size-dependent parameters $\gamma$ and K, and with boundary conditions (47) (Fig. 23) and (48) (Fig. 24), has also been investigated based on the NM.

Fig. 23

The value of the deflection function $w(0.5)$ in the nanobeam center subjected to temperature field depending on the type of porosity and the size-dependent parameter $\gamma$

Fig. 24

The value of the deflection function $w(0.5)$ in the nanobeam center subjected to temperature field depending on the type of porosity and the size-dependent parameter $\gamma$

From the analysis of the results regarding the static behavior of nanobeams, we can conclude that the functionally gradient porous structures have a significantly lower load-carrying capacity than homogeneous materials. The maximum difference between porous structures and homogeneous material is of the magnitude of 200%. The type of porosity also significantly affects the load-carrying capacity of nanobeams. For the considered materials with the porosity distributions modeled by various power functions [U-PFGM (14a)–(14c), X-PFGM (15a)–(15c), O-PFGM (16a)–(16c)], it was found that the material U-PFGM (uniform distribution of pores) has the lowest load-carrying capacity. In contrast, the X-PFGM (increased number of pores in the vicinity of the median surface) has the highest. Increasing the pore size to the maximum also significantly reduces the load-carrying capacity of the nanobeams. Porous structures of type 1 (17a) and type 2 (17b) have the most negligible differences between themselves, and for a small pore volume $K \le 0.1$, they coincide entirely. For the value of the size-dependent parameter $\gamma \ge 0.6$, the deflection values for a homogeneous material and a porous material of any type are the same.

Analysis of the results shows a significant influence of the size-dependent parameter $\gamma$ on the stress–strain state of the nanobeam. Furthermore, increasing the value of the size-dependent parameter $0 \le \gamma \le 0.7$ for all the beam types considered leads to a corresponding increase in their respective carrying capacity.

5 Concluding remarks

In this paper, the mathematical model of the general theory of functionally gradient Euler–Bernoulli nanobeams and Kirchhoff nanoplates subjected to temperature field, with an account of their porous structure, have been presented for the first time. The porous structure can change not only in thickness, as seen in the available scientific literature, but also in volume (x, y, z). For modeling size-dependent effects of the nanobeam and nanoplate, the modified couple stress theory has been adopted. Applying the proposed technique, mathematical models of nanobeams and nanoplates describe the more complex kinematic assumptions. Then, like the second (Timoshenko [47]), the third (Sheremetyev-Pelekh [25, 48], Reddy [50]), and higher-order formulations, the models were developed. Nano effects based on the set nonlocal elasticity theory [7], strain gradient theory [8], and nonlocal strain gradient theory (NSGT) [7] can also be considered. As a particular case, the porosity of the material is described by the functional gradient theory, when the properties of the porous structure change only on the thickness of the nanobeam and nanoplate. All known types of porous structures [13, 14] have been studied. Two-dimensional and three-dimensional heat conduction equations for rendering the temperature field in nanobeams and nanoplates are employed for the first time. Nanobeams and nanoplates, whose properties of porous materials depend on temperatures, have been studied. To study the stress–strain state of porous nanoplates, the methods of reducing partial differential equations to ordinary differential equations (the Kantorovich-Vlasov method [29,30,31], variational iteration method [29, 32,33,34], Vaindiner's method [29, 35], and the finite difference method of the second-order of accuracy have been adopted. The exact solution (by the technique of double trigonometric series) for porous nanoplates subjected to temperature field has been achieved. The above methods give precise solutions for two types of boundary conditions for nanoplates. The convergence of the solutions obtained by the various techniques mentioned has been investigated and compared.

For the variational iteration method, a high convergence rate and accuracy have been found. Machine time spent to obtain a solution for porous nanostructures with a given accuracy is much less than the time needed to get a reliable solution by the finite difference and finite element method. It has been illustrated how the size-dependent parameter $\gamma$ significantly affects the stress–strain state of nanobeams and nanoplates. At an increased value of the size-dependent parameter $\gamma \to 0.7,$ the solutions obtained for the considered porous nanobeams become the same.