1 Introduction

The desire to replicate birds’ flight has always fascinated humans. We always watch birds with wonder and envy as they are amazing examples of unsteady aerodynamics, high maneuverability and precision, attitude sensing, endurance, flight stability and control, and large aerodynamic efficiency. Birds are the result of millions of years of evolution.

In the late 1400s, Leonardo da Vinci designed a human-powered flapping wing machine or ornithopter (from the Greek word ornithos for bird and pteron for wing); however, there is no evidence that he actually attempted to build it. Bird wings generate lift and thrust due to a complex combination of wing kinematics (involving flapping, twisting, lagging, folding and phase angle), wing flapping frequency, flapping amplitude, and wing geometry; adding to this discussion the matters of stability and maneuverability, da Vinci’s design might have hardly worked as these concepts had not yet been developed.

Today, conventional man-made flying vehicles can fly over long distances at incredible altitudes and speeds, do remarkable maneuvers, transport passenger and freight safely, incorporate sophisticated guidance and navigation systems, and thanks to control system engineering they are the pinnacle of systems stability; nevertheless, they are heavy, noisy, and inefficient when compared to birds. Any of our designs pale in comparison with any of nature’s fliers.

Despite the progress made during the past years in the areas of unsteady aerodynamics and flight dynamics of birds flight, control system engineering, structural dynamics, aeroelasticity, materials science and robotics and automation [1–15], designing a biomimetic autonomous flapping unmanned aerial vehicle (UAV) remains a challenge for engineers and scientists.

From an engineering point of view, studying flapping flight in nature is not only of interest for the purpose of building flying machines inspired by birds and insects; these studies can also be extended to drag reduction, noise reduction, enhanced maneuverability, structural dynamics, guidance and control, flight dynamics and stability, and energy harvesting. From the standpoint of a biologist or zoologist, studying flapping flight in nature is of great importance for understanding the biology, allometry, flight patterns and skills, and the migratory habits of avian life.

In this manuscript, the preliminary design of a biologically inspired small-sized flapping UAV or ornithopter is presented; we focus our discussion on the aerodynamic performance and static longitudinal stability. Hereafter, we summarize some key technical issues of a flapping UAV, where the shape and size of the model are chosen using as a reference the morphological and allometric measurements of several birds [16–19], and in order to prove the concept we numerically simulate the proposed avian model in gliding and flapping flight. It is worth mentioning that our findings are not only limited to the engineering perspective, but can be extended to the biology or zoology field and used to study the allometry and flight characteristics of birds.

The remainder of the manuscript is organized as follows. In Sect. 2 we briefly review the design specifications. In Sect. 3 we present the avian model, reference geometry and design assumptions. In Sect. 4 we outline the wing kinematics. In Sect. 5 we give a brief summary of the solution strategy. Sections 6 and 7 are dedicated to the discussion of the results; in the former we present a detailed review of the results for the aerodynamic performance of the avian model in gliding and flapping flight, and in the latter we focus the discussion on the results concerning the longitudinal static stability of the model. Finally, in Sect. 8 we give conclusions and future perspectives.

2 Design specifications

In Table 1, the design specifications of the proposed flapping UAV are shown. One important design specification to highlight is that the vehicle is intended to be hand launched with a minimum velocity of 5.0 m/s. It is also interesting to point out that the flapping frequency can be modulated, but shall not exceed 3.0 Hz; this constraint is imposed for mechanical and structural reasons.

Table 1 Design specifications
Full size table

Based on these design specifications, we proceed to look for birds that closely match the specifications outlined in Table 1. We focus our attention on the literature pertaining to the biology and zoology fields [16–18]; this is done to have an initial idea of the body measurements and wing shape of the avian model. In Table 2, we list the bird species used as a reference to conduct this study.

Table 2 Bird species used for this study
Full size table

To select a bird species and use it as inspiration for our avian model, we look for the bird family that better meets the mass and flapping frequency requirements. Based on this selection criteria we pick the genus Larus (gulls family) as a reference for the initial sizing of the avian model. Moreover, our choice is also influenced by the fact that detailed data of the wing morphology is available in the literature [19].

3 Avian model, reference geometry, and design assumptions

Taking into account the design specifications given in Table 1, and the morphometrics/allometry and radar flight measurements of several birds [16–18] (as listed in Table 2), we proceed to sketch the initial form of the avian model. As mentioned in the previous section, the model shape and flight conditions are chosen to approximate those of the gulls family (specifically, the kelp gull and the yellow legged gull), which meet our design specifications. Our model will be bigger for reasons related to the housing of the mechanism, batteries, servo motors, etc., and the larger wing span and wing area needed to generate the required lift at a flapping frequency of 3.0 Hz (smaller than that of gulls) and forward velocity of 5.0 m/s. Furthermore, we have chosen wings which are not twisted, neither geometrically nor dynamically, for design simplicity and manufacturing considerations. Had we allowed for twist we would have been able to limit the dimensions of the model considerably. In Table 3, we list the geometrical information, from the symmetry line to the wing tip, of the proposed avian model.

Table 3 Avian model geometrical information
Full size table

The wing used in this study is a simplification of the actual wing of a gull. The morphology of the wing is obtained by Liu et al. [19], where they extracted the approximated wing surface coordinates and wing cross-section by using a 3D laser scanner. The simplified or engineered wing is used in order to parametrize the 3D model and to avoid potential surface modeling problems when conducting the parametric study. The use of the engineered wing is also driven by the potential restrictions in the manufacturing and mechanical realization.

The wing dimensions are chosen in such a way that they produce the minimum lift needed to keep the avian model aloft at the design conditions of forward velocity of 5.0 m/s and flapping frequency of 3.0 Hz, that is, the model is designed at minimum flight velocity and maximum flapping frequency.

The fuselage is designed in such a way that it provides enough room to house the mechanisms and flight systems with no interference, it produces low drag, it has a low negative contribution to the overall stability of the model and resembles a gull.

Finally, an horizontal stabilizer or tail is added to the model and its initial sizing, position and orientation is chosen in such a way that it guarantees the longitudinal static stability of the avian model, first in gliding flight and then in flapping flight. It is important to mention that the whole tail is allowed to move and the cross section is a symmetrical airfoil (NACA 0012).

In Fig. 1, we present an illustration of the avian model. In this figure, the point marked as 000 represents the junction between the fuselage and the internal wing and also serves as a reference point to define the wing kinematics, the position of the different components of the avian model, the position of the aerodynamic center of the wing and tail, and the position of the center of gravity of the model. The axis 100 (which passes through the point 000), is the axis about which the internal semi-wing oscillates (or rolls), and the axis 200 is the axis about which the external semi-wing is articulated and rolls.

Fig. 1
figure 1

Three-view of the avian model without vertical stabilizer. In the figure, EW stands for external semi-wing, and IW stands for internal semi-wing. All dimensions are in meters

Full size image

Hereafter, we list a few design assumptions used during this study:

  • For the flapping flight simulations, the wings are considered to be made of two parts, one internal semi-wing and one external semi-wing, with a gap between the internal and external parts. This gap is where the wing is articulated.

  • The junction between the wing and the body of the avian model is also modeled through a gap.

  • The individual components of the avian model are treated as rigid bodies.

  • The mass of the avian model is assumed to be distributed uniformly.

  • The fuselage is assumed to have a light shell making it look like a bird. This shell generates drag and lift, which are taken into account for the computation of the aerodynamic forces.

  • When accounting for the moments, all the moments produced by the pressure and viscous forces are taken into consideration.

  • The aerodynamic forces and moments, are due to the flapping motion of the wings and the contribution of the fuselage and tail.

  • The pitch attitude of the avian model is fixed at different values during the transient simulations. Thus, there is no aerodynamic damping nor inertial forces contribution.

  • The tail is articulated and is free to rotate about any axis, hinged at the tail’s point of junction with the fuselage.

  • The tail position is not fixed with reference to the center of gravity. Its position can be changed during the design stage in order to provide more stability.

  • The wings cross section is the high-lift airfoil Selig 1223.

  • The wings angle of attack is fixed during the flapping cycle. This choice has been dictated by manufacturing considerations and mechanical design simplicity. For completeness we have, however, carried out several simulations with dynamic twist (not reported here), which yielded larger aerodynamic forces and consequently would allow a reduction in the model dimensions.

  • The tail cross section is the symmetrical airfoil NACA 0012.

Of the previous design assumptions, the most prohibitive ones are the restrictions related to the gap between the inner wing and the fuselage, and the gap where the wing is considered to be articulated. Such restrictions are rendered necessary by the meshing and simulation methodology in order to deal with the moving wings and with the large mesh deformation of the simulations, and to avoid highly degenerated mesh elements. However, these gaps (which in the actual prototype would be absent, since the whole wings would be covered by a thin, light-weight plastic sheet) generate in the numerical simulations a large drag; they also create a discontinuity in the span-wise lift distribution, and all of this is detrimental for the aerodynamic performance of the avian model. This means that we are designing the model in a worse case, very conservative, scenario. These restrictions, together with the fact that we are not considering any pitch aerodynamic damping, might also have a negative effect on the static and dynamic stability of the model.

4 Wing kinematics

Birds and insects wings follow complex patterns, which often involve rotation and translation with several degrees of freedom and even deformation, e.g., rotation about one axis, folding about another axis, bending and twisting in different directions, and translation of the wing tip in a plane. Hereupon, and for the sake of simplicity, we represent the flapping motion as the rolling motion of the internal wing about the axis 100, and the rolling motion of the external wing about the axis 200 (Fig. 1). Despite this simplification, the wings’ kinematics resembles that of nature’s fliers and is realizable from a mechanical point of view, as discussed in part II of this work [20].

The equations that describe the wings’ motion are:

$$\begin{aligned} roll_{iw} &\,= \,A_{iw} sin (\omega t), \end{aligned}$$
(1)
$$\begin{aligned} droll_{iw} & \,= \, \omega A_{iw} cos (\omega t), \end{aligned}$$
(2)
$$\begin{aligned} roll_{ew} & \,= \, -\frac{A_{ie} \frac{\pi }{2} erf (\sqrt{2} \sqrt{B} cos (\omega t)) }{2 \sqrt{B} C}, \end{aligned}$$
(3)
$$\begin{aligned} droll_{ew} & \,= \, \frac{A_{ie} \omega sin (\omega t) e^{(B sin (2 \omega t - \frac{\pi }{2}) - B)} }{C}; \end{aligned}$$
(4)

where roll is the roll angle of the wing (measured in \(^\circ\)) and droll is the angular velocity of the wing (measured in \(^\circ /s\)). In this discussion the subscript iw stands for internal semi-wing, and the subscript ew stands for external semi-wing. In Eqs. 1–4, \(A_{iw}\) is the maximum roll amplitude of the internal semi-wing, \(A_{ie}\) is the maximum angle between the internal semi-wing and external semi-wing, \(\omega\) is the angular frequency (\(2 \pi f\)), f is the flapping frequency (Hz), t is the time (s) and erf is the error function (\(erf(x) = \frac{2}{ \sqrt{\pi }} \int _0^x e^{-t^2} dt\)). In Eqs. 1–2, the amplitude \(A_{iw}\) is equal to \(30^\circ\); whereas in Eqs. 3–4 the amplitude \(A_{ie}\) is equal to \(50^\circ\), and the constants B and C are equal to 1.0 and 1.1963 respectively. A description of the mechanism which realizes the desired movement is given in part II of this work [20].

In Figs. 2 and 3, the time evolution of the roll angle and the angular velocity are displayed, for both the internal and the external semi-wings. The kinematics is designed in such a way that it generates the minimum lift needed to keep the avian model aloft and it produces thrust at the design conditions of forward velocity equal to 5.0 m/s and flapping frequency equal to 3.0 Hz (refer to Fig. 4). Additionally, the kinematics has been carefully adjusted in order to have the internal and external semi-wings aligned as much as possible during the downstroke (refer to Fig. 2), and not to generate high angular velocities as the external semi-wing begins to rotate when it approaches the end of the downstroke and upstroke (refer to Fig. 3).

Fig. 2
figure 2

Time evolution of the roll angle for a flapping frequency of 3.0 Hz. The vertical black lines represent different instants during one flapping period

Full size image
Fig. 3
figure 3

Time evolution of the angular velocity for a flapping frequency of 3.0 Hz. The vertical black lines represent different instants during one flapping period

Full size image
Fig. 4
figure 4

Time evolution of the aerodynamic forces. The forces are computed for the avian model configuration with no tail. Flapping frequency \(f=3.0\) Hz. Forward velocity \(V = 5.0\) m/s. Mean lift = 4.95 N. Mean thrust = −1.35 N (a negative sign means thrust production). Mean sideslip = 0.25 N. The vertical black lines represent different instants during one flapping period

Full size image

In addition to Eqs. 1–4, the following equations are needed to track the spatial position of the articulation axis 200:

$$\begin{aligned} z_{iw}&\,= \,1.0 (l_{int} + l_{gap}) cos (roll_{iw}), \end{aligned}$$
(5)
$$\begin{aligned} y_{iw}&\,= -1.0 (l_{int} + l_{gap}) sin (roll_{iw}), \end{aligned}$$
(6)
$$\begin{aligned} dz_{iw} &\,= -1.0 (l_{int} + l_{gap}) sin (roll_{iw}) droll_{iw}, \end{aligned}$$
(7)
$$\begin{aligned} dy_{iw} & \,= -1.0 (l_{int} + l_{gap}) cos (roll_{iw}) droll_{iw}. \end{aligned}$$
(8)

Equations 5 and 6, tracks the position in the z axis and y axis of the points located at a distance equal to the length of the internal semi-wing or \(l_{int}\) plus the length of the gap between the semi-wings or \(l_{gap}\), where \(l_{int} = 0.3833\) m and \(l_{gap} = 0.0333\) m. This distance is measured with reference to the point 000 (refer to Fig. 1). Equations 7–8 are used to obtain the linear velocities dz and dy along the z axis and y axis, respectively.

Finally, to track the spatial position and compute the linear velocities of the external semi-wing in the direction of the axes z and y, Eqs. 9–12 are used. These equations are expressed in terms of the reference length \(l_{cg}^{ew}\) which, in our case, is equal to the distance of the center of gravity of the external semi-wing with respect to the axis 200 or \(l_{cg}^{ew}=0.2333\) m.

$$\begin{aligned} z_{ew}= & {} 1.0 (l_{cg}^{ew}) ( roll_{iw} + roll_{ew} ), \end{aligned}$$
(9)
$$\begin{aligned} y_{ew} &\,=\, -1.0 (l_{cg}^{ew}) sin ( roll_{iw} + roll_{ew} ), \end{aligned}$$
(10)
$$\begin{aligned} dz_{ew}= & {} -1.0 (l_{cg}^{ew}) sin ( roll_{iw} + roll_{ew} ) ( droll_{iw} + droll_{ew} ), \end{aligned}$$
(11)
$$\begin{aligned} dy_{ew} &\,= -1.0 (l_{cg}^{ew}) cos ( roll_{iw} + roll_{ew} ) ( droll_{iw} + droll_{ew} ). \end{aligned}$$
(12)

To reach this kinematics, we have conducted an extensive parametric study, where the values of several control variables have been varied. Hereafter, we list the control variables adjusted and we give a brief description of their effect on the aerodynamic performance:

  • Maximum flapping angle or roll amplitude (\(A1_{iw}\) and \(A2_{iw}\) in Fig. 5). Let us consider the case where \(A1_{iw}=A2_{iw}=A_{iw}\). This variable has a direct effect on both the lift and thrust generation. As this angle is increased, the lift (during the downstroke) and the downforce (during the upstroke) increase, and this is due to the higher angular velocities. This variable (together with the flapping frequency) is also responsible for the thrust generation; for the right combination of flapping angle and flapping frequency, the wing will produce thrust or drag. Let us now introduce the Strouhal number St; this number is a dimensionless parameter that characterizes the vortex dynamics and shedding behavior of unsteady flows. St is defined as \(St=f \; L/U\), where f is the flapping frequency, L is a characteristic length (\(L= b \; sin(A_{iw})\) as defined by Taylor et al. [21]), and U is the forward velocity. Clearly, St relates the flapping angle and the flapping frequency. Many authors have found that flying animals cruise at a Strouhal number tuned for high power efficiency [21–25]. The enhanced efficiency range has been found to be between Strouhal values corresponding to \(0.2 < St < 0.4\), with a maximum efficiency peak at approximately \(St=0.3\). For values of \(St < 0.2\), it has been found that there is little or no production of thrust, and the power efficiency drastically drops. For values of St higher than 0.4, there is thrust production but the power efficiency decreases, albeit more gently. The proposed avian model, operates in the regime \(0.2 < St < 0.4\).

  • Flapping frequency f. As we increase the flapping frequency, lift increases and this is due to the larger angular velocities. Flapping frequency is related to the flapping angle through the Strouhal number. For the right values of flapping frequency and flapping angle, thrust will be produced and, as previously mentioned, there is a narrow range of St where propulsive efficiency is high (\(0.2 < St < 0.4\)). Additionally, high values of flapping frequency impose structural and power constraints. In this study, we limit the maximum flapping frequency to 3.0 Hz.

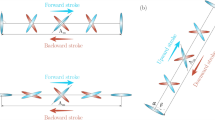
  • Maximum angle between the internal semi-wing and the external semi-wing, or articulation angle (\(A_{ie}\) in Fig. 5). The main reason to articulate the wings is to reduce the downforce and the amount of drag produced during the upstroke (cf. Fig. 4). During the downstroke the wing is totally extended, thus lift and thrust are maximized (as illustrated in Fig. 4). The maximum articulation angle used in this study is the one which provides the best trade-off among aerodynamic forces (including sideslip or lateral force). This variable is highly related to the angular velocity of the external semi-wing.

  • Angular velocity of the external semi-wing (\(droll_{ew}\)). In addition to the maximum articulation angle \(A_{ie}\), we carefully adjust the angular velocity of the external semi-wing in order not to generate high angular velocities, as the external semi-wing begins to rotate when it approaches the bottom-most and top-most positions (refer to Figs. 3 and 5), avoiding high aerodynamic forces and inertial loads that could destabilize or compromise the structural integrity of the avian model.

  • Position of the axis 200 or articulation axis (refer to Fig. 1). Similar to the articulation angle, this variable will reduce the downforce during the upstroke; however, it will have a positive or negative effect on the thrust generation and maximum lift peak according to the selected value. This variable also has a direct effect on the wing loading. The value of this design variable is varied between 30 and 70 % of the wing span b, and the best trade-off of lift, thrust/drag, and wing loading is found at approximately 40 % of the wing span b; consequently, all the simulations are conducted using this value. As illustrated in Fig. 1, the length of the internal semi-wing iw corresponds to about 40 % of the single wing span b, and for the external semi-wing ew is equal to about 60 % of b.

  • Velocity during the upstroke and downstroke (\(V_U\) and \(V_D\) in Fig. 5). By carefully designing the kinematics in order to have the wing going faster during the downstroke (\(V_D\)), and slower during the upstroke (\(V_U\)), the whole lift curve is shifted upwards (cf. Fig. 4). This effectively reduces the downforce during the upstroke; on the other hand the peak lift generated during the downstroke is higher (which could have a negative effect on the structural integrity due to an excessive wing loading), and higher mean lift values are produced. On the other side, this parameter has a marginal effect on the mean value of thrust, except for the variance of the instantaneous thrust/drag which is slightly larger. For all results presented in this study \(V_U=V_D\); this choice is taken to simplify the design of the mechanism, even though it is feasible to design a mechanism with \(V_D>V_U\).

  • Last but not least important, we discuss the implication of having an asymmetric flapping angle (\(A1_{iw} \ne A2_{iw}\) and \(A1_{iw} + A2_{iw} = 60^{\circ }\) in Fig. 5). This design variable is found to have a minimal effect on lift and thrust, hence we choose to use \(A1_{iw} = A2_{iw} = A_{iw}\). The only practical issue we evidence on using this design variable, is that if the model is set to take-off from the ground or fly in ground effect, by controlling this angle we can avoid the wing tip to hit the surface, that is, we increase the wing tip vertical clearance.

Fig. 5
figure 5

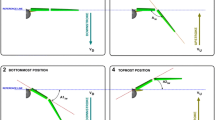
Illustration of the wing kinematics and design variables. \(A_{ie}=50^\circ\), \(A1_{iw} = A2_{iw} = A_{iw} = 30^\circ\), \(V_U=V_D\). The sequence is from 1 to 4, where 1 is the starting position, 2 is the bottom-most position, 3 is the mid-position during the upstroke, and 4 is the top-most position

Full size image

Finally, and using as a reference Fig. 5, all the simulations start with the wing totally extended in the middle position (1 in Fig. 5), then the wing goes down and starts to articulate as it reaches the bottom-most position (2 in Fig. 5). At this point, the wing starts to go up, passing again by the middle position but this time the wing is folded (3 in Fig. 5), until reaching the top-most position (4 in Fig. 5). As the wing reaches the top-most position it begins to articulate and starts its way back to the middle position (this time the wing is extended), to close one flapping cycle. A description of the mechanism which realizes the desired movement is given in reference [20].

5 Solution method overview and simulation setup

The unsteady, incompressible, Reynolds-Averaged Navier-Stokes (URANS) equations are solved by using the commercial finite volume solver Ansys® Fluent [26]. The cell-centered values of the computed variables are interpolated at the face locations using a second-order centered difference scheme for the diffusion terms. The convective terms at cell faces are interpolated by means of a second-order upwind scheme. For computing the gradients at cell-centers, the least squares cell-based reconstruction method is used. In order to prevent spurious oscillations, a multidimensional slope limiter is used, which enforces the monotonicity principle by prohibiting the linearly reconstructed field variables on the cell faces to exceed the maximum or minimum value of the neighboring cells. The pressure-velocity coupling is achieved by means of the PISO algorithm and, as the solution takes place in collocated meshes, the Rhie–Chow interpolation scheme is used to prevent the pressure checkerboard instability. For turbulence modeling, the shear-stress transport (SST) \(\kappa\)–\(\omega\) model [27] is used with blending wall functions [28, 29]. The turbulence quantities, namely, turbulent kinetic energy \(\kappa\) and specific dissipation rate \(\omega\), are discretized using the same scheme as for the convective terms. For the temporal discretization, we use a second order implicit method. The time-step is chosen in such a way that the CFL number is not >1.0. This results in a numerical method that is stable, bounded, and second order accurate in space and time.

To handle the moving bodies, the dynamic meshing model is employed [26], where we use mesh diffusion smoothing to deform the mesh, and in order to avoid degenerated cells, remeshing was used every 20 time steps. In the remeshing stage, we monitor two mesh quality metrics thresholds, namely, maximum skewness and minimum cell volume. Those cells with a skewness higher than the predefined threshold or with a volume less than the predefined threshold, are marked for refinement or coarsening. Prismatic cells are used near the wing surface and tetrahedral cells in the rest of the domain; only the latter are tagged for refinement/coarsening. In order to avoid an excessive cell count due to refinement, all the remeshing process is controlled in such a way that the final mesh does not exceed 3.0 millions cells.

The lift force L and drag force D are calculated by integrating the pressure and wall-shear stresses over the surface of the avian model. As for the lift and drag forces, the moment M is computed by integrating the pressure and wall-shear stresses over the surface of the model and it is calculated about a reference point (e.g., the center of gravity). As we are dealing with an unsteady aerodynamics case, i.e., the wings are flapping, the lift, drag and moment are averaged in time as follows:

$$\begin{aligned} \overline{L} = \frac{1}{\mathbb {T}} \int _t^{t+\mathbb {T}} L(t) dt ; \;\;\; \overline{D} = \frac{1}{\mathbb {T}} \int _t^{t+\mathbb {T}} D(t) dt ; \;\;\; \overline{M} = \frac{1}{\mathbb {T}} \int _t^{t+\mathbb {T}} M(t) dt, \end{aligned}$$
(13)

where \(\mathbb {T}\) is the period of the flapping motion (\(\mathbb {T}= 1/f\)). All aerodynamic forces and moments are averaged over the fourth period of the oscillations.

In Fig. 6, a sketch of the computational domain and the boundary conditions layout are shown. The inflow in this figure corresponds to a Dirichlet type boundary condition and the outflow to a Neumann type boundary condition. All the computations are initialized using free-stream values. For all the simulations, the incoming flow is characterized by a low turbulence intensity (TU = 1.0 %), and the working fluid is air at standard sea level (\(\rho\) = 1.225 kg/m\(^3\) and \(\mu = 1.81\times 10^{-5}\) Pa s ). The Reynolds number, based on the mean aerodynamic chord (\(MAC_w\)) and the minimum design velocity (\(V=5.0\) m/s) is \(Re = {\rho \; V_{\infty } \; MAC_w} / {\mu } \approx 115000\).

Fig. 6
figure 6

Computational domain and boundary conditions, all dimensions are in meters (sketch not to scale)

Full size image

Figure 7 displays quantitative and qualitative results for a typical simulation. In the figure, the avian model surface is colored using pressure, and the vortices are visualized by using the Q-criterion [30]. Notice in the figure the vorticity produced at the wing gaps; this vorticity penalizes the aerodynamic performance by increasing the drag. Also, the gaps generate a discontinuous lift distribution in the wing span, hence we are designing the model in a very conservative scenario. Most of the computations are carried out on two Intel Xeon X5670 at 2.93 GHz CPUs with 32 GB of RAM, and each simulation takes approximately 24–36 h. In total over a 1000 full simulations have been run to span the whole space of parameters.

Fig. 7
figure 7

Quantitative and qualitative results of a typical simulation. The case corresponds to a flapping frequency of 3.0 Hz, forward velocity of 6.0 m/s, pitch angle \(0^{\circ }\), and tail deflection of \(15^{\circ }\). For the half-model shown the mean lift is 4.79 N, the mean thrust is \(-\)1.12 N (positive sign would denote drag), and the mean sideslip = 0.76 N (the latter force is balanced by the other half of the model). Different animations are available on the first author’s website, http://www.dicat.unige.it/guerrero/flapuav.html

Full size image

6 Aerodynamic performance in gliding and flapping flight

In this section, we discuss the results of the aerodynamic performance of the avian model in gliding and flapping flight. As at this point we are not yet interested in the static stability of the model, the results presented are for the model configuration without tail and we limit our discussion to lift generation, thrust (or drag) production, and lift-to-drag ratio.

In Fig. 8, we show the drag polar in gliding flight for different cruise velocities and pitch angles. From this figure, we observe that the current design is able to generate the minimum lift required to keep the model aloft (minimum lift line in Fig. 8). In the figure, we do not show the results for the minimum velocity (V = 5.0 m/s), as we do not envisage the model operating for long periods in gliding configuration below a forward velocity of V = 6.0 m/s. If at any moment the velocity falls below this value the model enters into flapping mode.

Fig. 8
figure 8

Drag polar in gliding flight and different cruise velocities. The forces correspond to the no tail configuration and half the model. The numbers next to the curves indicate the pitch angle of the avian model. Positive pitch angle means nose up

Full size image

In Fig. 9, we show the lift-to-drag ratio (L / D) in gliding flight. In the figure, the maximum L / D ratio is between a pitch value of \(0^{\circ }\) and \(2^{\circ }\). It is in this range that the wings give their best all-round results, i.e., they generate as much lift as possible with a small drag production. Hence, it is desirable to operate in this range of pitch angles when gliding.

Fig. 9
figure 9

Lift-to-drag ratio in gliding flight and different cruise velocities for the no tail configuration and half the avian model. Positive pitch angle means nose up

Full size image
Fig. 10
figure 10

Drag polar in flapping flight and different cruise velocities. Flapping frequency is equal to 3.0 Hz. The forces correspond to the no tail configuration and half the model. In the figure, negative values of mean drag correspond to thrust generation

Full size image

Next, we discuss the lift generation and thrust (or drag) production in flapping flight. In Fig. 10, we show the polar plot in flapping flight for a flapping frequency of 3.0 Hz, several cruise velocities ranging from the minimum design velocity to the maximum cruise velocity (refer to Table 1), and different avian model pitch angles, in a range from \(-6^{\circ }\) to \(6^{\circ }\). Let us take a look at the minimum lift line in Fig. 10; all the values above this line correspond to configurations (in terms of forward velocity and pitch angle) that produce the minimum lift required (i.e., half the maximum weight). If we now look at the zero acceleration line in Fig. 10, we see that all values to the left of this line correspond to cases where we generate thrust (negative drag). We are interested in operating in the quadrant that is located above the minimum lift line and to the left of the zero acceleration line. All the cases located in this quadrant fulfill our design requirements; however, this does not necessarily mean that the avian model can operate in any of these scenarios.

For example, using Fig. 10 as a reference, at a forward velocity of 12.0 m/s and pitch attitude of \(0^{\circ }\), the avian model produces a mean lift of over 18.0 N, far more than the minimum lift required; consequently, this will generate controllability issues due to high vertical velocities. It will also compromise the structural integrity of the model because of the excessive wing loading. Hence, the possible operating scenarios are a compromise among lift, thrust, wing loading, stability and controllability issues.

Let us now take a look at the lift and drag values at our design conditions (\(f=3.0\) Hz and V = 5.0 m/s). From Fig. 10, it is evident that we meet our design requirements provided the pitch angle of the model exceeds \(0^{\circ }\); moreover, at this condition the model is operating at a \(St=0.3\), which corresponds to the maximum propulsive efficiency of many flying animals [21–25]. When the avian model is operating at these design conditions, the model will accelerate, as a consequence the lift will increase, and this will generate a vertical acceleration. Thus, to keep the model in level flight we shall resort to intermittent flight, where the model flaps its wings to accelerate and maintain a velocity above the minimum requirements, and then it switches to gliding flight to avoid producing too much lift. As soon as the cruise velocity falls below 6.0 m/s, the avian model starts to flap its wings again.

It is worth mentioning that in order to converge to the dimensions presented in Table 3, we have conducted a parametric study in gliding and flapping flight, where we have used as initial reference for the sizing of the avian model the body measurements of the gulls family, as presented in Table 2. This design iteration consists in assuring that at the design specifications of Table 1, the avian model is able to produce the minimum lift in gliding and flapping flight and it is also capable to produce thrust when it flaps its wings. By comparing the sizing of the proposed avian model (as described in Table 3) and the body measurements of the gulls family (shown in Table 2) it is clear that the dimensions of the model are larger than those of the gulls family, and this is due to the design constraints listed in Table 1. If we were able to flap the wings at frequencies close to 3.5 Hz, the ornithopter dimensions would be closer to those of the reference gulls (as shown in Table 2). Additionally, in order to provide the high lift required at low velocities (in gliding and flapping flight), and at a pitch angle between \(0^{\circ }\) and \(2^{\circ }\) (corresponding to the range of maximum lift-to-drag ratio), and as we can not use lift augmentation devices, the wing span and wing area requirements are over-dimensioned.

Finally, for the wings cross-section, we use the high lift Selig 1223 airfoil [31, 32], the choice of this airfoil help us in reducing the wing span and wing area requirements; however, this airfoil comes with an undesirable by-product, high residual pitching moment (nose down moment). This pitching moment needs to be taken into account when designing the tail if we want to get a stable configuration in gliding and flapping flight. The avian model static stability is addressed in the next section.

7 Longitudinal static stability in gliding flight

In this section, we discuss the results pertaining to the longitudinal static stability of the avian model in gliding flight. It is essential that the avian model remain stable in gliding flight before flapping flight is addressed.

For the avian model to have longitudinal static stability, two conditions must be fulfilled. First, the model must have positive longitudinal static stability, that is, if the model is perturbed from its original trim condition it must return to it. And second, the model must have a trim angle within the flight envelope, and preferably it has to be positive. The trim angle is the pitch angle at which the sum of the moments acting about the center of gravity (CG) is equal to zero.

It is clear that determining the position of the CG of the model is of great importance in order to have a stable configuration. Also, if we want to trim the model at a given pitch angle, somehow we need to generate a moment that will set the avian model to the desired pitch attitude. The vehicle component responsible for generating this moment is the tail or horizontal stabilizer. The tail position relative to the wing, its sizing, incidence angle, and its lift characteristics, are chosen in such a way that the avian model has positive longitudinal static stability and a trim condition at a positive pitch angle. The aforementioned tail design variables can be adjusted at any time in the design phase in order to satisfy further stability, trimmability and controllability requirements.

In Table 4, some of the CG locations explored during this study are listed. In the table, the CG location is measured with reference to the point 000 (as illustrated in Fig. 1). The influence of the CG position on the longitudinal static stability is shown in Fig. 11. In this figure, we plot the results for a configuration corresponding to a tail deflection of \(15^{\circ }\) and a forward velocity of 6.0 m/s, where a positive tail deflection is defined such that it generates a pitch up attitude of the whole model. In the figure, we can observe that for CG1 the model has positive stability, that is, the slope of the curve is negative:

$$\begin{aligned} \frac{\partial M}{\partial \alpha } < 0, \end{aligned}$$
(14)

where \(\alpha\) is the pitch angle. As we move the CG aft (i.e., towards CG2), we see how the stability of the model changes; CG2 corresponds to the neutral point of the model (aerodynamic center of the whole configuration). The neutral point is the point at which the moment about the CG is independent of the pitch angle, and if we go beyond this point the model will become unstable, as for CG3 in Fig. 11. For the sake of completeness, in the figure, positive pitch moment generates a nose up attitude, conversely, negative pitch moment generates a nose down attitude.

Fig. 11
figure 11

Gliding case. The influence of CG position on the longitudinal static stability. Stabilizer angle = \(15^{\circ }\). Velocity = 6.0 m/s

Full size image

To find the best position of the CG according to our requirements, for every single simulation we measure the avian model moment about different CG positions. As a result of this study, the best position of the center of gravity is found to be CG1 and, from now on, all results will be presented with reference to CG1 (for gliding and flapping flight). It is worth mentioning that for the CG selection we have also taken into consideration the possible limitations when positioning all the flight systems and mechanism inside the fuselage.

Table 4 Center of gravity (CG) location
Full size table

So far in our discussion we only have dealt with the longitudinal stability; let us now talk about longitudinal control and trimmability. These two properties of the flight vehicle are ensure by the tail surface. By looking at Figs. 12, 13 and 14, first we notice that all cases are stable, the slope of the curves \(\partial M / \partial \alpha\) is negative. Next, it can be seen that for different tail deflection angles the model has different trim angles, by changing the incidence angle of the tail we can control the longitudinal attitude (pitch angle) of the ornithopter. In the figures we also observe how the pitch stiffness or magnitude of the slope of the curve \(\partial M / \partial \alpha\), changes with the velocity. For higher velocities the pitch stiffness is larger, hence the tail restoring moment is higher.

Fig. 12
figure 12

Gliding case. Pitching moment about CG1 at different cruise velocities. Stabilizer angle = \(10^{\circ }\)

Full size image
Fig. 13
figure 13

Gliding case. Pitching moment about CG1 at different cruise velocities. Stabilizer angle = \(15^{\circ }\)

Full size image
Fig. 14
figure 14

Gliding case. Pitching moment about CG1 at different cruise velocities. Stabilizer angle = \(20^{\circ }\)

Full size image

For a tail deflection angle of \(10^{\circ }\) (Fig. 12) it can be seen that for all forward velocities studied the model trim is approximately between \(-6^{\circ }\) and \(-4^{\circ }\). This scenario is not desirable, we are looking for a trim condition with a positive pitch angle, and preferably close to the pitch angle corresponding to the maximum L/D ratio. If we now change the tail deflection to \(15^{\circ }\) (Fig. 13), the trim angle for the velocity range considered is now between \(0^{\circ }\) and \(1^{\circ }\), this is a desirable scenario. Finally, and as we keep increasing the tail deflection angle until we reach \(20^{\circ }\) (Fig. 14), we observe that the trim condition changes to a pitch angle between \(4^{\circ }\) and \(6^{\circ }\).

By changing the incidence angle of the tail we can control the longitudinal attitude of the model (as shown in Figs. 12, 13 and 14). When we deflect the tail, we change the lift, drag, and pitching moment of the avian model. For example, to reach a nose up attitude, we need to generate a downforce on the tail to develop a trim moment, and this moment generates trim drag that changes the aerodynamic performance. Also, the downforce generated by the tail reduces the mean lift of the whole model. We need to take into account these shortcomings when studying the aerodynamic performance. We will address in more details the trim drag and tail downforce when we study the stability in flapping flight.

Summarizing this discussion, for the tail deflection angles and CG locations studied in gliding flight, it is found that the avian model is stable, trimmable and controllable within the flight envelope.

8 Longitudinal static stability in flapping flight

Like in the gliding case, we first study how the position of the CG affects the stability of the model. The influence of the CG position on the longitudinal static stability in flapping flight is shown in Fig. 15, where we plot the results for a case corresponding to a tail deflection of \(15^{\circ }\) and a forward velocity of 6.0 m/s. From the figure, it can be seen that the model has positive static stability, but differently to the gliding case, the model is stable for all CG positions. We also observe that, as we move the CG aft, the magnitude of the slope of the curve \(\partial M / \partial \alpha\) decreases, and this changes the trim condition of the avian model to the point that the model does not have a trim point within the range of pitch angles explored. This situation is better illustrated in Fig. 16, where the influence of the CG position on the stability of the model for a forward velocity of 8.0 and 14.0 m/s is displayed. By inspecting this figure, we note that for CG3 and a forward velocity of 14.0 m/s it is not possible to trim the model within the chosen range of pitch angles; however, at a forward velocity of 8.0 m/s, the model has a trim condition at approximately \(6^{\circ }\). Another interesting observation from Figs. 15 and 16 is that the \(\partial M / \partial \alpha\) curves appear to show a trend to an unstable break-up, that is, for pitch angles larger than the maximum value shown in the figures, the slope of the curves might become positive and any contribution of the pitching moment will be destabilizing.

This difference between the stability in gliding and flapping flight, is chiefly due to a complex interaction between the highly unsteady aerodynamic forces generated by the wings during a flapping cycle, and the downforce and drag generated by the tail. During a flapping cycle the thrust line is not fixed, it changes in the vertical direction. Thus, according to the vertical position of the thrust line in reference to the CG, thrust can generate a nose up or nose down attitude; even more, during the upstroke the wings mainly generate drag and when the line of application of the drag force is above the CG, it has a positive effect on the stability of the model as it generates a pitch up moment. Additionally, the restoring moment generated by the tail produces a high trim drag. The line of application of the trim drag is above the CG, hence it contributes to the static stability.

Fig. 15
figure 15

Flapping case. Influence of CG position on the longitudinal static stability. Flapping frequency = 3.0 Hz. Stabilizer angle = \(15^{\circ }\). Velocity = 6.0 m/s

Full size image
Fig. 16
figure 16

Flapping case. Influence of CG position on the longitudinal static stability. Flapping frequency = 3.0 Hz. Stabilizer angle = \(15^{\circ }\). The continuous line corresponds to a velocity of 14.0 m/s, whereas the dashed line corresponds to a velocity of 8.0 m/s

Full size image

Let us focus our attention on the controllability and trimmability of the avian model in flapping flight. In Fig. 17 we show the results for a configuration with a tail deflection of \(10^{\circ }\). For the velocities plotted, it can be seen that the model is trimmable. Also, the trim angle changes as the pitch stiffness changes, which depends on the forward velocity. From the figure, the model trim is between \(-6^{\circ }\) and \(-3^{\circ }\), depending on the forward velocity.

Fig. 17
figure 17

Flapping case. Pitching moment about CG1 at different cruise velocities. Flapping frequency = 3.0 Hz. Stabilizer angle = \(10^{\circ }\)

Full size image

In Fig. 18, the aerodynamic performance for the same avian model configuration presented in Fig. 17 is shown. As for the gliding case, deflecting the tail changes the lift, drag, and pitching moment of the whole model. In this figure, we observe that for a forward velocity of 5.0 m/s and pitch angle of \(0^{\circ }\), the avian model produces just a little less lift than required. This degradation on the lift is due to the downforce generated by the tail. To avoid the problem of not producing enough lift, the model can be set to a pitch angle of \(2^{\circ }\). Also, if we compare Figs. 18 and 10, we note that now we are limiting the maximum cruise velocity. For the case shown in Fig. 10 the model reaches a maximum velocity above 14.0 m/s, whereas for the case presented in Fig. 18, the maximum cruise velocity is limited to about 12.0 m/s. Notice that we also lessen the amount of thrust produced for each pitch angle and forward velocity combination studied. This reduction in the maximum cruise velocity and thrust generated is due to the trim drag.

To circumvent the problem of high trim drag, we can use a thin asymmetrical airfoil in the tail, in this way we will able to produce an equivalent downforce at a smaller tail incidence angle; this will translate into a significant reduction of the trim drag and on an improvement of the controllability.

Fig. 18
figure 18

Drag polar in flapping flight and different cruise velocities. Flapping frequency is equal to 3.0 Hz. Stabilizer angle = \(10^{\circ }\)

Full size image

In Fig. 19, we show the results for the avian model with the tail at \(15^{\circ }\) of incidence. By inspecting the figure and comparing the results with those in Fig. 17, we note that the trim angle is different; now the model has a nose up attitude. For the case of forward velocity of 5.0 m/s the trim is approximately \(-3^{\circ }\) and as the velocity increases the pitch stiffness increases and the trim angle sets between \(0^{\circ }\) and \(2^{\circ }\). In order to get a positive trim angle at low velocities (5.0 m/s), we must increase the tail angle to reach the desired pitch angle. This is shown in Fig. 21, where for a tail deflection of \(20^{\circ }\), we get a trim condition around \(0^{\circ }\). As for the previous cases, as we increase the forward velocity the pitch stiffness increases. In this figure, for velocities larger than 6.0 m/s the trim angle is between \(4^{\circ }\) and \(6^{\circ }\).

Fig. 19
figure 19

Flapping case. Pitching moment about CG1 at different cruise velocities. Flapping frequency = 3.0 Hz. Stabilizer angle = \(15^{\circ }\)

Full size image
Fig. 20
figure 20

Drag polar in flapping flight and different cruise velocities. Flapping frequency is equal to 3.0 Hz. Stabilizer angle = \(15^{\circ }\)

Full size image

In Figs. 20 and 22, we show the results of the aerodynamic performance for a tail deflection of \(15^{\circ }\) and \(20^{\circ }\), respectively. As previously discussed, as we increase the tail deflection the downforce generated by the tail is higher, hence the mean lift of the model is lower. By simply changing the pitch angle, we can avoid operating in flight conditions where we produce less lift than needed. Additionally, the high trim drag is reflected in the reduced maximum cruise velocity and thrust generation for both cases (Fig. 21).

Fig. 21
figure 21

Flapping case. Pitching moment about CG1 at different cruise velocities. Flapping frequency = 3.0 Hz. Stabilizer angle = \(20^{\circ }\)

Full size image
Fig. 22
figure 22

Drag polar in flapping flight and different cruise velocities. Flapping frequency is equal to 3.0 Hz. Stabilizer angle = \(20^{\circ }\)

Full size image
Fig. 23
figure 23

Flapping case. Pitching moment with tail incidence angle variation. Flapping frequency = 3.0 Hz. Velocity = 8 m/s

Full size image

Drawing our attention to Fig. 23, and to illustrate that the avian model is controllable within the flight envelope, we show the tail effectiveness. By looking at this figure, we observe that changing the tail angle does not change the slope of the curve \(\partial M / \partial \alpha\). Changing the tail incidence angle, shifts the curve upwards at specific increments of \(\varDelta M\). This figure indeed shows that the model can be controlled and trimmed in flapping flight.

To conclude this discussion on the static stability of the model in flapping flight, and by looking at Figs. 18, 20 and 22, it is clear that is not trivial to find a scenario that holds for steady-level flight. One solution to this problem is intermittent flight, where the model flaps its wings to accelerate and generate the required lift, and then it switches to gliding flight at a pitch angle corresponding to the maximum L/D ratio. As soon as the lift produced is less than the minimum required lift, the model switches back to flapping flight. It is clear that to achieve intermittent flight, a proper control system must be designed and this is out of the scope of the present contribution.

Summarizing all the results presented for flapping flight, it can be stated that within the flight envelope and CG positions studied, the model is stable, controllable and trimmable.

9 Conclusions and perspectives

In this manuscript, the preliminary design of a biologically inspired flapping UAV has been presented. The shape and flight conditions of the avian model are based on the morphometrics/allometry and radar flight measurements of several bird species. The final shape of the proposed avian model approximates that of the gulls family, which meet our design specifications and operating requirements.

To design a flapping kinematics that mimics that of actual birds we have conducted an extensive parametric study. The flapping kinematics design variables adjusted are:

  • Maximum flapping angle on the internal wing.

  • Flapping frequency.

  • Maximum angle between the internal semi-wing and external semi-wing.

  • Angular velocity of the external semi-wing.

  • Position of the articulation axis.

  • Wing angular velocity during upstroke and downstroke.

  • Flapping angle in order to get a symmetric or asymmetric kinematics.

By carefully modifying the values of these design parameters, we have converged onto a flapping kinematics that resembles that of nature’s fliers, generates thrust and lift, does not generate high angular velocities and inertial loads that could compromise the structural integrity or destabilize the avian model and, most importantly, it is realizable from a mechanical point of view. By articulating the wings more energy efficient operations are allowed, since during the upstroke the downforce is highly reduced and the drag force is almost zeroed.

Regarding the aerodynamic performance of the avian model in flapping flight, and for the design goals and the wide range of velocities, pitch angles, and tail deflection angles studied, it is found that the proposed model and flapping kinematics are able to fulfill the design requirements. For the flight envelope studied, the avian model is able to produce thrust up to a velocity of approximately 14.0 m/s, and it generates enough lift to meet and exceed the weight constraints.

For the best location of the center of gravity (CG1), and for the tail configuration and deflection angles considered during the longitudinal static stability study, it has been found that the model has positive stability and it is trimmable in gliding and flapping flight. The tail effectiveness results show that the avian model is controllable and trimmable for the tail configuration used and pitch angles, forward velocity and tail deflection angles explored.

During this study, it also has been observed that the stability of the avian model is different in gliding and flapping flight, and this is chiefly due to a complex interaction between the unsteady aerodynamic forces generated by the wings during a flapping cycle, and the downforce and trim drag generated by the tail.

One limitation that has been observed during the stability study, is the trim drag penalization on the maximum cruise velocity. To have a stable and trimmable avian model, the tail needs to be set at high incidence angles, this in turn generates high trim drag. This trim drag reduces the maximum cruise velocity which for the worse case scenario (tail incidence angle at \(20^{\circ }\)), goes down to about 10.0 m/s. To avoid this problem, we can use a thin asymmetrical airfoil in the tail, in this way we will be able to produce an equivalent restoring moment at smaller tail incidence angles; this translates into a significant reduction of the trim drag and on an improvement of the controllability.

From the results shown in the drag polars for flapping flight, it is not trivial to find an operating condition for steady-level flight. A solution to this problem is the use of intermittent flight, where the model uses a combination of gliding and flapping flight in order to keep a steady-level flight condition.

It is clear that identical copies from nature to man-made technologies are not feasible in biomimetics. However, during the design iterations we have slowly converged to what is found in nature (in terms of morphology, wings’ kinematics, and operating conditions). Our results confirm the observations of many authors who have found that flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. The enhanced efficiency range has been found to lie in the range \(0.2 < St < 0.4\), with a maximum efficiency peak at approximately \(St=0.3\) [21–25]. The proposed avian model operates in this range of St at design conditions and low forward velocities.

Also, and in spite of the fact that our design does not closely match the body measurements of comparable natural fliers [16–18], if we were able to increase the flapping frequency to values close to 3.5 Hz, we would get a good agreement with respect to the morphology/allometry of analogous bird species [16–19]. However, taking blueprints of nature does not guarantee that the best solution will be found. It is possible that a more efficient flapping UAV design exist beyond what nature has explored. Nevertheless, designing a flapping UAV that exhibits some of the skills of natural fliers, is already a large step forward in biomimetics.

Finally, the extension of the current study is envisaged towards the study of the lateral-directional stability in gliding and flapping flight, the dynamic stability in flapping flight by using a multibody dynamics approach, and the design of a control system. We also look upon using an optimization method to design a better flapping kinematics and consequently reduce the dimension of the model and improve the overall aerodynamic performance, stability, trimmability and controllability of the ornithopter.