The effect of weak-inertia on droplet formation phenomena in T-junction microchannel

Abstract

We present droplet formation in a T-junction microfluidic device in five different regimes of squeezing, dripping, transition, jetting and parallel. Droplet is created as a result of interaction of two immiscible liquids. Effects of Capillary number (Ca) and Reynolds number (Re) are investigated which changes the regime of droplet formation and creates rotational flow inside droplet, respectively. Simulations were done with the open source code Gerris using volume of fluid method and adaptive mesh refinement techniques in order to track interface properly. Two kinds of jetting regimes, i.e., stable and unstable, were simulated in this work. For higher Re number the parallel regime is observed so Re number is limited to 25. This study shows that the results of Re > 1 have some differences compared with those of Re < 1. Using the effect of inertial forces, transition regime is limited to a range of Ca number. Simulations indicate that new vortices are created due to effect of inertial forces at a moment after droplet detachment, while it is fully creeping flow for Re < 1. The vortices which have appeared at the tail of droplet will become weaker with time. Also, at the downstream, two rotational flows were observed in droplet for both Re > 1 and Re < 1 which are due to wall shear stresses. Droplets with rotational flow can increase diffusivity, which is motivation of this work.

1 Introduction

Droplet formation of a fluid in a second immiscible fluid has many practical applications in microfluidic such as biological processes, chemical analyses, drug delivery, heat exchangers etc. T-junction microchannels are used for droplets formation, fusion, fission and microscale mass transportation such as proteins [1].

Many researchers have studied a droplet formation in T-shaped microchannel numerically and experimentally. Up to now, several experimental investigations have been reported on droplet formation. Thorsen et al. [2] performed experiments to investigate the formation of aqueous droplets in oil. They reported that the competition between shear force and surface tension dominates the droplet formation. Garstecki et al. [3] found out that at squeezing regime, the tip of the dispersed phase blocks the main channel due to the surface tension dominating the shear stress. In addition, the continuous phase confined to thin films, between the tip of the dispersed phase and the channel walls, increases viscous resistance and pressure build-up (in the continuous phase) at the upstream of the tip. Also, they offered a scaling law to determine droplet size depending on the channel geometry and flow rate ratio of two phases, which is $Q = {{u_{\text{c}} } \mathord{\left/ {\vphantom {{u_{\text{c}} } {u_{\text{d}} }}} \right. \kern-0pt} {u_{\text{d}} }}$ for microchannel with square cross-section, where u, subscripts “c” and “d” represent flow velocity, the continuous phase and the dispersed phase, respectively. Van Steijn et al. [4] reported that in squeezing regime for square microchannels, a thin film of the continuous fluid leaks around the tip of the disperse phase to downstream, besides there are 4 open corners at the channel 4 angles where the continuous fluid leaks from. The total amounts of these leaks include 25 % of continuous fluid volume. This phenomenon has been confirmed by Li et al. [5]. They used rectangular microchannel for their experiments and simulations that resulted in similar results to Oishi et al. [6]. Also several analytical equations were presented to predict the forming droplet diameter. Some of these equations were provided to predict the droplet diameter in squeezing and dripping regimes according to the balance between tangential shear stress and the interfacial tension, with this fact that Bond number (Bo), which signifies effect of gravitational force against interfacial force, is usually <1 (${\text{Bo}} < < 1$) [7]. Some others presented analytical equations to predict the droplet diameter in transition regime, which occurs between squeezing and dripping regimes [8]. Van Steijn et al. [9] proposed analytical equations involving the curvature of the dispersed phase to determine the formed droplet volume.

Through a series of simulations in T-junction microchannels, various mathematical methods have been employed. De Menech et al. [10] employed phase-field model to identify three different regimes of squeezing, dripping and jetting for droplet formation. In addition, they pointed out that in case of the two phases being liquid, the difference in their densities is negligible. They mentioned that the phases’ intensity difference effect on the results is negligible since in most microfluidic configurations buoyancy-driven speeds are much smaller than the actual flow speed. Of the 3D simulations performed is using Lattice Boltzmann Method (LBM). Gupta and Kumar [11] demonstrated the effect of geometry on the formed droplet size and presented an analytical model for predicting the droplet formation. They found that the dimensionless number λ = μ _d /μ _c , which is viscosity ratio between the dispersed phase and the continuous phase, has significant effect on the formed droplets size. Also they described the flow in the thin gap in the continuous thin film and between the dispersed fluid and the upper wall of the channel in the squeezing regime similar to Hagen–Poiseuille flow. Some other numerical modeling have been conducted through LBM for droplet formation simulation in square microchannel [4]. In the continuation, Wang et al. [12] simulated the droplet formation in microchannel with LBM in 2D and 3D. They used venturi-shaped microchannel to control the droplet formation. They also announced that the droplet size decreases and frequency increases with the presence of venturi. Their results show that 2D simulation can predict the overall droplet formation in T-junction microchannel. In addition, 2D simulation has not been predicted the transition regime, correctly. Yang et al. [13] applied LBM and combined it with the immersed boundary method (IBM) to simulate cell encapsulation as well as cell deformation inside the droplet. In addition, they explained pressure variation before and after droplet formation, for three regimes of squeezing, dripping and jetting. Furthermore, for the droplet formation simulation, some researchers used volume of fluid (VOF) method and found that in the squeezing regime, the pressure profile of the dispersed phase and the continuous phase changes during the droplet formation process. Their results revealed that the minimum pressure difference occurs at the last moment of the droplet break-up [14]. Based on the numerical simulations using level set method (LSM), Yan et al. [15] reported a 3D simulation using LSM for studying the droplet formation in a T-junction. They investigated pressure fluctuation near junction point to identify five different regimes. Bashir et al. [16] investigated pressure profile variation of both the dispersed and continuous phases during the droplet break-up process. In addition, they studied the effect of Capillary number ${\text{Ca}} = {{u_{\text{c}} \mu_{\text{c}} } \mathord{\left/ {\vphantom {{u_{\text{c}} \mu_{\text{c}} } \gamma }} \right. \kern-0pt} \gamma }$, which represents relative effect of viscous forces versus interfacial forces, and flow rate on the droplet formation. Also, γ is interfacial tension between the two phases.

To the authors’ knowledge, in T-junction microchannel, the effect of Reynolds number $\left( {\text{Re} = {{u_{\text{c}} \rho_{\text{c}} {\text{w}}} \mathord{\left/ {\vphantom {{u_{\text{c}} \rho_{\text{c}} {\text{w}}} {\mu_{\text{c}} }}} \right. \kern-0pt} {\mu_{\text{c}} }}} \right),$ which is defined as the ratio of inertial forces to viscous forces, has not yet been studied on droplet formation. ρ and w represent density and the channel width. For Re > 1, droplet formation at the break-up moment and after that is different from low Re, such as rotational flow inside droplet and this subject has been studied in this work. Various dimensionless parameters such as Q, Ca and Re have been taken into account and it has been tried to analyze their influence on droplet formation in different regimes. Five different regimes as squeezing, dripping, transition, jetting and parallel were simulated in this work but the jetting regime could be simulated only in 3D simulation. The reason is in 3D nature of complex hydrodynamics of droplet movement in this regime, in which shear stress and pressure drag are important parameters.

2 Governing equations

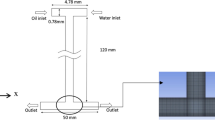
In the present study, the flow of the two immiscible liquids in T-junction microchannel has been simulated (Fig. 1). Using non-dimensional variables defined in Eq. (1), the formulation is based on incompressible Navier–Stokes equation Eq. (2), with variable-density flow pattern Eq. (3), and continuity equation for each phase Eq. (4). According to mass continuity, the advection equation for the density Eq. (5) takes the following form in terms of the volume fraction.

Fig. 1

Schematic of T-junction microchannel. Scale bar is 1 mm. a 2D simulation in x–y axis. b 3D simulation

$$ \varvec{x}^{*} = \frac{\varvec{x}}{\text{w}}\quad u^{*} = \frac{u}{{\text{U}_{0} }}\quad \rho^{*} = \frac{\rho }{{\rho_{\text{c}} }}\quad \mu^{*} = \frac{\mu }{{\mu_{\text{c}} }}\quad \text{t}^{*} = \text{t}\frac{{\text{U}_{0} }}{\text{w}}\quad \text{P}^{*} = \text{P}\frac{\text{w}}{{\rho_{0} .\text{U}_{0}^{2} }} $$

(1)

$$ \left( {{\partial }_{\text{t}}^{*} u^{*} + u^{*} .\nabla^{*} u^{*} } \right) = - {\nabla }^{*} p^{*} + \frac{1}{\text{Re}}{\nabla }^{*} \cdot \left( {D^{*} } \right) + \frac{1}{{{\text{Re}} \cdot {\text{Ca}}}}\kappa \delta_{s} n $$

(2)

$$ {\partial }_{\text{t}}^{*} \rho^{*} + {\nabla }^{*} \cdot \left( {\rho^{*} u^{*} } \right) = 0 $$

(3)

$$ {\nabla }^{*} \cdot \varvec{u}^{*} = 0 $$

(4)

$$ {\partial }_{\text{t}}^{*} c + {\nabla }^{*} \cdot \left( {c\varvec{u}^{*} } \right) = 0 $$

(5)

where u, p, D denotes the velocity vector, pressure and the deformation tensor, respectively. The deformation tensor defined as D _ij  = ( ∂  _i u _j  + ∂  _j u _i )/2. The Dirac delta function δ _s represented that the surface tension σ is concentrated on the interface. κ expresses the radius of curvature of the interface, and the unit outward vector normal to the interface is denoted by n [17].

3 Numerical method

The numerical method is based on solving the explicit governing equations of the flow pattern with direct numerical simulation (DNS) by using the open source code Gerris [17, 18]. In order to discretize the equations, a second-order accurate scheme has been used for the spatial and temporal variables. For the discretization of the geometry, the VOF method has been adopted with the staggered grids which velocity components locate at the face of the control volume while other variables are in the cell center. Uniform velocities (Dirichlet boundary condition) are set at the inlets, at the side channel inlet $u = u_{\text{d}}$ and at the main channel inlet $u = u_{\text{c}}$. The outflow boundary condition is considered at the outlet in which assumes a fully developed flow field at the end of the main channel; it deforms shape of droplets which reach to the outlet, because of Laplace pressure jump across an interface is forced to zero. In addition, it makes a curved interface become perpendicular to the outlet however it does not affect droplets at the upstream, significantly. The no-slip boundary condition was used for the microchannel walls. Assuming the above mentioned boundary conditions, we have net flux inlet and fully developed flow pattern for inlet and outlet, respectively. Furthermore, with few simulations with variable channel length, it is observed that changing the length of the main channel to approximately twice its original length has no effect on droplet size.

A VOF function $c(\varvec{x},t)$ is introduced to trace the multifluid interface. It is defined as the volume fraction of a given fluid in each cell of the computational mesh. The density and viscosity can thus be written as

$$ \rho^{*} \left( c \right) = c\rho_{\text{d}}^{*} + \left( {1 - c} \right)\rho_{\text{c}}^{*} $$

(6)

$$ \mu^{*} \left( c \right) = c\mu_{\text{d}}^{*} + \left( {1 - c} \right)\mu_{\text{c}}^{*} $$

(7)

where ρ and μ are density and viscosity of fluid, respectively [19]. For the interface reconstruction method, Popinet [17] applied piecewise-linear VOF scheme where the interface is represented in each cell by a line (resp. plane in 3D) which is described by equation

$$ \varvec{m} \cdot \varvec{x} = \alpha $$

(8)

where m is the local normal to the interface and x is the position vector. Given m and the local volume fraction c, α is uniquely determined by ensuring that the VOF contained in the cell and lying below the plane is equal to c. This volume can be computed relatively easily by taking into account the different ways that a square (resp. cubic) cell can be cut by a line (resp. plane). It leads to match linear and quadratic (resp. cubic) functions of α [17].

Zero velocities and T = 0, T defines a volume-fraction field advected using the geometrical VOF technique, are set to the wall boundary condition which means (1) no-slip condition and (2) non-wetting for the dispersed phase and perfect wetting for the continuous phase, respectively (Fig. 1a). In addition, the field variable $\tilde{c}$ is either identical to c or is constructed by applying a smoothing spatial filter to c. This smooth field is used to determine the density and viscosity fraction between the two phases and has indirect effect on velocity field and other properties. When spatial filtering is used, field $\tilde{c}$ is constructed by averaging the four (eight in 3D simulation) cell-corner values obtained by bilinear interpolation from the cell-centered values. The properties associated with the interface are thus “smeared” over three discretization cells [17].

A staggered temporal discretization of the volume fraction/density and pressure leads to a scheme which is second-order accurate in time [17]. Also Crank–Nicholson discretization is used in Gerris for the viscous terms that are second order accurate and unconditionally stable. Gerris uses Semi-Structure Quad/Octree spatial discretization for solving the advection equation and applied adaptive mesh refinement (AMR) in order to track interface properly. A cell of level n has a resolution of 2ⁿ in each coordinate [18]. Several refinements criteria are used concurrently, depending on the physical conditions encountered, to ensure numerical accuracy and robustness. These include refinements based on gradient, value, curvature, thickness, distance and topology-oriented [19, 20]. In this study, curvature-based refinement criterion is used to track the interface between two phases (Fig. 2a, b). In addition, topology-oriented refinement criterion is applied for grid refinement at the necking region near right corner (Fig. 2a). The two mentioned criteria in the AMR technique are used due to track interface in high resolution and increase accuracy of forces exerted to the neck of the dispersed phase at the detachment moment (Fig. 2).

Fig. 2

Discretization of geometry with AMR technique. a 7 level of refinement for curvature (dispersed phase) and topology-oriented (right corner of T-junction). b Quadtree mesh near an interface with 7 level of refinement. c Mesh refinement for emerging droplet in the jetting regime

4 Geometry and grid independency

Droplet formation was simulated in a T-junction microchannel with square cross-section and width of 100 µm. Channel width, length of the main channel and length of T-junction are w, 20w and 3w, respectively. For setting up this system, the continuous phase flow through the horizontal channel and the dispersed phase through the vertical channel were introduced until meet each other at the junction (Fig. 1b), which is located 3w downstream of the continuous phase inlet. It was assumed that the continuous phase completely wetted the wall and the dispersed phase not-wetted the wall, but being floated in the continuous phase (Fig. 1a).

Regarding the simulation of droplet formation, AMR technique was used with three-level refinements as 6, 7 and 8. Through this simulation, the droplet size changes about 12 and 5 % between mesh refinement level of 6–7, and 7–8, respectively. These are the maximum changes to increase 1 level of refinement in each step for the squeezing regime. In order to detach the dispersed phase form the necking place on the right corner, the interface thickness should be smaller than one grid size [20] which was considered in this work. Figure 2 shows an example of Quadtree AMR cells near an interface. The cells are colored by the volume fraction values in the cell centers (Fig. 2b). In this case, the value refinement level near junction is 7 and curvature refinement level for interface is 7 while level 4 is set for the continuous phase. Afterwards, in 3D simulation, the interface surface was well meshed with AMR technique (Fig. 2c). It should be noted that simulation time has got about three times for each refinement level increase. Run time for each step of simulation is about 20 h on 4 processors with 2.5 GHz frequency.

5 Results

Droplet formation in T-shape microchannel is influenced by several dimensionless numbers. Among these dimensionless numbers, Q, Ca and Re were investigated in this study. Flow pattern is divided into three different regimes such as squeezing, dripping and jetting. In the squeezing regime, the droplet size depends on Q number while Ca number does not have significant effect on it. In contrast, Ca number has significant role in dripping regime. In the squeezing regime, break-up occurs when the shear force and surface tension are in balance. For Ca < 0.02, three regimes of squeezing, dripping and transition can be observed while for larger Ca jetting and parallel flow patterns appear [3].

To be assured of the accuracy of the simulation, the presented results have been compared with the experimental data [5] which revealed a good agreement. For this purpose, all properties and geometrical characteristics were set similar to those of Li et al. [5]. Fluid properties are considered as $\rho_{\text{d}} = 1162\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }},\; \rho_{\text{c}} = 984\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }} ,\;\mu_{\text{d}} = 68.6 \times 10^{ - 3} \,{\text{Pa}}\,{\text{s}},\;\mu_{\text{c}} = 10.58 \times 10^{ - 3} \,{\text{Pa}}\,{\text{s}}.$ For all simulations, velocity of the dispersed phase and interfacial tension between the two phases were set to $u_{\text{d}} = 0.28 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$ and $\gamma = 12.5 \times 10^{ - 3} \,{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}$, respectively while the velocity of the continuous phase varies from $u_{\text{c}} = 3.46 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$ to $u_{\text{c}} = 0.73 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$ (Fig. 3). Due to the wall shear stress and the pressure difference between the tip and the tail of droplet, two vortices are created (Fig. 4). Figure 4c shows pressure contour for the confined droplet. As illustrated, there is a pressure jump across the interface, named Laplace pressure $\Delta p_{\text{L}}$, which is caused by the surface tension of the interface between two phases. This pressure jump for steady state of a droplet in the squeezing regime can be estimated by $\Delta p_{\text{L}} = {{2\gamma } \mathord{\left/ {\vphantom {{2\gamma } R}} \right. \kern-0pt} R}$. Having surface tension γ and characteristic radius of curvature of interface $\left( {R \simeq {{\text{w}} \mathord{\left/ {\vphantom {{\text{w}} 2}} \right. \kern-0pt} 2}} \right)$, Laplace pressure is obtained 50 Pa. Figures 5 and 6 show the droplet formation in good accuracy compared with the experimental data [4, 8].

Fig. 3

Dimensionless droplet size (L/W) for 2D simulations as a function of Ca number, which is compared with experimental data [5]. Capillary number is altered by changing velocity of the continuous phase

Fig. 4

Circulation motion inside the confined droplet. a Experimental picture [5]. b Streamline in 2D simulation for Ca = 0.0055, Re = 0.073 and Q = 0.7. c Pressure variation between the tip and the tail of the droplet. Laplace pressure jump is 50 Pa across the interface

Fig. 5

Comparison of velocity vector in 2D simulation with [4]. Ca = 0.0055, Re = 0.073 and Q = 0.7. a t = 0 s. b t = 44 × 10⁻³ s. c t = 121 × 10⁻³ s

Fig. 6

Cycle of droplet formation from penetration until detachment. 3D simulation for Ca = 0.031 and Q = 0.04 compared to experimental pictures of case (d) [8]. t_s and t_e represent simulation time and experimental time, respectively. a t_s = 9.42 × 10⁻³ s, t_e = 9.35 × 10⁻³ s. b t_s = 11.25 × 10⁻³ s, t_e = 11.21 × 10⁻³ s. c t_s = 11.55 × 10⁻³ s, t_e = 11.53 × 10⁻³ s. d t_s = 11.86 × 10⁻³ s, t_e = 11.84 × 10⁻³ s. e t_s = 12.12 × 10⁻³ s, t_e = 12.15 × 10⁻³ s

To increase Re number, four different values for density were selected. Also, the microchannel width increasing up to 1000 µm. In addition, the dimensionless numbers such as λ = 0.15, Q, ${{\rho_{\text{d}} } \mathord{\left/ {\vphantom {{\rho_{\text{d}} } {\rho_{\text{c}} }}} \right. \kern-0pt} {\rho_{\text{c}} }} = 1.18$ and Ca are similar to those of Ref [5], which means viscosity and density of the dispersed phase are changed to keep their ratio constant. Re number changed as the density of two phases altered. Viscosity of the continuous phase is set to $7 \times 10^{ - 3} \,{\text{Pa}}\,{\text{s}}$ and density of the continuous phase is altered to $1240\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$,$2060\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$, $3100\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$ and $4130\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$ for the curves A, B, C and D, respectively (Fig. 7). In addition, velocity of the continuous phase varies from $33.93 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$ to $5.36 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$ for different Ca numbers from 0.019 to 0.003, respectively. Velocity of the dispersed phase is set to $u_{\text{d}} = 2.72 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$ for all cases, to keep Q constant.

Fig. 7

Reynolds number is greater than one for dimensionless droplet size in 2D simulations as a function of Capillary number. Continuous phase density set to $\rho_{\text{c}} = 1240\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$,$\rho_{\text{c}} = 2060\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$, $\rho_{\text{c}} = 3100\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$ and $\rho_{\text{c}} = 4130\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$ for A, B, C and D, respectively. I Dripping regime; II transition regime; III squeezing regime

At Ca = 0.019 due to setting density of the continuous phase to $1240\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}$, Re number of the continuous phase and Re number of the dispersed phase $\left( {\text{Re}_{\text{d}} = {{u_{\text{d}} \rho_{\text{d}} {\text{w}}} \mathord{\left/ {\vphantom {{u_{\text{d}} \rho_{\text{d}} {\text{w}}} {\mu_{\text{d}} }}} \right. \kern-0pt} {\mu_{\text{d}} }}} \right)$ are 6 and 3.7, respectively (Fig. 7-curve A). In both phases, inertial forces overcome viscous forces (Re > 1). Accordingly, the dispersed phase separation is not influenced only by the balance of shear stress and interfacial tension, which are dominant parameters in Re < 1. Furthermore, inertial force influences droplet formation in itself. In this case, inertial force for the continuous phase results in droplet size decrease while for the dispersed phase it leads to droplet size increase. In addition to shear stress, balance of inertial force between the two phases plays its role in droplet formation. The maximum difference between Re for the two phases occurs at Ca = 0.019. Also, increasing this difference brings about the droplet size decrease as shown in Fig. 7, at region “I”. This density variation, which changes the Re number, influences the droplet size up to 15 % for this regime in Ca = 0.019.

As the continuous phase velocity decreases, Ca number drops while the dispersed phase velocity stays constant. This causes Q to increase and subsequently, Re number of the continuous phase drops while the Re number of the dispersed phase stays constant. In the transition region, (Ca = 0.011) Re number for both phases is approximately equal and inertial force has no significant effect on droplet formation which means balance of inertial force for the two phases. In this state, the effect of inertia reduces in this regime and balance of shear stress and interfacial tension dominates droplet formation (Fig. 7, at region “II”). In addition, this fact can distinguish this regime from the other regimes through Re number changing with different densities. So the droplet size for curve A-D is limited to a unique quantity. In addition, after this region, Re number of the continuous phase becomes smaller than that of the dispersed phase and pressure build-up at the upstream becomes pretty effective (Fig. 7, at region “III”).

Squeezing regime can be observed at Ca < 0.009. Due to emerging droplet length in this regime, the tip approached to the upper wall. In addition, this blocks the main channel and increases pressure build-up at the upstream of T-junction. Sharp corner of T-junction is considered as a singularity and causes a weak vortex to be created in the dispersed phase near the right corner (Fig. 8a). In the next step, tip penetrates into the channel until it blocks its cross-section resulting in pressure build-up. Consequently, the continuous phase moves along the channel and thins the neck of the dispersed phase, then leads to detachment and creates droplets. Due to the surface tension force, right after the detachment, the droplet tail accelerates towards the tip and causes to create vortices on the tail (Fig. 8b) and after that, another vortex is formed on the middle of droplet (Fig. 8c). Afterwards, the tip completely approaches the upper wall and this is first step that the tip is affected by the wall shear stress and it creates a vortex near the upper wall. Also, the created vortex on the tail near the lower wall is due to break-up (Fig. 8d). Later, effect of this vortex, which is created on the tip, disappears because of reaction from the tail on the tip and makes a gap between the tip and the upper wall. Droplet tends to be stable as moving through the channel. Thus, the tip and the tail of droplet tend to keep the hemisphere shape. Droplet size is more than twice the channel width in this regime. For this reason, the middle part of droplet completely approaches the upper wall. Afterwards, droplet tends to be stable but shear stress does not have enough time to properly influence droplet motion (Fig. 8e). As droplet approaches the upper wall, it decreases its velocity and increases effect of shear stress. As long as droplet moves towards the downstream, the effect of vortices induced by detachment decreases. Otherwise, the new vortices induced by shear stress merge with it. After droplet complete stability at the downstream, shear stress creates two vortices inside the entire length of droplet (Fig. 8f). Similar results are observed in last stage compared to low Re in the experiments (Fig. 4). These droplet formation steps were simulated in 2D for 1 < Re < 25 while in Re < 1, these behaviour are totally creeping flow and the vortices caused by detachment were not observed. Lack of inertial force and its effects causes lack of vortices (the vortices created because of droplet break-up) and creeping flow pattern appears. Vortices increase diffusion level and as a result, the two phases mixing. In addition, for Ca = 0.019 and Re > 25, the parallel regime is seen. The parallel regime not only depends on Ca number while the Re number can affect the droplet formation as well. Regarding the mentioned properties of the two phases, maximum Re number for all simulations is not exceeding 25.

Fig. 8

Droplet formation steps (2D) in the squeezing regime for Ca = 0.003, Re = 0.8 and Q = 0.5. a Dispersed phase completely blocks the main channel t = 0 s. b A moment after break-up. t = 195 × 10⁻³ s. c Appearing a vortex at the middle of the droplet t = 198 × 10⁻³ s. d Effect of the upper wall on the tip t = 202 × 10⁻³ s. e Vortices at the tail t = 294 × 10⁻³ s. f Steady state and effect of wall shear stresses on the droplet t = 831 × 10⁻³ s

Dripping regime is observed at 0.013 < Ca < 0.02. In the squeezing and dripping regimes, when the dispersed phase penetrates into the main channel, viscous drag of the continuous phase creates a vortex on the tip. In this regime, the dispersed phase is completely stretched near T-junction (because of fluid surface tension) and the tip is not influenced by the wall shear stress (Fig. 9a). When the dispersed phase penetrates enough, viscous drag (imposed by the continuous phase) increases on the tip and amplitude of the vortex on the tip is strengthened. Immediately after detachment, due to the break-up, two vortices are formed at the tail. Viscous drag still remains on the tip despite the existence of a thin gap between the tail and the lower wall. Also, the tail vortices are not influenced by the wall induced shear stress yet (Fig. 9b). This regime consists of smaller droplets and their stable shape is similar to bullet because of higher pressure for the continuous phase at the back of droplet compared to its front. For this reason, the tail approaches the wall and retains its hemispherical shape while the tip tends to be formed like a blunt body due to pressure decrease and small length of droplet. In addition, shear stress does not have any effect on the tip while some weak vortices are created at the tail. Also droplet size is approximately 1–1.5 times the channel width in this regime (Fig. 9d). Vortices, which are caused by inertial forces and detachment, quickly reach their steady state, and flow circulation in droplet is much less than that of the squeezing regime. In addition, it is observed that elapsed time, in the squeezing regime, for almost disappearance these vortices is $144 \times 10^{ - 3} \,{\text{s}}$, while it is $88.6 \times 10^{ - 3} \,{\text{s}}$ in the dripping regime. Also the region affected by these vortices in the squeezing regime is a greater extend compared with the dripping regime (Figs. 8c, 9c). The final state for droplet can be observed in Figs. 8f, 9d.

Fig. 9

Droplet formation cycle (2D) in the dripping regime for Ca = 0.017, Re = 13.43 and Q = 0.09. a Penetration of the dispersed phase. t = 0 s. b Droplet formation after break-up. t = 38 × 10⁻³ s. c Acceleration of the tail. t = 44 × 10⁻³ s. d Steady state and bullet shape of the droplet. t = 126 × 10⁻³ s

Transition regime is seen in 0.009 < Ca < 0.013. This is a kind of regime between the squeezing and the dripping which droplet formation has a state between these two regimes. For Re > 1, influence of this regime is shown clearly in Fig. 7. In addition, Re number for both phases approximately equals each other and inertial forces have little influence on droplet formation. As a result, the 4 lines of A, B, C and D would tend to approach a unique number of 1.45, which is at Ca = 0.011. In other words, as much as the inertial forces become effective, lines A, B, C and D diverge from each other and as much as the inertial forces become ineffective, lines would converge together that occurs on Ca = 0.011. Using effect of inertial forces addition to shear stress and pressure build up, boundaries of the transition regime is specified by assuming maximum 7 % divergence (0.1 variation of droplet dimensionless size from 1.45) of droplets size from each other. So the boundaries of this regime are defined based on influence of inertial forces. Considering effect of Re number on droplet size variation, the transition regime distinct from the dripping and squeezing regimes, which starts from ${L \mathord{\left/ {\vphantom {L {\text{w}}}} \right. \kern-0pt} {\text{w}}} = 1.35$ to 1.55 that results in 0.009 < Ca < 0.013. As Ca increases, shear forces will dominant drag forces, especially in the jetting regime

The jetting regime is observed clearly for constant Q = 0.5 and Ca > 0.05. In this regime, penetration of the tip coincides with influence of shear stress from the continuous phase applied on the disperse phase. It is worth mentioning, this shear stress is the greatest one compared to the other regimes. In addition, the dispersed phase does not detached at the junction but is pushed towards downstream. Then, the dispersed phase is affected by shear stress dramatically, due to moving through the main channel. This causes instability on the surface of the dispersed phase resulting in droplet creation from the reservoir. It’s worth noting that in 2D simulation, the jetting regime was not observed and the parallel regime could only be predicted in which the dispersed phase stretched to the downstream and not detached from the necking place (Fig. 10). It is due to this fact that in 2D simulation, shear stress is only applied on x–y axis on the dispersed phase. On the other hand, in 3D simulation, the jetting regime and droplet formation process can be seen. The most important parameters for droplet formation in the jetting regime are shear stress and pressure drag. Pressure drag pushes droplet to the downstream, while shear stress tends to detached it from the necking place. In 3D simulation, the shear stress is not only exerted on the x–y axis (Fig. 11a), from channel sides and the continuous phase, but also on the x–z (Fig. 11b) and y–z axis (Fig. 11c). As a result, the 2D simulation can not accurately estimate the forces applied to the dispersed phase. In this regime, before first droplet detachment, the tip penetration is affected by shear stress from the continuous phase (Fig. 12a). It should be mentioned, the most effective of shear stress direction is in x–z plan and exerts at the sides of the tip (Fig. 11b). This leads to thinning the reservoir at the back of the tip and causes instability at the surface of the dispersed phase. In addition, the first and the biggest droplet is created due to this instability (Fig. 12b). Afterwards, the dispersed phase is divided into two parts, the droplet and the reservoir. Immediately after droplet detachment, the tip of the reservoir slightly moves backward due to surface tension. This reaction makes reservoir experience an impact from the tip of the reservoir and increases the reservoir width compared to the separation before (Fig. 12c). However, the first droplet is always larger than next ones in this regime due to lack of collision (exerted from the tip of the reservoir) before detachment of the first droplet (Fig. 12d, e). Next, shear stresses have the required time to affect the tip of the reservoir due to thinning backside of the tip and to create more droplets (Fig. 12e). As new droplets are created, their size decreases and droplet break-up point moves to the downstream with time so this unstable jet will finally become the parallel flow in the main channel. It worth noting, droplet dimensionless size $\left( {{L \mathord{\left/ {\vphantom {L {\text{w}}}} \right. \kern-0pt} {\text{w}}}} \right)$ will get to the unique value of 1 after approximately 5–6 cycles. Also, the first droplet is similar to bullet shape in the dripping regime while others are similar to droplet in Co-Flow state (Fig. 12e). On the other hand, the unstable jetting regime is simulated in constant Q = 0.5 and Ca = 0.1 while the stable jetting regime is observed clearly for constant Q = 0.5 and Ca = 0.056 (Fig. 13a). Also, droplets were produced with the same size as each other in this regime. Unlike the unstable jetting regime, break-up points will not move to the downstream with time (Fig. 13b).

Fig. 10

Different steps of 2D simulation for the parallel regime for Ca = 0.055, Re = 1.43 and Q = 0.5. a t = 0 s. b t = 61 × 10⁻³ s. c t = 122 × 10⁻³ s. d t = 927 × 10⁻³ s

Fig. 11

Effect of channel sides and shear stresses on emerging droplet near necking place for Ca = 0.1, Re = 0.26 and Q = 0.5. a Velocity vector in x–y axis. b Velocity vector in x–z axis. c Velocity vector in y–z axis

Fig. 12

Droplet formation in the unstable jetting regime for Ca = 0.1, Re = 0.26 and Q = 0.5. 3D simulation with pressure contour at the middle of z axis. a Dispersed phase moves to the downstream. t = 0 s. b Shear stress exerted on back of the tip. t = 2.28 × 10⁻³ s. c First droplet separated. t = 6.93 × 10⁻³ s. d Creation of the second droplet. t = 9.17 × 10⁻³ s. e Reservoir pushes to the downstream with every droplet cycle and droplet size is decreased through every separation until L/W = 1. t = 33 × 10⁻³ s

Fig. 13

Droplet formation in the stable jetting regime (3D) for Ca = 0.056, Re = 0.15 and Q = 0.5. t = 0 s. b Dimensionless droplet size (L/W) is fixed on 1.14 after the first droplet detachment. t = 35 × 10⁻³ s

6 Conclusions

Five different regimes of squeezing, transition, dripping, jetting and parallel are simulated in a T-junction microchannel. Three regimes of squeezing, transition and dripping were simulated in both Re < 1 and Re > 1. Re number is increased up to maximum of 25 by alter two phases density and increase the channel width up to 1000 µm. For Re > 1 at the dripping regime, simulations show that droplet formation at the moment after detachment is not affected only by balance of shear stress and interfacial tension, while inertial forces also influenced its motion. As a result, inertial forces change droplet size and create some new vortices in droplet. Droplet size will varies up to 15 % in this regime for Ca = 0.019. This variation is decreased as Ca number approached to 0.011. In the transition regime, inertial forces have no significant effect on droplet formation, due to proximity of Re number for both phases. This restricts droplets size to a unique value. Using the mentioned concept, the transition regime distinct from the dripping and squeezing regimes by assuming maximum 7 % divergence of droplets size, from each other, by inertial forces. As a result, this regime is defined at 0.009 < Ca < 0.013. Inertial forces influence droplet formation in the squeezing regime with vortices which are stronger, pretty extensive and persistent compared with the dripping regime. As droplet moves to the downstream, the vortices caused by inertial forces are disappeared while some vortices are formed because of wall shear stress which have been seen in Re < 1. For Ca > 0.05, the jetting regime is observed only in 3D simulations because of shear stress on the z-axis, whereas only the parallel regime is seen in 2D simulations. The reason is that in the 2D simulation shear stress is only exerted on the x–y axis while in 3D it also affected the necking place on the x–z and y–z axis. At first, the stable jetting regime is appeared in which droplets are in the same sizes; while increasing Ca number up to near 0.1 changes it to the unstable jetting regime, which moves to the downstream because of high shear stresses exerted on the jet reservoir. Also, in this regime, droplets sizes are decreased continuously until reach to dimensionless size of 1.