The Kepler problem primigenial sphere

Abstract

The unitary ${\mathbf{S}}$-code description of the one-body Kepler problem is shown to unfold naturally from a primigenial sphere (with centre at the attracting gravitational centre and radius related to the universal constant of gravitation). In this spherical scenery all the Kepler problem fundamental elements are recovered by simple linear vector combinations.

1 Introduction

Our unitary ${\mathbf{S}}$-description [5–10] of the classical one-body Kepler problem is revisited and shown to find its primeval source in a sphere, which we denote by $S_{p^{-1}}$, and which has centre at the attractive centre of the gravitational force acting on the body and radius $p^{-1}$ related to the universal constant of gravitation. This primigenial sphere unravels, in a sort of inbred order of its elements, not only the cone of the orbital Kepler conic sections, but also the various, fundamental elements of the Kepler problem.

To begin with, we recall that the classical three-dimensional Kepler problem describes the motion of a particle in a central, attractive, inverse square law field. The Kepler motion occurs in a fixed plane, orthogonal to the constant angular momentum vector $\varvec{\Gamma }$ per unit of mass

$$ \varvec{\Gamma } = \mathbf{x}\wedge \dot{\mathbf{x}} \qquad \qquad \qquad (\cdot \equiv d/dt) $$

(1)

where ${\mathbf{x}}$ represents the particle position vector with respect to the attractive centre and $\wedge$ denotes the wedge product. The Kepler orbit is a conic, commonly expressed by the vector polar equation

$${\mathbf{x}} = \frac{p}{1+e\,\cos \,\theta }\,\,\,\varvec{\rho } \qquad \qquad \qquad ({\mathbf{x}}=r\varvec{\rho })$$

(2)

in the plane polar coordinate system $(r,\theta )$, with the origin at the fixed attracting centre and with the two orthogonal unit vectors $\varvec{\rho } = \varvec{\rho }\,(\theta )\,,\,\varvec{\tau }=\varvec{\tau }\,(\theta )$ pointing in the direction of increasing $r$ and $\theta$.

The two scalar parameters $p$ and $e$ represent, respectively, the semi-latus rectum and the eccentricity of the orbit, which is a circle for $e=0$, an ellipse for $0<e<1$, a parabola for $e=1$, the left branch of an hyperbola for $e>1$ (the right branch being excluded by the condition $r>0$, see Fig. 1).

Fig. 1

The family of Kepler confocal conics

In our previous works [5–10] we introduced the peculiar sum vector ${\mathbf{S}}$ which encompasses (in a sort of genetic code) all the geometrical and dynamical information about the Kepler problem.

For instance, the vector ${\mathbf{S}}$:

• 1. Allows to express the equation (2) of the whole family of the Kepler orbits as the simple scalar product

  $${\mathbf{S}} \cdot \mathbf{x} = 1;$$

  (3)

• 2. ‘Conceals’ a constant vector ${\mathbf{N}}$, unraveling the cone structure in $R^3$ which generates all the Kepler orbits as conic sections;

• 3. Discloses a peculiar genesis of the celebrated regularizing KS-map, devised to regularize at the origin (collision) the plane Kepler problem.

In this paper, we show how the two vectors ${\mathbf{S}}$ and ${\mathbf{N}}$ (together with the cone structure, the regularizing map and other features of the Kepler problem) turn up to be much more entangled and organized than what appeared in our previous papers on the ${\mathbf{S}}$-encoding: they are all originated by simple, linear combinations of the primitive elements that define the primigenial sphere $S_{p^{-1}}$.

This result ensues, first, from an autonomous and self-consistent review of the well known governing expression for the Newtonian law of gravitation

$${\mathbf{F}} =-\frac{K^2}{r^3}\,\,{\mathbf{x}},$$

(4)

and, secondly, by enlightening the role of both the spherical angles which parameterize a sphere. In this spherical scenario the well-known eccentricity vector ${\mathbf{e}}$, the Runge–Lenz vector and the Kepler mechanical energy $E$ acquire a particular interpretation.

2 Symmetry and planarity: both in Newton’s gravitation law

Our basic goal is to interlace strictly the two fundamental properties of the Kepler problem: symmetry and planarity. Commonly derived [1–3] from the Newtonian law of gravitation (4), these properties notoriously reveal that the central Kepler motion exhibits:

• a. Spherical symmetry (invariance under rotation in $R^3$ about any axis through the fixed attractive point) whence the motion is commonly described by spherical polar coordinates $(r,\theta ,\phi )$;

• b. Rotational symmetry (invariance under rotation about a given fixed axis, namely the constant direction of the conserved angular momentum vector ${\varvec{\Gamma }}$);

• c. Planarity, so that the motion occurs in the plane orthogonal to ${\varvec{\Gamma }}$ and through the fixed attractive centre, whence the motion is simply described by plane polar coordinates $(r,\theta )$ as in (2).

Our goal is to embody both symmetry and planarity directly in the classical expression (4) of the force ${\mathbf{F}}$. The result is achieved:

• a. By choosing a fixed right-handed unit system $\{F, {\mathbf{I}}, {\mathbf{J}}, {\mathbf{K}}\}$ in $R^3$, with the origin at the attractive centre $F$ and with ${\mathbf{K}}$ directed along ${\varvec{\Gamma }}$, so that

  $$ {\mathbf{{\Gamma}}} ={\mathbf{{\Gamma}}} \, {\mathbf{K}}$$

  (5)

• b. By identifying the ${\mathbf{I}}, {\mathbf{J}}$-plane with the polar $\{{\varvec{\rho }} , {\varvec{\tau }} \}$-plane, the particle position vector ${\mathbf{x}}$ being given by

  $${\mathbf{x}}= r\,\varvec{\rho }$$

  (6)

  (see Fig. 2).

Fig. 2

The cartesian $\{F,{\mathbf{I}},{\mathbf{J}},{\mathbf{K}}\}$ and the polar $\{F,{\varvec{\rho }},{\varvec{\tau }} \}$ frames

The two choices (5) and (6) enable us to introduce the vector ${\varvec{\Gamma }}$ in the expression (4), which can now be re-written as

$${\mathbf{F}} = -\frac{K^2}{r^2}\,\,\varvec{\rho }= -\frac{\Gamma ^2}{r^2}\,\frac{K^2}{\Gamma ^2}\,{\varvec{\rho}}.$$

If we denote by $p$ the constant ratio

$$ {p=\frac{\Gamma ^2}{K^2}} $$

(7)

so that

$${\mathbf{F}}= -\frac{\Gamma ^2}{r^2}\,\,p^{-1}\,{\varvec{\rho}},$$

we finally arrive at the wedge product

$${\mathbf{F}}=\frac{\varvec{\Gamma }\,\wedge \,\big (\varvec{\Gamma }\,\wedge \,p^{-1}\varvec{\rho }\big )}{r^2}.$$

(8)

This is the vector expression sought for. The Newton’s gravitational force ${\mathbf{F}}$, via the vector ${\varvec{\Gamma }}$, displays explicitly both the Kepler symmetry and the Kepler planarity.

What is now surprising is that the vector expression (8):

• Winds up with the parameter $p$ given by (7), which coincides exactly with the semi-latus rectum parameter of the literature;

• Discloses the existence of the following radial vector

  $$ {p^{-1}\varvec{\rho } }$$

  which turns out to be fundamental for the organization of the entire Kepler problem.

3 The primigenial sphere ${{S}_{p^{-1}}}$. The spherical angles and the rescaling vector ${\varvec{\epsilon }}$

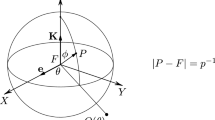
The radial vector $p^{-1}\varvec{\rho }= p^{-1}\varvec{\rho }(\theta )$ which appears in (8) may be interpreted as the vector which, for each ${\theta}$, defines the equator of a sphere with radius $p^{-1}$ and centre at $F$. We characterize this sphere by $S_{p^{-1}}$.

By adopting spherical coordinates (see Fig. 3)

$${ \left\{ \begin{array}{ll} X& \quad =p^{-1} \sin \phi \cos \theta \\ Y&\quad = p^{-1} \sin\phi \sin \theta \\ Z&\quad = p^{-1} \cos \phi \end{array} \right. }$$

where the longitude angle ${\theta}$ and the colatitude angle $\phi$ satisfy

$${ \theta \in [0,2\pi ], \quad \phi \in [0,\pi ], }$$

the sphere is notoriously characterized in $R^3$ by the set of vectors $P-F$, given explicitly by

$$ P-F = p^{-1}\,\, [\sin \,\phi \,\,(\cos \,\theta \,{\mathbf{I}}+ \sin \,\theta \,\mathbf{J})+\, \cos \,\phi \,\, \mathbf{K}\,]. $$

(9)

Fig. 3

The sphere $S_{p^{-1}}$ with radius $p^{-1}$, center $F$. The rescaling vector ${\varvec{\epsilon }}$

Now, since in the plane polar description we have that

$$\cos \,\theta \,{\mathbf{I}}+ \sin \,\theta \,{\mathbf{J}}={\varvec{\rho }},$$

we rewrite the vector expression (9) of the sphere as

$$P-F=p^{-1}\,\,[\sin \phi \,{\varvec{\rho }} + \,\cos \,\phi \, {\mathbf{K}}].$$

(10)

Let us notice that the longitude angle $\theta$ appears in (10), although indirectly, through ${{\varvec{\rho }}= {\varvec{\rho }} (\theta )}$.

As for the colatitude angle $\phi$, we can go further, and try to introduce in (10) its positive related range

$${ 0\,\le \,\sin \,\phi \,\le \,1 }$$

(obviously satisfied, being ${\phi \in [0,\pi ]}$).

To do so, we define the ‘rescaling vector’ ${\varvec{\epsilon }}$ by the following

Definition 3.1

For each fixed plane unit vector ${{\varvec{\rho }}={\varvec{\rho }}(\theta )}$ and for each fixed angle $\phi$, the ‘rescaling vector’ is the plane vector

$$ {\varvec{\epsilon } = \sin \,\phi \,\,\varvec{\rho } (\theta ) \, =\, \epsilon \,\varvec{\rho }}$$

(11)

which belongs to the equatorial plane of the sphere and whose magnitude

$${\epsilon \,=\, \mid \,\varvec{\epsilon } \,\mid \,=\, \sin \phi }$$

‘rescales’ the unit magnitude of ${\varvec{\rho }}$ and satisfies the range

$${ 0\le \epsilon \le 1\,. }$$

(12)

Consequently, the introduction of the vector ${\varvec{\epsilon }}$ in (10) leads us to the

Definition 3.2

We call ‘primigenial sphere’ of the Kepler problem the sphere $S_{p^{-1}}$ defined by the locus of vectors

$${P-F= p^{-1}\, (\varvec{\epsilon }+ \cos \,\phi \,{\mathbf{K}})}$$

(13)

that is the sphere with centre at the attractive origin $F$ of the inertial right-handed frame ${\{F, {\mathbf{I}}, {\mathbf{J}}, {\mathbf{K}}\}}$ of $R^3$ and with radius $p^{-1}$ related to the physical constants of the Kepler problem by (7) (see Fig. 3) .

Of course, if ${\phi = \frac{\pi }{2}}$, we recover, by (13), the equator ${P-F= p^{-1}\,\varvec{\rho }}$ of the sphere. And the equator plays a fundamental role, as shown in the following section.

4 Inside and outside the equator. The projection vector

The new rescaling vector ${\varvec{\epsilon }}$ allows to decompose the vectors (13) which define the primigenial sphere $S_{p^{-1}}$ as:

$$P-F= p^{-1}\, \varvec{\epsilon } \,+\, p^{-1}\,\cos \,\phi \,{\mathbf{K}}= (P_0-F)\,+\,(P-P_0)$$

(14)

(see Fig. 4).

We call the vector

$${ P_0-F = p^{-1}\,\varvec{\epsilon }}$$

(15)

the projection vector since it characterizes all the points P of the sphere $S_{p^{-1}}$ by giving their corresponding projections $P_0$ on the equatorial plane.

In particular, the point $P_0$ is:

• (a) At the center $F$ of the equator for ${\epsilon =0}$;

• (b) Inside the equator for $0<\epsilon <1$;

• (c) On the equator for ${\epsilon =1}$.

  For the future, we find it convenient to extend the range (12) by considering the points outside the equator, thus by adding

• (d) Outside the equator for ${\epsilon >1}$.

Fig. 4

The sphere and the projection vector ${P_0-F=p^{-1}\varvec{\epsilon }}$

5 From the sphere ${{S}_{p^{-1}}}$ to the ${\mathcal C}$-cone

Now we are ready to bring into life the cone which generates the Kepler conic orbits (the famous ‘conic’ sections).

As before we stick to the vector definition (13) of the sphere $S_{p^{-1}}$, considered as the ‘star’ of vectors $P-F$ of the same magnitude $p^{-1}$ issuing from its centre $F$ (and not as the equivalent definition, i.e. as the locus of equidistant points).

Accordingly, in the star of vectors (13) we select, for each fixed, constant value ${\phi ^*}$ of the colatitude ${\phi }$, the related vectors:

$$ {P^* -F= p^{-1}\, (\sin \,\phi ^*\,\varvec{\rho }\,+\, \cos \,\phi ^* \,{\mathbf{K}})}$$

(16)

which define a circular right cone with axis ${\mathbf{K}}$ and semi-aperture ${\phi ^*}$ (see Fig. 5).

Moreover, among the circular cones given by (16), we fix our attention to the cone corresponding to the particular relation

$${ \sin \,\phi ^*\,=\,\cos \,\phi ^*. }$$

(17)

Since ${\phi ^*= \frac{\pi }{4}}$, this particular cone (Fig. 5) is characterized by the vectors

$${P^* _{\frac{\pi }{4}}\, -F\,=\,\frac{\sqrt{2}}{2} p^{-1}\, (\varvec{\rho }\,+\, {\mathbf{K}})}.$$

(18)

Of course this circular cone is a ‘limited, finite’ one: the arrowed points $P^* _{\frac{\pi }{4}}$ belong to the sphere of finite radius $p^{-1}$ (the scalar factor ${\frac{\sqrt{2}}{2} p^{-1}}$ bringing the magnitude $\sqrt{2}$ of the sum vector $\varvec{\rho }\,+\, {\mathbf{K}}$ exactly to the finite value $p^{-1}$ and the magnitude of the projection vector $P^*_{0}-F$ corresponding to the finite value ${\epsilon \,=\,\frac{\sqrt{2}}{2}}$ of ${\varvec{\epsilon }}$).

Thus, with the aim at arriving at the (infinite) cone which generates the Kepler orbits, we rescale (18) and finally give the following

Definition 5.1

The circular ${\mathcal C}$ -cone associated to the primigenial sphere $S_{p^{-1}}$ of the Kepler problem, is the extended circular right cone, with vertex at $F$, characterized by the vector equation

$${\mathcal{{C}}} - F=\lambda \,p^{-1}\, (\varvec{\rho }\,+\, {\mathbf{K}})$$

(19)

with the positive scalar parameter $\lambda \in {\mathcal R}$ and with $p^{-1}$ given by (7).

In cartesian coordinates, being $F(0,0,0)$ and ${\mathcal C}\,=\, (X_{\mathcal{C}} \,, Y_{\mathcal{C}} \,,Z_{\mathcal{C}})$ where

$${\mathcal{X}}_{\mathcal{C}}= \lambda p^{-1}\,\cos \theta,\quad { {Y}}_{\mathcal{C}} = \, \lambda \,p^{-1}\,\sin \,\theta ,\quad {\mathcal{Z}}_{\mathcal{C}} \,= \, \lambda \,p^{-1} $$

the scalar cartesian equation of the right ${\mathcal {C}}$-cone is

$${{\mathcal{X}^{2}}_{\mathcal{C}}+ {\mathcal{{Y}}^{2}}_{\mathcal{C}} - {\mathcal{{Z}}^{2}}_{\mathcal{C}} = 0.}$$

(20)

Remarks (1) Of course, the cartesian equation (20) coincides with the standard one for a circular right cone with semi-aperture ${\frac{\pi }{4}}$. But the ${\mathcal {C}}$-cone, through its vector definition ${{\mathcal{C}} -F}$ given by (19), is intrinsically and explicitly related to the Kepler problem via the physical Kepler value $p^{-1}$and via its vertex, the attractive centre $F$ of the force ${\mathbf{F}}$. (2) How the ${\mathcal {C}}$-cone generates the Kepler orbits is revealed in the following section.

Fig. 5

The Sphere and its cones for ${\phi =cost}$. The ${\mathcal {C}}$-cone for ${\phi} ={ \frac{\pi }{4}}$

6 The primigenial role of the sphere ${{S}_{p^{-1}}}$

The vector expression (13) of the sphere $S_{p^{-1}}$ relies, at the core, on the two spherical coordinates ${\theta}$ and ${\phi }$: but, whereas the fixed unit vector ${\mathbf{K}}={\mathbf{K}} (0)$, corresponding to the angle $\phi =0$, appears explicitly, the fixed unit vector ${\mathbf{I}}= \varvec{\rho } (0)$, corresponding to the angle ${\theta =0}$, appears only implicitly through the particular rescaling vector ${\varvec{\epsilon } = \epsilon \, \varvec{\rho } (\theta )}$ corresponding to $\theta =0$.

We recover this (implicit) fixed direction ${{\mathbf{I}} =\varvec{\rho } (0)}$ by considering the particular, constant rescaling vector ${\varvec{\epsilon }_{0}}$ defined by setting $\theta =0$ and ${\phi =\phi _{0}}$ in the definition of ${\varvec{\epsilon }}$ given by (11) (the fixed, constant colatitude value ${\phi _{0}}$ and its physical meaning will be explored in Section 9).

The new constant vector ${\varvec{\epsilon }_0}$ is thus defined by:

$${\varvec{\epsilon }_{0}\,=\,\sin \,\phi _{0}\,\varvec{\rho } (0)=\, \sin \, \phi _{0}\, {{\mathbf{I}}}\,=\, \epsilon _{0}\,{\mathbf{I}}}$$

and lies on the ${\mathbf{I}}$-axis.

As a consequence, the sphere $S_{p^{-1}}$, via its $(P-F)$-vector definition (13) in the $\{{\mathbf{I}},{\mathbf{J}},{\mathbf{K}}\}$-frame, is characterized by the following four primitive elements

$$ p^{-1}, \varvec{\rho},\, {\mathbf{K}},\, \varvec{\epsilon }_{0} = \epsilon _{0} {\mathbf{I}}, $$

(21)

which are: the radius, two unit orthogonal vectors (the first one related to the longitude angle $\theta$, measured starting from ${\mathbf{I}}$) and the rescaling vector ${\varvec{\epsilon }_{0}}$ (related by ${{\epsilon _{0}}\,= \sin \,{\phi _{0}}}$ to the colatitude angle $\phi _{0}$, measured starting from ${\mathbf{K}}$).

Now, what is surprising is that simple combinations of these primitive elements, such as the following simple linear combinations:

$$ {p^{-1}\, ({\varvec{\rho }}\, +\,{\mathbf{K}})}$$

(22)

$$ {p^{-1}\, ({\varvec{\epsilon }}_{0}\, +\,{\mathbf{K}})}$$

(23)

$${ p^{-1}\, ({\varvec{\epsilon }}_{0}\,+\,{\varvec{\rho }})}$$

(24)

originate immediately all the fundamental elements of the Kepler problem.

That is why we called the sphere ‘primigenial’.

The combined vectors examined (Table 1).

We are now examining in detail the Table 1 which reassumes the combined vectors (22)-(24) (obtained exclusively by following our $S_{p^{-1}}$ spherical scheme) and compares them with the fundamental vectors we obtained by different procedures in [5–9].

a. The $\varvec{\mathcal {C}}$ -cone: a 3-dimensional characterization of Kepler orbits. The vectors (22), rescaled by $\lambda$, give, for each $\theta$, the whole ${\mathcal {C}}$-cone structure (19) or (20), strictly related to the primigenial sphere $S_{p^{-1}}$.

Table 1 The Combined primitive elements

We now compare the scalar equation (20) of the ${\mathcal {C}}$-cone with a scalar one obtained by considering the second combined vector (23). For a general representation in $R^3$, we rewrite this vector (which lies in the $\{{\mathbf{I}},{\mathbf{K}}\}$-plane) by relaxing the restriction $\varvec{\epsilon }_{0} =\epsilon _{0} {\mathbf{I}}$ so that this constant vector is ${\varvec{\epsilon }_{0}\,=\, \epsilon _{X}\,\,{\mathbf{I}}+\,\epsilon _Y\,{\mathbf{J}}}$ whence the vector (23) becomes

$$ {p^{-1}\, \big (\varvec{\epsilon }_{0}+{\mathbf{K}}\big ) \,=\, \frac{\epsilon _X}{p}\,{\mathbf{I}}\,+\, \frac{\epsilon _Y}{p}\,{\mathbf{J}}\,+\, \frac{1}{p}\,{\mathbf{K}}} $$

(25)

which has tip point, say $N$, with coordinates

$$ {X\,=\, p^{-1}\,\epsilon _X ,\quad Y\,=\,p^{-1}\epsilon _Y,\quad Z\,=\, p^{-1}} $$

(26)

which satisfy the scalar equation sought for

$${ X^2+ Y^2\, -Z^2=({\epsilon _{0}} ^2-1) p^{-2}} $$

(27)

where ${\epsilon _{0}\,=\,\mid \varvec{\epsilon }_{0} \mid \,=\, \sqrt{{\epsilon _X} ^2\, +\, {\epsilon _Y}^2}}$ and $Z>0$.

In this equation, the sign of the term ${({\epsilon _{0}}^2-1)}$ depends on the rescaling values ${0 \le \epsilon _{0} \le 1}$ and ${\epsilon _{0}>1}$.

But these ranges remind us that an ellipse, a parabola and the left branch of the hyperbola correspond to the same ranges of the well known eccentricity ${0\le e \le 1}$ and $e>1$.

Thus, by comparing the scalar Eq. (27) with (20), we may state that:

Proposition 6.1

The tip points $N$ of the combined vectors (23) which lie inside the ${\mathcal {C}}$-cone correspond to elliptical orbits, those on the cone to parabolic ones and those outside the cone to hyperbolic orbits (Fig. 6).

b. The cone structure. The ${\mathcal {C}}$-cone coincides exactly with what we have defined and called (for other reasons) $N$-cone in [9] . For uniformity we will call it here ${\mathcal {C}}$-cone.

c. The Rescaling vector ${{\varvec{\epsilon }}_{0}}$ and the Eccentricity vector e. As a consequence of the results obtained in a. we may set

$${ \epsilon _{0}\,=\, e \qquad \qquad \Longrightarrow \qquad \qquad \varvec{\epsilon }_{0}\,=\,{\mathbf{e}}}$$

so that:

Proposition 6.2

The constant rescaling vector ${\varvec{\epsilon }_{0}\,=\,\epsilon _{0}{\mathbf{I}}}$ corresponding to ${\theta =0}$ and to the particular angle ${\phi \,=\,{\phi _{0}}}$, turns out to be the eccentricity vector ${\mathbf{e}} \,=\, e\,{\mathbf{I}}$ of the literature which characterizes each type of the orbits ($e=0$ for circles, ${0<e<1}$ for ellipses, $e=1$ for parabolas, $e>1$ for hyperbolas).

Remark

The important fact is that in the literature the eccentricity vector is shown to rely on the concept of geometrical ratio (see [2, 3]), whereas in our description it comes from a completely different spherical approach.

d. The combined vector N. The vector defined in (23) has the same coordinate ${Z=p^{-1}}$ of the North pole of the sphere ${S_{p^{-1}}}$: that is why we denoted its tip point by $N$. This vector, deeply rooted into the spherical scheme of this work and strictly related to the Kepler conic orbits via the previous Proposition 5.1, coincides, being ${\varvec{\epsilon }_{0}={\mathbf{e}}}$, with the vector ${\mathbf{N}}$

$$ {\mathbf{N}} \,\equiv N-F \,\,\equiv \, p^{-1}\,({\mathbf{e}} \,+\, {\mathbf{K}}),$$

we introduced in [9] in a completely different way (see Fig. 7a) where ${\mathbf{e}}\,=\, e{\mathbf{I}}$.

(e) The Kepler orbits as conic sections. The polar plane. The sphere $S_{p^{-1}}$ may be considered as an extension of the unit sphere with centre at $F$, that is

$$ {X^2\,+\, Y^2\, +\,Z^2\,=\,1.} $$

(28)

It follows that (with respect to the unit sphere) each tip point $N$ of the vector ${\mathbf{N}}$ defines a polar plane, that is the plane (orthogonal to the line $FN$) which passes through the inverse point $N^*$ of $N$ so that ${\mid N^* -F\mid \,=\,\frac{1}{\vert N-F\vert }}$. The points $(X,Y,Z)$ belonging to the polar plane satisfy, recalling (26), (27) and (28), the equation

$$ {p^{ -1}} {e_{X}} X + {p^{-1}} {e_Y} Y + {p^{-1}}{Z-1} = 0 $$

(29)

As a consequence:

Proposition 6.3

The polar plane (29) intersects the ${\mathcal{C}}$-cone in the locus given by the equation

$${ \big (1-{e_X}^2\big )\,X^2+ \big (1-{e_Y}^2\big )\,Y^2+ 2pe_X X+ 2pe_Y Y-2e_X\,e_Y XY- p^2\,=\,0} $$

which is a conic section, which, projected orthogonally onto the $\{{\mathbf{I}},{\mathbf{J}}\}$-plane gives the Kepler conic section with focus at the vertex $F(0,0,0)$ of the ${\mathcal {C}}$-cone, eccentricity $e$ and parameter $p$. (The Fig. 8 shows an elliptic conic section).

Proposition 6.4

The polar plane makes an angle $\beta$ with the ${\mathbf{I}}$-axis such that

$${ \tan \beta =e} $$

which is exactly the eccentricity of the Kepler orbit (see Fig. 8).

Fig. 6

The ${\mathcal{C}}$-cone structure and the tip points $N$

f. The combined vector S. The combined vector (24), which is orthogonal to ${\mathbf{N}}$, coincides with the vector we defined in [6, 7] as the sum vector

$$ {\mathbf{S}} \equiv B-F\equiv p^{-1}({\mathbf{e}} + \varvec{\rho })$$

(see Fig. 7b)).

While the vector ${\mathbf{N}}$ gives a 3-dimensional picture of the conic orbits, the sum vector ${\mathbf{S}}$ gives a 2-dimensional one, for it allows to express the standard plane polar equation of the whole family of Kepler orbits

$${ r=\,\frac{p}{1+e\,\cos \,\theta } }$$

as the simple equation given by the scalar product

$$ {\mathbf{S}}\,\cdot \, {\mathbf{x}}=1.$$

Fig. 7

The constant vector ${\mathbf{N}}$. The plane sum vector ${\mathbf{S}}.$

7 Outburst of the Laplace–Runge–Lenz vector

A remarkable, well-known feature of the Kepler problem is the existence (beyond the constant angular momentum vector ${\varvec{\Gamma }}$) of an additional constant vector, the so called Laplace–Runge–Lenz vector, that is

$$ {\mathbf{V}} \,=\,K^2\,{\mathbf{e}}.$$

Now we notice that both our two important vectors ${\mathbf{N}}$ and ${\mathbf{S}}$ have in common the vector

$${ p^{-1}\, {\mathbf{e}} \,=\,\frac{K^2}{\Gamma ^2}\,{\mathbf{e}} }$$

(Fig. 7).

This is not a coincidence: in the spirit of the combined vectors generated by the sphere $S_{p^{-1}}$, if we simply rescale this vector by $\Gamma ^2$ we immediately recover the celebrated Laplace-Runge-Lenz vector

$$ {\mathbf{V}}\,=\,K^2\,{\mathbf{e}}$$

which satisfies

$$ {\mathbf{V}} \,\cdot \, \varvec{\Gamma } \,=\, {\mathbf{0}} $$

and which, being a constant vector, notoriously expresses the fact that a Kepler orbit does not precess in the plane of motion given by ${\varvec{\Gamma }}$.

Remark

The ‘origin’ of this extra conserved vector is related in the literature to the so called ‘hidden symmetry’ of the Kepler problem, for it arises from the invariance of the Hamiltonian function of the Kepler problem under the symmetry group of a four-dimensional real rotation group in the four-dimensional Euclidean space $R^4$.

For us the Laplace–Runge–Lenz vector is not completely hidden, but it already pops up by itself as an outstanding vector in the three-dimensional Euclidean arena: it is shared by the two fundamental vectors ${\mathbf{N}}$ and ${\mathbf{S}}$.

Fig. 8

The projection of an elliptic section onto the Kepler plane

8 The primigenial sphere and the regularizing KS-map

The well known singularity for $r=0$ in the equation of the Kepler motion

$${ \ddot{\mathbf{x}}\,+\, \frac{K^2}{r^3}\,{\mathbf{x}}\,=\,0 \qquad (.\equiv d/dt)}$$

was removed by Kustaanheimo and Stiefel ([4]) by means of the so called KS-regularization in real form, which relies on both a time transformation used by Levi–Civita and a peculiar coordinate transformation (briefly KS-map) given by

$$ {\big (R^4-\{0\}\big ) \longrightarrow \big (R^3-\{0\}\big ):\, \qquad {\mathbf{u}} \rightarrow {\mathbf{x}} }$$

(30)

which maps a parametric four-dimensional Euclidean space $R^4$ of real vectors ${{\mathbf{u}} \,=\,(u_1,u_2,u_3,u_4)}$ onto the ordinary three-dimensional Euclidean space or real vectors ${\mathbf{x}}\,=\, (x_1,\,x_2,\,x_3)$.

The regularized equation of motion is the linear regular differential equation

$$ {\mathbf{u}}\,''+ \omega ^2 \,{\mathbf{u}} \,=\,{\mathbf{0}} $$

where the symbol $'$ denotes the derivative with respect to the new time variable and

$$ {2\omega ^2\,\,=\,-E}$$

denotes the opposite of the Kepler mechanical energy $E$.

Now, the KS-map (30) acquires a simple, interesting interpretation in our spherical arena.

In fact, let us consider the particle position vector ${\mathbf{x}}\,=\,r\varvec{\rho }$ and the following spherical elements of the unit sphere (the sphere $S_{p^{-1}}$ reduced by $p^{-1}$, given by (28)), namely:

• a. The two unit vectors ${\mathbf{K}}$ and ${\varvec{\rho }}$.

• b. The right-handed colatitude angle $\phi$;

These elements suggest to consider (Fig. 9) the combination of:

• 1. A right-handed rotation of ${\phi \,=\,\frac{\pi }{2}}$ through the origin $F$, which carries directly the unit vector ${\mathbf{K}}$ onto the unit vector ${\varvec{\rho }}$;

• 2. A dilation in the ${\mathbf{I}}, {\mathbf{J}}$-plane by the positive factor $r$, which carries the unit vector ${\varvec{\rho }}$ onto the vector ${P-F\,=\,{\mathbf{x}}\,=\,r\varvec{\rho }}$, which is exactly the position vector of a point on the plane Kepler orbit.

This simple compound roto-dilation

$${\mathbf{K}} \rightarrow \varvec{\rho } \rightarrow r\varvec{\rho } $$

(which rotates the unit vector ${\mathbf{K}}$ about the origin $F$ and stretches it by the radial distance factor $r$) may be written in a simple quaternion form [7], bringing exactly to the KS-map (30) devised by Kustaanheimo and Stiefel.

Thus the primitive spherical elements of the primigenial sphere incorporate even the regularizing KS-map.

Let us add (as shown in [8] via the crazy fountain picture), that since ${\varvec{\rho }}$ depends on the longitude angle ${\theta}$, the whole collection of all these roto-dilations (for each fixed $\theta$) may be represented by the picture given in Fig. 9, where the sprays, spreading in a circular fashion from the arrowed point of ${\mathbf{K}}$, reach the point ${\varvec{\rho } (\theta )}$ on the plane and then spring away horizontally to reach the point ${\mathbf{x}} \,=\, r\varvec{\rho }$ on the same plane.

Fig. 9

The regularizing KS-map pictured as a roto-dilation ${{\text{K }} \to {\varvec{\rho}} \to r{\varvec{\rho}} }$

Fig. 10

The primigenial sphere ${S_{p^{-1}}}$ and its primitive elements${\varvec{\rho }\,, {\mathbf{K}}\,, \varvec{\epsilon }_{0}={\mathbf{e}}}$

9 The angle $\phi_{0}$ and the Kepler energy. Outlook

Throughout this paper we have endeavored to present a simple, spherical investigation of the well-known Kepler problem in its natural three-dimensional $R^3$-arena. We have shown how to construct all the characteristic elements of the Kepler problem via simple combinations of the basic, primitive elements of a primeval structure, the ‘primigenial’ sphere $S_{p^{-1}}$ (see Fig. 10).

Essentially, we have:

• a. Rewritten the governing Newtonian attractive force ${\mathbf{F}}$ so to keep track not only of the symmetries but also of the planarity of the Kepler motion in $R^3$;

• b. Emphasized the role of both the two spherical coordinates, the longitude $\theta$ and the colatitude $\phi$ of a sphere;

• c. Considered a sphere as a starry sphere, that is as a locus of vectors, whence it is precisely the vector equation of the primigenial sphere $S_{p^{-1}}$

  $$ {\text{P-F = }}{p^{-1}}\left( { \varvec{\in}} + {\text{cos}}\phi {\text{K}} \right) $$

  (31)

  which not only generates directly in $R^3$ the ${\mathcal C}$- cone structure which defines the ’conic’ orbits, but which also embodies in a natural way the geometrical and physical elements of the orbits: the centre of attraction $F$, the semilatus-rectum parameter $p$ and the eccentricity $e=\epsilon _{0}$ encapsulated in the extension vector ${{\varvec{\epsilon }_{0}}}$.

To further highlight the significance of the primigenial sphere description, let us add that there is more than meets the eye, since the colatitude angle ${\phi _{0}}$ is strictly related to the physical mechanical energy $E$ of the Kepler problem.

In fact let us rotate the unit vector ${\mathbf{K}}$ in the ${({\mathbf{K}}, {\mathbf{I}})}$-plane around $F$ through the particular angle $\phi _{0}$ defined by

$$ {\sin \,\phi _{0}}\,=\, \sqrt{2Ep\,K^{-2}\,+\,1} $$

(32)

where $E$ denotes the constant energy of the Kepler orbits. Since $E$ is notoriously related to $e$ by

$$ {\text{e}}^{{\text{2}}} {\text{ - 1 = 2E }}\Gamma ^{{\text{2}}} {\text{ K}}^{{{\text{ - 4}}}} $$

we find exactly that ${\sin \,\phi _{0}\,=\,e}$, which now has both a geometrical interpretation (see Fig. 10 where the rotating vector ${\mathbf{K}}$ is a unit one) and a physical one by (32).

This last result shows that the finding of a primigenial structure (such as the sphere $S_{p^{-1}}$ of the Kepler problem) is more than a fortuitous invention: suitably developed and extended, a primigenial structure may help in suggesting and obtaining the main features and the evolution of other different dynamical theories.