1 Introduction

Parallel robotic manipulators have been the subject of many robotic researches during the past three decades (Wang and Nace 2009; Arsenault and Gosselin 2006; Zhang et al. 2009a, b; Moon 2007; Palmer et al. 2008; Dong et al. 2007; Li and Xu 2006; Ukidve et al. 2008; Fang et al. 2004; Mitchell et al. 2006). A parallel manipulator typically consists of a moving platform that is connected to a fixed base by at least two kinematic chains in parallel. Parallel manipulators can provide several attractive advantages over their serial counterpart in terms of high stiffness, high accuracy, and low inertia, which enable them to become viable alternatives for wide applications (Zhang and Wang 2002; Bi et al. 2007; Chanal et al. 2009; Ottaviano et al. 2004; He and Lu 2007; Lessard et al. 2007; Zhang et al. 2009a, b; Wang et al. 2010; Wang and Nace 2009). But parallel manipulators also have disadvantages, such as complex forward kinematics, small workspace, complicated structures, and a high cost (Zhang 2009). To overcome the above shortcomings, progress on the development of parallel manipulators with less than 6-DOF has been accelerated.

Only recently, research on parallel manipulators with less than 6-DOF has been leaning toward the decoupling of the position and orientation of the end-effector. Kinematic decoupling for a parallel manipulator is that one motion of the up-platform only corresponds to input of one leg or one group of legs. Nevertheless, to date, the number of real applications of decoupled motion actuated parallel manipulators is still quite limited. This is partially because effective development strategies of such types of closed-loop structures are not so obvious. In addition, it is very difficult to design mechanisms with complete decoupling, but it is possible for fewer DOF parallel manipulators. To realize kinematic decoupling, the parallel manipulators are needed to possess special structures. Thus, investigating a parallel manipulator with decoupling motion remains a challenging task.

This paper focuses on the conceptual design, analysis and manufacturing of a 3-DOF non-over constrained translational parallel robotic manipulator with decoupled motions which can be utilized for parts assembly and light machining tasks that require large workspace, high dexterity, high loading capacity, and considerable stiffness. In what follows, conceptual generation, mobility analysis and inactive joint are presented in Sect. 2. Inverse and forward kinematics modelling is addressed in Sect. 3. Afterwards, performances including singularity, stiffness and workspace indices are derived in Sect. 4. In Sect. 5, genetic algorithm based workspace optimization is conducted for the 3-CRU manipulator. In Sect. 6, dynamics simulation is conducted based on Lagrangian method. In Sect. 7, the physical prototype is manufactured. Finally, conclusion and future work needed is given.

2 Geometrical design

2.1 Comparison between serial and parallel manipulators

A fully parallel manipulator is a parallel mechanism satisfying the following conditions:

  1. 1)

    The number of elementary kinematic chains equals the relative mobility between the base and the moving platform

  2. 2)

    Every kinematic chain possesses only one actuated joint

  3. 3)

    All the links in the kinematic chains are binary links; i.e., no segment of an elementary kinematic chain can be linked to more than two bodies

A fully parallel manipulator has one and only one solution to the inverse kinematics problem. Any parallel manipulator with multiple solutions for the inverse kinematics problem is a non-fully parallel manipulator. Table 1 specifies the physical characteristics of serial and parallel manipulators.

Table 1 Comparison between serial and parallel manipulators
Full size table

2.2 Design considerations

To simplify the design and development efforts, we have the following additional considerations,

  • Th parallel manipulators is composed of a base and a moving platform connected by three legs

  • Symmetric design—each leg is identical to the others. Hence, each leg should have the same number of actuated joints

  • Type of joints—four types of commonly used joints are considered:

    (i):

    1-DOF revolute (R) joint

    (ii):

    1-DOF prismatic (P) joint

    (iii):

    2-DOF universal (U) joint

    (iV):

    2-DOF cylinder (C) joint

Among them, the revolute and universal joints are only meant for passive (i.e. not actuated) joint, the prismatic or the prismatic in the cylinder joints are only meant for actuated joints.

  • Actuated joints are placed close to the base so as to reduce the moment of inertia and increase the loading capacity and motion acceleration.

  • At most one (actuated) prismatic or cylinder joint can be employed in each of the legs due to its heavy and bulky mechanical structure.

  • The number of redundant DOF of a leg is not greater than one.

  • The number of inactive joint of all legs is not greater than one.

  • Each leg is composed of a group of at least three revolute joints with parallel axes and at most one revolute joint whose axis is not parallel to the axes of the revolute joints in the group of revolute joints with parallel axes, while the axis of the actuated joint (prismatic or cylinder) is not perpendicular to the axes of the revolute joints in the group of revolute joints with parallel axes.

  • The axes of all the revolute joints in the group of revolute joints with parallel axes are not parallel to a plane.

  • The axes of all three actuated joints should be arranged perpendicular to each other to satisfy the parallel manipulator featuring decoupled motion.

2.3 Proposed CAD model

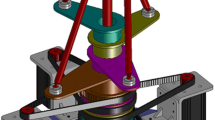
With these design considerations, a novel 3-CRU non-over constrained translational parallel manipulator with decoupled motions has been proposed. The 3-CRU (as shown in Figs. 1 and 2) is composed of a base and a moving platform connected by three CRU legs.

Fig. 1
figure 1

CAD model of 3-CRU

Full size image
Fig. 2
figure 2

Schematic model of 3-CRU

Full size image

The axes of the C and R joints, as well as the axe of the U joint, are arranged such that their joint axes are parallel to a common plane. As a result, the axe of outer R joint (the one connects to the moving platform) of the U joint is perpendicular to the axe of the U joint as well as all the axes of the C and R joints within a given leg. All above guarantee that instantaneous rotation of the moving platform about a direction that is perpendicular to the common plane of all the axes of the C, R, and inner R of the U joint is impossible. Since each C joint can be considered as a combination of one R joint and one P joint with parallel axes, each U joint consists of two intersecting R joints; each leg is kinematically equivalent to a PRRRR chain.

Through preliminary analysis, a 3-DOF parallel manipulator with such three CRU legs possesses the following advantages:

  1. 1)

    Simple kinematics and easy for analysis, design, trajectory planning, and motion control

  2. 2)

    Large and well shaped workspace

  3. 3)

    High stiffness

  4. 4)

    High loading capacity

2.4 Mobility analysis of the manipulator

Because most of the lower-mobility parallel mechanisms are over-constrained, it is necessary to take the common constraints of mechanism and the passive constraints into consideration in mobility analysis. Thus, the DOF of this manipulator can be obtained from the general Chebyshev–Grubler–Kutzbach formula,

$$ M = d(\eta - g - 1) + \sum\limits_{i = 1}^{g} {\mathop f\nolimits_{i} } + \nu = 6 \times (8 - 9 - 1) + 3 \times (2 + 1 + 2) + 0 = 3 $$
(1)

For a parallel manipulator with less than six degrees of freedom, the motion of each leg that can be treated as a twist system is guaranteed under some exerted structural constraints, which are termed as a wrench system. The wrench system is a reciprocal screw system of the twist system for the same leg, and a wrench is said to be reciprocal to a twist if the wrench produces no work along the twist. The mobility of the manipulator is then determined by the combined effect of wrench systems of all legs.

For the 3-CRU manipulator, the wrench system of a leg is a 1-system, which exerts one constraint couple to the moving platform with its axis perpendicular to the axis of C joint within the same leg. The wrench system of the moving platform, that is a linear combination of wrench systems of all the three legs, is a 3-system, because the three wrench 1-systems consist of three couples, which are linearly dependent and form a screw 3-system. Since the arrangement of all the joints shows on Fig. 2, the wrench systems restrict three rotations of the moving platform with respect to the fixed base at any instant, thus leading to a translational parallel manipulator.

2.5 Inactive joint

A general leg for a translational parallel manipulator with a liner actuator is composed of (ψ-1) R joints and one P or C joints. For the purposes of simplification, the P joint (or the P joint of the C joint) is labeled with one, while the R joints (including the R joint of C joint) are labeled with 2, 3…n, and \( \psi \) is the sequence from the base to the moving platform.

The infinitesimal change of orientation of the moving platform is a serial kinematic chain undergoing infinitesimal joint motion is (Kong and Gosselin 2002)

$$ \Updelta R = \sum\limits_{i = 2}^{n} {(\Updelta \theta_{i} } \cdot s_{i} ) $$
(2)

where ∆R and ∆θ i denote the infinitesimal change of orientation of the moving platform and the infinitesimal joint motion of joint i respectively; s i denotes the unit vector along the axis of joint i before the infinitesimal motion.

For a translational parallel manipulator, there exists

$$ \Updelta R = 0 $$
(3)

Substitution of Eq. (2) into Eq. (3), yields

$$ \sum\limits_{i = 2}^{n} {(\Updelta \theta_{i} } \cdot s_{i} ) = 0 $$
(4)

For the 3-CRU parallel manipulator, the only R joint whose axis is not parallel to the axes of the other R joints is labeled with five. It has

$$ {\mathbf{s}}_{ 5} \ne {\mathbf{s}}_{ 4} = {\mathbf{s}}_{ 3} = {\mathbf{s}}_{ 2} $$
(5)

Substitution of Eq. (5) into Eq. (4), yields

$$ {\mathbf{s}}_{ 5} \,\Updelta \theta_{5} + \sum\limits_{i = 2}^{4} {\Updelta \theta_{i} } {\mathbf{s}}_{i} = 0 $$
(6)

To satisfy Eq. (6), it has

$$ \Updelta \theta_{5} = 0 $$
(7)

and

$$ \sum\limits_{i = 2}^{4} {\Updelta \theta_{i} = 0} $$
(8)

Equation (7) proves that the outer R joint of the U joint of each leg is inactive. Equation (8) shows that the R joints with parallel axes within the same leg constitute a dependent joint group.

An inactive joint is a joint in a leg whose joint variable is constant during the motion of the manipulator. Although when an inactive joint is removed, the relative motion within the leg will not be changed, by using inactive joints, the number of over-constraints of the translational parallel manipulator can be reduced.

3 Kinematic modeling

The kinematics of a robot deal with finding the analytical relations between its input variables (the values of the actuated joints) and output variables (the position and orientation of the moving platform); the equations that connect the input and the output variables of a mechanism are called the kinematic equations of the mechanism. The equations that connect input and output velocities in a mechanism are called the instantaneous kinematic variables of the robot, i.e., the position and orientation of the moving platform, for a given set of input variables, namely, the actuated joints’ variables.

3.1 Inverse kinematics

The inverse kinematics problem (IKP) deals with finding the actuated joints’ values that correspond to a given set of output variables (position and orientation of the moving platform). The purpose of the inverse kinematics issue is to solve the actuated variables from a given position of the mobile platform.

The IKP of the Stewart–Gough manipulator is trivial with single solution, but when the number of kinematic chains is reduced, the number of solutions of the IKP increases and the problem becomes more challenging (Merlet 2006). The direct kinematics problem of parallel manipulators is by far more challenging than the IKP since it requires solving a set of polynomial equations in the output variables. While the IKP for a general Stewart–Gough manipulator has only one solution, the direct kinematic problem has up to forty real solutions (Tsai 1999).

To facilitate the analysis, referring to Fig. 3, a fixed reference frame O-xyz is attached at the centered point O on the base and a moving reference frame P-uvw at the centered point P on the moving platform, with the z and w axes perpendicular to the platform, and the x and y axes parallel to the u and v axes, respectively. The direction of the ith fixed C joint is denoted by unit vector c i . A reference point M i is defined on the axis of the ith fixed C joint, and the sliding distance is defined by d i ; point B i defined as the interaction of the axes of the U joint. Furthermore, the position vector of point M i in the fixed frame is denoted by m i  = [\( m_{xi} ,m_{yi} ,m_{zi}^{{}} \)]T, while the position vector of point B i is noted by \( {}^{p}{\mathbf{b}}_{i} \, = \,\left[ {b_{xi} ,b_{yi} ,b_{zi} } \right]^{\text{T}} \, \) in the moving frame and b i in the fixed frame. The u i is defined as a vector connecting Ai to Bi, and is orthogonal to the unit vector r i  = [\( r_{xi} ,r_{yi} ,r_{zi} \)]T.

Fig. 3
figure 3

Kinematic modeling of a leg

Full size image

Generally, the position and orientation of the moving platform with respect to the fixed base frame can be described by a position vector p = [\( p_{x} p_{y} p_{z} \)]T and a 3 × 3 matrix \( {}^{o}R_{P} \).

Since the moving platform of a 3-CRU possesses only translational motion \( {}^{o}R_{P} \) becomes an identity matrix. Then, it has

$$ b_{i} = {}^{p}b_{i} $$
(9)

Referring to Fig. 3, a vector-loop equation can be written for each leg as follows:

$$ u_{i} = p + b_{i} - m_{i} - d_{i} c_{i} $$
(10)

Substituting Eq. (9) into Eq. (10), it has,

$$ u_{i} = p + {}^{p}b_{i} - m_{i} - d_{i} c_{i} $$
(11)

As vectors u i and r i are orthogonal, it yields,

$$ u_{i}^{T} r_{i} = \, 0 $$
(12)

Substituting Eq. (11) into Eq. (12), it gets,

$$ (p + {}^{p}b_{i} - m_{i} - d_{i} c_{i} )^{\text{T}} r_{i} = \, 0 $$
(13)

For geometric parameters of this parallel manipulator, it has,

$$ c_{ 1} = r_{ 1} = \left[ { 1,0,0} \right]^{\text{T}} $$
(14)
$$ c_{ 2} = r_{ 2} = \left[ {0, 1,0} \right]^{\text{T}} $$
(15)
$$ c_{ 3} = r_{ 3} = \left[ {0,0, 1} \right]^{\text{T}} $$
(16)
$$ e_{ 1} = \left[ {0,0, 1} \right]^{\text{T}} $$
(17)
$$ e_{ 2} = \left[ {0,0, 1} \right]^{\text{T}} $$
(18)
$$ e_{ 3} = \left[ { 1,0,0} \right]^{\text{T}} $$
(19)

Substituting Eqs. (14)–(19) into Eq. (13), the solution of the inverse displacement analysis for the 3-CRU parallel manipulator is derived as,

$$ d_{ 1} = p_{\text{x}} + b_{\text{x1}} - m_{\text{x1}} $$
(20)
$$ d_{ 2} = p_{\text{y}} + b_{\text{y2}} - m_{\text{y2}} $$
(21)
$$ d_{ 3} = p_{\text{z}} + b_{\text{z3}} - m_{\text{z3}} $$
(22)

From Eqs. (20)–(22), it can easily observed that the motions of the 3-CRU parallel manipulator are decoupled. The actuator in leg 1 controls the translation along the X direction; the actuator in leg 2 controls the translation along the Y direction while the actuator in leg 3 controls the translation along Z direction.

The distance between the center of the moving plate and base is m i  = l 2i + b

3.2 Forward kinematics

The forward kinematics is to obtain the end-effector position, \( [p_{x} ,p_{y} ,p_{z} ]^{T} \), when the input sliding distance di is given.

By solving Eqs. (20)–(22) for variables x, y, and z, the forward kinematics can be performed. Thus, it yields,

$$ p_{x} = d_{1} - b_{x1} + m_{x1} $$
(23)
$$ p_{y} = d_{2} - b_{y2} + m_{y2} $$
(24)
$$ p_{z} = d_{3} - b_{z3} + m_{z3} $$
(25)

3.3 Velocity analysis

Equations (23)–(25) can be rewritten as:

$$ \left[ {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ {d_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {p_{x} + b_{x1} - m_{x1} } \\ {p_{y} + b_{y2} - m_{y2} } \\ {p_{z} + b_{z3} - m_{z3} } \\ \end{array} } \right] $$
(26)

Taking the derivative of Eq. (26) with respect to time yields,

$$ \left[ {\begin{array}{*{20}c} {\dot{d}_{1} } \\ {\dot{d}_{2} } \\ {\dot{d}_{3} } \\ \end{array} } \right] = J\left[ {\begin{array}{*{20}c} {\dot{p}_{x} } \\ {\dot{p}_{y} } \\ {\dot{p}_{z} } \\ \end{array} } \right] $$
(27)

where J is the 3 × 3 identity matrix. Since J is an identity matrix, the manipulator is isotropic everywhere within its workspace.

Therefore, the velocity equations of the 3-CRU parallel manipulator can be written as,

$$ \dot{d}_{1} = \dot{p}_{x} ,\,\dot{d}_{2} = \dot{p}_{y} ,\,\dot{d}_{3} = \dot{p}_{z} $$
(28)

4 Performance analysis

4.1 Singularity analysis

Singularity configurations are particular poses of the end-effector that will induce the mechanism itself to lose the inherent rigidity (Firmani and Podhorodeski 2009, Yang and Obrien 2010). The constraint singularity (Zlatanov et al. 2002) occurs when the moving platform of a translational parallel manipulator can rotate instantaneously. The constraint singularity occurs for a translational parallel manipulator if and only if its wrench system (a 3-system of \( \infty - \) pitch) degenerates into a 2-system or a 1-system.

For the 3-CRU translational parallel manipulator, as r i \( \ne \) e i, the CRU leg exerts one constraint on the moving platform, which prevents it from rotating about any axis parallel to r i \( \times \) e i. Therefore, the wrench system of the leg is invariant. The order of the wrench system of the 3-CRU is thus a constant. That is to say, the 3-CRU translational parallel manipulator is free from constraint singularity.

When type II kinematic singularity occurs for a parallel manipulator, the moving platform can undergo infinitesimal or finite motion when the inputs are specified. It will be proved below that, there is no type II singularity for the 3-CRU translational parallel manipulator.

It is known that no rotation singularity exists for the 3-CRU translational parallel manipulator. Thus, Eq. (27) is always satisfied. Uncertainty singularities for the 3-CRU translational parallel manipulator occur if and only if J is singular. As is known that the Jacobian matrix, J, is an identity matrix, thus, no type II singularity exists for the 3-CRU translational parallel manipulator.

4.2 Stiffness analysis

Stiffness is one of the most important indexes of parallel manipulator. The main reasons include: (1) the higher stiffness can improve the dynamic accuracy; (2) stiffness affects control performance. Compare with serial manipulators, parallel manipulators offer an improved stiffness and better accuracy. This feature makes them attractive for innovative machine tool structures for high speed machining (Tlusty and Ridgeway 1999). The stiffness properties of a manipulator can be defined through a 6 × 6 matrix that is called stiffness matrix K.

Several methods exist for the computation of the stiffness matrix: the finite element analysis (FEA) (Majou et al. 2007), the matrix structural analysis (MSA) (Bouzgarrou et al. 2002), and the virtual joint method (VJM) which is also called the lumped modelling (Gosselin 1990; Gosselin and Zhang 2002). The FEA is proved to be the most accurate and reliable; however, this method has the disadvantage that it requires an extensive computation time (Company and Pierrot 2002). The MSA also incorporates the main ideas of the FEA, but operates with rather large elements, 3D flexible beams describing the manipulator structure. This leads obviously to the reduction of the computational expenses, but does not provide clear physical relations required for the parametric stiffness analysis. Finally, the VJM method is based on the expansion of the traditional rigid model by adding the virtual joints, which describe the elastic deformations of the links.

The stiffness of a parallel mechanism is dependent on the joint’s stiffness, the legs structure and material, the platform and base stiffness, the geometry of the structure, the topology of the structure and the end-effector position and orientation.

The stiffness of a parallel mechanism at a given point of its workspace can be characterized by its stiffness matrix. This matrix relates the forces and torques applied at the gripper link in Cartesian space to the corresponding linear and angular Cartesian displacement. It can be obtained using kinematic and static equations. For the stiffness characterization in different directions, the eigenvalues of stiffness matrix may be utilized to describe the principal stiffness in each axis. Since the units of the different entries of the matrix are not uniform, the dimensions of the eigenvalues of the stiffness include both force/length and force–length. Hence, the eigenvalue problem for stiffness is dimensionally inconsistent and does not make sense physically. In this research, the stiffness mapping is derived based on the stiffness matrix which is usually represented as K L  = k J T J, where J is Jacobian matrix, k is the rigidity coefficient. On the other hand, the diagonal elements of stiffness matrix K L reflect the pure stiffness more clearly and reasonable.

Note, that link stiffness is not considered in conventional joint stiffness analysis approach. That means links of the mechanism are assumed strictly rigid.

The joint displacement, Δq, is related to the end-effector displacement in Cartesian space Δr, by the conventional Jacobian matrix J,

$$ \Updelta \mathbf{q} = \mathbf{J}\,\Updelta \mathbf{r} $$
(29)

Under the principle of virtual work, the end-effector force F in terms of the actuated joint torques \( \tau \) is given as the following:

$$ \mathbf{F} = \mathbf{J}^{\text{T}} \tau $$
(30)

Then τ can be related to Δq by a diagonal actuated joint stiffness matrix \( \mathbf{K}_{J} = diag[k_{1} , \ldots , k_{n} ], \) whose elements \( k_{i} \)are the stiffness of each actuator, as follow:

$$ \tau = \mathbf{K}_{J} \Updelta \mathbf{q} $$
(31)

Substituting Eq. (29) into Eq. (31) and the resulting equation into Eq. (30), then it has,

$$ \mathbf{F} = \mathbf{J}^{\text{T}} \mathbf{K}_{J} {\mathbf{J}}\Updelta r $$
(32)

Therefore, the stiffness matrix of a parallel manipulator is given by,

$$ \mathbf{K}_{r} = \mathbf{J}^{\text{T}} \mathbf{K}_{J} {\mathbf{J}} $$
(33)

Particularly, in the case for which all the actuators have the same stiffness, i.e., \( k_{1} = k_{2} = \cdots = k_{n} \), then Eq. (33) will be simplified to:

$$ \mathbf{K} = k\mathbf{J}^{\text{T}} \mathbf{J} $$
(34)

As J is a 3 × 3 identity matrix, so it has J T J = 1. The stiffness matrix of this 3-CRU manipulator is

$$ \mathbf{K} = diag\left( {k,k,k} \right) $$
(35)

The above model is now used to obtain the stiffness maps for this 3-DOF decoupled parallel manipulator. From the stiffness mesh graphs in X (Fig. 4a), Y (Fig. 4b), and Z (Fig. 4c), one can conclude that the stiffness in X, Y, and Z will not change while the position and orientation are changing. That means the stiffness of the actuators is the main factor to determine the stiffness in the situations. The results also indicate that the stiffness is a constant within its workspace; this will improve the kinematic accuracy.

Fig. 4
figure 4

Stiffness atlas in a x-direction, b y-direction, c z-direction

Full size image

As a result, the desired stiffness on X, Y, and Z directions can be achieved by adjusting the stiffness of the actuators. Moreover, when using this 3-DOF parallel manipulator for parts assembly or as a machine tool, one can judge if the parallel manipulator is stronger enough to perform the tasks by considering the workloads in X, Y, and Z directions.

4.3 Workspace analysis

The workspace of the parallel robot can be defined as a reachable region of the origin of a coordinate system attached to the center of the moving plate. Since its major drawback is a limited workspace, it is of primary importance to develop algorithms by which the workspace can be determined and the effect of different designs on the workspace can be evaluated.

Various approaches may be used to calculate the workspace of a parallel manipulator, such as geometrical approach, discretisation method, and numerical methods. The most common one is the geometrical approach. The purpose of this approach is to determine the boundary of the robot workspace geometrically.

From Eqs. (23)–(25), it appears clearly that the Cartesian workspace consists of a parallelepiped. A regular workspace (parallelepiped) is very attractive in practice.

Since the linear actuators are used for the 3-CRU parallel manipulator, the workspace is limited by the stroke lengths di. However, it is preferable to make the links of length l 1i and l 2i sufficiently long to ensure that additional constraints are not imposed on the mechanism, so that the ranges of motion of all linear actuators can be fully utilized. To implement this, the constraint is applied that the workspace volume is always equal to the product of the stroke lengths of the linear actuators.

Finally, the workspace of the parallel manipulator is obtained shown in Fig. 5.

Fig. 5
figure 5

Workspace representation

Full size image

5 Workspace optimization

Parallel mechanisms create great interest because they can be used for many applications in industrial such as machine tools or light assembly.

Obtaining high performance requires the choice of suitable mechanism dimensions especially as there is much larger variation in the performances of parallel architectures according to the dimensions than for classical serial ones. Indeed, with the development of manipulators for performing a wide range of tasks, the introduction of performance indices or criteria, which are used to characterize the manipulator, has become very important. A number of different optimization criteria for manipulators may be appropriate depending on the resources and general nature of tasks to be performed. The choice of any of the criteria for a given set of data would result in a manipulator whose performances do not necessarily match the optimum values of the other criteria.

Workspace is one of the most important properties because workspace determines geometrical limits on the task that can be performed. In this research, we will optimize the design of the 3-CRU architecture with its position workspace is suitably prescribed. The approach presented by Laribi et al. (2007) will be adopted and GA is applied. The flow chart in Fig. 6 shows the sequence of the basic operators used in genetic algorithms.

Fig. 6
figure 6

Genetic algorithm flow chart

Full size image

The optimum design problem for the 3-CRU architecture can be formulated as:

Objective function \( L = l_{1i}^{2} + l_{2i}^{2} + b^{2} \,(i = 1,2,3) \) where \( L \) denotes the size measure of the manipulator.

Assume that \( l_{11} = l_{12} = l_{13} ,l_{21} = l_{22} = l_{23} \)

In order to complete the design characterization and use prescribed data, the optimization problem is also subject to constraints from the position point of view:

$$ \begin{gathered} X_{\hbox{max} } \le X_{\hbox{max} }^{\prime } \hfill \\ Y_{\hbox{max} } \le Y_{\hbox{max} }^{\prime } \hfill \\ Z_{\hbox{max} } \le Z_{\hbox{max} }^{\prime } \hfill \\ \end{gathered} $$
(36)

where the left-hand values correspond to the orientation volume \( W_{L}^{*} \) and the prime values describe the prescribed parallelepiped \( W_{L} \).

Summarizing the optimum design for the 3-CRU architecture has been formulated by Eq. (36) and the W L by taking into account only workspace characteristics to give the smallest manipulator fitting the prescribed workspaces. In addition, the forward kinematics presented in Eqs. (23)–(25) are useful and computationally efficient to determine extreme reaches of Eq. (36).

The number of variables is to be determined. In this design, they are \( b,l_{11} \) and \( l_{21} \). So the vector of optimization variables is therefore:

$$ a = \left[ {l_{11} ,l_{21} ,b} \right] $$
(37)

and their bounds are:

$$ l_{11} \in [300,350], \, l_{21} \in [300,350], \, b \in [30,50]\,{\text{mm}} $$

The population size and the generation number have to be selected. The generation number is the maximum number of iterations the GA performs and the population size specifies how many individuals there are in each generation. In this case, the population size is set to TEN; the maximum generation number is 100.

The Fig. 7 displays a plot of the best and mean values of the fitness function at each generation.

Fig. 7
figure 7

The best fitness and the best individuals of the design optimization

Full size image

The following figure also displays the best and mean values in the current generation numerically at the top of the figure.

The optimal parameters obtained after 51 generations are given as follows:

$$ {\mathbf{a}} \, = [l_{11} ,l_{21} ,b] = \left[ { 30 2. 50 5 1 1,{ 324}. 9 70 6,{ 33}.0 10 2 9} \right] $$

which suggest the optimal design values for the length of links of the leg and the dimension of the end-effector are

$$ d\, = \,l_{ 1 1} \, = \, 30 3\,{\text{mm}}, \, l_{ 2 1} \, = \, 3 2 5\,{\text{mm}}, \, b\, = \, 3 4 {\text{ mm}} $$

6 Dynamics simulation

The dynamics analysis of parallel mechanism includes inertial force calculation, stress analysis, dynamic balance, dynamic modeling, computer dynamic simulation, dynamic parameter identification and elastic dynamic analysis, in which dynamic modeling is the most fundamental and important one. Generally, because of the complexity of parallel mechanism, the dynamic model is multi-degree-of-freedom, multi-variable, highly nonlinear and multi-parameter coupling.

There are many approaches for current analysis of dynamics, such as the methods of Lagrangian, Newton–Euler, Gauss and Kane. Lagrangian method can not only seek the simplest form to deduce related dynamics equations of complex system, but also has an explicit structure.

$$ \frac{d}{dt}\,\left( {\frac{\partial L}{{\partial \dot{q}_{i} }}} \right)\, - \,\frac{\partial L}{{\partial q_{i} }} = F_{i} \, + \,\sum\limits_{j = 1}^{k} {\lambda_{j} \frac{{\partial \Upgamma_{j} }}{{\partial q_{i} }}} \quad (i = 1,2,3) $$
(38)

where L is equal to the kinetic energy minus the potential energy of the system, q i is the generalized coordinate, F i is the generalized force with respect to the generalized coordinate, Γ j denotes the jth constraint function, k is the number of constraint function and λ j is the Lagrangian multiplier.

The external force applied on the centroid of moving platform is

$$ \left\{ {\begin{array}{*{20}c} {F_{x} } \hfill & { = 120 \cdot \sin (time) + 48} \hfill \\ {F_{y} } \hfill & { = 80 \cdot \cos (time) + 42} \hfill \\ {F_{z} } \hfill & { = 45 \cdot \sin (time) + 45 \cdot \cos (time) + 48} \hfill \\ \end{array} } \right. $$
(39)

Under the condition of joints motion and applied force, the curves with time of the driving force and corresponding torque of the four translational joints can be recorded as shown in Fig. 8a–g.

Fig. 8
figure 8

The results of each driven joint a force, b torque, c translational displacement, d translational velocity, e translational acceleration, f angular velocity, g angular acceleration

Full size image

7 Prototype and experiment

The key issues in the detailed design of the 3-CRU translational parallel manipulator are described as follows,

1. Adopt linear actuation layout; a linear actuator drives the C joint in each leg, whereas all the other joints are passive. One of the advantages is to have all actuators installed on the fixed base. The C joints will be driven using toothed belts connected to DC servomotors.

2. The selection of the assembly modes of each leg.

In selecting the assembly modes of each leg, the location of the work piece to be placed should be taken into consideration.

For the 3-CRU translational parallel manipulator, the work piece is placed under the moving platform.

3. The determination of the link lengths of \( l_{1i} \) and \( l_{2i} \).

In determining the link lengths \( l_{1i} \) and \( l_{2i} \), the issue of avoiding link interferences should be taken into consideration.

To address this issue, \( l_{1i} \) and \( l_{2i} \) are adjusted to avoid interference among links in the three legs and the moving platform by simulating the motion of the parallel manipulator using a CAD software.

Consider the requirements of feasibility concerning dimensional limits for manufacturing parts, encoders available in the market, and the need for a continuous working space with no interference of moving parts, the following choices for the geometric parameters of the 3-CRU manipulator,

Stroke length: \( d_{1} = d_{2} = d_{3} = 220 \) mm

Length of leg: \( l_{1i} = l_{2i} = 325 \) mm

Dimension of the moving plate: \( b = 30 \) mm

The distance between the center of the moving plate and base: \( m = l_{2i} + b = 355 \) mm

To more effectively prove the concept, the prototype is manufactured with some simple materials and basic hand tools. A threaded rod is utilized to create the wanted translations in the three orthogonal directions, by lodging a nut into guide blocks of the same thread size and pitch. The block is kept tracking straight using a steel guide rod through a hole in the guide block. The threaded rod will act similarly to the ball screws allowing the block to feed in the direction dependant on the screw movement. These threaded rods are powered by drills affixed to nuts brazed onto the end of the rod to crudely simulate the electric stepper motors that will ultimately power our final prototype. The threaded rod in combination with the variable drill speeds represented two types of machine tool motion in the form of a quick rapid to a slow and precise feed. This demonstrates the incredible resolution that can be achieved through this type of motion.

Aside from displaying the motion of the final unit, as well as how the system translates motion through the use of independent linked arms acting on independent axis, but it also displayed the physical size and shape of the overall unit. This includes height, footprint, and the generally robust design that it has. This not only helps the consumer imagine the part size that can be cut, but also how and where the final tool can be located. Figure 6 shows the physical prototype of the 3-CRU decoupled parallel robotic manipulator (as shown in Fig. 9).

Fig. 9
figure 9

The physical prototype, a side view, b top view

Full size image

The control unit will have to be of small stature and easily accessible in the event of a failure. The unit must be able to be powered from any 120 VAC source at 15 amps max, or a 220 VAC source at 7 amps max. The system must be compatible with both USB and parallel port input interfaces. Figure 10 illustrates the set up of control system.

Fig. 10
figure 10

The set up of control system

Full size image

The four characters “UOIT” are selected to test the cutting performance with this portable machine. Beginning with the “U” when the original plunge cut is made, the bit bites into the wood and then applies a force to the arms, that is generally referred to as “walking”. This walking force is the natural force implied on the router as the end mill bites the wood and cuts through it. Due to the amount of play at the end mill, the router simply walks until the slack or play in the arms is taken up, and proceeds straight down as normal (as shown in Fig. 11).

Fig. 11
figure 11

The characters cut by the parallel robotic manipulator

Full size image

8 Conclusion and future work

8.1 Conclusion

The major contribution of this research is to have proposed a novel 3-DOF parallel manipulator with features such as lower mobility, decoupled motions, and isotropic. These advantages have great potential for machine tools and coordinate measuring machine. The conceptual design of a novel 3-DOF non-over-constraint translational parallel manipulator with decoupled motion has been proposed. The kinematic modeling of the parallel manipulator has been examined, in terms of inverse and forward kinematics study, velocity analysis, singularity analysis, as well as stiffness analysis. It has been noticed that due to the isotropy and motion decoupling, the inverse and forward kinematic are easy for analysis; The Jacobian is a 3 × 3 identity matrix; and the kinematic accuracy can be well improved, as the stiffness is a constant within the parallel manipulator’s workspace. The geometrical method was selected to determine the workspace of the parallel manipulator. The workspace simulation graphically describes all the locations of operation points, which the end-effector can reach, which is very useful to define the reach ability of the parallel manipulator. Some of the key issues in the detailed prototype design of the 3-CRU manipulator were discussed as well. GA has been adopted into optimize the design parameters of the manipulator with suitable prescribed workspace.

8.2 Future work

The following issues may deserve more attentions in the future. (1) To conduct kinematics calibration and error compensation study; (2) To perform a comprehensive study of new parallel manipulator with kinematic decoupling of great potential application. The comprehensive study will include the constraint singularity analysis, the forward kinematics, the inverse kinematics, the kinematic error analysis, the workspace analysis and the kinematic design. (3) To investigate other practical applications, such as a parallel module with kinematic decoupling of a hybrid machine tool.