1 Introduction

Since the identification of carbon nanotubes (CNTs) (Iijima 1991) enormous efforts are being exerted by the researchers for developing CNT-reinforced composites because of the exceptionally attractive properties (Treacy et al. 1996; Li and Chou 2003; Shen and Li 2004; Batra and Sears 2007) of CNTs. For example, Thostensen and Chou (2003) have estimated the elastic moduli of CNT-reinforced composite through micromechanical analysis. Odegard et al. (2003) predicted the effective elastic moduli of CNT-reinforced composite using an equivalent-continuum modeling method. Gao and Li (2005) derived a shear lag model of CNT-reinforced polymer composites by replacing the CNT with an equivalent solid fiber. Song and Yoon (2006) numerically estimated the effective elastic properties of CNT-reinforced polymer based composites. Seidel and Lagoudas (2006) carried out a micromechanical analysis to estimate the effective properties of CNT-reinforced composites. Selmi et al. (2007) investigated several micromechanics models to predict the elastic properties of single walled CNT-reinforced polymer composite. Zhang and He (2008) theoretically investigated the viscoelastic behavior of CNT-reinforced composites developing a three-phase shear-lag model. Most recently, Ray and Batra (2009) carried out a micromechanical analysis to estimate the effective elastic and piezoelectric properties of hybrid composite reinforced with CNTs and piezoelectric fibers. Further research on improving the effective properties of fiber-reinforced polymer matrix composite has led to the growth of CNTs on the surface of the advanced fibers. For example, Zhang et al. (2008) produced CNT arrays on the host aluminum silicate and quartz fibers. Mathur et al. (2008) experimentally investigated that the flexural strength and modulus of the carbon fiber-reinforced composite can be improved by growing CNTs on the surface of the carbon fibers. Garcia et al. (2008) fabricated hybrid laminate in which the reinforcements are woven cloth of alumina fibers with in situ grown CNTs on the surface of the fibers. They demonstrated that both mechanical and electrical properties of such laminate are enhanced because of CNTs grown on the surface of the alumina fibers. Recently, Ray et al. (2009) carried out a load transfer analysis of short carbon fiber reinforced composite in which the aligned CNTs are radially grown on the surface of the carbon fibers.

In this paper, a novel CNT hybridized 1–3 piezoelectric composite is proposed. The piezoelectric fiber reinforcements are unidirectional and CNTs are considered to radially grow on the surfaces of these piezoelectric fibers. The objective of this work is to investigate the load transferred to such CNT-coated piezoelectric fibers from the matrix in the absence and the presence of the electric field along the length of the fibers. A closed-form shear lag model is developed for such investigation, incorporating a micromechanics model for predicting the radially-orthotropic properties of the aligned-CNT reinforced polymer matrix.

2 Shear lag model

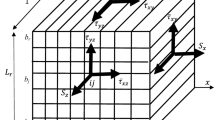
The proposed piezoelectric composite is a unidirectional continuous fiber-reinforced composite. Its shear lag model corresponds to that of the aligned long fiber-reinforced composite in which the fiber ends are treated as the fiber breaks and free of stress. Such shear lag model is concerned with the analysis of stress transfer to the portion of the fiber between the two fiber breaks from the matrix. Figure 1 illustrates a cylindrical representative volume element (RVE) of the proposed composite based on which the shear lag model is derived. The cylindrical coordinate system (r, θ and x) is considered in such a way that the axis of the RVE coincides with the x axis while the CNTs are aligned along the r-direction. The RVE consists of two concentric cylindrical phases. One of the phase is a solid micro-scale piezoelectric fiber reinforcement on which radially aligned CNTs have been grown. When this resulting fuzzy fiber is embedded in a polymer material, the CNT forest is filled with the polymer creating a nano-reinforced polymer matrix which may be called as a polymer nanocomposite (PNC). This cylindrical PNC is considered as the matrix phase of the RVE. The radius and the length of the piezoelectric fiber between two fiber breaks are denoted by a and 2L, respectively. The inner and outer radii of the CNT-reinforced matrix phase are a and R, respectively.

Fig. 1
figure 1

Cross-sections of the RVE of the CNT and piezoelectric fiber-reinforced composite

Full size image

As shown in Fig. 1, a tensile stress σ is applied to the RVE along x direction which results in a uniform stress level of σ′ = σR 2/(R 2 – a 2) over the cross-section of the matrix at x = ±L because of the fiber breaks. In order to derive this shear lag model, the effective properties of the PNC matrix phase are needed. This phase has transverse isotropy in a radial coordinate system due to the CNT alignment and isotropic nature of the polymer. A micromechanics model by Ray and Batra (2009) is used to calculate the effective elastic constants of the PNC matrix.

Returning to the shear-lag model, the governing equations for the different phases of this RVE concerning equilibrium along x direction are given by

$${\frac{{{\varvec{{{\partial}}}}{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{i}}} }}{{{\varvec{{{\partial}}}}{\mathbf{x}}}}}+{\frac{{\mathbf{1}}}{{\mathbf{r}}}}\;{\frac{{{\varvec{{{\partial}}}} ({\mathbf{r}}{\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{i}}} )}}{{{\varvec{\partial}} {\mathbf{r}}}}} = 0;\quad{\mathbf{i}}={\mathbf{f}}\;{\text{and}}\;{\mathbf{m}} $$
(1)

The relevant constitutive relations for the piezoelectric fiber are

$$ {\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} = {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} {\varvec{\epsilon}}_{{\mathbf{x}}}^{{\mathbf{f}}} + {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} {\varvec{\epsilon}}_{{\varvec{\uptheta}}}^{{\mathbf{f}}} + {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{f}}} {\varvec{\epsilon}}_{{\mathbf{r}}}^{{\mathbf{f}}} - {\mathbf{e}}_{\mathbf{33}} {\mathbf{E}}_{{\mathbf{x}}} \;{\text{and }}{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{f}}} = {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{f}}} {\varvec{\epsilon}}_{{\mathbf{x}}}^{{\mathbf{f}}} + {\mathbf{C}}_{\mathbf{23}}^{{\mathbf{f}}} {\varvec{\epsilon}}_{{\varvec{\uptheta}}}^{{\mathbf{f}}} + {\mathbf{C}}_{\mathbf{33}}^{{\mathbf{f}}} {\varvec{\epsilon}}_{{\mathbf{r}}}^{{\mathbf{f}}} - {\mathbf{e}}_{\mathbf{31}} {\mathbf{E}}_{{\mathbf{x}}} $$
(2)

while those of the matrix phase are

$$ {\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{m}}} = {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}} {\varvec{\epsilon}}_{{\mathbf{x}}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} {\varvec{\epsilon}}_{{\varvec{\uptheta}}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} {\varvec{\epsilon}}_{{\mathbf{r}}}^{{\mathbf{m}}} ,\;{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{m}}} = {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} {\varvec{\epsilon}}_{{\mathbf{x}}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} {\varvec{\epsilon}}_{{\varvec{\uptheta}}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}} {\varvec{\epsilon}}_{{\mathbf{r}}}^{{\mathbf{m}}} {\text{and }}{\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{m}}} = {\mathbf{C}}_{\mathbf{55}}^{{\mathbf{m}}} {\varvec{\epsilon}}_{{{\mathbf{xr}}}}^{{\mathbf{m}}} $$
(3)

In Eqs. 1–3, the superscripts f and m denote, respectively, the piezoelectric fiber and the PNC matrix. For the ith constituent phase, \( {\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{i}}} \) and \( {\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{i}}} \) represent the normal stresses in the x and r, directions, respectively; \( {\varvec{\epsilon}}_{{\mathbf{x}}}^{{\mathbf{i}}}, \) \( {\varvec{\epsilon}}_{\theta }^{i} \) and \( {\varvec{\epsilon}}_{{\mathbf{r}}}^{{\mathbf{i}}} \) are the normal strains along x, θ and r, directions, respectively; \( {\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{i}}} \) is the transverse shear stress, \( {\varvec{\epsilon}}_{{{\mathbf{xr}}}}^{{\mathbf{i}}} \) is the transverse shear strain and \({\mathbf{C}}_{\mathbf{ij}}^{\mathbf{i}}\) are the elastic constants. The electric field E x is considered to act along the length of the piezoelectric fiber. Also, e 33 and e 31 are the piezoelectric constants which account for the measure of the induced normal stresses in the piezoelectric fiber along x and r, directions respectively. It should be noted here that the principal material coordinates 1–3 axes are coincident with the problem coordinate axes x, θ, r, respectively. The strain–displacement relations for an axisymmetric problem relevant to this RVE are

$$ {\varvec{\epsilon}}_{{\mathbf{x}}}^{{\mathbf{i}}} ={\frac{{{\varvec{\partial}} {\mathbf{u}}^{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{x}}}}},\;{\varvec{\epsilon}}_{{\varvec{\uptheta}}}^{{\mathbf{i}}}= {\frac{{{\mathbf{w}}^{{\mathbf{i}}}}}{{\mathbf{r}}}},\;{\varvec{\epsilon}}_{{\mathbf{r}}}^{{\mathbf{i}}}= {\frac{{{\varvec{\partial}} {\mathbf{w}}^{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{r}}}}}\;{\text{and}}\;{\varvec{\epsilon}}_{{{\mathbf{xr}}}}^{{\mathbf{i}}}= {\frac{{{\varvec{\partial}} {\mathbf{u}}^{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{r}}}}} + {\frac{{{\varvec{\partial}} {\mathbf{w}}^{{\mathbf{i}}}}}{{{\varvec{\partial}} {\mathbf{x}}}}};\quad{\mathbf{i}} ={\mathbf{f}}\;{\text{and}}\;{\mathbf{m}} $$
(4)

in which u i and w i represent the axial and the radial displacements at any point of the ith phase along x and r, directions, respectively. The traction boundary conditions are given by

$$ \left. {{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{m}}} } \right|_{{{\mathbf{r}} = {\mathbf{R}}}} = 0 \quad {\text{and}} \quad \left. {{\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{m}}} } \right|_{{{\mathbf{r}} = {\mathbf{R}}}} = 0 $$
(5)

and the continuity conditions are

$$ \left. {{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{f}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} = \left. {{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{m}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} ,\;\left. {{\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{f}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} = \left. {{\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{m}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} = {\varvec{\uptau}}_{{\mathbf{i}}} {\mathbf{,}}\left. {{\mathbf{u}}^{{\mathbf{f}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} = \left. {{\mathbf{u}}^{{\mathbf{m}}} } \right|_{{{\mathbf{r = a}}}} {\text{and}}\left. {{\mathbf{w}}^{{\mathbf{f}}} } \right|_{{{\mathbf{r = a}}}} = \left. {{\mathbf{w}}^{{\mathbf{m}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} $$
(6)

where, τ i is the transverse shear stress at the interface between the piezoelectric fiber and the matrix. The average axial stresses in the different phases are defined as

$$ \left\langle {{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}}} \right\rangle ={\frac{1}{{\varvec{\uppi}}{\mathbf{a}^\mathbf{2}}}}\int\limits_{{\mathbf{0}}}^{{\mathbf{a}}}{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} }\;2{\varvec{\uppi}}{\mathbf{rdr}}\; {\text{and}}\;\left\langle{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{m}}} } \right\rangle= {\frac{1}{{{\varvec{\uppi}}\left({{\mathbf{R}}^\mathbf{2} -{\mathbf{a}}^\mathbf{2}}\right)}}}\int\limits_{{\mathbf{a}}}^{{\mathbf{R}}}{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{m}}}}2{\varvec{\uppi}}{\mathbf{rdr}}$$
(7)

Now, making use of Eqs. 1 and 5–7, it can be derived that

$$ {\frac{{{\varvec{\partial}} \left\langle{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle}}{{\varvec{\partial}{\mathbf{x}}}}} = -\frac{2}{\mathbf{a}}{\varvec{\uptau}}_{{\mathbf{i}}}\quad {\text{and}} \quad {\frac{{\varvec{\partial} \left\langle{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{m}}} } \right\rangle}}{{\varvec{\partial} {\mathbf{x}}}}} ={\frac{{2{\mathbf{a}}}}{{{\mathbf{R}}^{\mathbf{2}} -{\mathbf{a}}^{\mathbf{2}} }}}{\varvec{\uptau}}_{{\mathbf{i}}} $$
(8)

Since the radial dimension of this RVE is very small, it is reasonable to assume that the gradient of \( {\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{m}}}\) with respect to the axial coordinate (x) are independent of the radial coordinate (r). Thus using the equilibrium equation (1), the transverse shear stress in the matrix phase can be expressed in terms of the interface shear stress τ i as follows:

$$ {\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{m}}} = {\frac{{{\mathbf{a}}({\mathbf{R}}^{\mathbf{2}} - {\mathbf{r}}^{\mathbf{2}} )}}{{{\mathbf{r}}({\mathbf{R}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}} )}}}{\varvec{\uptau}}_{{\mathbf{i}}} $$
(9)

Also, since the RVE is an axisymmetric problem, it is usually assumed (Nairn 1997) that the gradient of radial displacements with respect to x-direction is negligible and so, from the constitutive relation (3) and the strain–displacement relation (4) between \( {\varvec{\upsigma}}_{{{\mathbf{xr}}}}^{{\mathbf{m}}}\) and \( {\varvec{\epsilon}}_{{{\mathbf{xr}}}}^{{\mathbf{m}}} \) one can write,

$$ {\frac{{{\varvec{\partial}} {\mathbf{u}}^{{\mathbf{m}}}}}{{{\varvec{\partial}}{\mathbf{x}}}}} ={\frac{1}{{{\mathbf{C}}_{\mathbf{55}}^{{\mathbf{m}}}}}}{\varvec{\upsigma}}_{{{\mathbf{rx}}}}^{{\mathbf{m}}} $$
(10)

Solving Eq. 10 and satisfying the continuity condition at r = a, the axial displacement of the PNC matrix phase along x direction can be derived as follows:

$$ {\mathbf{u}}^{{\mathbf{m}}} = {\mathbf{u}}_{{\mathbf{a}}}^{{\mathbf{f}}} + {\mathbf{A}}_{\mathbf{1}} {\varvec{\uptau}}_{{\mathbf{i}}} $$
(11)

in which

$$ {\mathbf{u}}_{{\mathbf{a}}}^{{\mathbf{f}}} = \left. {{\mathbf{u}}^{{\mathbf{f}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} \quad {\text{and}} \quad {\mathbf{A}}_{\mathbf{1}} = {\frac{{\mathbf{a}}}{{{\mathbf{C}}_{\mathbf{55}}^{{\mathbf{m}}} ({\mathbf{R}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}} )}}}\left\{ {{\mathbf{R}}^{\mathbf{2}} {\mathbf{ln}}{\frac{{\mathbf{r}}}{{\mathbf{a}}}} - \frac{1}{2}({\mathbf{r}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}} )} \right\} $$
(12)

The radial displacements in the two phases can be assumed as (Seidel and Lagoudas 2006)

$$ {\mathbf{w}}^{{\mathbf{f}}} = {\mathbf{A}}_{{\mathbf{f}}} {\mathbf{r}}\;{\text{and}}\;{\mathbf{w}}^{{\mathbf{m}}} = {\mathbf{A}}_{{\mathbf{m}}} {\mathbf{r}} + {\mathbf{B}}_{{\mathbf{m}}} /{\mathbf{r}} $$
(13)

where A f , A m , and B m are unknown constants. Invoking the continuity conditions for radial displacement at the interface r = a, the radial displacement in the matrix phase can be augmented as

$$ {\mathbf{w}}^{{\mathbf{m}}} = {\mathbf{a}}^{\mathbf{2}} {\mathbf{A}}_{{\mathbf{f}}} /{\mathbf{r}} + ({\mathbf{r}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}} ){\mathbf{A}}_{{\mathbf{m}}} /{\mathbf{r}} $$
(14)

Substituting (11), (13) and (14) into (4) and subsequently, employing the constitutive relations (2) and (3), the expressions for normal stresses can be written in terms of the unknowns A f and A m as follows:

$$ \left\langle {{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle = {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} {\frac{{{\varvec{\partial}} {\mathbf{u}}_{{\mathbf{a}}}^{{\mathbf{f}}} }}{{{\varvec{\partial}} {\mathbf{x}}}}} + 2{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} {\mathbf{A}}_{{\mathbf{f}}} - {\mathbf{e}}_{\mathbf{33}} {\mathbf{E}}_{{\mathbf{x}}},$$
(15)
$$ {\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{f}}} ={\frac{{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}}}}{{\bar{{\varvec{\upsigma}}}}}_{{\mathbf{x}}}^{{\mathbf{f}}} +\left\{ {{\mathbf{C}}_{\mathbf{23}}^{{\mathbf{f}}} +{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{f}}} -{\frac{{2({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} )^{\mathbf{2}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}}}\right\}{\mathbf{A}}_{{\mathbf{f}}} - ({\mathbf{e}}_{\mathbf{31}}- {\frac{{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}}}}\;{\mathbf{e}}_{\mathbf{33}} ){\mathbf{E}}_{{\mathbf{x}}},$$
(16)
$$ \begin{aligned}{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{m}}} &={\frac{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}}}}\bar{{\varvec{\upsigma}}}_{{\mathbf{x}}}^{{\mathbf{f}}} +\left[ {({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} -{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}}){\frac{{{\mathbf{a}}^{\mathbf{2}} }}{{{\mathbf{r}}^{\mathbf{2}} }}} -{\frac{{2{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}}{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}}}\right]{\mathbf{A}}_{{\mathbf{f}}} + \left[{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} +{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} -({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} -{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}}){\frac{{{\mathbf{a}}^{\mathbf{2}} }}{{{\mathbf{r}}^{\mathbf{2}} }}}}\right]{\mathbf{A}}_{{\mathbf{m}}} \\ &\quad+{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}}{\mathbf{A}}_{\mathbf{1}} {\frac{{{\varvec{\partial}}{\varvec{\uptau}}_{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{x}}}}} +{\frac{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}}}}{\mathbf{e}}_{\mathbf{33}} {\mathbf{E}}_{{\mathbf{x}}} \\\end{aligned} $$
(17)
$$ \begin{aligned}{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{m}}} &={\frac{{{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}}}}{{\bar{{\varvec{\upsigma}}}}}_{{\mathbf{x}}}^{{\mathbf{f}}} +\left[ {({\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} -{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}}){\frac{{{\mathbf{a}}^{\mathbf{2}} }}{{{\mathbf{r}}^{\mathbf{2}} }}} -{\frac{{2{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}}{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} }}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}}}}} \right]{\mathbf{A}}_{{\mathbf{f}}} + \left[{{\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} +{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}} -({\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} -{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}}){\frac{{{\mathbf{a}}^{\mathbf{2}} }}{{{\mathbf{r}}^{\mathbf{2}} }}}}\right]{\mathbf{A}}_{{\mathbf{m}}} \\ &\quad +{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}}{\mathbf{A}}_{\mathbf{1}} {\frac{{{\varvec{\partial}}{\varvec{\uptau}}_{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{x}}}}} +{\frac{{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}}}}{\mathbf{e}}_{\mathbf{33}} {\mathbf{E}}_{{\mathbf{x}}} \\\end{aligned} $$
(18)

Invoking the continuity condition \( \left. {{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{f}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} = \left. {{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{m}}} } \right|_{{{\mathbf{r}} = {\mathbf{a}}}} \) and satisfying the boundary condition \( \left. {{\varvec{\sigma}}_{\mathbf{r}}^{\mathbf{m}}}\right|_{{\mathbf{r=R}}}=0 ,\) the following equations for solving A f and A m are obtained:

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{A}}_{\mathbf{11}} }& {{\mathbf{A}}_{\mathbf{12}} } \\{{\mathbf{A}}_{\mathbf{21}}} & {{\mathbf{A}}_{\mathbf{22}} }\\ \end{array} } \right]\left\{ {\begin{array}{*{20}c}{{\mathbf{A}}_{{\mathbf{f}}} } \\ {{\mathbf{A}}_{{\mathbf{m}}} }\\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c}{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} -{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} } \\ { -{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} } \\ \end{array} }\right\}{\frac{{{{\bar{{\varvec{\upsigma}}}}}_{{\mathbf{x}}}^{{\mathbf{f}}}}}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}} + \left\{{\begin{array}{*{20}c} 0 \\ { -{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}}{\mathbf{A}}_{\mathbf{2}} } \\ \end{array} }\right\}{\frac{{{\varvec{\partial}}{\varvec{\uptau}}_{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{x}}}}} - \left\{ {\begin{array}{*{20}c}{{\bar{\mathbf{e}}}_{\mathbf{31}} } \\ { -{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}}{\mathbf{e}}_{\mathbf{33}}/{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} } \\ \end{array} }\right\}{\mathbf{E}}_{{\mathbf{x}}} $$
(19)

where,

$$ \begin{gathered} {\mathbf{A}}_{\mathbf{11}} = {\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} - {\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}} - 2{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} /{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} - {\mathbf{C}}_{\mathbf{23}}^{{\mathbf{f}}} - {\mathbf{C}}_{\mathbf{33}}^{{\mathbf{f}}} + 2({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} )^{\mathbf{2}} /{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} ,\;{\mathbf{A}}_{\mathbf{12}} = 2{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}} , \hfill \\ {\mathbf{A}}_{\mathbf{21}}= ({\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} - {\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}} ){\mathbf{a}}^{\mathbf{2}} /{\mathbf{R}}^{\mathbf{2}} - 2{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} /{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} ,\;{\mathbf{A}}_{\mathbf{22}} = {\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}} - ({\mathbf{C}}_{\mathbf{23}}^{{\mathbf{m}}} - {\mathbf{C}}_{\mathbf{33}}^{{\mathbf{m}}} ){\mathbf{a}}^{\mathbf{2}} /{\mathbf{R}}^{\mathbf{2}} , \hfill \\ {\bar{\mathbf{e}}}_{\mathbf{31}} = {\mathbf{e}}_{\mathbf{31}} - ({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} - {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} ){\mathbf{e}}_{\mathbf{33}} /{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} ,\;{\mathbf{A}}_{\mathbf{2}} = \left. {{\mathbf{A}}_{\mathbf{1}}} \right|_{{{\mathbf{r}} = {\mathbf{R}}}} . \hfill \\ \end{gathered} $$
(20)

From Eq. 20, the solutions of A f , A m and B m can be expressed as:

$$ {\mathbf{A}}_{{\mathbf{f}}} = {\mathbf{L}}_{\mathbf{11}}{{\bar{\varvec{\upsigma}}}}_{{\mathbf{x}}}^{{\mathbf{f}}} +{\mathbf{L}}_{\mathbf{12}} {\frac{{{\varvec{\partial}}{\varvec{\uptau}}_{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{x}}}}} - {\mathbf{L}}_{\mathbf{13}}{\mathbf{E}}_{{\mathbf{x}}} \;{\text{and}}\;{\mathbf{A}}_{{\mathbf{m}}} = {\mathbf{L}}_{\mathbf{21}}{{\bar{\varvec{\upsigma}}}}_{{\mathbf{x}}}^{{\mathbf{f}}} +{\mathbf{L}}_{\mathbf{22}} {\frac{{{\varvec{\partial}}{\varvec{\uptau}}_{{\mathbf{i}}} }}{{{\varvec{\partial}}{\mathbf{x}}}}} - {\mathbf{L}}_{\mathbf{23}}{\mathbf{E}}_{{\mathbf{x}}} $$
(21)

The expressions of the coefficients L ij are evident from Eq. 20 and are not shown here for the sake of brevity. Now, satisfying the equilibrium of force along the axial (x) direction at any transverse cross section of the RVE the following equation is obtained:

$$ \int\limits_{{\mathbf{0}}}^{{\mathbf{a}}}{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}}2{\varvec{\uppi}}\mathbf{rdr}} +\int\limits_{{\mathbf{a}}}^{{\mathbf{R}}}{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{m}}}2{\varvec{\uppi}}\mathbf{rdr}}={\varvec{\uppi}}({\mathbf{R}^\mathbf{2}}-{\mathbf{c}^\mathbf{2}}){{\varvec{\uppi}}^{\prime}}$$
(22)

Use of (17) and (21) in (22), yields

$$ {\frac{{{\varvec{\partial}} {\varvec{\uptau}}_{{\mathbf{i}}} }}{{{\varvec{\partial}} {\mathbf{x}}}}} = {\frac{1}{{{\mathbf{L}}_{\mathbf{1}}}}}({\mathbf{R}}^{\mathbf{2}} {\varvec{\upsigma}} - {\mathbf{L}}_{\mathbf{2}} \left\langle {{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle + {\mathbf{L}}_{\mathbf{3}} {\mathbf{E}}_{{\mathbf{x}}} ) $$
(23)

where,

$$ \begin{gathered} {\mathbf{L}}_{\mathbf{1}}= \left\{ { - {\frac{{2{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}} {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} }}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}}{\mathbf{L}}_{\mathbf{12}} + ({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} ){\mathbf{L}}_{\mathbf{22}} } \right\}({\mathbf{R}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}} ) + 2({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} - {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} ){\mathbf{a}}^{\mathbf{2}} ({\mathbf{L}}_{\mathbf{12}} - {\mathbf{L}}_{\mathbf{22}} ){\mathbf{ln}}{\frac{{\mathbf{R}}}{{\mathbf{a}}}} + {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}} {\mathbf{A}}_{\mathbf{3}} , \hfill \\ {\mathbf{L}}_{\mathbf{2}} = {\mathbf{a}}^{\mathbf{2}} + \left\{ {{\frac{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}} }}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}} - {\frac{{2{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}} {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} }}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}}{\mathbf{L}}_{\mathbf{12}} + ({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} ){\mathbf{L}}_{\mathbf{21}}} \right\}({\mathbf{R}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}} ) + 2({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} - {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} ){\mathbf{a}}^{\mathbf{2}} ({\mathbf{L}}_{\mathbf{11}} - {\mathbf{L}}_{\mathbf{21}}){\mathbf{ln}}{\frac{{\mathbf{R}}}{{\mathbf{a}}}}, \hfill \\ {\mathbf{L}}_{\mathbf{3}} = \left\{ { - {\frac{{2{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}} {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} }}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}}{\mathbf{L}}_{\mathbf{13}} + ({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} + {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} ){\mathbf{L}}_{\mathbf{23}} - {\frac{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{m}}} }}{{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}} }}}{\mathbf{e}}_{\mathbf{33}} } \right\}({\mathbf{R}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}} ) + 2({\mathbf{C}}_{\mathbf{12}}^{{\mathbf{m}}} - {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{m}}} ){\mathbf{a}}^{\mathbf{2}} ({\mathbf{L}}_{\mathbf{13}} - {\mathbf{L}}_{\mathbf{23}} ){\mathbf{ln}}{\frac{{\mathbf{R}}}{{\mathbf{a}}}} \hfill \\ {\text{and}} \quad {\mathbf{A}}_{\mathbf{3}} = 2\int\limits_{{\mathbf{a}}}^{{\mathbf{R}}} {{\mathbf{A}}_{\mathbf{1}}{\mathbf{rdr}}} . \hfill \\ \end{gathered} $$
(24)

Substituting Eq. 23 into the first equation of (8), the governing equation for the average axial stress in the piezoelectric fiber coated with radially grown aligned CNTs is obtained as follows:

$$ {\frac{{{\varvec{\partial}}^{\mathbf{2}} \left\langle{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle}}{{{\varvec{\partial}} {\mathbf{x}}^{\mathbf{2}} }}} -{\varvec{\upalpha}}^{\mathbf{2}} \left\langle{{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle= -{\varvec{\upeta \upsigma}}-{\varvec{\upbeta}}{\mathbf{E}_{{\mathbf{x}}}}$$
(25)
$$ {\text{where}},\;\;{\varvec{\upalpha}}^{\mathbf{2}} = {\frac{{2{\mathbf{L}}_{\mathbf{2}} }}{{{\mathbf{aL}}_{\mathbf{1}}}}},\;{\varvec{\upeta}} = {\frac{{2{\mathbf{R}}^{\mathbf{2}} }}{{{\mathbf{aL}}_{\mathbf{1}}}}} \quad {\text{and}} \quad {\varvec{\upbeta}} = {\frac{{2{\mathbf{L}}_{\mathbf{3}} }}{{{\mathbf{aL}}_{\mathbf{1}}}}} $$
(26)

Solution of Eq. 25 is given by:

$$ \left\langle {{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle = {\mathbf{c}}_{\mathbf{1}}{\mathbf{e}}^{{{\mathbf{\alpha x}}}} + {\mathbf{c}}_{\mathbf{2}} {\mathbf{e}}^{{ - {\mathbf{\alpha x}}}} + {\frac{{\varvec{\upeta}}}{{{\varvec{\upalpha}}^{\mathbf{2}} }}}{\varvec{\upsigma}} + {\frac{{\varvec{\upbeta}}}{{{\varvec{\upalpha}}^{\mathbf{2}} }}}{\mathbf{E}}_{{\mathbf{x}}} $$
(27)

in which c 1 and c 2 are the constants of integrations to be evaluated from the following end conditions:

$$ \left\langle {{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle = 0\;{\text{at }}\;{\mathbf{x}} = \pm {\mathbf{L}} $$
(28)

Utilizing the end conditions given by (28) in Eq. 27, the final solution of \( \left\langle {{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle\) can be derived as follows:

$$ \left\langle {{\varvec{\upsigma}}_{{\mathbf{x}}}^{{\mathbf{f}}} } \right\rangle = \left( {1 - {\frac{{{\mathbf{cosh}}\left( {{\mathbf{\alpha x}}} \right)}}{{{\mathbf{cosh}}\left( {{\mathbf{\alpha L}}} \right)}}}} \right)\left( {{\frac{{\varvec{\upeta}}}{{{\varvec{\upalpha}}^{\mathbf{2}} }}}{\varvec{\upsigma}} + {\frac{{\varvec{\upbeta}}}{{{\varvec{\upalpha}}^{\mathbf{2}} }}}{\mathbf{E}}_{{\mathbf{x}}} } \right) $$
(29)

Finally, substitution of Eq. 29 into Eq. 8 yields the expression for the interface shear stress τ i as follows:

$$ {\varvec{\uptau}}_{{\mathbf{i}}} = {\frac{{{\mathbf{a\alpha\;sinh}}\left( {{\mathbf{\alpha x}}} \right)}}{{2{\mathbf{cosh}}\left( {{\mathbf{\alpha L}}} \right)}}}\left( {{\frac{{\varvec{\upeta}}}{{{\varvec{\upalpha}}^{\mathbf{2}} }}}{\varvec{\upsigma}} + {\frac{{\varvec{\upbeta}}}{{{\varvec{\upalpha}}^{\mathbf{2}} }}}{\mathbf{E}}_{{\mathbf{x}}} } \right) $$
(30)

3 Results and Discussion

Arm chair type (5, 5) CNTs are used to compute the numerical results whose elastic coefficients (\( {\mathbf{C}}_{{{\mathbf{ij}}}}^{{\mathbf{n}}} \)) with respect to the coordinate system considered here are obtained from Shen and Li (2004) as follows:

$$ \begin{gathered} {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{n}}} = 668\,{\text{GPa}},{\mathbf{C}}_{\mathbf{22}}^{{\mathbf{n}}} = {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{n}}} ,\;{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{n}}} = 2 1 4 3\,{\text{GPa}},{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{n}}} = 40 4\,{\text{GPa}},{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{n}}} = 1 8 4\,{\text{GPa}}, \, {\mathbf{C}}_{\mathbf{23}}^{{\mathbf{n}}} = {\mathbf{C}}_{\mathbf{13}}^{{\mathbf{n}}} , \hfill \\ {\mathbf{C}}_{44}^{{\mathbf{n}}} = 7 9 1\,{\text{GPa}},{\mathbf{C}}_{\mathbf{55}}^{{\mathbf{n}}} = {\mathbf{C}}_{44}^{{\mathbf{n}}} , \, {\mathbf{C}}_{\mathbf{66}}^{{\mathbf{n}}} = 1 3 2\,{\text{GPa}}. \hfill \\ \end{gathered} $$

The isotropic elastic coefficients (\({\mathbf{C}}_{\mathbf{ij}}^{\mathbf{p}}\)) of the polymer material are given by

$$ {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{p}}} = 5.3\,{\text{GPa}} \quad {\text{and}} \quad {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} = 3.1\,{\text{GPa}} $$

while the elastic and piezoelectric coefficients of the piezoelectric fiber are (Ray and Batra 2009)

$$ \begin{gathered} \hfill{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{f}}}=124\;{\text{GPa}},\;{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}} =96\;{\text{GPa}},\;{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{f}}} ={\mathbf{C}}_{\mathbf{12}}^{{\mathbf{f}}},\;{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{f}}} =151\;{\text{GPa}},\;{\mathbf{C}}_{\mathbf{22}}^{{\mathbf{f}}} ={\mathbf{C}}_{\mathbf{33}}^{{\mathbf{f}}},\;{\mathbf{C}}_{\mathbf{23}}^{{\mathbf{f}}}= 98\;{\text{GPa}},\\ \hfill {\mathbf{C}}_{\mathbf{66}}^{{\mathbf{f}}} =23\;{\text{GPa}},\;{\mathbf{C}}_{\mathbf{55}}^{{\mathbf{f}}} ={\mathbf{C}}_{\mathbf{66}}^{{\mathbf{f}}}{\mathbf{,C}}_{44}^{{\mathbf{f}}} =({\mathbf{C}}_{\mathbf{33}}^{{\mathbf{f}}} -{\mathbf{C}}_{\mathbf{23}}^{\mathbf{f}})/2,{\mathbf{e}}_{\mathbf{33}}= 27\;{\text{C}}/\text{m}^{2},\;{\mathbf{e}}_{\mathbf{31}} = -5.1\;{\text{C}}/\text{m}^{2}. \\ \end{gathered} $$

A discussion on the effective properties of the PNC matrix is now in order. In the absence of piezoelectric fibers, the micromechanics model recently derived by Ray and Batra (2009) is reduced to the following model which predicts the effective elastic properties of the CNT-reinforced matrix phase:

$$ [{\mathbf{C}}^{{\mathbf{m}}} ] = [{\mathbf{C}}_{\mathbf{1}}][{\mathbf{V}}_{\mathbf{3}} ]^{ - 1} + [{\mathbf{C}}_{\mathbf{2}} ][{\mathbf{V}}_{\mathbf{4}} ]^{ - 1} $$
(31)

For a particular CNT volume fraction (V CNT ) the various matrices appearing in (31) are given by

$$ [{\mathbf{C}}_{\mathbf{1}}] = {\mathbf{v}}_{n} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ {{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{n}}} } & {{\mathbf{C}}_{\mathbf{23}}^{{\mathbf{n}}} } & {{\mathbf{C}}_{\mathbf{33}}^{{\mathbf{n}}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad [{\mathbf{C}}_{\mathbf{2}} ] = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{p}}} } & {{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & {{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & 0 & 0 & 0 \\ {{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & {{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{p}}} } & {{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & 0 & 0 & 0 \\ {{\mathbf{v}}_{{\mathbf{p}}} {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & {{\mathbf{v}}_{{\mathbf{p}}} {\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & {{\mathbf{v}}_{{\mathbf{p}}} {\mathbf{C}}_{\mathbf{11}}^{{\mathbf{p}}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {{\mathbf{C}}_{44}^{{\mathbf{p}}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\mathbf{C}}_{44}^{{\mathbf{p}}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {{\mathbf{C}}_{44}^{{\mathbf{p}}} } \\ \end{array} } \right], $$
$$ {\mathbf{v}}_{{\mathbf{n}}} = {\frac{{{\mathbf{R}}^{\mathbf{2}}}}{{{\mathbf{R}}^{\mathbf{2}} - {\mathbf{a}}^{\mathbf{2}}}}}{\mathbf{V}}_{{{\mathbf{CNT}}}} ,\;{\mathbf{v}}_{{\mathbf{p}}}= 1 - {\mathbf{v}}_{{\mathbf{n}}} ,[{\mathbf{V}}_{\mathbf{3}} ] =[{\mathbf{V}}_{\mathbf{1}}] + [{\mathbf{V}}_{\mathbf{2}}][{\mathbf{C}}_{\mathbf{4}} ]^{ - 1} \left[{{\mathbf{C}}_{\mathbf{3}} } \right],\left[{{\mathbf{V}}_{\mathbf{4}} } \right] = \left[{{\mathbf{V}}_{\mathbf{2}} } \right] + \left[{{\mathbf{V}}_{\mathbf{1}}} \right]\left[{{\mathbf{C}}_{\mathbf{3}} } \right]^{ - 1} \left[{{\mathbf{C}}_{\mathbf{4}} } \right], $$
$$ [{\mathbf{C}}_{\mathbf{3}} ] = \left[ {\begin{array}{*{20}c}{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{n}}} } &{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{n}}} } &{{\mathbf{C}}_{\mathbf{13}}^{{\mathbf{n}}} } & 0 & 0 & 0\\ {{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{n}}} } &{{\mathbf{C}}_{\mathbf{22}}^{{\mathbf{n}}} } &{{\mathbf{C}}_{\mathbf{23}}^{{\mathbf{n}}} } & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0& {{\mathbf{C}}_{44}^{{\mathbf{n}}} } & 0 & 0 \\ 0 & 0 & 0 & 0 &{{\mathbf{C}}_{\mathbf{55}}^{{\mathbf{n}}} } & 0\\ 0 & 0 & 0 & 0 & 0 &{{\mathbf{C}}_{\mathbf{66}}^{{\mathbf{n}}} } \\ \end{array} }\right],\quad [{\mathbf{C}}_{\mathbf{4}} ] = \left[{\begin{array}{cccccc} {{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{p}}}} & {{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } &{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & 0 & 0 & 0\\ {{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } &{{\mathbf{C}}_{\mathbf{11}}^{{\mathbf{p}}} } &{{\mathbf{C}}_{\mathbf{12}}^{{\mathbf{p}}} } & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0& {{\mathbf{C}}_{44}^{{\mathbf{p}}} } & 0 & 0 \\ 0 & 0 & 0 & 0 &{{\mathbf{C}}_{44}^{{\mathbf{p}}} } & 0\\ 0 & 0 & 0 & 0 & 0 &{{\mathbf{C}}_{44}^{{\mathbf{p}}} } \\ \end{array} } \right], $$
$$ \left[ {{\mathbf{V}}_{\mathbf{1}} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{{\mathbf{n}}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {{\mathbf{v}}_{{\mathbf{n}}} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {{\mathbf{v}}_{{\mathbf{n}}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\mathbf{v}}_{{\mathbf{n}}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {{\mathbf{v}}_{{\mathbf{n}}} } \\ \end{array} } \right]{\text{and}}\;[{\mathbf{V}}_{\mathbf{2}} ] = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{{\mathbf{p}}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {{\mathbf{v}}_{{\mathbf{p}}} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {{\mathbf{v}}_{{\mathbf{p}}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\mathbf{v}}_{{\mathbf{p}}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {{\mathbf{v}}_{{\mathbf{p}}} } \\ \end{array} } \right] $$
(32)

In the absence of the electric field, the results are normalized with respect to the applied stress σ while in the presence of electric filed only the results are normalized with respect to the applied electric filed. Unless otherwise mentioned, the radius of the piezoelectric fiber is assumed as 100 μm and its volume fraction (V f ) is used as 40% for computing the numerical results. For a given piezoelectric fiber volume fraction, the radius of the RVE is obtained from R 2 = a 2/V f . In order to validate the model derived in the previous section, first the long fiber and the matrix of the RVE are considered as the same as those used by Nairn (1997). The normalized average axial stresses in this fiber without coated with CNTs for different fiber volume fractions computed by the present model are compared with those obtained by Nairn (1997) as shown in Fig. 2. It may be noted that the excellent agreement between the two sets of results have been obtained verifying the present model. Next, the results are computed for the piezoelectric fibers coated with radially aligned CNTs.

Fig. 2
figure 2

Comparison of the present model with the earlier model (Nairn 1997)

Full size image

In the absence of the electric field, the variation of the axial normal stress in the piezoelectric fiber along the length of the fiber is shown in Fig. 3. It may be observed that the piezoelectric fiber coated with radially aligned-CNTs shares less load than the fiber without coated with CNTs. This is attributed simply to the radial and axial stiffening of the polymer matrix by the CNTs. In contrast, if the piezoelectric fiber is subjected to the applied electric filed only along the length of the fiber then the average axial stress induced in the fiber increases due to the radially growing of CNTs on the surface of the fiber as shown in Fig. 4. If the CNTs are radially grown on the surface of the piezoelectric fiber and the fiber is subjected to the electric field along its length only then the magnitude of the average radial stress \( \left\langle {{\varvec{\upsigma}}_{{\mathbf{r}}}^{{\mathbf{f}}}} \right\rangle\) induced in the fiber significantly increases over that in the piezoelectric fiber without coated with CNTs as shown in Fig. 5. This implies the probable improvement of the effective piezoelectric coefficient e 31 of this proposed composite. In Fig. 6, the variation of the interface shear stress (τ i ) along the length of the fiber has been illustrated. This figure reveals that augmenting the piezoelectric fiber with radially grown CNTs on its surface causes decrease in the maximum value of the interface shear stress if the piezoelectric fiber is not active (E z  = 0) while the maximum value of τ i increases when the fiber is active (E z  ≠ 0). Figures 7 and 8 illustrate the effect of variation of the CNT volume fraction (V CNT) on the maximum values of the average axial and radial stresses in the piezoelectric fiber, respectively. In these cases, the maximum values of the average stresses are computed in the presence of both the applied load and unit electric field along the length of the fiber. It may be observed that beyond a value of V CNT as 5%, the axial stress in the fiber is not significantly affected due to the radial growth of CNTs on the fiber surface while the maximum value of the average radial stress in the fiber increases with the increase in the CNT-volume fraction. The variation of the aspect ratio of the piezoelectric fiber does not appreciably affect the axial stress transferred to the fiber along the length of the fiber under the combined action of the applied stress and unit electric filed along the length of the fiber as shown in Fig. 9. The maximum value of the axial stress in the fiber is independent of the aspect ratio of the fiber while the length of the fiber being uniformly stressed slightly increases as the aspect ratio of the fiber changes from 10 to 30.

Fig. 3
figure 3

Variation of the average axial stress in the piezoelectric fiber along its length in the absence of electric field

Full size image
Fig. 4
figure 4

Variation of the average axial stress in the piezoelectric fiber along its length in the presence of the electric field along the length of the fiber only

Full size image
Fig. 5
figure 5

Variation of the average radial stress in the piezoelectric fiber along its length in the presence of the electric field along the length of the fiber only

Full size image
Fig. 6
figure 6

Variation of the interface shear stress along the length of the fiber

Full size image
Fig. 7
figure 7

Variation of the maximum values of the average axial stress in the piezoelectric fiber with the CNT volume fraction

Full size image
Fig. 8
figure 8

Variation of the maximum values of the average radial stress in the piezoelectric fiber with the CNT volume fraction

Full size image
Fig. 9
figure 9

Variation of the average axial stress in the piezoelectric fiber along its length for different aspect ratios (L/a) of the fiber

Full size image

4 Conclusions

In this paper, a novel hybrid piezoelectric composite has been proposed. The CNTs are considered to be radially grown on the surface of the piezoelectric fiber reinforcements. If such fuzzy piezoelectric fibers are embedded in a polymer matrix, the matrix phase of the resulting hybrid composite turns out to be a PNC. A shear lag model of this composite has been developed to analyze the axial load transferred to the piezoelectric fiber in the presence and the absence of the electric filed along the length of the fiber. If the piezoelectric fiber is coated with CNTs, the axial load transferred to the fiber and the maximum value of the interface shear stress at the interface between the fiber and the PNC matrix decrease in the absence of the electric filed along the length of the fiber. If the CNT-coated piezoelectric fiber is subjected to the applied electric field along its length only then the axial stress induced in the fiber increases. More importantly, the significant increase in the induced radial stress in the fiber reveals that the effective piezoelectric coefficient e 31 of this composite may be improved by means of engineering the surface of the piezoelectric fibers with CNTs. If the volume fraction of CNT increases beyond 5% then the axial load transferred to the fiber does not appreciably change but the radial stress in the fiber increases with the increase in the CNT volume fraction. For a particular value of CNT volume fraction, the maximum value of the axial stress in the piezoelectric fiber is independent of the aspect ratio of the fiber.