Abstract
Those who wish to claim that all facts about grounding are themselves grounded (“the meta-grounding thesis”) must defend against the charge that such a claim leads to infinite regress and violates the well-foundedness of ground. In this paper, we defend. First, we explore three distinct but related notions of “well-founded”, which are often conflated, and three corresponding notions of infinite regress. We explore the entailment relations between these notions. We conclude that the meta-grounding thesis need not lead to tension with any of the three notions of “well-founded”. Finally, we explore the details of and motivations for further conditions on ground that one might add to generate a conflict between the meta-grounding thesis and a well-founded constraint. We explore these topics by developing and utilizing a formal framework based on the notion of a grounding structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Some believe that the world can be organized into a hierarchy of fundamentality. The more fundamental facts (perhaps the facts about quarks, leptons, and bosons) metaphysically ground the less fundamental facts (e.g. the facts about cars, coffees, and koalas). Suppose this picture is correct, and that we possess a complete theory of how all these facts fit together – which are fundamental, which non-fundamental, and how the non-fundamental facts hold in virtue of the fundamental facts. If there are relations of metaphysical grounding between facts, a complete story of the world’s hierarchical grounding structure must tell us how these facts about grounding fit in. Are they themselves grounded? Or are they ungrounded, and fundamental?Footnote 1 It has been thought that if the grounding facts are themselves grounded, then certain paradoxes and problems arise (e.g. [3]). For example, Schaffer [18]: 373 (fn. 32) writes that if grounding is “derivative [i.e. grounded] there is a worrisome regress, because then the grounding relations themselves would need grounding.” This infinite regress is problematic because it conflicts with the popular well-founded constraint on ground, which says the structure of ground must be “well-founded”.
This paper simultaneously investigates two topics. First, we examine whether the claim that all grounding facts are grounded is coherent, and in particular whether this claim is in tension with the well-founded constraint. Second, we investigate what exactly the well-founded constraint is. We argue that there are at least three distinct notions of “well-founded”, all of which appear in the literature on ground and are often conflated and/or taken to be equivalent [5, 20]. We argue that the meta-grounding thesis (MG), which says that ground is grounded, does not entail that ground fails to be well-founded in any of the three senses of “well-founded”. In the end, this paper is as much or more about the well-founded constraint itself as it is about grounding grounding. A defense of grounded grounding is a useful lens through which to examine the well-founded constraint.
Our strategy will be as follows. We start by making some simplifying assumptions. In Sections 2–4, we deal only with full ground. We ignore partial ground and assume that ground relates only individual facts to individual facts, rather than pluralities to individual. This assumption is admittedly somewhat artificial. However, this simplifying move facilitates exposition and allows us to express several philosophical and formal results that will not change significantly when we move to a more sophisticated (and realistic) framework in Section 5. That framework will accommodate partial ground and grounding by pluralities. Throughout, the symbol ‘ <’ will stand for full ground and ‘\(\prec \)’ for partial ground.
2 Preliminaries: Grounds and Facts
Why does water expand when frozen? In virtue of the crystalline lattice structure formed by slow-moving H2O molecules. Why does the rock exist? In virtue of the fundamental particles that compose the rock. Why is it wrong to eat animals? In virtue of the fact that the practice causes unnecessary pain and suffering. These “in virtue of” claims express a relation of metaphysical grounding.Footnote 2 Grounding is a relation of metaphysical priority. Intuitively, some entities, properties, or facts are metaphysically prior to, and more fundamental than, others. The grounded derive their being from that which grounds.
Grounding can be partial or full. For example, the fact that Brooklyn is a borough east of Manhattan with a population of 2.5 million is partly grounded in the fact that Brooklyn is a borough east of Manhattan and partly grounded in the fact that Brooklyn has a population of 2.5 million. Together, these two facts form a full ground for the fact that Brooklyn is a borough east of Manhattan with a population of 2.5 million. We use the symbol ‘ <’ for full ground and ‘\(\prec \)’ for partial ground. The symbols should be read left to right. ‘p < q’ says that p fully grounds q. Any full ground is also a partial ground (in this sense a partial ground can be “improper”). Brackets - [...] - will be our “fact-maker” notation. For example, ‘[the twins are blonde]’ refers to the fact that the twins are blonde. ‘[...]’ refers to the fact that ... With these conventions in place, we represent as follows the grounding relations surrounding the fact that Brooklyn is a borough east of Manhattan with a population of 2.5 million.
-
[Brooklyn is a borough east of Manhattan] \(\prec \) [Brooklyn is a borough east of Manhattan with a population of 2.5 million]
-
[Brooklyn has a population of 2.5 million] \(\prec \) [Brooklyn is a borough east of Manhattan with a population of 2.5 million].
-
[Brooklyn is a borough east of Manhattan], [Brooklyn has a population of 2.5 million] < [Brooklyn is a borough east of Manhattan with a population of 2.5 million].
As illustrated by the above example, ground (partial or full) can relate a plurality, or collection, to an individual. For the first half of this paper (through Section 4), we focus exclusively on full ground. In Section 5, we expand the framework to accommodate partial ground.
The grounding relation (either full or part) is irreflexive and transitive. It follows that the grounding relation is asymmetric. For all p, q, r:
-
Irreflexivity: ¬(p < p).
-
Transitivity: If p < q and q < r, then p < r.
-
Asymmetry: ¬(p < q∧q < p)
Irreflexivity: No fact holds (even partly) in virtue of itself. Transitivity: If a fact holds in virtue of a second fact, which holds in virtue of third, then the first holds in virtue of the third as well. Asymmetry: If a fact holds in virtue of a second fact, then the second does not hold in virtue of the first. The same principles hold for partial ground.
Grounding is not mere necessitation. A fact may be necessitated by its grounds, but grounding cuts more finely than necessitation, since necessitation is reflexive while grounding is not. All facts necessitate themselves; no fact grounds itself. Necessitation is thereby potentially symmetric (i.e. not asymmetric). The existence of Socrates necessitates the existence of the singleton set {Socrates }, and the existence of {Socrates } necessitates the existence of Socrates. But the existence of Socrates grounds the existence of his singleton, and not vice versa. (At least that’s how the traditional story goes. Fine [11]: 269, Schaffer [18]: 375, Schaffer [20]: 35.)
We do not define ‘metaphysically grounds’ or ‘ <’. We take the notion as a primitive. Acceptance of grounding leads to a structured picture of reality. Reality contains the more and the less fundamental. The less fundamental derives its being from (or holds in virtue of) the more fundamental.
We concern ourselves only with grounding relations between facts. The question of whether the fact that Socrates exists grounds the fact that his singleton exists falls under our purview. The question of whether Socrates himself grounds his singleton does not. Grounding is, we think, in the first instance a relation between facts, not a relation between entities, properties, relations, or something else.Footnote 3 Perhaps good sense can be made of grounding relations between entities or properties themselves; we leave that task to others.Footnote 4
The grounding relation we are concerned with here is a transitive, irreflexive, asymmetric relation of metaphysical priority between facts. Intuitively, it is the relation of one fact holding in virtue of another.
3 Meta-Grounding and the Well-Founded Constraint
3.1 Meta-Grounding and the Well-Founded Constraint
Suppose there are relations of ground; some facts ground others. [P] grounds [P or Q]. What grounds the fact that [P] grounds [P or Q], i.e. [[P] grounds [P or Q]]? Are the facts about grounding grounded, or ungrounded?Footnote 5 This paper investigates the former answer, which claims that all grounding facts are grounded.
Proposition 1
(MG) All grounding facts are fully grounded.Footnote 6 , Footnote 7
There are some alleged problems with the thesis that grounding facts are grounded. One thought is that if the grounding facts are themselves grounded, an infinite regress of ground results. This infinite regress is undesirable because it is thought that the structure of reality must “ground out” in a fundamental level. The grounding hierarchy must be, in some important sense, “well-founded”. If so, then all facts must have an ultimate ground; chains of metaphysical dependence must end somewhere. The meta-grounding thesis seems to be in tension with the demand for well-foundedness.
Let’s get more specific about how this regress is supposed to get generated. Start with the grounding fact g 1, which is the fact that p grounds q (where neither p nor q are themselves grounding facts).
Given the meta-grounding thesis, this fact, g 1, must itself be grounded. Call its grounds r 1. We get a new grounding fact g 2:
This again is a grounding fact, and thus requires grounds. Call its grounds r 2, yielding g 3:
We continue this process, ad infinitum, to yield an infinite sequence of grounding facts, \(g_{1}, g_{2}, g_{3}, \dots \). Thus an immediate consequence of the meta-grounding thesis is that there are infinitely many grounding facts.Footnote 8
Theorem 1
Let G be the set of grounding facts. If for all p∈G, there is a \(p^{\prime }\) such that \(p^{\prime } < p\) , then the cardinality of G is infinite.
This result may be surprising. If we start with a world containing a few electrons and protons, facts about which ground the fact that a single hydrogen molecule exists, one might think that we could describe this world using finitely many facts. Not so, if the grounding facts are grounded. The claim that grounding is grounded immediately yields infinitely many facts, no matter how simple the world looks at first glance. But is this really all that worrisome? Any time we have the fact p we also thereby have the facts p∧p and p∧(p∧p), etc. Likewise, given the Tarski scheme, if p is true, then ‘p is true’ is true, and “‘p is true’ is true” is true, etc. Depending on how we individuate facts (an issue we wish to avoid), these cases may or may not yield infinitely many distinct facts. However, it seems clear that, at any world, the truths of mathematics hold. There are certainly infinitely many of these, and they are very likely distinct. Everyone is stuck with infinitely many facts, independently of the meta-grounding thesis.Footnote 9 We maintain that one should not be concerned if one’s system entails infinitely many facts.
Meta-grounding, however, implies more than that there are infinitely many facts. Meta-grounding implies that there are infinitely many facts about grounding, facts expressible using the relational predicate ‘grounds’ or ‘ <’. The existence of infinitely many grounding facts is, prima facie, more troubling, from the point of view of a coherent story about the world’s grounding structure, than the existence of infinitely many facts.
On the topic of how many grounding facts there are, we make two points. First, for any class of grounded facts, we think it should not matter much how many there are. It has been thought that the grounded facts are, in a sense, the “ontological free lunch” of which philosophers (e.g. Armstrong [1]) often speak.Footnote 10 We think it far more important to focus on how many ungrounded facts one endorses. Nothing we have said so far, about meta-grounding or not, makes commitments about how many ungrounded facts there are.
Second, the worry with meta-grounding was not merely that it generates an infinity of grounding facts. The real worry is that it generates an infinite regress of grounding facts. The charge is that the meta-grounding thesis violates the platitude that the grounding structure of reality must “ground out” in a fundamental level. Meta-grounding allegedly violates a maxim that might be called “the well-founded constraint”. The constraint captures the idea that all grounding relations must eventually come to an end. Cameron [5] states the principle thusly:
There must be a metaphysical ground, ... a realm of basic facts which provide the ultimate metaphysical grounding for all the derivative facts.
Metaphorically speaking, there can’t be turtles all they way down. Schaffer [20]: 62 states the driving intuition behind the well-founded constraint eloquently when he claims that if grounding were not well-founded, “being would be infinitely deferred, never achieved”.
-
The well-founded constraint: Grounding structures must be well-founded.
We’re not sure that the well-founded constraint is actually legitimate – why can’t every level of reality simply derive its being from a deeper, more fundamental, level?Footnote 11 But we needn’t weigh in on the issue over whether or not this type of regress is bad. Our aim is simply to investigate whether or not acceptance of the meta-grounding thesis leads to violations of the well-founded constraint. However, before we can do that, we must get clear about what the well-founded constraint actually comes to.
3.2 The Plan
The plan will be as follows. We start by making some simplifying assumptions. In Sections 3–4, we deal only with full ground. We ignore partial ground and assume that ground relates only individual facts to individual facts, rather than pluralities to individual. This assumption is admittedly somewhat artificial. However, this simplifying move facilitates exposition and allows us to express several philosophical and formal results that will not change significantly when we move to a more sophisticated (and realistic) framework in Section 5. That framework will accommodate partial ground and grounding by pluralities. Throughout, the symbol ‘ <’ will stand for full ground and ‘\(\prec \)’ for partial ground.
If facts stand in the grounding relation to one another, the world is sorted into layers of fundamentality. The full story of the world includes a chapter on the structure of reality, which tells us about dependencies between facts. The set of facts plus the relations of dependence given by the grounding relation yield the grounding structure of the world.
Definition 1
A grounding structure is an ordered pair 〈A, < 〉 consisting of a set of facts A and a grounding relation <.Footnote 12
Definition 2
A grounding structure 〈A, < 〉contains a structure 〈B, < 〉 iff \(B \subseteq A\). If 〈A, < 〉 contains 〈B, < 〉, we call 〈B, < 〉 a substructure of 〈A, < 〉.
Grounding structures are acyclic directed graphs. They can be perspicuously represented visually. For example, the following diagram represents the grounding structure 〈{p 0, p 1, p 2, p 3},<〉, where p 0 < p 1, p 0 < p 2, and p 2 < p 3 (Fig. 1).
To get these definitions to jive with our intuitions about “the structure of reality” we need to add a slight sophistication. A grounding structure 〈A, < 〉 might be intuitively non-well-founded, in the sense that it contains a fact whose complete chain of ground goes on forever, despite being such that 〈A, < 〉 itself does not contain an infinite descending chain. This can happen when A fails to include some fact that grounds a member of A. To remedy this lacuna, we introduce the grounding closure of a structure. The grounding closure of a structure 〈A, < 〉 is simply the collection of all the grounds of every fact in A (and no other facts) paired with <. A structure is grounding closed iff it is identical to its closure. The grounding structures of primary concern in this investigation are the grounding closed structures.
Definition 3
For a grounding structure 〈A, < 〉, the grounding closure of 〈 A, < 〉, GC (〈A, < 〉), is defined as 〈G C(A),<〉, where \(GC(A) = A \cup \{p \mid \exists q (q \in A \wedge p < q)\}\).
Definition 4
A structure is grounding closed iff it is identical to its grounding closure.
This definition makes the expression ‘ G C(ϕ)’ do “double-duty”. One can take the grounding closure of either a structure or a set. The closure of a structure is a structure; the closure of a set is a set. The closure of a set S is the set part of the structure (an ordered pair) generated by taking the closure of the structure 〈S, < 〉. We can use these definitions to precisely define when a grounding structure satisfies the meta-grounding thesis.
Definition 5
A structure S satisfies the meta-grounding thesis or is meta-grounded iff for all grounding facts g ∈ G C(S), there is some p ∈ G C(S) such that p < g.Footnote 13
3.3 Infinite Descent and Well-Foundedness
What does it mean to say that grounding structures must be well-founded? Schaffer [20]: 37 writes, “Well-foundedness is imposed by requiring that all priority chains terminate”. He also claims that well-foundedness requires the absence of “limitless chains of dependence”. Cameron [5]: 3 states that, “you cannot have dependence all the way down” and later (13) speaks against “infinitely descending chains of ontological priority”. One notion we would like to define, then, is “infinite chain of dependence”. On such a structure one could walk from facts to their grounds eternally.Footnote 14
Definition 6
A structure 〈A, < 〉 is a chain iff A is non-empty and for all p, q ∈ A either p < q, p = q, or q < p.
A chain is a set of facts all related to each other by the grounding relation.
Definition 7
A structure 〈A, < 〉 is an infinite descending chain iff (i) A is a chain and (ii) for every p ∈ A, there is a \(p^{\prime }\in A\) such that \(p^{\prime }< p\).
An infinite descending chain is a set of facts, all related to each other by the grounding relation, in which every fact is grounded by another member of the chain (Fig. 2).
Definition 8
A structure 〈A, < 〉 is finitely grounded iff its grounding closure does not contain an infinite descending chain.
Given this we can derivatively define what it is for a fact to be finitely grounded.
Definition 9
A fact p is finitely grounded iff 〈{p},<〉 is finitely grounded.
Intuitively, a fact fails to be finitely grounded if examination of its grounds leads to an infinite chain of ground. The definition of finitely grounded, then, seems to be a good candidate for what grounding theorists have meant by “well-founded”. In fact, it is the same as the definition of a well-founded relation in mathematics. In set theory, a set S is a well-founded set iff the set membership relation on the transitive closure of S contains no infinite chains.Footnote 15 Schaffer [20]: 37 explicitly says that grounding must provide a “well-founded partial ordering” (in the set-theoretic sense). However, we believe that there is no a priori reason to suppose that the appropriate grounding-theoretic notion of “well-foundedness” need be defined in the same way as a homophonic condition in set theory. In fact, one of the lessons of this paper will be that not enough attention has been paid to the grounding-theoretic notion of well-foundedness, and what exactly it might come to.
At the least, the notion of a grounding structure’s being finitely grounded is an obvious and straightforward formal way of capturing the intuitions behind well-foundedness.
3.4 Meta-Grounding and Infinite Descent
We wish to demonstrate that the meta-grounding thesis is compatible with the set of all facts being finitely grounded. If the definition of finitely grounded captures what it is for a grounding structure to be well-founded, then we will have demonstrated that meta-grounding is compatible with the well-founded constraint. First, we motivate the compatibility of meta-grounding with finite grounding by consideration of a possible world.
Consider the world Asgard, which in many respects is just like the actual world. There are protons, electrons, paramecia, and automobiles, and only finitely many of them. Let’s assume that the fact that the paramecium is swimming is, at least partly, grounded in facts about the protons, electrons, and other particles that make up the paramecium. The grounding structure goes from small to big. Facts about small things ground facts about the large things they make up.
At Asgard, the meta-grounding thesis is true - every fact about grounding is itself grounded. Suppose that some paramecium swims - call this fact [paramecium swims]. This fact is grounded in some complex configuration of microphysical particles. Call this fact C. C is the fact that particles such-and-such are arranged thisly-and-thatly and moving thus-and-so. C grounds [paramecium swims]. Now consider the fact [C < [paramecium swims]]. By the meta-grounding thesis, [C < [paramecium swims]] must be grounded. What fact grounds it? At Asgard, the answer is: “the fact that God exists”. This answer leads to a new question: What grounds the fact that the fact that God exists grounds [C < [paramecium swims]]? I.e. what fact grounds [[God exists] < [C < [paramecium swims]]]? At Asgard, the answer to such questions is always “the fact that God exists”. [God exists] grounds all the facts about grounding. In fact, we will assume that every fact at Asgard, is, after finitely many steps, ultimately grounded in the fact that God exists.
Asgard has only one fundamental fact: [God exists]. Every derivative fact, including every grounding fact, is ultimately grounded in the fact that God exists. So Asgard satisfies the meta-grounding thesis, while at the same time being such that the set of all facts at Asgard is finitely grounded.
Theorem 2
There are (non-empty) closed grounding structures that both satisfy the meta-grounding thesis and are finitely grounded.
If being a finitely grounded structure suffices for being a well-founded structure - which is both prima facie plausible and suggested by analogy with set theory - then the set of all facts at Asgard is well-founded and meta-grounding is compatible with the well-founded constraint.
To clarify we return to the alleged regress we started with. The meta-grounding thesis generates the following infinite sequence of facts.
The grounding structure generated by this situation, however, doesn’t include an infinite descending chain. To see this we need only notice that for each j>0, r j grounds the fact that r j−1 grounds g j−1, but r j does not ground r j−1 itself, nor does g j ground g j−1. There is no “chaining together” of the facts in the infinite sequence.
Such a grounding structure can be represented as follows:
The world Asgard itself fits the model just above. Asgard represents the special case in which [God exists] = r 0 = r 1 = \(\dots \).Footnote 16
The meta-grounding thesis, which demands that every grounding fact be grounded, does not entail that there are infinite descending chains (and therefore does not entail that a structure satisfying meta-grounding fails to be finitely grounded). The grounding structure in Fig. 3 appears perfectly well-founded. All chains of grounding terminate. Being is achieved, not infinitely deferred.
Bennett [3]: 6 disagrees. She writes that “requiring a ground for every grounding fact violates the well-foundedness of the grounding relation. If every grounding fact is grounded, there are priority chains that are not only infinitely long, but which also fail to terminate or ‘ground out’ in something ungrounded.” We disagree on several counts. The meta-grounding thesis does not yield infinite descending chains of ground (i.e. “priority chains that are infinitely long”). We’ll see shortly (Section 3.2) that there is a difference between an infinite descending chain and an infinite descending chain that fails to, in some intuitive sense, “ground out”. (The basic idea is that an infinite descending chain can either have or fail to have a “limit”). Meta-grounding leads to neither type of infinite descending chain, because it does not lead to infinite descending chains at all. Since meta-grounding does not lead to infinite descending chains, there is no conflict with the well-founded constraint.Footnote 17
In Section 4.1, we’ll see that adding extra (and independently motivated) conditions on ground might generate structures that fail to be finitely grounded. We will posit that such structures do not, despite failing to be finitely grounded, violate some intuitive notions of “well-founded”. However, before discussing these issues, we must get precise about the grounding-theoretic concept of “well-founded”.
4 Three Conceptions of Well-Founded
A forthcoming paper by Scott Dixon [10] covers much of the same material as this section. Our work was developed independently of his.
4.1 Well-Founded without Finite Grounding
First we argue that being finitely grounded may not be a necessary condition for being well-founded in the grounding theoretic sense. We offer an example of a world whose structure is not finitely grounded but which appears intuitively well-founded nonetheless.
Consider the world called ‘Space’. Let ‘Space’ denote the set of all facts at the world Space. Space consists of exactly that – empty space. We make some assumptions about the grounding structure of Space. Space has some ungrounded, perfectly fundamental facts - the facts about the existence of points of space. These facts ground the existence of regions, which in turn ground the existence of larger regions. If s is a sub-region of r, then [s exists\(] \prec [r\) exists]. If s 1, s 2, ... s n is a set of disjoint regions whose union is r, then [ s 1 exists ∧ s 2 exists ∧ ... s n exists ]<[r exists].
Similarly, if p is a point in r, then \(p \prec r\), and the existence of all the points in r fully grounds the existence of r. Grounding relations between facts about the existence of regions and points are the only grounding relations at Space.
Let s be a spherical region of Space. Let s 1 be a plurality consisting of two hemispheres whose union is s. Let s 2 be the four quarter spheres generated by halving each hemisphere of s 1. The union of the quarter spheres of s 2 will be s. Let s 3 be the eight eighth spheres generated by halving each quarter sphere of s 2. Let s n be the 2(n-1) regions generated by halving all the regions of s n−1. s, s 1, s 2, ... is a sequence of pluralities of regions. s is the sphere, s 1 the sphere’s two hemispheres, s 2 the sphere’s four quarter spheres, et cetera. Now let σ 0 = the fact that s exists and σ i = the fact that the sphere-parts of s i exist. Given this set-up, each σ i is grounded in σ i+1, because each region is fully grounded in the existence of any full plurality of its (non-overlapping) subregions (Fig. 4).
Consider the set of facts \({\Sigma } = \{\sigma _{0}, \sigma _{1}, \sigma _{2},\dots \}\). The facts in Σ form an infinite descending chain. Σ is contained in 〈Space ,<〉 - the grounding structure relating all the facts at the world Space. Therefore, 〈Space ,<〉 is not finitely grounded.
Nevertheless, there is a clear sense in which 〈Space ,<〉 is well-founded. σ 0 (the fact that the spherical region s exists) does have an ultimate, and perfectly fundamental, ground. Its ultimate ground is the existence of all the points contained in s. Call the fact that this plurality of points exists ¶. ¶ is an ungrounded, perfectly fundamental, full ground of σ 0. σ 0, and all the σ i , are grounded in ¶. This is so despite the fact there is an infinite chain of ground emanating downward from σ 0. ¶ functions as a lower bound for the infinite chain of ground Σ.
Grounding structures provide a pyramid of being. The higher, less fundamental, grounded layers of the pyramid derive their being from the lower, more fundamental layers. Well-foundedness is the claim that the pyramid has a bottom layer - a layer that grounds all the rest. There being such a bottom layer is compatible with the ability to traverse an infinite descending path in the pyramid. This is why being well-founded and being finitely grounded come apart. A grounding structure is finitely grounded if one can’t travel an infinite descending path of ground. But intuitively, a structure is well-founded if there is some set of ungrounded facts that ground the rest.
4.2 Bounded from Below
Let’s now take on board the claim that structures which fail to be finitely grounded can nevertheless be well-founded in some respectable grounding-theoretic sense.Footnote 19 , Footnote 20 But what exactly is this notion of “well-founded”? One candidate is “bounded from below”, which we define as follows.
Definition 10
A lower bound for a grounding structure 〈A, < 〉 is a p such that for all \(p^{\prime } \in \) A, either \(p = p^{\prime }\) or \(p< p^{\prime }\).
Definition 11
A grounding structure 〈A, < 〉 is bounded from below iff every chain in GC (〈A, < 〉) has a lower bound.
A lower bound is simply a limit to a descending chain of ground. It’s worth noting that (a) a lower bound needn’t be unique and (b) a lower bound to 〈A, < 〉 need not itself be a member of A. It will always be a member of GC(A).
A grounding structure that is bounded from below can contain infinite descending chains. But there must be a limit to every chain - an ultimate ground that (a) grounds every member of the chain and (b) is ungrounded. For example, the grounding structure 〈Σ,<〉 discussed above is not finitely grounded, but it is bounded from below, since the fact ¶ is a lower bound for the infinite descending chain 〈Σ,<〉.
Theorem 3
There are grounding structures that are bounded from below but fail to be finitely grounded.
Proof
By example. 〈Space ,<〉 and 〈Σ,<〉 are both bounded from below but fail to be finitely grounded. □
Furthermore, a structure which is finitely grounded is guaranteed to be bounded from below.
Theorem 4
If a structure is finitely grounded, it is bounded from below.
Proof
A structure 〈A, < 〉 is finitely grounded if every chain in GC(A) is finite. 〈A, < 〉 is bounded from below if every chain in GC(A) has a lower bound. Consider an arbitrary chain C in GC(A). Because C is a chain, every element of C is related by < to every other element of C. Since C is finite and < is asymmetric, there must be an element b in C s.t. b < c for all non-b c ∈ C. b is the lower bound. □
The problem with infinite chains of ground is not that they’re infinite. The problem arises only when they have no end (or limit). Being must originate from some ultimate source: the fundamental. It matters not that being is transferred from the fundamental to the non-fundamental via infinitely many steps. Only when there is no origin of being, no fundamental substratum to the hierarchy of ground, is (to crib Schaffer’s eloquent phrasing) being “infinitely deferred but never achieved”. In a grounding structure that is not finitely grounded (because it contains infinite chains) but bounded from below (because all such chains have a lower bound), being is infinitely deferred but nevertheless achieved.
4.3 Having a Foundation
In this section we define the notion of a structure’s “having a foundation”. In the next Section (4.4: “Relations between the three notions of “well-founded”) we compare the foundational conception of well-founded-ness with “bounded from below” and “finitely grounded”. A structure has a foundation if and only if there is some set of facts that (i) together ground all the derivative facts and (ii) are themselves ungrounded. We call such a set of facts a foundation for the grounding structure.
Definition 12
A foundation 〈F, < 〉 for a grounding structure 〈A, < 〉 is a substructure of GC(〈A, < 〉) such that (i) for all p∈ GC(〈A, < 〉) there is an f ∈ F, such that f = p or f < p and (ii) for all f ∈ F there is not a \(p^{\prime } \in \) GC(〈A, < 〉) such that \(p^{\prime } < f\).
Definition 13
A grounding structure 〈A, < 〉has a foundation iff its grounding closure contains a substructure 〈F, < 〉 this is a foundation for 〈A, < 〉.
We think that this definition of a structure’s having a foundation is a good candidate for capturing the intuitive grounding-theoretic notion of well-foundedness. It’s reasonable to think that what some philosophers have been after in demanding that grounding be well-founded is that grounding structures have a foundation. Schaffer [20]: 37 writes that the well-founded constraint “may be understood as a kind of metaphysical foundationalism.”
4.4 Relations between the Three Notions of “Well-Founded”
We’ve already seen that a structure can be bounded from below without being finitely grounded (Theorem 3), while a structure which is finitely grounded is thereby bounded from below (Theorem 4). With the introduction of third conception of “well-founded”, has a foundation, obvious questions arise about how this relation relates to the other two. On a moment’s reflection we see that there is the following entailment.
Theorem 5
If a grounding structure 〈A,<〉 is bounded from below, then it has a foundation.
Before commencing the proof, we sketch the main idea. We should be able construct a foundation F for A by collecting the lower bounds of all the chains in the grounding closure of 〈A, < 〉. Unfortunately, the set of all such bounds is much too large. It contains all the members of GC(A), because every fact is a lower bound for the chain consisting of its singleton paired with <. To avoid this overgeneration, we introduce the notion of a chain that is maximal with respect to S. A chain is maximal with respect to S when it is not a substructure of any other chain in S. 〈{p 0, p 1, p 2,..., l},<〉 is maximal if and only if there is no further fact in that grounds the lower bound l. Considering only maximal chains gives us what we want: l should be placed in the foundation only when there is no further fact that grounds l. The set consisting of every lower bound for every maximal chain in GC(A) will be a foundation for A.
Proof
First, we construct a foundation using the lower bounds guaranteed by the fact that 〈A, < 〉 is bounded from below. Then we demonstrate that this foundation satisifies the definition of a foundation for 〈A, < 〉.
Construction of the Foundation For any structure S, call any chain that is not a proper substructure of any other chain in S maximal with respect to S (or just “maximal”). 〈A, < 〉 is bounded from below, so every chain in G C(〈A, < 〉) has a lower bound. Thus every chain that is maximal with respect to GC(A) has a lower bound. Let F be the set of elements of GC(A) that are a lower bound for some maximal chain in GC(A). (A chain might have multiple lower bounds. F includes them all.)
Claim 〈F, < 〉 is a foundation for 〈A, < 〉.
Proof of Claim 〈F, < 〉 is a foundation for 〈A, < 〉 iff F is a subset of G C(A) and (i) for all p ∈ G C(A) there is a f ∈ F, such that f = p or f < p and (ii) for all f ∈ F there is not a \(p^{\prime } \in GC(A)\) such that \(p^{\prime } < f\). It’s obvious that \(F \subseteq GC(A)\), satisfying the requirement that 〈F, < 〉 be a substructure of G C(〈A, < 〉).
Condition (i) We need to show that for all p ∈ G C(A) there is a f ∈ F, such that f = p or f < p: Consider a chain M that contains p and is maximal with respect to GC(A). (There will always be such a chain. In the limit case it will be 〈{p},<〉). Since GC(A) is bounded from below, M is bounded from below. Consider a lower bound b. Since GC(A) is grounding closed, b ∈ G C(A). F is the set of lower bounds of maximal chains in A. M is such a maximal chain. So b ∈ F. If b = p then we have an f ∈ F (i.e. b) s.t. f = p and condition (i) is satisfied. If b≠p then b < p because b is a lower bound for a chain containing p. b ∈ F so we have an f ∈ F s.t. f < p; condition (i) is again satisfied.
Condition (ii) We need to show that for all f ∈ F there is not a \(p^{\prime } \in GC(A)\) such that \(p^{\prime } < f\). Suppose for reductio that there is a \(p^{\prime } \in GC(A)\) s.t. \(p^{\prime } < f\). By the construction of F, there is a maximal chain 〈M, < 〉 in GC(A) s.t. f is a lower bound for 〈M, < 〉. For all m ∈ M, f < m or f = m. This entails that for all \(m \in M, p^{\prime } < m\), since \(p^{\prime } < f\). Thus \(\langle M \cup \lbrace p^{\prime } \rbrace , < \rangle \) is a chain. By the asymmetry of ground, \(p^{\prime } < f\) entails that not: \(f < p^{\prime }\). Since f is a lower bound for 〈M, < 〉, and f is neither identical to nor grounds \(p^{\prime }\), \(p^{\prime } \notin M\). Thus \(M \subset M \cup \lbrace p^{\prime } \rbrace \) and 〈M, < 〉 is a proper substructure of the chain \(\langle M \cup \lbrace p^{\prime } \rbrace , < \rangle \). But this contradicts the maximality of 〈M, < 〉. We reject the supposition that there is a \(p^{\prime } \in GC(A)\) s.t. \(p^{\prime } < f\).
□
What about the other direction of implication? If a structure has a foundation, is it bounded from below? Interestingly, the answer is, “No”. Consider the following counter-example, involving infinite disjunction.Footnote 21 Let F = {f 1, f 2, f 3,...} be an infinite set of fundamental facts. Let D1 be the infinite disjunction of all these facts and D i be the disjunction of all f j such that i≤j. (This makes D1 the disjunction of all the f j s.) Let D be the set containing all the D i s.
-
D \(= \lbrace D_{1}, D_{2}, D_{3}, {\dots } \rbrace \)
-
D\(_{1} = f_{1} \vee (f_{2} \vee (f_{3} \vee \dots \)
-
D\(_{2} = f_{2} \vee (f_{3} \vee (f_{4} \vee \dots \)
-
D\(_{i} = f_{i} \vee (f_{i+1} \vee (f_{i+2} \vee \dots \)
We will argue that the grounding structure 〈D, < 〉 has a foundation (F) but is not bounded from below.
Any disjunction is fully grounded in any of its true disjuncts. Thus a disjunction can have more than one distinct full ground. In the infinite disjunction case just described, \(\langle D = \{D_{1}, D_{2}, D_{3}, {\dots } \}, < \rangle \) forms an infinite descending chain. D1 is grounded by D2 (one of D1’s disjuncts), D2 is grounded by D3 (one of D2’s disjuncts), et cetera. This chain has no lower bound because there is no f ∈ F (or ∈ G C(D)) such that for all d ∈ D, f < d. For example, f 78 grounds D 78, D 77, ..., D 1 but f 78 does not ground D 79. For any f i one chooses this situation will be repeated. Therefore, 〈D, < 〉 is not bounded from below. But the structure \(\langle \lbrace f_{1}, f_{2}, f_{3}, {\dots } \rbrace , < \rangle \) forms a foundation for 〈D, < 〉. Every fact in GC(〈D, < 〉) is either a member of F or grounded by a member of F. Therefore, not all structures that have a foundation are bounded from below (Fig. 5).
This example highlights the difference between having a foundation (an ungrounded set of fundamental facts that together ground all the rest) and being bounded from below (all infinite descending chains have a lower bound). The underlying reason these two notions come apart in simple. A structure has a foundation if every fact in it is fully grounded by some ungrounded fundamental. But a chain - itself a type of structure - has a lower bound only if there is some single fact that fully grounds every element in the chain. The requirements on being bounded from below are more strict - some fundamental fact needs to ground the entire chain. Having a foundation does not require that a single fact ground an entire chain. Instead it requires merely that each element of the chain be either ungrounded or grounded in something ungrounded.
Theorem 6
There are grounding structures that have a foundation but are not bounded from below.
The essential trick here is to have an infinitely large foundation. If the foundation is merely finite, then the equivalence between bounded from below and has a foundation holds.
Theorem 7
If a grounding structure has a finite foundation, then it is bounded from below.
Because a structure which is finitely grounded is bounded from below (Theorem 4), and a structure which is bounded from below has a foundation (Theorem 5), it follows that a structure which is finitely grounded has a foundation.
Corollary 1
A structure which is finitely grounded has a foundation. (From Theorems 4 and 5).
Lastly, a structure can have a foundation but not be finitely grounded. 〈D, < 〉, the structure formed by the disjuncts of the infinite disjunction above, provides an example.
Theorem 8
A structure that has a foundation can fail to be finitely grounded.
To summarize, “finitely grounded” is the strongest condition, both in the sense of being the most difficult to satisfy and in the sense of entailing the other two. “Bounded from below” and “has a foundation” follow in decreasing order of strength. The following diagram represents the relations of entailment between the three notions of well-founded (Fig. 6).
4.5 Whither Well-Foundedness?
We’ve now seen that there are grounding structures that have a foundation but which are not bounded from below. This is in itself an interesting result. The obvious question looms: Which of finitely grounded, bounded from below, and has a foundation best captures the intuition behind the well-founded constraint? Consider also the related question: “Which of the three candidate conceptions of well-founded-ness have authors had in mind when discussing the idea that grounding must be well-founded?”
There is likely no determinate answer to the second question (what authors have had in mind). Theorists of ground have worried about the ultimate source of being - the perfectly fundamental layer that grounds the rest. Many agree that the grounding cannot “go on forever”. The world’s grounding structure must be, in some sense, well-founded. There can’t be turtles all the way down.
Beyond that point, however, things start to get muddled. Different authors, and different time-slices of the same author, appear to have had different ideas about what well-founded grounding amounts to. If different formulations of well-founded-ness are considered at all, assumptions are made about how one formulation might be equivalent to, or entail, another. Consider the following three quotes:
-
“Well-foundedness is imposed by requiring that all priority chains terminate.” Schaffer [20]: 37.
-
“ “well-founded” in the sense that if a truth holds in virtue of any truth at all, then it is connected by an in-virtue-of chain to some truth that does not hold in virtue of any truth (“no unbounded descending chains of in-virtue-of”).” Sider [21]: 137
-
“The assumption of a well-founded partial ordering may be understood as a kind of metaphysical foundationalism.” Schaffer [20]: 37
These three quotes express the requirements of “finitely grounded”, “bounded from below”, and “has a foundation”, respectively.Footnote 22
In more careful moods, authors (e.g. Cameron [5]), after glossing the well-founded constraint as a prohibition against infinite chains, go on to say something like, “Of course, its not infinite chains per se that are bad, but infinite chains without a limit.” So the difference between infinite chains simpliciter and infinite chains that are somehow “based” is sometimes acknowledged. But the funny bit comes next. Those same authors then go on to explain that what really matters is having a foundation, a metaphysical basis from which all else is generated. Thus, having infinite chains, on the one hand, is contrasted with having chains without bound/having no foundation, on the other. But, to our knowledge, having chains without bounds has never been contrasted with having no foundation. It is just widely assumed that a structure has a foundation if and only if all the infinite chains have bounds. But that is not true, as this paper shows.
Upon reflection, it is not surprising that the possibility that ”has a foundation” and ”bounded from below” could come apart has heretofore been ignored. First, ”bounded from below” entails ”has a foundation” (Theorem 5). Second, structures that have a foundation but contain infinite unbounded chains nonetheless are quite recherché. They involve infinitary foundations in combination with structures that contain multiple distinct full grounds. We think that this partly explains why the possibility of the two coming apart has been completely ignored in the grounding literature. Nobody uses infinitary disjunction as the paradigm case that guides their thought about ground. But you need something as odd as infinitary disjunction to get a grounding structure that has a foundation but is not bounded from below.
The running together of different varieties of “well-founded” has been encouraged by comparison and/or conflation with the homophonic condition in set-theory. There is a well entrenched use of the term ‘well-founded’ in set theory. A set is well-founded if its closure under the set membership relation does not contain any infinite chains of set membership. In other words, a set is well-founded if and only if it meets the analog of “finitely grounded” for set membership. By now, it should be clear that the ground theoretic notion of “well-founded” has, on at least two of its plausible readings (“bounded from below” and “has a foundation”) quite a different content from the set-theoretic notion. A major lesson of this paper is that we must separate the ground-theoretic notion(s) of “well-founded” from the set-theoretic notion.
One of the reasons the three notions of ground-theoretic well-founded-ness discussed here have remained underappreciated is that in a set-theoretic framework the three distinct notions collapse. This occurs because, in a formal sense, set membership is a simpler relation than ground. For starters, a set-membership ordering is never dense. Any two elements in the order have finitely many elements between them. A ground-theoretic ordering can be dense; two elements in a chain of ground can contain infinitely many elements between them. Dense (and potentially dense) relations yield more complicated structures than non-dense relations. For non-dense relations, a structure will be finitely grounded if and only if it is bounded from below. In set theory, the difference between these two notions is invisible because the relation in question - set membership - is not dense.Footnote 23 Two further differences between ground and set-membership arise from (a) partial ground and (b) multiple distinct full grounds. There’s no “partial set membership”, and no situations in which two distinct pluralities P and P’ contain all and only the members of a set S. The result once again is that ground leads to more complicated structures than set membership.
The choice of the term “well-founded” for discussing a widespread intuition about ground is understandable, but perhaps unfortunate. The term has a well-established and quite distinct use in set-theory and the theory of relations more generally. However, it is probably too late to turn back and use a different term. The best we can do is be careful. If grounding theorists are going to co-opt a term from set theory, and use that term for a similar but distinct condition on the grounding relation, they must be extra careful not to conflate the notions or let thinking about well-founded sets and/or relations lead them astray when theorizing about ground. Hopefully this paper will help avoid such conflation by clarifying the differences between set-theoretic and ground-theoretic well-foundedness.
Unlike in set theory, in research on ground it’s not clear what being well-founded amounts to. We’ve tried to get precise about different formal structures at which philosophers might aim when they speak of “well-founded grounding”. Clarifying formal conditions that purport to represent an intuitive concept should purify the philosophical waters and allow us to see deeper into the nature of ground.
Reconsider the first question posed above: “Which of our three formal notions best captured the intuitive idea behind well-founded grounding?” We think that “has a foundation” is the core conception of ground-theoretic well-foundedness. The idea of a basic realm of facts (or objects) from which everything else is generated comes before any more sophisticated claims about infinite descending chains. We have relied on this intuition when we claimed that even if a grounding structure contains infinite descending chains it can be well-founded nonetheless.
Regardless of whether one decides to model ground-theoretic well-foundedness with (i) “finitely grounded” (ii) “bounded from below”, or (iii) “has a foundation”, the meta-grounding thesis will be in good shape. A grounding structure can satisfy the meta-grounding thesis and be finitely grounded, bounded from below, and have a foundation. The grounding of Asgard (2.3) provides one example. Meta-grounding itself yields no conflict with the claim that grounding structures must be well-founded.
5 A Framework for Partial Ground
5.1 Partial Ground
Thus far, we have considered (for the most part) only relations of full ground. We also considered only cases of ground that related single facts. In this section, we expand the framework to accommodate partial ground and the possibility of grounding by pluralities. The restriction in previous sections to full ground by non-pluralities is admittedly somewhat artificial. However, the restriction significantly simplifies presentation without doing harm. The increased sophistication required to handle partial ground will not significantly alter the main results. The three different notions of well-founded remain and interact with the meta-grounding thesis in the same ways. The main difference is that we must bifurcate the notions of chain and of lower bound. There will be chains of full ground and chains of partial ground. There will be partial lower bounds and full lower bounds. The definitions will be intuitive.
Suppose that some facts p 1, p 2, \(\dots \) together fully ground a fact q. We write: \(p_{1}, p_{2}, \dots < q\). We abbreviate this as P < q, where P is the set of all the p i s. One should keep in mind that the set P does not do the grounding. On our official terminology, facts ground, not sets. When a plurality of facts (the p i s) grounds another fact (q), we represent this using the set (P) that contains the many facts (the p i s). But the set itself does not do the grounding, the facts do. In the definitions to follow, we’ll speak of sets as grounders, but this is a shorthand.
Grounding by pluralities is non-monotonic. If some plurality of facts grounds q, adding an arbitrary fact to the plurality may not generate a plurality that remains a full ground. This is partly because grounding is a relation of metaphysical explanation. The grounders must, in some sense, be “relevant” to that which is grounded.
We define partial ground in terms of full ground. A partial ground is a member of a plurality that fully grounds. Pluralities can also be partial grounds.
Definition 14
(partial ground) p \(\prec \) q \(=_{def} (\exists P)(P < q \wedge (p \in P \vee p \subseteq P))\)
Before delving into the nitty-gritty details, we offer a preview. First we modify some definitions to accommodate partial and many-one grounding. Then we define two types of chains - chains of full ground and chains of partial ground - and two types of lower bounds - full lower bounds and partial lower bounds. A chain of full ground (or partial ground) may have a full lower bound, or it may have a partial lower bound, or it may have neither. We then discuss the relationship between a structure’s having a foundation and having all the structure’s chains fully or partly bounded from below. In the end, the results will not be significantly different than those that have come before.
5.2 The Details
To accommodate full ground by pluralities, we modify the definitions of the grounding closure and of a foundation.
Definition 15
The grounding closure \(_{\prec }\) GC\(_{\prec }(\langle A, < \rangle )\) of a structure 〈A, < 〉 is the structure \(\langle GC_{\prec }(A), < \rangle \) where \(GC_{\prec }(A) = \cup S\) and S = {G|(∃a ∈ A)(G < a)}.
The grounding closure of A is the union of all the collections of facts that fully ground some fact in A. Equivalently, GC\(_{\prec }\)(A) is the set of all facts that partly ground some fact in A.
Definition 16
〈A, < 〉has a full foundation 〈F, < 〉 iff \(\exists F \subseteq GC_{\prec }(\langle A, < \rangle )\) s.t.:
-
(i)
(∀f ∈ F)(¬∃Y)(Y < f)
-
(ii)
\((\forall s \in GC_{\prec }(A))(\exists F^{\prime } \subseteq F)(F^{\prime } < s \vee s \in F^{\prime })\) Footnote 24
A full foundation for a structure S is a structure which contains facts that are (i) ungrounded and (ii) together ground all the facts in S (in these sense that every fact in S is fully grounded by some subset of the facts in the foundation).
Once we allow full ground by pluralities, we must expand the transitivity of full ground into a full-blown cut rule:
-
(Cut) If P < p and Q, p < r, then Q, P < r.
In Section 3.3 we defined an infinite descending chain of full ground. We now define an infinite descending chain of partial ground.
Definition 17
A structure 〈A, < 〉 is an infinite descending chain of partial ground iff:
-
(i) A is non-empty
-
(ii) for every p ∈ A, there is a \(p^{\prime }\in A\) such that \(p^{\prime }\prec p\)
-
(iii) for all p, q ∈ A either \(p \prec q\), p = q, or \(q \prec p\).
An infinite descending chain of partial ground is exactly what it sounds like: an infinite set of facts all related to each other by partial ground. Every chain of full ground is a chain of partial ground because full grounding entails partial grounding. In this section, we’ll primarily be concerned with the ways in which infinite chains of partial ground interact with bounds (both partial and full) and with having a full foundation. We define a partial and full lower bound in the obvious way.
Definition 18
A partial lower bound b for a grounding structure 〈A, < 〉 is a b such that for all a∈ A, \(b\prec a\) or b = a.
A partial lower bound is a fact that partly grounds every fact in a structure. A full lower bound is a set of facts that fully grounds every fact in a structure.
Definition 19
A full lower bound B for a grounding structure 〈A, < 〉 is a set B of facts such that (i) for all a∈ A, B < a or a ∈ B and (ii) (∀b ∈ B)(¬∃a∈ A\()(a \prec b)\).
We also define “partially bounded from below” and “fully bounded from below” in the obvious way.
Definition 20
A structure 〈A, < 〉 is partially bounded from below iff every infinite descending chain of partial ground in GC\(_{\prec }\langle A, < \rangle \) has a partial lower bound.
Definition 21
A structure 〈A, < 〉 is fully bounded from below iff every infinite descending chain of partial ground in GC\(_{\prec }\langle A, < \rangle \) has a full lower bound.
5.3 Results
With these definitions in tow, we can ask the obvious questions: “How does partially bounded from below interact with having a full foundation?” “How does fully bounded from below interact with having a full foundation?” The answer to the first question is that neither “has a full foundation” nor “partially bounded from below” entails the other. The answer to the second question is that if a structure is fully bounded from below, then it will have a foundation, but the converse implication does not hold.
Theorem 9
A structure can be partially bounded from below but not have a full foundation.
The reason for this result is simple. The existence of ungrounded partial grounds does not guarantee the existence of ungrounded full grounds.
Consider the following case. Suppose that the fact that God exists is fully fundamental and partially grounds every fact at a world. God’s existence plays some role, albeit a small and partial role, in sustaining all of reality. [God exists] is a partial lower bound for every infinite descending chain of partial ground. But there need not be a fully fundamental basis - a foundation - which fully grounds every fact. In fact, there might be no ungrounded facts other than [God exists]!
Theorem 10
A structure can have a full foundation but not be partially bounded from below.
The infinite disjunction case from Section 4.4 provides an example of a structure that has a full foundation but which is not even partially bounded from below.
Theorem 11
If a structure is fully bounded from below, then it has a full foundation.
We can use a procedure similar to the one used in the proof of theorem 4 to generate a foundation by collecting the full lower bounds.
Theorem 12
A structure can have a full foundation but not be fully bounded from below.
The reason why a structure can have a foundation but fail to be bounded from below is the same as before. Lower bounds are required to ground every element of the chain. The foundation need not contain any fact that grounds every element of the chain. This is why structures can have a foundation but not be bounded from below (in either the full or partial sense).
5.4 Meta-Grounding
How does the meta-grounding thesis, which says that all facts about ground are themselves grounded, interact with the more sophisticated framework incorporating partial ground? First, there are two versions of the meta-grounding thesis - one which says that all facts about ground are fully grounded, the other which says that all facts about ground are only partially grounded. The thesis we have been concerned with thus far is the former, stronger, thesis. This is the more intuitive and straightforward claim - the one that comes to mind when one says, “What if the facts about grounding are themselves grounded?”
The move to a framework involving partial ground generates a dizzying array of notions of well-founded-ness. In Section 5.2 (“The Details”), we discussed only the most theoretically interesting ones. A structure can generate finite or infinite chains of full ground and finite or infinite chains of partial ground. Each such chain might be fully or partially bounded from below. The structure might have a full foundation or it might have a merely partial foundation. We do not go through all the sordid details. The basic result is the same. A structure can satisfy either the full or partial meta-grounding thesis and still be well-founded in every sense of the term we have covered so far (and then some). The structure can be finitely grounded, bounded from below, and have foundation (in every sense of those terms).
In sum, the move to a framework that accommodates relations of partial ground generates no extra tension between the meta-grounding thesis and the well-founded constraint.
6 Meta-Grounding and LC
6.1 Meta-Grounding in Wonderland
We’ve seen that meta-grounding, by itself, yields no conflict with the well-founded constraint, however one chooses to capture well-foundedness. In this section, we attempt to assess whether or not some further condition, in combination with meta-grounding, yields non-well-founded structures.
Suppose we want to list the complete grounds for a fact q. Let p ground q. The list of grounds of q should answer the question: “Why is it that q?” Here are two potential answers: (i) because p or (ii) because p and p grounds q. The intuition behind answer (ii) is that it is not in virtue of p alone that q is the case, but rather q is so because of p in conjunction with the fact that p metaphysically supports q. We can in fact formalize this intuition in the form of a condition on grounding structures. Those who believe that an answer of form (ii) is always correct will want to accept the following condition on grounding structures.
Proposition 2
(LC) For any facts p and q, if \(p \prec q\) , then \([p \prec q] \prec q\).Footnote 25
If a grounding structure satisfies the LC condition we will call it an LC-structure. Consider the world called Wonderland, whose grounding structure \(\langle \underline {Wonderland}, < \rangle \) is an LC-structure. The first thing to note about the grounding structure of Wonderland is that every non-fundamental fact has infinitely many grounds, since if \(p_{0} \prec q_{0}\), then \([p_{0} \prec q_{0}] \prec q_{0}\) and \([[p_{0} \prec q_{0}] \prec q_{0}] \prec q_{0}\) and \([[[p_{0} \prec q_{0}] \prec q_{0}] \prec q_{0}] \prec q_{0}\), etc.
Theorem 13
If a grounding structure is an LC-structure, then every grounded fact has infinitely many grounds.
This is an interesting result, but it is not immediately troubling. It’s certainly odd that every non-fundamental fact has infinitely many grounds. But the mere presence of a fact with infinitely many grounds yields no problem yet, as far as well-foundedness is concerned (Fig. 7).
Let’s also assume that Wonderland also satisfies the meta-grounding thesis - every fact about grounding at Wonderland is itself grounded. Is the grounding structure of Wonderland well-founded? Do grounding structures that satisfy both the LC-condition and meta-grounding thesis violate the well-founded constraint? First we notice that \(\langle \underline {Wonderland}, < \rangle \) is not finitely grounded.
Theorem 14
If a grounding structure satisfies meta-grounding and the LC-condition, and has at least one grounding fact, then it is not finitely grounded.
Proof
We need to show that if a structure satisfies meta-grounding and LC, then it has an infinite descending chain g 1, g 2, g 3, … such that g i grounds g i−1 for all i1. For any g i we demonstrate that there is a fact g i+1 that grounds g i . g i is a fact about grounding. By meta-grounding, there is some fact r i that grounds g i : \(r_{i} \prec g_{i}\). By LC, \([r_{i} \prec g_{i}] \prec g_{i}\). Let \(g_{i+1} = [r_{i} \prec g_{i}]\). Thus, for any g i there is a fact g i+1 that grounds g i . For every element in the chain there is an element that grounds it. The chain gets started by the assumption that there is at least one fact about grounding. Let g 1 be any such fact (Fig. 8). □
Even if Wonderland is very simple, containing only a single macroscopic object whose existence is grounded in facts about smaller particles, Wonderland will not be finitely grounded. The meta-grounding thesis, when applied to an LC-structure, yields an infinite chain of ground. When theorists assume that the claim that grounding facts are grounded leads to infinite descending chains of ground, they might be tacitly assuming that all grounding structures satisfy the LC-condition.
The LC-condition in combination with meta-grounding entails that a grounding structure is not finitely grounded. However, a grounding structure can satisfy both the LC-condition and the meta-grounding thesis and be either bounded from below or have a foundation.
Theorem 15
There are grounding structures that satisfy the LC-condition and the meta-grounding thesis while being bounded from below.
Proof
It is trivial to create models in which LC and MG are both satisfied and all chains are bounded from below. Any structure in which one fundamental fact F (perhaps [God exists]) grounds all other facts will suffice. □
Corollary 2
There are grounding structures that satisfy the LC-condition and the meta-grounding thesis while having a foundation.
Proof
This follows from Theorems 16 and 5, which says that structures that are bounded from below have a foundation. □
Finite grounding is not the most intuitive way to capture the intuitive ground-theoretic notion of well-foundedness. Given this fact, it’s very plausible that not even the combination of the LC-condition with the meta-grounding thesis results in a violation of the well-founded constraint on grounding structures. Grounding grounding looks to be in good shape.
6.2 For and Against LC
It remains interesting in itself to consider the LC-condition. We offer one argument for and one argument against accepting it as a requirement on ground. The argument against draws on an analogy with Carroll [7]’s story of what the tortoise said to Achilles. The condition is called ‘LC’ in honor of Lewis Carroll, because it reminds us of the position that the tortoise adopts. The tortoise’s endless request for extra premises is intuitively misguided – it’s p, and \(p \rightarrow q\), that yields q, not p, and \(p \rightarrow q\), and \((p \wedge (p \rightarrow q)) \rightarrow q\), and \(((p \wedge (p \rightarrow q) \rightarrow q) \rightarrow q\), and et cetera, ad infinitum. The LC-condition makes demands similar to the Tortoise’s. It requires that, if p \(\prec \) q, then also [p \(\prec \) q] \(\prec \) q, and [[p \(\prec \) q] \(\prec \) q] \(\prec \) q, et cetera, ad infinitum. The LC-condition results in every grounded fact having infinitely many grounds. In the same way, the tortoise’s position yields the result that every valid argument has infinitely many premises.
Carroll’s parable teaches us not to conflate the premises that entail a conclusion with the rule of inference (in this case modus ponens) by which we move from the premises to the conclusion. The Carrollian thought behind rejecting the LC-condition is that the grounding relation itself is like the inference rule by which we move from premises to conclusion, not like the premises that serve as input to the inference rule. It is true that every instance of grounding yields a fact about that instance of grounding, but the Carrollian line of thought is that this fact about grounding is not itself a ground of the grounded fact, but rather an ancillary fact. Likewise, the statement that \((p \wedge (p \rightarrow q)) \rightarrow q\) is not an implicit premise in every modus ponens argument from p and \(p \rightarrow q\) to q. The complex statement is true if and only if the modus ponens argument is valid but it does not enter in as rational justification for q. If this line of thought can be fleshed out it would suggest that that the LC-condition is not a general requirement on grounding structures.
The argument in favor of requiring the LC-condition revolves around a comparison with mereological composition. It has been thought by many that mereological composition is a grounding relation [4,20]. Wholes exist in virtue of their parts; the bicycle exists in virtue of its parts existing (and perhaps in virtue of some relations between those parts). If we ask, “Why is it that the bicycle exists?”, there are two potential answers. The first goes, “Because of the existence of its parts.” The second goes, “Because of the existence of the parts, and because the parts compose the whole.” The first answer is analogous to rejecting the LC-condition as a truth about ground, while the second answer is analogous to accepting it. The second answer is not uncommon in the literature on mereological composition. So thinking about mereological composition as a grounding relation favors accepting the LC-condition as a truth about grounding structures.
Both of these arguments are far from conclusive. Our only goal is to bring forth considerations that tell for and against adopting the LC-condition. We should be cautious about inferences from the case of mereological composition to the general case. Perhaps there are many grounding relations – perhaps composition is merely one species of the genus “grounding relation”. The LC-condition might describe the correct grounding structure for some members of this genus, but not for others. In any case, we recognize that some metaphysicians may have principled reason to accept the LC-condition as a requirement on grounding structures.
There are other conditions one might have principled reasons to require grounding structures to satisfy. We have focused on the LC-condition, since it seems to have something going for it and it leads to infinite descending chains (a topic in which we are already interested).
If one interprets the well-founded constraint on grounding as a requirement either that grounding structures be bounded from below or have a foundation (or something else of their ilk), we know of no well-motivated principles that combine with the meta-grounding thesis to produce a violation of the well founding constraint. We leave the hunt for such principles to others.
7 Conclusion
We started with an inchoate worry about grounding grounding, and about grounding structures in general: the hierarchy of ground must be well-founded. But what does ‘well-founded’ mean? We have studied three different, related, but non-equivalent candidates for a technical formulation of ‘well-founded’.
-
finitely grounded
-
bounded from below
-
has a foundation.
These three core notions bifurcate even further given the possibility of chains of partial and full ground, and the possibility of partial and full lower bounds for those chains.
There seem to be many grounding relations. Composition, constitution, realization, set membership, and causation are a few candidates.Footnote 26 There is a thought that at least some of these grounding relations must be well-founded; if they aren’t, they simply fail to ground. We have two methodological suggestions. First, we encourage the replacement of vague worries about well-foundedness with more specific worries about being finitely grounded, being bounded from below, and having a foundation. In Section 4.5 we complained about how contemporary theorists of ground run together these distinct notions. In all likelihood, most talk of “well-founded grounding” is indeterminate between these three types of structures. Second, we suggest a type of pluralism about grounding relations, and about the variety of well-foundedness they require. Perhaps there are many grounding relations, but different relations have different requirements with respect to how the grounding structure is founded. For the grounding relationship of set membership (if it is a grounding relation), perhaps the sets must be finitely grounded. As much is suggested by the mathematical definition of ‘well-founded set’. For composition, perhaps every grounding structure must be bounded from below, or satisfy the LC-condition. Other grounding relations might only need their structures to have foundations, potentially without being finitely bounded or bounded from below. Still others might not need to satisfy any variety of the well-founded constraint at all.
One of the main goals of this paper is to replace vague talk about “well-founded ground” with more specific talk about finite grounding, having a foundation, and being bounded from below. We leave it to particular theorists of ground, who are sympathetic to the well-founded constraint, to decide which of our three notions best suits their conception of well-found-ness and their target grounding relations.
What about grounding grounding? We have offered no argument that either (i) the facts about ground are, in general, grounded or (ii) the facts about ground are ungrounded. Structures that satisfy both the meta-grounding thesis and the LC-condition will fail to be finitely grounded, but need not fail to be bounded from below or have a foundation. This result is mitigated by two points. First, being finitely grounded (i.e. lacking infinite chains of ground) is plausibly not what most theorists have in mind when they claim that the grounding relation must be well-founded. Second, the LC-condition itself is quite controversial.
While we have not weighed in on the question of whether grounding is itself grounded, we have cleared the way. Much of the intuitive resistance to grounding grounding comes from a felt tension with the well-founded constraint. However one chooses to cache out the notion of a well-founded grounding structure, the meta-grounding thesis does not lead to structures that fail to meet any of the three conditions above. The tension between grounding grounding and the well-founded constraint is not real. It is merely felt. Grounding grounding can do better than survive under the long shadow of infinite regress. There is no shadow. Grounding grounding is ready to step into the sun.
Notes
A third possibility is that grounding facts aren’t the type of facts that can enter into grounding relations - they are somehow “outside” the hierarchy of grounding. On this picture, these facts are neither fundamental nor non-fundamental. Attempts to apply the notion of fundamentality to them, and the search for their metaphysical ground, involve a category mistake. Dasgupta [8] for such a view.
We leave open the possibility that the three examples involve different relations. There may be a genus - grounding - of which the relations in the three examples are species. Or there may be no such genus. Either way, we take the examples to involve conceptually, metaphysically, and formally similar relations that share enough important features that it makes sense to study them together. They all involve a metaphysical “in virtue of” claim. We shall, for the most part, speak as if there is one grounding relation (which we call ‘grounding’). But no substantive claims turn on this manner of speaking. In fact, we are sympathetic to the idea that there are many grounding relations, each governed by different principles. (Cf. Section 7 for more on this idea).
Schaffer [18].
Of course, some grounding facts might be grounded, others ungrounded. We do not consider this option, but that choice has negligible import here.
There is a meta-grounding thesis that says that all grounding facts are merely partly grounded. We don’t consider such a thesis here, mainly because we find it far less theoretically interesting.
The “grounding facts” we target are those facts in which the grounding relation is the “main connective”. Perhaps all such facts will be expressible using a sentence of the form ‘p grounds q’, where ‘p’ and ‘q’ refer to facts. These facts aren’t the same as the facts that contain the grounding relation. The fact that reading about grounding is fun contains the grounding relation, but isn’t a “grounding fact” in our sense. The meta-grounding thesis does not entail that the fact that reading about grounding is fun is grounded.
This result does require some minimal claims about the individuation of facts, and specifically about the relationship between sentences that express facts and the facts themselves. Without any guidelines whatsoever, it’s unclear that the facts \(p, g_{1}, g_{2}, g_{3}, \dots \) are distinct. Two assumptions enable the proof that these facts are distinct. First assumption: if fact P concerns grounding, and fact Q does not, then P and Q are not the same fact. Second assumption: if P and Q are both facts about grounding, then they are the same fact if and only if they relate the same two relata via the grounding relation. Both assumptions are tremendously plausible. These assumptions imply that, for each i, g i and g i+1 are not the same fact. The proof proceeds by induction.
We admit that even the claim that there are infinitely many mathematical facts requires some minimal assumptions about the individuation of facts. We’re willing to commit ourselves to the claim that any reasonable individuation of mathematical facts will yield the result that there are infinitely many mathematical facts (but not necessarily infinitely many fundamental, or ungrounded, facts).
Cameron [6], Schaffer [18–20], and Sider [21] all agree that non-fundamental, derivative, grounded facts are an “ontological free lunch”. The ontological commitments of a theory should be determined by measuring what the theory takes as fundamental, or ungrounded. The non-fundamental, derivative, or grounded posits of the theory incur no ontological cost. For a dissenting view, cf. Audi [2].
Cameron [5], Nolan [15], and Schaffer [17] for more on this topic. To add some fuel to the fire, we offer an example of a world whose grounds appear not to be well-founded.
Let the world Escher be a near-duplicate of the actual world, in so far as this is possible given the rest of the construction. Escher has microscopic fundamental particles, called fundamentons, facts about which ground the macroscopic facts about Escher. However, every fundamenton at Escher is itself a miniature replica of Escher. This miniature replica also contains fundamentons, which are themselves miniature miniature replicas. The 2 nd level of replicas is grounded in its fundamentons, which are themselves replicas of Escher. And so on ad inifinitum. You get the idea.
We see nothing wrong with the grounding structure of Escher. We’re liberal about modality, and see no reason to rule out a world like Escher as metaphysically impossible.
Importantly, we assume that the < part of a grounding structure 〈A, < 〉 includes all the facts about grounding, not just the facts about grounding relations between members of A. This is slightly odd, but makes the definitions simpler and exposition clearer.
This definition requires us to divide up the grounding facts from the non-grounding facts. Cf. footnote 7.
This would be structurally similar to what Hans Herzberger called “groundlessness”, which he describes as being like “the bureaucratic regress in which each clerk endlessly refers you to the next to settle your accounts” [14].
A binary relation R is well-founded on a domain D iff every non-empty subset of D has a minimal element with respect to R. Assuming the axiom of dependent choice (thanks to an anonymous referee for pointing out this need), this is equivalent to the descending chain condition on partially ordered sets, which demands that there be no infinite descending chains. A set S is a well-founded set iff the set membership relation is a well-founded relation on the transitive closure of S.
Bennett [3] claims that the ground of g 0, i.e. p < q, is p itself. She claims that, in the general case, when A grounds B, A also grounds the fact that A grounds B, and the fact that A grounds the fact that A grounds B, etc. Such a structure provides another example of a grounding structure that satisfies the meta-grounding thesis without generating infinite descending chains.
The grounding relation on a non-finitely grounded structure will fail to be well-founded in the relation- or set- theoretic sense. The grounding relation on that structure will not be a well-founded relation precisely because it contains infinite chains. On such a structure, grounding will not provide a well-founded partial ordering. Schaffer [18]: 376 demands that grounding provide such an ordering. Thus, non finitely-grounded structures may run afoul of the Schafferian well-founded constraint.
We don’t think this point should be that controversial. Cameron [5]: 4 certainly appears to agree. He writes, “The intuition under discussion [well-foundedness] does not demand that we should be able to reach the ultimate ontological ground in a finite number of steps... It demands only that there is a fundamental ground. This is compatible with a situation where no entity depends directly on that fundamental ground, but every entity has a chain of dependence with an infinite number of steps taking that entity to the ultimate ground.” Not every philosopher is as careful as Cameron in discussing what the well-founded constraint amounts to. It’s common to hear or read the constraint glossed as a ban on infinite descending chains of ground.
One need not believe in infinitely disjunctive facts in order to generate structures that have a foundation but are not bounded from below. We choose the case of infinite disjunction to provide a concrete illustration of a formal claim.
In fairness to Schaffer, he says only that well-foundedness is imposed by requiring that all priority chains terminate. One can reasonably interpret Schaffer as endorsing only the mild conditional that if all priority chains terminate, then grounding is well-founded, rather than claiming that well-foundedness amounts to all priority chains terminating. We agree with the conditional. Theorem 4 and Corollary 8 demonstrate that any structure that is finitely grounded, i.e. in which all priority chains terminate, is also bounded from below and has a foundation. It is thus well-founded in all three senses.
Thanks are to due here to an anonymous referee.
The type of foundation defined here is a foundation that fully grounds a set of facts. On could define the notion of a partial foundation - a set of perfectly fundamental facts that at least partly grounds every member of the facts founded thereby. Such a notion might serve some theoretical purposes. However, we think it clear that a partial foundation is not what anyone who favors a well-founded constraint on ground is after. We do not investigate partial foundations here.
Bennett [3]: 36-7 discusses something quite close to the LC-condition. She motivates the principle in much the same way we do. However, her discussion is limited to deflecting an LC-motivated objection to her super-internality principle, which says that if p < q then p<[p < q]. Our discussion of LC is independent of super-internality.
Bennett [4] for a good overview.
References
Armstrong, D.M. (1997). A World of states of affairs. Cambridge: Cambridge University Press.
Audi, P. (2012). A clarification and defense of the notion of grounding. In F. Correia, B. Schneider (Eds.), Metaphysical grounding: understanding the structure of reality. Cambridge University Press.
Bennett, K. (2011a). By our bootstraps. Philosophical Perspectives, 25(1), 27–41.
Bennett, K. (2011b). Construction area: No hard hat required. Philosophical Studies, 154(1), 79–104.
Cameron, R. (2008a). Turtles all the way down: regress, priority and fundamentality. The Philosophical Quarterly, 58(230), 1–14.
Cameron, R.P. (2008b). Truthmakers and ontological commitment. Philosophical Studies, 1(140), 1–18.
Carroll, L. (1895). What the tortoise said to achilles. Mind, 4, 278–80.
Dasgupta, S. (forthcoming). The possibility of physicalism. The Journal of Philosophy.
deRosset, L. (2013). Grounding explanations. Philosophers’ Imprint .
Dixon, S. (forthcoming). What is the well-foundedness of ground? Mind.
Fine, K. (1995). Ontological dependence. Proceedings of the Aristotelian Society, 95, 269–290.
Fine, K. (2001). The question of realism. Philosopher’s Imprint, 1, 1–30.
Fine, K. (2012). A guide to ground. In F. Correia, B. Schneider (Eds.), Metaphysical grounding: understanding the structure of reality. Cambridge University Press.
Herzberger, H. (1970). Paradoxes of grounding in semantics. The Journal of Philosophy, 67(6), 145–167.
Nolan, D. (2001). What’s wrong with infinite regresses. Metaphilosophy, 32, 523–538.
Rosen, G. (2010). Metaphysical dependence, grounding, and reduction. In B. Hale, A. Hoffman, (Eds.), Modality: metaphysics, logic, and epistemology. Oxford University Press.
Schaffer, J. (2003). Is there a fundamental level? Nous, 37(3), 498–517.
Schaffer, J. (2009). On what grounds what. In D. Chalmers, D. Manley, R. Wasserman, (Eds.), Metametaphysics. Oxford: Oxford University Press.
Schaffer, J. (2010a). The internal relatedness of all things. Mind, 119(474), 341–376.
Schaffer, J. (2010b). Monism: The priority of the whole. The Philosophical Review, 119(1), 31.
Sider, T. (2012). Writing the Book of the World, Oxford University Press.
Acknowledgments
Thanks for helpful comments and discussion to Karen Bennett, Jonathan Cusbert, Louis deRosset, Kit Fine, Holger Thiel, Daniel Nolan and participants in Karen Bennett’s metaphysics seminar at NYU in autumn 2010. Thanks also to audiences at the Conference on the Philosophy of Kit Fine, Sinaia, Romania, May 2012, the 2012 meeting of the Australasian Association of Philosophy in Dunedin, New Zealand, and the “Fundamentality and Metaphysical Infinitism” Workshop at the University of Helsinki, June 2014.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rabin, G.O., Rabern, B. Well Founding Grounding Grounding. J Philos Logic 45, 349–379 (2016). https://doi.org/10.1007/s10992-015-9376-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-015-9376-4




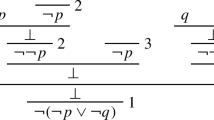



 functions to label which fact about grounding g
i
is, while the arrows emanating to and from
functions to label which fact about grounding g
i
is, while the arrows emanating to and from  demonstrate the grounding relations into which g
i
enters)
demonstrate the grounding relations into which g
i
enters)



 labels which fact about grounding p
i
is, while the arrows emanating to and from
labels which fact about grounding p
i
is, while the arrows emanating to and from
 represent the grounding relations into which p
i
enters)
represent the grounding relations into which p
i
enters)