Introduction

Anthropogenic landscape alteration can result in both habitat loss (a reduction in the proportion of a landscape composed of suitable habitat for a focal species, commonly measured as reduced habitat amount) and habitat fragmentation (a change in the arrangement or configuration of the remaining habitat such as increased edge density, or reduced core area). Because habitat loss and fragmentation are inevitably correlated to some degree, they are often combined into a single concept—“habitat loss and fragmentation” (Ewers and Didham 2006, 2007) or even simply “fragmentation” (e.g., Gelling et al. 2007). However, in the context of landscape planning for conservation, combining these two processes may be counter-productive, because: (1) they can be managed independently to some degree (e.g., creating corridors to link existing habitat patches could have a strong effect on fragmentation but a comparatively weak effect on habitat amount); and, (2) their effects on populations and biodiversity may be different in magnitude and even direction (e.g., creating corridors may have a positive influence on a population through increased connectivity but have a concurrent negative influence through increased edge habitat in the landscape; Fahrig 2003). As a result, it is important to understand their independent effects so that management recommendations result in the most efficient and effective use of limited conservation resources (Lindenmayer and Fischer 2007; Sutherland et al. 2004).

The current understanding of the relative importance of habitat loss and fragmentation is limited because of the high degree of correlation between them (McGarigal and Cushman 2002; Fahrig 2003). Indeed, Koper et al. (2007) recently demonstrated that one of the most common statistical approaches for separating their effects—residual regression—is highly biased. The approach involves using the residuals of a regression of one correlated predictor on another as an orthogonal predictor in a classic regression framework (see Koper et al. 2007 for a detailed review). If residuals are used to create a measure of fragmentation that is orthogonal to habitat amount (or vice versa), the assessment of relative importance may be inherently biased towards habitat amount (or fragmentation). Presumably, any shared effect is allocated to amount which is usually the intact (i.e., non-residual) predictor (Freckleton 2002). In some contexts, an a priori bias may be appropriate (e.g., if habitat amount is inherently easier to manage but see Ewers and Didham 2007); however, these residual regression studies have also been incorrectly cited as evidence that amount is more important than fragmentation (e.g., in Flather and Bevers 2002; Fahrig 2003; Turner 2005).

The bias inherent in residual regression may be even more complicated than has been suggested. The presumed bias towards habitat amount assumes that the effects of habitat amount and fragmentation on biodiversity do not conflict, but they may. For example, if an increase in habitat amount has a positive effect on biodiversity but is positively correlated with a measure of fragmentation that has a negative effect, then the two processes will conflict and suppress (mask) each other’s effects. Variables that have these conflicting effects (opposite qualitative effects and a positive correlation or similar qualitative effects and a negative correlation) are referred to as suppressor variables (Cohen and Cohen 1983). In these conditions, residual regression may underestimate both effects. In addition, suppressor effects likely influence other statistical methods. For example, if an influential suppressor variable is removed from a multiple regression, the effects of the remaining predictor will be underestimated (Legendre and Legendre 1998). These serious consequences should clearly be addressed in comparing the relative effects of habitat loss and fragmentation.

There are many statistical approaches for estimating the relative effects of correlated predictor variables such as habitat amount and fragmentation (Graham 2003; Burnham and Anderson 2002; Gromping 2007) but synthesizing the literature is difficult if previous results have been determined by the statistical methods rather than the actual biological effects. Therefore, in this paper we have three objectives: (1) to review the statistical methods that have been used to estimate the relative importance of habitat amount and fragmentation; (2) to compare the accuracy and precision of these different statistical estimates of relative importance under identical conditions using simulated but realistic data; and (3) to make recommendations on the best approaches to use in future studies. In our simulations, we compared 7 statistical methods: standard multiple regression, residual regression, variable or model selection, two multi-model inference measures (sensu Burnham and Anderson 2002), and two variance partitioning approaches.

Methods

Literature review

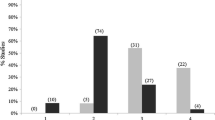
We searched the literature for studies that compared the effects of habitat amount and fragmentation on an ecological response variable. After excluding patch-scale studies (sensu Fahrig 2003), our review included 33 empirical studies that compared the relative effects of habitat amount and fragmentation, measured at the landscape scale. We reviewed the statistical methods used in the studies and the conclusions on which (habitat amount or fragmentation) was more influential.

The studies in our review employed some combination of 6 statistical tools to evaluate the relative importance of fragmentation and amount. These included: (1) residual regression, (2) variable or model selection procedures (stepwise significance or AIC-based selection), (3) averaged coefficients that account for uncertainty in model selection, (4) summed Akaike weights [3 and 4 relate to multi-model inference (MMI); Burnham and Anderson 2002], (5) classical variance partitioning, and (6) hierarchical variance partitioning (HVP, Chevan and Sutherland 1991). We categorized metrics from these methods as either “confidence metrics” (i.e., those that estimate the confidence or uncertainty in a particular predictor’s effect, based on either statistical significance or the inclusion of a predictor in a best or final model) or “strength metrics” (i.e., those that estimate the relative strength of a predictor’s effect, based on a regression coefficient or an estimate of explained variation).

Simulations

Landscapes variables

We used 350 real landscapes to provide the landscape variables used in our simulations. The landscapes were 10 × 10 km regions of Southern Ontario, Canada; which were clipped from a pre-existing, landcover map of the province with 28 classes and 30 m cell-resolution (OMNR 1998). We used four landscape variables in our simulations. One variable represented habitat amount (“Amount” = the area of forest cover). Two variables represented habitat fragmentation; habitat edge (“Edge” = length of the edge between forest and all non-forest landcover) and mean patch size (“MnPatch” = average size of forest patches). A fourth variable represented the heterogeneity of natural landcover (“Hetero” = number of natural, landcover classes present in the landscape). This fourth variable could be grouped with habitat amount in the broader category of landscape composition variables but in our simulations, it primarily serves to demonstrate the effects of variables that are less strongly correlated (r ~0.5). For the first three measures, the original landcover data was reclassified into a binary, forest/non-forest landscape. For the fourth measure (Hetero), the original landcover classification was used. We chose these variables because they are relatively common in landscape ecology studies and they are correlated in these landscapes (Fig. 1).

Fig. 1
figure 1

Correlation matrix of standardized landscape predictor variables (n = 350). Numbers in parentheses are the variance inflation factors for each predictor, and numbers below the diagonal are Pearson correlation coefficients for all predictor pairs

Full size image

In our simulations, Edge acts as a suppressor variable because all predictors are positively correlated (Fig. 1) but Edge’s effects are opposite in sign to all other predictors (i.e., negative). As an example of this suppressor relationship, a regression coefficient for Amount would be effectively zero when \( Y = a + 2.0 * {\text{Amount}} - 2.0 * {\text{Edge}} + \varepsilon \) is regressed on Amount only, because the effects of Edge on Y suppress those of Amount (and vice versa). However, if Y is regressed on both predictors then the partial regression coefficients are accurate (|β| = 2.0).

We used both the pair-wise correlation matrix among all predictors as well as each predictor’s variance inflation factor (Neter et al. 1990) to quantify collinearity. Variance inflation factors (VIF) were calculated for each predictor as the inverse of the coefficient of non-determination (1/(1−R 2)) for a regression of that predictor on all others. VIF is a positive value representing the overall correlation of each predictor with all others in a model. Generally, VIF >10 indicate “severe” collinearity (Neter et al. 1990).

We used real landscapes because we wanted a realistic representation of the covariance structure among predictor variables in empirical studies of habitat loss and fragmentation. We limited our selection of landscapes to 350 that contained <30% habitat cover because theoretical studies suggest that fragmentation effects should be most evident in landscapes with low habitat amount and therefore questions of relative importance are most relevant here (Fahrig 1998; Flather and Bevers 2002) and the relationships between many fragmentation metrics and habitat amount are simplified in this range (approximately linear instead of curvilinear). We standardized all predictors to a mean of 0 and a standard deviation of 1.0 so that equal coefficients implied equal effect-strength and to simplify expected variance partitions for each predictor.

Simulated response data

We generated simulated response data for all 350 landscapes, using a linear equation with coefficients of known value (e.g., Y = a + β 1 Amount + β 2 Fragmentation + ε). The values of these response data could be interpreted as a measure of average abundance of a species within each landscape or any other response with an approximately normal distribution. We used each of the following linear equations to represent 6 true models:

$$ Y_{\text{aeph}} = a + 2.0 * {\text{Amount}} - 2.0 * {\text{Edge}} + 2.0 * {\text{MnPatch}} + 2.0 * {\text{Hetero}} + \varepsilon $$
$$ Y_{\text{ae}} = a + 2.0 * {\text{Amount}} - 2.0 * {\text{Edge}} + \varepsilon $$
$$ Y_{\text{ap}} = a + 2.0 * {\text{Amount}} + 2.0 * {\text{MnPatch}} + \varepsilon $$
$$ Y_{\text{a}} = a + 2.0 * {\text{Amount}} + \varepsilon $$
$$ Y_{\text{e}} = a - 2.0 * {\text{Edge}} + \varepsilon $$
$$ Y_{\text{p}} = a + 2.0 * {\text{MnPatch}} + \varepsilon $$

.

The subscripts indicate “influential predictors”—predictors used to create the relevant simulated response (e.g., “e” in Y e refers to Edge). “Uninfluential predictors” are those that were not used to create a particular response (e.g., Edge in Y ap). The error term (ε) was normally distributed with mean of zero and a variance adjusted so that a correct statistical model (i.e., one that included the same predictors as the true model) explained approximately 50% of the variation in the response. Response data from each of the 6 true models were replicated 100 times. Among the 100 replications, only the random values of the error (ε) in the linear equation varied.

Comparing statistical methods

To compare the different statistical methods, the simulated response data from each of the 6 true models were analyzed using each of the 7 statistical methods of relative importance (i.e., partial coefficients from a multiple regression, plus the methods identified in our literature review). We assessed the accuracy (in comparison to the true value) and variation across the 100 replications in the estimates of relative importance from each statistical method (i.e., the mean and variation in the; partial coefficients, relative proportion of variance explained, or relative importance according to the summed Akaike weight). Finally, each of the 7 statistical methods were compared under each of 3 conditions, by varying which predictors were included in the statistical analyses for each true model: (1) correct predictors—the analysis contained all of the influential predictors and no uninfluential predictors; (2) too many predictors—the analysis contained all of the influential predictors as well as some uninfluential predictors; and (3) too few predictors—the analysis contained only a subset of the influential predictors. The entire simulation experiment consisted of 7 statistical methods applied under 3 different conditions to simulated data created under 6 true models where the data creation was replicated 100 times.

All simulations were conducted using R statistical software (www.r-project.org) with additional packages for some of the specific statistical analyses including “hier.part” for HVP and “MuMIn” for MMI calculations across all possible sub-models (available online at: http://r-forge.r-project.org/projects/mumin/).

Results

A majority of the studies that we reviewed found that habitat amount was generally more important than fragmentation in determining the effects of landscape structure on biodiversity (Table 1). There were no clear trends in published results that would suggest particular methods were more likely than others to find amount or fragmentation most important. Additional results of the literature review are in the following, method-specific sections.

Table 1 Summary of results and the statistical methods used in studies that have measured the relative effects of habitat loss and fragmentation
Full size table

Partial coefficients from a multiple regression

This approach was not used on its own in any of the reviewed studies, yet we found that multiple regression coefficients were unbiased estimates of effect strength when the correct predictors were available (Fig. 2A) and also when too many predictors were available (Fig. 2D). However, as for all methods, coefficients were biased if too few predictors were available. If the missing predictor was not a suppressor, then the absolute values of the coefficients were over-estimated (see Amount in Fig. 3A). If the missing predictor was a suppressor, then the absolute values of the coefficients of the included predictors were underestimated (Fig. 3B). In both cases, the coefficients were biased to a degree dependent on their correlation with the missing predictor.

Fig. 2
figure 2

Partial regression coefficients from three statistical methods were unbiased estimates of effect strength, even with highly correlated predictor variables. Estimates were unbiased for—(1) multiple regression (A, D), (2) the best model selected using AIC in a step-wise variable selection (B, E), and (3) the MMI averaged coefficients (C, F)—when the influential predictors were available (i.e., correct predictors A–C or too many predictors D–F). Points and error bars indicate the mean partial regression coefficients and 95th percentiles from 100 replications of simulated Y data. True Y indicates the influential predictors (see text for definition). Horizontal dotted lines indicate the true effect strength and any arrows show deviations of the means from it. %sig indicates the percent of replications where each predictor’s regression coefficient was significantly different from zero (P < 0.05), % incl indicates the percent of replications where each predictor was included in the best model, and % excl indicates the percent of replications where each predictor was excluded from at least one of the supported models (i.e., ΔAIC < 4)

Full size image
Fig. 3
figure 3

Partial regression coefficients were biased if influential predictors were missing from the model and the strength and direction of bias depended on suppressor relationships. In A, the missing influential predictors were non-suppressors and therefore the most highly correlated predictor (Amount) was overestimated. In B, one of the missing influential predictors (Edge) was a suppressor and therefore the most highly correlated predictor (Amount) was underestimated. Partial regression coefficients from a multiple regression are shown here but the same bias applied to all three coefficient-based estimates included in Fig. 2. See Fig. 2 for explanation of text and symbols in the plot

Full size image

Residual regression

Residual regression was used in 10 of the 33 studies we reviewed (Table 1). All 10 used residuals for the fragmentation variables, leaving the habitat amount variables intact and were therefore supposedly biased towards the effects of habitat amount. However, this bias was not evident in the results. Indeed, only 50% of the residual regression studies, compared to approximately 70% of the remaining studies, concluded that amount was more important than fragmentation (Table 1).

In our simulations, if the amount and fragmentation predictors had similar effect directions and were positively correlated then residual regression overestimated the importance of the intact predictor and underestimated the importance of the residual predictor (Fig. 4B) as suggested by Koper et al. (2007). However, if the two predictors had a suppressor relationship (e.g., Amount and Edge), the importance of both predictors was underestimated (Fig. 4A). In addition, with a suppressor relationship, the presumed bias in residual regression was actually reversed because the residual predictor’s coefficient was less underestimated than the intact predictor’s (i.e., the residual predictor was more likely to be significant and had a larger coefficient value, Fig. 4A).

Fig. 4
figure 4

Residual regression is biased but the bias depends on suppressor effects. With suppressor effects (A), both amount and fragmentation effects are underestimated and the analysis is biased towards the residual predictor whether fragmentation (left side of A) or amount (right side of A). When there is no suppressor relationship (B) the analysis is biased towards the intact predictor. The prefix “R.” indicates the residual predictor in each of the 4 separate analyses. See Fig. 2 for explanation of text and symbols

Full size image

Variable/model selection

Fourteen of the studies in our review used some sort of stepwise selection procedure to identify important variables for inclusion in a final or best model (Table 1). Some (but not all) studies took steps to limit correlations among predictors to avoid potentially spurious models (Kruskal and Majors 1989; Clark and Troskie 2006). This was generally done by removing one of a pair of correlated predictors from the model (either during the stepwise selection or before the analysis by removing one of each pair of highly correlated predictors). No studies provided estimates of potential effect strength for any of the removed predictors.

In our simulations, we used AIC to choose the best model from among all possible combinations of a global model (i.e., a model that includes all of the available predictors). When the correct predictors were available, this approach almost always selected the global model (i.e., the correct model, Fig. 2B). When too many predictors were available, the best model included uninfluential predictors at least 14% of the time (Fig. 2E). However, this inclusion of uninfluential predictors did not strongly bias the regression coefficients of the influential variables. If too few predictors were available, the influential predictors were retained in the best model but the coefficients were biased in the same way as partial coefficients from a multiple regression (Fig. 3).

Weighted mean coefficients

Ten of the studies we reviewed used coefficients averaged across models to estimate relative importance (Table 1). In MMI, these averaged coefficients are a strength metric for each predictor, which is calculated as the weighted mean partial regression coefficient, averaged across all supported models (i.e., models for which Akaike weight >0.05, or ΔAIC <4) and weighted by the Akaike weight (an estimate of the support for each model in the data, Burnham and Anderson 2002). In our simulations, when the influential predictors were available (i.e., the correct predictors or too many predictors), this method generated unbiased estimates but the variance around the estimates was slightly higher than for other coefficient-based approaches (compare Fig. 2C, F). When too few predictors were available, the coefficients were biased in the same way and to the same degree as for the model selection and multiple regression approaches (results similar to those in Fig. 3).

Summed Akaike weights

The same ten studies that used MMI averaged coefficients, also included a confidence metric for each predictor, which was calculated as the sum of the Akaike weights for all supported models that include each predictor (“variable importance” sensu Burnham and Anderson 2002). With this metric, if there are numerous competing models for which there is some support, then variables that are included in models with higher weights and/or included in more of the supported models will be ranked higher in relative importance. This measure is biased towards predictors that are included in more candidate models (Burnham and Anderson 2002, p. 169) but we found no acknowledgement of this potential bias in the reviewed studies.

In our simulations, the summed Akaike weight was a liberal confidence metric, in that uninfluential predictors were always allocated some importance. Although the average estimate was generally lower for uninfluential predictors, there was much variation and in some replications uninfluential predictors received very high importance scores (Fig. 5B). In addition, this metric underestimated the importance of influential predictors that were more highly correlated (e.g., Amount and Edge in Fig. 5A).

Fig. 5
figure 5

Summed Akaike weights overestimated the importance of uninfluential predictors (B) and in some replications, underestimated the importance of influential predictors that were more highly correlated (A). Text below each figure indicates range in the number of supported models (i.e., ΔAIC < 4) across 100 replications and the percent of replications for which more than 1 model was supported. Points and error bars indicate the mean summed Akaike weights and 95th percentiles from 100 replications of simulated Y data. See Fig. 2 for explanation of other text and symbols

Full size image

Classical variance partitioning

Five of the reviewed studies partitioned the variation in the response into portions that were explained independently by each predictor and portions that were shared among predictors (Legendre and Legendre 1998, p. 528). These studies used this approach to estimate effect strength and importance of predictors in a full model, by comparing the size of the independently explained portions. However, when the predictors are highly correlated, then the independent portions represent only a fraction of the predictor’s true effect or importance.

In our simulations, this approach could generally distinguish between influential and uninfluential predictors but the ranking of influential predictors was biased. Uninfluential predictors did not, on average, explain any of the variation independently (Fig. 6A). In contrast, even highly correlated influential predictors were always allocated a non-zero share. However, the ranking of influential predictors was highly dependent on the correlations among predictors. When all four predictors contributed an equal share (25%) to the response (i.e., Y aeph) the average across all 100 replications of the independently explained variation for each predictor ranged from 4 to 21% (Fig. 6A).

Fig. 6
figure 6

Independent variance partitions were biased estimates of effect strength for all true models in all conditions (Classical, A–D and HVP, E and F). Classical variance partitioning underestimated the effects of influential predictors (A and B) but was unbiased for uninfluential predictors (B). If missing influential predictors were not suppressors, the effects of some predictors were overestimated (C) and when missing influential predictors were suppressors the effects of the remaining predictors were underestimated (D and Edge in C). HVP estimates were biased for influential and uninfluential predictors (E and F) and were particularly biased against suppressors (Edge in E). Points and error bars indicate the mean and 95th percentiles from 100 replications of simulated Y data of the percent of the variation explained by the model that is independently attributed to each predictor. See Fig. 2 for explanation of text and symbols

Full size image

As for all methods, this approach was also biased when too few predictors were available but the type of bias depended on suppressor effects. The importance of influential predictors was underestimated in all situations (Fig. 6A, B, D) except when a substantial, non-suppressor variable was missing from the analysis (Fig. 6C). In that case, the importance of the modeled predictor with similar qualitative effects as the missing predictor was overestimated because it was allocated the explanatory power of the missing predictor while the modeled predictor with different qualitative effects (suppressor relationship) was not. In contrast, when the missing predictor had a suppressor relationship with both retained predictors neither took on its explanatory power; instead, the missing predictor’s effect reduced the variation explained by all retained predictors (Fig. 6D).

Hierarchical variance partitioning

The HVP approach was applied in 4 of the 33 studies (Table 1). HVP decomposes all of the variation explained by the full model (including the shared component) into components that can be allocated to individual predictors (Chevan and Sutherland 1991). HVP partitions the shared components of the full model by assuming that shared component within each hierarchical level of all possible sub-models can be divided equally among correlated predictors. HVP is one of a number of closely related metrics of relative importance that are more commonly applied in the social sciences (Kruskal 1987; Gromping 2007).

In our simulations, the strength estimates from HVP analyses were strongly affected by both the predictor’s correlation with other predictors and the direction of its effect. When all predictors had equal absolute effects on the response (i.e., Y aeph, Fig. 6E), importance was overestimated for those that were less correlated and had positive effects (i.e., MnPatch and Hetero) and underestimated for those that were more correlated and had positive effects (i.e., Amount). Importance of the suppressor variable Edge was greatly underestimated. HVP always allocated some of the explained variation to every predictor in the model, even uninfluential ones (Fig. 6F). The importance was consistently overestimated for the following three groups: uninfluential predictors, predictors that were less correlated than the others (lower VIF), and all predictors when influential, non-suppressor predictors were missing from the analysis.

Discussion

Comparing methods

The main finding of our simulation experiment was that standard multiple regression performed as well or better than all of the methods that have been used to account for collinearity. Standardized partial regression coefficients within a reasonably well specified model are useful measures of effect strength even for correlated predictors. Within the range of true models and conditions that we simulated, standardized partial regression coefficients of highly correlated predictors were unbiased whether from a straight-forward multiple regression, the best model identified by AIC, or averaged across all supported models using MMI in an information theoretic framework—although the MMI approach slightly increased the variance around the estimate (Fig. 2). Perhaps the strong performance of multiple regression should not come as a surprise since there is a long history of using regression to control for potentially confounding effects and continuous predictors are almost always correlated to some degree (Legendre and Legendre 1998). However, considering the added complexity from many statistical manipulations intended to remove collinearity or the alternative methods intended to circumvent the issue, it is remarkable that these efforts may be worse than doing nothing at all.

Even though collinearity causes high variance around partial regression coefficient estimates and reduced statistical power (Neter et al. 1990; Graham 2003), our simulations suggest that the alternatives to multiple regression have similar or even worse problems. The summed Akaike weights of highly correlated predictors were underestimated and more highly variable than for less correlated predictors (Fig. 5). In addition, the estimates from variance partitioning approaches and residual regression were both highly variable and biased (Figs. 4, 6). By contrast, although more correlated predictors were more likely to be found erroneously insignificant (i.e., increased Type II error—reduced statistical power), in the context of our simulations, multiple regression identified even the most highly correlated influential predictors as statistically significant in >90% of the replications (Fig. 2).

Ecologists have been trained to remove collinearity from ecological regression models, in part, because of suggestions that collinearity causes “biased” coefficient estimates (Petraitis et al. 1996; Graham 2003). However, in our simulations partial regression coefficients were unbiased for influential predictors, even when the predictors were highly correlated. The difference between our results and the results of these previous studies is entirely due to interpretation. Interpreting partial coefficients as “biased” assumes that the simple or univariate coefficient of each predictor with the response represents the “truth”. In fact, if the two correlated predictors have additive functional relationships with the response (e.g., distinct ecological processes such as population size and negative edge effects), then the partial coefficients are the best representation of the true effects and the univariate coefficients are the “biased” estimates. We only observed bias in the partial regression coefficients when an important confounding effect was missing from the model; and indeed, this was true for all methods. Controlling for confounding effects requires knowledge of the relevant ecological processes in the system being studied and clear links between those processes and the predictor variables in the statistical model.

Residual regression studies are known to have predictable bias (Koper et al. 2007) but our results show they may also be biased in unexpected ways. Residual regression is biased towards the intact variable (usually habitat amount) if the effects of amount and fragmentation do not conflict (i.e., conditions that lead to box B in Fig. 7 and similar to the bias shown in Koper et al. 2007). However, effect strength and statistical significance in published studies may have been underestimated for both amount and fragmentation if the variables were suppressors (i.e., conditions that lead to box A in Fig. 7). Indeed, some published estimates may even have been biased in favor of the residual variable (usually fragmentation), because our simulations suggest the residual variable’s effect is less underestimated than the intact variable. Therefore, even if a researcher had wished to impose an initial priority on one of the variables, residual regression may have given inaccurate results. Suppressor effects may explain why the results of studies that used residual regression did not reflect the presumed bias of habitat amount over fragmentation (Table 1). Our results cast serious doubt on previous research that applied residuals to distinguish between the effects of habitat fragmentation and amount.

Fig. 7
figure 7

The bias in residual regression depends on suppressor effects (i.e., the correlation between amount and fragmentation and whether the fragmentation measure has a positive or negative effect on the response). This figure shows the qualitative bias in published studies that used residual regression to create fragmentation metrics orthogonal to habitat amount. The strength of the bias is directly related to the magnitude of correlation between the original predictors in the published study. If habitat loss was measured instead of amount, a negative effect of loss on the response would be expected. In this case, switching the contents of boxes A and B would show the resulting bias

Full size image

Partitions of independently explained variation should be avoided as measures of the relative effects of amount and fragmentation because they reveal as much about the correlation structure among predictors as their relative effects. When true effects were identical across predictors, the classical independent variance partitions ranked the predictors according to their level of correlation with the other predictors. The independent partitions were approximately what would be expected considering the correlation structure of the predictors but they did not accurately represent the true independent contributions of each predictor. Similarly, estimates of relative importance using HVP depended on how correlated a predictor was but were further biased by the direction of a predictor’s effect (i.e., underestimated for highly correlated predictors and suppressor variables and overestimated for others). The flaw in using partitions of independently explained variation as estimates of importance is that they combine estimates of effect strength and confidence. It is not clear from an independent variance partition (classical or HVP) whether a variable has a strong but uncertain effect or a certain but weak effect. In a management context, this distinction is clearly important. Less confounded metrics of effect strength (such as coefficient-based estimates) presented in combination with confidence estimates (such as summed Akaike weights or the coefficient’s confidence intervals) will be more informative than estimates of explained variation.

Toward a synthesis

Future studies of the relative importance of amount and fragmentation should explicitly report both the variance inflation factor for each predictor and the pair-wise correlations among all predictors. Without this information, we could not synthesize the literature in our review while accounting for the biases identified here. Many studies reported only a maximum, pair-wise correlation coefficient (e.g., r < 0.8), or removed predictors that were “highly” correlated with another predictor in the analysis using an arbitrary cut-off value for pair-wise correlations (usually r > 0.5–0.7). These simple criteria give no information on the remaining correlations, which may still influence results. Indeed, considering only pair-wise correlations may not actually reduce the statistical problems caused by collinearity. Complicated relationships among predictors can result in large increases in error around coefficient estimates for predictors that nonetheless have very low pair-wise correlations with all other predictors (Neter et al. 1990).

We did not find a single reference to potentially conflicting effects of correlated predictors (suppressor effects) in any of the reviewed studies. However, suppressor effects have very likely influenced the results of studies that used residual regression or HVP; they may also have led to underestimates of effect strength for retained variables in any of the methods, if one of a pair of suppressor variables was removed from the analysis because it was “highly correlated”. In an ecological context, suppressor variables may represent important effects. For example, increasing habitat amount may have a positive effect on a population through an increase in population size but the concurrent increase in edge length may have a negative effect that acts through an unrelated mechanism (e.g., increases in mortality rates from predators that use habitat edges). In conditions of conflicting ecological processes, using residual regression, HVP, or arbitrarily removing one of a pair of highly correlated variables from a regression model, will give biased estimates of relative importance.

Confronting collinearity

There are two considerations that should inform decisions on including particular variables in future studies of the relative effects of habitat amount and fragmentation. First, if two predictors are thought to represent distinct ecological processes or mechanisms then both should be included in the analysis. An understanding of the important ecological processes and mechanisms is essential if statistical modeling is to advance ecological understanding (MacNally 2000). Removing variables simply because they are highly correlated with each other or have a weak univariate correlation with the response can lead to uncontrolled, confounding effects that decrease the explanatory power of the final model and generate biased measures of effect strength. Second, the direction of the effect and the correlation between two variables must be considered. If two predictors have a suppressor relationship (i.e., opposite qualitative effects and a positive correlation or similar qualitative effects and a negative correlation), removing one will underestimate the effects of the remaining predictor. If two predictors do not have a suppressor relationship (i.e., similar qualitative effects and a positive correlation or opposite qualitative effects and a negative correlation), removing one will overestimate the effects of the other. If these two considerations are followed, standardized partial regression coefficients will be unbiased estimates of the relative importance of amount and fragmentation, even when predictors are highly correlated.