Introduction

It is now generally agreed that the molecular mechanism of muscle contraction is driven by a rotation of the lever arm of myosin-S1 (a ‘working stroke’) when bound to actin. This ‘swinging lever-arm’ model (Huxley 1974; Squire 1994; Holmes 1997) is supported by a host of mechanical experiments (Woledge et al. 1985), firstly the tension response to length steps (Huxley and Simmons 1971; Ford et al. 1977; Lombardi et al. 1992) and, more recently, optical trap experiments with a single molecule of myosin-S1 (Finer et al. 1994; Veigel et al. 1998; Steffen et al. 2001) or a single myosin cofilament (Kaya and Higuchi 2010). The biochemical cycle of actin, myosin and ATP has been extensively studied, supporting the original proposal of Lymn and Taylor (1971) that the ATP-driven cycle is such that S1 detaches from actin when it binds ATP, and the subsequent hydrolysis of bound ATP occurs when myosin is detached (for example Geeves 1991; Ma and Taylor 1994). This mechanism is supported by atomic-structure determinations of myosin-S1 (Rayment et al. 1993; Geeves and Holmes 2005) and EPR/FRET studies (Ostap et al. 1995; Shih et al. 2000) which reveal three different configurations, one of which is the post-stroke or ‘rigor’ state of actomyosin. The other two are associated with detached myosin; one is the ‘post-rigor’ state of M.ATP and the second is the pre-stroke M.ADP.Pi state, generated after the lever arm has reprimed to allow hydrolysis (Malnasi-Czizmadia et al. 2001; Fischer et al. 2005). A fourth configuration, the pre-stroke configuration of the myosin-products state when bound to actin, is required to confirm the swinging lever-arm model. Nevertheless, the structure of the M.ADP.Pi state suggests that, when this state binds to actin, the phosphate group (Pi) bound to the active site must be released before the stroke can take place (Reubold et al. 2003).

The first attempt to include the effects of added phosphate into a model of muscle contraction was made by Pate and Cooke (1989), who assumed that the phosphate-release step was part of the working stroke. The forward stroke rate was unaffected by the concentration [Pi] of phosphate ions in the medium, but the reverse rate was proportional to [Pi], which implies that Pi is released after the stroke. This led to modest reductions in isometric tension and ATPase rate with added phosphate (23 and 13 % respectively per decade). Bigger tension decreases have been observed experimentally, whereas the ATPase rate drops very slowly with phosphate. Despite numerous modelling efforts, this problem has remained open.

Subsequent experiments with caged phosphate compounds cast a rather different light on the effects of added phosphate. Flash photolysis generated a step increase in phosphate concentration, and the transient tension responses of glycerinated fibres were measured at different final concentrations. The response rate varied from 30 to 70 s−1 as [Pi] was increased 2–12 mM (Dantzig et al. 1992). This slow response suggested that the phosphate-release step was distinct from the stroke, whose rate constant is very fast (104–105 s−1) when not blocked by elastic strain in myosin. While Pi-jump transients can be modelled in this way (Smith and Sleep 2004, Takagi et al. 2004), attempts to insert a slow Pi-release step into a complete mechanokinetic model are bound to fail. If this step occurs before the stroke, then pre-stroke A.M.ADP heads are driven into negative strain, reducing the unloaded shortening velocity. If Pi is released slowly after the stroke, the same difficulty arises for post-stroke A.M.ADP.Pi heads (Smith and Mijailovich 2008). Thus phosphate must be released rapidly and reversibly from its active site in bound myosin-S1, as part of the contraction cycle.

If this conclusion is accepted, then energetics shows why phosphate release from the active site should occur before any stroke. The phosphate sensitivity of isometric tension can be maximised by supposing that tethered M.ADP.Pi heads in the half-sarcomere bind weakly to actin, with affinity K A < 1 where K A = [A.M.ADP.Pi]/[M.ADP.Pi]. When Pi is released, the net affinity to the pre-stroke A.M.ADP state increases by a factor of 10 if [Pi] = 1 mM and the Pi dissociation constant is 10 mM; this extra affinity is lost as phosphate concentration is increased beyond 10 mM, giving a large reduction in tension. On the other hand, if the stroke occurs before Pi release, the net affinity to the post-stroke A.M.ADP state must be at least 104 to make the stroke energetically possible, and 10 mM of added Pi would reduce this number to 1,000, which has very little effect on the post-stroke population.

The paradox presented by rapid reversible phosphate release and the slow tension response to phosphate jumps can be resolved if the slow transition is not phosphate release from the active site but an associated reaction linked by a common state. The simplest choice is detachment from actin, which allows tension to be regenerated during shortening by rebinding to another actin monomer. Thus the dominant pathway in the myosin-S1 contraction cycle is as follows (Scheme 1): where the states linked by phosphate release are boxed to indicate a rapid equilibrium.

Scheme 1
scheme 1

Minimal actomyosin-ATPase cycle

Full size image

The two A.M.ADP states, first identified by Sleep and Hutton (1980), are linked by the “working stroke,” an 8–10 nm swing of the lever-arm (Holmes 1997) which moves an unloaded actin filament towards the M-band. If the actin site is held fixed, the same transition generates tension by a “power stroke” where the lever-arm flexes in its converter domain (Kohler et al. 2002). Against an elastic load, the swinging lever-arm displaces the actin filament by a smaller distance and mechanical work is done.

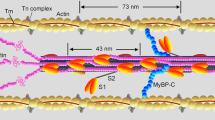
The model used here operates at the level of one actin filament in one half-sarcomere, and is based on the biochemical cycle shown in Fig. 1. Two 4 nm sub-strokes are required to give sufficient isometric tension; the first stroke generates tension while the second stroke acts as a strain-dependent gate. Distributed elasticity in filaments was replaced by a lumped elastic element in series with the actin filament, and quantitative predictions were generated by Monte Carlo simulation. The model also uses dimeric myosin-S1’s attached to a myofilament backbone by S2 rods, which buckle under very small amounts of compressive strain (Kaya and Higuchi 2010; Adamovic et al. 2008), so that during rapid shortening, many bound heads enter the buckling range of strains in which their apparent stiffness is almost zero. The evidence for S2 buckling from Kaya and Higuchi’s single-myofilament experiment translates directly to the muscle fibre, and is responsible for two Pi-dependent observations that are otherwise difficult to explain, namely (1) the very slight decrease of ATPase rate with added phosphate and (2) the extra tension seen in shortening muscle at high Pi, approaching that seen under physiological conditions at the same shortening speed. Both effects are generated by buckling rods which enhance S1-actin binding rates at negative strain, and buckling is generated by dimeric myosins.

Fig. 1
figure 1

The biochemical actin-myosin-nucleotide cycle used for modelling, in which the release of phosphate ion (Pi) is rapid, reversible and lumped into state 5. The abbreviations D,T are used for adenosine diphosphate (ADP) and triphosphate (ATP). Cartoons show detached states and pre-stroke, paused and post-stroke (A-state, P-state and R-state) configurations of the lever-arm of bound myosin relative to its motor domain. For A.M.ADP, all three forms are present, and the existence of two such states was deduced from oxygen-exchange experiments (Sleep and Hutton 1980). Detached states for all myosin-nucleotide combinations and their actin-binding pathways are included; only M.ADP.Pi executes a stroke after binding to actin, whereas M.ADP and apo-myosin (M) do not (Steffen et al. 2003). The A-state form of M.ATP, in which the R-state form (state 1) has reprimed to allow ATP to hydrolyse, is not shown. To accommodate ramp stretch responses, the model also assumes that state 6 can detach to state 3 via an intermediate detached state whose lever arm is in the paused configuration

Full size image

Mathematical details of the model are presented in the Supplementary Material.

The results of modelling

Muscle mechanics and the associated biochemistry is a mature field where many experimental protocols have been explored in depth. The task of this paper is not to find optimised sets of model parameters which fit them all, but rather to demonstrate how the model behaves with a single set of parameters, chosen to fit various properties of rabbit muscle at 10 °C with reasonable accuracy. The parameter values of Table 1 were optimised to provide the best possible fit to observed rates of tension response to phosphate jumps on rabbit psoas fibres at 10 °C (Dantzig et al. 1992), which constitute a primary test of how the model predicts phosphate-dependent behaviour. The model also predicts observed reductions in isometric tension with added phosphate, which vary with the amount of tension generated under physiological conditions (Caremani et al. 2008); this behaviour can be attributed to variations in the actin affinity of tethered heads, but only if phosphate release occurs immediately after M.ADP.Pi heads bind to actin. This model also explains why the tension response to a quick stretch is highly phosphate-dependent, while the response to a quick release is much less so (Ranatunga et al. 2002).

Table 1 Values of the parameters used for modelling
Full size table

Shortening muscle was simulated under isotonic conditions as a function of the applied load, giving the shortening velocity and ATP turnover as a function of load described by Hill (1938), with appropriate values for the maximum power and efficiency. The approach to rigor at low ATP and the tension response to ramp stretches are not included, but the present model anticipates these applications by incorporating all detached myosin-nucleotide states in Fig. 1, plus the Arrhenius mechanism for strain-dependent enhancement of actin attachment rates. All simulations describe the fully Ca2+-activated state.

Isometric muscle and added phosphate

Under physiological conditions, the sarcomeric phosphate concentration in a freshly activated fibre is under 1 mM. With the parameters of Table 1, the model predicts the following steady-state isometric properties per actin filament at low and high phosphate: Table 2 gives results for isometric tension T o, stiffness S o, N Bo heads bound to actin and N Do bound heads on doubly-bound dimers. R o is the ATPase rate, calculated as the net rate of ADP release. These values can be compared with measurements on skinned rabbit psoas fibres, for which data at low and high Pi is available. At 1 mM Pi, the predicted tension is within the range of observed values of 125–250 kPa at 10 °C (Coupland et al. 2001; Linari et al. 2007; Ranatunga et al. 2002), or 125–250 pN per actin for 1 × 1015 actin filaments/m2. At 25 mM Pi, observed tensions are typically reduced by 40–50 % (Dantzig et al. 1992; Fryer et al. 1995; Coupland et al. 2001), although larger decreases have been observed (Tesi et al. 2000). The predicted ATPase rate increases very slightly with Pi, whereas experiments (Kawai et al. 1987; Bowater and Sleep 1988; Potma et al. 1995) show a slight decrease. Predictions for the phosphate sensitivity of isometric properties are shown in Fig. 2a.

Fig. 2
figure 2

The phosphate dependence of isometric properties predicted by the model. a The ratios of tension, stiffness, the number of bound heads and the ATPase rate, relative to their values at 1 mM Pi and calculated from Table 1. b Tension ratios for different values of actin affinity; as in Table 1 (circles), with all actin affinities halved (triangles) and quartered (squares). c Absolute values of isometric tension as a function of log10[Pi], for the same reductions in affinity. d Phosphate dependence of the normalised ATPase rate for the three levels of actin affinity. Experimental data (Potma et al. 1995; Kawai et al. 1987; Bowater and Sleep 1988) lie near the middle level, for which the predicted isometric tension per actin is 185 pN

Full size image

For isometric stiffness there is no agreement with experiments on skinned fibres. From Table 2, the ratio T o/S o which estimates the release step required to reduce tension T 1 to zero is 4.13 nm. However, Linari et al. (2007) and Ranatunga et al. (2002) found intercepts of 8-9 nm, which implies that the net stiffness of their fibres was about half that predicted from Table 2. In intact frog fibres, the release step for zero T 1 is 4.5 nm (Ford et al. 1977), and similar values may be expected for rabbit psoas muscle. The extra compliance seen in skinned fibres is presumably due to the difficulty of making non-compliant attachments (D.G. Stephenson, personal communication). Thus the following predictions for length-step experiments show what could be expected in the absence of compliant attachments.

Table 2 Isometric predictions
Full size table

The predicted fraction of heads bound to actin (0.24) is lower than the value of 0.33 estimated by Linari et al. (2007) for rabbit psoas muscle. On the other hand, the ATPase rate per azimuthally competent head (defined in the Supplementary Material) is 1.95, or 0.975 s−1 per head if all 300 heads are counted, compared with a measured value of 1.2 s−1 for rabbit at 8 °C (Bowater and Sleep 1988).

The variability of isometric tension

As quoted above, reported isometric tensions per unit area from different fibres of rabbit psoas muscle under the same conditions can vary by a factor of two. How can this variability be explained? The predicted tension in Table 2 is at the upper end of this range, and the most likely explanation appears to be in terms of variable actin affinity of myosin-S1. Myosin dimers are linked to the myofilament backbone by S2 rods, which must bend under Brownian forces to allow them to approach the actin filament; such thermally-activated binding should be sensitive to variations in lattice spacing, electrostatic interfilament interactions and the ionic strength and pH of the sarcoplasm (Brenner 1987). Actin binding rates should vary in proportion to actin affinity.

This idea can be explored quantitatively, starting from the observation that tension for pre-stroke actin affinity K A is roughly proportional to ln K A (Karatzaferi et al. 2004). In the model used here, actin affinity and the phosphate sensitivity of isometric properties are very closely linked. If \( \tilde{K}_{P} \) is the second-order phosphate dissociation constant from the pre-stroke (A-state) form of A.M.ADP.Pi, then the combined probability of these A.M.ADP.Pi and A.M.ADP states (state 5 in Fig. 1) for an actin site at distance x is

$$ p_{A} (x) = \frac{{K_{A} (x)(1 + \tilde{K}_{P} /[\text{Pi}])}}{{1 + K_{A} (x)(1 + \tilde{K}_{P} /[\text{Pi}])}} \equiv \, \frac{{K_{A} (x)}}{{K_{A} (x) + C_{A} ([\text{Pi}]])}}, $$
(1)

where \( C_{A} ([\text{Pi}]) = [\text{Pi}]/([\text{Pi}] + \tilde{K}_{P} ), \) and \( K_{A} (x) = K_{A} \exp ( - v_{A} (x)/k_{B} T) \) includes the strain energy v A(x). Here kB is Boltzmann’s constant and T the absolute temperature. Figure 3 shows how A-state occupancy varies with actin affinity at low and high phosphate levels, taking \( \tilde{K}_{P} \) = 5 mM. These hyperbolic plots converge at low and high affinity. In between, there is a window of affinities in which binding is phosphate-sensitive and added phosphate has the ability to switch the dominant A-state from A.M.ADP to A.M.ADP.Pi. This argument does not apply to heads which make a stroke, but the occupancy of post-stroke states reflects the value of p A(x) which would apply if they did not.

Fig. 3
figure 3

The phosphate sensitivity of bound-state occupancy and tension is a function of actin affinity. From Eq. 1, the A-state occupancy \( p_{A} (K_{A} ,[\text{Pi}]) = \) \( K_{A} /(K_{A} + C_{P} ([\text{Pi}])) \) is plotted as a function of actin affinity K A, for \( \tilde{K}_{P} = 5\,{\text{mM}} \) and low and high phosphate levels as shown, for which C P(1) = 1/6, C P(25) = 5/6. Phosphate sensitivity \( \Delta p_{A} (K_{A} ) \) is defined as the difference \( p_{A} (K_{A} ,1) - p_{A} (K_{A} ,25), \) here equal to \( 2K_{A} /(3K_{A}^{2} + 3K_{A} + 5/12). \) This function has a maximum at K A = 0.37, and approaches zero when K A → 0 and K A ≫ 1

Full size image

In many ways Eq. 1 is a central result of this paper, and can be tested by changing actin affinities with added salt. Actin affinity is expected to be temperature-dependent; if so, then Fig. 3 also shows why phosphate sensitivity is confined to a certain range of temperatures (Coupland et al. 2001) and suggests why tension is phosphate-dependent in some muscles but not in others (Park-Holohan et al. 2010).

The other graphs in Fig. 2 show the variation of isometric properties with actin affinity as well as phosphate. By reducing all actin affinities and actin binding rates by factors of two and four, the predicted isometric tension at 1 mM Pi falls from 239 to 185 and 124 pN respectively (Fig. 2b), which covers the reported range of tensions in rabbit psoas muscle. The fractional reduction in tension produced by 25 mM Pi is 0.44, rising to 0.50 and 0.55 as actin affinities are halved and quartered. For rabbit psoas, these trends are confirmed by Caremani et al. (2008), who find that 10 mM Pi induces fractional tension reductions of 0.43 and 0.48 from physiological tensions of 156 and 131 pN respectively. The authors also find much smaller reductions in stiffness. Figure 2d shows that the predicted variation of ATP-ase rate with phosphate also falls into line with experiments when actin affinity is halved. The larger decrease predicted by earlier models (Pate and Cooke 1989), is avoided by S2 buckling, where heads bind at negative strain without a penalty in strain energy. Conversely, the model predicts a slight increase in ATPase rate with Pi when actin affinity is raised; this could be tested by lowering the ionic strength of the sarcoplasm.

Many studies have demonstrated the logarithmic dependence of isometric tension on phosphate level, namely

$$ T_{o} [\text{Pi}] = T_{o} [1] - A\,{ \ln }[\text{Pi}] $$
(2)

which is approximately obeyed over two decades. Figure 2c shows that this law is also obeyed by our model, with different values of A (from 33 to 21 pN) for the three levels of actin affinity. If A were independent of affinity, then the fractional reduction \( A\,{ \ln }[\text{Pi}]/T_{o} [1] \) at a given Pi level relative to 1 mM Pi is larger when T o[1] is smaller, which helps explain why the phosphate sensitivity of isometric tension is enhanced when actin affinity is reduced. Moreover, a simplified single-head model described in the Supplementary Material shows that

$$ A \approx k_{B} T{\text{M}}/b, $$
(3)

where M is the number of competent heads per actin and b = 36 nm is the actin half-period; this formula is remarkably free of mechanokinetic parameters. With M = 150, A = 16.7 pN. Approximately twice this value is obtained for the dimeric model.

Phosphate jumps

A step increase in phosphate concentration over a period of 1 ms can be generated from flash photolysis of caged compounds. The resulting tension transient is faster when the final concentration is higher, and the dominant phase can be fitted to a single exponential decay with rate constants from 20 to 100 s−1. In rabbit psoas fibres, the response rate λ([Pi]) has been fitted to a hyperbolic law with a characteristic concentration \( \tilde{K}_{P} \) of 12 mM at 10 °C or 4 mM at 20 °C (Dantzig et al. 1992). In the absence of Arrhenius enhancements, \( \tilde{K}_{P} \) is the true Pi dissociation constant of the pre-force A.M.ADP.Pi state.

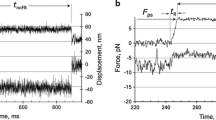
Monte-Carlo modelling with the cycle of Fig. 1 generates the phosphate-jump tension transients of Fig. 4a, which compare well with experiment. Over 0.1 s, the responses are well fitted by a single exponential decay. The rate constant is a hyperbolic function of the final concentration, giving good agreement with the data of Dantzig et al. for rabbit psoas muscle at 10 °C (Fig. 4b). This behaviour can be understood in terms of actin-binding and Pi-release transitions in isolation, namely the reaction scheme (Scheme 2) for a head with actin site at distance x along the filament. If Arrhenius factors are excluded, the detachment rate k −A is strain-independent, \( \tilde{K}_{P} \) is the second-order Pi release constant, and states in the box are in rapid equilibrium. The rate equation for binding to this lumped state gives a rate constant

$$ \lambda (x) = k_{A} (x) + \, \frac{[\text{Pi}]}{{\tilde{K}_{P} + [\text{Pi}]}}k_{ - A} . $$
(4)

which depends on the final Pi level. The net tension response requires a weighted average of exp(-λ(x)t) over x, which also depends on the initial x-distribution of bound states. If the second term in Eq. 4 is x-independent, then the averaged rate constant has a hyperbolic dependence on [Pi]. However, Tesi et al. (2000) found that the response to a downward Pi-jump is slower than for an upward jump to the same final Pi level; this puzzling result is explored in the Supplementary Material.

Fig. 4
figure 4

a Tension transients from phosphate jumps from 1 to 2–12 mM Pi, as predicted from Table 1. On the time-scale shown, each transient is well fitted by a single exponential. b The rate constant from exponential fitting (filled circles) is in reasonable agreement with experimental data of Dantzig et al. (1992) for glycerinated rabbit psoas fibres at 10 °C. Both curves can be fitted by a hyperbola, as in Eq. 4. The experimental data is fitted with \( \tilde{K}_{P} \) = 12.5 ± 2.6 mM and k −A = 104 ± 11 s−1, whereas the predicted curve is fitted with \( \tilde{K}_{P} \) = 7.0 ± 0.8 mM and k −A = 95 ± 2 s−1

Full size image
Scheme 2
scheme 2

Actin-binding coupled to phosphate release

Full size image

Similar behaviour can be expected when actin affinities and actin-binding rates are lowered by the same factor, because k −A would not be affected. Thus the hyperbolic increase in Pi-jump response rate with Pi level should be independent of actin affinity, and not subject to the variations of isometric tension found in different fibres of the same type.

To conclude, the model shows that, for the first time, Pi-jump kinetics can be modelled without using a slow Pi-release step in the kinetic scheme. The tension response to a phosphate jump is entirely due to detachment of pre-stroke A.M.ADP.Pi heads from actin, provided that Pi release from the active site is fast and reversible, and that pre-stroke A.M.ADP heads do not detach from actin or detach more slowly.

The response to length steps

The transient tension response to a quick release or a quick stretch, as a function of step size ΔL, is a hallmark of fast striated muscle. The fastest phase of the response was interpreted as evidence for the working stroke (Huxley and Simmons 1971; Ford et al. 1977). Responses were predicted over a time sufficient to generate the fast phases 2a and 2b, because the rate of the 2b response is phosphate sensitive whereas that of phase 2a is not. Moreover, this sensitivity is manifested only for stretches and not releases (Ranatunga et al. 2002). The current model, in which rapid reversible phosphate release occurs before any stroke, provides a natural explanation for this behaviour. The response to a quick stretch triggers stroke reversals which populate the A-state form of A.M.ADP, and rapid phosphate binding triggers detachment from actin at a rate proportional to the fraction of heads in the A.M.ADP.Pi form of the lumped state with A.M.ADP (state 5 in Fig. 1). This mechanism also generates the Pi dependence of the rate of tension change after a Pi jump.

Monte-Carlo simulations with this model can reproduce Pi-dependent length-step behaviour. Release steps certainly cause buckling in some of the S2 rods supporting bound myosins, but the general effect is benign, appearing as curvature in the elastic response tension T 1(ΔL). The main problem in fine-tuning the model is the presence of two strokes, whose kinetics and equilibrium constants need to be carefully adjusted to avoid overlapping tension transients.

For 1 and 25 mM Pi, Fig. 5 shows the results of fitting the predicted tension transients to two exponentials, which describe phases 2a and 2b of the response. The transients are shown in Figure S5 of the Supplementary Material. As a function of step size ΔL, the characteristic tensions T 1 after the elastic response, and T 2a after phase-2a recovery, are essentially as observed by Ford et al. (1977) for frog muscle at 3 °C and Ranatunga et al. (2002) for rabbit psoas muscle at 10 °C. The rate constants λ2a and λ2a of the two phases are also shown here. Slower phases exist (Burton et al. 2006) but were not modelled here.

Fig. 5
figure 5

Properties of the predicted tension response to length steps at 1 mM Pi (upper graphs) and 25 mM Pi (lower graphs), from the transients shown in Figure S6 of the Supplementary Material. a, d The characteristic tensions T 1,T 2a,T 2b after the zero-time elastic response, phase-2a and phase-2b recovery respectively. The other graphs show the rate constants of these phases for releases (b, e) and stretches (c, f). Additional slow phases exist since T 2b decreases with release steps of increasing size

Full size image

With added phosphate, modelling yielded similar rates of tension recovery for releases, but not for stretches. For stretches, phase 2a is approximately twice as fast as at 1 mM Pi (Figs. 5b, d) but the phase-2b rate is six-fold faster (Figs. 5c, f). Most of this recovery lies in phase 2b; the amplitude of phase-2a recovery is under 0.3T o at low and high Pi. Thus the model is able to explain why the stretch response is the only essentially phosphate-dependent aspect of length step behaviour.

Isotonic shortening

The most modelled aspect of muscle contraction, namely the speed of shortening and the ATP turnover rate as a function of sub-isometric load, appears to be the least dependent on added phosphate. Measurements of Cooke and Pate (1985) show no difference in the zero-load shortening velocities at 1 and 12 mM Pi. There is very little phosphate dependence of the ATPase at zero load (Potma and Steinen 1996).

Monte-Carlo modelling was carried out under isotonic conditions as a function of applied force F per actin filament. The half-sarcomere length shortens rapidly for small loads and goes through a single cycle of oscillation, analogous to the two phases of the tension response to a quick release (Figure S7, Supplementary Material), before settling down to a steady shortening after 10 ms, as seen by Edman (1988) for frog muscle. Simulations were made with 50–100 nm of shortening (less than the plateau of the tension-length curve), and average shortening velocities were calculated over the second half of the sampling time.

Figure 6 shows all results generated for isotonic shortening as a function of load, at low and high phosphate (upper and lower graphs respectively). Shortening velocities as a function of load F are shown in Fig. 6a, d. They can be fitted to Hill’s equation (Hill 1938) in the form

$$ \frac{v}{{v_{o} }} = \frac{1 - \tau }{1 + \tau /\alpha } \, \left( {\tau = \frac{F}{{T_{o} }}} \right), $$
(5)

where α = a/T o in Hill’s terminology. At 1 mM Pi, v o = 1,730 nm/s and α = 0.20, in very close agreement with measurements of Cooke et al. (1988), namely v o = 1,790 nm/s and the same value of α. Lower values of α (0.09) are associated with higher zero-load velocities (Sun et al. 2001), while higher values (0.42, He et al. 1999) may be expected when the concentration of ATP is reduced (Cooke and Bialek 1979). At 25 mM Pi, the predicted unloaded shortening velocity is 20 % smaller at 25 mM Pi, rather than Pi-independent, and α = 0.35. The higher value of α indicates that the velocity-load curve is raised mid-range by excess phosphate, moving it towards the curve for low [Pi] as seen by Cooke and Pate (1985).

Fig. 6
figure 6

Muscle properties for isotonic shortening as a function of applied load F. a Shortening speed v(F) and ATPase rate R(F). b Half-sarcomere stiffness per actin (circles), the number of bound heads (triangles) and the number on doubly bound dimers (squares). c Mechanical power output Fv(F) and mechanochemical conversion efficiency η = Fv(F)/R(F)|ΔH|, where ΔH = −34.7 kJ/mole = −53.5 zJ/molecule (Woledge et al. 1985) is the enthalpy of phosphocreatine splitting, appropriate for measurements with this ATP-regenerating system. The upper and lower graphs are for 1 mM and 25 mM Pi respectively

Full size image

The same figure show that the ATP-ase rate rises as load falls, not quite linearly as proposed by A.V. Hill. The ratio of the ATP-ases at zero load and isometric load is 5.68 at 1 mM Pi and 5.38 at 25 mM Pi, a measure of the Fenn effect (Fenn 1924). Lower ratios are sometimes (He et al. 1999) but not always (Sun et al. 2001) observed. The Fenn ratio can be lowered by increasing the fraction of cycling time when the myosin-nucleotide complex is detached from actin, for example by slowing the hydrolysis rate of M.ATP, but this reduces the unloaded shortening velocity.

Figures 6b, e show how muscle stiffness, the number of heads bound to actin, and the number in doubly-bound dimers all vary with load. With loads below 0.5T o, the number of bound heads drops almost linearly with load, but the intercept at zero load is finite; in Fig. 6b the number bound is 29 % of the isometric value, while the net stiffness falls to 20 %. If the stiffness κ per bound head were to remain constant, the combination of NB bound heads and a lumped series compliance C S would generate stiffness S such that 1/S = 1/κNB + C S. Let S(F) and NB(F) be stiffness and the number of bound heads at load F. Then

$$ \frac{{S(0)/S(T_{o} )}}{{N_{B} (0)/N_{B} (T_{o} )}} = \frac{{1 + \kappa C_{S} N_{B} (T_{o} )}}{{1 + \kappa C_{S} N_{B} (0)}} > 1. $$
(6)

However, predictions with the buckling model put the left-hand side at 20/29 < 1. Buckling rods cause the net stiffness per bound head to decrease with load, and this decrease occurs in conjunction with a decreasing number of bound heads.

The mechanical power output of muscle is the rate of working Fv against the load. At constant pressure, the rate at which the chemical energy of ATP hydrolysis is converted into work and heat is R|ΔH|, where R is the ATPase rate and ΔH is the enthalpy of ATP hydrolysis supported by phosphocreatine (Smith et al. 2005). Hence muscle efficiency is defined as η = Fv/R|ΔH|. Figures 6c, f show that the model predicts the same maximal power output and the same maximal efficiency (0.5) at 1 and 25 mM Pi, which is surprising in view of the difference in isometric tensions. This behaviour arises because phosphate boosts the lumped pre-stroke state, helped by buckling rods which assist actin binding at negative strain (Supplementary Material, Figure S2). Is this a mechanism to guard against fatigue (Westerblad et al. 2002)?

Discussion

Actin affinity links the effects of phosphate and temperature

The main conclusion of this paper is that the phosphate sensitivity of skinned muscle fibres is linked to the actin affinity of myosin heads, provided that the Pi-release transition occurs rapidly and reversibly immediately after the products state M.ADP.Pi binds to actin; in Fig. 3 the phosphate sensitivity of isometric tension is maximal for a critical value (0.37) of actin affinity. This conclusion applies equally to isometric properties and the transient responses induced by length steps and phosphate jumps. Actin affinities are expected to increase with temperature, and in rabbit psoas fibers, the temperature dependence of isometric tension T o is phosphate sensitive in a range of temperatures from 0 to 30 °C (Coupland et al. 2001). This behaviour is strikingly similar to the variation of phosphate sensitivity with actin affinity shown in Fig. 3, which suggests that T o is a monotonic increasing function of p A and K A is a monotonic increasing function of temperature. Preliminary modelling suggests that quantitative agreement with Coupland’s measurements can be achieved. Other muscles with high isometric tension do not display phosphate sensitivity over their working range of temperatures (Park-Holohan et al. 2010), which suggests that their actin affinity stays well above the critical value.

Buckling rods and working strokes

One might imagine that buckling S2 rods could function as an alternative mechanism for tension generation, but this is not possible under equilibrium conditions. Once the rod has buckled, some work is required for further buckling, but the energy cost for heads binding under compressive strain is very small. Hence positive tension from heads on straight rods is balanced by negative tension from heads on buckled rods at large negative strains. Similarly, no net tension is generated under cycling conditions.

Although strokes are still required to generate tension, S2 buckling has no effect on the number of sub-strokes required for a workable model. The present model requires only two sub-strokes to generate adequate length-step responses, and there appears to be no need for a larger number.

Piazzesi et al. (2007) have proposed a model for shortening muscle where the tension per bound head stays constant near 6 pN, but the number of bound heads drops linearly with load force. The implication is that there are no negatively-strained heads at any load, and this concept is consistent with an idealized buckling model. However, the real situation is more complicated. Their measurements (on frog muscle) show that for loads below 0.5T o the tension per bound head decreased, and while the high-frequency stiffness fell steadily with reduced load, it appears to asymptote at zero load to 11 % of the isometric value. However, these estimates were made by assuming that the number of bound heads fell in proportion to stiffness, which is true only if stiffness per bound head were constant; this assumption is not correct if the rods buckle in compression. Monte-Carlo simulations predicted 33 % of heads bound at zero load, which includes heads on buckled rods with an apparent stiffness near zero, while the force per bound head dropped from 6.67 to 4.36 pN.

Strong evidence for S2 buckling in compression comes from the single-myofilament experiment of Kaya and Higuchi (2010) and not from muscle fibre experiments. Buckling generates curvature in the elastic response function T 1(ΔL), but the amount of curvature seen experimentally varies with the speed of the length step (Ford et al. 1977). No such curvature is seen in the rigor state (Piazzesi et al. 2007, Fusi et al. 2010), presumably because of the extra stiffness. However, in the activated state there is no reason to doubt that S2 rods will buckle whenever their myosin dimers exert negative tension.

Biochemical aspects of the model

Rapid reversible release of phosphate from the active site is the central ingredient of the model, but this assumption appears to be contradicted by the slow rates of phosphate release on activation observed in different laboratories. An early burst of phosphate release (Curtin and Woledge 1979; He et al. 1997) precedes steady-state conditions, in which the net rate of phosphate release must be equal to the rate of ADP release calculated in the model. A particularly challenging experimental result is the slow (75 s−1) rate of phosphate release observed in solution with the phosphate binding protein (White et al. 1997), in the limit of high actin concentrations where the expected actin binding rates were too fast to measure. These results can be reconciled with the model by distinguishing between Pi release from its active site at the base of the nucleotide pocket and Pi appearing in the sarcoplasm. The escape route from the vicinity of the active site is thought to be through a narrow tube to the base of the actin-binding cleft, so that Pi escapes through the ‘back door’ rather than ‘front-door’ entry to the nucleotide pocket when bound to M.ADP (Lawson et al. 2004). However, other escape pathways may exist after the stroke (Reubold et al. 2003; Cecchini et al. 2010). The phosphate concentration in the vicinity of the active site may not equilibrate to the external concentration, as assumed in modelling phosphate jumps, but the time scale of the measured tension response is probably slow enough.

Much modelling of phosphate-dependent phenomena has been wedded to the idea that Pi is released after the stroke. Dantzig et al. (1992) have modelled Pi jumps and Pi-dependent tension in this way, but their pre-stroke state carried no tension at any strain and their stroke transition was too slow to account for length-step responses. Linari et al. (2010) proceeded in the same way but used no strain-dependent transitions and were forced to postulate a post-stroke A.M.ADP.Pi state as well as the pre-stroke state formed by hydrolysis; such a state seems structurally dubious and would short-circuit tension generation by detaching from actin. These difficulties disappear if the Pi-dependent equilibration rate k + + k −[Pi] common to these analyses is assigned to actin binding rather than a lever-arm stroke.

The model cycle of Fig. 1 omits the closed-pocket form of M.ATP, which follows the open-pocket form (state 1) after the lever-arm reprimes to the pre-stroke position. State 1 is populated at the end of the cycle, in the form of negatively-strained states during rapid shortening. After repriming, the closed-pocket form of M.ATP would generate negative tension if it binds to actin, lowering the unloaded shortening velocity. Thus the closed-pocket form of M.ATP probably has a similar affinity for actin as the open-pocket form, which is so low that this pathway is effectively closed.

Another bound state would also be required if phosphate binds to the rigor state. If this occurs, the ATPase rate and the zero-load shortening velocity would both be reduced at high phosphate. However, solution kinetics with rabbit myosin indicates very weak binding (McKillop and Geeves 1990); at pH 7.0 and an ionic strength of 0.175 M, the Pi binding constant to A.M was 27 M−1.

Finally, the model developed here applies only to fully activated muscle. The kinetics of muscle activation and relaxation by Ca2+ lie beyond the scope of this paper. Because the time course of tension development at the start of a tetanus is determined not only by actin binding rates, but also by localised unblocking of actin sites by tropomyosin (Lehman and Craig 2008). This cooperative process is probably responsible for a four-fold increase in the half-time required for tension rise, relative to what is expected from actin-binding rates alone (Geeves et al. 2011). Similarly, rapid shortening may partially deactivate the regulated actin filament by reducing the number of bound heads (Edman 1975). This would explain why the rate of tension rise when a muscle shortening under zero load is suddenly held at constant length or restretched (the ‘ramp-restretch’ protocol) is itself calcium-dependent (Brenner 1988).