Introduction

Fluids flowing over bluff bodies like squares, circles, etc., are typical engineering applications associated with the fluid flowing over an obstacle. A few real-life problems include the tubes used in power plants, flow over heat exchanger tubes, risers in the offshore pipelines, subsea cables for electronic communication and power transmission, submarine oil pipelines, etc. The future application also includes the vortex-induced energy harvesting systems, the micro-underwater vehicles, etc. It is crucial to study these numerous fluid–structure interaction problems to avoid the failure of the structural members due to fatigue or fretting. It has also been observed that predicting and simulating the flow patterns developed for such flows are complex and challenging due to the presence of moving boundaries as well as interactions occurring therein.

Flow over a single oscillating (forced or vortex-induced) circular cylinder is one of the classical problems exhaustively studied for the last several decades. The experimental studies by Leung et al. [1], Williamson et al. [2, 5], Cheng et al. [3], Park et al. [4], Quintino [7] and numerical studies by Bearman [6], Zhang et al. [8] on forced oscillating (in transverse to the flow or in streamwise direction) circular cylinder revealed the interesting lock-in phenomenon where synchronization between the vibrating cylinder frequencies and the vortex shedding can be observed. The nonlinear flow is found [9, 10] to be governed by Reynolds number, Re, Prandtl number, Pr, the amplitude of vibration (A) and cylinder vibrating frequency (f0). Hence, understanding and numerically predicting the vortex-shedding pattern produced behind the oscillating cylinder is one of the fundamental challenges to fluid-dynamics researchers. Hence, this complex fluid–structure interaction problem still draws the attention of many researchers and has become the classical test problem for validating the new numerical methods. Based on the detailed reviewed by Sarpkaya et al. [9] and Williamson [10], it can be seen that forced oscillating cylinder performing rectilinear oscillations, i.e., transverse oscillation and/or ln-line oscillation in the presence of uniform flow, are extensively studied by several researchers. It has been seen that when a cylinder oscillates with oscillation frequency, the nonlinear interaction causes two kinds of phenomena to occur. Firstly, the natural vortex shedding frequency gets suppressed, and vortex shedding occurs at forced cylinder frequency. Secondly, the lock-in or synchronization can be seen with a considerable increase in the drag coefficient. For the in-line oscillating cylinder, it has been observed that the natural shedding frequency becomes twice the oscillating cylinder frequency during lock-in with a significant increase in lift coefficient.

The early numerical work on forced oscillating cylinder includes the finite difference-based numerical simulation by Karanth et al. [11]. They evaluated the forced heat transfer from both in-line as well as transverse oscillating cylinder at Re 200. They studied the effect of various oscillating cylinder velocity amplitude on Nusselt number. The heat transfer rate is observed to be increasing with an increase in velocity amplitude. Cheng et al. [12] used the SOLA method to simulate transversely oscillating cylinder at 0 ˂ Re ˂ 300 with cylinder oscillation frequency varying 0–0.3 and amplitude of cylinder oscillation (A/D) 0.7. They obtained an increase in heat transfer of 1.6%, 3.9%, 7.5%, and 12.5% for A/D ratio of 0.14, 0.3, 0.5, and 0.7, respectively. They also proposed a correlation for a heat transfer in the lock-on regime. Cheng et al. [3] observed by an experimental study that the surface heat transfer enhanced by 34% when the circular cylinder was forced to oscillate transversely. Their experimental studies also extended to the turbulent region; however, the increase in heat transfer for the turbulence region is presumed to be connected with some unsteadiness of the flow pattern and boundary layer developed during the flow. Fu and Tong [13] numerically simulated transversely oscillating heated circular cylinder using penalty method-based arbitrary Lagrangian–Eulerian formulation. They investigated the effect of Reynolds number, oscillating speed, and amplitude of oscillation. They observed that the flow and heat transfer become periodic, which is enhanced considerably in the lock-in regime.

Pottebaum and Gharib [14] experimentally studied the forced oscillating cylinder using digital particle image thermometry and velocimetry (DPIT/V)-based temperature and velocity field measurements. They observed that the heat transfer from the circular cylinder oscillating in the transverse direction is strongly dependent on synchronization of natural vortex shedding frequency, the oscillating cylinder velocity, and vortex pattern mode developed behind the cylinder. They also observed that the vortex roll-up process formed due to transverse oscillation significantly affects the heat transfer coefficients. The higher oscillating cylinder velocity will also help to shed the vortex to the larger distances contributing to heat transfer enhancement. Placzek et al. [15] used finite volume-based industrial code to simulate the transversely oscillating cylinder and investigated the effect of frequency ratio (ratio of cylinder oscillation frequency to the Strouhal frequency) on the fluid flow and heat transfer characteristics. They also represented the aerodynamic coefficients in terms of power spectral densities to identify the possible frequencies dominating the flow. Zhang et al. [16] used an immersed boundary method to simulate the transversely oscillating cylinder and observed that the Nusselt number increases with the increase in Reynolds number. They also observed that most of the heat is transferred from the front part of the cylinder as compared to the rare part of the cylinder.

Bao et al. [17] simulated the two-dimensional streamwise oscillating cylinder using the lattice Boltzmann method. The Reynolds numbers are varied from 100–200, and the cylinder is forced to oscillate with a frequency ratio of 0.2–3.0 and amplitude of 0.1–0.4. They observed that heat transfer could be enhanced when the cylinder was forced to oscillate with small frequencies and low amplitude; however, the heat transfer decreased for the larger frequencies with large amplitude. They also observed that the RMS value of the Nusselt number increases with the oscillation frequency, whereas the average Nusselt number decreases with an increase in cylinder oscillation frequency. For lock-in conditions, both Nusselt number values are found to be maximum. Liao and Lin [18] simulated transversely oscillating heated cylinder using an immersed boundary method. They observed that when the cylinder oscillated with different oscillating frequencies, both lift and drag were increased due to phase-locked oscillations. Al-Mdallal et al. [19, 20] used Fourier spectral analysis to evaluate the heat transfer characteristics of a circular cylinder moving in a circular path. They evaluated forced convection from the isothermal cylinder and found that heat transfer increases with the vibration amplitude of the cylinder. They obtained around a 50% increase in heat transfer for a higher Reynold number and high-frequency ratio. Hoseinzadeh et al. [41, 42] also explored the artificial intelligence-based predictive way for Newtonian flow scenarios [43].

As per as fluid–structure problem solvers are concerned, three numerical approaches, i.e., the overset grid method, immersed boundary method and arbitrary Lagrangian–Eulerian (ALE) method, are popular. Immersed boundary method [21] is one of the most widely used approaches. However, as Gillebaart et al. [22] mentioned, there are a few problems, particularly for describing the fluid nodes and solid boundary nodes on structured boundaries during the interpolation/extrapolation process, which may create a problem distribution of pressure and viscous components. At high Reynolds number, the interpolation accuracy of boundary conditions is another problem encountered. On the other hand, the overset grid method uses meshes of different types, i.e., overlapping sub-mesh and background mesh [23]. Interpolation is necessary to find the values at the overset and main grid interfaces. In contrast to both methods mentioned above, the ALE formulation moves the meshes to adapt the moving boundary movements with no modifications in the topology of the mesh. The ALE formulation uses both Eulerian as well as Lagrangian features. Hence, this method is better than the immersed boundary method and oversets grid method as it could be more accurate and robust. Its body-conforming mesh is also an added advantage until there is a requirement for re-meshing.

No study is available on forced convective heat transfer characteristics of circular cylinder forced to perform an elliptical path based on the literature studied. Note that the elliptical path is more relevant in practical scenarios as the cyclic variation in lift forces is more than the cyclic variation of drag forces. Hence, cylinder following an elliptical path provides a more realistic approach than that of only transversely or only in-line forced path. It has also been observed that very few research has been conducted using arbitrary Lagrangian–Eulerian formulation for the forced vibration for a circular cylinder. Hence, developing and validating an accurate incompressible solver can be justified here. In this paper, forced heat transfer from the circular cylinder forced to oscillate in an elliptical path in an incompressible fluid flow is numerically simulated. Incompressible laminar unsteady flow at three Reynolds numbers, Re = 100, 150, 200, is studied. The amplitude of vibration, A, both in X-direction, Ax and Y-direction, Ay is varied 0.1D to 0.6 D (D is the cylinder diameter) such as to form typical elliptical path. The frequency ratio, F(fc/fs), is varied from 0.5 to 3.0, where fs is the vortex shedding frequency. An attempt is made to accurately predict the flow physics and heat transfer characteristics and validate the current approach against the present literature results. To the author's knowledge, no work has been reported on moving boundary forced oscillating circular cylinder using Artificial Compressibility (HLLC-AC) Riemann solver with ALE approach.

The paper is summarized as Sect. 2 describes the basic mathematical formulation of a forced oscillating circular cylinder. Section 3 details the computational domain and necessary code validation cases for stationary cylinder, transverse oscillating cylinder and in-line oscillating cylinder are presented. The results and discussion on the unsteady incompressible flow over circular cylinder performing elliptical path are also presented in Sect. 3. At last, conclusions are provided.

Arbitrary Lagrangian–Eulerian (ALE) formulation

The dimensionless form of the Navier–Stokes equations for laminar incompressible flows is modified using artificial compressibility method [24] with a dual-time stepping approach [25] and utilizing the arbitrary Lagrangian–Eulerian formulation [26] as

$$\frac{1}{{\beta }^{2}}\frac{\partial P}{\partial \tau }+\frac{\partial U}{\partial \mathrm{X}}+\frac{\partial V}{\partial Y}=0$$
(1)
$$\frac{\partial U}{\partial \tau }+\frac{\partial U}{\partial t}+(U-{U}_{\text{m}})\frac{\partial U}{\partial \mathrm{X}}+(V-{V}_{\text{m}})\frac{\partial U}{\partial \mathrm{Y}}=-\frac{\partial P}{\partial \mathrm{X}}+\frac{1}{Re}{\nabla }^{2}\left(\mathrm{U}\right)$$
(2)
$$\frac{\partial V}{\partial \tau }+\frac{\partial V}{\partial t}+(U-{U}_{\text{m}})\frac{\partial V}{\partial \mathrm{X}}+(V-{V}_{\text{m}})\frac{\partial V}{\partial \mathrm{Y}}=-\frac{\partial P}{\partial \mathrm{Y}}+\frac{1}{Re}{\nabla }^{2}\left(\mathrm{V}\right)$$
(3)
$$\frac{\partial \theta }{\partial \tau }+\frac{\partial \theta }{\partial t}+(U-{U}_{\text{m}})\frac{\partial \theta }{\partial X}+(V-{V}_{\text{m}})\frac{\partial \theta }{\partial Y}=\frac{1}{Re.Pr}{\nabla }^{2}\left(\uptheta \right)$$
(4)

where the dimensionless velocity (\(\mathrm{U}\) and \(V\)), dimensionless time (t), dimensionless temperature difference (\(\theta\)), and dimensionless pressure (\(P\)) are,

$$\begin{gathered} U = \frac{u}{{u_{\infty } }};\;V = \frac{v}{{u_{\infty } }};\;t = \frac{{t_{\text{r}} u_{\infty } }}{D};\;\theta = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }};\;P = \frac{{p - p_{\infty } }}{{\rho u_{\infty }^{2} }};\;X = \frac{x}{D};\;Y = \frac{y}{D}; \hfill \\ \;U_{\text{m}} = \frac{{u_{\text{m}} }}{{u_{\infty } }};\;V_{\text{m}} = \frac{{v_{\text{m}} }}{{u_{\infty } }};\;F_{c} = \frac{{f_{0} D}}{{u_{\infty } }} \hfill \\ \end{gathered}$$
(5)

The governing flow parameters, i.e., Reynolds number, \(Re\) and Prandtl number, can be defined as,

$${\text{Re}} = \frac{{\rho u_{\infty } D}}{\mu };\;\Pr = \frac{\nu }{\alpha }$$
(6)

where \(v\) represents flow velocity in the respective x, \(y\) directions, \(p\) denotes pressure, \({T}_{\text{w}}\) is cylinder wall temperature, \({T}_{\infty }\) represents far-field fluid's temperature. \({u}_{\infty }\) is the reference far-field fluid velocity, \(D\) is the cylinder’s diameter (characteristic dimension), \(\rho\) and \(\mu\) represent the fluid density and dynamic viscosity, respectively, \(\nu\) and \(\alpha\) are the kinematic viscosity and thermal diffusivity of the fluid, respectively. \({u}_{\text{m}}\) and \({v}_{\text{m}}\) are the moving meshes' velocity, \({\beta }^{2}\) is the artificial compressibility parameter, and \(\uptau\) is the pseudo-time representing an auxiliary variable similar to real-time tr. \({f}_{0}\) is cylinder oscillation frequency. Note that walls of the cylinder have a higher temperature than the fluid flowing over it, hence the term: \(\left({T}_{\text{w}}-{T}_{\infty }\right)\) is larger than zero, indicating that the heat is transferred from the cylinder surface. While formulating Eqs. (1)–(6), the following assumptions are made:

  1. 1)

    The maximum Reynolds number considered here is 200; hence it is assumed that the fluid is air and the flow field is two-dimensional, laminar and incompressible.

  2. 2)

    The cylinder cross section is taken in a horizontal direction; hence, gravity's effect is neglected.

  3. 3)

    At the cylinder wall surface, no-slip conditions are specified. However, the fluid at the cylinder wall acquires the vibrating cylinder velocity.

As the current approach utilizes the finite volume method [29], hence Eqs. (1)–(4) can be re-casted in compact integral form for the two-dimensional case as,

$${\Theta }^{M}{\iint }_{\Omega }\frac{\partial \mathrm{W}}{\partial\uptau }\mathrm{dxdy}+{\mathrm{I}}^{\mathrm{M}}{\iint }_{\Omega }\frac{\partial \mathrm{W}}{\partial \mathrm{t}}\mathrm{dxdy}+{\Theta }^{\mathrm{M}}\underset{\mathrm{A}}{\overset{}{\oint }}\left[\left({\mathrm{E}}^{\mathrm{c}}+{\mathrm{E}}^{\mathrm{v}}\right){\mathrm{n}}_{\mathrm{x}}+\left({G}^{\mathrm{c}}+{G}^{\mathrm{v}}\right){\mathrm{n}}_{\mathrm{y}}\right]\mathrm{dA}= 0$$
(7)

where \(W\) is the unknown primitive variables vectors, \({E \& G}\) represent the fluxes where superscript 'c ' indicates the convective flux, and 'v' indicates the viscous flux part.

The artificial compressibility method (ACM) converts the incompressible flow system of Eqs. (1–4) into a hyperbolic–parabolic type of time-dependent system of equations that looks similar to the compressible gas dynamics equations. Therefore, in principle, all advanced algorithms that used incompressible flows can be applied to these modified incompressible flows formulations. With the advancement of calculation, Eq. (7) converges to a steady-state solution, \(\left(\frac{\partial \mathrm{P}}{\partial\uptau }=\frac{\partial \mathrm{U}}{\partial\uptau }=\frac{\partial \mathrm{V}}{\partial\uptau }=\frac{\partial \theta }{\partial\uptau }\cong 0\right)\) i.e., Eqs. (1 – 4) no longer depends upon the pseudo-time, \(\uptau\). Hence, the solution obtained at this pseudo-time steady-state does not influence \({\text{the} \, \beta }^{2}\) term, and the \({\beta }^{2}\) could be considered as a disposable parameter, similar to a relaxation parameter. Thus, Eq. (8) system gets converted into equations for compressible fluid with a very small Mach number; hence, the artificial compressibility relaxes the strict condition of satisfying mass conservation in every step.

The convective fluxes (\({E}^{\text{c}}\) and \({G}^{\text{c}}\)) of Eq. (7) is can further be divided into stationary flux part and moving grid flux part, i.e., ale flux part as [28],

$${\iint }_{\Omega }\frac{\partial \mathrm{W}}{\partial\uptau }\mathrm{dxdy}+{\mathrm{I}}^{\mathrm{M}}{\iint }_{\Omega }\frac{\partial \mathrm{W}}{\partial \mathrm{t}}\mathrm{dxdy}+{\Theta }^{\mathrm{M}}\underset{\mathrm{A}}{\overset{}{\oint }}\left[\left({\mathrm{E}}_{\mathrm{St}}^{\mathrm{c}}+{\mathrm{E}}^{\mathrm{v}}\right){\mathrm{n}}_{\mathrm{x}}+\left({G}_{\mathrm{st}}^{\mathrm{c}}+{G}^{\mathrm{v}}\right){\mathrm{n}}_{\mathrm{y}}\right]\mathrm{dA}-\underset{\mathrm{A}}{\overset{}{\oint }}\left[\left({\mathrm{E}}_{\mathrm{ale}}^{\mathrm{c}}\right){\mathrm{n}}_{\mathrm{x}}+\left({\mathrm{G}}_{\mathrm{ale}}^{\mathrm{c}}\right){\mathrm{n}}_{\mathrm{y}}\right]\mathrm{dA}= 0$$
(8)

The meshing of the 2-D geometry is split up into triangular and quadrilateral cells, whereas the 3D meshing is split into hexahedral and tetrahedral cases. The data structure used for any grid in the present computation is unstructured. The discretized form of the Navier–Stokes Eqs. (8) applied to a 2D geometry with finite volume formulation over structured or unstructured grid can be written for particular cell 'i’ as,

$${\Omega }_{\text{i}}\frac{\partial \overline{{W }_{\text{i}}}}{\partial \tau }+{I}^{\text{M}}\frac{\partial {(\Omega }_{\text{i}}\overline{{W }_{\text{i}}})}{\partial t}+ {\Theta }^{\mathrm{M}}\sum_{{k}=1}^{{K}}{\left[\left({\mathrm{E}}_{\mathrm{St}}^{\mathrm{c}}+{\mathrm{E}}^{\mathrm{v}}\right){l}_{\text{x}}+\left({G}_{\mathrm{st}}^{\mathrm{c}}+{G}^{\mathrm{v}}\right){l}_{\text{y}}\right]}_{\text{k}}^{\text{n}}-{\Theta }^{\mathrm{M}}\sum_{{k}=1}^{{K}}{\left[\left({\mathrm{E}}_{\mathrm{ale}}^{\mathrm{c}}\right){l}_{\text{x}}+\left({\mathrm{G}}_{\mathrm{ale}}^{\mathrm{c}}\right){l}_{\text{y}}\right]}_{\text{k}}^{\text{n}}=0$$
(9)

here k = 1, 2, …, K; where K refers to the neighboring cells connected to each boundary of the control volume \({\Omega }_{i}\). The \(\overline{{W }_{\text{i}}}\) denotes the cell average at the cell center 'i'.

Now approximating the real-time derivative part \((\frac{\partial }{\partial t})\) by second-order implicit backward formula, the finite volume discretization of Eq. (9) will be an ordinary differential equation in pseudo-time, \(\tau\), and its integration is done using the five-stage Runge–Kutta scheme [27].

$${\Omega }_{\text{i}}^{\text{n}+1}\frac{\partial \overline{{W }_{\text{i}}}}{\partial \tau }+{I}^{\text{M}}\left[\frac{3{\Omega }_{\text{i}}^{\text{n}+1}{\overline{W} }_{\text{i}}^{\text{n}+1}-4{\Omega }_{\text{i}}^{\text{n}}{\overline{W} }_{\text{i}}^{\text{n}}+{\Omega }_{\text{i}}^{\text{n}-1}{\overline{W} }_{\text{i}}^{\text{n}-1}}{2\Delta t}\right]+{\Theta }^{\mathrm{M}}\sum_{{k}=1}^{{K}}{\left[\left({\mathrm{E}}_{\mathrm{St}}^{\mathrm{c}}+{\mathrm{E}}^{\mathrm{v}}\right){l}_{\text{x}}+\left({G}_{\mathrm{st}}^{\mathrm{c}}+{G}^{\mathrm{v}}\right){l}_{\text{y}}\right]}_{\text{k}}^{\text{n}}-{\Theta }^{\mathrm{M}}\sum_{{k}=1}^{{K}}{\left[\left({\mathrm{E}}_{\mathrm{ale}}^{\mathrm{c}}\right){l}_{\text{x}}+\left({\mathrm{G}}_{\mathrm{ale}}^{\mathrm{c}}\right){l}_{\text{y}}\right]}_{\text{k}}^{\text{n}}=0$$
(10)

Hence for the real-time solution at (n + 1)th time level during flow simulation, the pseudo-time steady-state is achieved by marching Eq. (10) to \(\left(\frac{\partial \mathrm{P}}{\partial\uptau }=\frac{\partial \mathrm{U}}{\partial\uptau }=\frac{\partial \mathrm{V}}{\partial\uptau }=\frac{\partial \theta }{\partial\uptau }\le {10}^{-6}\right)\). Thus, the unsteady flow calculation gets converted to a series of pseudo-time steady-state flow calculations. In this method, the real-time remains constant, whereas the solution marches in pseudo-time.

The current paper utilized the local time-stepping method [27] to accelerate the pseudo-time step calculation so that the real-time accuracy is not affected. The local time stepping used here is estimated based on the local convective and diffusive time steps. Hence, the pseudo-time step \(\Delta {\tau }_{\text{i}}\), required in Eq. (10) for a cell ‘i’ is calculated using the harmonic formula as

$$\frac{1}{\Delta {\tau }_{\text{i}}}=\frac{1}{\Delta {\tau }_{\left(\text{conv}\right)\text{i}}}+\frac{1}{\Delta {\tau }_{(\text{diff})\text{i}}}$$
(11)

where \(\Delta {\tau }_{\left(\text{conv}\right)\text{i}}\) is the inviscid time step and \(\Delta {\tau }_{\text{(diff)i}}\) is the viscous time step for cell ‘i’. The inviscid time step is given by formula [27],

$$\Delta {\tau }_{\text{(conv)i}}= \frac{CFL . {\Omega }_{\text{i}}}{\sum_{{m}=1}^{M}\left(\left|{V}_{\text{m}}{S}_{\text{m}}\right|+a|{S}_{\text{m}}|\right)}$$
(12)

and the viscous time step is given by,

$$\Delta {\tau }_{\text{(diff)i}}= \frac{CFL. {\Omega }_{\text{i}}^{2}}{\sum_{\text{m}=1}^{M}\left(\frac{8}{3}\frac{\mu }{\rho } |{S}_{\text{m}}^{2}|\right)}$$
(13)

Here \({V}_{\text{m}}\) is the velocity vector, \({S}_{\text{m}}\) is the surface normal vector, \({\Omega }_{\text{i}}\) is the cell area, a is the modified speed of sound, \((\frac{\mu }{\rho })\) is the kinematic viscosity, and m is the face index for the cell ‘i,’ which has M number of faces.

In the incompressible flow Eq. (10), two types of fluxes need to be evaluated: convective and diffusive flux. The discretization of these two fluxes is carried out according to their nature. The stationary convective fluxes are discretized applying the HLLC-AC upwind methods developed by Mandal et al. [29, 30]. This scheme is based on the highly efficient and accurate Harten Lax and van Leer with contact (HLLC) [31] upwind scheme, originally developed for compressible flows, to the present incompressible flow formulation. Detailed for the HLLC-AC upwind Riemann solver is available at [28], whereas the diffusive fluxes by central differencing technique. The additional efforts are required for the evaluation of the ale flux vector in Eq. (10), which can be readily evaluated using Geometric Conservations Law (GCL.) [32, 33].

Before evaluating the ALE fluxes and the new cell volume \(\Omega\) at (n + 1)th level, one first needs to move the boundaries and meshes; the present approach utilizes the radial basis function [34]-based interpolation technique for mesh movements. The radial basis function (RBF) is the functions whose values are only dependent on the radial distance from the center or a reference point hence producing more accurate mesh move movements, especially in case of rotation/twisting of mesh. Also, the computational efforts required are much less than that of the connectivity of the internal grid points strategy.

To obtain the high order accuracy, the cell interface values of solution variables are found using Taylor series expansion about the cell center. The left and right state values of any solution variable W at the interface between two adjacent cells i and j are given by [31]

$$\begin{gathered} W_{\text{L}} = \overline{W}_{\text{i}} + \left( {r_{{\text{int}}} - r_{\text{i}} } \right)^{\text{T}} \nabla \overline{W}_{\text{i}} + \frac{1}{2}\left( {r_{{\text{int}}} - r_{\text{i}} } \right)^{\text{T}} H_{\text{i}} \left( {r_{{\text{int}}} - r_{\text{i}} } \right) + \ldots \hfill \\ W_{\text{R}} = \overline{W}_{\text{j}} + \left( {r_{{\text{int}}} - r_{\text{j}} } \right)^{\text{T}} \nabla \overline{W}_{\text{j}} + \frac{1}{2}\left( {r_{{\text{int}}} - r_{\text{j}} } \right)^{\text{T}} H_{\text{j}} \left( {r_{{\text{int}}} - r_{\text{j}} } \right) + \ldots \hfill \\ \end{gathered}$$
(14)

where the Hessian matrices, \({H}_{\text{i}}\) and \({H}_{\text{j}},\) computed at the left and right cell centers, the position vectors ri, rj and rint are evaluated for the cell center i, cell center j. The interface between the cell i and j, the cell average of primitive variables are \({\overline{W} }_{\text{i}}\) and \({\overline{W} }_{\text{j}}\), and the gradients are \(\nabla {\overline{W} }_{\text{i}}\) and \(\nabla {\overline{W} }_{\text{j}}\) at cell i and j, respectively. The interpolated values \({W}_{\text{L}}\) and \({W}_{\text{R}}\) were evaluated at the face interface on the left and right sides.

To obtain the quadratic reconstruction, i.e., third-order accuracy on two-dimensional unstructured/structured grids, one needs to keep three terms of the R.H.S. of Taylor series expansion (14). Thus, quadratic reconstruction demands evaluating the following five derivatives (for two-dimensional cases) at the cell center.

$$\frac{\partial \overline{W}}{\partial x }, \frac{\partial \overline{W}}{\partial y } , \frac{{\partial }^{2}\overline{W}}{\partial {x }^{2}} , \frac{{\partial }^{2}\overline{W}}{\partial {y }^{2}} \frac{{\partial }^{2}\overline{W}}{\partial x\partial y }$$
(15)

These five derivatives are evaluated using solution-dependent least square-based gradient calculations [35,36,37].

Step by step computational procedure for ALE-HLLC-AC method: A brief outline of a step-by-step computational solution is as follows.

  1. (1)

    Based on the mesh convergence study and literature available, determine and develop the mesh with an optimum number of elements and nodes. In the current computation, CGNS-based unstructured data structure is utilized.

  2. (2)

    Simulate the steady-state simulation and use it as the initial condition (U, V, P, and \(\theta\)) for unsteady as well as forced cylinder problems.

  3. (3)

    Based on the optimized mesh, evaluate pseudo-time step using local time stepping.

  4. (4)

    A real-time step can be taken per literature or by conducting a time study analysis.

  5. (5)

    For the forced circular cylinder problem, move the cylinder as well as domain mesh using the radial basis function and evaluate the new coordinates.

  6. (6)

    Evaluate incremental volume for moving mesh by applying geometric conservation law.

  7. (7)

    Incorporate proper boundary conditions.

  8. (8)

    Evaluate the convective fluxes by applying the HLLC-AC upwind method and viscous fluxes by central difference manner.

  9. (9)

    Use solution-dependent weighted least square-based gradients to evaluate the necessary gradient of the primitive variables.

  10. (10)

    Evaluate the ODE Eq. (10) using RK-5.

  11. (11)

    Iterate in pseudo-time such that pseudo-time steady-state \(\left(\frac{\partial \mathrm{p}}{\partial\uptau }=\frac{\partial \mathrm{u}}{\partial\uptau }=\frac{\partial \mathrm{v}}{\partial\uptau }=\frac{\partial \theta }{\partial\uptau }\cong {10}^{-6}\right)\) is achieved for each real-time step.

  12. (12)

    Once the solution is obtained, update the solution by advancing in real-time and moving the cylinder to a new location.

  13. (13)

    Repeat steps 4 to 12 until the steady periodic solution is attained.

Result and discussion

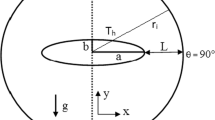
Figure 1 shows the physical model considered for the present numerical study. The computational domain consists of the circular cylinder having a diameter (D) and the outer boundaries having a size of 40 × 40 times the cylinder diameter. The circular cylinder is located at 8 units from the inlet and kept 20 units from the top and bottom far-field sides. The downstream length of the domain is 31.5, which is sufficient to capture the vortex shedding generated. Also, the present computational domain is sufficiently large to neglect the influence caused by the various nearby boundaries like inlet, outlet and side boundaries.

Fig. 1
figure 1

Physical model considered for present simulation

Full size image

The various boundary conditions enforced are:

Inlet: U \(=1,\) V = 0, \(\theta =0,\) and the pressure is interpolated from the interior domain.

Outlet: The exit pressure is specified as \({p}_{\infty }\), and other primitive variables are extrapolated as

$$p_{\infty } = 0{ }\left( {{\text{gauge}}} \right),\;\frac{\partial U}{{\partial X}} = 0,\;\frac{\partial V}{{\partial X}} = 0,\;\frac{\partial \theta }{{\partial X}} = 0$$

Top and Bottom far-field boundaries:

$$\frac{\partial U}{{\partial Y}} = 0,\;V = 0,\;\frac{\partial P}{{\partial Y}} = 0,\;\frac{\partial \theta }{{\partial Y}} = 0$$

Cylinder wall: For Stationary cylinder case: no-slip boundary condition U = V = 0, the cylinder surface, \(\theta =1\), and \(\frac{\partial P}{\partial n}=0\)

Forced oscillating cylinder case: the circular cylinder is forced to oscillate in a transverse direction to the flow with a forced oscillation equation

$$y\left(t\right)={A}_{\text{y}} \mathrm{Sin}\left(2\pi {f}_{\text{c}} t\right)$$
(16)

and, for in-line oscillating cylinder case: the cylinder oscillates with forced oscillation equation

$$x\left(t\right)={A}_{\text{x}} Cos\left(2\pi {f}_{\text{c}} t\right)$$
(17)

here \({A}_{x}\) and \({A}_{y}\) are the maximum amplitude of the oscillating cylinder in the X and Y direction, respectively, \({f}_{\text{c}}\) is the forced oscillating cylinder frequency. The frequency ratio, F, relates cylinder oscillation frequency (\({f}_{\text{c}})\) with vortex shedding frequency (\({f}_{0})\) as F = \({f}_{\text{c}}/{f}_{0}\).

Now the cylinder displacement is evaluated using Eqs. (13) and (14), and the cylinder wall (as well as the mesh) is displaced to a new location. The cylinder wall velocity is then specified based on this displacement, U = \(\dot{X}\), V = \(\dot{Y}\). The cylinder surface temperature was maintained at \(\theta =1\). The pressure condition \(\frac{\partial P}{\partial n}=0\) is specified.

Figure 2 shows the mesh generated and utilized for the present computational problem. A detailed mesh convergence study is conducted on three different meshes: mesh-1 having 10,410 mesh elements and 10,816 nodes; mesh-2 having 27,900 mesh elements and 28,300 nodes and mesh-3 having 48,150 mesh elements and 48,765 nodes. Figure 3 shows the comparison lift coefficient obtained for unsteady incompressible laminar flow at Reynolds number 150 over three meshes. Mesh-2 and mesh-3 show less than 5% change in lift coefficient values. Hence, mesh-2 is selected here for all presented simulations. The first quadrilateral mesh is at a distance of 0.0015 m from the cylinder wall.

Fig. 2
figure 2

Mesh used for the present simulation

Full size image
Fig. 3
figure 3

Mesh convergence study: comparison of lift coefficient for stationary flow over a cylinder at Re = 150

Full size image

Code validation: unsteady incompressible flow at Re = 100, 150, 200

Although the present HLLC-AC scheme [35] and solution-dependent weighted least square-based gradients [36, 37] are successfully applied to various incompressible benchmark problems as well as practical heat transfer cases, further tests considered here to show the validation for the unsteady incompressible flow over a stationary cylinder at Reynolds number of 100, 150 and 200 with Prandtl number of 0.7.

The local Nusselt number is evaluated at cylinder wall surface as [35]:

$${Nu}_{\uptheta }= {\left(\frac{\partial \theta }{\partial n}\right)}_{\text{D}=1/2}$$
(18)

Note that, as cylinder temperature is higher than fluid flow temperature, the heat transfer will be cylinder surface to the flowing fluid. The average Nusselt number around the circular cylinder wall is given as [35]

$$Nu=\frac{1}{2\pi }{\int }_{0}^{2\pi }{Nu}_{\theta } \text{d}\theta$$
(19)

The time average Nusselt number per cycle is given as [35]

$$\overline{Nu }=\frac{1}{{t}_{\text{p}}}{\int }_{0}^{{t}_{\text{p}}}{Nu}_{\text{n}} \text{d}{t}_{\text{p}}$$
(20)

Figure 4 compares the average Nusselt Number around the circular cylinder wall for Reynolds number 100, 150 and 200. The average Nusselt number shows small but cyclic fluctuating nature for unsteady incompressible flows. The Nusselt number increases with an increase in Reynolds number. Table 1 compares the Average Nusselt Number, Strouhal Number, Lift and drag coefficient obtained by the present computation and compares with literature results. The results show a good match with the literature results showing the capability and accuracy of the present solver.

Fig. 4
figure 4

Comparison of average Nusselt number for unsteady laminar flow at Re = 100, 150 and 200, Pr = 0.7

Full size image
Table 1 Unsteady flow over stationary circular cylinder: comparison with literature results
Full size table

Code validation: forced oscillating circular cylinder at Re = 200

The cylinder has oscillated forcefully only in transverse directions and only in the in-line direction to the fluid stream as per Eqs. (13) and (14), respectively. Various numerical tests are carried out for the cylinder frequency ratio, F = \({f}_{\text{c}}/{f}_{\text{s}}\) of 0.25 – 3.0 and oscillation amplitude of 0.1–0.4. The three Reynolds number cases 100, 150 and 200 keeping fixed Prandtl number of 0.7 are simulated. The transverse oscillation cases were kept similar to Fu and Tong [13], whereas in-line oscillation cases were similar to Bao et al. [17]. The intention is to reproduce the results for validation purposes only.

Figure 5 shows the comparison of variation of the Nusselt number with frequency ratio obtained for in-line oscillation of circular cylinder scenario at Reynolds number, 100 and Prandtl number 0.7. Three cases of oscillation amplitude of 0.1, 0.25 and 0.4 are simulated and compared with Bao et al. [17]. The Nusselt number decreases with an increase in frequency ratio for given oscillation amplitude. Also, for small oscillation amplitude, the maximum heat transfer occurs. The local maxima are achieved at the respective lock-in region.

Fig. 5
figure 5

Variation of average Nusselt number with frequency ratio for the forced in-line oscillating cylinder at Re = 100, Pr = 0.7

Full size image

Figure 6 shows the comparison of the Nusselt number ratio (Nuavg/Nu0), i.e., the ratio of average Nusselt number for forced oscillation case to the Nusselt number for stationary cylinder case evaluated for the range of cylinder frequency ratio of 0.25 – 2.5. The Reynolds number of 200 and cylinder amplitude of 0.4 is maintained as per literature [13, 17] values. The maximum heat transfer is achieved during locked regime for both transversely oscillating and in-line oscillating cylinder cases. There is an almost 17% increase in heat transfer for transversely oscillating cylinder cases, whereas only a 4% increase is due to in-line oscillations. For a higher value of frequency ratio, the adverse effect on heat transfer is observed and reduced almost by 8%. From Figs. 4 and 5, it can be seen that the results produced by the present ALE-HLLC-AC solver agree well with the literature results, i.e., Fu and Tong [13] results for transverse oscillation case and with Bao et al. [17] results for in-line oscillation.

Fig. 6
figure 6

Variation of Nusselt number ratio (Nuavg/Nu0) with frequency ratio at Re = 200, Pr = 0.7 for forced oscillating cylinder amplitude Ay (Transverse oscillation) = Ax (inline oscillation) = 0.4

Full size image

Forced oscillating cylinder performing elliptical path

From the results of forced transverse oscillation [17] and in-line [13], it is clear that the fluid flow and heat transfer are mainly affected by Reynolds number, Re, Prandtl number, Pr, The cylinder vibration frequency (fc) and the oscillation amplitude, (Ax and/or Ay). Literature results also reveal that the heat transfer is larger in the case of transverse oscillation than in-line oscillations. In fact, there is a decrease in heat transfer seen at the higher frequency ratio for the in-line oscillating cylinder case. Now to study the combined effect of transverse oscillation and in-line oscillation, the cylinder is forced to follow the elliptical path. The cyclic variation in lift forces is more than the cyclic variation of drag forces; hence cylinder made to follow the elliptical path is relevant with the practical scenario. The cylinder forced to oscillate in the elliptical path provides a more realistic approach than that of only transversely or only in-line forced path.

In this section, incompressible laminar unsteady flow at three different Reynolds number, Re = 100, 150, 200, are studied. The flow over circular cylinder is observed to be two-dimensional till Re = 200. However, the three-dimensional effects and turbulence start observing beyond Re = 250. The proposed application of the current work involves the design of low speed energy harvesting system where flow below Reynolds number of 200 is expected. The amplitude of vibration, both in X-direction, Ax and Y-direction, Ay is varied 0.1D to 0.6 D (D is the cylinder diameter) such as to form a typical elliptical path. Table 2 shows different configurations studied by varying Ax and Ay. There are total 24 different configurations simulated for each Reynolds number and frequency ratio. The cylinder is forced to move in an anti-clockwise direction as per Eqs. (14) and (15). Figure 7 shows three sample elliptical paths formed by setting Ax = 0.6, Ay = 0.1 (orange), Ax = 0.1, Ay = 0.6 (gray), Ax = 0.6, Ay = 0.6 (blue). The frequency ratio, (F = fc/fs), is varied from 0.5 to 3.0. Attempt here is made to predict the heat transfer due to forced convection of oscillating cylinder forced to follow an elliptical path.

Table 2 Details of elliptical movement of a forced circular cylinder, Amplitude ratio = Ay/Ax
Full size table
Fig. 7
figure 7

Elliptical path generated for different values of oscillation amplitude Ax and Ay. (three sample elliptical path plotted: orange—Ax = 0.6, Ay = 0.1; gray—Ax = 0.1, Ay = 0.6; blue—Ax = 0.6, Ay = 0.6)

Full size image

Firstly, the flow patterns and heat transfer characteristics are presented for the case study at Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 and F(fc/f0) = 0.5. This case lies in the non-lock-on region for the considered forced oscillation cylinder flow. Figure 8 shows the temperature contours (left) and vorticity (right) contours over one oscillation cycle. The vortex shedding generation can be seen from the cylinder surface for both temperature and vorticity contours. The temperature contours clearly show how effectively the heat transfer from the cylinder surface gets convected by the flowing fluid. The thermal vortex shedding helps to diffuse this convected heat into the cylinder wake. A thin thermal boundary layer is observed at the frontal cylinder area (i.e., front stagnation region), indicating a higher temperature gradient in these regions. Hence, most heat will be transferred from the left-half side of the oscillating cylinder, indicating a higher local Nusselt number on this surface. This can be confirmed from Fig. 9, which shows the variation of local Nusselt number over cylinder surface for all mentioned (as mentioned in Fig. 8) locations. From Fig. 8, it can also be seen that the vorticity is generated from the cylinder surface as well as heat conducted from the cylinder surface is transported to the cylinder wake hence the contours of vorticity and temperature look very much similar. As the cylinder is forced to oscillate in an anti-clockwise direction, the heated fluid from the frontal stagnation region flows along the cylinder surface and increases the thickness of the thermal boundary layer. The thick thermal boundary layer causes a reduction in temperature gradients and hence a decrease in Nusselt number. However, cyclic vortex shedding contributes to an increase in heat transfer, which shows another small peak in the Nusselt number in the wake region. It is also worth noting that, the circular versus elliptical motion of the cylinder has slightly different flow patterns. Mostly in practical life the cylinder is tend to oscillate in elliptical manner due to the non-similar magnitude of lift and drag forces produced.

Fig. 8
figure 8

Temperature contours (left) and vorticity (right) contours over one oscillation cycle for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 and F (fc/f0) = 0.5

Full size image
Fig. 9
figure 9

Local Nusselt number plotted over cylinder surface one oscillation cycle for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 and F (fc/f0) = 0.5

Full size image

Figure 10 shows the variation of average Nusselt number, cylinder center x location, cylinder center y location over one oscillation cycle for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 and F(fc/f0) = 0.5. At non-dimensional time 107.78, i.e., at the start of the cycle, the cylinder is located at the extreme right (x = 0.1, y = 0) location. As cylinder forced to move in elliptical path in anti-clockwise direction, it reaches the topmost (x = 0, y = 0.1), extreme left (x = −0.1, y = 0) and bottom most (x = 0, y = −0.1) location at non-dimensional time 110.77, 113.77 and 119.76, respectively. The average Nusselt number attained a maximum value of 5.85 when a cylinder is slightly moving away from the bottom-most location. In contrast, it attains a minimum of 4.56, slightly moving away from the topmost position. Hence, heat transfer is found to increase if the cylinder moves from top location to bottom-most location in an anti-clockwise direction. The higher relative velocity between the flowing fluid and oscillating cylinder causes this heat transfer.

Fig. 10
figure 10

Time variation of (a) cylinder (center) location (b) average Nusselt number over one oscillation cycle for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 and F(fc/f0) = 0.5

Full size image

Figure 11 shows the time variation of average Nusselt number for Re = 100, Pr = 0.7, Ax = 0.4, Ay = 0.1 and F(fc/f0) = 2.0, whereas Fig. 12 shows the time variation of average Nusselt number for Re = 150, Pr = 0.7, Ax = 0.1, Ay = 0.4 and F(fc/f0) = 2.0 for two oscillation cycles. These two cases fall near to the only in-line oscillation only transverse oscillation scenarios, respectively. From Fig. 11, it is seen that the heat transfer pattern is becoming complex due to the in-line dominant oscillation. The Nusselt number is maximum when a cylinder is located at the extreme left (Ax = 0.4, Ay = 0.1) position. A smaller peak was also found to be appearing at the extreme right location (Ax = −0.4, Ay = 0.1); however, due to lower relative velocity between the fluid and the cylinder, the heat transfer is limited. The Nusselt number is found to be minimum when a cylinder is at the bottom-most location (Ax = 0.0, Ay = −0.1).

Fig. 11
figure 11

Time variation of (a) cylinder (center) location (b) average Nusselt number over one oscillation cycle for Re = 100, Pr = 0.7, Ax = 0.4, Ay = 0.1 and F(fc/f0) = 2.0

Full size image
Fig. 12
figure 12

Time variation of (a) cylinder (center) location (b) average Nusselt number over two oscillation cycle for Re = 150, Pr = 0.7, Ax = 0.1, Ay = 0.4 and F(fc/f0) = 2.0

Full size image

From Fig. 12, it can be seen that, for transversely dominant cylinder oscillating with elliptical amplitude Ax = 0.1, Ay = 0.4 shows two peaks during one oscillation cycle. The first peak occurs at extreme left (Ax = 0.1, Ay = 0.0) and another peaks at extreme right (Ax = -0.1, Ay = 0.0) location. Hence, average heat transfer is more for cylinder oscillating with larger Ay amplitude (transverse dominated) values for given Ax. In practice, higher cyclic variation in lift forces may cause the cylinder to oscillate in a transverse direction more, hence promoting heat transfer for transversely dominating oscillating cylinder cases. (The temperature and vorticity contours are not shown here, if required we can add them with the reviewer's opinion.)

Figure 13 (a) and (b) shows variation of average Nusselt number for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 for the range of frequency ratio, F(fc/f0) of 0.5 – 3. As the frequency of the cylinder oscillation increases, the heat transfer increases. The maximum value attained by the average Nusselt number is found to be increased with higher cylinder oscillation frequency. Increased frequency of the cylinder oscillation produces larger relative velocities between the flowing fluid and cylinder hence promoting more heat transfer. However, at a very high cylinder oscillation frequency, the increase in heat transfer is not that appreciable due to the less time for heat transfer. Similar observations are noted for almost all test scenarios, i.e., all combinations mentioned in Table 1. Figure 14 shows the effect of various cylinder oscillation amplitude for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 oscillating at frequency ratio, F = 0.5. With an increase in oscillation amplitude, the heat transfer is promoted, and the average Nusselt number is found to increase. The maximum value attained is increased, whereas the minimum value decreases due to an increase and decrease in the respective max and min values of the relative velocity attained during the flow.

Fig. 13
figure 13

a variation of average Nusselt number for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 for the range of frequency ratio, F(fc/f0) of 0.5 – 1. b variation of average Nusselt number for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 for the range of frequency ratio, F(fc/f0) of 1.5 – 3

Full size image
Fig. 14
figure 14

variation of average Nusselt number for Re = 100, Pr = 0.7, Ax = 0.1, Ay = 0.1 for the range of frequency ratio, F(fc/f0) of 1.5 – 3

Full size image

Tables 3, 4 and 5 summarize the time average Nusselt number obtained by simulation for Prandtl number of 0.7, Reynolds number, Re 100, 150 and 200, respectively. As mentioned above, Tables 3, 4 and 5 show that, in the given case of cylinder oscillation amplitude (Ax and Ay), the time average Nusselt number increases with Reynolds number. At a higher Reynolds number, the high velocity flowing fluid helps to increase heat transfer by improving the heat by convection. Also, for particular cylinder x-direction oscillation amplitude, Ax, the time average Nusselt number is increasing with cylinder y-direction oscillation amplitude, Ay. As mentioned previously, the Nusselt number increases with an increase in cylinder oscillation amplitude at a particular cylinder oscillation frequency. An increase in Nusselt number at lower cylinder amplitude is not appreciable, which is only 2%, 4% and 13% for Re 100, 150 and 200, respectively, compared to the stationary cylinder. A maximum increase of 28.7%, 29.9% and 39.6% in Nusselt number is observed for Re 100, 150 and 200, respectively, compared to the stationary cylinder. At a higher Reynolds number, Re = 200, the three-dimensional effects are contributing; hence larger increase in the Nusselt number can be seen. Also, for fixed cylinder oscillation amplitude (fixed values of Ax and Ay), the Nusselt number increases with an increase in cylinder oscillation frequency ratio. The rate of increase in Nusselt number is observed to be increasing till oscillation frequency ratio of 1.5–2; however, then the rate of increase in Nusselt number is decreasing at higher frequency ratio (F > 2.5). The heat transfer is found to be maximum for the frequency ratio range of 0.75 – 2, mainly due to the lock-on phenomenon.

Table 3 Time average Nusselt number at Reynolds number 100, Pr = 0.7
Full size table
Table 4 Time average Nusselt number at Reynolds number 150, Pr = 0.7
Full size table
Table 5 Time average Nusselt number at Reynolds number 200, Pr = 0.7
Full size table

Conclusions

In the present paper, convective heat transfer from a circular cylinder forced to oscillate elliptically in an incompressible flow is numerically simulated. The two-dimensional laminar incompressible viscous fluid–structure interaction problem is simulated first time using an in-house ALE-HLLC-AC Riemann solver. During validation, the heat transfer rate is found to be increased maximum by 15.46% for the transverse oscillation in the lock-in region. For in-line oscillation cases, a maximum of 3.5% heat transfer is increased in the lock-in region; however, the heat transfer decreases by 4% for a higher frequency ratio.

From the present computation of a convective heat transfer from a circular cylinder forced to oscillate elliptically, it can be observed that the heat characteristics are completely different from a transversely and in-line oscillation case. The heat transfer characteristics show a higher Nusselt number but complex flow patterns for elliptical oscillations. Although no specific trend for lock-on region is seen, heat transfer is increasing for a higher cylinder frequency ratio, F. Present study also shows that the heat transfer is promoted for the higher amplitude of cylinder oscillation. For elliptical oscillations path having larger oscillation amplitude in a transverse direction, Ay shows a higher increase in Nusselt number than that of oscillation amplitude in in-line direction, Ax. Hence, it can be concluded that cylinder oscillating with higher oscillation amplitude and at higher frequency ratio shows the highest increase in heat transfer. A maximum increase of 28.7%, 29.9% and 39.6% in Nusselt number is observed for Re 100, 150 and 200, respectively, compared to the stationary cylinder. The vortex-induced vibration of circular cylinder will help in designing and understanding many future potential application like vortex-induced energy harvesting systems, unmanned water/aerial vehicles, etc.