Free convection/radiation and entropy generation analyses for nanofluid of inclined square enclosure with uniform magnetic field

Abstract

This paper studies the generation of entropy and free convective heat transfer of Al₂O₃/water nanofluid in an inclined enclosure affected by a magnetic field considering radiation effects. There is a circular quadrant at temperature $T_{\text{h}}$ in the bottom section of the left wall of the enclosure. The right wall of enclosure is kept at a fixed temperature $T_{\text{c}}$. The other walls are insulated. The governing equations for fluid flow are resolved using the algorithm of SIMPLE. The effect of variations of Rayleigh number (Ra), Hartmann number (Ha), the enclosure angle and concentration of nanoparticles ($\varphi$) on the flow field, isothermal field, entropy field, Nusselt number (Nu), Bejan number (Be) and total generation of entropy is investigated. The results indicate that the Nu enhances by 160% and 40% by augmenting the Ra and decreasing the Ha, respectively. Be diminishes by enhancing the Ra and reducing the Ha. The maximum generation of entropy intensifies by 288% and 39% by augmenting the Ra and reducing the Ha, respectively. The highest average Nusselt umber (${\text{Nu}}_{\text{M}}$) and an overall generation of entropy occur at the inclination angle of 30°.

Introduction

The free convection heat transfer has distinct applications in closed enclosures in distinct industries. These enclosures are used in many professions such as aerospace, defense, aerospace and solar collectors [1,2,3]. With regard to the widespread use of enclosures in various industries, scientific scholars have been studying the rate of heat transfer (HTR) in the enclosures [4,5,6,7]. The researchers studied the HTR in the enclosures by adding various fluids to closed enclosures [8,9,10,11]. For the purpose of using the enclosures as higher HTR and NFs have been proven to have better thermal properties than simple fluids, many researchers studied the HTR by using NFs in the enclosures [12,13,14]. Pordanjani et al. [15] studied natural convection of alumina/water NF in a closed enclosure. The enclosure’s right wall was at low temperature, and the upper and bottom walls were insulated. They imposed distinct temperature profiles on the left wall and studied the HTR. They found that the HTR intensifies by augmenting the Ra.

Since the addition of fins can increase the HTR [16,17,18,19], according to a previous study, some scientific scholars have attempted to increase the HTR by adding fins to the enclosures [20,21,22,23]. Miroshnichenko et al. [24] examined the free convection in an enclosure filled by alumina/water NF using the finite distinctial method. The enclosure had an angle with the horizon line, and a heat source was placed at its bottom. They concluded that the maximum HTR occurred at the inclination angle of 60°.

In many industries, the enclosures are placed next to the electric current. Since the electric current generates a MF around the enclosure, some scientific scholars have also studied the effects of MF on the HTR [25,26,27,28,29]. Pordanjani et al. [30] examined the free convection in a closed enclosure filled by a NF. There were two heat sources in the middle of the enclosure, which creates the buoyancy force in the enclosure. Also, a MF was applied to the cavity and the results indicated that the HTR diminishes by enhancing the Ha. Selimefendigil and Öztop [9] studied the free convection in a closed enclosure filled by a NF. They put the enclosure affected by a MF and examined the effect of it on the HTR. They demonstrated that the HTR enhances by increasing the Ra and reducing the Ha.

Due to the importance of efficiency in various engineering and industrial applications, researchers have tried to examine the efficiency of various devices. One of the best methods is to study the generation of entropy in various devices [31,32,33]. This method is based on the thermodynamics second law and is a suitable method for investigating the efficiency of various devices [34, 35]. Many researchers studied the generation of entropy in the enclosures [36,37,38]. Rahimi et al. [39] examined the free convection and the generation of entropy in a closed enclosure filled by a hybrid NF. A high-temperature fin was located in the enclosure. They concluded that the HTR intensifies by enhancing the Ra and φ. Ghasemi and Siavashi [40] examined the free convection and the generation of entropy in a square cavity. The enclosure was applied by a MF, and there was an obstacle inside the enclosure.

Heat transfer of radiation in addition of convection and conduction processes is important, especially at high temperatures [41,42,43]. Since this kind of heat transfer cannot be ignored in many cases, many researchers investigated the thermal and flow distributions considering the radiation heat transfer process [44,45,46,47,48,49,50,51,52,53,54,55]. Alnaqi et al. [56] studied the free convection and the generation of entropy in an inclined enclosure by using the volume control method. A fin filled with a NF was placed on a hot wall of the enclosure. A MF also affects the enclosure. They also considered the effects of radiation and found that radiation leads to an enhancement in the HTR and generation of entropy in the enclosure. Safaei et al. [47] examined the free convection and heat transfer in the radiation mode for NF containing alumina/water. They revealed that the value of conduction heat transfer is more than that of the convection one, and both are more than radiation heat transfer.

Due to the importance of free convection in the enclosures equipped with fins filled by NFs, the HTR in an inclined closed enclosure with a fin is studied. Since the enclosures affected by a MF have many applications in various professions such as aerospace, petrochemicals and solar collectors, the effect of MF on the thermal and flow distributions is investigated in the present work. Also, the generation of entropy and Be is calculated to evaluate the efficiency of the enclosure. There is also a volumetric radiation in the enclosure. The principal objective of this study is the type of the fin used in the enclosure. The blade has a circular quadrant shape. Most of the articles that have studied the effects of the fins on the HTR used rectangular fins. The circular blade is of less interest to researchers due to the difficulty in simulations, especially if the simulations are performed by computational codes. According to the review, radiation and free convection heat transfer in an inclined enclosure filled by alumina/water NF applied by a MF are studied. Finally, the effect of the variations of the parameters including Ra, Ha, angle of enclosure and the φ on the HTR, the generation of entropy and the Be is studied.

Geometry of problem and governing equations

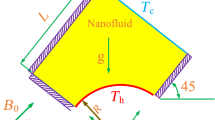
The schematic of the considered geometry consists of a two-dimensional square enclosure with a γ-angle relative to the horizontal axis. A constant MF along the horizon also affects the enclosure. The enclosure is filled with NF containing Al₂O₃/water. The NF is considered to be homogeneous with a coefficient of thermal conductivity of $K_{\text{nf}}$ and viscosity of $\mu_{\text{nf}}$. The enclosure’s right wall is fixed at cold temperature $T_{\text{c}}$. A circular quadrant with the temperature of $T_{\text{h}}$ is placed at the bottom of the left side of the enclosure. The other walls of the enclosure are insulated. Figure 1 shows a schematic of the problem.

Fig. 1

A schematic illustration of problem study

Conservation equations

The conservation equations conducted the fluid flow by using the following assumptions:

(i) Laminar and steady flow, (ii) Newtonian and incompressible fluid, (iii) neglecting the volumetric forces except the gravitational one and (iv) considering the Boussinesq approximation [30, 57]:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(1)

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{1}{\rho }\frac{\partial p}{\partial x} + \frac{1}{{\rho_{\text{nf}} }}\left( {\frac{\partial }{\partial x}\left( {\mu_{\text{nf}} \frac{\partial u}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\mu_{\text{nf}} \frac{\partial u}{\partial y}} \right)} \right) + g\beta_{\text{nf}} (T - T_{\text{c}} ){ \sin }\gamma$$

(2)

$$u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = - \frac{1}{{\rho_{\text{nf}} }}\frac{{\partial \bar{P}}}{\partial y} + \frac{1}{{\rho_{\text{nf}} }}\left( {\frac{\partial }{\partial x}\left( {\mu_{\text{nf}} \frac{\partial v}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\mu_{\text{nf}} \frac{\partial v}{\partial y}} \right)} \right) - \frac{{\sigma_{\text{nf}} B^{2} }}{{\rho_{\text{nf}} }}v + g\beta_{\text{nf}} (T - T_{\text{c}} ){ \cos }\gamma$$

(3)

$$\begin{aligned} & \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} } \right) = \frac{{k_{\text{nf}} }}{{\left( {\rho C_{\text{P}} } \right)_{\text{nf}} }}\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - \frac{1}{{\rho C_{\text{P}} }}\frac{{\partial q_{\text{r}} }}{\partial y}, \\ & \quad \left[ {q_{\text{r}} = - \frac{4}{3}\frac{{\sigma_{\text{e}} }}{{\beta_{\text{R}} }}\frac{{\partial T^{4} }}{\partial y},\;\;T^{4} = 4T_{\text{c}}^{3} T - 3T_{\text{c}}^{4} } \right] \\ \end{aligned}$$

(4)

$$S_{\text{gen}} = \frac{{k_{\text{nf}} }}{{T_{0}^{2} }}\left( {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right) + \frac{{\mu_{\text{nf}} }}{{T_{0} }}\left\{ {2\left[ {\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial v}{\partial y}} \right)^{2} } \right] + \left( {\frac{\partial u}{\partial y} + \frac{{\partial {\text{v}}}}{\partial x}} \right)^{2} } \right\} + \frac{{\sigma_{\text{nf}} B^{2} }}{{T_{0} }}v^{2}$$

(5)

The parameters used to non-dimensionalize the governing equations are described in the following equation in which Ha and Ras and the radiation parameter are also defined.

$$\begin{aligned} X & = \frac{x}{l},\quad Y = \frac{y}{l},\quad U = \frac{ul}{{\alpha_{\text{f}} }}, \\ V & = \frac{vl}{{\alpha_{\text{f}} }},\quad P = \frac{{\bar{P}l^{2} }}{{\rho_{\text{nf}} \alpha_{\text{f}}^{2} }}, \\ \theta & = \frac{{T - T_{\text{c}} }}{{T_{\text{h}} - T_{\text{c}} }},\quad L = \frac{l}{l}, \quad R = \frac{r}{l} \\ \Pr & = \frac{{\vartheta_{\text{f}} }}{{\alpha_{\text{f}} }},\quad {\text{Ra}} = \frac{{g\beta_{\text{f}} l^{3} (T_{\text{h}} - T_{\text{c}} )}}{{\alpha_{\text{f}} \vartheta_{\text{f}} }}, \\ {\text{Ha}} & = B_{0} l\sqrt {\frac{{\sigma_{\text{f}} }}{{\rho_{\text{f}} \vartheta_{\text{f}} }}} ,\quad {\text{Rd}} = \frac{{4T_{\text{c}}^{3} \sigma_{\text{e}} }}{{\beta_{\text{R}} k_{\text{f}} }} \\ \end{aligned}$$

(6)

Applying the mentioned parameters, the governing equations in the non-dimensional form are as follows.

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$

(7)

$$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} \alpha_{\text{f}} }}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) + \frac{{\beta_{\text{nf}} }}{{\beta_{\text{f}} }}{\text{Ra}}\Pr \theta \sin \gamma$$

(8)

$$U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} \alpha_{\text{f}} }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + \frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}\Pr {\text{Ha}}^{2} \left( { - V} \right) + \frac{{\beta_{\text{nf}} }}{{\beta_{\text{f}} }}{\text{Ra}}\Pr \theta \cos \gamma$$

(9)

$$\left( {U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} } \right) = \frac{{\alpha_{\text{nf}} }}{{\alpha_{\text{f}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) + \frac{4}{3}\frac{{k_{\text{nf}} /k_{\text{f}} }}{{\left( {\rho C_{\text{P}} } \right)_{\text{nf}} /\left( {\rho C_{\text{P}} } \right)_{\text{f}} }}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)^{ - 1} {\text{Rd}}\frac{{\partial^{2} \theta }}{{\partial Y^{2} }}$$

(10)

$$S_{\text{gen}} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\left( {\left( {\frac{\partial \theta }{\partial X}} \right)^{2} + \left( {\frac{\partial \theta }{\partial Y}} \right)^{2} } \right) + \zeta \left\{ {2\left[ {\left( {\frac{\partial U}{\partial X}} \right)^{2} + \left( {\frac{\partial V}{\partial Y}} \right)^{2} } \right] + \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)^{2} } \right\} + \zeta \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}\frac{{\mu_{\text{f}} }}{{\mu_{\text{nf}} }}{\text{Ha}}^{2} V^{2}$$

(11)

The definition of Be and local Nu calculated on cold wall and also the definition of the entropy parameter are presented in Eq. (12).

$$\begin{aligned} {\text{Be}} & = \frac{{S_{\text{gen,T}} }}{{S_{\text{Total}} }},\quad {\text{Nu}} = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\left( {\frac{\partial \theta }{\partial X}} \right) + \frac{4}{3}{\text{Rd}}\left( {\frac{\partial \theta }{\partial X}} \right) = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\left( {1 + \frac{4}{3}{\text{Rd}}\frac{{k_{\text{f}} }}{{k_{\text{nf}} }}} \right)\frac{\partial \theta }{\partial X}, \\ \zeta & = \frac{{\mu_{\text{nf}} T_{0} }}{{k_{\text{f}} }}\left( {\frac{{\alpha_{\text{f}} }}{{L(T_{\text{h}} - T_{\text{c}} )}}} \right)^{2} \\ \end{aligned}$$

(12)

In the above relation, the local Nusselt number is obtained from the following relation:

$${\text{Nu}}_{\text{Y}} = \frac{hL}{{k_{\text{f}} }} + {\text{Nu}}_{\text{Rd}}$$

(13)

Natural convection heat transfer coefficient is as Eq. (14):

$$h = \frac{{q_{\upomega} }}{{T_{\text{h}} - T_{\text{c}} }}$$

(14)

The heat flux is calculated using Eq. (15):

$$q_{\upomega} = k_{\text{nf}} \left( {\frac{\partial T}{\partial X}} \right)$$

(15)

The overall entropy, the average Bejan number ($B_{\text{Ave}}$) and ${\text{Nu}}_{\text{M}}$ on cold wall are obtained by integrating over the whole solution range:

$$S_{\text{Total}} = \mathop \int \nolimits S_{\text{gen}} {\text{d}}\varOmega = \mathop {\iint }\limits_{0}^{1} S_{\text{gen}} {\text{d}}X{\text{d}}Y$$

(16)

$${\text{Nu}}_{\text{M}} = \frac{1}{L}\mathop \int \limits_{0}^{L} {\text{Nu}}_{{({\text{x}} = 0,1)}} {\text{d}}Y = - \frac{1}{L}\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\mathop \int \limits_{0}^{L} \left( {\frac{\partial \theta }{\partial X}} \right)_{{({\text{x}} = 0 ,1)}} {\text{d}}Y$$

(17)

$$B_{\text{Ave}} = \mathop {\iint }\limits_{0}^{1} {\text{Bed}}X{\text{d}}Y$$

(18)

The hydrodynamic and thermal boundary conditions applied to the enclosure are presented in Table 1.

Table 1 Dimensional boundary conditions

According to the dimensionless equations (6), boundary conditions in the non-dimensional form are presented in Table 2.

Table 2 Non-dimensional boundary conditions

NF specifications

The coefficient of electrical conductivity, the density, coefficient of volumetric expansion, thermal capacity and coefficient of thermal diffusivity of the NF are calculated using the specifications of the nanoparticles and fluid:

$$\sigma_{\text{nf}} = (1 - \varphi )\sigma_{\text{f}} + \varphi \sigma_{\text{s}}$$

(19)

$$\rho_{\text{nf}} = (1 - \varphi )\rho_{\text{f}} + \varphi \rho_{\text{s}}$$

(20)

$$(\rho \beta )_{\text{nf}} = (1 - \varphi )(\rho \beta )_{\text{f}} + \varphi (\rho \beta )_{\text{p}}$$

(21)

$$(\rho c_{\text{p}} )_{\text{nf}} = (1 - \varphi )(\rho c_{\text{p}} )_{\text{f}} + \varphi (\rho c_{\text{p}} )_{\text{s}}$$

(22)

$$\alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{(\rho c_{\text{p}} )_{\text{nf}} }}$$

(23)

The Vajjha model [58] is used for viscosity and thermal conductivity of NF. (In these relations, the subclasses s and f refer to the ${\text{Al}}_{2} {\text{O}}_{3} \;{\text{and}}\;$ water properties, respectively. These properties are presented in Table 3.) This model considers the Brownian motion of nanoparticles that can help to more accurately predict the simulations. Brownian motion is one of the physical phenomena in NFs. This model involves thermal conductivity coefficient of stationary fluid, in addition to the coefficient of thermal conductivity of Brownian motion, where $k_{\text{Static}}$ is obtained from the Maxwell relation [59]. Finally, the coefficient of thermal conductivity of the NF is derived as Eq. (24):

$$k_{\text{nf}} = k_{\text{Static}} + k_{\text{Brownian}} = \frac{{k_{\text{s}} + 2k_{\text{f}} - 2(k_{\text{f}} - k_{\text{s}} )}}{{k_{\text{s}} + 2k_{\text{f}} + (k_{\text{f}} - k_{\text{s}} )\varphi }}k_{\text{f}} + 5 \times 10^{4} \beta \varphi \rho_{\text{f}} \left( {C_{\text{p}} } \right)_{\text{f}} \sqrt {\frac{kT}{{\rho_{\text{s}} d_{\text{s}} }}} f(T,\varphi )$$

(24)

Table 3 Thermophysical properties of Al2O3 and water [30]

For the viscosity model, the term $\mu_{\text{Static}}$ is derived from the Brinkman relationship [60]. Finally, the viscosity relation is written as Eq. (25):

$$\mu_{\text{nf}} = \mu_{\text{Static}} + \mu_{\text{Brownian}} = \frac{{\mu_{\text{f}} }}{{(1 - \varphi )^{2.5} }} + 5 \times 10^{4} \beta \varphi \rho_{\text{f}} \left( {C_{\text{p}} } \right)_{\text{f}} \frac{{\mu_{\text{f}} }}{{k_{\text{f}} \Pr }}\sqrt {\frac{{k_{\text{b}} T}}{{\rho_{\text{p}} d_{\text{s}} }}} f(T,\varphi )$$

(25)

In Eqs. (24) and (25), the terms f(T, φ) and β are expressed with relations (26) and (27) for Al₂O₃/water NF [58]:

$$f(T,\varphi ) = \left( {2.8217 \times 10^{ - 2} \varphi + 3.917 \times 10^{ - 3} } \right)\left( {\frac{T}{{T_{0} }}} \right) + \left( { - 3.0669 \times 10^{ - 2} \varphi - 3.91123 \times 10^{ - 3} } \right)$$

(26)

$$\beta = 8.4407(100\varphi )^{ - 1.07304}$$

(27)

Numerical method

Equations (7)–(11) are solved using a control volume-based finite difference method. The computational domain is discretized by a staggered grid. In a staggered grid, moreover the comfort of calculating flows on the control volume, in the main points of the grid, the values of pressure are calculated due to that the velocity of the surfaces is known. For solving simultaneously the algebraic equations, the algorithm of SIMPLE is used, the full details of which are given in Ref. [61]. Finally, the SIMPLE code is applied by means of FORTRAN and the results are shown in figures and tables. The criterion of convergence is demonstrated as follows:

$$\varPhi = \mathop \sum \limits_{\text{J}} \mathop \sum \limits_{\text{I}} \left| {\frac{{\varphi^{{{\text{n}} + 1}} - \varphi^{\text{n}} }}{{\varphi^{{{\text{n}} + 1}} }}} \right| \le 10^{ - 8}$$

(28)

For all simulations, the base effective parameters are ${\text{Ra}} = 10^{5} ,\; \gamma = 45, \;\varphi = 0.03, \;{\text{Ha}} = 20, \;{\text{Rd}} = 1, \;\omega = 0, \;{\text{AR}} = 0.3.$ By changing each of the effective parameters, its effect on the HTR and the generation of entropy can be evaluated.

Code validation

In order to verify the code validation, the results of this numerical work are compared with the previous results. In the first comparison, the thermal and flow distribution and also ${\text{Nu}}_{\text{M}}$ are compared to the work performed by Ghasemi et al. [62]. The ${\text{Nu}}_{\text{M}}$ values are illustrated in Table 4, and the flow and thermal fields are presented in Fig. 2. The comparison is performed at ${\text{Ra}} = 10^{5}$ and ${\text{Ha}} = 30$ for alumina/water NF. According to the results, the written code is acceptable.

Table 4 Comparing the ${\text{Nu}}_{\text{M}}$ obtained from this simulation and the results obtained by Ghasemi et al. [62] at ${\text{Ra}} = 10^{5}$ and ${\text{Ha}} = 30$ for various φ

Fig. 2

Flow and thermal distributions at ${\text{Ra}} = 10^{5}$ and ${\text{Ha}} = 30$ obtained from the present simulations compared to the one reported by Ghasemi et al. [62]

In Fig. 3, the present results with the results obtained by Krane and Jessee [63] are compared. The velocity profile achieved in the present work is compared with the empirical results reported by Krane and Jessee [63]. Comparison of the two profiles showed a proper agreement between them.

Fig. 3

The dimensionless horizontal velocity profile for the present simulations and experimental work [63] carried out for free convection of the air in an enclosure

A comparison was also made to check the accuracy of the values obtained for entropy generation. Table 5 compares the results of the production entropy with the results of Oliowski et al. [64] inside the square cavity. As shown in Table 5, the production entropy values show that the discrepancy between the results of the present work and the Ref. [64] is low.

Table 5 Comparison of mean entropy inside a square cavity for ζ = 10⁻² and distinct Ra

Grid study

The results gained from numerical simulations must be independent of the grid points number. In Table 6, the ${\text{Nu}}_{\text{M}}$ and the generation of entropy are presented for ${\text{Ha}} = 20$, φ = 0.03, Y = 0.6 AR = 0.5, Rd = 1, ω = 45°, and ${\text{Ra}} = 10^{5}$ for distinct grid resolutions. It is seen that the grid resolution of 120 × 120 is sufficient to perform the simulations; and further increase in the number of the grid points does not affect both parameters.

Table 6 Grid study for distinct grid resolutions

Calculation results

Changing Ra

In Fig. 4, the streamlines, isothermal lines and isentropic lines are displayed for ${\text{Ha}} = 20,\; \gamma = 45,\; \varphi = 0.03$ and various Ras. The figure shows that the density of the streamlines enhances by increasing the Ra. The density of the streamlines means that the velocity intensifies in the enclosure. The Ra represents the amount of buoyancy force in the enclosure, and its increase means that the buoyancy force intensifies. The fluid in the enclosure moves faster, and the vortex flow velocity in the cavity intensifies by augmenting the buoyancy force. The vortex formed in the chamber rotates clockwise. The formation of the vortex is such that the fluid is heated when it is placed in the vicinity of the fin, causing the molecules to be separated and the density of the fluid diminishes. By decreasing the density of the fluid, it moves upward and replaces the heavier fluid that has a low temperature. The force that causes this displacement is buoyancy force. The greater the difference in the density, the greater the buoyancy force. The fluid is placed near to the wall with the low temperature of the enclosure, and its temperature diminishes leading to a reduction in the molecular momentum. As a result, the density of the fluid intensifies and moves downward, and the warmer fluid will be replaced by a lower density than the upper part of the enclosure. This permanent fluid’s displacement in the cavity leads to the formation of a vortex in the enclosure. The stream function’s maximum value is illustrated in the middle of each vortex. This number indicates the velocity and vortex’s strength. Stronger vortex has the largest number. It can be concluded that the vortex strength enhances by augmenting the Ra. It is because of that augmenting the Ra leads to augmenting the buoyancy force, which ultimately causes an enhancement in the fluid flow velocity in the cavity. Isotherms show that two events happen with an enhancement in the Ra. The first thing is an enhancement in the compression of the isothermal lines close to the fixed-temperature fin and the constant-temperature wall. The second one is an enhancement in the curvature of the isothermal lines and their collapse. An enhancement in the compression of the isothermal lines means an enhancement of the temperature gradient due to an enhancement in the velocity of fluid flow, which causes an enhancement in the HTR. Three heat transfer mechanisms in the enclosure include: convection, conduction and radiation. The HTR in the radiation mode does not change much by changing the Ra, and its rate does not change because of the constant magnitude the parameter of radiation. But, the velocity of flow in the enclosure enhances and natural convection intensifies by increasing the Ra. Hence, this mechanism of heat transfer has more contribution than the two other ones. At low Ra and fluid velocities with low value, conduction is the dominant heat transfer process. This is concluded from the regular shape of the isothermal lines and their curvature. As the velocity intensifies, natural convection intensifies and the mechanism of conduction is weakened. Since the conduction has a lower order than natural convection in the same conditions, this can cause an enhancement in the HTR by augmenting the Ra. Entropy filed also demonstrates that the density of the isentropic lines enhances by increasing the Ra. Overall generation of entropy includes three sections: thermal generation of entropy, generation of entropy because of viscous dissipation and generation of entropy because of MF.

Fig. 4

Streamlines, isotherms and isentropic lines at ${\text{Ha}} = 20,\;\gamma = 45,\;\varphi = 0.03$ and distinct Ra

While each entropy generations rises, the overall generation of entropy enhances. The flow velocity and the HTR increase by enhancing the Ra. Thermal generation of entropy is temperature gradient dependent and intensifies with augmenting the temperature difference. The generation of entropy because of viscous dissipation also depends on the velocity difference and intensifies with the temperature gradient. The generation of entropy because of the MF is the Ha and y-component of the velocity dependent. As the Ra rises, the velocity and temperature gradients increase leading to an enhancement in thermal generation of entropy and generation of entropy due to viscous dissipation. This is concluded from the increase in the density of isentropic lines. The generation of entropy because of the MF is due to the small value of the coefficient of the Ha at vertical velocity. Also, it is concluded that the compression of the isotherms and isentropic lines is identical in the same points. This illustrates that the generation of entropy at this point is due to the temperature gradient.

In Fig. 5, the local Nu number calculated on the cold wall of the enclosure is displayed for various Ras and ${\text{Ha}} = 20, \;\gamma = 45,\; \varphi = 0.03$. At low Ra, the Nu is a line. In this state, the conduction is the dominant process of heat transfer which caused obtaining the constant HTR on the wall. The Nu intensifies in the upper section of the wall with low temperature and diminishes in the lower part by enhancing the Ra. It is because of that the process of heat transfer converts to the convection mode by augmenting the Ra. Whenever the Ra enhances, the vortex formed in the enclosure becomes faster causing an enhancement in free convection mechanism. In the top section of the wall, where the hot fluid collides with the wall with low temperature for the first time, there is a high temperature difference. So, the HTR is high in this area. By moving the fluid throughout the wall with low temperature and reducing its temperature, the temperature gradient also diminishes, which finally causes a decrease in the HTR.

Fig. 5

The local Nu number calculated on the wall with the low temperature of the enclosure of distinct Ra and ${\text{Ha}} = 20,\; \gamma = 45, \;\varphi = 0.03$

In Table 7, the changes in the ${\text{Nu}}_{\text{M}}$ calculated on the wall with low temperature, the overall generation of entropy and the Be are presented for ${\text{Ha}} = 20, \;\gamma = 45,\; \varphi = 0.03$ and distinct Ras. It was shown that the ${\text{Nu}}_{\text{M}}$ enhances by increasing the Ra. This is because of an enhancement in the velocity of fluid inside the enclosure by augmenting the buoyancy force, which causes an enhancement in the HTR. As the flow velocity intensifies, the mechanism of heat transfer converts from conduction to convection mode and causes an enhancement in the HTR. As the Ra rises, the overall generation of entropy enhances as well as the HTR. As Ra rises, the vortex velocity inside the enclosure intensifies. Therefore, the velocity gradient intensifies and the generation of entropy due to viscous dissipation intensifies. The temperature difference intensifies by augmenting the Ra and leads to an enhancement in thermal generation of entropy. The entropy of the MF also intensifies because of the high velocity in the cavity. Therefore, overall generation of entropy enhances by increasing its three parts. It was shown that the Be reduces by enhancing the Ra. The Be is the proportion of thermal entropy and overall generation of entropy. Overall generation of entropy intensifies by enhancing the Ra. Thermal entropy also intensifies with the Ra, but since the increase in the overall generation of entropy is greater than thermal entropy, the Be diminishes based on its definition.

Table 7 The ${\text{Nu}}_{\text{M}}$ calculated on the wall with low temperature, overall generation of entropy and the Be for ${\text{Ha}} = 20,\;\gamma = 45,\; \varphi = 0.03$ and various Ras

Changing Ha

In Fig. 6, streamlines, isotherms and isentropic lines are displayed for ${\text{Ra}} = 10^{5} ,\; \gamma = 45, \;\varphi = 0.03$ and distinct Ha. It can be noted that streamlines and the vortex strength inside the enclosure decrease by enhancing the Ha. By applying a MF, a new force was produced which is called the Lorentz force. This force prevents the motion of fluid molecules and keeps them stationary. Therefore, the Lorentz force is applied against the buoyancy force and prevents the vortex velocity. When the Ha rises, the Lorentz force enhances, resulting in low fluid velocity in the enclosure which reduces the strength of the vortex. Isothermal lines show that the compression of the isotherms diminishes close to the fixed-temperature walls and become more regular with augmenting the Ha. An ascent in the Ha causes an enhancement in the fluid velocity in the enclosure. As a result, mechanism of free convection is weakened and the conduction mode is dominant. This can reduce the HTR. Also, the temperature difference close to the walls diminishes with decreasing the fluid velocity due to the lower HTR by reducing the vortex’s strength. It is also concluded that the compression of the isentropic lines diminishes with the Ha. As the Ha rises, the temperature and velocity difference decrease. This is concluded from the flow fields and isothermal lines. Therefore, the values of thermal generation of entropy and generation of entropy due to viscous dissipation decrease. Hence, the amount of overall generation of entropy is also reduced leading to a decrement in the compression of the isentropic lines in the enclosure. Since the fin’s bottom and the top wall of the low-temperature wall have high temperature difference, the generation of entropy is also higher in these places.

Fig. 6

Streamlines, isothermal lines and entropy generation for Ra = 10⁵, γ = 45, φ = 0.03 and various Ha

In Fig. 7, the local Nu calculated on the low-temperature wall is shown for various Ha and ${\text{Ra}} = 10^{5} , \;\gamma = 45, \;\varphi = 0.03$. It was shown that the local Nu number reduces by enhancing the Ha. For a constant Ha, the local Nu number on the wall enhances by augmenting the wall height. The reason is that the hot fluid collides with the cold wall in the top section of the hot wall for the first time, and higher temperature gradient rests in an enhancement in the HTR. The HTR is reduced by moving the fluid on the low-temperature wall and reducing the temperature gradient. As the Ha intensifies, the Lorentz force intensifies and the fluid velocity in the enclosure diminishes. The temperature difference also diminishes with decreasing the fluid flow velocity. As a result, the local Nu number diminishes by increasing the Ha.

Fig. 7

The local Nu number calculated on the low-temperature wall for various Ha and ${\text{Ra}} = 10^{5} ,\; \gamma = 45,\; \varphi = 0.03$

In Table 8, the variations of ${\text{Nu}}_{\text{M}}$ calculated on the low-temperature wall, overall generation of entropy and the Be are shown for ${\text{Ra}} = 10^{5} ,\; \gamma = 45,\; \varphi = 0.03$ and various Ha. While the Ha rises, the overall generation of entropy and ${\text{Nu}}_{\text{M}}$ decrease. The Lorentz force prevents the formation of the vortex, and eventually the vortex strength diminishes by augmenting the Ha. When the velocity of fluid diminishes, the process of heat transfer converts to conduction and the Nu number diminishes. Also, the temperature gradient diminishes close to the cold wall causing a decrement in the HTR. The velocity and temperature gradients decrease by decreasing the vortex velocity. Thus, the values of thermal generation of entropy and generation of entropy due to viscous dissipation decrease. The generation of entropy due to the MF also changes a little. It is because of that the velocity reduces by increasing the Ha, which does not vary the generation of entropy because of the MF. Because this part of generation of entropy is the Ha, multiply the Y-component velocity in the chamber. Hence, the overall generation of entropy reduces by 39% with the decrement of two parts of the overall generation of entropy. The Be intensifies by increasing the Ha. Since the Be is the proportion of thermal entropy and the overall generation of entropy, the Be intensifies by decreasing the overall generation of entropy. It is worth noting that the thermal generation of entropy also diminishes, but the total entropy reduction is greater than the thermal one.

Table 8 The ${\text{Nu}}_{\text{M}}$ calculated on the low-temperature wall, overall generation of entropy and the Be for ${\text{Ra}} = 10^{5} ,\;\gamma = 45,\;\varphi = 0.03$ and various Ha

Changing angle of cavity

In Fig. 8, the streamlines, isotherms and generation of entropy are shown for ${\text{Ra}} = 10^{5} , \;{\text{Ha}} = 20, \;\varphi = 0.03$ and distinct enclosure angles. It is concluded that the strength of the vortex enhances first by augmenting the enclosure angle, and then the vortex is converted into two vortices. This concludes that the vortex strength enhances by augmenting in the inclination angle initially, and it is weakened by more augmenting. The reason for this increase is that the conditions for vortex formation are improved and the vortex becomes stronger by augmenting the angle of the enclosure. This can be explained as follows: The hot fin is placed in the bottom section of the enclosure, and the cold fluid with a high density is placed in the vicinity of the fin. It is heated causing an enhancement in the buoyancy force. As the angle of the enclosure intensifies, the conditions for vortex formation are weakened. The compression of the isothermal lines intensifies by enhancing the enclosure angle to 45°, indicating intensification in the temperature difference. The reason is the enhancement in the fluid velocity by augmenting the enclosure angle. With further increase in the inclination angle, the vortex is converted into two vortices, which intensifies the isothermal lines curvature. In places with higher temperature gradients, the generation of entropy is higher and the entropy field is also affected by flow and thermal fields.

Fig. 8

Streamlines, isotherms and entropy generation for ${\text{Ra}} = 10^{5} ,\;{\text{Ha}} = 20,\;\varphi = 0.03$ and distinct inclination angles

In Fig. 9, the local Nu number calculated on the low-temperature wall is drawn for various inclination angles and ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20,\; \varphi = 0.03$. It was shown that the HTR rises and then diminishes by increasing the enclosure angle. The vortex strength intensifies initially by enhancing the enclosure angle, but it diminishes by more augmenting of the angle resulting in a decrement in the HTR. At the inclination angle of 90°, two vortices are created in the enclosure. These two vortices move in opposite directions, causing the hot fluid collision with the middle of the cold wall for the first time, and the HTR becomes high in this region. The fluid moves toward the two sides of the low-temperature wall, is cooled and moves along the insulated walls to the bottom of the enclosure. Consequently, the temperature difference is low on the side of the cold wall and the local Nu number is negligible.

Fig. 9

The local Nu number calculated on the low-temperature wall for various inclination angles and ${\text{Ra}} = 10^{5} ,\;{\text{Ha}} = 20, \;\varphi = 0.03$

In Fig. 10, the ${\text{Nu}}_{\text{M}}$ calculated on the low-temperature wall is displayed for various inclination angles and ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20, \;\varphi = 0.03$. It was shown that the maximum HTR corresponds to the angle of 30°, and its minimum is related to the angle of 60°. This indicates that the best conditions for vortex formation exist at the angle of 30°, and the worst conditions are at the 60° angle. The amount of HTR from the walls depends on the strength of the vortex. The higher vortex strength leads to the better HTR in the enclosure. On the other hand, the HTR diminishes by reducing the strength of the vortex. In Fig. 11, the generation of entropy is displayed for various angles of inclination and ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20, \;\varphi = 0.03$. It is observed that the maximum generation of entropy corresponds to the angle of 30°. The maximum Nu number also happened at this angle. Since generation of entropy is temperature and velocity gradients dependent, entropy is also high when a strength vortex is formed in the enclosure. The generation of entropy because of viscous dissipation is enhanced by augmenting the velocity gradient and thermal generation of entropy which are temperature gradient dependent. As a result, it causes an enhancement in the overall generation of entropy. At the angle of 75°, the Nu number and the velocity gradient are small. The overall generation of entropy has also no significant value.

Fig. 10

The ${\text{Nu}}_{\text{M}}$ calculated on the low-temperature wall for various angles of inclination and ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20,\; \varphi = 0.03$

Fig. 11

Overall generation of entropy for various angles of inclination and ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20, \;\varphi = 0.03$

In Fig. 12, the Be is displayed for various angles of inclination and ${\text{Ra}} = 10^{5} , \;{\text{Ha}} = 20,\; \varphi = 0.03$. It can be noted that the minimum amount of the Be occurs at the angle of 45°. In a situation where thermal entropy has a smaller contribution than an overall generation of entropy, the Be diminishes. At 45°, there are good conditions for vortex formation leading to an enhancement in the velocity of fluid in the enclosure. On the other hand, the enhancement of the HTR is not much as the thermal entropy diminishes. As a result, thermal generation of entropy is less than the overall entropy. At the angle of 0°, the contribution of the thermal entropy to the overall generation of entropy is high, which indicates that the velocity gradient is low and the temperature gradient is high and causes an enhancement in the Be.

Fig. 12

The Be for distinct inclination angles and ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20, \;\varphi = 0.03$

Changing volume friction

In Fig. 13, the streamlines, isotherms and entropy generation are shown for ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20,\; \gamma = 45$ and distinct $\varphi$. It can be concluded that the strength of the vortex intensifies by enhancing the $\varphi$. The reason is that the fluid thermal conductivity intensifies with $\varphi$. The fluid has better HTR in the vicinity of the hot fin and the cold wall. This means that the fluid is hotter than before close to the hot fin and becomes colder alongside the cold wall. This results in a higher density difference leading to an enhancement in the buoyancy force in the enclosure. As the buoyancy force intensifies, the fluid rotates faster and a stronger vortex is created. The density of isothermal lines intensifies close to the high-temperature fin and the low-temperature wall. This means the higher temperature gradient in these areas, especially in the lower part of the fin and the top of the cold wall. As noted above, the fluid thermal conductivity enhances by augmenting the $\varphi$, and as a result an enhancement occurred in the temperature gradient in these areas. The density of isentropic lines intensifies due to an enhancement in the generation of entropy with increase in the temperature gradient and an enhancement in the velocity of fluid in the enclosure. This leads to an enhancement in thermal generation of entropy and the entropy because of viscous dissipation, which finally causes an enhancement in the overall generation of entropy in the enclosure.

Fig. 13

Streamlines, isotherms and entropy generation for ${\text{Ra}} = 10^{5} ,\;{\text{Ha}} = 20,\;\gamma = 45$ and distinct volume fractions of nanoparticles

In Fig. 14, the local Nu number calculated on the low-temperature wall is drawn for various $\varphi$ and ${\text{Ra}} = 10^{5} ,\; {\text{Ha}} = 20, \;\gamma = 45$. It was shown that the HTR from the low-temperature wall enhances by increasing the $\varphi$. This increase is higher in areas where better HTR is made. By increasing the $\varphi$ and the fluid thermal conductivity, more HTR occurred between the wall and the fluid. This can be best observed in the regions with higher temperature gradient. For this reason, the maximum HTR occurs in the top section of the low-temperature wall, where the heated fluid collides with the wall for the first time. In this region, the variation of fluid thermal conductivity is higher.

Fig. 14

The local Nu number calculated on the low-temperature wall for various $\varphi$ and ${\text{Ra}} = 10^{5} ,\;{\text{Ha}} = 20,\;\gamma = 45$

Conclusions

In the present work, the generation of entropy and free convection and radiation heat transfer of NF containing the Al₂O₃/water into an inclined enclosure applied by a MF was studied. A heat source was placed in the lower section of the left wall. The following results were obtained by changing the effective parameters.

• 1. The rate of the generation of entropy enhances by 288% by increasing the Ra from ${\text{Ra}} = 10^{3}$ to ${\text{Ra}} = 10^{5}$.

• 2. By increasing the Ha from 0 to 40, the ${\text{Nu}}_{\text{M}}$ is enhanced by 40%. The Be is also increased by 15%.

• 3. The maximum of ${\text{Nu}}_{\text{M}}$ occurs at the angle of inclination equal to 30°.

• 4. The minimum of generation of entropy occurs at the angle of inclination equal to 75°.

• 5. The HTR is enhanced by augmenting the $\varphi$.