Introduction

Heat exchanger (HE) is a device for exchanging heat among various streams. Various types of the HEs have been used in different places [1,2,3]. Plate heat exchangers (PHE) are a kind of the HEs which offer many advantages making it the most appropriate HE in the industrial applications. Their expandability, easy to remove and clean, high efficiency and lower costs compared to the other common HE types are among those advantages [4,5,6].

The PHEs have been subjected to many studies. The studies could be categorized into two main topics as: (a) investigating heat transfer and flow characteristics and (b) optimizing design parameters.

There are a few studies about first topic. In one of the recently published works, an experimental investigation was carried out by Nilpueng et al. [7] to study thermal performance of a PHE. They considered the roughness of the plate surface in their model and developed correlations for estimating the Nusselt number and friction factor. Their results showed that the optimum thermal performance of a PHE occurs at chevron angle of 30°. In another work, Arsenyeva et al. [8] proposed an approach to design pillow-plate HE with minimal heat transfer area. They assumed the working fluid to be single-phase and investigated heat transfer coefficient and pressure drop inside the HE. Kumar et al. [9] performed an experimental study to investigate the effect of the Reynolds number (800 ≤ Re ≤ 2300) and chevron angle on the pressure drop and efficiency of a U-type PHE. As a final result, they developed correlations for friction factor and efficiency. In another experimental work, Yang et al. [10] proposed a few correlations to calculate heat transfer characteristics of the PHE. They considered the mixture of ethylene glycol and water (EG/W) with single-phase assumption as the working fluid. The accuracy of their proposed correlation was 50%.

There are also a few numerical studies in this field. Lee and Lee [11] utilized finite volume method (FVM) and large-eddy simulation (LES) to perform a numerical study of corrugated chevron-type PHE (CPHE). They applied their model for both laminar and turbulent flow. They concluded that the optimum chevron angle is 30° and 60° for laminar and turbulent flows, respectively. Han et al. [12] investigated velocity, pressure and temperature distribution inside a CPHE using a three-dimensional numerical simulation. Dovic et al. [13] proposed a mathematical model for estimating heat transfer and flow characteristics in a sinusoidal corrugated PHE. They also presented new semi-analytical equations for Nusselt number and friction factor.

Recently, the researchers paid attention to perform investigations about the second topic in order to optimizing the heat exchangers. In one of the recently published works, Raja et al. [14] used heat transfer search (HTS) optimization algorithm for thermal–hydraulic optimization of a PHE. They applied multi-objective optimization for maximizing the total heat transfer coefficient and minimizing the total pressure drop. Their optimization results indicate 98.2% and 72.1% reduction in heat transfer coefficient and pressure drop, respectively. Farzaneh-Gord et al. [15] performed an analytical optimization of tube-in-tube helical HE. They presented optimum values of the geometrical parameters for both of the laminar and turbulent conditions. Zhou et al. [16] found the optimal design parameters of a plate-fin HE based on the second law of thermodynamics. Babaelahi et al. [17] considered the entropy generation as objective function and utilized LINMAPFootnote 1 multi-objective optimization method to find optimal design of the cross-flow plate-fin HE. In another study, Guo et al. [18] combined the entropy generation minimization (EGM) and genetic algorithm (GA) methods for optimizing some of the geometrical parameters of the shell-and-tube HE. They minimized the entropy generation number (EGN) for three different examples.

Reviewing the previous literatures and the above-mentioned studies reveals that although there are a few studies in the field of heat transfer and fluid-flow characteristics or the second-law-based analysis of a CPHE, However, no system optimization has been carried out based on the EGM approach. The current study tries to fill the gap by determining optimum parameters of a CPHE based on EGM as the optimization criteria. For bridging this gap, in present study, a complete optimization of the CPHE is carried out using EGM approach. Firstly, a comprehensive sensitivity analysis is carried out to study the effects of the important geometrical parameters and flow conditions on CPHEs performance by considering the minimizing of entropy generation rate. The optimization is carried out by using genetic algorithm and taking into account all of the geometrical and hydrodynamical parameters. Finally, based on the optimization process, a useful correlation is developed for finding optimum Reynolds number. The correlation could be useful during CPHE operation.

Methodology

Problem statement and geometry

The CPHE could be studied based on the only first or both the first and the second law of thermodynamics. In the researches, which are based only on the first law of thermodynamics, despite improving heat transfer, the pressure drop also increases. In the other words, the first-law-based analysis investigates only heat transfer characteristics of a HE and doesn’t give any information about the pressure drop and mechanical work lost [19,20,21,22]. However, in designing real systems, the impact of both factors (heat transfer and pressure drop) should be considered for finding optimal conditions.

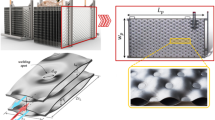
Bejan [23] was the first who proposed, in 1995, an optimization method (called EGM method) based on the second law of thermodynamics. The method could be bridged the gap between fluid flow, heat transfer and thermodynamics [24,25,26,27,28]. The main objective of the present study is to propose a thermal optimization of the CPHE (with the schematic of Fig. 1a) based on the second law of thermodynamics employing EGM approach. As it can be seen in this figure, there are two fluids which a certain amount of heat is exchanged between them (a constant heat flux is mounted from the hot fluid to the cold fluid). The CPHEs have wavy walls. Those corrugations improve heat transfer along with increasing frictional losses. Consequently, the target function (for optimization process) should be contained both of the thermal and frictional losses.

Fig. 1
figure 1

A schematic sketch of the a CPHE, b plate and design parameters

Full size image

The entropy generation represents the level of irreversibility during a process [23]. It could be employed as a criterion for accessing the performance of the thermal devices [23]. In general, the entropy generation is composed of two terms: thermal and frictional entropy generations. The first term (thermal) represents the irreversibility due to heat transfer, and the second term (frictional) is related to the irreversibility due to the fluid flow. Therefore, less entropy generation leads to the better system performance [29,30,31,32,33].

Considering real CPHE systems which are used previously [34, 35], the effect of the geometrical parameters is found to be important in a wide range including: The corrugation of V shape embossed on the plates which is termed as chevron plate angle (30° ≤ β ≤ 60°); the surface enlargement factor, ϕ, which is defined as the ratio of actual heat transfer area to the projected area (1.1 ≤ ϕ ≤ 1.4); the dimensionless plate width, \({\mathcal{W}}\), which is obtained as the ratio of plate width to the equivalent diameter (19 ≤ \({\mathcal{W}}\) ≤ 79). The initial value of the other geometric parameters is considered as de= 5.08 mm (equivalent diameter) and t = 0.6 mm (plate thickness). These parameters are presented schematically in Fig. 1b.

Problem formulation

It should be noted that the entropy generation within the CPHE, as a thermodynamic system, is selected as target function for optimization purpose in the current study. As a result, in the first step, the entropy generation should be calculated considering the effective parameters. The entropy generation rate for an internal fluid flow could be written as Eq. (1) [23, 36]. Details about the derivation process of Eq. (1) are presented in “Appendix 1”.

$$\dot{S}'_{\mathrm{gen,tot}} = \dot{S}'_{{{\text{gen}},\Delta {\text{T}}}} + \dot{S}'_{{{\text{gen}},\Delta {\text{P}}}} = \frac{{q'^{2} d_{\mathrm{e}} }}{{4T^{2} \dot{m}C_{\mathrm{p}} {\text{St}}}} + \frac{{2\dot{m}^{3} f}}{{\rho^{2} Td_{\mathrm{e}} A_{\mathrm{c}}^{2} }}$$
(1)
$$St = \frac{Nu}{{\text{Re} \Pr }},\quad A_{\mathrm{c}} = \frac{{d_{\mathrm{e}} w}}{2}$$
(2)

in which the parameters \(q^{\prime}\), \(T\), \(\dot{m}\), \(C_{\mathrm{p}}\), \(St\), f, \(\rho\) and Ac represent heat flux per unit length, average flow temperature, mass flow rate, fluid specific heat, Stanton number, friction factor, fluid density and channel flow cross-sectional area, respectively. Substituting Eq. (2) into Eq. (1), the entropy generation rate per unit length could be rewritten as Eq. (3) [37,38,39].

$$\dot{S}'_{\mathrm{gen,tot}} = \frac{{q^{2} d_{\mathrm{e}} Pr}}{{2wT^{2} \mu C_{\mathrm{p}} Nu}} + \frac{{8\dot{m}^{3} f}}{{\rho^{2} Td_{\mathrm{e}}^{3} w^{2} }}$$
(3)

For analyzing the results in a good manner, it would be better to present the entropy generation as a dimensionless parameter. For this purpose, the following dimensionless parameters are considered:

$$Q = \frac{{q{\prime}}}{Tk},\Psi^{2} = \frac{{q{\prime}^{2} \rho^{2} \dot{m}^{2} }}{{kT\mu^{5} }} \left( {\frac{d_{\mathrm{e}}}{w}} \right)^{4}$$
(4)

Combining these dimensionless parameters with Eq. (3), the dimensionless entropy generation rate could be written as:

$$N_{\mathrm{g,tot}} = N_{{{\text{g}},\Delta {\text{T}}}} + N_{{{\text{g}},\Delta {\text{P}}}} = \frac{1}{2Nu} + \frac{{Re^{5} f}}{{4\Psi^{2} }}$$
(5)

in which:

$$N_{\mathrm{g,tot}} = \frac{{\dot{S}'_{\mathrm{gen,tot}} }}{{\frac{{k{\text{Q}}^{2} }}{{\mathcal{W}}}}} ,\quad \text{Re} = \frac{{\dot{m}d_{\mathrm{e}} }}{{A_{\mathrm{c}} \mu }} = \frac{{2\dot{m}}}{w\mu }$$
(6)

where \({\mathcal{W}} = w/d_{\mathrm{e}}\) is the dimensionless plate width.

In the EGM approach of the second-law-based analysis, two important parameters (Bejan number, Be, and irreversibility distribution ratio, Φ) are used to evaluate the contribution of the thermal and frictional irreversibility in the total irreversibility. These dimensionless numbers are defined as Eqs. (7) and (8), respectively [40, 41].

$$Be = \frac{{\dot{S}_{{{\text{gen}},\Delta {\text{T}}}} }}{{\dot{S}_{\mathrm{gen,tot}} }} = \frac{{N_{{{\text{g}},\Delta {\text{T}}}} }}{{N_{\mathrm{g,tot}} }}$$
(7)
$$\Phi = \frac{{\dot{S}_{{{\text{gen}},\Delta {\text{P}}}} }}{{\dot{S}_{{{\text{gen}},\Delta {\text{T}}}} }} = \frac{{N_{{{\text{g}},\Delta {\text{P}}}} }}{{N_{{{\text{g}},\Delta {\text{T}}}} }}$$
(8)

For determining heat transfer and pressure drop, the following correlations are used in present study to evaluate Nusselt number and friction factor [35]. These correlations are accurate for laminar and turbulent flow (2.6 ≤ Pr ≤ 6.4 and 600 ≤ \({\text{Re}}\) ≤ 104) through CPHEs with a uniform heat transfer per unit length from the hot fluid [35].

$$\begin{aligned} Nu & = \left[ {0.2668 - 0.006967\beta + 7.244 \times 10^{ - 5} \beta^{2} } \right] \times \left[ {20.78 - 50.94\phi + 41.16\phi^{2} - 10.51\phi^{3} } \right] \\ & \quad \times Re^{{\left( {0.728 + 0.0543\sin \left[ {\left( {\pi \beta /45} \right) + 3.7} \right]} \right)}} Pr^{1/3} \left( {\frac{\mu }{{\mu_{\mathrm{w}} }}} \right)^{0.14} \\ \end{aligned}$$
(9)
$$\begin{aligned} f & = \left[ {2.917 - 0.1277\beta + 2.016 \times 10^{ - 3} \beta^{2} } \right] \times \left[ {5.474 - 19.02\phi + 18.93\phi^{2} - 5.341\phi^{3} } \right] \\ & \quad \times Re^{{ - \left( {0.2 + 0.0577\sin \left[ {\left( {\pi \beta /45} \right) + 2.1} \right]} \right)}} \\ \end{aligned}$$
(10)

Finally, Fig. 2 presents the procedure for calculating the system entropy generation in order to study effects of investigated parameters.

Fig. 2
figure 2

The procedure of the problem formulation

Full size image

Optimization using genetic algorithm

Generally, the systematic formulation of an optimization problem requires the three basic steps. First, an objective function should be identified. Secondly, there is need to characterize a set of design variables which can influence the optimization goals. Finally, a set of restriction(s) should be applied to the design variables in order to constrain the optimization problem.

There are several optimization approaches which could be classified as enumerative methods, calculus methods and heuristic methods. As one of the most precise heuristic methods, genetic algorithm (GA) is widely used for optimizing many systems. GAs are computerized optimization algorithms designed based on the mechanics of natural genetics and natural selection and known as nontraditional optimization methods. There are some fundamental differences between GA and traditional methods which could be divided into five items:

  1. 1.

    GA works on the coding of parameters, instead of parameters.

  2. 2.

    GA exploits the coding similarities to achieve a parallel search.

  3. 3.

    GA works on a population of points, instead of a single point. That is why GA is likely to find global solutions.

  4. 4.

    GA does not require any derivative or auxiliary information which this benefit extends the application of GA to a wide variety of problem domains and that is why GA is robust.

  5. 5.

    GA uses probabilistic transition rules, instead of deterministic transition rules which this option reduces the bias in the search. Initially, the search direction is random and as repetition progresses, GA obtains a directed search adaptively.

Because of the mentioned advantages, the current investigation employed GA as an optimization algorithm to find optimum PHEs parameters by minimizing entropy generation.

As it is discussed in the previous sections, the entropy generation consists of two terms: the first term is due to heat transfer and the second one is the impact of pressure drop caused by fluid friction. Consequently, the entropy generation could be studied as a comprehensive objective function in order to optimize the HEs [42,43,44]. Based on the thermodynamics laws, lower system irreversibility follows from less entropy generation and it results in a higher thermal efficiency. A diagram of the optimization process is drawn in Fig. 3.

Fig. 3
figure 3

Flowchart diagram of the optimization procedure

Full size image

It should be noted that there are two basic kinds of optimization design variables of any energy system such as HEs. The first kind of optimization design variables is related to conditions of the fluid flow, and the second one is about geometrical parameters. If optimization process is applied for a constructed PHE which currently is in use as a part of cooling or heating facilities, we just utilize conditions of the fluid flow as optimization variables and the geometrical parameters (which describe structural features of a system) are fixed during the process and they can’t be varied. On the other hand, for designing a PHE, we can utilize both conditions of the fluid flow and the geometrical parameters as optimization variables.

Model validation

In this section, the effort has been made to validate the calculations by comparison with the available experimental data. Focke et al. [45] performed experiments and presented the Nusselt number and friction factor at different \({\text{Re}}\) numbers. Here, the results of the entropy generation in present study are compared (at a compatible conditions) with the entropy generation which are calculated based on experimental data of Focke et al. [45]. The root-mean-squared error (RMSE), defines as Eq. (11), has been employed to evaluate the accuracy of the results.

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} e_{\mathrm{i}}^{2} }$$
(11)

where the parameter ei represents the difference of the experimental and the calculated values.

Figure 4a, b depicts the comparison of the entropy generation between this study and the experimental data reported in [45]. As it can be seen in these figures, the results of the present approach agree well with the experimental data. Comparison of the results indicates that the amount of RMSE is 0.061931, 0.008516 and 0.06300 for thermal, frictional and total entropy generations, respectively. This demonstrates the accuracy of the present approach for calculating entropy generation.

Fig. 4
figure 4

Comparison of the a thermal and frictional entropy generations, b total entropy generation, between the results of the proposed approach and the experimental data [45]

Full size image

Results and discussion

In this section, the effects of several geometrical and operational parameters (that are applied in practice) on the entropy generation of the CPHEs are presented.

Sensitivity analysis

Investigating the effect of plate chevron angle and surface enlargement factor

Figure 5a–c illustrates the effect of plate chevron angle β on dimensionless total entropy generation, thermal/frictional entropy generations and Be number, respectively. As it can be seen in Fig. 5a, chevron angle plays an important role in the total entropy generation. More importantly, the graph shows that for each enlargement factor ϕ, there is a chevron angle in which minimum entropy generation occurs. Obviously, by minimizing entropy generation, exergy lost is minimized, which means the system efficiency is improved. It is also worth noting that, as enlargement factor ϕ increases, the optimum chevron angle decreases. For instance, for ϕ = 1.27, 1.29 and 1.31, the minimum entropy generation occurs at β = 46°, 41° and 37.5°, respectively. The reason can be attributed to the fact that the increase in enlargement factor as well as chevron angle leads to higher level of turbulence through the HE channel. Therefore, for a plate with low enlargement factor, large chevron angle is required in order to increase turbulence intensity, which is essential for enhancement of heat transfer coefficient of the plate. On the contrary, increasing chevron angle for a plate with high enlargement factor would significantly increase pressure lost, while heat transfer improvement would be negligible. Therefore, according to the second law of thermodynamics, high chevron angles should be utilized in conjugation with large corrugation pitch and vice versa. According to Fig. 5b, as expected, by increasing β, frictional entropy generation increases and thermal entropy generation decreases. Consequently, based on Eq. (7), the reduction of thermal entropy generation causes the reduction of Be number (see Fig. 5c).

Fig. 5
figure 5

Variations of a dimensionless total entropy generation, b thermal and frictional entropy generations, c Bejan number, in terms of plate chevron angle

Full size image

Investigating the effect of plate width

Figure 6a shows the effect of dimensionless plate width (\({\mathcal{W}} = w/d_{\mathrm{e}}\)) on the dimensionless entropy generation rate. This figure investigates this matter for three different chevron angles from β = 30° to β = 60°. As it can be seen, lower chevron angles result in lower rates of the entropy generation. In this case, the minimum \(N_{\mathrm{g,tot}}\) varies from 0.0075 up to 0.0078 for different chevron plate angles. On the other hand, the dimensionless width corresponding to the \(\left( {N_{\mathrm{g,tot}} } \right)_{ \hbox{min} }\) value decreases significantly so that for β = 30° the \({\mathcal{W}}_{ \hbox{min} }\) is equal to almost 51, while a lower optimum dimensionless width of approximately 30 is observed for β = 60°. Evidently, in this case, both of the entropy generation rate and minimum plate width number change at uniform paces as the surface enlargement factor (ϕ) varies.

Fig. 6
figure 6

Variations of a dimensionless entropy generation rate, b thermal and frictional entropy generations, c Bejan number, in terms of dimensionless plate width

Full size image

Figure 6b illustrates the variations of entropy generation rate as a function of dimensionless plate width for a particular value of β and \(\phi\). As it is expected, frictional entropy generation increases with \({\mathcal{W}}\) and thermal entropy generation decreases by increasing plate width. It is noticeable that by increasing the width of plate, the friction factor based on Eq. (7) “Appendix 1” should increase as well as the generation of frictional entropy. Additionally, when the surface of heat transformation rises, thermal gradient between the surface and fluid flow will decrease; therefore, we expect thermal entropy generation reduces.

Figure 6c shows the variations of Be number with dimensionless plate width for different chevron plate angles at a certain ϕ. As it can be seen in Fig. 6c, the Be number decreases by increasing \({\mathcal{W}}\) and it could be understood that the Be number has the lower value at higher chevron plate angles. For example, at \({\mathcal{W}}\) = 40, increasing chevron plate angle from β = 30° to β = 60° causes a reduction of 33.5% in Be number.

Based on Eq. (7) and the above-mentioned contents, it could be realized that by increasing the amount of frictional entropy generation, the Be value becomes smaller.

Investigating the effect of Prandtl number

Variations of dimensionless entropy generation rate against Pr number for three different chevron angles are depicted in Fig. 7a. As it can be observed, the minimum plate chevron angle decreases by increasing Pr number. Here, the optimum Pr for β = 30°, 45° and 60° is 4.7, 3.8 and 3.5, respectively. Accordingly, for fluids with low Pr number such as molten metals, high chevron angle plates are preferable and for fluids with large Prandtl such as oils, low chevron angle plates are recommended.

Fig. 7
figure 7

Variations of a dimensionless entropy generation rate, b thermal and frictional entropy generations, c Bejan number, in terms of Prandtl number

Full size image

In Fig. 7b, the effect of Pr number on thermal and frictional entropy generations is studied. As it can be seen, the thermal entropy generation decreases by increasing Pr number. According to Eq. (9), Nu number is related to fluid Pr number. Therefore, increasing Pr number enhances the heat transfer coefficient, and consequently, thermal entropy generation decreases. Another key point in Fig. 7b is that frictional entropy generation is more significant at higher Pr numbers. It is noted that in order to keep Re as a constant value, mass flow rate should be increased when Pr increases. Clearly, higher mass flow through the HE causes higher pressure drop, which increases frictional entropy generation.

Based on the above statements (decreasing \(\dot{S}_{{{\text{gen}},\Delta {\text{T}}}}\) with Pr number), Fig. 7c indicates that by increasing Pr number, Be number decreases. So, increasing Pr number from 2.5 to 6.5 causes 23.91%, 35.28% and 48.73% reduction in Be number for β = 30°, β = 45° and β = 60°, respectively.

Investigating the effect of Reynolds number

Figure 8a displays variations of \(N_{\mathrm{g,tot}}\) with Reynolds number for the specific values of ϕ = 1.29 and \({\mathcal{W}}\) = 40 at various chevron plate angles. As it could be realized, there is an optimum Reynolds number for each \(\beta\), which minimizes \(N_{\mathrm{g,tot}}\). In the other words, this figure shows that the amount of entropy generation drops as Reynolds number increases before the minimum \(N_{\mathrm{g,tot}}\) and after the minimum point, \(N_{\mathrm{g,tot}}\) increases as Reynolds number increases. Also, the minimum entropy generation point is significantly affected by the chevron plate angel. So, in order to optimize the system in the permitted range, for Re < 4750 the biggest \(\beta\) and for Re > 4750 the smallest β should be elected.

Variations of the thermal and frictional entropy generations as a function of Reynolds number are plotted in Fig. 8b (for ϕ = 1.29, β = 45° and \({\mathcal{W}}\) = 40). As it can be seen, increasing the Reynolds number causes an increment in the thermal entropy generation and a decline in the entropy generation of frictional. Analyzing the results indicates that the thermal and frictional entropy generations have same order of magnitude. But, based on this figure, for Re < 4900, the amount of the thermal entropy generation is greater than the amount of frictional one (\(\dot{S}_{{{\text{gen}},\Delta {\text{T}}}} > \dot{S}_{{{\text{gen}},\Delta {\text{P}}}}\)) and for Re > 4900, the viscous entropy generation is greater than the entropy generation due to heat transfer (\(\dot{S}_{{{\text{gen}},\Delta {\text{T}}}} < \dot{S}_{{{\text{gen}},\Delta {\text{P}}}}\)).

Fig. 8
figure 8

Variations of a dimensionless entropy generation rate, b thermal and frictional entropy generations, c Bejan number, in terms of Reynolds number

Full size image

Figure 8c presents variations of Be number in terms of Reynolds number for different chevron angles at a certain surface enlargement factor (ϕ = 1.29) and constant dimensionless plate width (\({\mathcal{W}}\) = 40). It could be understood that for bigger chevron angles, Be number has a lower grade. For instance at Re = 5000, the amount of Be is decreased around 45% if β = 60° selected instead of β = 30°. As it can be obtained, increasing the Reynolds number at specific \(\beta\) causes an increment in the frictional entropy generation and a decrease in the thermal entropy generation; so based on the irreversibility distribution ratio formula (Eq. (8)), increasing Reynolds number causes more irreversibility.

Optimization results

In this section, the efforts have been made to optimize design parameters using the EGM approach and the GA method. As mentioned in previous sections, the optimization process has been done for two cases:

  1. (1)

    A CPHE is under construction, and the objective is to design the optimum parameters.

  2. (2)

    A constructed CPHE is in operation mode, so only operational parameters need to be optimized.

Due to the existence of powerful toolbox for GA optimization method in Matlab software, the optimization problem is solved by using Matlab software. According to the reasonable range of the design variables, a random initial population of the design variables is produced. Then the iterative search process is given as shown in Fig. 9 until the stop measures are satisfied. The maximum number of generations is fixed at 500. The normalized geometric selection, arithmetic crossover, and non-uniform mutation are operated. After 500 generations, the optimum solution of the CPHE optimization design problem under consideration is found as \(\left( {N_{\mathrm{g,tot}} } \right)_{\mathrm{opt}}\) = 0.006775. The optimum values of the investigated parameters are presented in Table 1. The difference in the fitness function with regard to the number of generations is represented in Fig. 9. It is obvious that the fitness value is essentially stable and the solution has been converged.

Fig. 9
figure 9

Convergence of the optimization process (fitness = min(Ng,tot))

Full size image
Table 1 The optimum values of the parameters after the evolution of 500 generations
Full size table

By considering the fact that the geometric parameters are passive (i.e., unchangeable for a constructed system), the provided results for geometric parameters can only be used before the construction of the HE. For a constructed HE, the only variable parameter with an effect on system entropy generation is the Reynolds number. Therefore, having a Reynolds number corresponding to the optimum amount of entropy generation can be particularly beneficial for the industry. Accordingly, in this section, a correlation is developed to estimate the optimum Reynolds number in terms of geometric parameters β and ϕ (see Fig. 10 and Eq. (12)). The error analysis including RMSE= 0.003986 and R2 = 0.9965 demonstrates the goodness of the curve fitting process (the required formula for determining R2 is presented in “Appendix 2”).

$$Re_{\mathrm{opt}} \left( {\beta ,\phi } \right) = m_{00} + m_{10} \beta + m_{01} \phi + m_{20} \beta^{2} + m_{11} \beta \phi + m_{02} \phi^{2} + m_{30} \beta^{3} + m_{21} \beta^{2} \phi + m_{12} \beta \phi^{2} + m_{03} \phi^{3} + m_{40} \beta^{4} + m_{31} \beta^{3} \phi + m_{22} \beta^{2} \phi^{2} + m_{13} \beta \phi^{3} + m_{04} \phi^{4}$$
(12)

in which the values of the 15 constant coefficients are listed in Table 2. Also, it should be noted that the constant amounts of Pr = 4.485 and \({\mathcal{W}}\) = 50.79 are received from optimization process (which are listed in Table 1)

Fig. 10
figure 10

Optimum values of the Reynolds number and fitted curve as a function of the geometrical parameters

Full size image
Table 2 Details of the constant coefficients in Eq. (12)
Full size table

Concluding remarks

This work intends to optimize CPHEs geometry and flow conditions based on the entropy generation minimization approach. For this objective, a wide Reynolds range including laminar and turbulent flow within CPHEs is considered and the amount of entropy generation is calculated. The effect of the chevron plate angle (β), surface area enlargement factor (ϕ), dimensionless plate width (\({\mathcal{W}}\)), Prandtl number (Pr) and Reynolds number (Re) are investigated. The following remarks can be expressed as key conclusions:

  • It is found out from the sensitivity analysis that for each ϕ there is a β in which minimum entropy generation occurs. For instance, for ϕ = 1.27, 1.29 and 1.31, minimum entropy generation occurs at β = 46°, 41° and 37.5°, respectively.

  • The amount of \(\left( {N_{\rm g,tot} } \right)_{\rm opt}\) and \(Pr_{\rm opt}\) decreases by increasing β (at certain amount of the other parameters). For example, \(Pr_{\rm opt}\) for \(\beta\) = 30°, 45° and 60° is 4.7, 3.8 and 3.5, respectively.

  • For designing a CPHE at the optimal conditions, the geometrical and fluid-flow parameters can be selected as βopt= 40.564°, ϕopt= 1.362, \({\mathcal{W}}_{\rm opt}\) = 50.79, \(Pr_{\rm opt}\) = 4.485 and \({Re}_{\rm opt}\) = 2881 (within the range of the investigated parameters in present study).

  • As a final result, a correlation is developed for constructed CPHEs to estimate \({Re}_{\rm opt}\) in terms of geometric parameters β and ϕ. The goodness quantities for this curve fitting are RMSE = 0.003986 and R2 = 0.9965.