Introduction

The existence of very small-sized (micro or millimeter) particles or impurities in the fluid is quite natural. Such fluids are called the dusty fluids. Due to these dust particles, the thermal property of such fluids is increased [1]. The suspension of dust particles in the base fluid can degrade its efficiency in the devices or machines, but still it is beneficial in respect of fluid flow and increment in thermal conductivity. There are several scientific and engineering processes where the involvement of dusty particles plays an important role such as slurries movements in chemical and nuclear processes, lunar ash flows and powder technology, oceanography , medicine, blood flow in arteries, steel manufacturing industry, waste water treatment, dust in gas cooling systems and corrosive particles in engine oil flow. Initially, Farbar and Morley [2] analyzed experimentally about the transport of heat for the gas-solid suspensions. Stability analysis and influences of dust particles in viscous and laminar flow were first time studied by Saffman [3]. Hazem et al. [4] studied the combined effects of viscous dissipation, Hall current, Joule heating and ion slip effects on unsteady Couette flow of a dusty fluid which is electrically conducting and incompressible with strong magnetic field and injection suction phenomenon. They found that the dust velocities are highly influenced by Hall and ion-slip effects. Koneri et al. [5] have discussed numerically about the dusty upper-convected Maxwell fluid over the convectively heated sheet with nonlinear thermal radiation, viscous dissipation and magnetic field. Shooting method is opted to solve the problem. Unsteady dusty nanofluid flow over the permeable exponentially stretching sheet with strong magnetic field and radiation effects was covered by Sandeep et al. [6]. Copper and copper oxide are used with dust particles. They observed the increment in heat transfer rate when the fluid particle interaction is enhanced. Pop et al. [7] addressed the dusty fluid flow over the two-dimensional shrinking surface. Problem is formulated using boundary layer approximation and solved by bvp4c. Ghadikolaei et al. [8] investigated boundary layer dusty micropolar nanofluid flow and heat transfer with MHD and thermal radiation embedded in the porous medium. They considered the \(\hbox {TiO}_{2}\) as a nanoparticles in water. Heat and fluid flow of Casson dusty fluid in the presence of nonlinear radiation over a vertical wavy cone is addressed numerically by Sadia et al. [9]. Gireesha et al. [10] considered the time-dependent flow of water-based copper nanofluid having dust particles with effective viscosity and thermal conductivity using additionally the Hall effects over the stretching sheet. It is witnessed that the heat transfer rate is increased due to the higher concentration of dust particles.

Henry Darcy, a French engineer, suggested the flow model of liquids or gases or their mixtures through a porous sand bed medium in 1856. It links the velocity of the fluid and the pressure drop during the flow. It can be stated in mathematical form as follows [11,12,13]:

$$\begin{aligned} -\frac{\hbox {d}p}{\hbox {d}x}=\frac{1}{k}\cdot \left( \mu \cdot \nu _{\mathrm{f}}\right) , \end{aligned}$$

where \(\nu _{\mathrm{f}}\) is the filtration velocity. This law works correctly for the low porosity and the fluid having smaller velocity. On the other hand, if the velocities are higher, then a discrepancy appears between the experimental data and the obtained results. Darcy’s law can only be applicable when the range of Reynold’s number is \(1\le Re\le 10\) [11, 14]. This flaw in Darcy’s law is linked with inertial impacts by Forchheimer [15] proposing the kinetic energy term [11, 12, 16].

$$\begin{aligned} -\frac{\hbox {d}p}{\hbox {d}x}=\frac{1}{k}\cdot \left( \mu \cdot \nu _{\mathrm{f}}\right) +F\cdot \left( \rho +\nu _{\mathrm{f}}^{2}\right) , \end{aligned}$$

where F is the non-Darcy coefficient also know an Forchheimer coefficient. Fluids having high flow rate in the porous medium have significant importance in engineering and industries like petroleum technology, hydrology, agriculture, mining and mineral processes, catalytic reactors, geophysics and many others [17]. Rami et al. [18] modeled mathematically the mixed convective non-Darcian flow through a vertical flat plate under mass and thermal diffusion effects embedded in a porous medium and found its similarity solutions. Sobieskil and Trykozko [19] conduct an experimental study based on the pressure drop and flow rate in which the Forchheimer and permeability coeffcients are studied. They have correctly determined the ranges for Darcy’s and Forchheimer’s laws and determined their related issues. Hayat et al. [20] conducted a study on the Darcy–Forchheimer viscoelastic fluids flowing with Cattaneo-Christov heat flux and homogeneous heterogeneous reactions over the sheet. They have used two different types of viscoelastic fluids and compared their results. Darcy–Forchheimer flow of MHD Maxwell nanofluid over the convective sheet is discussed by Taseer et al. [21]. Brownian motion and thermophoresis effects along with zero mass flux condition is also considered. The work of Taseer et al. [21] is extended by Sajid et al. [22] in which the effects of nonlinear thermal radiation, variable thermal conductivity and activation energy are also incorporated. Three-dimensional convective flow of Darcy–Forchheimer porous medium over bidirectional stretching sheet in the presence of water-based single- and double-walled carbon nanotubes is discussed by Abdullah [23].

In recent era, the use of conventional fluids in industries for the heat transfer purpose is almost ceased, and these are replaced with nanofluid, comprising of pure liquid and nanosized particles [24,25,26,27,28,29,30,31,32,33,34]. The main purpose of the fluid flow is to analyze the heat and mass transfer over different geometries [35,36,37,38]. After numerous experiments, it is believed that different nanoparticles have different capacity to conduct heat. Shape and size of the nanoparticles are also matters [39]. Experiments yield about six times greater thermal conductivity of the nanofluid in the presence of carbon nanotubes (CNT) instead of other nanoparticles [40]. Carbon nanotubes are in cylindrical shape and are crystalline allotropes of carbon. Their uni-dimensional structure enhances their mechanical and electronic properties [41, 42]. Choi and his coworker [43] first time experimentally reported the enhanced thermal properties of base fluid in the presence of cylindrical carbon nanotubes. The applications of CNT can be seen in nanotechnology, I/R optics industries, semiconductor devices, ultra-capacitors, atomic force microscope, radar-absorbing coating, etc. Single-walled and multiwalled CNT are two basic categories of carbon nanotubes. In the present article, we have focused the single-walled carbon nanotubes, because of their ability to form a network of carbon atoms with surrounding atoms and thereby responsible to increase the thermal conductivity.

The literature review reveals that there have been studies about the CNTs in varied geometries. However, fewer are reported in case of dust particles. The main purpose of this dissertation is to model and analyze the Darcy–Forchheimer time-dependent flow and heat transfer of water-based SWCNTs over the convective sheet and in the presence of nonlinear thermal radiation, heat generation/absorption and Hall current effects. Due to the impurities, the dust phase of nanofluid is also discussed in detail. To the best of our knowledge, no such study is conducted before in the literature. A mathematical model is solved numerically by bvp4c, a built-in MATLAB function. The Nusselt number and the skin friction coefficients are computed and discussed. Results are calculated and presented in tables and graphs. Finally, the prominent findings are highlighted.

Mathematical formulation

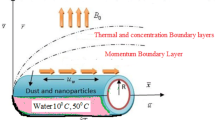
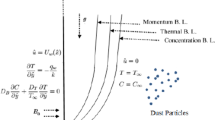
Time-dependent two-dimensional non-Darcian laminar, rotational and incompressible water-based CNT over the convectively stretching sheet is considered to flow along the x-axis. Strong magnetic field which is responsible to generate the Hall current effects is applied normal to the flow by ignoring the induced magnetic field. During the formulation of energy equation, the Khanafer Vafai Lightstone (KVL) model is used for the effective thermal conductivity and viscosity of the fluid, along with nonlinear thermal radiation and heat generation absorption effects. The presence of dust particles in the fluid is assumed to be uniform in size and conducting which are initially in rest. The number density of dust particles is consistence all through the stream. The mixture theory and phenomenological laws for the CNT are as follows [44]: Mixture theory

$$\begin{aligned}&\rho _{\mathrm{nf}}=\left( 1-\varkappa \right) \rho _{\mathrm{f}}+\varkappa \rho _{\mathrm{s}}, \end{aligned}$$
(1)
$$\begin{aligned}&\left( \rho \beta _{\mathrm{T}}\right) _{\mathrm{nf}}=\left( 1-\varkappa \right) \left( \rho \beta _{\mathrm{T}}\right) _{\mathrm{f}}+\varkappa \left( \rho \beta _{\mathrm{T}}\right) _{\mathrm{s}}, \end{aligned}$$
(2)
$$\begin{aligned}&\left( \rho C\right) _{\mathrm{nf}}=\left( 1-\varkappa \right) \left( \rho C\right) _{\mathrm{f}}+\varkappa \left( \rho C\right) _{\mathrm{s}}, \end{aligned}$$
(3)
$$\begin{aligned}&\sigma _{\mathrm{nf}}=\sigma _{\mathrm{f}}\left[ 1+\frac{3\left( \frac{\sigma _{\mathrm{s}}}{\sigma _{\mathrm{f}}}-1\right) \varkappa }{\frac{\sigma _{\mathrm{s}}}{\sigma _{\mathrm{f}}}+2--\left( \frac{ \sigma _{\mathrm{s}}}{\sigma _{\mathrm{f}}}-1\right) \varkappa }\right] . \end{aligned}$$
(4)

Phenomenological Laws:

$$\begin{aligned}&\frac{\kappa _{\mathrm{nf}}}{\kappa _{\mathrm{f}}}=\frac{\kappa _{\mathrm{s}}+2\kappa _{\mathrm{f}}-2\varkappa \left( \kappa _{\mathrm{f}}-\kappa _{\mathrm{s}}\right) }{\kappa _{\mathrm{s}}+2\kappa _{\mathrm{f}}+2\varkappa \left( \kappa _{\mathrm{f}}-\kappa _{\mathrm{s}}\right) }, \end{aligned}$$
(5)
$$\begin{aligned}&\frac{\mu _{\mathrm{nf}}}{\mu _{\mathrm{f}}}=\left( 1-\varkappa \right) ^{-2.5}. \end{aligned}$$
(6)

Nanofluid phase [10]:

$$\begin{aligned}&\nabla \cdot U=0, \end{aligned}$$
(7)
$$\begin{aligned}&\rho _{\mathrm{nf}}\left( \frac{\partial U}{\partial t}+\varOmega \times U+\left( U\cdot \nabla \right) U\right) =\nabla P+\nabla \left( \mu _{\mathrm{nf}}\nabla \cdot U\right) +F_{\mathrm{p}}+F_{\mathrm{b}}+J\times B, \end{aligned}$$
(8)
$$\begin{aligned}&\left( \rho C\right) _{\mathrm{nf}}\left( \frac{\partial T}{\partial t}+\left( U\cdot \nabla \right) T\right) =\nabla \left( \kappa _{\mathrm{nf}}\nabla \cdot T\right) +Q_{\mathrm{p}}. \end{aligned}$$
(9)

Dust phase:

$$\begin{aligned}&\nabla \cdot V=0, \end{aligned}$$
(10)
$$\begin{aligned}&\rho _{\mathrm{p}}\left( \frac{\partial V}{\partial t}+\left( V\cdot \nabla \right) V\right) =-\nabla P-F_{\mathrm{p}}, \end{aligned}$$
(11)
$$\begin{aligned}&\rho _{\mathrm{p}}C_{\mathrm{p}}\left( \frac{\partial T_{\mathrm{p}}}{\partial t}+\left( V\cdot \nabla \right) T_{\mathrm{p}}\right) =-Q_{\mathrm{p}}. \end{aligned}$$
(12)

The generalized Ohm’s law [45]:

$$\begin{aligned} J+\frac{\omega _{\mathrm{e}}\tau _{\mathrm{e}}}{B_{0}}\times \left( J\times B\right) =\sigma _{\mathrm{nf}}\left( E+U\times B+\frac{1}{en_{\mathrm{e}}}P_{\mathrm{e}}\right) , \end{aligned}$$
(13)

here, \(U=(u_{\mathrm{f}},v_{\mathrm{f}},w_{\mathrm{f}})\) and \(V=(u_{\mathrm{p}},v_{\mathrm{p}},w_{\mathrm{p}})\) are, respectively, the velocity vectors of fluid and dust phase, \(F_{\mathrm{p}}\) and \(F_{\mathrm{b}}\) are dust particles and body forces, respectively. Equations (7) and (10) are the continuity equations of nanofluid and dust particle flows, respectively. The right-hand side of Eq. (8) is the convective part, whereas \(\varOmega \times U\) is due to rotational flow. The first term in the left-hand side is due to the pressure gradient; the second one is viscous term. \(J \times B\) is because of the applied magnetic field. The right-hand side of Eq. (9) deals with advection, whereas the first term of left-hand side deals with conduction. Thermal interaction between dust particles and nanofluid is \(Q_{\mathrm{p}},E\) the electric field intensity, \( B=(0,B_{0},0)\)-magnetic induction. The term \(F_{\mathrm{p}}\) is the drag force between the fluid-particles and is defined as

$$\begin{aligned} F_{\mathrm{p}}=6\pi Nr_{\mathrm{p}}\mu _{\mathrm{f}}\left( V-U\right) =\frac{\rho _{\mathrm{p}}\left( V-U\right) }{\tau _{v}}, \end{aligned},$$
(14)

where the momentum relaxation time of dust phase is \(\ \tau _{v}=m_{\mathrm{p}}/6\phi v_{\mathrm{f}}r_{\mathrm{p}}\). The thermal interaction between the particles and the fluid is given by

$$\begin{aligned} Q_{\mathrm{p}}=\frac{\rho _{\mathrm{p}}C_{\mathrm{p}}\left( T_{\mathrm{p}}-T\right) }{\tau _{\mathrm{T}}}, \end{aligned}$$
(15)

and the thermal relaxation time of the dust phase is \(\tau _{\mathrm{T}}=\frac{m_{\mathrm{p}}C_{\mathrm{p}} }{4\phi r_{\mathrm{p}}}.\) After ignoring the electric field, the Eq. (13) is

$$\begin{aligned}&J_{\mathrm{x}}=\frac{\sigma _{\mathrm{nf}}B_{0}}{\left( 1+m^{2}\right) }\left( mu-w\right) , \end{aligned}$$
(16)
$$\begin{aligned}&J_{\mathrm{z}}=\frac{\sigma _{\mathrm{nf}}B_{0}}{\left( 1+m^{2}\right) }\left( u+mw\right) , \end{aligned}$$
(17)

with \(m_{\mathrm{e}}=\omega _{\mathrm{e}}\tau _{\mathrm{e}}\) is hall parameter. The governing equations in component forms are [10]:

Nanofluid phase:

See Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image
$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(18)
$$\begin{aligned}&\left( \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{ \partial u}{\partial y}\right) =\nu _{\mathrm{nf}}\left( \frac{\partial ^{2}u}{ \partial y^{2}}\right) +2\omega w+\frac{\rho _{\mathrm{p}}}{\rho _{\mathrm{nf}}\tau _{v}} \left( u_{\mathrm{p}}-u\right) \\&\quad +g\frac{\left( \rho \beta _{\mathrm{T}}\right) _{\mathrm{nf}}}{ \rho _{\mathrm{nf}}}\left( T-T_{\infty }\right) -\frac{\sigma _{\mathrm{nf}}B_{0}^{2}}{\rho _{\mathrm{nf}}\left( 1+m^{2}\right) }\left( u+mw\right) -\frac{\nu _{\mathrm{nf}}}{K^{*}} u-Fu^{2}, \end{aligned}$$
(19)
$$\begin{aligned}&\left( \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{ \partial w}{\partial y}\right) =\nu _{\mathrm{nf}}\left( \frac{\partial ^{2}w}{ \partial y^{2}}\right) -2\omega u+\frac{\rho _{\mathrm{p}}}{\rho _{\mathrm{nf}}\tau _{v}} \left( w_{\mathrm{p}}-w\right) \\&\quad -\frac{\sigma _{\mathrm{nf}}B_{0}^{2}}{\rho _{\mathrm{nf}}\left( 1+m^{2}\right) }\left( mu-w\right) -\frac{\nu _{\mathrm{nf}}}{K^{*}} w-Fw^{2}, \end{aligned}$$
(20)
$$\begin{aligned}&\left( \rho C\right) _{\mathrm{nf}}\left( \frac{\partial T}{\partial t}+u\frac{ \partial T}{\partial x}+v\frac{\partial T}{\partial y}\right) =\kappa _{\mathrm{nf}} \frac{\partial ^{2}T}{\partial y^{2}}+\frac{\rho _{\mathrm{p}}C_{\mathrm{p}}}{\tau _{\mathrm{T}}}\left( T_{\mathrm{p}}-T\right) -\frac{\partial q_{\mathrm{r}}}{\partial z}. \end{aligned}$$
(21)

Dust phase:

$$\begin{aligned}&\frac{\partial u_{\mathrm{p}}}{\partial x}+\frac{\partial v_{\mathrm{p}}}{\partial y}=0, \end{aligned}$$
(22)
$$\begin{aligned}&\rho _{\mathrm{p}}\left( \frac{\partial u_{\mathrm{p}}}{\partial t}+u_{\mathrm{p}}\frac{\partial u_{\mathrm{p}} }{\partial x}+v_{\mathrm{p}}\frac{\partial u_{\mathrm{p}}}{\partial y}\right) =\frac{\rho _{\mathrm{p}} }{\tau _{v}}\left( u-u_{\mathrm{p}}\right) , \end{aligned}$$
(23)
$$\begin{aligned}&\rho _{\mathrm{p}}\left( \frac{\partial w_{\mathrm{p}}}{\partial t}+u_{\mathrm{p}}\frac{\partial w_{\mathrm{p}} }{\partial x}+v_{\mathrm{p}}\frac{\partial w_{\mathrm{p}}}{\partial y}\right) =\frac{\rho _{\mathrm{p}} }{\tau _{v}}\left( w-w_{\mathrm{p}}\right) , \end{aligned}$$
(24)
$$\begin{aligned}&\rho _{\mathrm{p}}C_{\mathrm{p}}\left( \frac{\partial T_{\mathrm{p}}}{\partial t}+u_{\mathrm{p}}\frac{\partial T_{\mathrm{p}}}{\partial x}+v_{\mathrm{p}}\frac{\partial T_{\mathrm{p}}}{\partial y}\right) =\frac{\rho _{\mathrm{p}}C_{\mathrm{p}}}{\tau _{\mathrm{T}}}\left( T-T_{\mathrm{p}}\right) . \end{aligned}$$
(25)

The corresponding boundary conditions for the governing PDEs are

$$\begin{aligned} u\left( x,0,t\right) =U_{\mathrm{w}},v\left( x,0,t\right) =w\left( x,0,t\right) =0,T\left( x,0,t\right) =T_{\mathrm{w}}, \end{aligned}$$
(26)
$$\begin{aligned} \left. \begin{aligned}&u\left( x,y,t\right) =u_{\mathrm{p}}\left( x,y,t\right) =w\left( x,y,t\right) =w_{\mathrm{p}}\left( x,y,t\right) =0, \\&u_{\mathrm{p}}\left( x,y,t\right) =v\left( x,y,t\right) ,T\left( x,y,t\right) =T_{\mathrm{p}}\left( x,y,t\right) =T_{\infty ,} \end{aligned}\right\}\; \text {as}\;y\rightarrow \infty . \end{aligned}$$
(27)

We, now, introduce the following dimensionless variables:

$$\begin{aligned} \left. \begin{aligned}&\eta =\sqrt{\frac{b}{\nu _{\mathrm{f}}\left( 1-\alpha t\right) }}y,u=\frac{bx}{1-\alpha t}f^{\prime }\left( \eta \right) ,v=-\sqrt{\frac{b\nu _{\mathrm{f}}}{\left( 1-\alpha t\right) }}f\left( \eta \right) ,\theta \left( \eta \right) =\frac{T-T_{\infty }}{T_{\mathrm{w}}-T_{\infty }}, \\&w =\frac{bx}{1-\alpha t}h\left( \eta \right) , u_{\mathrm{p}}=\frac{bx}{1-\alpha t}F^{\prime }\left( \eta \right) ,v_{\mathrm{p}}=-\sqrt{\frac{b\nu _{\mathrm{f}}}{\left( 1-\alpha t\right) }}F\left( \eta \right) ,w_{\mathrm{p}}=\frac{bx}{1-\alpha t}H\left( \eta \right) . \end{aligned}\right\} \end{aligned}$$
(28)

Both the continuity equations are identically satisfied, while the rest of the equations are transformed as:

$$\begin{aligned}&M_{2}f^{\prime \prime \prime }+M_{1}\left( ff^{\prime \prime }-f^{\prime 2}-S\left( f^{\prime }+\frac{\eta }{2}f^{\prime \prime }\right) \right) +M_{4}\lambda \theta +l\beta _{v}\left( F^{\prime }-f^{\prime }\right) +2M_{1}\varOmega h \\&\quad -\frac{M_{3}M^{2}}{1+m^{2}}\left( f^{\prime }+mh\right) -M_{2}\delta f^{\prime }-M_{1}Frf^{\prime 2}=0, \end{aligned}$$
(29)
$$\begin{aligned}&M_{2}h^{\prime \prime }+M_{1}\left( fh^{\prime }-f^{\prime }h-S\left( h+ \frac{\eta }{2}h^{\prime }\right) \right) +l\beta _{v}\left( H-h\right) -2M_{1}\varOmega f^{\prime } \\&\quad +\frac{M_{3}M^{2}}{1+m^{2}}\left( mf^{\prime }-h\right) -M_{2}\delta h-M_{1}Frh^{2}=0, \end{aligned}$$
(30)
$$\begin{aligned}&\left[ \frac{\kappa _{\mathrm{nf}}}{\kappa _{n}}\frac{1}{\Pr }+\frac{4}{3}Rd\left( 1+\left( \theta w-1\right) \theta \right) ^{3}\right] \theta ^{\prime \prime }+M_{5}\left[ f\theta ^{\prime }-2f^{\prime }\theta -S\left( \frac{\eta }{2} \theta ^{\prime }+2\theta \right) \right] \\&\quad +l\gamma \beta _{\mathrm{T}}\left( \phi -\theta \right) +4Rd\left( \theta w-1\right) \left( 1+\left( \theta w-1\right) \theta \right) ^{2}\theta ^{\prime 2}=0. \end{aligned}$$
(31)

Dust phase:

$$\begin{aligned}&F^{\prime \prime }F-F^{\prime 2}-S\left( F+\frac{\eta }{2}F^{\prime \prime }\right) +\beta _{{\upnu }}\left( f^{\prime }-F^{\prime }\right) =0, \end{aligned}$$
(32)
$$\begin{aligned}&H^{\prime }F-HF^{\prime }-S\left( H+\frac{\eta }{2}H^{\prime }\right) +\beta _{{\upnu }}\left( h-H\right) =0, \end{aligned}$$
(33)
$$\begin{aligned}&\phi ^{\prime }F-2F^{\prime }\phi -S\left( \frac{\eta }{2}\phi ^{\prime }+2\phi \right) +\beta _{\mathrm{T}}\left( \theta -\phi \right) =0. \end{aligned}$$
(34)

The transformed boundary conditions are:

$$\begin{aligned} \left. \begin{aligned}&f^{\prime }\left( 0\right) =1,~~f\left( 0\right) =0,~~h\left( 0\right) =0,~~\theta ^{\prime }\left( 0\right) =\frac{\kappa _{n}}{\kappa _{\mathrm{nf}}} Bi\left( 1-\theta \left( 0\right) \right) , \\&f^{\prime }\left( \infty \right) \rightarrow 0,~~h\left( \infty \right) \rightarrow 0,~~\theta \left( \infty \right) \rightarrow 0,~~\phi \left( \infty \right) \rightarrow 0, \\&F^{\prime }\left( \infty \right) \rightarrow 0,~~H\left( \infty \right) \rightarrow 0,~~F\left( \infty \right) \rightarrow f\left( \infty \right) . \end{aligned}\right\} \end{aligned}$$
(35)

where

$$\begin{aligned} \left. \begin{aligned}&M_{1} =\left( \left( 1-\varkappa \right) +\varkappa \frac{\rho _{\mathrm{s}}}{\rho _{\mathrm{f}}}\right) ,~~~~~ M_{2}=\left( 1-\varkappa \right) ^{-2.5}, \\&M_{3} =\left( 1+\frac{3\left( \frac{\sigma s}{\sigma f}-1\right) \varkappa }{\frac{\sigma s}{\sigma f}+2-\left( \frac{\sigma s}{\sigma f}-1\right) \varkappa }\right) , \\&M_{4} = \left( \left( 1-\varkappa \right) +\varkappa \frac{\left( \rho \beta _{\mathrm{T}}\right) _{\mathrm{s}}}{\left( \rho \beta _{\mathrm{T}}\right) _{\mathrm{f}}}\right) ,~~~~~M_{5}=\left( \left( 1-\varkappa \right) +\varkappa \frac{\left( \rho C\right) _{\mathrm{s}}}{\left( \rho C\right) _{\mathrm{f}}}\right) . \end{aligned}\right\} \end{aligned}$$
(36)

The different dimensionless parameters are defined as

$$\begin{aligned} \left. \begin{aligned}&l =\frac{\rho _{\mathrm{p}}}{\rho _{\mathrm{f}}},\quad \beta _{{\upnu }}=\frac{1-\alpha t}{\tau _{v}b} ,\quad Gr_{\mathrm{x}}=\frac{g\beta _{Tf}}{b^{2}\nu _{\mathrm{f}}^{2}}\left( T_{\mathrm{w}}-T_{\infty }\right) U_{\mathrm{w}}^{2},\quad \beta _{\mathrm{T}}=\frac{1-\alpha t}{\tau _{\mathrm{T}}b}, \\&Pr = \frac{\mu _{\mathrm{p}}C_{\mathrm{p}}}{\kappa _{\mathrm{p}}},\quad \gamma =\frac{C_{\mathrm{p}}}{C_{\mathrm{f}}},\quad M^{2}= \frac{\sigma _{\mathrm{f}}B_{0}^{2}\left( 1-\alpha t\right) }{\rho _{\mathrm{f}}b},\quad \lambda = \frac{Gr_{\mathrm{x}}}{{Re}_{\mathrm{x}}^{2}}, \\&{Re}_{\mathrm{x}} = \frac{Uwx}{\nu f},\quad S=\frac{\alpha }{b},\quad \varOmega =\frac{\omega }{b}\left( 1-\alpha t\right) ,\quad \delta =\frac{\nu f}{K^{*}b}\left( 1-\alpha t\right) , \\&F_{\mathrm{r}} = \frac{C_{\mathrm{b}}}{K^{*1/2}},\quad Rd=\frac{4\sigma ^{*}}{ \rightthreetimes \left( \mu C\right) _{\mathrm{f}}},\quad \theta _{\mathrm{w}}=\frac{T_{\mathrm{w}}}{ T_{\infty }},\quad Bi=\frac{h_{\mathrm{f}}}{\kappa _{\mathrm{f}}}\sqrt{\frac{\left( 1-\alpha t\right) \nu _{\mathrm{f}}}{b}}. \end{aligned}\right\} \end{aligned}$$
(37)

The important quantities of interest are the coefficient of skin friction in x and z directions and the local Nusselt number. These are defined as

$$\begin{aligned}&{Re}_{\mathrm{x}}^{1/2}C_{fx}=\frac{\mu _{\mathrm{nf}}\left( \frac{\partial y}{\partial y} \right) _{y=0}}{\rho _{\mathrm{f}}U_{\mathrm{w}}^{2}}=\frac{1}{\left( 1-\varkappa \right) ^{2.5}}f^{\prime \prime }\left( 0\right) , \end{aligned}$$
(38)
$$\begin{aligned}&{Re}_{y}^{1/2}C_{fy}=\frac{\mu _{\mathrm{nf}}\left( \frac{\partial w}{\partial y} \right) _{y=0}}{\rho _{\mathrm{f}}U_{\mathrm{w}}^{2}}=\frac{1}{\left( 1-\varkappa \right) ^{2.5}}h^{\prime }\left( 0\right) , \end{aligned}$$
(39)
$$\begin{aligned}&{Re}_{\mathrm{x}}^{-1/2}Nu_{\mathrm{x}}=\frac{-\kappa _{\mathrm{nf}}\left( \frac{\partial T}{\partial y}\right) _{y=0}}{\kappa _{\mathrm{f}}\left( T_{\mathrm{w}}-T_{\infty }\right) }=\frac{\kappa _{\mathrm{nf}}}{\kappa _{\mathrm{f}}}\theta ^{\prime }\left( 0\right) . \end{aligned}$$
(40)

Numerical solution and results

The Eqs. (29–34) supporting with boundary conditions (35) are solved numerically by a MATLAB built-in function bvp4c, which is frequently used due to its efficiency and accuracy [46,47,48]. Recently, Mustafa [49] has discussed the closed analytical solution of two-phase MHD dusty fluid; however, due to nonlinearity, the current problem is addressed numerically. The domain \([0,\infty )\) is replaced with [0, 5], and the results are approximated with the tolerance of \(10^{-5}.\) The higher-order differential equations are transformed to the first-order system of equations along with boundary conditions. The MATLAB function bvp4c is finite difference code that works on three-stage Lobatto IIIa formula. It provides a collocation fourth-order accurate \(C^{1}\)-continuous solution as this is based on collocation formula. Error control and mesh size based on the residual of the continuous solution. Table 1 shows the calculated results in limiting case using bvp4c code. This table shows the excellent agreement with the results of previously published article. In Table 2, the effect of unsteadyness parameter S, momentum dust parameter \(\beta _{{\upnu }}\) and thermal dust parameter \(\beta _{\mathrm{t}}\) on wall shear stress are presented. It is observed that higher values of unsteadyness parameter S have increasing trend on \(f^{\prime \prime }(0),\) whereas a reverse relation is noticed for \(F^{\prime }(0)\). Both \(f^{\prime \prime }(0)\) and \(F^{\prime }(0)\) increase for the increasing values of momentum and thermal dust parameters; however, this increase is negligible for thermal dust parameter \(\beta _{\mathrm{t}}\).

Table 1 Comparison of \(-\theta ^{\prime }(0)\) values for different values of Pr when the rotational effects, Darcy Forchimer flow and nonlinear thermal radiations are ignored
Full size table
Table 2 Tabular comparison between nanofluid phase and dust phase flow
Full size table

Figures 2–15 are plotted to understand the impact of different parameters on velocity and temperature profiles. Figure 2 depicts the influence of momentum dust parameter \(\beta _{\upupsilon }\) on the dusty fluid. Figure illustrates that the dust phase moment is enhanced for the higher values of \(\beta _{\upupsilon }\). This velocity enhances until it matches with the velocity of nanofluid. This increment occurs because of the higher momentum of the dust particles. Both the velocity profiles \(f^{\prime }\) and \(F^{\prime }\) are declined for the larger porosity parameter \(\delta \) as can be verified in Fig. 3. The existence of porous medium produces a resistance in the flow, and by increasing the porosity parameter means, the size of the pours are enhanced, and hence, a more resistance is produced which decline the velocity as well as the momentum boundary layer thickness. As previously discussed that the velocity decreases because of the porous medium, however, this decrement is more prominent after the inclusion of inertial effects Fr, and this phenomenon is presented in Fig. 4. The impact of mass concentration of dust particles l on velocity profiles for the dusty and nanofluid flow is shown in Fig. 5. It is observed that by adding the more dust particles, the drag force is enhanced which reduces the speed of the fluid. The Lorentz forces are generated more hastily when the applied magnetic field is enhanced. As these are the opposing forces in nature, so the velocities \( f^{\prime }\) and \(F^{\prime }\) are lessens as shown in Fig. 6. Figure 7 illustrates how the increasing rotational parameter effects the velocities profiles. It is noticed that both the velocities of dusty fluid \(F^{\prime }\) and nanofluid \(f^{\prime }\) are diminished along with hydrodynamic boundary layer thickness due to higher rotation in fluid when compared with the stretching rate. Effects on temperature profiles for the different parameters are portrayed in Figs. 8–10. Figure 8 predicts the Prandtl number effects on the temperature profiles for nanofluid and dusty fluid flows. Prandtl number is the ratio of momentum diffusivity to thermal diffusivity. Thermal diffusivity is reduced when Pr is increased. Due to this decrement in thermal diffusion, the thermal boundary layer got thinner, and hence, the temperature of the fluid decreases. The temperature of the fluid \(\theta (\eta )\) and \(\phi (\eta )\) is rapidly enhanced when the thermal radiation parameter is taken larger as stated in Fig. 9. Due to the radiation, the heat is transferred into the fluid which augments the thermal boundary layer of nanofluid and dusty fluid. Figure 10 shows the variation of temperature ratio parameter \(\theta _{\mathrm{w}}\) in the temperature profile of nanofluid and dusty fluid, respectively. \(\theta _{\mathrm{w}}\) is the ratio between the wall temperature and ambient temperature. As wall temperature escalates when temperature ratio parameter is increased, the temperature rises. In Fig. 11, the characteristics of Hall current parameter m on transverse velocity components \(h(\eta )\) and \(H(\eta )\) are considered. Both the velocities are upgraded significantly when the value of m is uprooted. It happens because of the reason that the larger values of m decrease the conductivity of \( \frac{\sigma _{\mathrm{f}}}{1+m^{2}},\) and magnetic damping force rises up. Through Fig. 12, it is observed that the tangential velocities of nanofluid phase \(h\left( \eta \right) \) and dust phase \(H\left( \eta \right) \) both are increased near the surface \(\eta <1,\) but gradually, they decreases away \(\eta >1\) from the wall when the magnetic field is increased. The skin friction coefficient along the x-axis for the magnetic parameter M, unsteadiness parameter S, Hall current parameter m and momentum dust phase parameter \(\beta _{\upupsilon }\) is highlighted in Figs. 13 and 14. These figures shows that the Hall current parameter enhances the skin friction where as the increasing values of magnetic parameter, unsteadiness parameter and momentum for the dust particles parameter are responsible for the reduction of drag force on the surface. Figure 15 shows the rate of heat transfer on the wall for different parameters such as thermal radiation parameter Rd and Prandtl number Pr. The dimensionless Nusselt number escalates for the higher values of Prandtl number; however, a reverse relation is noticed for the thermal radiation parameters i.e., Rd.

Fig. 2
figure 2

Influence of \(\beta _{{\upnu }}\) on \(F^\prime \)

Full size image
Fig. 3
figure 3

Influence of \(\delta \) on \(f^\prime \) and \(F^\prime \)

Full size image
Fig. 4
figure 4

Influence of Fr on \(f^\prime \) and \(F^\prime \)

Full size image
Fig. 5
figure 5

Influence of l on \(f^\prime \) and \(F^\prime \)

Full size image
Fig. 6
figure 6

Influence of M on \(f^\prime \) and \(F^\prime \)

Full size image
Fig. 7
figure 7

Influence of \(\varOmega \) on \(f^\prime \) and \(F^\prime \)

Full size image
Fig. 8
figure 8

Influence of Pr on \(\theta \) and \(\phi \)

Full size image
Fig. 9
figure 9

Influence of Rd on \(\theta \) and \(\phi \)

Full size image
Fig. 10
figure 10

Influence of \(\theta _{\mathrm{w}}\) on \(\theta \) and \(\phi \)

Full size image
Fig. 11
figure 11

Influence of m on \(h(\eta )\) and \(H(\eta )\)

Full size image
Fig. 12
figure 12

Influence of M on \(h(\eta )\) and \(H(\eta )\)

Full size image
Fig. 13
figure 13

Influence of S and M on \(Cf_{\mathrm{x}}Re_{\mathrm{x}}^{1/2}\)

Full size image
Fig. 14
figure 14

Influence of m and \(\beta _{{\upnu }}\) on \(Cf_{\mathrm{x}}Re_{\mathrm{x}}^{1/2}\)

Full size image
Fig. 15
figure 15

Influence of Rd and Pr on \(Nu_{\mathrm{x}}Re_{\mathrm{x}}^{-1/2}\)

Full size image

Concluding remarks

This article comprises the numerical discussion of unsteady MHD dusty nanofluid rotating flow over the convected surface with nonlinear thermal radiation and non-Darcian effects. Carbon nanotubes are considered as the nanoparticles, and Hall current phenomenon is produced due to the higher magnetic strength. A MATLAB function bvp4c is utilized to solve the equations. The main findings are as listed below.

  • Due to the increment of inertial coefficient, the velocity of the dust phase and nanofluid phase both decreases..

  • Rotational coefficient and velocity profiles are reciprocal of each other.

  • The thermal and flow field of nanofluid are much more higher than the dust phase.

  • Thermal boundary layer of nanofluid and dust phase fluids are raised for the higher values of radiation parameter.

  • Temperature and velocity boundary layer are enhanced in the presence of dust particles.

  • Thermal field is declined, while velocities are inclined for the Hall current effect.

  • The Nusselt number is reduced when the temperature ratio is increased