Introduction

Today, due to the consumption of irreversible energy sources and the production of environmental prolusions, optimizing heat transfer process by using cooling fluids has become very important in the numerous industries such as energy generation industries, aerospace, petrochemicals, transportation, machining and electronic industries. In order to obtain high efficiency, the heat transfer equipment needs minimized dimensions and the enhancement of heat transfer in each unit of surface area. The development of technology in recent decades, the changes of rheological properties of cooling fluids and generating steady solid–liquid suspensions called nanofluid cause the optimization of thermal efficiency of industrial tools and heat exchangers. Hence, increasing heat transfer through nanofluids has been reported by many researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. In recent decades, for minimizing the dimensions of heat transfer equipment, producing channels with microdimensions as heat exchangers (microchannels) has been widely considered. Microchannel is an equipment used for controlling the temperature of electronic chips with high heat fluxes. Some advantages of microchannel are compressibility, high ratio of surface to volume, high heat transfer and thermal performance and lightweight. These advantages of microchannel along with novel heat transfer methods entail more heat transfer enhancement in the electronic industries. Therefore, numerous researchers have studied the nanofluid flow in micro- and macro-dimensions [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Nikkhah et al. [32] numerically investigated the laminar flow of water/functionalized multi-walled carbon nanotubes in a two-dimensional rectangular microchannel by applying oscillating heat flux and slip velocity boundary condition on walls. Their numerical results revealed that the increase in volume fraction, slip velocity coefficient and Reynolds number entail the enhancement of Nusselt number and heat transfer. Safaei et al. [33] numerically studied the laminar flow of water/Cu nanofluid in an inclined ribbed microchannel with the angles of 0°–90° and volume fractions of 0–4% of solid nanoparticles in Reynolds number of 50 and Richardson numbers of 0.1–10. They figured out that, in low Reynolds numbers, the gravity force has an important effect on heat transfer and fluid flow, and by increasing volume fraction of nanoparticles, the inclined angle of microchannel and Richardson number, heat transfer improves. Raisi et al. [34] numerically studied the laminar flow and heat transfer in a two-dimensional rectangular microchannel with constant thermal boundary condition and constant surface temperature with slip boundary condition on walls. Their results indicated that the existence of slip boundary condition on solid walls in low Reynolds numbers does not have any considerable effect on heat transfer enhancement and in higher Reynolds numbers causes significant enhancement of heat transfer. Elshazly et al. [35] investigated the convection heat transfer on the internal surface of vertical and inclined elliptical tubes placed in front of flow. In their research, the applied heat flux on the internal surface of tubes and the effect of inclined angle and flow direction on heat transfer coefficient have been investigated. They stated that, in constant Rayleigh number, by increasing the inclined angle and flow direction, the average Nusselt number enhances. Lotfi et al. [36] simulated the nanofluid flow in a horizontal tube by using three different methods of single-phase, two-phase mixture model and two-phase Euler model. By comparing their numerical results with the results of an experimental study, they found that two-phase mixture model is more accurate than other models. Behzadmehr et al. [37] numerically investigated the turbulent and developed nanofluid flow in different Reynolds numbers with volume fraction of 1% of Cu nanoparticles inside a circular tube. In this research, they used two-phase and single-phase models for investigating the fluid flow and heat transfer and indicated that two-phase mixture model has better coincidence with the experimental results. Akbari et al. [38] numerically studied the laminar and forced nanofluid flow in a two-dimensional ribbed microchannel and revealed that, by increasing the number of ribs, volume fraction of nanoparticles and Reynolds number, the rate of heat transfer enhances. On the other hand, the existence of rib on the direction of flow motion causes the creation of velocity gradients and the enhancement of contact surface and average friction coefficient. Behnampour et al. [39] investigated the effect of using different shapes of rib on laminar flow and heat transfer of water/Ag nanofluid with different volume fractions inside a rectangular ribbed microchannel. They concluded that, in all Reynolds numbers, the optimization of heat transfer is not observed in the rectangular rib shape, and in high Reynolds numbers, using trapezoidal rib is not recommended.

In many industrial tools, the existence of timed fans causes the creation of oscillating thermal removal from these equipments. In the present numerical research, the mixed and laminar flow and heat transfer of nanofluid in a two-dimensional microchannel with oscillating heat flux boundary condition are numerically simulated using finite volume method in Cartesian coordinates. The results of the present research indicate the dependency of flow and heat transfer parameters such as Nusselt number, thermal resistance, pressure drop and friction coefficient with thermal boundary condition (oscillating heat flux) and hydrodynamical (slip and no-slip boundary conditions), volume force of gravity acceleration and volume fraction of nanoparticles. The advantage of this research is considering vertical microchannel and applying inconstant heat flux and slip boundary condition on microchannel walls in contact with fluid. Also, in order to simulate different phases of solid (nanoparticles) and liquid (base fluid) more accurately, two-phase mixture model is used.

Problem statement

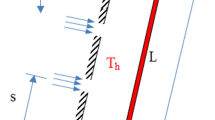
In the current study, the mixed, laminar and two-phase flow and heat transfer of water/Ag nanofluid in vertical microchannel have been numerically simulated. The studied microchannel is rectangular and two dimensional. The length of microchannel is L = 4.8 mm, and its height is H = 40 µm. The wall of microchannel is made of silicon, and its thickness is t = 15 µm. The external wall of microchannel at the left side is insulated, and the right side wall is under the influence of oscillating heat flux with the function of \(q^{\prime \prime } (X) = 2q_{0}^{\prime \prime } + q_{0}^{\prime \prime } \,\sin \,(\frac{\pi X}{4})\). The inlet cooling fluid enters the channel with uniform velocity with the temperature of Tc = 293 K. This simulation has been carried out in volume fractions of 0, 2 and 4% of Ag nanoparticles and Reynolds numbers of 150, 400, 700 and 1000. Also, the effect of gravity domain on laminar flow and heat transfer behavior in Grashof numbers of 1000 and 10,000 is investigated. Figure 1 demonstrates the simulated geometry of the present study.

Fig. 1
figure 1

Schematic of studied geometrics in the present research

Full size image

The present study has been carried out for no-slip (B = 0) and slip (B = 0.1) velocity boundary conditions on the internal walls of microchannel which are in contact with fluid. Also, the solid nanoparticles are uniform and spherical with the diameter of 10 nm. The suspension of pure water as the base fluid and nanoparticles in the studied volume fractions is simulated by two-phase mixture model as a Newtonian and steady fluid. The nanofluid properties are constant and independent from temperature. In Table 1, the properties of base fluid and Ag nanoparticles are presented [40].

Table 1 Thermophysical properties of base fluid and solid nanoparticles [40]
Full size table

Mathematical modeling

Governing equations and boundary conditions

The governing equations on laminar and two-phase nanofluid flow are continuity, momentum and energy equations [41,42,43]:

$$\nabla \cdot (\rho_{\text{m}} \vec{V}_{\text{m}} ) = 0$$
(1)
$$\vec{V}_{\text{m}} = \frac{{\sum\nolimits_{{\text{Z}} = 1}^{\text{n}} {\varphi_{\text{Z}} \rho_{\text{Z}} \vec{V}_{\text{Z}} } }}{{\rho_{\text{m}} }} = V_{\text{Z}}$$
(2)
$$\rho_{\text{m}} = \sum\limits_{{{\text{Z}} = 1}}^{\text{n}} {\varphi_{\text{Z}} \rho_{\text{Z}} }$$
(3)
$$\nabla \cdot (\rho_{\text{m}} \vec{V}_{\text{m}} \vec{V}_{\text{m}} ) = - \nabla P_{\text{m}} + \nabla \cdot \left[ {\mu_{\text{m}} \left( {\nabla \vec{V}_{\text{m}} + \nabla \vec{V}_{\text{m}}^{T} } \right)} \right] + \nabla \cdot \left( {\sum\limits_{Z = 1}^{n} {\varphi_{\text{Z}} \rho_{\text{Z}} \vec{V}_{\text{dr,Z}} \vec{V}_{\text{dr,Z}} } } \right) + (\rho \beta )_{\text{m}} (T - T_{\text{c}} )\vec{g}$$
(4)
$$\vec{V}_{\text{dr,Z}} = \vec{V}_{\text{Z}} - \vec{V}_{\text{m}}$$
(5)
$$\mu_{\text{m}} = \sum\limits_{Z = 1}^{n} {\varphi_{\text{Z}} \mu_{\text{Z}} } = \varphi_{\text{bf}} \mu_{\text{bf}} + \varphi_{\text{np}} \mu_{\text{np}} \to \mu_{\text{np}} = - 0.188 + 537.42\varphi_{\text{np}}$$
(6)
$$\nabla \cdot (\rho_{\text{m}} h_{\text{m}} \vec{V}_{\text{m}} ) + \nabla \cdot (P\vec{V}_{\text{m}} ) = \nabla \cdot \left( {k_{\text{m}} \nabla T} \right)$$
(7)
$$\rho_{\text{m}} h_{\text{m}} = \sum\limits_{Z = 1}^{n} {\left( {\varphi_{\text{Z}} \rho_{\text{Z}} h_{\text{Z}} } \right)} ,\quad k_{\text{m}} = \sum\limits_{Z = 1}^{n} {\varphi_{\text{Z}} \left( {k_{\text{Z}} } \right)}$$
(8)

In the above equations, Vm is the average velocity of mixture, Vdr,z is driving velocity for the secondary phase of z and the indexes of T, P, φ, µ and ρ are, respectively, the temperature, pressure, volume fraction, dynamic viscosity and density. In Eqs. (1–8), the indexes of z, dr and m are, respectively, the secondary phase of z, driving and the mixture (solid–liquid phases).

For non-dimensioning the parameters explained in results and discussion section, the following definitions are used [44],

$$\begin{array}{*{20}l} {X = \frac{x}{H} = \bar{x}} \hfill & {Y = \frac{y}{H} = \bar{y}} \hfill & {\bar{v} = \frac{v}{{\alpha _{{\text{f}}} /H}}} \hfill \\ {\theta = \frac{{T - T_{{\text{c}}} }}{{\Delta T}}} \hfill & {\bar{u} = \frac{u}{{\alpha _{f} /H}}} \hfill & {B = \frac{\beta }{H}} \hfill \\ {\Delta T = \frac{{q^{\prime\prime}_{0} \,H}}{{k_{{\text{f}}} }}} \hfill & {Pr = \frac{{\upsilon _{{\text{f}}} }}{{\alpha _{{\text{f}}} }}} \hfill & {P = \frac{{\overline{P} }}{{\rho _{{\text{m}}} (\alpha _{{\text{f}}} /H)^{2} }}} \hfill \\ \end{array}$$
(9)

The non-dimensional equations for two-phase and laminar flow are as follows:

Continuity equation [42]:

$$\frac{{\partial \bar{u}_{\text{m}} }}{{\partial \bar{x}}} + \frac{{\partial \bar{v}_{\text{m}} }}{{\partial \bar{y}}} = 0$$
(10)

x-momentum equation:

$$\begin{aligned} & \left[ {\bar{u}_{\text{m}} \frac{{\partial \bar{u}_{\text{m}} }}{{\partial \bar{x}}} + \bar{v}_{\text{m}} \frac{{\partial \bar{v}_{\text{m}} }}{{\partial \bar{y}}}} \right] = - \frac{{\partial \bar{p}}}{{\partial \bar{x}}} + \frac{{\rho_{\text{f}} }}{{\rho_{\text{m}} }}\left[ {\frac{\partial }{{\partial \bar{x}}}\left( {Pr \frac{{\mu_{\text{m}} }}{{\mu_{\text{f}} }}\frac{{\partial \bar{u}_{\text{m}} }}{{\partial \bar{x}}}} \right) + \frac{\partial }{{\partial \bar{y}}}\left( {Pr \frac{{\mu_{\text{m}} }}{{\mu_{\text{f}} }}\frac{{\partial \bar{u}_{\text{m}} }}{{\partial \bar{y}}}} \right)} \right] \\ & \quad + (1 - \varphi )\frac{{\rho_{\text{f}} }}{{\rho_{\text{m}} }}\left[ {\bar{u}_{\text{dr,f}} \frac{{\partial \bar{u}_{\text{dr,f}} }}{{\partial \bar{x}}} + \bar{v}_{\text{dr,f}} \frac{{\partial \bar{u}_{\text{dr,f}} }}{{\partial \bar{y}}}} \right] + \varphi \frac{{\rho_{\text{p}} }}{{\rho_{\text{m}} }}\left[ {\bar{u}_{\text{dr,p}} \frac{{\partial \bar{u}_{\text{dr,p}} }}{{\partial \bar{x}}} + \bar{v}_{\text{dr,p}} \frac{{\partial \bar{u}_{\text{dr,p}} }}{{\partial \bar{y}}}} \right] \\ \end{aligned}$$
(11)

y-momentum equation:

$$\begin{aligned} & \left[ {\bar{u}_{\text{m}} \frac{{\partial \bar{v}_{\text{m}} }}{{\partial \bar{x}}} + \bar{v}_{\text{m}} \frac{{\partial \bar{v}_{\text{m}} }}{{\partial \bar{y}}}} \right] = - \frac{{\partial \bar{p}}}{{\partial \bar{y}}} + \frac{{\rho_{\text{f}} }}{{\rho_{\text{m}} }}\left[ {\frac{\partial }{{\partial \bar{x}}}\left( {Pr \frac{{\mu_{\text{m}} }}{{\mu_{\text{f}} }}\frac{{\partial \bar{v}_{\text{m}} }}{{\partial \bar{x}}}} \right) + \frac{\partial }{{\partial \bar{y}}}\left( {Pr \frac{{\mu_{\text{m}} }}{{\mu_{\text{f}} }}\frac{{\partial \bar{v}_{\text{m}} }}{{\partial \bar{y}}}} \right)} \right] \\ & \quad + (1 - \varphi )\frac{{\rho_{\text{f}} }}{{\rho_{\text{m}} }}\left[ {\bar{u}_{\text{dr,f}} \frac{{\partial \bar{v}_{\text{dr,f}} }}{{\partial \bar{x}}} + \bar{v}_{\text{dr,f}} \frac{{\partial \bar{v}_{\text{dr,f}} }}{{\partial \bar{y}}}} \right] + \varphi \frac{{\rho_{\text{p}} }}{{\rho_{\text{m}} }}\left[ {\bar{u}_{\text{dr,p}} \frac{{\partial \bar{v}_{\text{dr,p}} }}{{\partial \bar{x}}} + \bar{v}_{\text{dr,p}} \frac{{\partial \bar{v}_{\text{dr,p}} }}{{\partial \bar{y}}}} \right] \\ & \quad + \frac{{(\beta \rho )_{\text{m}} }}{{(\beta \rho )_{\text{f}} }}\frac{{\rho_{\text{f}} }}{{\rho_{\text{m}} }}RaPr \theta \\ \end{aligned}$$
(12)

Energy equation:

$$\frac{{\rho_{\text{p}} C_{{P_{\text{p}} }} }}{{\rho_{\text{f}} C_{{P_{\text{f}} }} }}\left[ {\bar{u}_{\text{p}} \frac{\partial }{{\partial \bar{x}}}(\varphi \theta ) + \bar{v}_{\text{p}} \frac{\partial }{{\partial \bar{y}}}(\varphi \theta )} \right] + \left[ {\bar{u}_{\text{f}} \frac{\partial }{{\partial \bar{x}}}(\left( {1 - \varphi } \right)\theta ) + \bar{v}_{\text{f}} \frac{\partial }{{\partial \bar{y}}}(\left( {1 - \varphi } \right)\theta )} \right] = \frac{\partial }{{\partial \bar{x}}}\left( {\frac{{k_{\text{m}} }}{{k_{\text{f}} }}\frac{\partial \theta }{{\partial \bar{x}}}} \right) + \frac{\partial }{{\partial \bar{y}}}\left( {\frac{{k_{\text{m}} }}{{k_{\text{f}} }}\frac{\partial \theta }{{\partial \bar{y}}}} \right)$$
(13)

Volume fraction equation:

$$\frac{{\partial (\varphi \bar{u}_{\text{m}} )}}{{\partial \bar{x}}} + \frac{{\partial (\varphi \bar{v}_{\text{m}} )}}{{\partial \bar{y}}} + \frac{{\partial (\varphi \bar{u}_{dr,p} )}}{{\partial \bar{x}}} + \frac{{\partial (\varphi \bar{v}_{dr,p} )}}{{\partial \bar{x}}} = 0$$
(14)

The thermal and hydrodynamical boundary conditions used in different sections of microchannel are as follows:

$$U = 1,\;V = 0\;{\text{and}}\;\theta = 0\;{\text{for}}\;X = 0\;{\text{and}}\;0.375 \le Y \le 1.375$$
(15)
$$V = 0\;\,{\text{and}}\,\;\frac{\partial \theta }{\partial X} = \frac{\partial U}{\partial X} = 0\quad {\text{for}}\;\,X = 120\;\,{\text{and}}\;\,0.375 \le Y \le 1.375$$
(16)
$$V = 0,\;\,U = 0\;\,{\rm and}\;\,\frac{\partial \theta }{\partial Y} = 2q_{0}^{\prime \prime } \, + q_{0}^{\prime \prime } \,\sin \,\left( {\frac{\pi X}{4}} \right)\,\,\,\,\,\,\,{\text{for}}\;\,Y = 0\;\,{\text{and}}\;\,0 \le X \le 120$$
(17)
$$V = 0,\;\,U_{\text{s}} = B\frac{\partial U}{\partial Y}\,\,\,{\text{and}}\,\,\,k_{\text{nf}} \frac{\partial \theta }{\partial Y} = k_{\text{s}} \frac{\partial \theta }{\partial Y}\,\,\,\,\,{\text{for}}\,\,\,\,Y = 0.375\,\,\,{\text{and}}\,\,0 \le X \le 120$$
(18)
$$V = 0\,\,,\,\,U = 0\,\,\,\,\,{\rm and}\,\,\,\,\,\frac{\partial \theta }{\partial Y} = \,\,0\,\,\,\,\,\,\,{\text{for}}\,\,Y = 1.75\,\,\,\,{\rm and}\,\,\,0\, \le X \le 120\,\,$$
(19)
$$V = 0\,\,,\,\,U_{s} = - B\,\frac{\partial U}{\partial Y}\,\,\,\,\,{\rm and}\,\,\,\,\,k_{nf} \frac{\partial \theta }{\partial Y} = \,k_{s} \frac{\partial \theta }{\partial Y}\,\,\,\,\,\,\,{\text{for}}\,\,\,\,\,\,Y = 1.375\,\,\,\,\,{\rm and}\,\,\,\,0 \le X \le 120$$
(20)

The equations of thermophysical properties of nanofluid

Chon equation is used for calculating the thermal conductivity of nanofluid [45]. In Chon equation, the effects of fluid molecules and solid nanoparticles diameter, volume fraction of nanoparticles and fluid temperature are considered for calculating the thermal conductivity of nanofluid. This equation is considered for nanoparticle diameters of 11–150 nm.

$$\begin{aligned} & \frac{{k_{\text{m}} }}{{k_{\text{f}} }} = 1 + 64.7\,\phi^{0.746} \,\left( {\frac{{d_{\text{f}} }}{{d_{\text{np}} }}} \right)^{0.369} \left( {\frac{{k_{\text{np}} }}{{k_{\text{f}} }}} \right)^{0.7476} \,Pr ^{0.9955} \,\text{Re}^{1.2321} \\ & \text{Re} = \frac{{\rho_{\text{f}} k_{\text{b}} T}}{{3\pi \mu^{2} l_{\text{f}} }},\,\,\,\,\,\,Pr = \frac{{\mu_{\text{f}} }}{{\rho_{\text{f}} \alpha_{\text{f}} }},\quad \mu = A \times 10^{{\frac{B}{T - C}}} ,\,C = 140\,({\text{K}}), \\ & B = 247\,({\text{K}}),\quad A = 2.414 \times 10^{ - 5} \,({\text{Pa}}\,{\text{s}}),\quad T = T_{\text{in}} \\ \end{aligned}$$
(21)

The dynamic viscosity is calculated by the following equation [46],

$$\mu_{\text{eff}} = \left( {123\varphi^{2} + 7.3\varphi + 1} \right)\mu_{\text{f}}$$
(22)

The specific heat capacity can be determined by the following equation [47],

$$\left( {\rho \,c_{\text{p}} } \right)_{\text{m}} = (1 - \varphi )(\rho \,c_{\text{p}} )_{\text{f}} + \varphi (\rho \,c_{\text{p}} )_{\text{np}}$$
(23)

Nanofluid density is calculated by the following equation [48],

$$\rho_{\text{m}} = \varphi \rho_{\text{np}} + (1 - \varphi )\rho_{\text{f}}$$
(24)

Thermal expansion coefficient is calculated by the following equation [49, 50],

$$\frac{{\beta_{\rm eff} }}{{\beta_{\text{f}} }} = \left[ {\frac{1}{{1 + \frac{{\left( {1 - \varphi } \right)\rho_{\text{f}} }}{{\varphi \,\rho_{\rm P} }}}} \times \frac{{\beta_{\rm P} }}{{\beta_{\text{f}} }} + \frac{1}{{1 + \frac{{\varphi \,\rho_{\rm P} }}{{\left( {1 - \varphi } \right)\rho_{\text{f}} }}}}} \right]$$
(25)

Equations for calculating the output parameters

Friction coefficient is a parameter for investigating microchannel performance and can be calculated by the following equation,

$$Cf = \frac{{2 \times \tau_{\rm w} }}{{\rho u_{\text{in}}^{2} }}$$
(26)

The average Nusselt number can be obtained as [51],

$$Nu_{x} = \frac{h \times H}{{k_{\text{f}} }}\,\,\,\, \to \,\,\,\,\,\,Nu_{\rm ave} = \frac{1}{L}\int_{0}^{L} {Nu_{\rm x} (X)} \,dX$$
(27)

The pressure drop in the inlet and outlet sections is defined as [52]:

$$\Delta P = P_{\text{in}} - P_{\text{out}}$$
(28)

The thermal resistance of hot wall of microchannel is calculated by the following equation [53],

$$R = \frac{{T_{\hbox{max} } - T_{\hbox{min} } }}{{q^{\prime\prime}_{0} \,\, \times A}} = \frac{{T_{\hbox{max} } - T_{\text{in}} }}{{q^{\prime\prime}_{0} \, \times \,A}}\, \to \,\,A = W \times L \to R \times \,W = \frac{{T_{\hbox{max} } - T_{\hbox{min} } }}{{q^{\prime\prime}_{0} \,\, \times L}}$$
(29)

In Eq. (24), Tmax, Tmin, A and q0″ are, respectively, the maximum temperature of bottom wall, the minimum temperature (temperature of inlet fluid), cross section of applied heat flux and the applied heat flux to the hot wall. The entropy generation caused by thermal irreversibility (heat transfer) equals with [54].

$$S_{gen} = \frac{{k_{\rm eff} }}{{\overline{T}^{2} }}\left[ {\left( {\frac{{\partial \overline{T} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial \overline{T} }}{\partial y}} \right)^{2} } \right]$$
(30)

The entropy generation caused by flow irreversibility (friction coefficient) equals with [54],

$$S_{gen} = \frac{{\mu_{\rm eff} }}{{\overline{T} }}\left\{ {2\left[ {\left( {\frac{{\partial \overline{u} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial \overline{v} }}{\partial y}} \right)^{2} } \right] + \left( {\frac{{\partial \overline{u} }}{\partial x} + \frac{{\partial \overline{v} }}{\partial y}} \right)^{2} } \right\}$$
(31)

Total entropy generation including the entropy enhancement caused by heat transfer and flow friction is obtained as [55],

$$S_{gen} = \frac{{k_{\rm eff} }}{{\overline{T}^{2} }}\left[ {\left( {\frac{{\partial \overline{T} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial \overline{T} }}{\partial y}} \right)^{2} } \right] + \frac{{\mu_{\rm eff} }}{{\overline{T} }}\left\{ {2\left[ {\left( {\frac{{\partial \overline{u} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial \overline{v} }}{\partial y}} \right)^{2} } \right] + \left( {\frac{{\partial \overline{u} }}{\partial x} + \frac{{\partial \overline{v} }}{\partial y}} \right)^{2} } \right\}$$
(32)

Numerical procedure

Assumptions and solving methods

In the current study, by using finite volume method, the mixed and laminar nanofluid flow is simulated as steady and Newtonian. Nanofluid properties are constant (homogeneous) and independent from temperature, and the behavior of two-phase nanofluid is determined by two-phase mixture model. On the right side wall of microchannel shown in Fig. 1, the sinusoidal heat flux is applied. In this research, the radiation effects are neglected. The second-order upwind discretization [56] and SIMPLEC algorithm [57] are employed for solving the governing equations. The maximum residual of present numerical procedure is considered 10−6.

Mesh study and numerical solving procedure

In the current investigation, in order to ensure the results independency, the considered grid number has been changed to the regular and rectangular grids from 20,000 to 95,000. The studied parameters in the validation of the present study are Nusselt number along the hot wall and pressure drop differences in the inlet and outlet sections of microchannel. The changes of these two parameters are studied in Reynolds numbers of 150 and 700 for pure water fluid in no-slip boundary condition (B = 0) and Grashof number of 1000. According to Table 2, the grid number of 95,000 indicates more accurate results than other grid numbers. However, because the grid number of 70,000, comparing to the grid number of 95,000, has an acceptable error and needs less computational time, the grid number of 70,000 is used in the present numerical simulation. The gridding of present geometry with the selected grid number is shown in Fig. 2.

Table 2 Changes of studied grid number in the present research
Full size table
Fig. 2
figure 2

Regular grid structure on the part of the desired geometry

Full size image

Validation

The results of the present study are validated with the numerical study of Safaei et al. [33] and the experimental study of Chein and Chuang [58]. Safaei et al. [33] numerically investigated the laminar flow and heat transfer of water/Cu nanofluid inside a two-dimensional microchannel with the angle of 90° (completely vertical channel) in Reynolds number of 50, 2% nanoparticles volume fraction and Richardson number of 10 (Fig. 3a). Also, Chein and Chuang [58] studied the hydrodynamical behavior of flow and heat transfer of water/CuO nanofluid in microchannel heat sink. They increased the heat transfer by using copper nanoparticles with volume fractions of 0–4% and different flow rates (Fig. 3b). According to Fig. 3, proper coincidence of present results with the studies of Safaei et al. [33] and Chein and Chuang [58] indicates that the present solving procedure and the applied boundary conditions are accurate.

Fig. 3
figure 3

Validation of present problem with the study of Safaei et al. [33] and Chein and Chuang [58]. a Numerical study, b experimental study

Full size image

Results and discussion

Figure 4 demonstrates the dimensionless temperature lines in Grashof numbers of 1000 and 10,000 and slip velocity coefficients of 0 and 0.1 for pure water fluid in Reynolds number of 100. Figure 4a investigates the effect of slip velocity coefficient on dimensionless temperature distribution inside the microchannel. It is observed that, by increasing slip velocity coefficient, cooling enhances on the solid wall. The reason of this behavior is because of nonzero velocity of fluid, which is in contact with solid wall in slip coefficient of 0.1. Figure 4b investigates the effect of Grashof number on temperature domain, and it is seen that, in hot areas of solid wall, the heat transfer improves considerably. Also, due to the enhancement of gravity domain and the influence of buoyancy force in Grashof number of 10,000, the cooling of these areas becomes considerable.

Fig. 4
figure 4

Changes of dimensionless temperature lines in different Grashof numbers and slip velocity coefficients for pure water fluid in Reynolds number of 100. a Gr = 10,000, bB = 0.1

Full size image

Figure 5 indicates the behavior of dimensionless temperature lines in different volume fractions and Grashof number of 1000 and slip velocity coefficient of 0 for pure water fluid in Reynolds number of 100. This figure studies the effect of using higher volume fractions on temperature distribution in different areas of microchannel. According to the contours of Fig. 5, by increasing volume fraction of nanoparticles, the heat transfer distribution inside the microchannel and especially on the solid walls becomes considerably uniform and temperature gradients reduce. The reason of this behavior is due to the augmentation of thermal conductivity coefficient of cooling fluid in contact with hot surfaces in higher volume fractions of nanoparticles. Also, by using pure water fluid, on the heated walls of microchannel areas with lower heat transfer are created which are marked by red color, and these areas become more significant from the middle of microchannel to later on.

Fig. 5
figure 5

Changes of dimensionless temperature lines in different volume fractions of nanoparticles and Grashof number of 1000

Full size image

Figure 6 indicates the changes of dimensionless temperature lines in volume fraction of 4% of nanoparticles and Grashof number of 10,000 and slip velocity coefficient of 0.1 in different Reynolds numbers. In this study, the effect of Reynolds number changes on dimensionless temperature lines for the balanced values is investigated. By increasing fluid velocity, the convection heat transfer mechanism enhances significantly and the temperature distribution becomes uniform. By decreasing fluid velocity, because heat penetration to the upper layers of heated surface takes more time and fluid has sufficient time to be in contact with the heated surface, the non-uniform heat penetration to the upper layers of heated surface is completely obvious in Reynolds number of 150. By increasing fluid velocity, the dominancy of lower temperature of cooling fluid throughout the microchannel causes better distribution and the elimination of hot areas from microchannel walls.

Fig. 6
figure 6

Changes of dimensionless temperature lines in different Reynolds numbers

Full size image

In Fig. 7, the local friction coefficient on the heated wall for Reynolds numbers of 150 and 700 in Grashof numbers of 1000 and 10,000 with slip and no-slip boundary conditions on the solid walls is shown for investigating the effect of mentioned parameters and the enhancement of volume fraction of nanoparticles on the changes of local friction coefficient along the microchannel. According to Fig. 7a, in lower velocities of fluid, because of more contact with solid walls, temperature gradients enhance causing the augmentation of shear stress and friction coefficient. Therefore, in all states, the level of Fig. 7a is higher than Fig. 7b. By increasing volume fraction of nanoparticles, due to the enhancement of nanoparticles collusion with the heated wall, fiction coefficient increases. Also, the slip velocity on solid walls does not prevent the fluid motion in these areas; hence, by increasing slip velocity coefficient, the friction coefficient reduces considerably. The increase in Grashof number causes significant changes in velocity gradients and consequently the augmentation of friction coefficient. According to the stated analogies and the relationship between the heat transfer enhancement and friction coefficient, in Fig. 7a and Grashof number of 10,000, the behavior of friction coefficient is affected by the oscillating heat transfer, and this behavior is not considerable in other figures. The reason is because of the great effect of buoyancy force (caused by oscillating heat transfer of heated surface) on fluid velocity parameters in Grashof number of 10,000 and Reynolds number of 150.

Fig. 7
figure 7

Local friction coefficient on the heated wall. aRe = 150, bRe = 700

Full size image

Figure 8 shows the behavior of local Nusselt number on the heated wall in Grashof number of 10,000 and slip velocity coefficient of 0.1 for Reynolds numbers of 400 and 1000. As it is seen, the behavior of local Nusselt number is affected by thermal boundary condition, and the changes of this parameter are oscillating. In all graphs of Fig. 8, by increasing volume fraction of nanoparticles and Reynolds number, the local Nusselt number improves. The maximum value of heat transfer accomplishes at the beginning of microchannel, and the reason is because of the maximum temperature differences of heated surface and fluid temperature in these areas. On the direction of fluid motion, the heat transfer intensity reduces gradually because of the enhancement and penetration of average temperature of fluid and the reduction of temperature difference of surface and fluid. According to the behavior of Fig. 8, in Reynolds number of 1000, the level of graphs is higher than Reynolds number of 400.

Fig. 8
figure 8

Local Nusselt number on the hated wall. aRe = 400, bRe = 1000

Full size image

Figure 9 compares the values of average Nusselt number on the heated wall in different Grashof numbers, slip velocity coefficients and volume fractions. In all graphs, the maximum amount of heat transfer is related to Reynolds number of 1000 and volume fraction of 4% of solid nanoparticles and the slip velocity boundary condition on the solid wall and Grashof number of 10,000. By increasing volume fraction of nanoparticles, due to the improvement of thermal conductivity coefficient of cooling fluid and micron heat transfer mechanism of nanoparticles, heat transfer enhances. The existence of slip velocity on the solid walls causes better heat transfer and the enhancement of convection heat transfer coefficient and Nusselt number and the reduction of temperature gradients. By increasing Grashof number, the buoyancy force along the fluid motion improves and the natural convection heat transfer becomes significant. Hence, in Grashof number of 10,000, graphs have higher levels. By increasing fluid velocity, the forced convection heat transfer enhances; therefore, Reynolds number of 1000 has the maximum value of heat transfer. It is observed that, in lower Reynolds numbers, the impressionability of heat transfer enhancement caused by Grashof number enhancement becomes more significant. Regarding this behavior, in constant B and in lower Reynolds numbers, graphs become divergent. Also, in higher Reynolds numbers, the importance of slip velocity on heat transfer enhancement caused by this boundary condition is more considerable. Therefore, by increasing Reynolds number and in constant φ, the average Nusselt number graphs become divergent.

Fig. 9
figure 9

Average Nusselt number on the heated wall. aφ = 0, bφ = 0.02, cφ = 0.04

Full size image

Figure 10 indicates the changes of average pressure drop in different Grashof numbers, slip velocity coefficients, volume fractions of nanoparticles and Reynolds numbers. This figure investigates the effect of the enhancement of slip velocity and Grashof number on the changes of average pressure drop in different Reynolds numbers ranging from 150 to 1000. By increasing nanoparticles volume fraction, the density and viscosity of fluid are enhanced. Also, fluid with higher density has more momentum depreciation on its direction along the channel. On the other hand, fluid with higher viscosity has more contact with solid surfaces, and the transfer of velocity gradients among fluid layers happens with more pressure drop. By increasing slip velocity on the solid wall, due to the less prevention of solid surface on the direction of fluid motion and simple movement of fluid on walls, pressure drop reduces. Also, by increasing fluid velocity, due to the more momentum depreciation of fluid, pressure drop enhances.

Fig. 10
figure 10

Average pressure drop in different Reynolds numbers

Full size image

Figure 11 demonstrates the behavior of average thermal resistance on the heated wall in Grashof numbers of 1000 and 100,000, slip velocity coefficients of 0 and 0.1 and volume fractions of 0–4%. This figure investigates the relationship between thermal resistance of heated surface with different slip velocity coefficients, Reynolds numbers, volume fractions of nanoparticles and Grashof numbers. According to this figure, by increasing Reynolds number, the buoyancy force, slip velocity coefficient on the solid wall, volume fraction and every factor causing the enhancement of heat transfer on the heated surfaces and the reduction of maximum temperature of surfaces entail the reduction thermal resistance of wall. By considering constant slip velocity coefficient, the ratio of thermal resistance to Grashof number reduces with the increase in Reynolds number. Therefore, by increasing Reynolds number, in constant B, the graphs of thermal resistance become convergent. Also, by increasing Grashof number and slip velocity coefficient, the reduction of thermal resistance is significant in lower Reynolds numbers.

Fig. 11
figure 11

Changes of average thermal resistance on the heated wall. aφ = 0, bφ = 0.02, cφ = 0.04

Full size image

Figure 12 indicates the average entropy in different Grashof numbers, slip velocity coefficients and volume fractions of nanoparticles. The changes of entropy generation on flow direction are due to the entropy enhancement caused by heat transfer and friction coefficient. If fluid becomes irreversible on its direction, entropy generation enhances. According to the studied temperature contours and in Reynolds number of 150, the existence of hot areas on solid walls and on the top of the heated wall causes the augmentation of entropy generation. Also, because of the existence of no-slip boundary condition in collusion areas of fluid with wall, fluid velocity becomes 0. This behavior causes the increase in entropy generation caused by friction coefficient enhancement. The distribution of solid nanoparticles with higher volume fraction causes the reduction of temperature gradients and the dominancy of inlet cooling fluid temperature in most areas of microchannel. Therefore, the increase in volume fraction of nanoparticles, slip velocity coefficient, Reynolds number and Grashof number cause the reduction of entropy.

Fig. 12
figure 12

Behavior of entropy generation on the solid wall. aφ = 0, bφ = 0.02, cφ = 0.04

Full size image

Figure 13 shows the changes of local dimensionless temperature on the central line of flow in Grashof number of 1000 with the existence of no-slip boundary condition on solid walls. By entering the cooling fluid to microchannel, because of the existence of hated wall, temperature gradients grow gradually and the penetration of thermal boundary layer to the central core of flow becomes observable. The penetration of thermal boundary layer starts in Reynolds number of 150 in X = 10, and before this area, the inlet fluid temperature becomes dominated in central line of flow. By increasing Reynolds number, the heat penetration to the central core of flow postpones and in Reynolds number of 700 starts in X = 40. In fact, this postponement and the dominancy of cooling fluid temperature on channel entail heat transfer enhancement with the augmentation of Reynolds number. Also, the increase in volume fraction of nanoparticles causes the enhancement of dimensionless temperature in central line of flow.

Fig. 13
figure 13

Distribution of dimensionless temperature in the central line of flow. a Re = 150, b Re = 700

Full size image

Conclusions

In the present paper, the effect of using water/Ag nanofluid with 0–4% nanoparticles volume fractions with slip and no-slip boundary conditions on the solid walls of a two-dimensional rectangular microchannel with Reynolds numbers of 150–1000 has been investigated by applying gravity acceleration domain in Grashof numbers of 1000 and 10,000 using finite volume method in Cartesian coordinates. The obtained results indicate that, in vertical microchannel, the heat transfer enhancement depends on boundary condition, velocity domain and gravity acceleration. Also, the changes of local friction coefficient profile in low fluid velocities (Reynolds number of 150) and Grashof number of 10,000 depend on temperature profile. According to the average Nusselt number figures, in low Reynolds numbers, the increase in this parameter caused by Grashof number augmentation is more significant. Based on this behavior, in constant slip velocity coefficient and low Reynolds numbers, the figures become divergent. Also, in higher Reynolds numbers, the importance of slip velocity boundary condition on heat transfer enhancement becomes more considerable. Therefore, by increasing Reynolds number, the average Nusselt number figures in constant volume fraction of nanoparticles become divergent. The enhancement of Reynolds number, slip velocity coefficient, Grashof number and volume fraction of nanoparticles entail the augmentation of Nusselt number and the reduction of thermal resistance.