Molecular dynamics and thermodynamic simulations of segregation phenomena in binary metal nanoparticles

Abstract

An approach combining atomistic molecular dynamics (MD) and thermodynamic simulations has been applied to predict the distribution of components in binary Ni–Cu and Au–Ag nanoparticles consisting of 2000 atoms (of about 4 nm in size). The term ‘thermodynamic simulation’ has referred to solving, in some approximations, the Butler equation for a core–shell particle model. Both atomistic and thermodynamic approaches predict the surface segregation of Cu atoms in Ni–Cu nanoparticles and segregation of Ag to the surface of Au–Ag nanoalloys. Then, contrary to the Ni–Cu systems, some Au–Ag nanoparticles demonstrated an onion-like structure with the outer Ag monolayer. The results of MD and thermodynamic simulations agree with each other and with some available direct and indirect experimental data.

Introduction

Metal nanoclusters are objects of interest for physicists, chemists and engineers since the 1970s in view of noticeable deviations of their properties from those of corresponding bulk phases. It opens prospects of many important practical applications. The available results on one-component metal nanoclusters have been published in a number of papers and monographs. As a matter of fact, the first serious works on properties of metal nanoclusters were published long before the terms ‘nanotechnology’, ‘nanoscience’ and ‘nanoparticle’ have appeared and widely spread. As an example of early publications on this topic, paper [1] by Buffat et al. can be mentioned where the size dependence of the melting temperature of Au nanoclusters was experimentally investigated by using the X-ray diffraction method. Up to the present time, interest to Au nanoclusters has been growing in connections with well-known and quite new prospects of their applications in nanotechnology. In particular, Au nanoclusters have the ferromagnetic spin and their ensembles demonstrate properties of superparamagnets [2] that open brand new prospects of their applications as magnetic memory units. Even more interesting seems to be paper [3] where a new way was reported of the GaAs nanocrystal production by using Au nanoclusters as centres of the heterogeneous nucleation.

No doubt that when using binary and multicomponent nanoparticles and nanosystems, the scope of related phenomena and their possible applications is significantly extended. Such a conclusion has been entirely confirmed and exemplified on bulk alloys [4, 5] and, to a lesser extent, on nanostructured materials [6]. At the same time, properties of binary nanoparticles (referred also to as nanoalloys in what follows) have only begun to be studied. On the one hand, binary nanosystems are of interest themselves, on the other their studying may be considered as a step towards the further investigations of multicomponent systems. As for binary metal nanoparticles, interest to them relates, first of all, to prospects of their applications as catalysts [7]. In particular, the catalytic activity of Pd–Pt nanoclusters was discussed in [8]. Nanoalloys on the basis of Au seem to be less used as catalysts. However, they are also applied as catalysts for the epoxidation of alkenes [9]. A number of other applications of nanoalloys can be also highlighted: accumulation of energy, including the hydrogen storage, design of sensors, supercapacitors and materials resistant to radiation. Among binary metal nanoparticles bimetallic ones are of special interest. This term will be referred to binary metal nanoparticles with sharply segregated components. For example, the core–shell structures with the particle core presented by one metal and the shell consisting of another may be treated as patterns of bimetallic nanostructures. However, experimental results on the structure and properties of binary metal nanoclusters seem to advance their theoretical interpretation and development of computer simulations in this field of research. Accordingly, there remain a number of open questions and, respectively, some experimental results are not properly understood and systematized.

The surface segregation, i.e. the surface enrichment of one of the two components of the binary nanoparticle or another nanosized unit, seems to relate to most of phenomena in binary nanosystems which are of interest in view of potential applications. In the case of nanoparticles, the surface segregation phenomenon can result in the core–shell and other Janus structure formation. However, the laws governing the formation of these structures and degree of their stability remain unclear. In particular, it seems that such nanostructures, in contrast to corresponding microstructures, can be unstable because of their non-equilibrium nature. For example, Ag(core)–Au(shell) and Au(core)–Ag(shell) nanostructures have been already obtained and intensively studied [10, 11]. However, in [10], the shells enriched by the more noble component (Au) were obtained by using an electrochemical method, namely, the surface dealloying. In [11], some Au and Ag shells were chemically deposited on a preliminary prepared cores presented by the second component of the desired core–shell structure. In other words, the possibility of the spontaneous Ag–Au core–shell structure formation remains unclear. Moreover, it is not clear whether Ag or Au atoms should spontaneously segregate to the particle surface in the Ag–Au nanoalloys with the initially uniform distribution of components.

Taking into account that experimental study of the segregation phenomena in nanoparticles and nanosystems faces many difficulties, computer simulation methods seem to be promising to elucidate the laws and mechanisms of the surface segregation in binary nanosystems. By the present time, computer simulation methods are divided into atomistic, including molecular dynamics (MD), and ab initio methods, including the density functional theory (DFT). When using the atomistic simulations, a semi-empirical potential of the interatomic interaction should be used, whereas ab initio methods take into account directly, to a greater or lesser extent, the electronic structure of the investigated system. However, ab initio calculations are usually applicable to systems containing not more than several dozens of atoms, i.e. to very small nanoclusters. Besides, different approximations of ab initio methods can give principally differing results. In [9], binary metal nanoclusters, including Au–Ag ones, containing up to several dozens of atoms, were investigated using both the DFT calculations and some atomistic simulations employing the tight-binding potential (TBP) with the parameterization proposed and justified in [12]. According to DFT results [9], segregation of Au should take place, whereas the atomistic simulations performed in [9] predicted segregation of Ag atoms. The DFT results [9] for the Au–Ag nanoalloy seem to be more disputable as experimental data [13] do not predict segregation of Au but of Ag atoms. The deviations between the energies of different configurations of Au–Ag nanoclusters studied in [9] by involving one of the above two methods (DFT or TBP calculations) are very low. At the same time, the binding energies evaluated by using DFT and TBP differ very significantly. For other nanoalloys, qualitative divergences between DFT and TBP results are not reported in [9]. It is also worth to mention that in [9], MD method or any other conventional atomistic simulation method was not used at all, i.e. TBP was applied to calculate the binding energies of some arbitrary but reasonably chosen (hand-made) cluster configurations.

So, some predictions of segregation in binary metal nanoparticles and nanosystems on the basis of atomistic and ab initio simulations may be not quite reliable. Besides, in many cases, not only very small particles or structural units of nanomaterials may be of interest but also nanoparticles containing up to several millions of atoms and even more (of order of 100 nm in size). Such a size region is practically not available for both ab initio and MD simulations. For this and some other reasons, it seems to be of interest development of approaches combining the atomistic simulations, by involving reliable multiparticle potentials, with thermodynamic simulation methods. When using the term ‘thermodynamic simulation’, we mean that the problem under discussion hardly can be solved by using some simple ready thermodynamic equations. In particular, the thermodynamic simulation of the segregation phenomena is a complex enough problem which, however, can be solved mainly by means of numerical calculations, employing some particle models and sequential approximations.

The approach to the thermodynamic simulation used in this paper is based on application of the Butler equations [14] to a modelling spherical particle that is arbitrary, in general, divided into its central core and a shell, i.e. the surface area. The goal of our thermodynamic simulations is to evaluate the equilibrium distributions of components of binary metal nanoparticles between the above regions. Being proposed long ago, Butler’s approach has provoked some critical remarks [15]. Presumably, the main Butler’s disadvantage was that he in advance related his derivation to the Gibbs surface phases method. In [16], Kaptay proposed a new derivation of the Butler equations not relating them strongly to Gibbs’ method. Using these equations, the segregation of Cu atoms to the grain boundaries in Ni–Cu nanoalloys was predicted. And it is worth to mention that the pronounced segregation of Cu to the grain boundaries in Ni–Cu polycrystalline alloys was discovered and studied before experimentally [17]. These experimental data may be treated as an indirect confirmation of the Cu surface segregation in Ni–Cu nanoparticles as well. Presumably, there are no direct experimental data on the segregation in Ni–Cu nanoparticles.

The thermodynamic simulation of binary metal nanoparticles on the bases of the Butler equations was performed in [18,19,20]. And it is noteworthy that in [20], the case was discussed when the particle core cannot be treated as an unlimited source for the segregating atoms. So, there are some direct and indirect experimental data as well as some theoretical results on the segregation phenomena in Au–Ag and Ni–Cu nanoalloys as well as in the corresponding nanostructured materials. At the same time, laws and mechanisms of the surface segregation in nanoalloys are not quite clear yet. Respectively, they are worth to be studied combining the atomistic and thermodynamic simulations.

Method of atomistic simulation

Our atomistic simulation results presented in the present paper were obtained by using the well-known open program LAMMPS developed and distributed by Sandia National Laboratories (USA). Usually, when using LAMMPS, the embedded atom method (EAM) is employed to describe the interatomic interactions in the system under investigation. The choice of the Au–Ag and Ni–Cu systems as the objects of the research has been already justified before. In addition, it is worth to mention that corresponding bulk alloys have relatively simple phase diagrams, and it seems to be reasonable that some simpler modelling systems should be investigated before systems with more complex phase diagrams revealing some intermetallic compounds. For the Ni–Cu system, we have used parametrization [21] recommended just for this alloy. As for the Au–Ag alloy, a ready parametrization seems to be absent. However, there exists a special method [22] and a subsidiary but well-approbated program that makes it possible to design the EAM multiparticle potential for binary systems on the basis of potentials proposed for the corresponding pure components. So, we have used parametrizations [23] and [24] for Au and Ag, respectively, to obtain the EAM parameters for the Au–Ag alloy.

The EAM potential was proposed just for metals to adequately take into account both the atomic and electronic subsystems. At the same time, the degree of the adequacy of the EAM parametrization is very principal to provide adequate simulation results. Obliviously, it is hardly possible to assess the quality of a force field on the basis of the binary nanoparticle properties. However, some basic properties of nanoparticles of pure Ni, Cu, Au and Ag and of the corresponding bulk phases can be straightforwardly proved and compared to the available experimental data and some MD results of other authors. Of course, a verification of the chosen parametrization was performed by the authors of papers [21, 23, 24] themselves. At the same time, before simulating binary nanoalloys, we investigated some basic properties of Ni, Cu, Au and Ag nanoparticles as well as of the corresponding bulk phases. These results cannot be discussed here in details. However, in what follows such properties as the melting temperature, the density and the structure will be sampled on our MD results for Au, Ag and Ni nanoparticles and corresponding the bulk phases.

Usually, in computer experiments, the particle melting T_m and crystallization T_c temperatures are fixed by observing some jumps (sharp moves upwards and downwards, respectively) in the temperature dependence of the cohesive term u in the specific (per atom) internal energy of the particle [25,26,27]. For this purpose, a nanocluster can be subjected to a predetermined number of the melting (in the course of heating) and crystallization (in the course of cooling) cycles. Such a method results in a melting-crystallization hysteresis, i.e. in a difference ΔT = T_m − T_c between T_m and T_c. And as it was shown in our paper [28], ΔT diminishes from 100 to 200 K down to about 10 K when the heating and cooling rates are diminished from 1 TK s⁻¹ down to 0.1 TK s⁻¹. However, to exclude the melting-crystallization hysteresis, in the present paper, we have used an alternative variant of determination of T_m by means of subsequent relaxations for about 100 ns of the initially solid particles at different constant temperatures in a vicinity of the bulk melting point T ^(∞)_m . In this case, we have also observed a jump of u at a definite temperature T ^(e)_m interpreted as the equilibrium melting temperature of the particle. A more detailed discussion on the methods of the determination of the melting temperature of nanoparticles in MD experiments is beyond the frames of this paper. Let us only note that T ^(e)_m lies within the interval T_c ≤ T ^(e)_m  ≤ T_m.

The size dependence of T ^(e)_m obtained in our MD experiments on Au nanoparticles is presented in Fig. 1 by the solid straight line. Fortunately, for Au nanoparticles, there are some experimental data which are also presented in the figure. One can see that our MD results satisfactorily agree with the available experimental data. For Cu nanoparticles, experimental data on the T_m(N) dependence (N is the number of atoms the particle consist of) seem to be absent. However, our MD dependence T_m(N^−1/3) shown in Fig. 2 agrees with the MD results of other authors presented here as well. The independent variable N^−1/3 was chosen as it is proportional to the reciprocal particle radius r ⁻¹₀ figuring in the well-known Thomson formula [33, 34] that predicts the linear dependence of T_m on r ⁻¹₀ . The linear approximation of the T_m(N^−1/3) dependence to N^−1/3 = 0 makes it possible to evaluate the macroscopic melting temperature T ^(∞)_m . For Au obtained, the value T ^(∞)_m  = 1188 K is underestimated in comparison with experimental value 1337 K [35]. However, such a deviation does not testify incontrovertibly that the MD dots directly obtained for Au nanoparticles should be also underestimated. Really, some deviations from linear T_m(N^−1/3) dependence are quite possible just for very small values of N^−1/3, i.e. for very large particle sizes which cannot be reproduced so far in computer experiments. For Cu particles, the value T ^(∞)_m  = 1352 K found from  our T_m(N^−1/3) dependence by means of linear approximation to N^−1/3=0 ideally agrees with the experimental value 1357 K [35].

Fig. 1

Dependence of T_m on N^−1/3 for Au nanoparticles. Circles ☉ and the solid line present our MD results, dots ■, ▲ and ▼ depict experimental data [1, 29, 30], respectively

Fig. 2

Comparison of our MD results for the size dependence of the melting temperature of Cu nanoparticles (circles ☉ and the solid line) with MD results of other authors (dots ■ [31] and ▲ [32])

Besides, all the chosen potentials for Au, Ag, Cu and Ni adequately predict the fcc structure of mesoscopic in size metal nanoparticles consisting of several thousand atoms and of the corresponding bulk metals. As a result, these potentials predict reasonable values of densities as well. For example, in Fig. 3, the local density ρ(r) is presented for Ni nanoparticles of different sizes (0 ≤ r ≤ r₀ is the radial coordinate). All the dependences correspond to the same temperature 1600 K but to the liquid (curves 1, 2 and 3) and solid (curve 4) states of the particles. One can see that in spite on some oscillations, the average local densities in the particle cores coincide with the corresponding bulk values. So, a conclusion can be made that all the chosen EAM potentials adequately enough describe the interatomic interactions in metal nanoparticles and corresponding bulk phases.

Fig. 3

Radial distributions of the local density ρ(r) in Ni nanoparticles of different sizes at T = 1600 K. Curves 1, 2, 3 and 4 correspond to N equal to 500, 5000, 10,000 and 15,000, respectively. Straight dashed lines correspond to experimental densities ρ ^(bulk)_s  = 8.30 × 10³ kg m⁻³ and ρ ^(bulk)_l  = 7.85 × 10³ kg m⁻³ for the bulk Ni in the solid and liquid states, respectively [35]

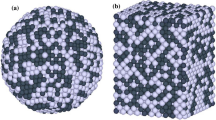
The initial configurations of binary nanoparticles, to be subjected then to the further MD evolution, corresponded to spherical fragments of the bulk fcc lattice with a random distribution of A and B components. A sample of such a configuration of a Ni–Cu nanoparticle (30% of Cu atoms) is presented in Fig. 4a. After placing the initial configuration in the centre of the simulation cell, the particle is uniformly heated to reach its liquid state above the particle melting temperature T_m which, generally speaking, can be determined by observing a jump of u(T). However, it is worth to mention that the exact definition of T_m is not principal for the further investigation of segregation. Moreover, up to now, even the interpretation itself of T_m and T_c for binary nanoalloys in terms of the liquidus and solidus temperatures is problematic and worth to be discussed separately. Really, contrary to the liquidus and solidus temperatures in the bulk phase diagram, T_m and T_c relate to the particle melting-crystallization hysteresis. However, the problem of the nanoalloy phase diagram cannot be solved not studying before the segregation phenomena in nanoparticles.

Fig. 4

MD snapshots of the initial (a) and final (b) configurations of a binary Ni–Cu nanoparticle consisting of 2000 atoms (30% of Cu atoms). Cu atoms are depicted by dark spheres

So, the particles were preliminary heated up to a temperature knowingly higher than the melting points of both components. Then, after cooling down to 400 K for Ni–Cu nanoparticles and down to 300 K for Au–Ag ones, the objects under consideration were relaxed for about 100 ns before further determination of the segregation parameters. The melting of binary nanoparticles before the subsequent cooling and observation of the segregation parameters has been used to facilitate the rearrangement of the initially non–equilibrium particle structure, i.e. to promote the possible tendency to the surface segregation of one of the particle components. Segregation has been studied when the particle structure and properties do not change in the course of time, i.e. the particle state could be treated, to a greater or lesser extent, as equilibrium or at least close to equilibrium. A snapshot of the final Cu nanoparticle configuration is presented in Fig. 4b (its initial configuration is shown in Fig 4a).

Method of thermodynamic simulation

It is hardly possible to strictly differentiate between conventional thermodynamic calculations and the thermodynamic simulation. However, as it has been already mentioned, the last term seems to be used when there are no ready thermodynamic formulas to adequately describe a system or a phenomenon of interest. In other words, the thermodynamic simulation reduces to solving an equation or a set of equations using as a rule some sequential approximations. In what follows, we will use the thermodynamic simulation method based on the Butler equations [14]. In [16], a new derivation of the Butler equations is given and exemplified on the investigation of the grain boundary segregation. Later [18,19,20] this method was extended to the segregation in nanoparticles. In our paper, the approach in question will be applied to a modelling nanoparticle presented by a core (its central part) surrounded by a shell. The goal of the thermodynamic simulation will be to find the equilibrium distribution of components in the modelling binary nanoparticle between its core and the shell. The modelling system in question will be considered in the frames of two sequential approximations:

• (i) the approximation of an unlimited source of the segregating component;

• (ii) the approximation of a limited source of the segregating component.

In the case of our modelling system just the particle core will be treated as the source for the segregating atoms. First, we will assume that the partial excess Gibbs energies of mixing ΔG ^(E)_m,i of components are zero, i.e. for this quantity the ideal solution approximation will be used. Afterwards (“Discussion”), the terms ΔG ^(E)_m,i will be also taken into account. However, independently on the chosen approximation, we will use one of the basic results of papers [16, 18,19,20] that the specific partial surface free energies of all the particle components should be equal to each other, i.e. the specific partial surface free energy σ_i of component i should be equal to the specific partial free energy σ_j of component j:

$$\sigma_{\rm i} = \sigma_{\rm j} .$$

(1)

As Eq. (1) is central for the further thermodynamic simulation, in what follows it will be explained in more detail. The Gibbs energy G of a multicomponent particle can be presented as follows

$$G = G_{0} + \sigma S,$$

where the summand G₀ may be interpreted either as the bulk Gibbs energy (when the Gibbs surface phases method is used being extended to small objects [36, 37]) or as the Gibbs energy of the particle core (if the alternative Guggenheim’s method of the finite thickness layer [38] is engaged). The addend σS corresponds to the particle surface free energy where σ is the specific (per unit area) free energy and S is the particle surface area (in m²). In [16, 18,19,20],  a novel enough concept of the partial surface area S_i of the component i was used. Introducing such a quantity seems to be quite reasonable as it is a direct analogue of the partial volume widely used in thermodynamics of multicomponent systems. Finally, as the conditions σS = ∑ σ_iS_i and S = ∑ S_i are satisfied, the equality $\sigma_{\rm i} = \sigma = {\text{const}}$ should be also valid that, in turn, justifies Eq. (1).

Then, according to [16, 18,19,20], the specific partial surface free energy σ_i of the component i can be presented as the next function of the relative molar fraction x ^(s)_i /x ^(c)_i of this component i:$\sigma_{\rm i} = \sigma_{\rm i}^{\left( 0 \right)} \frac{{\omega_{\rm i}^{\left( 0 \right)} }}{{\omega_{\rm i} }} + \frac{RT}{{\omega_{\rm i} }}\ln \left( {\frac{{x_{\rm i}^{(\rm s)} }}{{x_{\rm i}^{(\rm c)} }}} \right) + \frac{{\Delta G_{\text{m,i}}^{{\left( {\rm E,s} \right)}} - \Delta G_{\text{m,i}}^{{\left( {\rm E,c} \right)}} }}{{\omega_{\rm i} }}$where x ^(s)_i is the molar fraction of componentiin the surface area and x ^(c)_i is the value of x_i for the particle core, R is the molar gas constant, ω_i is the partial molar surface of component i, i.e. the partial surface in m² mol⁻¹, ω ⁽⁰⁾_i is the specific molar surface area for the pure component i, σ ⁽⁰⁾_i is the specific surface free energy of the pure component i, ∆G_m,i^(E,s) and ∆G_m,i^(E,c) are the partial molar excess Gibbs energies of component i in the surface layer and in the particle core, correspondingly. Here and in what follows, superscripts s and c correspond to the surface layer and the particle core, respectively.

In the frames of the approximation of the infinite reservoir for the segregating component, we assume that x ^(c)_i remains equal to its initial average value x_i which is treated as a constant input parameter. So, for binary A–B particles, under an additional assumption that ΔG ^{(E, s)}_m,A  = ΔG ^{(E, c)}_m,A =ΔG ^(E,s)_m,B = ΔG ^(E,c)_m,B  = 0 (the ideal solution approximation), Eq. (1) can be rewritten as

$$\sigma_{\text{A}}^{\left( 0 \right)} + \frac{RT}{{\omega_{\text{A}} }}\ln \left( {\frac{{1 - x_{\text{B}}^{(\rm s)} }}{{1 - x_{\text{B}} }}} \right) = \sigma_{\text{B}}^{\left( 0 \right)} + \frac{RT}{{\omega_{\text{B}} }}\ln \left( {\frac{{x_{\text{B}}^{(\rm s)} }}{{x_{\text{B}} }}} \right) .$$

(2)

We have also taken into account that, according to [16, 18,19,20], the equality ω_i ≈ ω ⁽⁰⁾_i should be also fulfilled. Then, under the assumption that $\omega_{\text{A}} = \omega_{\text{B}} = \omega$ (some quantitative evaluations will be discussed in “Discussion” section) Eq. (2) can be readily solved:

$$x_{\text{B}}^{(\rm s)} = \frac{{K_{{{\text{B,s}}}} x_{\text{B}} }}{{1 + x_{\text{B}} \left( {K_{{{\text{B,s}}}} - 1} \right)}} ,$$

(3)

where

$$K_{{{\text{B,s}}}} = \exp \left[ {\frac{{\omega \left( {\sigma_{\text{A}}^{\left( 0 \right)} - \sigma_{\text{B}}^{\left( 0 \right)} } \right)}}{RT}} \right]$$

(4)

is the segregation coefficient for the B component. In our following calculations, we will assume that $\omega = \left( {\omega_{\text{A}}^{\left( 0 \right)} + \omega_{\text{B}}^{\left( 0 \right)} } \right)/2$

For binary nanoparticles of 1–10 nm in size, the particle core cannot be adequately interpreted as an infinite reservoir of the segregating component. Therefore, the average molar fractions

$$\left\langle {{x_{\rm{A}}}} \right\rangle = \frac{{\nu_{\text{A}} }}{\nu } = \frac{{N_{\text{A}} }}{N}\quad {\text{and}}\quad \left\langle {{x_{\rm{B}}}} \right\rangle = \frac{{\nu_{\text{B}} }}{\nu } = \frac{{N_{\text{B}} }}{N}$$

should differ from the next similar quantities

$$x_{\text{A}}^{(\rm c)} = \frac{{\nu_{\text{A}}^{(\rm c)} }}{{\nu^{(\rm c)} }} = \frac{{N_{\text{A}}^{(\rm c)} }}{{N^{(\rm c)} }}; \;x_{\text{B}}^{(\rm c)} = \frac{{\nu_{\text{B}}^{(\rm c)} }}{{\nu^{(\rm c)} }} = \frac{{N_{\text{B}}^{(\rm c)} }}{{N^{(\rm c)} }};\;x_{\text{A}}^{(\rm s)} = \frac{{\nu_{\text{A}}^{(\rm s)} }}{{\nu^{(\rm s)} }} = \frac{{N_{\text{A}}^{(\rm s)} }}{{N^{(\rm s)} }}\quad {\text{and}}\quad x_{\text{B}}^{(\rm s)} = \frac{{\nu_{\text{B}}^{(\rm s)} }}{{\nu^{(\rm s)} }} = \frac{{N_{\text{B}}^{(\rm s)} }}{{N^{(\rm s)} }}$$

for the particle core and the particle surface area, respectively, where $\nu_{\text{A}}$ and $\nu_{\text{B}}$ are the numbers of moles of components A and B, respectively, $\nu = \nu_{\text{A}} + \nu_{\text{B}}$ is the total number of moles, $N_{\text{A}}$ and $N_{\text{B}}$ are the numbers of A and B atoms, respectively, and $N = N_{\text{A}} + N_{\text{B}}$ is the total number of atoms in the particle.

The thermodynamic approach under consideration does not put any restrictions on the surface layer thickness. However, the fraction of the surface atoms ξ = N^(s)/N should be preassigned as one of the input parameters. In the surface monolayer approximation the ξ parameter is equal to the reduced (dimensionless) dispersion degree D^*:

$$\xi = \frac{{n^{(\rm s)} 4\pi r_{0}^{2} }}{{n\left( {4/3} \right)\pi r_{0}^{3} }} = \frac{{n^{\left( s \right)*} }}{{n^{*} }}\frac{{4\pi r_{0}^{*2} }}{{\left( {4/3} \right)\pi r_{0}^{*3} }} \simeq \frac{3}{{r_{0}^{*} }} = D^{*} .$$

(5)

In (5) n = N/(4/3)πr ³₀ is the average density (concentration) of atoms in the particle, n^(s) = N^(s)/4πr ²₀ is the average surface density and r ^*₀  = r₀/a, where the average atomic diameter a can be interpreted as average value of the atomic diameters a_A and a_B. The corresponding reduced densities n^* and n^(s)*are defined as na³ and n^(s)a², respectively. A loose but reliable approximation ξ ≃ D^* corresponds to n^* ≃ n^(s)* ≃ 1. Of course, Eq. (5) does not exclude some more exact approximations of the ξ parameter.

So, the evaluation of $x_{\text{B}}^{(\rm s)}$, in the frames of the limited source for the segregating component approximation, reduces to solving the next set of two algebraic equations:

$$\left\{ {\begin{array}{l} {x_{\text{B}}^{(\rm s)} = \frac{{K_{{{\text{B,s}}}} x_{\text{B}}^{(\rm c)} }}{{1 + x_{\text{B}}^{(\rm c)} \left( {K_{{{\text{B,s}}}} - 1} \right)}}} \\ {x_{\text{B}}^{(\rm s)} \xi + x_{\text{B}}^{(\rm c)} \left( {1 - \xi } \right) = \left\langle {{x_{\rm{B}}}} \right\rangle ,} \\ \end{array} } \right.$$

(6)

and the solution in question reduces, in turn, to solving a quadratic algebraic equation for $x_{\text{B}}^{(\rm c)}$. If the particle is non-volatile, the average molar fraction $\left\langle {{x_{\rm{B}}}} \right\rangle$ of the component B in the particle will not depend on time, i.e. the condition $\left\langle {{x_{\rm{B}}}} \right\rangle = {\text{const}}$ should be fulfilled. The second equation of the set (6) has a simple physical meaning: it is the mass balance equation for the B component in the core–shell modelling particle. In what follows, the subscript B will be used for Cu atoms in the case of the Ni–Cu nanoalloy and for Ag atoms when the Au–Ag nanoalloy will be treated.

Results of atomistic and thermodynamic simulations

To determine the surface segregation, i.e. $x_{\text{B}}^{(\rm s)}$ as a function of $\left\langle {{x_{\rm{B}}}} \right\rangle$ for the Ni–Cu and Au–Ag nanoalloys, we have chosen low enough temperatures (400 and 300 K, respectively). For these temperatures, binary Ni–Cu and Au–Ag nanoparticles will knowingly be in the solid state. One can see that the snapshot presented in Fig. 4b demonstrates a pronounced surface segregation of Cu in this Ni–Cu nanoparticle containing 30% of Cu atoms. Quantitatively, the segregation of Cu is demonstrated by Fig. 5 where the dependences of the local molar fractions $x_{\text{Ni}} \left( r \right)$ and $x_{\text{Cu}} \left( r \right)$ of Ni and Cu atoms, respectively, on the radial coordinate r are presented for a Ni–Cu nanoparticle consisting of 2000 atoms (r₀ = 1.9 nm, 50% concentration of each component). The value r₁ of r, corresponding to an intersection of $x_{\text{Ni}} \left( r \right)$ and $x_{\text{Cu}} \left( r \right)$ curves, can be chosen as a geometrical boundary between the particle core and its surface area. The surface area thickness r₀ − r₁ ≃ 0.5 nm corresponds to two outer atomic monolayers enriched by Cu atoms. The dependence of $x_{\text{Cu}}^{(\rm s)}$ on $\left\langle {{x_{\rm{Cu}}}} \right\rangle$ for binary Ni-Cu nanoparticles consisting of 2000 atoms is presented in Fig. 6. One can see that our MD results agree very well with the approximation of the limited source of the segregating component (curves 2 and 3). The dashed line in Fig. 6 corresponds to $x_{\text{B}}^{(\rm s)} = \left\langle {{x_{\rm{B}}}} \right\rangle$, i.e. to the absence of segregation. So, if segregation of B component takes place, the dots $x_{\text{B}}^{(\rm s)} \left( {\left\langle {{x_{\rm{B}}}} \right\rangle } \right)$ will be located above the dashed line in question. When evaluating $x_{\text{B}}^{(\rm s)}$ in the frames of the thermodynamic approach, values of the specific surface free energies $\sigma_{\text{A}}^{\left( 0 \right)}$ and $\sigma_{\text{B}}^{\left( 0 \right)}$, i.e. of the surface tensions of Ni and Cu in the solid state, figuring in the segregation coefficient (4), were calculated using experimental data [39] on the surface tensions and their temperature derivatives.

Fig. 5

MD radial distributions of local molar fractions $x_{\text{Ni}} \left( r \right)$ and $x_{\text{Cu}} \left( r \right)$ in the final equilibrated configuration of a binary Ni–Cu nanoparticle consisting of 2000 atoms (50% of each component). Curve 1 corresponds to Ni and curve 2 to Cu atoms

Fig. 6

Evaluations of the surface molar fraction $x_{\text{Cu}}^{(\rm s)}$ in Ni–Cu nanoparticles consisting of 2000 atoms. Curve 1 corresponds to the approximation of the unlimited source of the segregating component, curves 2 and 3 to the limited source approximation. MD results are depicted by dots. Curves 1 and 2 correspond to the ideal solution approximation. Curve 3 takes into account the differences between the partial Gibbs mixing energies for Ni and Cu. Dashed line corresponds to $x_{\text{Cu}}^{(\rm s)} = \left\langle {{x_{\rm{Cu}}}} \right\rangle$, i.e. to the limiting case of the absence of segregation

Structural transformations in binary Au–Ag nanoparticles in the course of the spontaneous rearrangement of their structure seem to be more complex and more interesting. Really, according to Fig. 7a, the onion-like structure is not inherent to binary Au–Ag nanoparticles containing 20% of Ag atoms. At the same time, the surface segregation in Au–Ag nanoparticles, containing more than 20% of Ag atoms, results in an onion-like structure formation. In fact, as one can see in Fig. 7b, corresponding to the 1:1 composition, the outer atomic monolayer of thickness r₀ − r₁ = 0.3 nm consists almost entirely of Ag atoms, whereas the second monolayer, having the same thickness r₂ − r₁ = 0.3 nm, is enriched by Au atoms. Therefore, for such Au–Ag nanoparticles, r = r₂ corresponds to the most adequate choice of the boundary between the particle core and its surface bilayer. It is also noteworthy that some onion-like layering in the particle core has been observed as well. However, such a layering demonstrated by the $x_{\text{Au}} \left( r \right)$ and $x_{\text{Ag}} \left( r \right)$ dependences shown in Fig. 7a for r<r₂ is rather poorly pronounced.

Fig. 7

MD radial distributions of the local molar fractions $x_{\text{Au}}$ and $x_{\text{Ag}}$ in binary Au–Ag nanoparticles consisting of 2000 atoms: a 20% of Ag atoms; b 50% of Ag atoms. Curve 1 corresponds to $x_{\text{Au}} \left( r \right)$ and curve 2 to $x_{\text{Ag}} \left( r \right)$

The dependence of $x_{\text{Ag}}^{(\rm s)}$ on $\left\langle {{x_{\rm{Ag}}}} \right\rangle$ for binary Au–Ag nanoparticles is presented in Fig. 8. One can see that our MD results, corresponding to the monolayer model of the surface area and presented by black circles satisfactorily agree with the thermodynamic simulation results presented by curve 2 corresponding to approximation of the limited source of the segregating component. Then, when handling the MD results, the bilayer surface area model was also employed (white circles in Fig. 8), $x_{\text{Ag}}^{(\rm s)}$ diminishes almost down to $\left\langle {{x_{\rm{Ag}}}} \right\rangle$, i.e. the surface segregation of Ag considered in the frames of the surface bilayer model is negligibly small.

Fig. 8

Dependence of the molar fraction $x_{\text{Ag}}^{(\rm s)}$ of Ag atoms on <x_Ag> in the surface layer of Au–Ag nanoparticles consisting of 2000 atoms (50% of each component). Curve 1 corresponds to the thermodynamic simulation results in the approximation of unlimited source of the segregating component; curve 2 corresponds to the limited source approximation. MD results corresponding to the surface monolayer model are depicted by black dots; white circles depict the MD results corresponding to the bilayer surface area model

Discussion

According to the results, presented in the previous section, both atomistic and thermodynamic simulations predict the surface segregation of Cu in Ni–Cu nanoparticles and the segregation of Ag in Au–Ag nanoalloys. One can see that the MD results agree well enough with the thermodynamic simulation results corresponding to the approximation of the limited source for the segregating component even if the ideal solution approximation for the excess Gibbs energy of mixing is also used, i.e. it is assumed that ΔG ^{(E, s)}_m,i  = ΔG ^{(E, c)}_m,i  = 0 for both components. However, in Appendices to paper [16], all the parameters and some semi-empirical equations are given that make it possible to evaluate the partial molar Gibbs energies ΔG ^{(E, c)}_m,i and ΔG ^{(E, s)}_m,i for both components of the Ni-Cu alloy. With respect to these terms, Eq. (1) allows a numerical solution only and a discussion on details of these calculations is beyond the frames of this paper. The results of the numerical solution of Eq. (1) are presented by curve 3 in Fig. 6. So, the realistic counting for the values of the Gibbs mixing energy results in a diminishing of the $x_{\text{Cu}}^{(\rm s)}$ values in comparison with the ideal solution approximation (curve 2). At the same time, the thermodynamic simulation results presented by both curves 2 and 3 satisfactory agree with each other and with our MD results. The explanation is that such an agreement between these thermodynamic results takes place not only when $\Delta G_{\text{m, Ni}}^{{\left( {\rm E,s} \right)}} = \Delta G_{\text{m, Ni}}^{{\left( {\rm E,c} \right)}} = \Delta G_{\text{m,Cu}}^{{\left( {\rm E,s} \right)}} = \Delta G_{\text{m, Cu}}^{{\left( {\rm E,c} \right)}} = 0$, but also when the terms $\left( {\Delta G_{\text{m, Ni}}^{{\left( {\rm E,s} \right)}} - \Delta G_{\text{m, Ni}}^{{\left( {\rm E,c} \right)}} } \right)/\omega_{\text{Ni}}$ and $\left( {\Delta G_{\text{m, Cu}}^{{\left( {\rm E,s} \right)}} - \Delta G_{\text{m, Cu}}^{{\left( {\rm E,c} \right)}} } \right)/\omega_{\text{Cu}}$ are close enough to each other being not equal to zero separately. For components of the Au–Ag alloys, the ΔG ^(E)_m,i contributions should be much closer to each other and, respectively, they cannot change noticeably the dependence of $x_{\text{Ag}}^{(\rm s)}$ on $\left\langle {{x_{\rm{Ag}}}} \right\rangle$ presented by curve 2 in Fig. 8. In other words, it is more principal that the particle core is really the limited source for the segregating component.

As it was already mentioned in Introduction, the problem of the segregation in Au–Ag nanoalloys is disputable [9]. We mean that it was not quite clear before which of two components of this nanoalloy should segregate to the particle surface. Therefore, it is noteworthy that both thermodynamic and MD simulations predict segregation of Ag atoms that entirely agrees with experimental data presented in paper [13] that seems to be the only experimental work on segregation in Au-Ag nanoparticles. It is also worth to be emphasized that when segregation of Ag atoms was estimated in the frames of the monolayer model of the surface area, thermodynamic results (curve 2 in Fig. 8) satisfactorily agree with the MD results corresponding to the same model of the surface area. At the same time, our MD results for the Au–Ag system predict an interesting phenomenon of the onion-like structure formation. Because of the phenomenon in question, the MD estimations of $x_{\text{Ag}} \left( r \right)$ in the frames of the surface bilayer approximation predict a very low segregation of Ag, i.e. give the values of $x_{\text{Ag}}^{(\rm s)}$ close to $\left\langle {{x_{\rm{Ag}}}} \right\rangle$ (see Fig. 8). Such a result seems to be quite reasonable taking into account the onion-like structure observed in our MD experiments.

In our thermodynamic calculations, we have used the average value $\omega = \left( {\omega_{\text{A}} + \omega_{\text{B}} } \right)/2$ of the partial molar areas of components A and B. Besides, following to [16, 18,19,20], we have also assumed that $\omega_{\text{A}} = \omega_{\text{A}}^{\left( 0 \right)}$ and $\omega_{\text{B}} = \omega_{\text{B}}^{\left( 0 \right)}$ where $\omega_{\text{A}}^{\left( 0 \right)}$ and $\omega_{\text{B}}^{\left( 0 \right)}$ are the molar surfaces of pure components A and B. In turn, for the components of the Ni-Cu and Au–Ag alloys, the values of $\omega_{\text{A}}^{\left( 0 \right)}$ and $\omega_{\text{B}}^{\left( 0 \right)}$ are close to each other. Really, at the room temperature $\omega_{\text{Cu}}^{\left( 0 \right)} = 3.12\;10^{4}$ × m² mol⁻¹ and $\omega_{\text{Ni}}^{\left( 0 \right)} = 2.89\;10^{4}$  × m² mol⁻¹. So, when the quantities $\omega_{\text{A}}^{\left( 0 \right)}$ and $\omega_{\text{B}}^{\left( 0 \right)}$ had been separately taken into account, it would not noticeably change the results of the thermodynamic simulations. For Au and Ag, the values of ω⁽⁰⁾ practically coincide. Really, $\omega_{\text{Au}}^{\left( 0 \right)} = 3.97\;10^{4}$ × m² mol⁻¹ and $\omega_{\text{Ag}}^{\left( 0 \right)} = 3.99\;10^{4}$ × m² mol⁻¹, respectively. To evaluate the $\omega_{\text{A}}^{\left( 0 \right)}$ and $\omega_{\text{B}}^{\left( 0 \right)}$ quantities, we have used the values of densities of metals taken from handbook [35].

In monograph [9], the next factors affecting segregation in nanoalloys are mentioned:

• (i) Bond strength, i.e. the relative strengths of A–A, B–B and A–B bonds between metal atoms: the component forming stronger bonds should tend to segregate to the core, while stronger A–B bonds will favour mixing. Obviously, the bond strength is determined by the binding energies of components A and B;

• (ii) Surface energy: the metal with lower surface energy will tend to segregate to the nanoparticle surface;

• (iii) Atomic size: this relates to the release of strain effects in the nanoparticle with smaller atoms tending to the core position;

• (iv) Specific electronic effects for certain metals (directionality of bonding);

• (v) Charge transfer between atoms: the most electronegative atom will tend to occupy a surface site.

All the above factors seem to be quite reasonable and their quantitative role remains unclear. However, all the above factors should be treated as different aspects of the interatomic interactions that fully determine all the thermodynamic properties, including the surface energy which cannot be considered as an independent factor. And taking into account this conclusion and the results of our work, we put forward a hypothesis that the segregation coefficient (4) determined by the difference $\left( {\sigma_{\text{A}}^{\left( 0 \right)} - \sigma_{\text{B}}^{\left( 0 \right)} } \right)$ can be treated as a criterion which makes it possible to predict, at least qualitatively, the surface segregation in binary nano- and microparticles. Really, $K_{{{\text{B,s}}}} > 1$ for both Cu in the Ni–Cu particles and Ag in the Au–Ag nanoalloy. Another example can be also given: for Au-Cu nanoparticles K_Au,s>1 that predicts the surface segregation of Au atoms. And such a prediction agrees with theoretical results [40] not relating to the thermodynamic simulation method we have used in the present paper. However, a detailed justification of the segregation coefficient (4) as a criterion of segregation is beyond the frames of this paper.

Conclusions

So, to predict the segregation in binary metal nanoparticles, we have used and approbated the approach combining atomistic and thermodynamic simulations. Being also complemented in some cases by ab initio simulations, such an approach seems to be promising taking into account that all the available theoretical treatments of the segregation phenomena are, to a greater or lesser extent, disputable when extended to nanoalloys. In particular, it concerns the extension of concept and methods of thermodynamics to small objects. Moreover, as it has been already mentioned in Introduction, Buttler’s approach provoked before some critical objections as well. In turn, DFT and some other ab initio methods may be effectively applied to very small clusters consisting of several dozens of atoms only. Besides, the basic ab initio approaches do not take into account the non-zero temperature and, respectively, the entropy factor. No doubt that the size rage of the objects suitable for the atomistic simulations is much wider. However, some doubts may be also provoked concerning the adequacy of the counting for the electronic term into the interatomic interaction in metal systems and, especially, in metal nanoparticles. From this point of view, the agreement of our results obtained by combining the thermodynamic and atomistic simulations for Ni–Cu and Au–Ag nanoalloys can be considered as a corroboration of the adequacy of the both approaches. It is also worth to mention that our thermodynamic simulations were based on the equilibrium thermodynamics. And the agreement of the results of the thermodynamic and atomistic simulations confirms our assumption that the final relaxed configurations of nanoparticles in our MD experiments can be treated as equilibrium ones. Then, as it has been already mentioned, the available experimental data on the segregation phenomena in nanoparticles and nanosystems are rather scanty and very often not quite reliable. So, we hope that our paper has demonstrated that the further development of theoretical approaches is promising by combining different structural levels of simulation to adequately predict the segregation phenomena in small objects.