Thermal analysis of cadmium addition on the glass transition and crystallization kinetics of Se–Te–Sn glassy network

Abstract

Calorimetric measurements have been performed in quaternary glassy system Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4, and 6) to study the thermally induced glass transition and crystallization phenomena. The characteristics kinetic temperatures (glass transition temperature $T_{\text{g}}$, onset crystallization temperature $T_{\text{o}}$, peak crystallization temperature $T_{\text{c}}$) and static melting temperature $T_{\text{m}}$ of the quaternary glassy series have been determined using their non-isothermal DSC curves. These temperatures were utilized to calculate the thermal stability $S$ and the Hruby parameter $H_{\text{R}}$ for the studied glasses. Both the activation energy of glass transition $E_{\text{t}}$ and the activation energy of crystallization $E_{\text{c}}$ for all compositions were evaluated using the well-known Kissinger's relation and the method of Augis–Bennett. Values of the fragility index $m$ and the crystallization rate factor $K_{\text{p}}$ were estimated using the activation energy values $E_{\text{t}}$ and $E_{\text{c}}$, respectively. The compositional dependence of the above-mentioned parameters was discussed on the basis of rigidity models and according to the formation of iono-covalent bonds when our glassy Se–Te–Sn system is doped with a heavy element as Cd.

Introduction

Chalcogenide glasses have been involved in many applications in our daily life such as digital X-ray imaging solar cells, biosensing, lithography, optical elements (lenses, waveguides, gratings, fibers, etc.) and switching devices [1,2,3]. Moreover, the ease of the phase change between high-conductive (crystalline) and low-conductive (amorphous) states in these materials makes them as good candidates in the phase-change rewritable optical disk. This disk has a large capacity and is easily handled like the floppy disk and the digital versatile disk (DVD) [4,5,6,7,8,9,10,11]. Kinetic analysis is considered as an important tool in determining the utility of chalcogenide alloys as recording materials or other practical applications [12]. This is due to the fact that the phase change of optical recording and erasing techniques are based on the laser-induced thermal amorphization and crystallization of chalcogenide glasses [13].

Much attention has been paid to study the relation between the composition of glassy alloys and their thermal stability and glass-forming ability because of their importance in yielding valuable information concerning the evaluation of network connectivity and the network rigidity as well [14]. Se-based chalcogenide glasses are promising materials due to their several applications like optical fibers, memory devices, switching devices and solar cells. Se in its pure state has disadvantages such as short lifetime, low sensitivity and low crystallization temperature [15]. In order to overcome these demerits, the addition of Te improves the corrosion resistance and optical sensitivity [16]. Adding Sn to the Se–Te alloys make them more promising glasses for infrared optical films due to their good thermo-mechanical properties. The addition of metallic impurity as Cd to Se–Te–Sn forms a prototypical system suitable for devices fabrication [17, 18]. The present work was undertaken to study the influence of replacing Se by Cd in our quaternary alloys of Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6). Both the Te percentage (20 at.%) and the Sn percentage (2 at.%) have been fixed in the studied series. The DSC characteristic temperatures were used to determine several important parameters such as the thermal stability, glass-forming ability, the Hruby number and the reduced glass transition temperature. A theoretical prediction of some important physical parameters related to the composition viz., average coordination number, average constraints, lone-pair electrons, fraction of floppy modes, heat of atomization, theoretical energy gap, electronegativity was made. Both the activation energy of glass transition and the activation energy of crystallization were calculated. All the above-mentioned parameters have been reflected the growing interest in these materials and the effect of Cd on the chemical ordering of the existing bonds as well as the compositional and configurational disorders in the alloys under study.

Experimental

Multi-component glasses of Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4, and 6) system were prepared by using uncomplicated melt-quench technique. Uncontaminated Se, Te, Sn and Cd elements having 99.999% purity were first weighed according to their atomic percentages and after that the materials were evacuated in quartz ampoules having length ~ 5 cm and internal diameter ~ 8 mm. For this purpose, we used a bench mark high vacuum pumping system that was able to create satisfactory vacuum (~ 10⁻⁶ Torr). Every sample containing ampoule was reserved inside the furnace for heating at appropriate high temperature at a constant rate of 4 °C min⁻¹ for 12 h. During heating, the rocking of all the ampoules was done continuously to make sure homogeny of the samples. Finally, we quenched the molten samples rapidly in ice-cooled water. The ingots of the samples were then taken out by breaking the quartz ampoules.

We used differential scanning calorimeter (TA Instruments, USA; Model: Q20 MDSC) for study of thermal behavior of preset multi-component glasses. Almost equal mass (~ 5 mg) of each sample in powdered form was used for thermal analysis in DSC unit in non-isothermal mode. The temperature precision of this equipment is ± 0.1 K with an average standard error of about ± 1 K in the measured values.

Theoretical basis

The understanding of glass transition and crystallization kinetics is one of the most significant problems in the area of glasses. This can be studied in terms of glass transition temperature (T _g) and crystallization temperature (T _c) and the corresponding activation energies of glass transition (E _t) and crystallization (E _c).

Dependence of the glass transition temperature on heating and cooling rate in chalcogenide glasses is interpreted by Moynihan et al. [19,20,21] in terms of thermal relaxation phenomenon. In his interpretation, he assumed that enthalpy is the function of time and temperature. During cooling or heating at constant pressure (i.e., isobaric process), the enthalpy relaxes from value H _o (at t = 0) at a particular temperature to some equilibrium value H _e at temperature T instantaneously. This whole process may assume to consist of large number of slow processes (isothermal processes). Thus, it can be expressed as:

$$\left( {{{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\text{T}} = \sum\limits_{i = 1}^{n} {\left( {{{\partial H_{\text{i}} } \mathord{\left/ {\vphantom {{\partial H_{\text{i}} } {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\text{T}} } .$$

(1)

The rate of isothermal change H _i is given by time and temperature relaxation time

$$\left( {{{\partial H_{\text{i}} } \mathord{\left/ {\vphantom {{\partial H_{\text{i}} } {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\text{T}} = - \,\,\left( {H_{\text{i}} - H_{\text{ei}} } \right)/\tau_{\text{i}} .$$

(2)

According to Moynihan et al., the difference between total observed heat capacity (C _p) and glass heat capacity (C _pg) during the heating process of glass under isobaric condition can be written as:

$$(C_{\text{p}} - C_{\text{pg}} ) = \pm \mathop {\,\sum }\limits_{i = 1}^{n} \frac{{(H_{\text{i}} - H_{\text{ie}} )}}{{\beta \tau_{\text{i}} }} .$$

(3)

Here, β is the heating or cooling rate, H _i is the enthalpy associated with some order parameter as 1,2,3,…..i,…n which changes during structural relaxation and H _ie is the enthalpy at new equilibrium value at some order parameter.

According to Moynihan’s theory [21], the structural relaxation process can be described by more than one order parameter and associated relaxation time. In such condition, the corresponding relaxation heat capacity associated with each order parameter can be written as:

$$(C_{\text{p}} - C_{\text{pgi}} ) = \mp \,\mathop \sum \limits_{i = 1}^{n} \frac{{(H_{\text{i}} - H_{\text{ie}} )}}{{\beta { \exp }\left[ { - \,c\left( {{\text{H}} - H_{\text{e}} } \right)} \right]}}\exp \left\{ { - \ln \left| \beta \right| + bT} \right\}.$$

(4)

Here, b = (E _g/RT ²_τ ) is a constant, E _g is the activation energy, T _τ is the temperature in the middle of the transition range and R is the gas constant.

For two heat capacity curves, A and B, produced during cooling/heating at respective rates β _A and β _B, the condition will hold that:

$$(C_{\text{p}} - C_{\text{pg}} )_{\text{A}} |\;at\;T_{\text{A}} = (C_{\text{p}} - C_{\text{pg}} )_{\text{B}} |\;at\;T_{\text{B}} .$$

(5)

T _g is the temperature at which some particular value of relaxation heat capacity (C _p − C _pg) is observed. For two heat capacity curves, A and B, produced during cooling or heating at respective rates ∣β _A∣ and ∣β _B∣:

$$- \,\ln |\beta_{\text{A}} | + bT_{\text{gA}} = - \,\ln |\beta_{\text{B}} | + bT_{\text{gB}} .$$

(6)

Here,

$$(H - H_{\text{e}} )_{\text{A}} |\;at\;T_{\text{A}} = (H - H_{\text{e}} )_{\text{B}} |\;at\;T_{\text{B}} .$$

(7)

They further assumed that the difference between the equilibrium liquid and glass heat capacities (C _pe − C _pg) is constant over the experimental range of T _g. The total heat capacity at any temperature is the sum of individual process:

$$\left( {C_{\text{p}} - C_{\text{pg}} } \right) = \sum\limits_{i = 1}^{n} {\left( {C_{\text{pi}} - C_{\text{pgi}} } \right)}$$

(8)

Finally, we conclude for whole process:

$$(\partial H/\partial T) = - \,(H - H_{\text{e}} )/\tau .$$

(9)

Here, τ is a temperature dependent structural relaxation time and is given by the following relation:

$$\tau = \tau_{\text{o}} \exp ( - \,E_{\text{g}} /RT)\exp [ - \,c(H - H_{\text{e}} )].$$

(10)

Here, τ _o and c are constants and E _g is the activation energy associated with thermal relaxation. Using the above equations, it can be shown [19,20,21] that:

$${\text{d}}(\ln \,\beta )/{\text{d}}(1/T_{\text{g}} ) = - \,E_{\text{g}} /R.$$

(11)

Equation (11) states that ln β versus 1/T _g plot should be straight line and the activation energy involved in the molecular motions and rearrangements around T _g can be calculated from the slope of this plot.

The Kissinger method [22] is devised to analyze crystallization and generally known as peak shift method. During the isothermal transformation, the extent of crystallization (α) at any time t of a certain material is expressed by well-known Avrami’s equation [23, 24]:

$$\alpha (t) = [1 - \exp \{ ( - \,Kt)^{\text{n}} \} ].$$

(12)

Here, “K” is rate constant and “n” is the order parameter or Avrami exponent which depends upon the mechanism of crystal growth.

The form of rate constant K is generally accepted to be given by Arrhenius equation:

$$K = K_{\text{o}} \exp [ - \,E_{\text{c}} /kT].$$

(13)

Here, K _o is pre-exponential factor.

According to Kissinger, the time derivative of α of Eq. (12) can be approximated as:

$${\text{d}}\alpha /{\text{d}}t = (1 - \alpha )nK^{\text{n}} t^{{\text{n}} - 1} .$$

(14)

Expressing t in terms of α from Eq. (12), the crystallization rate dα/dt becomes:

$${\text{d}}\alpha /{\text{d}}t = AnK(1 - \alpha ).$$

(15)

Here, $A = [ - \,\ln (1 - \alpha )]^{({\text{n}} - 1)/{\text{n}}}$.

In non-isothermal mode of DSC, the sample is heated at constant heating rate during the experiment. Thus, the relation between the sample temperature T and the heating rate β can be written as:

$$T = T_{\text{i}} + \beta t.$$

(16)

Here, T _i is the initial temperature.

The derivative of K with respect to time can be obtained by differentiating Eq. (8) and using Eq. (16) in the following form:

$${\text{d}}K/{\text{d}}t = ({\text{d}}K/{\text{d}}T) \cdot ({\text{d}}T/{\text{d}}t) = (\beta E_{\text{c}} /RT^{2} )K.$$

(17)

Using Eqs. (15) and (17), Kissinger showed that:

$$\ln (\beta /T_{\text{c}}^{2} ) = - \,E_{\text{c}} /RT_{\text{c}} + \text{constant}{.}$$

(18)

Here, T _c is the peak crystallization temperature.

Although originally derived for the crystallization process, it is suggested that this relation is valid for glass transition process [25, 26] and hence the above equation takes the following form for its use in glass transition kinetics:

$$\ln (\beta /T_{\text{g}}^{2} ) = - \,E_{\text{g}} /RT_{\text{g}} + \text{constant}{.}$$

(19)

Augis and Bennett [27] developed an accurate method for evaluation of activation energy of crystallization and the pre-exponential factor of rate constant K. They took proper account of the temperature dependence of the reaction rate, and their approach resulted in a linear relation between ln β/(T _c) versus 1/T _c.

They used a substitution “u” for “Kt,” and then they expressed the rate of reaction as:

$$\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right) = n\left( {\frac{{{\text{d}}u}}{{{\text{d}}t}}} \right)u^{{\text{n}} - 1} \;(1 - \alpha ).$$

(20)

Here,

$$\left( {\frac{{{\text{d}}u}}{{{\text{d}}t}}} \right) = u\left[ {\frac{1}{t} + a} \right].$$

(21)

The second derivatives of Eqs. (20) and (21) are given by:

$$\frac{{{\text{d}}^{2} \alpha }}{{{\text{d}}t^{2} }} = \left[ {\frac{{{\text{d}}^{2} u}}{{{\text{d}}t^{2} }}u - \left( {\frac{{{\text{d}}u}}{{{\text{d}}t}}} \right)^{2} \;(nu^{\text{n}} - n + 1)\;} \right]nu^{{\text{n}} - 2} \;(1 - \alpha ) = 0$$

(22)

$$\frac{{{\text{d}}^{2} u}}{{{\text{d}}t^{2} }} = \frac{{{\text{d}}u}}{{{\text{d}}t}}\left[ {\frac{1}{t} + a} \right] + u\left[ { - \frac{1}{{t^{2} }} + \frac{{{\text{d}}a}}{{{\text{d}}t}}} \right]$$

(23)

Recalling that T = T _i + βt and substituting for (da/dt) = – (2β/T)a, Eq. (23) can be written as:

$$\frac{{{\text{d}}^{2} u}}{{{\text{d}}t^{2} }} = u\left[ {a^{2} + \frac{{2aT_{\text{i}} }}{tT}} \right]$$

(24)

The last term in the above equation was omitted in the original derivation of Augis and Bennett (T _i ≪ T) and resulted in the simple form:

$$\frac{{{\text{d}}^{2} u}}{{{\text{d}}t^{2} }} = a^{2} u$$

(25)

Substitution of (du/dt) and (du ²/dt ²) from Eqs. (21) and (25) into Eq. (22) gives:

$$(nu^{\text{n}} - n + 1) = \left[ {\frac{at}{1 + at}} \right]^{2}$$

(26)

For E/RT ≫ 1, the right-hand bracket approaches its maximum limit and consequently u (at the peak) = 1, then we have

$$u = (Kt)_{\text{c}} = K_{0} \exp \left( {\frac{{ -\, E_{\text{c}} }}{kT}} \right)\left[ {\frac{{T_{\text{c}} - T_{\text{i}} }}{\beta }} \right] \approx 1$$

(27)

In logarithm form, for T _i ≪ T _c, we have:

$$\ln \left( {\frac{\beta }{{T_{\text{c}} }}} \right) = \left( {\frac{{ -\, E_{\text{c}} }}{{RT_{\text{c}} }}} \right) + \ln K_{0}$$

(28)

Equation (28) shows that a linear relation exists between ln(β/T _c) versus 1/T _c, with (− E _c/R) as the slope and value of pre-exponential factor of rate constant in terms of natural logarithmic. Thus, one can determine both parameters using Augis–Bennett’s approximation method.

Results and discussion

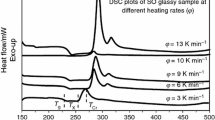
It is well known that the characteristic temperatures of a given material depend upon various factors. Consequently, structural information is essential to understand the dependence of the characteristic temperatures on the composition. To determine the characteristic temperatures of Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) samples, they were heated at different heating rates and their thermograms were obtained. DSC curves of Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) at heating rates of 5, 10, 15 and 20 °C min⁻¹ are shown in Fig. 1. Table 1 displays the peak values of glass transition temperature T _g and crystallization temperature T _c derived from DSC thermograms of samples.

Fig. 1

DSC curves for Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) at heating rates of 5, 10, 15 and 20 K min⁻¹

Table 1 Characteristic temperatures $T_{\text{g}}$, $T_{\text{c}}$, $T_{\text{p}}$ and $T_{\text{m}}$ at different heating rates for the studied compositions

Activation energy of glass transition $\varvec{E}_{\text{t}}$

It was observed that the glass transition temperature increases with increasing heating rate from 5 to 20 °C min⁻¹. It was noticed that when Cd is introduced in glass matrix of parent glass then the value of T _g is raised, while an opposite behavior is obtained for further addition of Cd. This is an expected behavior where the glass transition temperature T _g usually increases with increasing chain length. Furthermore, the increase in T _g may be related to the decrease in Se-rings concentration on decreasing Se concentration [28, 29].

The decreasing trend of T _g with raise in Cd atoms in quaternary glasses can be understood by considering the structural modifications. According to universally accepted structural model, glassy Se and Se-rich glasses consist of two molecular species: tortuous chains having helical chains of trigonal Se and Se₈ ring molecules of monoclinic Se [28, 29]. The structure of the Se–Te–Sn system prepared by melt quenching is regarded [28, 29] as a mixture of Se₈ rings, Se₆Te₂ rings and Se–Te copolymer chains. In the present case, we have entered the Cd atoms in glass matrix of parent glass by replacing Se atoms. Thus, it is obvious that Cd makes bonds with Se and is probably dissolved in the Se chains. The number of Se₈ rings increases, while the number of long Se–Te polymeric chains and Se–Te mixed rings decreases. Since T _g increases [28, 29] with increasing chain length and decreases with increasing ring concentrations, T _g decreases with increasing Cd content.

Lasocka [30] postulated a relation that proves the dependence of T _g on the heating rate β in the form:

$$T_{\text{g}} = A + B\ln \,\beta$$

(29)

Here, A and B are constants for a given glass composition. The value of $A$ indicates the glass transition temperature for the heating rate 1 °C min⁻¹, while $B$ is proportional to the time taken by the system for reducing T _g. Figure 2 represents the plots of T _g versus ln β for the four compositions under study.

Fig. 2

Plots of $T_{\text{g}}$ versus ${ \ln }\,\beta$ for glassy Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) alloys

The activation energy of glass transition $E_{\text{t}}$ is an indicator of thermal stability. It can be evaluated from the variation of T _g with the heating rate $\beta$ using the well-known Kissinger’s relation described in “Theoretical basis” section. The values of E _t (Table 2) for studied compositions are obtained using the slope values of the relation between $\ln \left( {\frac{\beta }{{T_{\text{g}}^{2} }}} \right)$ and $1000/T_{\text{g}}$ (cf., Fig. 3). Furthermore, the dependence of T _g on the heating rate β was found to obey the theory of structural relaxation developed by Moynihan et al. as mentioned in “Theoretical basis” section.

Table 2 Activation energy of glass transition $E_{\text{t}}$ and the activation energy of crystallization $E_{\text{c}}$ obtained using both Kissinger and Augis–Bennett equations, and the fragility index $m$ and the crystallization rate factor $K_{\text{p}}$ for the compositions under investigation

Fig. 3

Plot of $\ln \left( {\frac{\beta }{{T_{\text{g}}^{2} }}} \right)$ versus $1000/T_{\text{g}}$ for glassy Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) alloys

Figure 4 reveals the plot of $\ln \left( \beta \right)$ versus $1000/T_{\text{g}}$ for studied samples. The values of $E_{\text{t}}$ were estimated from the slopes of the obtained straight lines. Table 2 represents values of $E_{\text{t}}$ obtained using the above two methods. From Table 2, we find that the increasing sequence of E _t is (E _t)_x=4 < (E _t)_x=0<(E _t)_x=6 < (E _t)_x=2. It is interesting to note that the increasing trend of B is also same. The plot of E _t versus B is shown in Fig. 5. From this figure, it is clear that the glass having higher activation energy takes less time in completing the configurational adjustment in glass transition regime.

Fig. 4

Plot of $\ln \left( \beta \right)$ versus $1000/T_{\text{g}}$ for glassy Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) alloys

Fig. 5

Plot of E _t versus B for glassy Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) alloys

Knowing the values of both $T_{\text{g}}$ and $E_{\text{t}}$, we have determined the value of the fragility index $m$ via the expression, $m = \frac{{E_{\text{t}} }}{{RT_{\text{g}} \ln 10}}$ [31, 32]. Values of $m$ have also been listed in Table 2. The fragility index $m$ for the investigated glasses was evaluated in order to see whether these materials are obtained from strong or fragile glass-forming liquid. It was reported that $m$ varies between 16 for strong systems and 200 for fragile ones [33].The obtained values of $m$ were varied in the range 20–45. This indicates that our glassy system is obtained from strong glass-forming liquid which is characterized by covalent directional bonds that form a spatial network.

Thermal stability and glass-forming ability

Thermal stability and glass-forming ability are interesting parameters that reveal the nature of the studied glass. Both parameters have been determined using the characteristic temperatures ($T_{\text{g}}$, $T_{\text{o}}$, $T_{\text{c}}$ and $T_{\text{m}}$) of the studied compositions. The $T_{\text{g}}$ offers a valuable information about the thermal stability of the glassy system and also represents the strength or rigidity of the glass structure in the chalcogenide glasses. The higher values of the term $\left( {T_{\text{o}} - T_{\text{g}} } \right)$ delay the nucleation process [34]. Values of this term were found to increase with increasing Cd content. Also, this term is considered as a strong indicator of both thermal stability and glass-forming ability. The thermal stability $S$ is a parameter that reflects the resistance to devitrification after formation of the glass and it can be calculated using the expression [34, 35]:

$$S = \frac{{(T_{\text{c}} - T_{\text{o}} )(T_{\text{o}} - T_{\text{g}} )}}{{T_{\text{g}} }}.$$

(30)

The term $\left( {T_{\text{c}} - T_{\text{o}} } \right)$ is related to the rate of devitrification transformation of the glassy phase. The obtained values of $S$ and related parameter for the four compositions under study are given in Table 3.

Table 3 Values of $N_{\text{c}}$, $N_{\text{con}}$, $V$, $L$, $\left( {V - N_{\text{c}} } \right)/2$, $N_{\text{c}} /2$ and $f$ for compositions under study

The glass-forming ability can be determined by calculating $T_{\text{rg}}$, which is the reduced glass transition temperature, $T_{\text{rg}} = \frac{{T_{\text{g}} }}{{T_{\text{m}} }}$ [36]. The values of the ratio $(T_{\text{g}} /T_{\text{m}} )$ for the four compositions under investigation are also presented in Table 3. The values of $T_{\text{g}} /T_{\text{m}}$ are found to be nearly equal 0.66 for different compositions at each heating rate. This is evident that our compositions obey the “two-third rule,” which states that $T_{\text{rg}} = \frac{{T_{\text{g}} }}{{T_{\text{m}} }} = \frac{2}{3}$. Several researchers [33, 34, 37] reported that $T_{\text{rg}}$ is almost constant for all glassy alloys. This means that $T_{\text{rg}}$ does not reflect any difference of the glass-forming ability of different compositions. Therefore, there was a need for another parameter that can reveal the difference of glass-forming ability between different compositions. The used parameter is the Hruby number $H_{\text{R}}$.

The theory of homogeneous nucleation and growth [38] of a crystalline phase from a liquid phase indicates that the nucleation rate decreases with an increase in the interfacial energy between the liquid and solid phase. The Hruby number is a strong indicator of the glass-forming tendency and is defined as the ratio of the term $(T_{\text{c}} - T_{\text{g}} )$ that represents the nucleation process and the term $(T_{\text{m}} - T_{\text{c}} )$ that retards the growth process, and is given by [39]:

$$H_{\text{R}} = \frac{{T_{\text{C}} - T_{\text{g}} }}{{T_{\text{m}} - T_{\text{C}} }}.$$

(31)

The average values of $H_{\text{R}}$ for the compositions under study are given in Table 3. According to Hruby, glasses with $H_{\text{R}} \le 0.1$ are difficult to form and require higher cooling rate, whereas with $H_{\text{R}} \ge 0.4$ can be easily formed with moderate quenching rate. It is clear from Table 3 that the average values of $H_{\text{R}}$ for the four compositions under study are less than 0.4. This further means that the ability of the formation for our composition is improved with the increase in cooling rate. The addition of Cd concentration to Se_78−xTe₂₀Sn₂Cd_x system cross-links the already existing chains. Hence, the formed cross-linked structure enforces the composition to be more rigid which results no significant enhancement in values of $H_{\text{R}}$ for quaternary glasses. Literature [40, 41] shows that the atoms of different types are combined more favorably than those of similar types. Observed data can be visualized by using the chemical order network model [40, 41]. The heteropolar bond energies of Se–Te, Se–Sn and Se–Cd are 44.2, 49.2 and 58.7 kcal/mole, respectively. Hence, the bond formation probability of Se–Cd bond is the largest. So the increase in Cd causes insignificant change in $T_{\text{rg}}$ and other related parameters. Thus, adding Cd and reducing Se replace the weaker bonds with stronger ones.

Glass transition and network rigidity

The glass transition temperature $T_{\text{g}}$ is related to the rigidity of the network which is created by the broken bonds. The rigidity of the network is usually associated with the mean coordination number $N_{\text{c}}$, which is an important parameter for describing the glass-forming tendencies topologically [40]. The average coordination number $N_{\text{c}}$ for Se_78−xTe₂₀Sn₂Cd_x compositions has been calculated in terms of covalent bonding using the relation [42, 43]

$$N_{\text{c}} = \frac{{aN_{\text{Se}} + bN_{\text{Te}} + cN_{\text{Sn}} + dN_{\text{Cd}} }}{a + b + c + d}.$$

(32)

Here, $a$, $b$, $c$ and $d$ are the concentrations of Se, Te, Sn and Cd, whereas the coordination numbers of the used elements are $N_{\text{c}} \left( {\text{Se}} \right) = 2$, $N_{\text{c}} \left( {\text{Te}} \right) = 2$, $N_{\text{c}} \left( {\text{Sn}} \right) = 4$ and $N_{\text{c}} \left( {\text{Cd}} \right) = 6$. The calculated values of $N_{\text{c}}$ are listed in Table 3. It is observed that $N_{\text{c}}$ increases with increasing Cd content. This proves that the cross-linking of chains between the atoms increases with the increase in Cd percent. Covalent network is mechanically constrained by bond stretching $N^{\alpha } = N_{\text{c}} /2$ and bond bending $N^{\beta } = 2N_{\text{c}} - 3$, respectively. The calculated values of the average constraints $N_{\text{con}} = N^{\alpha } + N^{\beta }$ are given in Table 3 for the four compositions of Se_78−xTe₂₀Sn₂Cd_x system. Values of $N_{\text{con}}$ were found to increase with increasing Cd content. The increase in $N_{\text{con}}$ is a result of the increase in the cross-linking of chains between atoms, and it is considered as an evidence of the compactness of the system under study. According to [40, 44], the lone-pair electrons play an important role in chalcogenide glass formation. Bridging atoms with lone-pair electrons eliminates the strain forces that are created by the formation of amorphous materials. Increasing the number of lone-pair electrons decreases the strain energy and favors the glass formation. The number of lone-pair electrons has been calculated using the formula [45] $L = V - N_{\text{c}}$, where $L$ and $V$ are the lone-pair electrons and valence electrons, respectively. The calculated values of $L$ and $V$ are tabulated in Table 3. It is known that the system with large number of lone-pair electrons favors the glass formation as the strain energy of the system decreases with the increase in the lone-pair electrons. The variation of $L$ with the increase in Cd might be due to the interaction between Cd ion and lone-pair electrons of bridging Se atoms. According to Dembovsky [38], the condition of preparation of any alloy is a function of the average number of lone-pair electrons per atom $\left( {V - N_{\text{c}} } \right)/2$ and the number of covalent bonds per atom $N_{\text{c}} /2$. Since the physical basis of the structural modification is expressed by the possibility of obtaining structural configuration in the glassy alloy, this possibility increases with the increase in the degree of freedom as well as the number of lone-pair electrons. In view of Dembovsky [46] consideration, one can see that $\left( {V - N_{\text{c}} } \right)/2$ decreases, while $N_{\text{c}} /2$ increases with increasing Cd content (cf., Table 3). The above assumption was confirmed by the chain-crossing model (CCM) proposed by Tronc et al. [47]. Thorpe [48] has suggested the existence of vibrational modes called floppy modes in the absence of weaker long-range forces. The fraction of floppy modes is related to $N_{\text{c}}$ by the relation [48, 49], $f = 2 - \frac{5}{6}N_{\text{c}}$. The values of fraction of floppy modes are calculated and reported in Table 3. It is clear that the fraction of floppy modes decreases with the increase in N _c. These results prove that the four compositions of our Se_78−xTe₂₀Sn₂Cd_x system undergo transition toward more rigidity with increasing Cd content.

Estimation of activation energy of crystallization $\varvec{E}_{\text{c}}$

The activation energy of crystallization $E_{\text{c}}$ can be estimated from the variation of $T_{\text{c}}$ with the heating rate using the Kissinger equation. The slope of the graphs between $\ln \left( {\frac{\beta }{{T_{\text{c}}^{2} }}} \right)$ and $1000/T_{\text{c}}$ gives the values of activation energy of crystallization $E_{\text{c}}$ (cf., Figure 6). The $E_{\text{c}}$ values for different compositions of our system are given in Table 2. It is observed that $E_{\text{c}}$ decreases with the increase in Cd content and the heating rate β.

Fig. 6

Plots of $\ln \left( {\frac{\beta }{{T_{\text{c}}^{2} }}} \right)$ versus $1000/T_{\text{c}}$ for glassy Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) alloys

The activation energy $E_{\text{c}}$ can also be deduced using the formula suggested and approximated by Augis and Bennett. The Augis–Bennett plot for the studied compositions is presented in Fig. 7. Extracted $E_{\text{c}}$ values are also listed in Table 2. The obtained values of $E_{\text{c}}$ from the two methods are in a good agreement with each other. This means that one can use any of these two equations to calculate the activation energy of crystallization.

Fig. 7

Plots of $\ln \left( {\frac{\beta }{{T_{\text{c}} }}} \right)$ versus $1000/T_{\text{c}}$ for glassy Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) alloys

Table 2 reveals that the value of E _c for quaternary glasses is more than that of parent alloy. Such increment in E _c values for Cd containing quaternary alloys can be explained to some extent in terms of molar volume of these alloys. We are familiar with the fact that the growth and nucleation phenomena govern the devitrification of glassy materials [50,51,52,53] and the crystallization activation energy is well connected with both of these phenomena. In the current exertion, we have incorporated Cd in parent alloy by replacing Se at the cost of Cd. The atomic weight of Cd (118.7 gm/mol) is more than that of Se (78.9 gm/mol). Thus, the molar volume of quaternary glasses increases owing to which an enhancement in the nucleation and growth rate is possible. This is perhaps the cause behind the occurrence of crystallization in present quaternary alloys at relatively higher activation energies.

Gao–Wang model [52] has proposed a parameter that can reveal information about the morphology of crystal growth of the studied material. This parameter is the crystallization rates factor $K_{\text{p}}$ that corresponding to the temperature at which the crystallization rate is maximum. The values of $K_{\text{p}}$ can be deduced using the value of $E_{\text{c}}$ through the formula $K_{\text{p}} = \beta E_{\text{c}} /RT_{\text{c}}^{2}$. The obtained values of $K_{\text{p}}$ for various heating rates are tabulated in Table 4. Abdel-Rahim et al. [53] have been reported that the glass with a minimum rate of crystallization will have the maximum stability. Composition with the highest percent of doped Cd presents such case. This reveals that Se₇₂Te₂₀Sn₂Cd₆ glass has the greatest stability against devitrification which means that this composition requires the longest time to be fully crystallized. The composition dependence of K _p can be understood in terms of thermal stability parameter S as shown in Fig. 8. Figure 8 shows the plots of ln K _p against S at various heating rates. This figure clearly shows that values of ln K _p are decreased with increasing S. Thus, Fig. 8 signifies the scientific fact that the enhancement in the thermal stability of glassy alloy causes slower crystallization rate. Similar results were observed by our group in the past in various multi-component glasses of other system [54]. Thus, our present observation is in good agreement with the previous results.

Table 4 Values of K _p for different glasses at various heating rates

Fig. 8

Plots of ln K _p against S for glassy Se_78−xTe₂₀Sn₂Cd_x (x = 0, 2, 4 and 6) alloys

Conclusions

The calorimetric measurements have been utilized to study the kinetics and thermal stability of the studied quaternary alloys Se_78−xTe₂₀Sn₂Cd_x. The DSC curves revealed a well-defined glass transition temperature peaks. Various physical parameters have been calculated theoretically, and good correlations have been made between the various kinetic parameters and physico-chemical parameters. These linkages have been interpreted in the view of increasing the Cd content. The fragility index values revealed that the prepared glasses were obtained from strong glass-forming liquids. The composition with lowest Cd percent was found to be the most stable glass among the prepared ones. This has been confirmed as it has the minimum value of crystallization rate as compared to other two quaternary alloys. The activation energy of crystallization is more for the quaternary alloys as compared to parent ternary glass. Moreover, the increase in Cd content was accompanied with the increase in $N_{\text{c}}$ and $N_{\text{con}}$ as well as with the decrease in $V$ and $L$. The parameters T _rg and H _r (that showing the glass-forming ability) are also found maximum for the composition with lowest Cd percent. Thus, the Cd containing quaternary glass Se₇₆Te₂₀Sn₂Cd₂ of present systems is more suitable for optical memory application due to optimized values of various physico-chemical and kinetic parameters.