Introduction

In these last years torrefaction, a thermolysis process that subjects biomasses to a relative low thermal treatment in the range of 473–600 K is expected to play an important role in upgrading the quality of raw lignocellulosic materials for their uses in several applications [1–4]. This process can improve the properties, and therefore the chain value, of low-value woody material as agroforestry, industrial residues and agricultural crops [5–8]. Regarding the critical factors for the torrefaction’s diffusion, the mains are the lack of consolidated knowledge on both the design and the procedures to optimize the working process conditions [9, 10]. Recent studies [11–13] have identified the role of mass and energy yield as strategic parameters to optimize torrefaction plants exercise and characterize the quality of the final treated material. Within this scenario, the implementation of reliable kinetics procedures is a strategic task to support the industrial evolution of this process. Among the relevant amount of kinetics schemes till now proposed to describe the decomposition reactions involving solids [14–19], most methodologies investigate the thermal degradation of the solid matrix in terms of a single reaction composed of two contributions, Eq. 1: one depending solely on temperature, the k(T) term; the other, f(a), as a function of only the conversion fraction α.

$${\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = k\left( T \right) \cdot f\left( \alpha \right)}.$$
(1)

The parameter α is defined as follows:

$${\alpha = \frac{{m_{\text{o}} - m_{{{\text{t}},{\text{T}}}} }}{{m_{\text{o}} - m_{\infty } }}}$$
(2)

where m o is the initial mass of the sample and m ∞ the mass measured at the end of the imposed thermal treatment. For isothermal conversion, m t,T becomes m t and represents the mass of the sample at time t while, for non-isothermal mode, m t,T becomes m T and represents the same quantity at temperature T.

The temperature-dependent function k(T) is generally assumed to follow an Arrhenius form:

$${k\left( T \right) = A \times { \exp }\left( {\frac{{ - E_{\text{a}} }}{RT}} \right)}$$
(3)

where A is the frequency factor, E a the activation energy and R the universal gas constant. It is to underline that the two Arrhenius parameters in the original formulation are intended to be constant. Through this approach, a single reaction is assumed to be indicative of the solid degradation process. Hence the resulting kinetics parameters are more correctly identified as “global” or “apparent” parameters, to stress the fact that their values could deviate from those effectively pertaining to each single step of a hypothetical multiple reactions scheme. In addition, the determination of the so-called kinetics triplet (Eqs. 1, 3): f(α), A and E a usually involves fitting procedures implemented by preliminary selecting the f(α) term. As a consequence, the obtained Arrhenius parameters strongly depend on the f(α) function that, if not correct, makes the two parameters meaningless. In conclusion the determination of the Arrhenius parameters appears as an interlinked problem and, for a selected f(α), the data fitting procedure can be satisfied by several couples of A and E a for the contribution of compensation effects.

Among the different approaches, isoconversional methods are confirmed as the more consolidated to investigate thermal degradation processes, in particular for those involving solids materials [15, 20–22]. With these methods the apparent activation energy is a function of the extent of conversion (α), so it will be indicated as E a(α). One of the main advantages of these methods is that they allow the determination of the “apparent activation energy” without any assumption of the reaction mechanism. For this reason, these “model-free” methods appear particularly suitable to evaluate the effects of the TG data sets on the E a results.

Considering the heterogeneous fibrous structure and the involved solid-state reactions, for biomasses the sensitivity analysis of the implemented models becomes essential. The experimental TG tests were therefore replayed several times to evaluate the random effects connected to: samples and particles size distribution, heating rate, impurities and gaseous atmosphere in and around the samples. Then this study investigates the impact of several TG replicates on the obtained E a(α) values. Besides, further interesting and practical outcomes achieved are:

  • To make available supplemental data on torrefaction kinetics, improving the existing data bank;

  • To test the reliability of several isoconversional methods, traditionally applied to solids, in determining the E a(α) of biomasses in the torrefaction range;

  • To compare the E a(α) resulting from different isoconversional methods and to test the application ranges of the proposed approach and methods.

Experimental

Material characterization and preparation

Three types of biomasses, all belonging to hardwood, have been considered in this study: ash-wood, beech-wood and hornbeam. To make the samples representative of the raw materials, bulk samples have been collected from different sawmills. About 600 g. of each species have been oven-dried in laboratory. These dried samples have been carefully selected in terms of defect, bark and knots free, sieved to pass through a 600-μm trapezoidal mesh and then kept to a desiccator prior to store the powdery sample in an artificial plastic container for replicates and further applications. Before beginning each test, the moisture content of the received samples was determined in triplicate according to AOAC standard method 930.15 [23]. All the analyses of this study and specifically the TG measurements have been performed on these conditioned powders.

Samples have preliminary been characterized in terms of ultimate analysis (UA), higher heating value (HHV) and fibres composition comprehensive of ash content. The carbon, hydrogen, nitrogen and sulphur (CHNS) content was determined by using the Elemental Analyzer Mod. Vario Macro Cube-Elementar (Elementar Analysen Systeme GmbH, Hanau, D), while the oxygen content was calculated by subtracting the ash and the CHNS amount from the total. The ash content was determined according to the standard method DD CEN/TS 14775:2004 [24]. The HHV was measured by using the Oxigen Bomb Calorimeter Mod. IKA C5000 (Isoperibolic Calorimeter). These quantities are tabulated on the following Table 1.

Table 1 Ultimate, chemical analysis and higher heating value (HHV) of the raw biomasses
Full size table

Equipment

The thermogravimetric dynamic analyses were performed by an analyser Labsys Setaram, refer to [25] for a detailed description of the apparatus. To guarantee an inert atmosphere, nitrogen is used as purge gas at a flow rate of 100 mL min−1. It also sweeps the evolving gases from the reaction zone and limits the extent of secondary reactions such as thermal cracking and recondensations. For each run, approximately 20 mg of specimen was placed in the aluminium oxide crucible of the furnace chamber microbalance. To test the reproducibility of the measurements, five replicates have been performed at each selected constant heating rate (β) runs.

Experimental procedure and quantities calculation

Non-isothermal thermogravimetric analysis (TG) are one of the most extensively technique used to study the kinetics of biomass. Several reasons lean towards the adoption of this approach as alternative to the isothermal methodology. Some are debated and still open questions not strictly interwoven with the main purpose of this work. For an in-depth analysis of these topics, reference is made to [22, 26, 27]. An extension of both the isothermal conditions and the complete kinetic triplet determination will be presented on a further work of the authors actually in progress. All the experiments have been carried out with constant heating rates and covering a temperature range from ambient to 1180 K including, therefore, the entire samples decomposition. This allowed the determination of the final amount of the samples, m ∞ in Eq. 2, required to calculate the α parameter. Regarding the treatment conditions, four constant heating rates (β) have been selected: 3, 5, 10, and 20 K min−1. The initial mass weight m o, Eq. 2, is referred to the mass of the sample after the complete removal of water and light volatiles. This condition occurs at temperature close to the 420 K. The m o quantity defined in this way is coherent with works of [26] and represents a reproducible state condition for all the replicates.

Kinetics investigation

Isoconversional methods

The basic assumption of the isoconversional methods states that, for a given extent of the conversion, the reaction rate depends only on temperature while the reaction mechanism is independent on the heating rate.

By computing the logarithmic derivative of the reaction rate, Eq. 1, it comes:

$${\left[ {\frac{{\partial { \ln }\left( {{\text{d}}\upalpha/{\text{d}}}{t} \right)}}{\partial T}} \right]_{\alpha } = \left[ {\frac{{\partial { \ln }K\left( T \right)}}{\partial T}} \right]_{a} + \left[ {\frac{{\partial { \ln }f\left( \alpha \right)}}{\partial T}} \right]_{\alpha } }.$$
(4)

As each term is assumed at a defined (constant) α value, f(α) is also constant. Considering the Arrhenius k(T) function, Eqs. 3, 4 reduces to:

$${\left[ {\frac{{\partial { \ln }\left( {{\text{d}}\upalpha/{\text{d}}}{t} \right)}}{\partial T}} \right]_{\alpha } = \frac{{E_{\text{a}} \left( \alpha \right)}}{R}}$$
(5)

so the temperature dependence of the reaction rate dα/dt can be exploited to determine the activation energy E a(α) without any particular assumption of the reaction model. The E a(α) is determined step by step at a fixed α value, thus the name of isoconversional or multi-curve attributed to these methods [28, 29].

Considering the non-isothermal heating mode of this study and the constant heating rate quantity \({\beta = \frac{{{\text{d}}T}}{{{\text{d}}t}}}\), Eq. 1 can be rearranged to give the differential form of the non-isothermal rate law:

$${\frac{{{\text{d}}\upalpha}}{\text{d}T} = \frac{A}{\beta } \times { \exp }\left( { - \frac{{E_{\text{a}} \left( \alpha \right)}}{RT}} \right) \times f\left( \alpha \right)}.$$
(6)

This equation lays the computational basis of the isoconversional approaches classified into two main categories: differential and integral methods.

Differential isoconversional methods

By applying the logarithmic derivative of the fundamental form, Eq. 6, the following relationship, proposed by Friedman [30, 31], can be derived:

$${{ \ln }\left( {\beta \cdot \frac{{{\text{d}}\upalpha}}{{\text{d}}T}} \right) = {\text{lnA}} + {\text{ln}}f\left( \alpha \right) - \frac{{E_{\text{a}} \left( \alpha \right)}}{RT}}.$$
(7)

An alternative to this approach is represented by the method of Flynn [18, 21, 32], simply derived from Eq. 7:

$${{ \ln }\left( \beta \right) = { \ln }\left[ {A \cdot \frac{f\left( \alpha \right)}{{{\text{d}}\upalpha/{\text{d}T}}}} \right] - \frac{{E_{\text{a}} \left( \alpha \right)}}{{RT}}}.$$
(8)

Looking at these equations, the E a(α)·R −1 quantity can be determined by plotting against T −1 the terms: \({\ln (\beta \cdot \frac{{{\text{d}}\alpha }}{{{\text{d}}T}}})\) or \({\ln (\beta )}\) for the two methods, respectively. This analysis does not involve any approximations and appears, potentially, particularly attractive. Furthermore, as emerged on the results section, the instabilities introduced by computing the term \({\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}}\) can limit both the accuracy and the stability of the differential methods. Besides, investigations have evidenced inconsistencies due to the influence of the baseline inaccuracy [14] for those cases for which the heat of reaction shows a noticeable dependence on the heating rate [33]. For these reasons and to test the performances of different isoconversional approaches, several integral methods have also been included.

Integral isoconversional methods

The general equation of the isoconversional methods, Eq. 6, can be referred to a constant heating rate and rearranged as follows:

$${\frac{{{\text{d}}\upalpha}}{f\left( \alpha \right)} = \frac{A}{\beta } \times { \exp }\left( { - \frac{{E_{\text{a}} \left( \alpha \right)}}{RT}} \right) \cdot {\text{d}T}}.$$
(9)

By adopting the following change of variable: y = E a(α ).(RT)−1, Eq. 9 can be rewritten in its integral form:

$${\int\limits_{ 0}^{\alpha } {\frac{{{\text{d}}\upalpha}}{f\left( \alpha \right)}} = \frac{A}{\beta } \cdot \int\limits_{ 0}^{T} {{ \exp }\left( { - \frac{{E_{\text{a}} \left( \alpha \right)}}{RT}} \right)} \cdot {\text{d}T = }\frac{{A \cdot E_{\text{a}} \left( \alpha \right)}}{\beta \cdot R}\int\limits_{\infty }^{y} {\frac{{{ \exp }\left( { - y} \right)}}{{y^{ 2} }}} {\text{d}y}}$$
(10)

where T is the temperature at an equivalent (fixed) state of transformation. The integral \({\int\limits_{\infty }^{y} {\frac{{{ \exp }\left( { - y} \right)}}{{y^{ 2} }}} {\text{d}}y}\), traditionally named the temperature integral or Arrhenius integral, can be indicated in a generalized h(y) form as follows:

$${g\left( y \right) = \frac{{{ \exp }\left( { - y} \right)}}{{y\left( {\upomega{\text{ + y}}} \right)}} \cdot h\left( y \right)} .$$
(11)

This integral does not have an analytical solution so a variety of approximate solutions have been proposed by defining suitable values for the constant parameter ω and the h(y) function. For the most important ones, reference is made to [34–37]. This study considers those proposed by Murray and White [37] that assumes h(y) = 1 and the parameter ω = 0. This leads to the so-called direct isoconversional methods represented by the following generalized equation:

$${{ \ln }\left( {\frac{\beta }{{T^{\text{e}} }}} \right){ = + }F \cdot \frac{{E_{\text{a}} \left( \alpha \right)}}{RT} + {\text{const}}}.$$
(12)

Through this equation, the activation energy can be directly deduced by the slope of the plot of \({\ln (\frac{\beta }{{T^{\text{e}} }})}\) vs. T −1 once the two parameters e and F are assigned. Reference is made to [38–40] for a deep analysis of their determination. Four integral methods, reported on Table 2, have been selected by assigning suitable values to the e and F parameters: Kissinger–Akahira–Sunose (KAS); Doyle [41–43]; Starink-1 [38] and Starink-2 [39]. On the following Fig. 1 a representation of the lines obtained from the application of the KAS method to the ash-wood data is depicted; as case test the results for a regular α increment covering the range 0.05 < α < 0.85 are proposed. This procedure has been likewise replicated for all the methods considering a regular α increment of 0.005.

Table 2 Parameters and equations form of the adopted integral isoconversional methods
Full size table
Fig. 1
figure 1

Arrhenius-like plot for the KAS method applied to ash-wood at selected α values

Full size image

Results

Before discussing in details the main results of this study, a preliminary overview of the experiments (“Experimental Results Overview“section) and models (“Models Results Overview“section) results is presented. For a clear explanation and for sake of brevity, on the most of the plots and tables, only the results pertaining to ash-wood have been included: similar trends have been verified for hornbeam and beech-wood too. The results of this section make reference to the average values of the five replicates, as detailed on “Sensitivity Analysis“section.

Experimental results overview

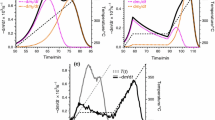
The experimental investigation temperature range includes the torrefaction decomposition, assumed to occur from 473 K to a maximum temperature close to 600 K. Considering that hemicellulose degradation is substantially complete at temperature below 600 K (it decomposes in the range 493 K < T < 553 K [44, 45]), torrefaction usually leads to a nearly complete degradation of this fibre. However, as reported on the following plots, the upper scale limit of the experimental TG runs has been extended up to 673 K, beyond the torrefaction temperature limit. This is due to the fact that at 600 K the degradation of a part of the cellulose fraction is unavoidable, as it occurs in the range 510 K < T < 643 K [46]. Therefore, for all the samples and replicates, the upper TG temperature limit has been conventionally assumed to correspond to the complete degradation of cellulose. In this sense lignin decomposition has not been considered as its degradation slowly occurs on a wide temperature range from 373 to 1170 K [44]. Figure 2 reports the TG and DTG curves for the selected four heating rates. Figure 2a evidences that, at a selected temperature, the higher is the heating rate, the lower is the mass loss; in coherence with this observation, Fig. 2b shows that an increase in the heating rate entails a shift towards right of the curves and a corresponding shift towards higher temperatures of the DTG peaks. The effects of the different heating rates are hence confirmed in this case too as well documented on similar studies [47–51]. Thermal degradation process appears very slow beyond the limit of 650 K, where a further long tail zone occurs for a wide temperature range (not reported due to the adopted limit of 673 K) that corresponds, as extensively investigated [48, 50–53], to the slow mass loss of lignin without any evidence of significant peaks. In the range of 483–573 K, a complex region is exhibited due to the overlapping of the ranges incorporating both the decomposition of hemicellulose and cellulose. A distinct separation of the hemicellulose peak is not evident also because of the relative low heating rates, as evidenced by Biagini et al. [50].

Fig. 2
figure 2

Ash-wood TG (a) and DTG (b) curves at the selected heating rates: β = 3, 5, 10, 20 K min−1

Full size image

Models results overview

The models analysis has been intentionally limited to the torrefaction range and the upper temperature fixed at 600 K. As evidenced on Fig. 2, for a selected temperature, the lower is the heating rate (β) the higher is the mass loss. Considering the upper torrefaction limit of 600 K, the maximum value of α achieved at the lower heating rate (β = 3 K min−1) results nearby α = 0.7. Therefore, in this section, the reported graphs depict the models performances for α varying in the range 0.05 < α < 0.7.

For all the adopted methods, a global view of the E a (α) evolution trends vs. α is reported on the following Fig. 3. From these results it emerges that the apparent activation energy increases for α moving from 0.05 to 0.4, while a plateau can be observed for α ranging from 0.4 up to the assumed torrefaction limit of 0.7. Even if each biomass presents its own E a(α) behaviour, these trends are consistent with those of recent investigations involving biomasses and kinetic analysis adopting isoconversional methods: rice husks [47, 50], Nigerian lignocellulosic resources [54], olive pomace [48], Tucuma endocarp [17], elephant grass [47]. Despite the discrepancies among the adopted models, in the range: 0.05 < α < 0.4 the E a(α) reaches values normally encountered for hemicellulose decomposition, from 134 to 196 kJ mol−1, as confirmed also by Lopez-Velazquez et al. [55] and Wang et al. [56].

Fig. 3
figure 3

E a(α)/kJ mol−1 vs. α for ash-wood as result of the application of the proposed models

Full size image

From a kinetics point of view, the variation of activation energy with α reflects the presence of multiple and competitive reactions. This is consistent with the hypothesis lying behind the multi-step model mechanism proposed by Prins et al. [26]. For an extended and deeper discussion on the significance of the E a(α) behaviour trend, reference is made to [20, 57–59].

Analysing the performances of the differential methods, the Friedman model confirms an unstable behaviour evidenced also by Vyazovkin [60] and Golikeri and Luss [57]. This is mainly due to the introduction of the term \({\frac{{{\text{d}}\alpha }}{{{\text{d}}T}}}\) in Eqs. 7 and 8 that requires a numerical calculation procedure. A more regular trend is observed for the integral methods. Despite the introduction of the crude temperature integral approximations, these methods are claimed to give better results with respect to the differential ones and, for the selected hardwood family, they give also similar results: the differences among E a (α) values are set significantly below the limit of 10% accepted as the conventionally accuracy level for this quantity [22, 35]. These results, if compared with similar studies available in the literature [53, 55], appear satisfactory to suggest the use of these methods. It is even to note that the Starink-1 and Starink-2 methods give nearly the same results when applied to biomasses, on the contrary to what happens when they are applied to other types of solids [39].

Approaches, involving numerical integrations as the methods of Vyazovkin [16, 49, 60] and Senum and Yang [36], are claimed to reach high accuracies. These have not been included due to the more complex computation load required and the very slightly improvement of the results obtained when compared with those of the models here included. This statement has also been confirmed by the applications of the cited models to different type of biomasses [48].

Sensitivity analysis

Definition of the TG confidential boundary range

Considering the heterogeneity of both the reactions and structure of the biomasses jointly with the relevant amount of data required for the application of the isoconversional procedures, several replicates have been carried out for each of the TG test run. Starting from the same initial conditions for both the samples and the apparatus, among the five mass loss replicates available at each β, the lower and the higher ones have been selected to establish the TG Confidential Boundary Range (CBR). As case test, the following Fig. 4 depicts the two curves (minimum and maximum TG) of the CBR for ash-wood at β = 3 K min−1 with the mean TG and the TG variance trends. It is to point out that this variance is a punctual quantity referred to the five replicates and calculated at each temperature. For the introduced CBR, Table 3 reports, for the three biomasses, the variance and the mean absolute deviation (MAD) values. The MAD indicates the mean value of the Absolute Deviation of each mass loss point of the five replicates with respect to the mean TG curve. For the minimum and maximum TG curves of the CBR boundary, the absolute average deviation (AAD) and the maximum error (ME), calculated with respect to the mean TG curve, are reported in Table 3.

Fig. 4
figure 4

Confidential Boundary Range (CBR) curves, mean TG curve and variance of the TG data sets for ash-wood referred to β = 3 K min−1

Full size image
Table 3 Result of the statistical analysis of the Confidential boundary range (CBR) for the three investigated biomasses
Full size table

Sensitivity analysis of the models

Defined the uncertainty of the TG results in terms of the CBR, the sensitivity analysis of the models is introduced to evaluate the impact of different TG data sets on the achieved E a(α) results. This analysis allows to determine the activation energy boundary range (E a BR) corresponding to the defined CBR. This procedure is complicated by considering that:

  • Each activation energy value (E a(α)) depends from a number of experimental TG points equal to the number of the considered heating rates (four in this study);

  • The reliability of the resulting E a(α) depends on the capability of the calculated points to represent, as best as possible, a straight line from which the E a(α) is computed on the base of the adopted model, (ref. Figure 1).

Considering these constrains, for each α the maximum and minimum E a(α) values are calculated as the results of the combinations of those points that provide the maximum and minimum slopes selected among all the possible interpolating lines.

Considering the complexity of this procedure, it is explained step by steps by applying, as case test, the KAS model to beech-wood. On the first step the E a (0.4), only for α* = 0.4, is evaluated in the following way: for the three heating rates: 5, 10 and 20 K min−1, the TG curves are referred to the average of the five replicates, while for the heating rate β = 3 K min−1, all the five points of the replicates have been considered. Consequently, five different slopes have been obtained, corresponding to five E a (α*) results as well. On the following Fig. 5, the obtained straight lines are evidenced. Due to the very close values of points 2 and 3, only four lines can be graphically appreciated.

Fig. 5
figure 5

Effects of the different mass loss of the five replicates for β = 3 K min−1 on the straight lines slope for the KAS model applied to beach-wood at α* = 0.4

Full size image

On the second step, for the same conversion fraction α* = 0.4, this methodology is extended by including the whole amount of TG data points: all the five replicates for all the heating rates β = 3, 5, 10 and 20 K min−1. So, considering that the variation of one TG replicate impacts on the slopes of the curves, all the combinations of the different replicates (54 = 625) are considered and, with an optimization procedure, those points providing the highest and lowest values of the slopes are selected. With these points it has been possible to compute, for α* = 0.4 and KAS model applied to beech-wood, the bounds of the E a BR: E a,max = 179.55 kJ mol−1; E a,min = 152.29 kJ mol−1.

As third and final step, the computational procedure illustrated for the second step is repeated to cover the entire α range considered in this study: 0.05 < α < 0.7. Even if this extended calculation could be based, for this study, only on the data available for the five replicates, an alternative and more generalized approach has been adopted considering that:

  • From an experimental point of view within the CBR, each TG replicates has the same probability to occur by chance;

  • If this analysis involves only TG replicates available (five in this study), usually, a good distribution of the data over the entire CBR is not guaranteed.

Therefore, a family of “10 artificial” TG curves, equally spaced and covering the entire CBR, has been generated for each β. Then the procedure described on the second step has been applied to find the combinations of the four values, each one pertaining to a selected curve among the 10 artificial TG that maximizes and minimizes the slopes of the interpolated straight lines. This has been replicated for each α by selecting a regular increment of Δα = 0.005 spanning the 0.05 < α < 0.7 range. The resulting minimum E a (α)min and maximum E a (α)max curves define, therefore, the Activation Energy Boundary Range (E a BR) based on the previously determined CBR. A graphical representation of the E a BR is depicted on Fig. 6 considering, as example, the Doyle method applied to hornbeam. The following Table 4 summarizes the global results, for each of the biomasses and models, in terms of Absolute Average Deviation (AAD) and Maximum Error (ME), respectively, for the E a (α) maximum (Ea(α)max ) and the E a (α) minimum (Ea(α)min) curves (the boundary curves of the E a BR) with respect to the E a (α) mean curve assumed as reference. It has to be stressed that the selection of the 10 artificial TG curves is just to limit the computational load: several tests verified that the proposed analysis is not sensible to the number of artificial curves used. So to guarantee the stability of the obtained results, on the base of the CBRs obtained in this study, an increase of the number of the artificial TG curves appear excessive. A decrease in this number has to be tested case by case. A free software version of the proposed sensitivity analysis is available at the link indicated on Appendix.

Fig. 6
figure 6

E a(α) curves: Max, and Min curves trends defining the Activation Energy Boundary Range (E a BR) and the Mean curve trend of the five replicates for Doyle model applied to hornbeam

Full size image
Table 4 AAD% and ME (%) of the E a (α) max and the E a (α) min curves of the activation energy boundary range (E a BR) with respect to the E a(α) mean curve for the analysed methods and the three biomasses
Full size table

Sensitivity analysis results

Considering at first the results resumed on Table 3 for the CBR, the mean AAD of both the minimum and maximum mass loss curves set around a similar level and almost symmetrically distributed with respect the mean TG curves: from the 0.633% (ash-wood)—0.663% (beech-wood) values for the minimum curve to 0.696% (beech-wood)—0.766% (ash-wood) for the maximum curves. Similar trends are confirmed for the ME values that set around −2 to 2% and for the mean of the MAD parameter that sets close to 0.26%. From a general point of view, this proves the good quality of both procedures and performances carried out during the entire experimental campaign. Higher discrepancy affects the variance that appears to be influenced by the heating rates. Moving to Table 4, it emerges that the Doyle method achieves the best performances for all the three biomasses: for this reason, this method is assumed as reference on the occurring discussion. This method reaches a significant accuracy in particular for ash-wood. Considering the obtained statistical results, the following correspondence from the CBR (Table 3) and the E a BR (Table 4) can be observed: for ash-wood as example, the mean AAD (Table 3) of the two boundary mass loss curves results is: 0.633 and 0.766% for minimum and maximum mass loss curve, respectively. The corresponding two boundary curves of the E a BR, in terms of a mean AAD, present these results (Table 4, Doyle method): 3.263% for E a (α)min and 3.427% E a (α)max. For beech-wood and hornbeam, similar values of the CBR curves are obtained (mean AAD of the Table 3) to which the corresponding E a BR curves set around 6–7% (Table 4, Doyle model: for beech-wood: E a (α)max 6.130%, E a (α)min 6.031%; for hornbeam: E a (α)max 6.983%, E a (α)min 5.257%). Considering further the maximum error (ME), this quantity reaches values higher then 10% only for hornbeam (Doyle model, Table 4, ME of E a (α)max curve: 11.194%). Therefore, the following main remarks can be pointed out:

  • The uncertainties of the experimental TG have an amplifying impact on the final Activation Energy Boundary Range (E a BR) around one order of magnitude as maximum value in terms of mean AAD;

  • If the mean AAD of the boundary CBR sets at values lower than 1%, the resulting uncertainties of the E a (α) curves, in terms of mean AAD%, achieves values significantly lower than 10%, the conventional maximum limit accepted for this quantity;

  • The correspondence between the CBR and E a BR boundary ranges can be different for each biomass and a generalized statement cannot be deduced. If reference is made to similar types of feedstocks (as hardwood in this study), the correspondence can be limited within reasonable ranges. These results have, however, to be confirmed for other biomasses of the hardwood family and, furthermore, for different families of feedstocks;

  • Considering the proposed analysis, the Doyle method appears to reach the best performances.

Range of validity and limits and of the proposed approach

The adopted integral isoconversional methods involve the use of a logarithm function, Eq. 12, whose value depends on the specific approximations assumed for each method. In literature [40, 42] the approximation accuracy of the temperature integral is expressed in terms of the tolerance of the parameter y = E a (α)·(RT) −1. The most cited [39] and accurate approximations assign the variability of this parameter in the range 15 < y < 60. This constrain limits the reliability of the integral isoconvertional methods when very low or extremely high values of y occur. For the investigated biomasses and models, it has been verified that the corresponding y values set at a very convenient position; they place on the central part of the assumed variability range, as evidenced by the following Table 5. Considering that the resulting y values are also influenced by the heating rate, for sake of brevity, on the indicated Table 5 only the mean, minimum and maximum values are reported. For an extended analysis, reference is made to Fig. 1 of the cited Starink paper [39].

Table 5 Mean and maximum and minimum values of the parameter y = E a(α)·(RT) for −1 for the adopted integral methods applied to the selected biomasses
Full size table

The proposed approach has been moreover verified for very low and high α values. For congruence with the previous validations tests, the KAS method has been applied to ash-wood in this case too and the results are reported on the following Fig. 7: for very low α values: case a: α = 0.005; case b: α = 0.035; for high α values: case c: α = 0.855; case d: α = 0.86. When α approaches these limits, the definition of the activation energy appears unsatisfactory due to the lower accuracy of the linear correlations, the usually called correlation coefficient (R 2) is lower than 0.97. This analysis, verified for all the methods and biomasses, recommends to limit the application of these methods within: 0.05 < α < 0.85. The upper α value covers the higher torrefaction limit assumed in this work while the lower, based of the limits here considered, has been therefore fixed at α = 0.05.

Fig. 7
figure 7

E a(α) determination procedure for the KAS method applied to ash-wood. Low α values, cases (a, b); high α values, cases(c, d) Case a: KAS method for α = 0.005, Case b: KAS method for α = 0.035, Case c: KAS method for α = 0.855, Case d: KAS method for α = 0.86

Full size image

Conclusions

Thermogravimetric analysis (TG) of three biomasses, ash-wood, beech-wood and hornbeam, all belonging to the hardwood family, has been carried out covering the torrefaction range condition up to 600 K. Several isoconversional models have been considered to test their reliability in determining the activation energy E a(α). This has been achieved by identifying a Confidential Boundary Range (CBR) for the TG measurements in correspondence to which the Activation Energy Boundary Range (E a BR) is calculated basing on the sensitivity analysis of the investigated models. The uncertainty of the CBR sets within 1% and it was verified that the differences among the mean values of the E a(α) are lower than 10%. Furthermore, by applying the proposed analysis to the obtained experimental TG measurements, the resulting E a (α) values are of good quality: they satisfy the conventional criterion usually accepted for this quantity. This analysis, if confirmed for other biomasses, feedstock families and for further non homogeneous materials, looks promising to exploit, jointly with the adopted isoconversional methods, the role of TG data sets on activation energy determination.

Appendix: Supplementary material

The on line software version of the proposed sensitivity analysis is available at the following link: https://marcobrighenti.wordpress.com/sensitivity-of-the-methods-to-the-tg-data-sets/.