The mechanism and kinetics of NiO reduction by hydrogen

Abstract

The thermochemical approach to analysis of thermal decomposition of solids, developed earlier by L’vov, is extended here, for the first time, to interpret the kinetics and mechanism of the reduction of an oxide (NiO) by a gas (H₂). This approach is based on the mechanism of congruent dissociative vaporization of the reactant, Langmuir kinetics and determination of the Arrhenius E parameter by the third-law method. The calculated enthalpy of the reaction is in good agreement with the experimentally measured E value. Many other mechanistic and kinetic features of the reaction are explained within the framework of the given theoretical approach. These include: the formation of metal nuclei; the initial autocatalytic behavior; the formation of nanocrystalline structure of the reduced metal product; the equimolar and isobaric modes of reduction; the dependence of reduction rate on hydrogen pressure; the more than twofold decrease of the E parameter with the extent of reaction α, and the systematic increase of E with temperature.

Introduction

Many studies of the reductions of metal oxides by gases have characterized the chemical properties and kinetic behavior of these (often) simple reactions. Among the numerous investigations reported, the reduction of nickel oxide by hydrogen [1–23] has attracted wide interest and is now identified as a particularly suitable reaction for kinetic and mechanistic analysis by the thermochemical approach [24–32] presented and discussed here.

In their pioneering study of NiO reduction by H₂, Benton and Emmett [1] established the following characteristics: (i) reduction proceeds in a boundary layer consisting of the solid phases NiO and Ni; (ii) autocatalytic behavior is due to changes in the area of this layer during reaction; (iii) the induction (or incubation) period, before onset of reaction, depends on temperature and on the nature of the sample; and (iv) the presence of water vapour in the reaction zone decreases the reduction rate and increases the induction period. These regularities have been confirmed in virtually all the subsequent investigations.

From the dozens of studies of nickel oxide reduction by hydrogen, we select those (22) listed in Table 1 as reporting quantitative kinetic measurements of the Arrhenius activation energy, E, and the dependence of reaction rate, ν, on hydrogen pressure. The following trends and regularities in E are found within these data: E values from the (13) earlier studies, published in 1950–1976, show considerable variation, with E = 97 ± 28 kJ mol⁻¹. (Data from [5] have been omitted due to the presence of water vapour, together with high temperature measurements that gave curved Arrhenius plots [12, 14].) Activation energies published during the last 20 years, 1989–2009, show much less variation, 93 ± 4 kJ mol⁻¹ (omitting values obtained in the presence of water vapour [18, 19]). We regard this value as the more reliable, attributable to improvements in equipment and measuring techniques. The value of E is increased by the presence of water vapour [18, 19]. The dependence of reduction rate on hydrogen pressure in the presence of water vapour, ν ~ P ^1.5 [5], is greater than in its absence, ν ~ P ^0.5 [4, 7, 13, 15].

Table 1 Values of the activation energy, E, reported in the literature for the reduction of NiO by hydrogen

Throughout the long, 85-year, history of this research, the kinetic features of NiO reduction, originally described by Benton and Emmett [1], together with other regularities found later, have remained a puzzle and a subject for discussion. The traditional theoretical approach, based on the kinetic Arrhenius equation and the mechanism of direct reduction of solid oxide to solid metal, have failed to provide a reliable quantitative interpretation of the kinetic characteristics. These include the induction period, the autocatalytic behavior and the several quantitative kinetic features of the process, mentioned above. This article, therefore, uses the thermochemical approach to interpret the kinetics and mechanism of nickel oxide reduction by hydrogen. This alternative theoretical model has been developed during the last 20 years [24–33] to explain the kinetics and mechanisms of thermal decompositions of solids. It is applied to metal oxide reduction here, replacing the more generally accepted (conventional) approach used hitherto. Significant differences between these two approaches are found in all parts of the alternative theories (mechanism, kinetics, and methodology); these are summarized in Table 2.

Table 2 Differences between the conventional and the thermochemical approaches to kinetic and mechanistic analysis of rate data for oxide reduction by gases

Mechanism

Congruent and incongruent mechanisms of reduction

Conventional approaches to the interpretation of kinetic data for oxide reductions recognize two alternative mechanisms: either congruent reduction, forming gaseous metal for volatile metals, or incongruent reduction, involving direct (solid → solid) formation of a solid product for low-volatility metals. In contrast, the thermochemical approach is based on the congruent formation of gaseous products in the reductions of all metal oxides: this is followed, for metals of low volatility, by condensation of the supersaturated metal vapour. Thus, by analogy with recent investigations of thermal decompositions of a range of oxides [27, 28], the reductions of CdO and NiO are described by similar reactions:

$$ {\text{CdO}}\left( {\text{s}} \right){\text{ + H}}_{ 2} \rightleftarrows {\text{Cd}}\left( {\text{g}} \right){\text{ + H}}_{ 2} {\text{O}} $$

(1)

$$ {\text{NiO}}\left( {\text{s}} \right){\text{ + H}}_{ 2} \rightleftarrows {\text{Ni}}\left( {\text{g}} \right){\text{ + H}}_{ 2} {\text{O}} \to {\text{Ni}}\left( {\text{s}} \right){\text{ + H}}_{ 2} {\text{O}} $$

(2)

For convenience, the two steps in reaction (2) can be expressed:

$$ {\text{NiO}}\left( {\text{s}} \right){\text{ + H}}_{ 2} \rightleftarrows {\text{Ni}}\left( {\text{g}} \right) \downarrow {\text{ + H}}_{ 2} {\text{O}} $$

(3)

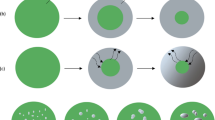
The condensation of a supersaturated Ni vapor explains the formation of finely divided metallic product (in the form of nanoparticles) on the oxide (reactant) surface. This mechanistic concept was originally proposed by Volmer in 1929 [34] and subsequently forgotten for 60 years [35]. Its renaissance, to explain the thermal decompositions of solids through the congruent dissociative vaporization of reactant (CDV mechanism), occurred only in the early 1990s [24–26].

The radius r of a spherical particle of liquid or solid formed by vapor condensation, at supersaturation S and temperature T, is expressed by the Gibbs–Thomson equation:

$$ r = 2M\gamma /(\rho RT\,{ \ln }\,S) $$

(4)

Here, M is molar mass, γ surface tension (or formation energy/unit surface area) and ρ, the density of the substance (e.g., metal). Supersaturation S is the ratio of the actual pressure P _act of metal in the equilibrium part of reaction (2) to its saturated vapor pressure P _sat, or:

$$ S = P_{\text{act}} /P_{\text{sat}} $$

(5)

Analysis of the data available [27, 28] confirms that the dependence of r on S is expressed by Eq. 4.

Condensation energy transfer to the reactant

Another important distinction between the CDV mechanism and the conventional incongruent mechanism, first reported in [24–26], concerns that part of the condensation energy that is transferred to the reactant within the thin reaction zone (interface) formed at the contact of the two solid phases (reactant and product). This energy is responsible for the considerable increase in the rate of the reduction reaction within this zone, as compared with the open reactant surface. (In the absence of an interface, most of the condensation energy is scattered/released to the open space above the reactant oxide surface.) This explains both the induction period, during which reaction is limited to specific small areas of the surface, and the subsequent autocatalytic behavior which leads to the formation of a comprehensive layer of product across all oxide surfaces. The energy transfer process has been discussed in detail and, for thermal decompositions of solids, confirmed experimentally [27, 28].

To calculate the enthalpy of the reduction reaction, the supplementary term $\tau \times \Updelta_{\text{c}} H_{T}^{^\circ }$(M) was introduced to take into account the partial transfer of condensation energy to the (reactant) oxide. The transfer coefficient τ represents the fraction of the $\Updelta_{\text{c}} H_{T}^{^\circ }$(M) energy that is returned to the oxide, by analogy with thermal decomposition reactions [27, 28]. Therefore,

$$ \begin{gathered} \Updelta_{\text{r}} H_{T}^{^\circ } \; = \;\Updelta_{\text{f}} H_{T}^{^\circ } ({\text{M}}) + \Updelta_{\text{f}} H_{T}^{^\circ } \left( {{\text{H}}_{ 2} {\text{O}}} \right) - \Updelta_{\text{f}} H_{T}^{^\circ } ({\text{MO}}) - \Updelta_{\text{f}} H_{T}^{^\circ } \left( {{\text{H}}_{2} } \right) + \tau \;\Updelta_{\text{c}} H_{T}^{^\circ } ({\text{M}}) \hfill \\ \end{gathered} $$

(6)

Here, the $\Updelta_{\text{f}} H_{T}^{^\circ }$ terms represent the enthalpy of formation of each participant in the reaction and $\tau \,\Updelta_{\text{c}} H_{T}^{^\circ }$(M) the enthalpy of oxide reduction with due to regard for the metal condensation. Initially, in studies of thermal decompositions, the coefficient τ was introduced to reconcile the enthalpy calculated for a particular reaction with the measured parameter E. Next, it was suggested [26] that the condensation energy would divide equally between the solid reactant and product phases, i.e., τ = 0.50. However, after calculating τ coefficients, by comparing $\Updelta_{\text{r}} H_{T}^{^\circ }$ and E values for a wide range of thermal decompositions, it became clear that the suggested equidivision of condensation energy was incorrect. From an analysis of the magnitudes of τ obtained for decompositions of 15 different compounds [27, 28], it was found possible to relate these values to the supersaturation degree of the low-volatile product during the decomposition. This dependence, with a correlation coefficient of 0.96, is expressed [31] by the equation:

$$ \tau = 0. 3 5 1\,{ \log }\,{ \log }\,S + 0.0 1 7 $$

(7)

The above dependence is very weak: variation of supersaturation by an order of magnitude (at the average value, S = 10³²) changes τ by only 0.1%. Unfortunately, no physical explanation for this dependence has yet been found.

Thermochemical calculation of the reaction enthalpy

Now let us apply the given model to the thermochemical calculation of the enthalpy of reaction (2) between 400 and 600 K to enable the calculated values to be compared with those obtained experimentally. The values of the thermodynamic functions from Table 3 [36–38] are used as input data. First, to estimate τ magnitudes, we calculate the saturated vapor pressures of Ni and supersaturation values S. As seen from Table 4, P _sat varies by nearly 19 orders of magnitude in the temperature range considered. The average value of actual vapour pressure for Ni, P _act, corresponding to the experimental conditions prevailing during reaction (2), was estimated (from data in Tables 7 and 8 below) to be about 10⁻⁵ bar at these temperatures. Thus, supersaturation decreases from 2.50 × 10⁴² at 400 K to 1.47 × 10³² at 500 K and to 4.55 × 10²⁵ at 600 K (Table 4). According to Eq. 7, these S values correspond to τ values of 0.592, 0.546, and 0.506 respectively (Table 5).

Table 3 Values of thermodynamic functions used in the thermochemical calculations

Table 4 Estimation of saturated vapor pressures of Ni, and its supersaturation

Table 5 Calculated values of thermodynamic functions for reaction (2)

Table 5 also includes the final results of the calculations: the enthalpies $\Updelta_{\text{r}} H_{T}^{^\circ }$ and the equilibrium constant

$$ K_{P} = P_{\text{Ni}} \times P_{{{\text{H}}_{2} {\text{O}}}} /P_{{{\text{H}}_{2} }} $$

(8)

for the reduction of NiO by H₂, with and without allowance for the condensation energy of supersaturated Ni vapor. We note that these results show that the calculated values of the molar enthalpy, or the reaction enthalpy per mole of primary gaseous products (87, 95, and 101 kJ mol⁻¹ at 400, 500, and 600 K, respectively), agree with the most reliable value of the E parameter measured in the same temperature interval (93 ± 4 kJ mol⁻¹, see Table 1).

Variations of enthalpy with temperature and the extent of reaction

It is significant that the increase in enthalpy with temperature corresponds with the experimentally observed rise in E. This effect was discovered, and described, several years ago for the decomposition of CaCO₃ [27, 28] and is identified with the transfer of condensation energy (from gaseous CaO) to the reactant. The value of τ decreases with temperature rise, so that the contributions of the condensation energy to the enthalpy and, to a lesser degree, to the condensation energy itself (see Tables 4, 5), both diminish. Consequently, instead of the expected small enthalpy decrease with temperature rise, its magnitude increases. In CaCO₃ decomposition, the temperature rise from 900 to 1,200 K results in an increase of $\Updelta_{\text{r}} H_{T}^{^\circ }$ by about 50 kJ mol⁻¹, instead of the expected reduction by 10 kJ mol⁻¹. Theoretically calculated values were in satisfactory agreement with experimental measurements [27, 28].

Janković [39] observed, for NiO reduction by H₂, that $\Updelta_{\text{r}} H_{T}^{^\circ }$ increased by about 13 kJ mol⁻¹ for the temperature rise 518–573 K. It is difficult to overestimate the significance of this effect. It is convincing proof that condensation energy is transferred to the reactant and validates the above calculations of reaction enthalpies for metal oxide reductions. Another of Janković’s [39] important results is the more than twofold decrease of the E parameter with the extent of reaction, α: from 155.2 kJ mol⁻¹ at α = 0.05 (where there is effectively no transfer of condensation energy to the reactant) to 70.4 kJ mol⁻¹ when α = 0.95 (in its presence). This effect is in agreement with our calculations: at 600 K the molar enthalpy (without and with the condensation contribution) is 211 and 102 kJ mol⁻¹ (Table 5).

At a hydrogen pressure of 1 bar, K _P ** values within the range 10⁻¹³–10⁻⁸ bar correspond to partial pressures of gaseous products between 10⁻⁶ and 10⁻⁴ bar, in good agreement with measured $P_{{{\text{H}}_{2} {\text{O}}}}$ values (reported below). For comparison, the partial pressures of gaseous products corresponding to K _P * values (excluding the contribution from condensation energy) are between 10⁻²³ and 10⁻¹⁴ bar. This distinction explains the origin and extension of the induction period, during the initiation of reduction, when most of the condensation energy is scattered/released in the open space above the reactant oxide surface. The reduction rate attains its maximal value only gradually, when the number and sizes of the nuclei have increased sufficiently to form a complete layer of metal product that covers all reactant surfaces.

From these results, we can conclude that the reaction of hydrogen with metal oxide occurs in the interface between the two solid phases (reactant/product) through interaction of H₂ molecules with oxygen released by the congruent dissociation of metal oxide (NiO). The interaction occurs with O₂ molecules adsorbed at the oxide surface so that the enthalpy of this exothermic reaction (H₂ + 0.5O₂ = H₂O) is a part of total enthalpy of NiO reduction by hydrogen. In contrast with this, the energy of condensation of gaseous Ni atoms (Ni(g) → Ni(s)) is distributed almost equally between the two solid phases, reactant and product. Indeed, τ diminishes from 0.6 to 0.5 between 400 and 600 K (Table 5).

It is interesting to compare the results of this thermochemical study of NiO reduction by H₂ with similar studies for some other metal oxides. As a base for this comparison, we can use the criterion proposed in [40] and further developed in [27, 28]. From the very well-known thermodynamic equation

$$ \Updelta_{\text{r}} H_{T}^{^\circ } = T(\Updelta_{\text{r}} S_{T}^{^\circ } - R\,\ln \,K_{P} ) $$

(9)

we have

$$ T/\Updelta_{\text{r}} H_{T}^{^\circ } = 1/\left( {\Updelta_{\text{r}} S_{T}^{^\circ } - R\,\ln \,K_{P} } \right) $$

(10)

For reactions of similar stoichiometry, and where the initial reaction temperatures (T _in) have been determined under similar conditions, the values of $\Updelta_{\text{r}} S_{T}^{^\circ }$ and K _P for different oxides are expected to be approximately equal. Therefore, it can be anticipated that the ratio $T/\Updelta_{\text{r}} H_{T}^{^\circ }$ (or the ratio T _in/E) for the reduction of different oxides by hydrogen will have similar values. Experimental data (obtained by Electrothermal Atomic Absorption Spectrometry [40]) and theoretically calculated values for several oxides (MgO, CaO, SrO, BaO, and MnO) are given in Table 6. The average ratio T _in/E = 3.6 (Table 6) is about 20% higher than the ratio T _in/E = 2.6–2.9 for NiO reduction (Table 5). This discrepancy can be ascribed to the large differences in reaction temperature (×3–4) and, accordingly, in reaction entropy. Instead of the average value 132 J mol⁻¹ K⁻¹ (from Table 6), the entropy change for NiO reduction is about 190 J mol⁻¹ K⁻¹ (Table 5). Thus, the significantly higher temperatures required for metal oxide reduction (Table 6) are ascribed to the absence of the metal condensation stage and, consequently, the higher enthalpy change for reduction of these (very stable) oxides. These regularities provide further proof of the validity of the mechanism described here.

Table 6 Reduction of solid oxides by hydrogen (isobaric mode)

Kinetics

Langmuir’s equations for evaporation of simple substances

In contrast with the usual approach to kinetic (and mechanistic) analysis, applied conventionally in studies of reactions of solids, based on the Arrhenius equation:

$$ k = A\,{ \exp }\left( {-E/RT} \right) $$

(11)

the thermochemical approach uses Langmuir’s quasi-equilibrium equations for the evaporation of simple substances (such as a metal) in vacuum or an inert gas:

$$ J = MP/( 2\pi MRT)^{ 1/ 2} $$

(12)

$$ J = MDP/\left( {zRT} \right) $$

(13)

$$ J = MDP/\left( {rRT} \right) $$

(14)

Here, J is the absolute evaporation rate (kg m⁻² s⁻¹), M is molar mass, D is the diffusion coefficient of the vapor in an inert gas, z is the distance from the vaporization surface to the sink, where the vapor concentration is zero and r is the radius of a spherical particle of the substance. Equation 12, for vacuum, was derived by Hertz, Knudsen, and Langmuir: the diffusion Eqs. 13 and 14 were developed by Langmuir (see [27, 28]). All absolute vaporization rates J are directly proportional to the equilibrium vapor pressure P of the substance.

Isobaric and equimolar modes of reduction

Before considering the applications of these equations in kinetic calculations, it must be noted that, in thermal decompositions and in reductions of solid reactants, two different reaction modes (regimes) exist: equimolar and isobaric. The equimolar mode (e) refers to reaction in the absence of excess (added) water vapour (product), or $P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} \, > \,P_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}}$, and the isobaric mode (i), represents reaction in excess product, with $P_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}} > P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} .$ These different reaction modes were distinguished more than 25 years ago [41], but nobody, except L’vov, has recognized this important kinetic distinction. Indeed, when gaseous product, here H₂O vapor, is present in the reaction zone, Eq. 8 becomes:

$$ K_{P} = \tfrac{{P_{\text{M}}^{\text{int}} (P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} + P_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}} )}}{{P_{{{\text{H}}_{2} }} }} $$

(15)

where $P_{\text{M}}^{\text{int}}$ and $P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}}$ are equilibrium partial pressures for metal and water, determined by the reaction itself (internal) and $P_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}}$ is an externally introduced (constant) partial pressure of water vapor.

When the reduction reaction is congruent, and yields equal numbers of product molecules, i.e., J _M/M _M = $J_{{{\text{H}}_{2} {\text{O}}}}$/$M_{{{\text{H}}_{2} {\text{O}}}}$, it follows from Eq. 12 that:

$$ P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} /P_{\text{M}}^{\text{int}} = \left( {M_{{{\text{H}}_{2} {\text{O}}}} /M_{\text{M}} } \right)^{ 1/ 2} \equiv \beta^{\text{e}} $$

(16)

Under this condition, Eq. 15, for the equimolar mode, is:

$$ K_{P}^{\text{e}} = \tfrac{{(P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} )^{2} }}{{\beta^{\text{e}} P_{{{\text{H}}_{2} }} }} $$

(17)

In the case of the isobaric mode, Eq. 14, the congruence condition corresponds to:

$$ P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} /P_{\text{M}}^{\text{int}} = D_{{{\text{H}}_{2} {\text{O}}}} /D_{\text{M}} \equiv \beta^{\text{i}} $$

(18)

Under this condition, Eq. 15, for the isobaric mode, is:

$$ K_{P}^{\text{i}} = \tfrac{{P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} P_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}} }}{{\beta^{\text{i}} P_{{{\text{H}}_{2} }} }} $$

(19)

Taking into account the molar masses (0.0587, 0.0160, and 0.028 kg mol⁻¹) and radii (2.06, 0.96, and 1.09 Å) of Ni, H₂O and N₂ gaseous species [42, 43], we calculated β ^e = 0.554 for equimolar mode and β ⁱ = 3.10 for isobaric mode. (Calculation of the magnitude of β ⁱ was based on the Chapman–Enscoge theory of diffusion [43].)

Dependence of reduction rate on H₂ pressure and reaction regime

These relationships identify the dependence of reduction rate on H₂ pressure in the absence and in the presence of H₂O vapor in the reaction zone. Reported values, for the dependence of reduction rate on hydrogen pressure in the absence of H₂O, range from ν ~ P ^0.35 [4] to ν ~ P ^1.0 [20], Table 1. In contrast, Hauffe and Rahmel [5] found a higher dependence, ν ~ P ^1.5, with water vapour present. While there is a possibility that this magnitude may be an overestimation, the correspondence between theory and experiment may be regarded as fairly reliable, consistent with the CDV mechanism. When oxide is reduced in hydrogen, alone or with an inert gas, the vapor of the low-volatile metal is condensed and the reduction rate is limited solely by diffusion of water vapor from the oxide surface. Consequently, for reactions in the equimolar mode, the diffusion Eqs. 13 and 14 are valid. However, during the isobaric mode, in a constant excess H₂O pressure, diffusion limitations are fully eliminated, so that the relation between reaction rate and $P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}}$ in vacuum is defined by Eq. 12. Thus, these reaction regimes must correspond to the following equations for $P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}}$:

$$ \left( {P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} } \right)^{\text{e}} = \tfrac{zRT}{MD}J^{\text{e}} $$

(20)

$$ \left( {P_{{{\text{H}}_{2} {\text{O}}}}^{\text{int}} } \right)^{\text{e}} = \tfrac{rRT}{MD}J^{\text{e}} $$

(21)

$$ \left( {P_{{{\text{H}}_{ 2} {\text{O}}}}^{\text{int}} } \right)^{\text{i}} = \tfrac{{(2{{\uppi}}MRT)^{1/2} }}{M}J^{\text{i}} $$

(22)

Methodology

Methods for determination of the E parameter

The equilibrium constant K _P for oxide reduction, measured at various temperatures, allows the second-law method to be used to determine the reaction enthalpy $\Updelta_{\text{r}} H_{T}^{^\circ }$, through Eq. 9. Compared with the conventional Arrhenius method, in which the reaction enthalpy is calculated from the lnJ − 1/T plot, the second-law method enables both thermodynamic parameters to be determined. The magnitude of $\Updelta_{\text{r}} H_{T}^{^\circ }$ may be found from the slope of the plot, which in the lnK _P  − 1/T coordinates is a straight line, and the magnitude of $\Updelta_{\text{r}} S_{T}^{^\circ }$ is obtained from its intersection on the ordinate axis. In addition, this analysis includes the dependence of absolute reduction rate J (or rate constant k) on temperature, disregarded in the Arrhenius-plot method.

Furthermore, if the equilibrium constant can be determined, then $\Updelta_{\text{r}} H_{T}^{^\circ }$ may be also calculated directly from Eq. 9, in which the $\Updelta_{\text{r}} S_{T}^{^\circ }$ value is known. For most substances of interest, absolute values of the standard entropy $S_{298}^{^\circ }$ and corresponding temperature increments $S_{T}^{^\circ } - S_{298}^{^\circ }$ have been calculated and their values tabulated (see, e.g., [36–38]). This approach, referred to as the third-law method [27, 28], yields more reliable and precise values than can be obtained from the differential Arrhenius-plot and the second-law methods. Its advantages have been analyzed in [44, 45], showing that the ratio of random errors from both second-law and Arrhenius methods to the error from the third-law method is proportional to the ratio T _max/(T _max − T _min), where T _max and T _min are maximal and minimal temperatures of the measurement range. In most thermochemical investigations this ratio is about 10 but sometimes it rises up to 30 or even 50. Therefore, errors in the third-law method are much smaller, often by an order of magnitude. Moreover, because measurements are required at only one or two average temperatures, experiments can be completed considerably more quickly than by the conventional approaches. Indeed, at least 3, and up to 10 (or more), rate constant determinations are usually used for an Arrhenius plot, including prolonged low-temperature experiments.

The third-law method applied to the data reported in [18]

Hitherto, the third-law method has not been used in kinetic analysis of rate data for metal oxide reductions. Its value is convincingly demonstrated by reanalyzing experimental kinetic data for NiO reduction by H₂ (X-ray diffraction analysis) by Richardson et al. [18]. The NiO and Ni reflections were scanned periodically during the continuous reduction of NiO samples at temperatures between 175 and 300 °C. Each single scanning cycle was completed in 30 s, during reactions in flowing gas mixtures (200 cm³ min⁻¹): N₂–H₂ containing 0.2 bar H₂ and N₂–H₂–H₂O containing 0.2 bar H₂ and 0.022 bar H₂O. The NiO reactant sample was disintegrated into small particles, about 20 μm diameter. These were dispersed in ethanol and placed on a Pt–Rh strip, through which a heating current was passed. After drying, a uniform layer of NiO reactant particles about 50 μm in thickness was produced on the strip surface. The E parameter was determined [18] from the Arrhenius plots of log k − 1/T. The rate constant k for each temperature was found by fitting the experimental α − t data (reduction extent and time, respectively) to the (first-order) rate equation:

$$ \alpha = 1 - {\text{e}}^{{ - k (t - t_{ 0} )}} $$

(23)

where t ₀ is the induction period. The time of each experiment varied with reduction temperature, from several minutes at 300 °C to 8 h at 175 °C.

The third-law method was used to calculate the enthalpy of NiO reduction with H₂ (in a flow with N₂), using experimental data from [18], in the absence and presence of water vapour, through Eqs. 20 and 21, respectively. These equations relate partial pressure $P_{{{\text{H}}_{ 2} {\text{O}}}}^{\text{int}}$ to absolute reduction rate J and, consequently, the measured rate constants k require recalculation. The relationship between these kinetic parameters (J and k) for spherical particles, initial radius r ₀ and density ρ, was theoretically derived in [46]:

$$ J = \rho r_{0} k $$

(24)

The density of NiO is 7,450 kg m⁻³, r ₀ = 10 μm = 10⁻⁵ m [18] and the diffusion coefficient D for H₂O molecules in pure N₂ [27, 28] was calculated from

$$ D = 0. 20 4\left( {T/ 2 7 3} \right)^{ 2.0 7 2} $$

(25)

Calculated values are estimated to differ from those for the N₂–H₂ reactant mixtures by 10–20% or less.

Tables 7 and 8 report values of E ^e and E ⁱ calculated by the third-law method from the experimental results in [18]. Input data are shown, together intermediate steps in the calculation, undertaken in the sequence $k \to J \to P_{{{\text{H}}_{ 2} {\text{O}}}}^{\text{int}} \to K_{P} \to \Updelta_{\text{r}} H_{T}^{^\circ } \to E.$ Parameters obtained by the Arrhenius-plot method in [18] are also included in both tables (last column). Comparative analyses of these results lead to the following conclusions. Within experimental accuracies, the results from both methods give good agreement for E ^e and satisfactory agreement for E ⁱ. Use of the third-law method reduces the random error by an order of magnitude compared with the Arrhenius method. The third-law method gives the E ⁱ/E ^e ratio as 2.0 (164/82), coinciding with theoretical expectation. K _P values at 498 and 524 K calculated by the alternative methods differ by factor of 1.5 and 1.1. We point out, in addition, that the time required for a full set of experiments, measuring rate constants across an adequate range of temperatures [18], may be reduced several-fold by the third-law approach, necessitating experiments at only one or two temperatures between 200 and 250 °C.

Table 7 E ^e parameter values calculated by the third-law method from the primary data (T, k and $P_{{{\text{H}}_{2} }}$) reported in [18]

Table 8 E ⁱ parameter values calculated by the third-law method from the primary data (T, k, $P_{{{\text{H}}_{2} }}$ and $P_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}}$) reported in [18]

Conclusions

The thermochemical approach, previously used to interpret the kinetics and mechanisms of solid-state thermal decompositions [27, 28], has been extended here, for the first time, to analyze rate data for the reduction of a metal oxide (NiO) by hydrogen.

For both types of reaction, the mechanism considered involved the congruent decomposition of solid reactant into gaseous products, followed by the condensation of supersaturated vapor of the low-volatile product. For both types of reaction, Langmuir’s quasi-equilibrium equations have been used instead of the Arrhenius kinetic equation. Finally, replacing the traditional Arrhenius-plot method, the third-law method has been used to determine the E parameter, guaranteeing the reliability and precision of the values obtained, and reducing the experimental time involved. The analysis shows that the thermochemical approach quantitatively accounts for the kinetic characteristics of the reduction reactions. Furthermore, this approach theoretically accounts for kinetic features not previously recognized. In particular, the dependence of reduction rate on hydrogen pressure, in the equimolar and the isobaric modes, a more than twofold decrease of the E parameter with the extent of reaction, and a systematic increase of E with temperature are explained.

The present authors suggest that this theory may profitably be extended to interpret the reduction kinetics of oxides of many other metals (Ag, Co, Cu, Fe, Mn, Mo, Ni, Pb, Pd, Pt, Rh, W) with H₂ (and CO). Confirmation of the wide applicability of the method is expected to contribute towards the developing a general (universal) theory that might be valuable throughout pyrometallurgy and may even be capable of extension to heterogeneous catalytic reactions.