Introduction

The mechanism of solidification behavior of polyphase alloys, particularly monotectic alloys, are of potential importance for fundamental and industrial applications such as self-lubricating alloys [1, 2]. Metallic systems [3, 4] constitute an interesting area of investigations but they are not suitable for detailed study because of wide density difference, opacity, and high transformation temperature of the components involved. However, low transformation temperature, transparency, wider choice of materials, and minimized convection effects are the special features which have prompted a number of research groups to work on binary organic eutectics, monotectics, and molecular complexes [5–9]. To begin with organic systems are used as model systems for detailed investigation of several parameters which control the mechanism of solidification and decide the properties of materials, and thus the understanding of controlling parameters could be applied for metallic systems. During the last two decades, the potential use of organic materials for non-linear optical (NLO) and other electronic applications [10, 11] has prompted the researchers to undertake their various physicochemical investigations. Furthermore, synthesis of binary organic materials have shown the potential to produce, as well as to modify, the NLO and white light-emitting diode (WLED) materials [12–15].

The studies on monotectic alloys have been less scarce due to several inherent difficulties associated with systems forming monotectic. Nonetheless, some of the articles [1, 16, 17] explain various interesting phenomena of monotectic alloys. The wide freezing range, large density differences, and immiscibility between two liquid phases are the prime issues. Thus, the roles of wetting behavior, interfacial energy, thermal conductivity, and buoyancy during the phase separation process have been a subject of great discussion. In this article, the details of phase diagrams, thermochemistry, linear velocity of crystallization at different undercoolings, heat of fusion, Jackson’s roughness parameter, interfacial energy and microstructures of the HB–BNA, BN–RC and U–DNB systems are reported.

Experimental

Materials and purification

Starting materials, 3-hydroxybenzaldehyde, 4-bromo-2-nitroaniline, benzoin, urea and 1,3-dinitrobenzene were received from Sigma-Aldrich (Germany), whereas resorcinol was received from Thomas Baker, India. Urea was purified by recrystallization from deionized water below 60 °C; benzoin was purified by crystallization from CCl4, 3-hydroxybenzaldehyde, 4-bromo-2-nitroaniline and 1,3-dinitrobenzene was purified by recrystallization from ethanol, and resorcinol was purified by crystallization from hot water. The purity of each compound was verified by comparing its melting temperature with that of the reported values in the literature [18, 19].

Phase diagram

The phase diagram was determined by the thaw–melt method. In this method [20, 21], mixtures of two components covering the entire range of compositions were prepared, and these mixtures were homogenized by repeating the process of melting followed by chilling in ice cooled water 4–5 times. The melting temperatures of different composition were determined using a melting point apparatus (Toshniwal melting point) attached with thermometer with an accuracy of ±0.5 °C. The graphs were plotted between melting temperatures and their respective compositions.

Enthalpy of fusion

The values of heat of fusion of the pure components, the eutectics, and the monotectic were determined [22, 23] by differential scanning calorimeter (Mettler DSC-4000 system). Indium and Zinc samples were used for calibrating the DSC unit. The amounts of the test sample and heating rate were about 5–7 mg and 5 °C/min, respectively. The values of enthalpy of fusion are reproducible within ±0.01 kJ/mol. To assess the uncertainty, the experiment for the determination of heat of fusion values was repeated by taking different weights between 5 and 7 mg as well as using the heating rates from 5–10 °C/min, for the same samples and several times.

Growth kinetics

The influence of temperature on growth kinetics of the pure components and their eutectics and the monotectic was studied [21, 23] by measuring the rate of movement of the solid–liquid interface at different undercoolings in a capillary tube (U-shape) of 150-mm horizontal portion and 5 mm internal diameter. Molten samples of the pure components, the eutectics and the monotectic were separately taken in a capillary and placed in a silicone oil bath. The temperature of the oil bath was maintained using microprocessor temperature controller of accuracy ±0.1 °C. At a particular temperature, below the melting point of the sample, a seed crystal of the same composition was added to start the nucleation, and the rate of movement of the solid–liquid interface was measured using a traveling microscope and a stop watch. The same procedure was repeated at different undercoolings for different material to plot the graph.

Microstructure

Microstructures of the pure components, the eutectics, and the monotectic were recorded [20] by placing a drop of molten compound on a hot glass slide. To avoid the inclusion of the impurities from the atmosphere, a cover slip was glided over the melt, and it was allowed to cool to obtain a super-cooled liquid. The melt was nucleated with a seed crystal of the same composition at one end, and care was taken to ensure unidirectional freezing. The directionally solidified crystal system on the glass slide was then placed on the platform of an optical microscope (Leitz Labourlux D). The different regions of the slide were viewed with suitable magnification and photographs of interesting region were recorded using a camera attached with the microscope.

Results and discussions

Phase diagram

The phase diagrams of BNA–HB and BN–RC systems, reported in terms of melting temperature–composition curves, show the formation of simple eutectics (Figs. 1, 2). The melting points of BNA and HB are 111.0 and 103. 0 °C, respectively, and the melting point of BNA decreases with the addition of HB. The mixture having 0.5 mol fraction of HB shows the minimum melting temperature, 78.0 °C, and it is the eutectic of BNA–HB system. Similarly, in case of BN–RC, the melting temperature of BN is 133.0 °C, and it decreases with the addition of RC and reaches to the minimum melting temperature, i.e., the eutectic temperature of BN–RC. Further addition of RC increases the melting point and reaches to the 110.5 °C, which is the melting point of resorcinol. The eutectic temperature and composition of BN–RC system are 87.0 °C and 0.75 mol fraction of resorcinol, respectively. Three phases, namely, a binary liquid phase, L, and two solid phases, S 1 and S 2, are in equilibrium at the eutectic point which is invariant point of the system. When a solution of the eutectic composition is cooled below the eutectic temperature, it dissociates into two solid phases as

$$ L \leftrightarrow S_{ 1} + S_{ 2} $$
(1)

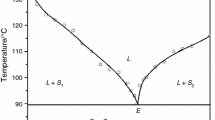
However, the solid–liquid equilibria data of the third system (U–DNB) show the formation of a monotectic and a eutectic where the mole fractions of DNB are 0.025 and 0.989, respectively (Fig. 3). The eutectic and the monotectic melting temperatures correspond to 131.5 and 87.5 °C, respectively. A portion of the studies of U–DNB system concerning the phase diagram, formation of solid solution, solubility, crystal growth, and their optical and nonlinear optical properties, of has been reported earlier [24]. Moreover, solidification behavior, details of thermal study including excess thermodynamic properties and microstructural investigation of this system were due to report.

Fig. 1
figure 1

Phase diagram of 4-bromo-2-nitroaniline and 3-hydroxybenzaldehyde

Full size image
Fig. 2
figure 2

Phase diagram of benzoin and resorcinol

Full size image
Fig. 3
figure 3

Phase diagram of urea and 1,3-dinitrobenzene [24]

Full size image

Growth kinetics

In order to study the crystallization behavior of the pure components, the eutectic and the monotectic, the crystallization rate (v) are determined at different undercoolings (ΔT) by measuring the rate of movement of solid–liquid interface in a capillary. The plots between log ΔT and log v are depicted in Fig. 4. The linear dependence of these plots is in accordance with the Hillig and Turnbull [25] equation

$$ v = u\left( {\Updelta T} \right)^{n} $$
(2)

where u and n are constants and depend on the solidification behavior of the materials involved. The values of u and n are given in Table 1. These findings may be explained by the mechanism given by Winegard et al. [26]. According to those authors, the crystallization of eutectic/monotectic begins with the formation of the nucleus of one of the phases. This phase grows until the surrounding liquid becomes rich in the other component, and a stage is reached when the second component also starts nucleating. Now, there are two possibilities: either the two initial crystals grow side-by-side, or there may be alternate nucleation of the two phases. The values of n for the monotectic being close to 1 suggest that there is direct relationship between growth velocity and undercoolings. The values of n being close to 2 suggest the square relationship between growth velocity and undercooling (ΔT). The deviation of n values from 2 observed in some cases is due to difference in temperature of bath and temperature of growing interface. From the values of u (Table 1), it can be concluded that growth velocity of eutectic and monotectic is higher than the parent components in case of U–DNB system. These findings suggest that the two phases of monotectic and eutectic solidify via the side-by-side growth mechanism.

Fig. 4
figure 4

Linear velocity of BNA–HB, BN–RC and U–DNB systems

Full size image
Table 1 Values of n and u for pure components, monotectic and eutectics
Full size table

Thermochemistry

The knowledge of enthalpy of fusion values of the pure components, the eutectics and the monotectic is important for understanding the mechanism of solidification, structure of eutectic melt, and the nature of interaction between two components forming the eutectic and the monotectic. The values of enthalpy of fusion of the pure components, the eutectics, and the monotectic, as determined by the DSC method, are reported in Table 2. For comparison, the values of enthalpy of fusion of eutectics calculated by the mixture law [20] are also included in the same table. The values of enthalpy of mixing which mark the difference between experimental and the calculated values of the enthalpy of fusion of the eutectics are found to be 0.03, −6.14, and 0. 32 kJ mol−1 for BNA–HB, BN–RC, and U–DNB systems, respectively. As such, three types of structures are suggested [27]; quasi-eutectic for Δmix H > 0, clustering of molecules for Δmix H < 0, and molecular solution for Δmix H = 0. In present system, the positive value of Δmix H for the eutectic suggests the formation of quasi-eutectic structure in the binary melt of the eutectic of BNA–HB and U–DNB systems. The highly negative value of enthalpy of mixing in case of BN–RC system suggests that there is associative interaction in the molecules in the eutectic melt [28]. The entropy of fusion (Δfus S) values, for different materials, has been calculated by dividing the enthalpy of fusion by their corresponding absolute melting temperatures (Table 2). The positive values suggest that the entropy factor favors the melting process. This is a common observation in the melting of a material.

Table 2 Heat of fusion, entropy of fusion and roughness parameters of three systems
Full size table

The deviation from the ideal behavior can best be expressed in terms of excess thermodynamic functions, namely, excess free energy (g E), excess enthalpy (h E), and excess entropy (s E), which give a more quantitative idea about the nature of molecular interactions. The excess thermodynamic functions could be calculated [20, 29] using the following equations and the values are given in Table 3:

$$ g^{\text{E}} {\text{ = R}}T\left[ {x_{ 1} { \ln }\gamma_{ 1}^{\text{l}} + x_{ 2} \ln \gamma_{ 2}^{\text{l}} } \right] $$
(3)
$$ h^{\text{E}} = - {\text{R}}T^{ 2} \left[ {x_{ 1} {\frac{{\partial \ln \gamma_{ 1}^{\text{l}} }}{\partial T}} + x_{ 2} {\frac{{\partial \ln \gamma_{ 2}^{\text{l}} }}{\partial T}}} \right] $$
(4)
$$ s^{\text{E}} = - {\text{R}}\left[ {x_{ 1} { \ln }\gamma_{ 1}^{\text{l}} + x_{ 2} \ln \gamma_{ 2}^{\text{l}} + x_{ 1} T{\frac{{\partial \ln \gamma_{ 1}^{\text{l}} }}{\partial T}} + x_{ 2} T{\frac{{\partial \ln \gamma_{ 2}^{\text{l}} }}{\partial T}}} \right] $$
(5)

where \( { \ln }\gamma_{i}^{\text{l}} ,\;x_{i} \), and \( {\frac{{\partial \ln \gamma_{i}^{\text{l}} }}{\partial T}} \) are activity coefficients in the liquid state, the mole fraction and the variation of log of activity coefficients in liquid state as a function of temperature of the component i.

Table 3 Excess thermodynamic functions for the eutectics of three systems
Full size table

It is evident from equations, (3)–(5), that activity coefficients and thier variation with temperature are required to calculate the excess functions. Activity coefficient \( \left( {\gamma_{i}^{\text{l}} } \right) \) could be evaluated [20, 30] using the equation:

$$ - \ln \,\left( {x_{i} \,\gamma_{{_{i} }}^{l} } \right)\,\, = \,\,{\frac{{\Updelta_{\rm fus} H_{i} }}{R}}\left( {{\frac{1}{{T_{\rm fus} }}} - {\frac{1}{{T_{{_{i} }} }}}} \right) $$
(6)

where \( x_{i} ,\;\Updelta_{\rm fus} H_{i} ,\;T_{{_{i} }} \) and T fus are mole fraction, enthalpy of fusion, melting temperature of component i and melting temperature of a eutectic, respectively. The variation of activity coefficient with temperature could be calculated by differentiating Eq. 6 with respect to temperature:

$$ {\frac{{\partial \ln \gamma_{{_{i} }}^{l} }}{\partial T}}\,\, = \,\,{\frac{{\Updelta_{\rm fus} H_{i} }}{{RT^{2} }}} - {\frac{{\partial x_{{_{i} }} }}{{x_{{_{i} }} \partial T}}} $$
(7)

∂x i /∂T in this expression can be evaluated by considering two points around the eutectic. The positive values of excess free energy in case of BNA–HB and U–DNB in eutectics indicate that the interaction between the like molecules (BNA–BNA, HB–HB, U–U, and DNB–DNB) are stronger than the interaction between the unlike molecule (BNA–HB and U–DNB), whereas the negative values of excess free energy in case of BN–RC eutectic suggest that there is an associative interaction between unlike molecules [29].

The solid–liquid interfacial tension affects the enthalpy of fusion value and plays an important role in determining the kinetics of phase transformation [31]. When liquid is cooled below its melting temperature, the melt does not solidify spontaneously because under equilibrium condition, it contains number of clusters of molecules of different sizes. As long as the clusters are well below the critical size [32], they cannot grow to form crystals and, therefore, no solid would result. Also during growth, the radius of critical nucleus gets influenced by undercooling as well as the interfacial energy. The interfacial energy (σ) is given by

$$ \sigma \, = \,\,{\frac{{C.\,\Updelta_{\rm fus} H}}{{\left( {N_{\rm A} } \right)^{1/3} \,\left( {V_{\rm m} } \right)^{2/3} }}} $$
(8)

where N A is the Avogadro Number, V m is the molar volume, and parameter C lies between 0.30 and 0.35. The calculated interfacial energy of the three systems are given in Table 4. The literature during the last two decades is replete with various attempts to understand and to explain the process of solidification of monotectic alloys [33, 34]. The role of wetting behavior in a phase separation process is of immense importance. In view of this, the applicability of Cahn’s wetting condition, given by the following equation, has been tested in case of U–DNB system.

$$ \sigma_{{SL_{2} }} < \sigma_{{SL_{1} }} + \sigma_{{L_{1} L_{2} }} $$
(9)

where σ is the interfacial energy between the faces denoted by the subscripts. The interfacial energy between two liquids, \( \sigma_{{L_{1} L_{2}}} . \) has been calculated using the equation:

$$ \sigma_{{L_{1} L_{2} }} = \sigma_{{SL_{1} }} + \sigma_{{SL_{2} }} - 2\surd \left( {\sigma_{{SL_{1} }} \sigma_{{SL_{2} }} } \right) $$
(10)

The values of interfacial energy (Table 4) show that the Cahn’s wetting condition could be applicable in this system.

Table 4 Interfacial energy of the three systems
Full size table

To study the critical nucleus (r*) and the influence of undercooling on it, the following equation was used:

$$ r*\,\,\,\, = \,\,\,\,{\frac{{2\,\sigma \,T_{\rm fus} }}{{\Updelta_{\rm fus} \,H\,.\,\Updelta T}}} $$
(11)

where T fus, Δfus H, and ΔT are melting temperature of eutectic, heat of fusion and degree of undercooling, respectively. The computed values of the size of critical nucleus at different undercoolings using the Eqs. 8 and 11 of the three systems are given in Table 5. The size of critical nucleus decreased with increase in undercooling. Thus, high undercooling favors the formation of critical nucleus of smaller size. This may be ascribed to the increase amplitude of molecular vibration at higher temperature.

Table 5 Critical radius of three systems
Full size table

Microstructure

It is well known that in polyphase materials, the microstructure gives information about shape and size of the crystallites, which plays a very significant role in deciding mechanical, electrical, magnetic, and optical properties of materials. According to Hunt and Jackson [35], the type of growth from melts depends upon the interface roughness (α) defined by

$$ \alpha = \xi \Updelta_{\text{\rm fus}} H/{\text{R}}T $$
(12)

where ξ is a crystallographic factor which is generally equal to one or less than one. The calculated values of α are reported in Table 2. If α > 2, then the interface is quite smooth and the crystal develops with a faceted morphology. On the other hand, if α < 2, then the interface is rough and many sites are continuously available, and the crystal develops with a non-faceted morphology. In the above three systems, the values of α are greater than 2 in all the cases which suggests that the phases grow with facets morphology.

Microstructure of monotectic and eutectic

The study of interfacial energy reveals the applicability of non wetting condition, i.e., both phases are not wetting to each other. The effect of wetting behavior reflects from the microstructure of monotectic and eutectic. According to the wetting model [36] in the monotectic reaction (L 1 → S 1 + L 2), the reaction constituents are in contact as represented in Fig. 5. Chadwick [36] proposed that monotectic composites cannot be grown unless the relative surface energies equilibrium contact between S 1, L 1, and L 2 occurs. As such when L 2 does not wet S 1, monotectic growth cannot take place. Cahn [37] suggested monotectic growth in the light of critical wetting, critical velocity, and disjoining pressure. The nucleation of liquid L 2 depends on the balance of interfacial tensions and as such the following three situations arise:

Fig. 5
figure 5

Schematic representation of monotectic reaction component

Full size image
  1. (i)

    If \( \gamma_{{S_{1} L_{2}}} > \gamma_{{S_{1} L_{1}}} + \gamma_{{L_{1} L_{2}}}, \) then non-wetting behavior would result, a steady-state growth of the monotectic will be observed, and droplets of L 2 will be formed. They will sink or float as given by the Stokes formula:

$$ V = \,\frac{2}{9}{\frac{{gr^{2} (D_{1} - D_{2} )}}{{\eta_{1} }}} $$
(13)

where, V is the liquid droplet float velocity, g is the acceleration due to gravity, r is the radius of droplet, D 1 is the density of liquid L 1, D 2 is the density of liquid L 2, and η1 is the viscosity of liquid L 1. If R is the solid–Liquid interface advance velocity, and V > R, then L1 will solidify at the bottom and L 2 will solidify at the top. On the other hand if V < R, steady state fibrous growth of L 2 will be observed.

If \( \gamma_{{S_{1} L_{2} }} = \gamma_{{S_{1} L_{1} }} + \gamma_{{L_{1} L_{2} }} { \cos }\theta , \) the partial-wetting behavior would result, and a steady-state fibrous growth of L 2 will be obtained.

  1. (ii)

    If \( \gamma_{{S_{1} L_{2} }} < \gamma_{{S_{1} L_{1} }} + \gamma_{{L_{1} L_{2} }} , \) then the complete wetting behavior and a steady-state growth of L 2 will be observed.

The unidirectional solidify microstructure of eutectic of BNA–HB system (Fig. 6a) shows showing the federal nucleation which has grown with dendritic structure. One of the phase has solidified in dendritic shape over the another phase which has solidified uniformly. The microstructure of eutectic of BN–RC system (Fig. 6b) shows the lamellar structure. The closure view of structure shows that some of the lamellas are broken. The proportion of the two phases present in eutectic structure is being reflected from the microstructure. The directionally solidified microstructure of U–DNB monotectic (Fig. 6c) shows the droplets formation for one of the phases. The alignment of the droplets indicates the direction of solidification. Lower half of the structure shows that the droplets are regularly arranged in parallel fashion similar to broken lamella. The droplets have got sufficient time to become spherical in shape. On the other hand, the upper half portion shows branching and misalignment (some portion) in array of droplets. This type of microstructures is frequently observed in case of metal–nonmetal systems [34] where the Cahn-wetting condition is obeyed. For metallic systems, such structure are more demanding for the application of self-lubricating bearing. The eutectic of U–DNB system has grown with lamellar morphology (Fig. 6d). The right portion of the microstructure shows the parallel lamella; however, in left corner, parallelisms have not been maintained uniformly. This may be due to the lack of uniform temperature gradient.

Fig. 6
figure 6

Microstructure of (a) BNA–HB eutectic, (b) BN–RC eutectic, (c) U–DNB monotectic and (d) U–DNB eutectic

Full size image

Conclusions

The phase diagram of BNA–HB and BN–RC systems show the formation of simple eutectics with 0.5 mol fraction of HB and 0.75 mol fraction of RC, respectively. The phase diagram between urea and m-dinitrobenzene shows the formation of a monotectic (with 0.025 mol fraction of DNB) and a eutectic (with 0.9896 mol fractions of DNB) with their melting temperatures 131.5 and 87.5 °C, respectively. The growth kinetics suggests that growth data obey the Hillig–Turnbull equation for each material of the three systems, and the size of critical nucleus depends on the undercoolings. The enthalpies of mixing and excess free energy were found to be positive in two systems, namely, BNA–HB and U–DNB, and negative in BN–RC eutectic. The interfacial energy data confirm that the Cahn’s condition, \( \sigma_{{SL_{2} }} < \sigma_{{SL_{1} }} + \sigma_{{L_{1} L_{2} }} , \) is applicable in the case of U–DNB system. In the case of monotectic of U–DNB, microstructural investigations show the formation of regular lamellar droplet morphology, and the eutectic shows the formation of lamellar morphology.